1.8: עשרוניות
- Page ID
- 205714
בסוף פרק זה, תוכל:
- תן שם וכתוב עשרונים
- עשרוניות עגולות
- הוסף וחסר עשרונים
- להכפיל ולחלק עשרונים
- המרת עשרונים, שברים ואחוזים
מבוא יסודי יותר לנושאים המכוסים בחלק זה ניתן למצוא בפרק Prealgebra, עשרוניות.
שם וכתיבה עשרוניות
עשרונים הם דרך נוספת לכתוב שבריר s שהמכנים שלהם הם סמכויות של 10.
\[\begin{array} {ll} {0.1 = \frac { 1 } { 10 }} &{0.1 \text { is "one tenth" }} \\ {0.01 = \frac { 1 } { 100 }} &{0.01 \text { is "one hundredth }} \\ {0.001 = \frac { 1 } { 1,000 }} &{0.001 \text { is "one thousandth }} \\ {0.0001 = \frac { 1 } { 10,000 }} &{0.0001 \text { is "one ten-thousandth" }} \end{array}\]
שימו לב ש"עשרת אלפים "הוא מספר גדול מאחד, אך" עשרת אלפים "הוא מספר קטן מאחד. ה- "th" בסוף השם אומר לך שהמספר קטן מאחד.
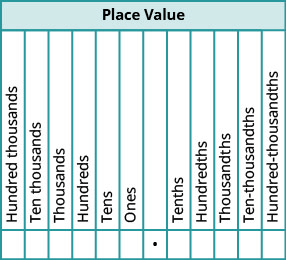
כאשר אנו מציינים מספר שלם, השם מתאים לערך המקום המבוסס על הסמכויות של עשר. אנו קוראים 10,000 כ"עשרת אלפים "ו -10,000,000 כ"עשרה מיליון". באופן דומה, שמות המקומות העשרוניים תואמים את ערכי השבר שלהם. איור \(\PageIndex{1}\) מציג את שמות ערכי המקום משמאל ומימין לנקודה העשרונית.
תן שם לעשרוני\(4.3\).
- תשובה
-




תן שם לעשרוני\(6.7\).
- תשובה
-
שש ושבע עשיריות
תן שם לעשרוני\(5.8\).
- תשובה
-
חמש ושמונה עשיריות
אנו מסכמים את הצעדים הדרושים לשם שם עשרוני להלן.
- תן שם למספר משמאל לנקודה העשרונית.
- כתוב "ו" עבור הנקודה העשרונית.
- תן שם לחלק "מספר" מימין לנקודה העשרונית כאילו היה מספר שלם.
- תן שם למקום העשרוני של הספרה האחרונה.
תן שם לעשרוני:\(−15.571\).
- תשובה
-
\(−15.571\) תן שם למספר משמאל לנקודה העשרונית. חמש עשרה שליליות __________________________________ כתוב "ו" עבור הנקודה העשרונית. חמש עשרה שליליות ו __________________________________ תן שם למספר מימין לנקודה העשרונית. חמש עשרה וחמש מאות שבעים ואחת __________ שלילי \(1\)זה נמצא במקום האלפים. שלילי חמש עשרה וחמש מאות שבעים ואחד אלפים
תן שם לעשרוני:\(−13.461\).
- תשובה
-
שלוש עשרה וארבע מאות שישים ואחת אלפים שליליים
תן שם לעשרוני:\(−2.053\).
- תשובה
-
שלילי שניים וחמישים ושלושה אלפים
כשאנחנו כותבים צ'ק אנו כותבים גם את הספרות וגם את שם המספר. בואו נראה איך לכתוב את העשרוני מהשם.
כתוב "ארבע עשרה ועשרים וארבע אלפים" כעשרוני.
- תשובה
-




כתוב כעשרוני: שלוש עשרה ושישים ושמונה אלפים.
- תשובה
-
13.068
כתוב כעשרוני: חמש ותשעים וארבעה אלפים.
- תשובה
-
5.094
אנו מסכמים את השלבים לכתיבת עשרוני.
- חפש את המילה "ו-" - היא מאתרת את הנקודה העשרונית.
- מקם נקודה עשרונית מתחת למילה "ו-". תרגם את המילים לפני "ו" למספר השלם והנח אותו משמאל לנקודה העשרונית.
- אם אין "ו", כתוב "0" עם נקודה עשרונית מימין.
- סמן את מספר המקומות העשרוניים הדרושים מימין לנקודה העשרונית על ידי ציון ערך המקום המצוין במילה האחרונה.
- תרגם את המילים אחרי "ו" למספר מימין לנקודה העשרונית. כתוב את המספר ברווחים - שים את הספרה הסופית במקום האחרון.
- מלא אפסים למחזיקי מקום לפי הצורך.
עשרוניות עגולות
עיגול עשרונים דומה מאוד לעיגול מספרים שלמים. נעגל עשרונים בשיטה המבוססת על זו שהשתמשנו בה כדי לעגל מספרים שלמים.
סיבוב 18.379 למאה הקרובה ביותר.
- תשובה
-




סיבוב למאה הקרובה ביותר: 1.047.
- תשובה
-
1.05
סיבוב למאה הקרובה ביותר: 9.173.
- תשובה
-
9.17
אנו מסכמים כאן את השלבים לעיגול עשרוני.
- אתר את ערך המקום הנתון וסמן אותו בחץ.
- הדגיש את הספרה מימין לערך המקום.
- האם הספרה הזו גדולה או שווה ל -5?
- כן - הוסף 1 לספרה בערך המקום הנתון.
- לא — אל תשנה את הספרה בערך המקום הנתון.
- כתוב מחדש את המספר, מחק את כל הספרות מימין לספרת העיגול.
סיבוב 18.379 הקרוב ביותר
- עשירי
- מספר שלם.
- תשובה
-
סיבוב 18.379
1. לעשירית הקרובה
אתר את המקום העשירי בעזרת חץ. 
הדגיש את הספרה מימין לערך המקום הנתון. 
מכיוון ש- 7 גדול או שווה ל- 5, הוסף 1 ל- 3. 
כתוב מחדש את המספר, מחק את כל הספרות מימין לספרת העיגול. 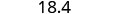
שימו לב שהספרות שנמחקו לא הוחלפו באפסים. אז, 18.379 מעוגל לעשירית הקרובה ביותר הוא 18.4.
2. למספר השלם הקרובאתר את המקום עם חץ. 
הדגיש את הספרה מימין לערך המקום הנתון. 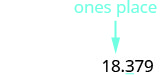
מכיוון ש- 3 אינו גדול או שווה ל- 5, אל תוסיף 1 ל- 8. 
כתוב מחדש את המספר, מחק את כל הספרות מימין לספרת העיגול. 
אז, 18.379 מעוגל למספר השלם הקרוב ביותר הוא 18.
סיבוב 6.582 הקרוב ביותר
- המאה
- עשירי
- מספר שלם.
- תשובה
-
- 6.58
- 6.6
- 7
סיבוב 15.2175 אל הקרוב
- האלף
- המאה
- עשירית.
- תשובה
-
- 15.218
- 15.22
- 15.2
הוספה וחיסור עשרוניות
כדי להוסיף או לחסר עשרונים, אנו מיישרים את הנקודות העשרוניות. על ידי יישור הנקודות העשרוניות בדרך זו, אנו יכולים להוסיף או לחסר את ערכי המקום המתאימים. לאחר מכן אנו מוסיפים או מחסרים את המספרים כאילו היו מספרים שלמים ואז מניחים את הנקודה העשרונית בסכום.
- כתוב את המספרים כך שהנקודות העשרוניות יתיישרו אנכית.
- השתמש באפסים כמחזיקי מקום, לפי הצורך.
- הוסף או הפחת את המספרים כאילו היו מספרים שלמים. לאחר מכן מקם את הנקודה העשרונית בתשובה מתחת לנקודות העשרוניות במספרים הנתונים.
הוסף:\(23.5+41.38\).
- תשובה
-
\[\text{Write the numbers so that the decimal points line up vertically.} \quad \begin{array} {r} { 23.50 } \\ { + 41.38 } \\ \hline \end{array}\]
\[\text{Put 0 as a placeholder after the 5 in 23.5. Remember, } \frac{5}{10} = \frac{50}{100}, \text{ so } 0.5 = 0.50 \quad \begin{array} {r} { 23.50 } \\ { + 41.38 } \\ \hline \end{array}\]
\[\text{Add the numbers as if they were whole numbers . Then place the decimal point in the sum.} \quad \begin{array} {r} { 23.50 } \\ { + 41.38 } \\ \hline 64.88 \end{array}\]
הוסף:\(4.8+11.69\).
- תשובה
-
\(16.49\)
הוסף:\(5.123+18.47\).
- תשובה
-
\(23.593\)
חיסור:\(20−14.65\).
- תשובה
-
\[\begin{array} {ll} {\text{Write the numbers so that the decimal points line up vertically.}} &{ \begin{align} {20 - 14.65} \\ {20.} \\ {-14.65} \\ \hline \end{align}} \\ {\text{Remember, 20 is a whole number, so place the decimal point after the 0.}} &{} \end{array}\]
\[\begin{array} {ll} {\text{Put zeros to the right as placeholders.}} &{ \begin{align} {20.00} \\ {-14.65} \\ \hline \end{align}} \end{array}\]
\[\begin{array} {ll} {\text{Write the numbers so that the decimal points line up vertically.}} &{ \begin{align} {\tiny{9} \quad \tiny{9}\qquad} \\ {\small{1} \not{\small{10}} \not{\small10}\not{\small10}}\\ {\not{2}\not{0.}\not{0}\not{0}} \\ {-14.65} \\ \hline \\{5.35} \end{align}} \end{array}\]
חיסור:\(10−9.58\).
- תשובה
-
0.42
חיסור:\(50−37.42\).
- תשובה
-
12.58
להכפיל ולחלק עשרונים
הכפלת עשרונים דומה מאוד להכפלת מספרים שלמים - עלינו רק לקבוע היכן למקם את הנקודה העשרונית. ההליך להכפלת עשרונים יהיה הגיוני אם נמיר אותם תחילה לשברים ואז נכפיל.
אז בואו נראה מה היינו מקבלים כתוצר של עשרונים על ידי המרתם לשברים תחילה. נעשה שתי דוגמאות זו לצד זו. חפש דפוס!
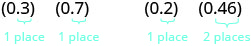 |
|
המר לשברים. |
 |
| להכפיל. |  |
| המר לעשרונים. |  |
שימו לב, בדוגמה הראשונה הכפלנו שני מספרים שלכל אחד מהם הייתה ספרה אחת אחרי הנקודה העשרונית ולמוצר היו שני מקומות עשרוניים. בדוגמה השנייה הכפלנו מספר עם מקום עשרוני אחד במספר עם שני מקומות עשרוניים ולמוצר היו שלושה מקומות עשרוניים.
אנו מכפילים את המספרים בדיוק כפי שאנו עושים מספרים שלמים, תוך התעלמות זמנית מהנקודה העשרונית. לאחר מכן אנו סופרים את מספר הנקודות העשרוניות בגורמים והסכום הזה אומר לנו את מספר המקומות העשרוניים במוצר.
הכללים להכפלת מספרים חיוביים ושליליים חלים גם על עשרונים, כמובן!
כאשר מכפילים שני מספרים,
- אם הסימנים שלהם זהים המוצר חיובי.
- אם הסימנים שלהם שונים המוצר שלילי.
כאשר אנו מכפילים עשרונים חתומים, ראשית אנו קובעים את סימן המוצר ואז מכפילים כאילו המספרים היו חיוביים. לבסוף, אנו כותבים את המוצר עם הסימן המתאים.
- קבע את סימן המוצר.
- כתוב בפורמט אנכי, מסדר את המספרים בצד ימין. הכפל את המספרים כאילו היו מספרים שלמים, תוך התעלמות זמנית מהנקודות העשרוניות.
- מקם את הנקודה העשרונית. מספר המקומות העשרוניים במוצר הוא סכום מספר המקומות העשרוניים בגורמים.
- כתוב את המוצר עם הסימן המתאים.
הכפל:\((−3.9)(4.075)\).
- תשובה
-
\((−3.9)(4.075)\) הסימנים שונים. המוצר יהיה שלילי. כתוב בפורמט אנכי, מסדר את המספרים בצד ימין. 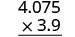
להכפיל. 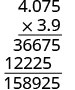
הוסף את מספר המקומות העשרוניים בגורמים\((1 + 3)\).

מקם את הנקודה העשרונית 4 מקומות מימין.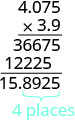
הסימנים שונים, ולכן המוצר שלילי. \((−3.9)(4.075) = −15.8925\)
הכפל:\(−4.5(6.107)\).
- תשובה
-
\(−27.4815\)
הכפל: -10.79 (8.12).
- תשובה
-
\(−87.6148\)
ברבים מהשיעורים האחרים שלך, במיוחד במדעים, תכפיל עשרונים בכוחות של 10 (10, 100, 1000 וכו '). אם תכפיל כמה מוצרים על נייר, ייתכן שתבחין בתבנית המתייחסת למספר האפסים בעוצמה של 10 למספר המקומות העשרוניים אנו מעבירים את הנקודה העשרונית ימינה כדי לקבל את המוצר.
- הזז את הנקודה העשרונית ימינה את אותו מספר מקומות כמו מספר האפסים בעוצמה של 10.
- הוסף אפסים בסוף המספר לפי הצורך.
הכפל 5.63
- על ידי 10
- על ידי 100
- על ידי 1,000.
- תשובה
-
על ידי התבוננות במספר האפסים בכפולה של עשרה, אנו רואים את מספר המקומות הדרושים לנו כדי להזיז את העשרוני ימינה.
ⓐ
\(5.63(10)\) יש 1 אפס ב 10, אז להזיז את הנקודה העשרונית 1 מקום ימינה. 
ⓑ
\(5.63(100)\) ישנם 2 אפסים ב 100, אז להזיז את הנקודה העשרונית 2 מקומות ימינה. 
ⓒ
ישנם 3 אפסים ב -1,000, אז הזז את הנקודה העשרונית 3 מקומות ימינה. 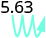
יש להוסיף אפס בסוף. 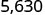
הכפל 2.58
- על ידי 10
- על ידי 100
- על ידי 1,000.
- תשובה
-
- 25.8
- 258
- 2,580
הכפל 14.2
- על ידי 10
- על ידי 100
- על ידי 1,000.
- תשובה
-
- 142
- 1,420
- 14,200
בדיוק כמו בכפל, חלוקת העשרונים דומה מאוד לחלוקת מספרים שלמים. עלינו רק להבין היכן יש למקם את הנקודה העשרונית.
כדי לחלק עשרונים, קבע באיזה כוח של 10 להכפיל את המכנה כדי להפוך אותו למספר שלם. ואז להכפיל את המונה על ידי אותו כוח של 10. בגלל מאפיין השברים המקביל, לא שינינו את ערך השבר! ההשפעה היא להזיז את הנקודות העשרוניות במונה ובמכנה את אותו מספר מקומות ימינה. לדוגמה:
\[\begin{array} { c } { \frac { 0.8 } { 0.4 } } \\ { \frac { 0.8 ( 10 ) } { 0.4 ( 10 ) } } \\ { \frac { 8 } { 4 } } \end{array}\]
אנו משתמשים בכללים לחלוקת מספרים חיוביים ושליליים גם עם עשרונים. כאשר מחלקים עשרונים חתומים, קבעו תחילה את סימן המנה ואז חלקו כאילו המספרים היו חיוביים. לבסוף, כתוב את המנה עם הסימן המתאים.
אנו בודקים את הסימון ואוצר המילים לחלוקה:
\[\begin{array} {ll} {} &{\underset{\text{quotient}}{c}} \\ {\underset{\text{dividend}}{a} \div \underset{\text{divisor}}{b} = \underset{\text{quotient}}{c}} & {\underset{\text{divisor}}{b})\overline{\underset{\text{dividend}}{a}}} \end{array}\]
נכתוב את הצעדים שיש לנקוט בעת חלוקת עשרונים, לעיון קל.
- קבע את סימן המנה.
- הפוך את המחלק למספר שלם על ידי "הזזת" הנקודה העשרונית עד ימינה. "העבר" את הנקודה העשרונית בדיבידנד למספר זהה של מקומות - הוספת אפסים לפי הצורך.
- לחלק. מקם את הנקודה העשרונית במנה מעל הנקודה העשרונית בדיבידנד.
- כתוב את המנה עם הסימן המתאים.
לחלק:\(−25.65\div (−0.06)\).
- תשובה
-
זכור, אתה יכול "להזיז" את העשרונים במחלק ובדיבידנד בגלל נכס השברים המקבילים.
\(−25.65\div (−0.06)\) הסימנים זהים. המנה חיובית. הפוך את המחלק למספר שלם על ידי "הזזת" הנקודה העשרונית עד ימינה. "העבר" את הנקודה העשרונית בדיבידנד באותו מספר מקומות. 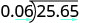
לחלק.
מקם את הנקודה העשרונית במנה מעל הנקודה העשרונית בדיבידנד.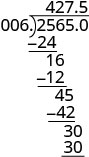
כתוב את המנה עם הסימן המתאים. \(−25.65\div (−0.06) = 427.5\)
לחלק:\(−23.492\div (−0.04)\).
- תשובה
-
687.3
לחלק:\(−4.11\div(−0.12)\).
- תשובה
-
34.25
יישום נפוץ של חלוקת מספרים שלמים לעשרונים הוא כאשר אנו רוצים למצוא את המחיר של פריט אחד שנמכר כחלק ממארז מרובה. לדוגמה, נניח שמקרה של 24 בקבוקי מים עולה\($3.99\). כדי למצוא את המחיר של בקבוק מים אחד, נחלק \($3.99\) ב 24. אנו מראים חלוקה זו בתרגיל\(\PageIndex{31}\). בחישובים עם כסף, נעגל את התשובה לסנט הקרוב ביותר (המאה).
לחלק:\($3.99\div 24\).
- תשובה
-
.99 מחולק ב -24 ניתן. בעיית חלוקה ארוכה מוגדרת עם 24 מחלקים 3.99. טבלה ניתנת עם כיוונים משמאל והצעדים המתמטיים מימין. בשלב הראשון כתוב "מקם את הנקודה העשרונית במנה מעל הנקודה העשרונית בדיבידנד. מחלקים כרגיל. מתי אנחנו עוצרים? מכיוון שחלוקה זו כרוכה בכסף, אנו מעגלים אותה לסנט הקרוב ביותר (מאית). לשם כך עלינו לשאת את החלוקה למקום האלף". מימין לכך, יש לנו בעיית חלוקה ארוכה שהוקמה עם 24 חלוקת 3.990. המנה ניתנת כ- 0.166. כדי להציג את העבודה, מתחת 3.990 הוא קורא 24, קו אופקי מוצק, 159, 144, קו אופקי מוצק, 150, 144, קו אופקי מוצק, ולבסוף 6. השלב החמישי קורא "סיבוב לסנט הקרוב ביותר". מימין לכך, יש לנו 0.166$ שווה בערך ל 0.17$ ומכאן >.99 חלקי 24 הוא 0.17$." >
\($3.99\div 24\) מקם את הנקודה העשרונית במנה מעל הנקודה העשרונית בדיבידנד. מחלקים כרגיל.
מתי אנחנו עוצרים? מכיוון שחלוקה זו כרוכה בכסף, אנו מעגלים אותה לסנט הקרוב ביותר (המאה). כדי לעשות זאת, עלינו לשאת את החלוקה למקום האלפים.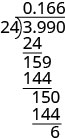
סיבוב לסנט הקרוב ביותר. \($0.166\approx $0.17\)
\($3.99\div 2\approx $0.17\)
לחלק:\($6.99\div 36\).
- תשובה
-
\($0.19\)
לחלק:\($4.99\div 12\).
- תשובה
-
\($0.42\)
המר ספרות עשרוניות, שברים ואחוזים
אנו ממירים עשרונים לשברים על ידי זיהוי ערך המקום של הספרה האחרונה (הימנית הרחוקה ביותר). בעשרוני 0.03 ה -3 נמצא במקום המאות, ולכן 100 הוא המכנה של השבר השווה ל 0.03.
\[00.03 = \frac { 3 } { 100 }\]
שימו לב, כאשר המספר משמאל לעשרוני הוא אפס, אנו מקבלים שבר שהמונה שלו פחות מהמכנה שלו. שברים כאלה נקראים שברים מתאימים.
השלבים שיש לנקוט כדי להמיר עשרוני לשבר מסוכמים בתיבת ההליך.
- קבע את ערך המקום של הספרה הסופית.
- כתוב את השבר.
- המספר - "המספרים" מימין לנקודה העשרונית
- מכנה - ערך המקום המתאים לספרה הסופית
כתוב 0.374 כשבריר.
- תשובה
-
0.374 קבע את ערך המקום של הספרה הסופית. 
כתוב את השבר עבור 0.374:
- המונה הוא 374.
- המכנה הוא 1,000.
\(\dfrac{374}{1000}\) פשט את השבר. \(\dfrac{2\cdot 187}{2\cdot 500}\) לחלק את הגורמים המשותפים. \(\dfrac{187}{500}\)
כך, \(0.374=\dfrac{187}{500}\)האם שמת לב שמספר האפסים במכנה של \(\dfrac{374}{1000}\) זהה למספר המקומות העשרוניים ב- 0.374?
כתוב 0.234 כשבריר.
- תשובה
-
\(\dfrac{117}{500}\)
כתוב 0.024 כשבריר.
- תשובה
-
\(\dfrac{3}{125}\)
למדנו להמיר עשרונים לשברים. כעת נעשה את ההיפוך - נמיר שברים לעשרונים. זכור כי סרגל השבר פירושו חלוקה. אז \(\dfrac{4}{5}\) אפשר לכתוב \(4\div 5\) או\(5)\overline{4}\). זה מוביל לשיטה הבאה להמרת שבר לעשרוני.
כדי להמיר שבר לעשרוני, חלק את מונה השבר במכנה השבר.
כתוב \(-\dfrac{5}{8}\) כעשרוני.
- תשובה
-
מכיוון שסרגל שברים פירושו חלוקה, אנו מתחילים בכתיבה \(\dfrac{5}{8}\) כ\(8)\overline{5}\). עכשיו לחלק.

כתוב \(-\dfrac{7}{8}\) כעשרוני.
- תשובה
-
-0.875
כתוב \(-\dfrac{3}{8}\) כעשרוני.
- תשובה
-
-0.375
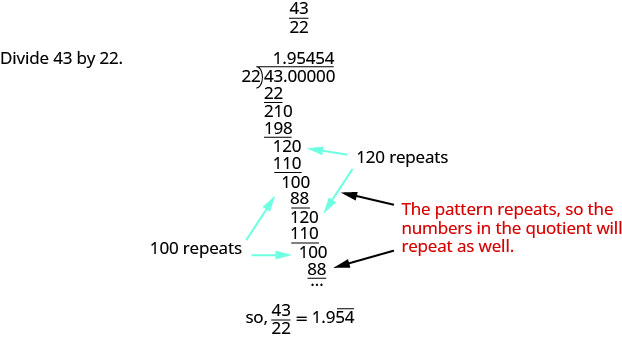
כשאנחנו מתחלקים, לא תמיד נקבל שארית אפס. לפעמים המנה מסתיימת בעשרוני שחוזר על עצמו. עשרוני חוזר הוא עשרוני שבו הספרה האחרונה או קבוצת הספרות חוזרת על עצמה בלי סוף. סרגל ממוקם מעל גוש הספרות החוזר כדי לציין שהוא חוזר.
עשרוני חוזר הוא עשרוני שבו הספרה האחרונה או קבוצת הספרות חוזרת על עצמה בלי סוף.
סרגל ממוקם מעל גוש הספרות החוזר כדי לציין שהוא חוזר.
כתוב \(\dfrac{43}{22}\) כעשרוני.
- תשובה
-
כתוב \(\dfrac{27}{11}\) כעשרוני.
- תשובה
-
\(2.\overline{45}\)
כתוב \(\dfrac{51}{22}\) כעשרוני.
- תשובה
-
\(2.3\overline{18}\)
לפעמים יתכן ונצטרך לפשט ביטויים עם שברים ועשרונים יחד.
פשט:\(\dfrac{7}{8}+6.4\).
- תשובה
-
ראשית עלינו לשנות מספר אחד כך ששני המספרים יהיו באותה צורה. אנו יכולים לשנות את השבר לעשרוני, או לשנות את העשרוני לשבר. בדרך כלל קל יותר לשנות את השבר לעשרוני.
\(\dfrac{7}{8}+6.4\) שנה \(\dfrac{7}{8}\) לעשרוני. 
להוסיף. \(0.875+6.4\) \(7.275\) אז, \(\dfrac{7}{8}+6.4 = 7.275\)
פשט:\(\dfrac{3}{8}+4.9\).
- תשובה
-
\(5.275\)
פשט:\(5.7 + \dfrac{13}{20}\).
- תשובה
-
\(6.35\)
אחוז הוא יחס שהמכנה שלו הוא 100. אחוז פירושו למאה. אנו משתמשים בסמל האחוזים,%, כדי להראות אחוזים.
אחוז הוא יחס שהמכנה שלו הוא 100.
מכיוון שאחוז הוא יחס, הוא יכול לבוא לידי ביטוי בקלות כשבריר. אחוז פירושו לכל 100, ולכן המכנה של השבר הוא 100. לאחר מכן אנו משנים את השבר לעשרוני על ידי חלוקת המונה במכנה.
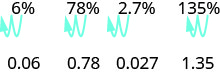
\[\begin{array} {llll} {} &{\text{6%}} &{\text{78%}} &{\text{135%}} \\ {\text { Write as a ratio with denominator } 100. } &{\dfrac{6}{100}} &{\dfrac{78}{100}} &{\dfrac{135}{100}} \\ { \text { Change the fraction to a decimal by dividing}} &{0.06} &{0.78} &{1.35}\\ {\text{the numerator by the denominator.}} &{} &{} &{} \end{array}\]
אתה רואה את התבנית? כדי להמיר מספר אחוז למספר עשרוני, אנו מעבירים את הנקודה העשרונית שני מקומות שמאלה.
המר כל אחוז לעשרוני:
- 62%
- 135%
- 35.7%.
- תשובה
-
1. 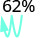
הזז את הנקודה העשרונית שני מקומות שמאלה. 0.62 2. 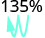
הזז את הנקודה העשרונית שני מקומות שמאלה. 1.35 3. 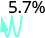
הזז את הנקודה העשרונית שני מקומות שמאלה. 0.057
המר כל אחוז לעשרוני:
- 9%
- 87%
- 3.9%.
- תשובה
-
- 0.09
- 0.87
- 0.039
המר כל אחוז לעשרוני:
- 3%
- 91%
- 8.3%.
- תשובה
-
- 0.03
- 0.91
- 0.083
המרת עשרוני לאחוז הגיוני אם נזכור את ההגדרה של אחוזים ונזכור את ערך המקום.
כדי להמיר עשרוני לאחוז, זכור שאחוז פירושו למאה. אם נשנה את העשרוני לשבר שהמכנה שלו הוא 100, קל לשנות את השבר הזה לאחוז.
\[\begin{array} {llll} {} &{0.83} &{1.05} &{0.075} \\ {\text {Write as a fraction }} &{\frac{83}{100}} &{\small{1}\frac{5}{100}} &{\frac{75}{1000}} \\ { \text {The denominator is 100.}} &{} &{\frac{105}{100}} &{\frac{7.5}{100}}\\ {\text{Write the ratio as a percent.}} &{\text{83%}} &{\text{105%}} &{\text{7.5%}} \end{array}\]
מזהים את התבנית? כדי להמיר עשרוני לאחוז, אנו מעבירים את הנקודה העשרונית שני מקומות ימינה ואז מוסיפים את סימן האחוז.
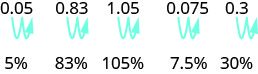
המר כל עשרוני לאחוז:
- 0.51
- 1.25
- 0.093.
- תשובה
-
1. 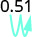
הזז את הנקודה העשרונית שני מקומות ימינה. \(51%\) 2. 
הזז את הנקודה העשרונית שני מקומות ימינה. \(125%\) 3. 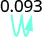
הזז את הנקודה העשרונית שני מקומות ימינה. \(9.3%\)
המר כל עשרוני לאחוז:
- 0.17
- 1.75
- 0.0825
- תשובה
-
- 17%
- 175%
- 8.25%
המר כל עשרוני לאחוז:
- 0.41
- 2.25
- 0.0925.
- תשובה
-
- 41%
- 225%
- 9.25%
מושגי מפתח
- שם עשרוני
- תן שם למספר משמאל לנקודה העשרונית.
- כתוב" ו-" לנקודה העשרונית.
- תן שם לחלק "מספר" מימין לנקודה העשרונית כאילו היה מספר שלם.
- תן שם למקום העשרוני של הספרה האחרונה.
- כתוב עשרוני
- חפש את המילה 'ו-' - היא מאתרת את הנקודה העשרונית. הצב נקודה עשרונית מתחת למילה 'ו'. תרגם את המילים לפני 'ו' למספר השלם והנח אותו משמאל לנקודה העשרונית. אם אין "ו", כתוב "0" עם נקודה עשרונית מימין.
- סמן את מספר המקומות העשרוניים הדרושים מימין לנקודה העשרונית על ידי ציון ערך המקום המצוין במילה האחרונה.
- תרגם את המילים אחרי 'ו' למספר מימין לנקודה העשרונית. כתוב את המספר ברווחים - שים את הספרה הסופית במקום האחרון.
- מלא אפסים למחזיקי מקום לפי הצורך.
- סיבוב עשרוני
- אתר את ערך המקום הנתון וסמן אותו בחץ.
- הדגיש את הספרה מימין לערך המקום.
- האם הספרה הזו גדולה או שווה ל -5? כן - הוסף 1 לספרה בערך המקום הנתון. לא — אל תשנה את הספרה בערך המקום הנתון.
- כתוב מחדש את המספר, מחק את כל הספרות מימין לספרת העיגול.
- הוספה או הפחתה של מספרים עשרוניים
- כתוב את המספרים כך שהנקודות העשרוניות יתיישרו אנכית.
- השתמש באפסים כמחזיקי מקום, לפי הצורך.
- הוסף או הפחת את המספרים כאילו היו מספרים שלמים. לאחר מכן מקם את העשרוני בתשובה מתחת לנקודות העשרוניות במספרים הנתונים.
- הכפל עשרוניות
- קבע את סימן המוצר.
- כתוב בפורמט אנכי, מסדר את המספרים בצד ימין. הכפל את המספרים כאילו היו מספרים שלמים, תוך התעלמות זמנית מהנקודות העשרוניות.
- מקם את הנקודה העשרונית. מספר המקומות העשרוניים במוצר הוא סכום המקומות העשרוניים בגורמים.
- כתוב את המוצר עם הסימן המתאים.
- הכפל עשרוני בכוח של עשר
- הזז את הנקודה העשרונית ימינה את אותו מספר מקומות כמו מספר האפסים בעוצמה של 10.
- הוסף אפסים בסוף המספר לפי הצורך.
- מחלקים עשרוניים
- קבע את סימן המנה.
- הפוך את המחלק למספר שלם על ידי "הזזת" הנקודה העשרונית עד ימינה. "העבר" את הנקודה העשרונית בדיבידנד אותו מספר מקומות - הוספת אפסים לפי הצורך.
- לחלק. מקם את הנקודה העשרונית במנה מעל הנקודה העשרונית בדיבידנד.
- כתוב את המנה עם הסימן המתאים.
- המרת עשרוני לשבר תקין
- קבע את ערך המקום של הספרה הסופית.
- כתוב את השבר: מונה - 'המספרים' מימין לנקודה העשרונית; מכנה - ערך המקום המתאים לספרה הסופית.
- המרת שבר לעשרוני חלק את מונה השבר במכנה.


