7.9: Kutatua Mifumo na Utawala wa Cramer

Malengo ya kujifunza

• Tathmini 2 × 2 determinants.
• Matumizi Cramer ya Utawala wa kutatua mfumo wa milinganyo katika vigezo viwili.
• Tathmini vigezo 3 × 3.
• Matumizi Cramer ya Utawala wa kutatua mfumo wa milinganyo tatu katika vigezo tatu.
• Jua mali ya determinants.

Tumejifunza jinsi ya kutatua mifumo ya equations katika vigezo viwili na vigezo vitatu, na kwa njia nyingi: badala, kuongeza, kuondoa Gaussia, kutumia inverse ya tumbo, na graphing. Baadhi ya njia hizi ni rahisi kutumia kuliko wengine na zinafaa zaidi katika hali fulani. Katika sehemu hii, tutajifunza mikakati miwili zaidi ya kutatua mifumo ya equations.

Kutathmini Uamuzi wa Matrix 2 × 2

Kitambulisho ni namba halisi ambayo inaweza kuwa na manufaa sana katika hisabati kwa sababu ina maombi mengi, kama vile kuhesabu eneo, kiasi, na kiasi kingine. Hapa, tutatumia vigezo ili kufunua kama tumbo haiwezi kuingizwa kwa kutumia maingizo ya tumbo la mraba ili kuamua kama kuna suluhisho la mfumo wa equations. Labda moja ya maombi ya kuvutia zaidi, hata hivyo, ni matumizi yao katika cryptography. Ishara salama au ujumbe wakati mwingine hutumwa encoded katika tumbo. Data inaweza tu kufutwa na tumbo invertible na kuamua. Kwa madhumuni yetu, tunazingatia uamuzi kama dalili ya invertibility ya tumbo. Kuhesabu uamuzi wa tumbo huhusisha kufuata mifumo maalum ambayo imeelezwa katika sehemu hii.

PATA UAMUZI WA MATRIX 2 × 2

Uamuzi wa tumbo la 2 × 2, lililopewa

\(A=\begin{bmatrix}a&b\\c&d\end{bmatrix}\)

hufafanuliwa kama

Angalia mabadiliko katika nukuu. Kuna njia kadhaa za kuonyesha uamuzi, ikiwa ni pamoja\(\det(A)\) na kuchukua nafasi ya mabano katika tumbo na mistari ya moja kwa moja,\(| A |\).

Mfano\(\PageIndex{1}\): Finding the Determinant of a \(2 × 2\) Matrix

Pata uamuzi wa tumbo lililopewa.

\(A=\begin{bmatrix}5&2\\−6&3\end{bmatrix}\)

Suluhisho

\[\begin{align*} \det(A)&= \begin{vmatrix}5&2\\-6&3\end{vmatrix}\\ &= 5(3)-(-6)(2)\\ &= 27 \end{align*}\]

Kutumia Utawala wa Cramer Kutatua Mfumo wa Equations mbili katika Vigezo viwili

Sasa tutaanzisha njia ya mwisho ya kutatua mifumo ya equations ambayo inatumia vigezo. Inajulikana kama Utawala wa Cramer, mbinu hii ilianza katikati ya karne ya 18 na ni jina la mvumbuzi wake, mtaalamu wa hisabati wa Uswisi Gabriel Cramer (1704-1752), ambaye aliianzisha mwaka 1750 katika Utangulizi à l'Analyse des lignes Courbes algébriques. Utawala wa Cramer ni njia inayofaa na yenye ufanisi ya kutafuta ufumbuzi wa mifumo yenye idadi ya kiholela ya haijulikani, ikiwa ni pamoja na kwamba tuna idadi sawa ya milinganyo kama haijulikani.

Utawala wa Cramer utatupa suluhisho la kipekee kwa mfumo wa milinganyo, ikiwa ipo. Hata hivyo, ikiwa mfumo hauna suluhisho au idadi isiyo na kipimo cha ufumbuzi, hii itaonyeshwa kwa uamuzi wa sifuri. Ili kujua kama mfumo haukubaliani au unategemea, njia nyingine, kama vile kuondoa, itatakiwa kutumika.

Ili kuelewa Utawala wa Cramer, hebu tuangalie kwa karibu jinsi tunavyoweza kutatua mifumo ya usawa wa mstari kwa kutumia shughuli za msingi za mstari. Fikiria mfumo wa equations mbili katika vigezo viwili.

\[\begin{align} a_1x+b_1y&= c_1 (1) \label{eq1}\\ a_2x+b_2y&= c_2 (2) \label{eq2}\\ \end{align}\]

Tunaondoa variable moja kwa kutumia shughuli za mstari na kutatua kwa mwingine. Sema kwamba tunataka kutatua\(x\). Ikiwa Equation\ ref {eq2} imeongezeka kwa kinyume cha mgawo wa\(y\) katika Equation\ ref {eq1}, Equation\ ref {eq1} huongezeka kwa mgawo wa\(y\) katika Equation\ ref {eq2}, na tunaongeza equations mbili, variable\(y\) itaondolewa.

\[\begin{align*} &b_2a_1x+b_2b_1y = b_2c_1 & \text{Multiply }R_1 \text{ by }b_2 \\ -&\underline{b_1a_2x−b_1b_2y=−b_1c_2} & \text{Multiply }R_2 \text{ by }−b_1 \\ & b_2a_1x−b_1a_2x=b_2c_1−b_1c_2 \end{align*}\]

Sasa, tatua\(x\).

\[\begin{align*} b_2a_1x−b_1a_2x &= b_2c_1−b_1c_2 \\ x(b_2a_1−b_1a_2) &= b_2c_1−b_1c_2 \\ x &= \dfrac{b_2c_1−b_1c_2}{b_2a_1−b_1a_2}=\dfrac{\begin{bmatrix}c_1&b_1\\c_2&b_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}} \end{align*}\]

Vile vile, ili kutatua\(y\), tutaondoa\(x\).

\[\begin{align*} & a_2a_1x+a_2b_1y = a_2c_1 & \text{Multiply }R_1 \text{ by }a_2 \\ -& \underline{a_1a_2x−a_1b_2y=−a_1c_2} & \text{Multiply }R_2 \text{ by }−a_1 \\ & a_2b_1y−a_1b_2y =a_2c_1−a_1c_2 \end{align*}\]

Kutatua kwa\(y\) anatoa

\[ \begin{align*} a_2b_1y−a_1b_2y &= a_2c_1−a_1c_2 \\ y(a_2b_1−a_1b_2) &= a_2c_1−a_1c_2 \\ y &= \dfrac{a_2c_1−a_1c_2}{a_2b_1−a_1b_2}=\dfrac{a_1c_2−a_2c_1}{a_1b_2−a_2b_1}=\dfrac{\begin{bmatrix}a_1&c_1\\a_2&c_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}} \end{align*}\]

Angalia kwamba denominator kwa wote\(x\) na\(y\) ni uamuzi wa tumbo la mgawo.

Tunaweza kutumia fomula hizi kutatua kwa\(x\) na\(y\), lakini Cramer ya Utawala pia utangulizi nukuu mpya:

• \(D\):kuamua ya tumbo la mgawo
• \(D_x\):determinant ya nambari katika suluhisho la\(x\)

  \[x=\dfrac{D_x}{D}\]

• \(D_y\):determinant ya nambari katika suluhisho la\(y\)

  \[y=\dfrac{D_y}{D}\]

Funguo la Utawala wa Cramer ni kuchukua nafasi ya safu ya kutofautiana ya riba na safu ya mara kwa mara na kuhesabu vigezo. Tunaweza kisha kueleza\(x\) na\(y\) kama quotient ya determinants mbili.

CRAMER YA UTAWALA KWA\(2×2\) SYSTEMS

Utawala wa Cramer ni njia inayotumia vigezo kutatua mifumo ya milinganyo ambayo ina idadi sawa ya milinganyo kama vigezo.

Fikiria mfumo wa equations mbili linear katika vigezo viwili.

\[\begin{align*} a_1x+b_1y&= c_1\\ a_2x+b_2y&= c_2 \end{align*}\]

Suluhisho kwa kutumia Utawala wa Cramer hutolewa kama

\[\begin{align} x&= \dfrac{D_x}{D} = \dfrac{\begin{bmatrix}c_1&b_1\\c_2&b_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}}\; , D\neq 0\\ y&= \dfrac{D_y}{D} = \dfrac{\begin{bmatrix}a_1&c_1\\a_2&c_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}}\; , D\neq 0 \end{align}\]

Ikiwa tunatatua\(x\),\(x\) safu inabadilishwa na safu ya mara kwa mara. Ikiwa tunatatua\(y\),\(y\) safu inabadilishwa na safu ya mara kwa mara.

Mfano\(\PageIndex{2}\): Using Cramer’s Rule to Solve a \(2 × 2\) System

Kutatua\(2 × 2\) mfumo wafuatayo kwa kutumia Cramer ya Utawala.

\[\begin{align*} 12x+3y&= 15\\ 2x-3y&= 13 \end{align*}\]

Suluhisho

Kutatua kwa\(x\).

\[\begin{align*} x&= \dfrac{D_x}{D}\\ &= \dfrac{\begin{bmatrix}15&3\\13&-3\end{bmatrix}}{\begin{bmatrix}12&3\\2&-3\end{bmatrix}}\\ &= \dfrac{-45-39}{-36-6}\\ &= \dfrac{-84}{-42}\\ &= 2 \end{align*}\]

Kutatua kwa\(y\).

\[\begin{align*} y&= \dfrac{D_y}{D}\\ &= \dfrac{\begin{bmatrix}12&15\\2&13\end{bmatrix}}{\begin{bmatrix}12&3\\2&-3\end{bmatrix}}\\ &= \dfrac{156-30}{-36-6}\\ &= -\dfrac{126}{42}\\ &= -3 \end{align*}\]

Suluhisho ni\((2,−3)\).

Zoezi\(\PageIndex{1}\)

Tumia Utawala wa Cramer kutatua\(2 × 2\) mfumo wa equations.

\[\begin{align*} x+2y&= -11\\ -2x+y&= -13 \end{align*}\]

Jibu

\((3,−7)\)

Kutathmini Uamuzi wa Matrix 3 × 3

Kupata uamuzi wa tumbo la 2 × 2 ni moja kwa moja, lakini kutafuta uamuzi wa tumbo la 3 × 3 ni ngumu zaidi. Njia moja ni kuongeza tumbo la 3 × 3 na kurudia kwa nguzo mbili za kwanza, kutoa tumbo la 3×5. Kisha tunahesabu jumla ya bidhaa za kuingizwa chini ya kila diagonal tatu (juu kushoto kwenda chini kulia), na uondoe bidhaa za kuingizwa hadi kila diagonal tatu (chini kushoto kwenda kulia juu). Hii inaeleweka kwa urahisi kwa kuona na mfano.

Kupata determinant ya 3 × 3 Matrix.

\(A=\begin{bmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{bmatrix}\)

1. Kuongeza\(A\) na nguzo mbili za kwanza.

   \(\det(A)=\left| \begin{array}{ccc|cc} a_1&b_1&c_1&a_1&b_1\\a_2&b_2&c_2&a_2&b_2\\a_3&b_3&c_3&a_3&b_3\end{array} \right|\)

2. Kutoka juu kushoto kwenda chini kulia: Kuzidisha entries chini diagonal kwanza. Ongeza matokeo kwa bidhaa ya maingizo chini ya diagonal ya pili. Ongeza matokeo haya kwa bidhaa ya maingizo chini ya diagonal ya tatu.
3. Kutoka chini kushoto kwenda juu kulia: Ondoa bidhaa ya entries up diagonal kwanza. Kutokana na matokeo haya Ondoa bidhaa ya entries hadi diagonal pili. Kutoka kwa matokeo haya, toa bidhaa ya kuingizwa hadi diagonal ya tatu.

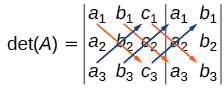
Algebra ni kama ifuatavyo:

\(| A |=a_1b_2c_3+b_1c_2a_3+c_1a_2b_3−a_3b_2c_1−b_3c_2a_1−c_3a_2b_1\)

Mfano\(\PageIndex{3}\): Finding the Determinant of a 3 × 3 Matrix

Pata uamuzi wa\(3 × 3\) tumbo uliotolewa

\(A=\begin{bmatrix}0&2&1\\3&−1&1\\4&0&1\end{bmatrix}\)

Suluhisho

Kuongeza tumbo na nguzo mbili za kwanza na kisha ufuate formula. Hivyo,

\[\begin{align*} | A | &= \left| \begin{array}{ccc|cc}0&2&1&0&2\\3&-1&1&3&-1\\4&0&1&4&0\end{array}\right| \\ &= 0(−1)(1)+2(1)(4)+1(3)(0)−4(−1)(1)−0(1)(0)−1(3)(2) \\ &=0+8+0+4−0−6 \\ &= 6 \end{align*}\]

Zoezi\(\PageIndex{2}\)

Pata uamuzi wa tumbo la 3 × 3.

\(\det(A)=\begin{vmatrix}1&−3&7\\1&1&1\\1&−2&3\end{vmatrix}\)

Jibu

\(−10\)

Q & A: Je, tunaweza kutumia njia hiyo ili kupata determinant ya tumbo kubwa?

Hapana, njia hii inafanya kazi tu kwa matrices 2 × 2 na 3 × 3. Kwa matrices kubwa ni bora kutumia matumizi ya graphing au programu ya kompyuta.

Kutumia Utawala wa Cramer Kutatua Mfumo wa Equations Tatu katika Vigezo Tatu

Sasa kwa kuwa tunaweza kupata determinant ya\(3 × 3\) tumbo, tunaweza kutumia Utawala Cramer ya kutatua mfumo wa milinganyo tatu katika vigezo tatu. Utawala Cramer ni moja kwa moja, kufuatia mfano sambamba na Utawala Cramer kwa\(2 × 2\) matrices. Kama utaratibu wa tumbo huongezeka kwa\(3 × 3\), hata hivyo, kuna mahesabu mengi zaidi yanahitajika.

Tunapohesabu uamuzi wa kuwa sifuri, Utawala wa Cramer hautoi dalili kama mfumo hauna suluhisho au idadi isiyo na kipimo cha ufumbuzi. Ili kujua, tunapaswa kufanya uondoaji kwenye mfumo.

Fikiria\(3 × 3\) mfumo wa equations.

\[\begin{align} a_1x+b_1y+c_1z &= \color{blue}d_1 \\ a_2x+b_2y+c_2z &= \color{blue}d_2 \\ a_3x+b_3y+c_3z &= \color{blue}d_3 \\ \end{align}\]

\(x=\dfrac{D_x}{D}\),\(y=\dfrac{D_y}{D}\),\(z=\dfrac{D_z}{D}\),\(D≠0\)

wapi

\[D = \begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix}\; ,\; D_x = \begin{vmatrix} \color{blue}d_1 & b_1 & c_1\\ \color{blue}d_2 & b_2 & c_2\\ \color{blue}d_3 & b_3 & c_3 \end{vmatrix}\; ,\; D_y = \begin{vmatrix} a_1 & \color{blue}d_1 & c_1\\ a_2 & \color{blue}d_2 & c_2\\ a_3 & \color{blue}d_3 & c_3 \end{vmatrix}\; ,\; D_z = \begin{vmatrix} a_1 & b_1 & \color{blue}d_1\\ a_2 & b_2 & \color{blue}d_2\\ a_3 & b_3 & \color{blue}d_3 \end{vmatrix}\]

Ikiwa tunaandika uamuzi\(D_x\), tunachukua nafasi ya\(x\) safu na safu ya mara kwa mara. Kama sisi ni kuandika determinant\(D_y\), sisi kuchukua nafasi yao y safu na safu ya mara kwa mara. Ikiwa tunaandika uamuzi\(D_z\), tunachukua nafasi ya\(z\) safu na safu ya mara kwa mara. Daima angalia jibu.

Mfano\(\PageIndex{4}\): Solving a \(3 × 3\) System Using Cramer’s Rule

Kupata ufumbuzi wa\(3 × 3\) mfumo kutokana na kutumia Cramer ya Utawala.

\[\begin{align*} x+y-z&= 6\\ 3x-2y+z&= -5\\ x+3y-2z&= 14 \end{align*}\]

Suluhisho

Matumizi Cramer ya Utawala.

\(D=\begin{vmatrix}1&1&−1\\3&−2&1\\1&3&−2\end{vmatrix}\),\(D_x=\begin{vmatrix}6&1&−1\\−5&−2&1\\14&3&−2\end{vmatrix}\),\(D_y=\begin{vmatrix}1&6&−1\\3&−5&1\\1&14&−2\end{vmatrix}\),\(D_z=\begin{vmatrix}1&1&6\\3&−2&−5\\1&3&14\end{vmatrix}\)

Kisha,

\[\begin{align*} x&= \dfrac{D_x}{D}&= \dfrac{-3}{-3}&= 1\\ y&= \dfrac{D_y}{D}&= \dfrac{-9}{-3}&= 3\\ z&= \dfrac{D_z}{D}&= \dfrac{6}{-3}&= -2\\ \end{align*}\]

Suluhisho ni\((1,3,−2)\).

Zoezi\(\PageIndex{3}\)

Tumia Utawala wa Cramer wa kutatua\(3 × 3\) tumbo.

\[\begin{align*} x-3y+7z&= 13\\ x+y+z&= 1\\ x-2y+3z&= 4 \end{align*}\]

Jibu

\(\left(−2,\dfrac{3}{5},\dfrac{12}{5}\right)\)

Mfano\(\PageIndex{5A}\): Using Cramer’s Rule to Solve an Inconsistent System

Tatua mfumo wa milinganyo kwa kutumia Utawala wa Cramer.

\[\begin{align} 3x-2y&= 4 \label{eq3}\\ 6x-4y&= 0 \label{eq4}\end{align}\]

Suluhisho

Tunaanza kwa kutafuta vigezo\(D\),\(D_x\), na\(D_y\).

\(D=\begin{vmatrix}3&−2\\6&−4\end{vmatrix}=3(−4)−6(−2)=0\)

Tunajua kwamba uamuzi wa sifuri ina maana kwamba ama mfumo hauna suluhisho au ina idadi isiyo na kipimo cha ufumbuzi. Ili kuona ni moja, tunatumia mchakato wa kuondoa. Lengo letu ni kuondoa moja ya vigezo.

1. Kuzidisha Equation\ ref {eq3} na\(−2\).
2. Ongeza matokeo kwa Equation\ ref {eq4}.

\[\begin{align*} &−6x+4y=−8 \\ &\;\;\;\underline{6x−4y=0} \\ &\;\;\;\;\;\;\;\;\;\; 0=−8 \end{align*}\]

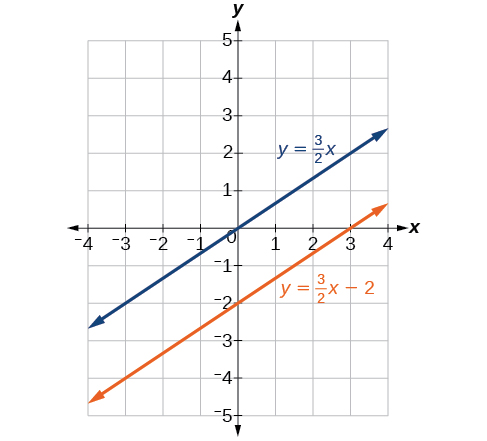
Tunapata equation\(0=−8\), ambayo ni ya uongo. Kwa hiyo, mfumo hauna suluhisho. Graphing mfumo inaonyesha mistari miwili sambamba. Angalia Kielelezo\(\PageIndex{1}\).

Kielelezo\(\PageIndex{1}\)

Mfano\(\PageIndex{5B}\): Use Cramer’s Rule to Solve a Dependent System

Tatua mfumo na idadi isiyo na kipimo cha ufumbuzi.

\[\begin{align} x-2y+3z&= 0 \label{eq5}\\ 3x+y-2z&= 0 \label{eq6}\\ 2x-4y+6z&= 0 \label{eq7} \end{align}\]

Suluhisho

Hebu tupate uamuzi wa kwanza. Weka tumbo lililoongezwa na nguzo mbili za kwanza.

\(\left| \begin{array}{ccc|cc}1&−2&3&1&-2\\3&1&−2&3&1\\2&−4&6&2&-4\end{array}\right|\)

Kisha,

\(1(1)(6)+(−2)(−2)(2)+3(3)(−4)−2(1)(3)−(−4)(−2)(1)−6(3)(−2)=0\)

Kama uamuzi sawa na sifuri, kuna ama hakuna suluhisho au idadi isiyo na kipimo cha ufumbuzi. Tunapaswa kufanya uondoaji ili kujua.

1. Ongeza Equation\ ref {eq5}\(−2\) na kuongeza matokeo kwa Equation\ ref {eq7}:

\[\begin{align*} &−2x+4y−6x=0 \\ &\;\;\underline{2x−4y+6z=0} \\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0=0 \end{align*}\]

2. Kupata jibu la\(0=0\), taarifa ambayo daima ni kweli, ina maana kwamba mfumo una idadi isiyo na kipimo ya ufumbuzi. Graphing mfumo, tunaweza kuona kwamba wawili wa ndege ni sawa na wote wawili intersect ndege ya tatu kwenye mstari. Angalia Kielelezo\(\PageIndex{2}\).

Kielelezo\(\PageIndex{2}\)

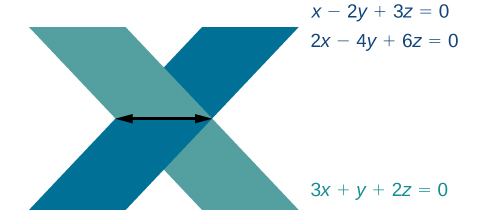
Kuelewa Mali ya Maamuzi

Kuna mali nyingi za maamuzi. Waliotajwa hapa ni baadhi ya mali ambayo inaweza kuwa na manufaa katika kuhesabu determinant ya tumbo.

MALI YA VIKWAZO

1. Ikiwa tumbo iko katika fomu ya juu ya triangular, uamuzi huo unafanana na bidhaa za kuingizwa chini ya diagonal kuu.
2. Wakati safu mbili zinabadilishana, ishara ya mabadiliko ya kuamua.
3. Ikiwa safu mbili au nguzo mbili zinafanana, uamuzi huo unafanana na sifuri.
4. Ikiwa tumbo lina safu ya zero au safu ya zero, uamuzi huo ni sawa na sifuri.
5. Uamuzi wa tumbo la inverse\(A^{−1}\) ni usawa wa uamuzi wa tumbo\(A\).
6. Ikiwa mstari wowote au safu huongezeka kwa mara kwa mara, uamuzi huongezeka kwa sababu sawa.

Mfano\(\PageIndex{6}\): Illustrating Properties of Determinants

Onyesha kila moja ya mali ya determinants.

Suluhisho

Mali 1 inasema kwamba ikiwa tumbo iko katika fomu ya juu ya triangular, uamuzi ni bidhaa ya entries chini ya diagonal kuu.

\(A=\begin{bmatrix}1&2&3\\0&2&1\\0&0&−1\end{bmatrix}\)

Kuongeza\(A\) na nguzo mbili za kwanza.

\(A=\left[ \begin{array}{ccc|cc}1&2&3&1&2\\0&2&1&0&2\\0&0&−1&0&0\end{array}\right]\)

Kisha

\[\begin{align*} \det(A)&= 1(2)(-1)+2(1)(0)+3(0)(0)-0(2)(3)-0(1)(1)+1(0)(2)\\ &= -2 \end{align*}\]

Mali 2 inasema kuwa safu za kubadilishana hubadilisha ishara. Kutokana

\[\begin{align*} A&=\begin{bmatrix}-1&5\\4&-3\end{bmatrix}\\ \det(A)&= (-1)(-3)-(4)(5)\\ &= 3-20\\ &= -17 \end{align*}\]

\[\begin{align*} B&= \begin{bmatrix}4&-3\\-1&5\end{bmatrix}\\ \det(B)&= (4)(5)-(-1)(-3)\\ &= 20-3\\ &= 17 \end{align*}\]

Mali 3 inasema kwamba ikiwa safu mbili au nguzo mbili zinafanana, uamuzi huo ni sawa na sifuri.

\[\begin{align*} A&=\left[ \begin{array}{ccc|cc}1&2&2&1&2\\2&2&2&2&2\\-1&2&2&-1&2\end{array}\right]\\ \det(A)&=1(2)(2)+2(2)(-1)+2(2)(2)+1(2)(2)-2(2)(1)-2(2)(2)\\ &=4-4+8+4-4-8\\ &=0 \end{align*}\]

Mali 4 inasema kwamba kama mstari au safu ni sawa na sifuri, determinant sawa na sifuri. Hivyo,

\[\begin{align*} A&=\begin{bmatrix}1&2\\0&0\end{bmatrix}\\ \det(A)&=1(0)-2(0)\\ &=0 \end{align*}\]

Mali 5 inasema kwamba uamuzi wa tumbo la inverse\(A^{−1}\) ni usawa wa kuamua\(A\). Hivyo,

\[\begin{align*} A&=\begin{bmatrix}1&2\\3&4\end{bmatrix}\\ \det(A)&=1(4)-3(2)\\ &=-2 \end{align*}\]

\[\begin{align*} A^{-1}&=\begin{bmatrix}-2&1\\\dfrac{3}{2}&-\dfrac{1}{2}\end{bmatrix}\\ \det(A^{-1})&=-2\left(-\dfrac{1}{2}\right)-\dfrac{3}{2}(1)\\ &=-\dfrac{1}{2} \end{align*}\]

Mali 6 inasema kwamba ikiwa mstari wowote au safu ya tumbo huongezeka kwa mara kwa mara, uamuzi huongezeka kwa sababu sawa. Hivyo,

\[\begin{align*} A&=\begin{bmatrix}1&2\\3&4\end{bmatrix}\\ \det(A)&=1(4)-2(3)\\ &=-2 \end{align*}\]

\[\begin{align*} B&=\begin{bmatrix}2(1)&2(2)\\3&4\end{bmatrix}\\ \det(B)&=2(4)-3(4)\\ &=-4 \end{align*}\]

Mfano\(\PageIndex{7}\): Using Cramer’s Rule and Determinant Properties to Solve a System

Pata suluhisho la\(3 × 3\) mfumo uliopewa.

\[\begin{align} 2x+4y+4z&=2 \label{eq8}\\ 3x+7y+7z&=-5 \label{eq9}\\ x+2y+2z&=4 \label{eq10}\end{align}\]

Suluhisho

Kwa kutumia Cramer ya Utawala, tuna

\(D=\begin{bmatrix}2&4&4\\3&7&7\\1&2&2\end{bmatrix}\)

Angalia kwamba nguzo ya pili na ya tatu ni sawa. Kwa mujibu wa Mali 3, uamuzi utakuwa sifuri, kwa hiyo hakuna suluhisho au idadi isiyo na kipimo cha ufumbuzi. Tunapaswa kufanya uondoaji ili kujua.

1. Ongeza Equation\ ref {eq10}\(–2\) na kuongeza matokeo kwa Equation\ ref {eq8}.

\[\begin{align*} -2x-4y-4x&=-8\\ 2x+4y+4z&=2\\ 0&=-6 \end{align*}\]

Kupata taarifa ambayo ni utata ina maana kwamba mfumo hauna suluhisho.

vyombo vya habari

Kupata rasilimali hizi online kwa maelekezo ya ziada na mazoezi na Utawala Cramer ya.

• Tatua Mfumo wa milinganyo miwili Kutumia Utawala wa Cramer
• Kutatua Systems ya Equations Tatu kwa kutumia Utawala Cramer

Dhana muhimu

• Determinant kwa\(\begin{bmatrix}a&b\\c&d\end{bmatrix}\) ni\(ad−bc\). Angalia Mfano\(\PageIndex{1}\).
• Utawala wa Cramer hubadilisha safu ya kutofautiana na safu ya mara kwa mara. Ufumbuzi ni\(x=\dfrac{D_x}{D}\),\(y=\dfrac{D_y}{D}\). Angalia Mfano\(\PageIndex{2}\).
• Ili kupata uamuzi wa\(3×3\) tumbo, ongezeko na nguzo mbili za kwanza. Ongeza entries tatu za diagonal (juu kushoto kwenda chini kulia) na uondoe entries tatu za diagonal (chini kushoto kwenda juu kulia). Angalia Mfano\(\PageIndex{3}\).
• Ili kutatua mfumo wa milinganyo mitatu katika vigezo vitatu kwa kutumia Utawala wa Cramer, badala ya safu ya kutofautiana na safu ya mara kwa mara kwa kila suluhisho la taka:\(x=\dfrac{D_x}{D}\),\(y=\dfrac{D_y}{D}\),\(z=\dfrac{D_z}{D}\). Angalia Mfano\(\PageIndex{4}\).
• Utawala wa Cramer pia ni muhimu kwa kutafuta suluhisho la mfumo wa equations na hakuna suluhisho au ufumbuzi usio na mwisho. Angalia Mfano\(\PageIndex{5}\) na Mfano\(\PageIndex{6}\).
• Mali fulani ya kuamua ni muhimu kwa kutatua matatizo. Kwa mfano:
  • Ikiwa tumbo iko katika fomu ya juu ya triangular, uamuzi huo unafanana na bidhaa za kuingizwa chini ya diagonal kuu.
  • Wakati safu mbili zinabadilishana, ishara ya mabadiliko ya kuamua.
  • Ikiwa safu mbili au nguzo mbili zinafanana, uamuzi huo unafanana na sifuri.
  • Ikiwa tumbo lina safu ya zero au safu ya zero, uamuzi huo ni sawa na sifuri.
  • Uamuzi wa tumbo la inverse\(A^{−1}\) ni usawa wa uamuzi wa tumbo\(A\).
  • Ikiwa mstari wowote au safu huongezeka kwa mara kwa mara, uamuzi huongezeka kwa sababu sawa. Angalia Mfano\(\PageIndex{7}\) na Mfano\(\PageIndex{8}\).