13E: Kazi za Trigonometric (Mazoezi)

5.1: Pembe

Katika sehemu hii, tutachunguza mali ya pembe.

Maneno

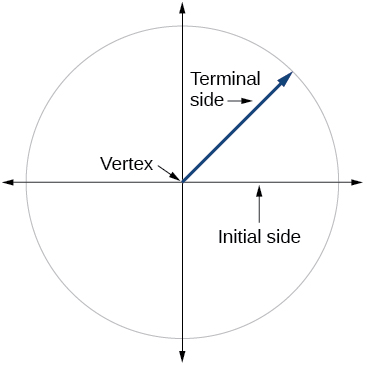
1) Chora angle katika nafasi ya kawaida. Weka kipeo, upande wa awali, na upande wa terminal.

Jibu

2) Eleza kwa nini kuna idadi isiyo na kipimo ya pembe ambazo ni coterminal kwa pembe fulani.

3) Eleza nini angle nzuri au hasi inaashiria, na kuelezea jinsi ya kuteka kila mmoja.

Jibu

Ikiwa angle ni chanya au hasi huamua mwelekeo. Pembe nzuri hutolewa katika mwelekeo wa kinyume chake, na angle hasi hutolewa katika mwelekeo wa saa.

4) Je, kipimo cha radian cha angle kinalinganishwa na kipimo cha shahada? Jumuisha maelezo ya$1$ radian katika aya yako.

5) Eleza tofauti kati ya kasi ya mstari na kasi ya angular wakati wa kuelezea mwendo kando ya njia ya mviringo.

Jibu

Kasi ya mstari ni kipimo kinachopatikana kwa kuhesabu umbali wa arc ikilinganishwa na wakati. Kasi ya angular ni kipimo kinachopatikana kwa kuhesabu angle ya arc ikilinganishwa na wakati.

Graphic

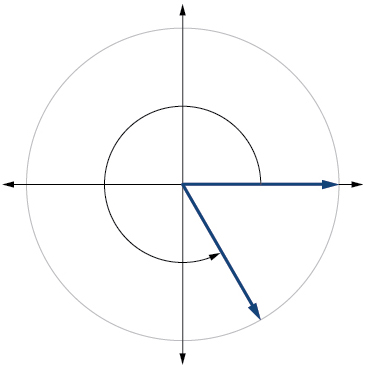
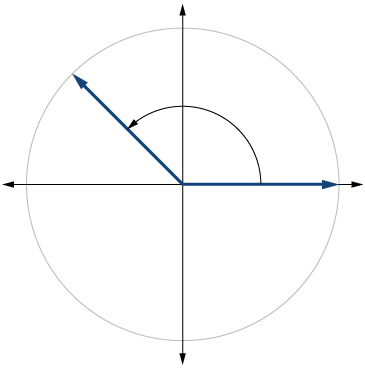
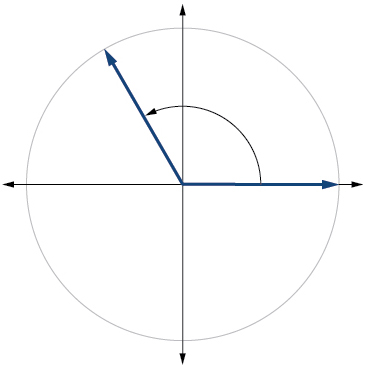
Kwa mazoezi 6-21, futa angle katika nafasi ya kawaida na kipimo kilichopewa.

6)$30^{\circ}$

7)$300^{\circ}$

Jibu

8)$-80^{\circ}$

9)$135^{\circ}$

Jibu

10)$-150^{\circ}$

11)$\dfrac{2π}{3}$

Jibu

12)$\dfrac{7π}{4}$

13)$\dfrac{5π}{6}$

Jibu

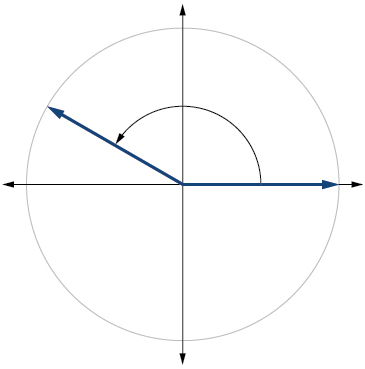
14)$\dfrac{π}{2}$

15)$−\dfrac{π}{10}$

Jibu

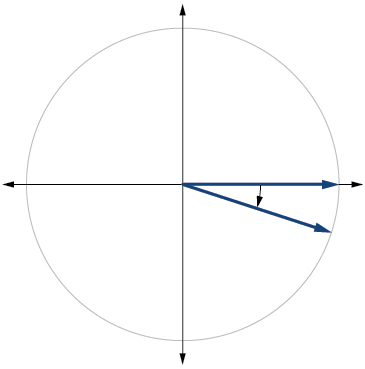
16)$415^{\circ}$

17)$-120^{\circ}$

Jibu

$240^{\circ}$

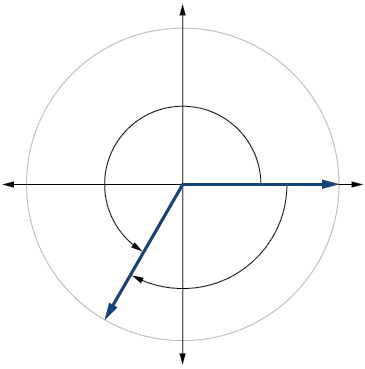
18)$-315^{\circ}$

19)$\dfrac{22π}{3}$

Jibu

$\dfrac{4π}{3}$

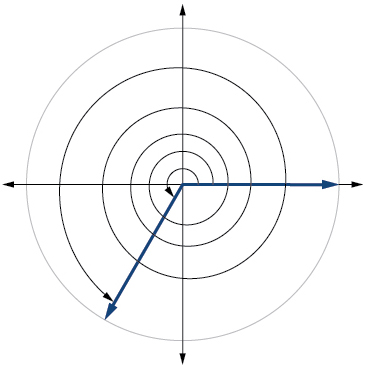
20)$−\dfrac{π}{6}$

21)$−\dfrac{4π}{3}$

Jibu

$\dfrac{2π}{3}$

Kwa mazoezi 22-23, rejea Kielelezo hapa chini. Pande zote kwa maeneo mawili ya decimal.

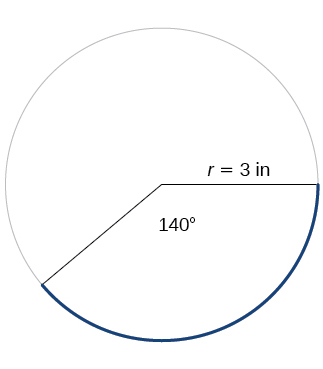
22) Pata urefu wa arc.

23) Pata eneo la sekta hiyo.

Jibu

$\dfrac{27π}{2}≈11.00 \text{ in}^2$

Kwa mazoezi 24-25, rejea Kielelezo hapa chini. Pande zote kwa maeneo mawili ya decimal.

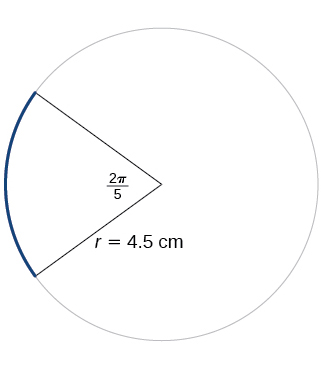
24) Pata urefu wa arc.

25) Pata eneo la sekta hiyo.

Jibu

$\dfrac{81π}{20}≈12.72\text{ cm}^2$

Kialjebra

Kwa mazoezi 26-32, kubadilisha pembe katika radians kwa digrii.

26)$\dfrac{3π}{4}$ radians

27)$\dfrac{π}{9}$ radians

Jibu

$20^{\circ}$

28)$−\dfrac{5π}{4}$ radians

29)$\dfrac{π}{3}$ radians

Jibu

$60^{\circ}$

30)$−\dfrac{7π}{3}$ radians

31)$−\dfrac{5π}{12}$ radians

Jibu

$-75^{\circ}$

32)$\dfrac{11π}{6}$ radians

Kwa mazoezi 33-39, kubadilisha pembe kwa digrii kwa radians.

33)$90^{\circ}$

Jibu

$\dfrac{π}{2}$radiani

34)$100^{\circ}$

35)$-540^{\circ}$

Jibu

$−3π$radiani

36)$-120^{\circ}$

37)$180^{\circ}$

Jibu

$π$radiani

38)$-315^{\circ}$

39)$150^{\circ}$

Jibu

$\dfrac{5π}{6}$radiani

Kwa mazoezi 40-45, tumia taarifa iliyotolewa ili kupata urefu wa arc mviringo. Pande zote kwa maeneo mawili ya decimal.

40) Pata urefu wa arc ya mduara wa$12$ inchi za radius zinazotengwa na angle ya kati ya$\dfrac{π}{4}$ radians.

41) Kupata urefu wa safu ya mduara wa$5.02$ maili Radius subtended na angle ya kati ya$\dfrac{π}{3}$.

Jibu

$\dfrac{5.02π}{3}≈5.26$maili

42) Kupata urefu wa arc ya mduara wa$14$ mita kipenyo subtended na angle ya kati ya$\dfrac{5\pi }{6}$.

43) Kupata urefu wa safu ya mduara wa$10$ sentimita radius subtended na angle ya kati ya$50^{\circ}$.

Jibu

$\dfrac{25π}{9}≈8.73$sentimita

44) Kupata urefu wa safu ya mduara wa$5$ inchi Radius subtended na angle ya kati ya$220^{circ}$.

45) Kupata urefu wa arc ya mduara wa$12$ mita kipenyo subtended na angle ya kati ni$63^{circ}$.

Jibu

$\dfrac{21π}{10}≈6.60$mita

Kwa mazoezi 46-49, tumia taarifa iliyotolewa ili kupata eneo la sekta hiyo. Pande zote hadi sehemu nne za decimal.

46) Sekta ya mduara ina pembe ya kati ya$45^{\circ}$ na$6$ cm ya radius.

47) Sekta ya mduara ina pembe ya kati$30^{\circ}$ na radius ya$20$ cm.

Jibu

$104.7198\; cm^2$

48) Sekta ya mduara na$10$ miguu ya kipenyo na angle ya$\dfrac{π}{2}$ radians.

49) Sekta ya mduara na radius ya$0.7$ inchi na angle ya$π$ radians.

Jibu

$0.7697\; in^2$

Kwa mazoezi 50-53, pata angle kati$0^{\circ}$ na$360^{\circ}$ hiyo ni coterminal kwa angle iliyotolewa.

50)$-40^{\circ}$

51)$-110^{\circ}$

Jibu

$250^{\circ}$

52)$700^{\circ}$

53)$1400^{\circ}$

Jibu

$320^{\circ}$

Kwa mazoezi 54-57, pata angle kati$0$ na$2\pi$ katika radians ambayo ni coterminal kwa angle iliyotolewa.

54)$−\dfrac{π}{9}$

55)$\dfrac{10π}{3}$

Jibu

$\dfrac{4π}{3}$

56)$\dfrac{13π}{6}$

57)$\dfrac{44π}{9}$

Jibu

$\dfrac{8π}{9}$

Real-World Matumizi

58) Lori yenye magurudumu$32$ -inch kipenyo ni kusafiri saa$60$ mi/h Kupata kasi ya angular ya magurudumu katika rad/min. Je, magurudumu hufanya mapinduzi ngapi kwa dakika?

59) Baiskeli na magurudumu$24$ -inch kipenyo ni kusafiri saa$15$ mi/h Kupata kasi angular ya magurudumu katika rad/min. Je, magurudumu hufanya mapinduzi ngapi kwa dakika?

Jibu

$1320$rad$210.085$ RPM

60) Gurudumu la$8$ inchi za radius linazunguka$15^{\circ}/s$. Je, ni kasi ya mstari$v$, kasi ya angular katika RPM, na kasi ya angular katika rad/s?

61) Gurudumu la$14$ inchi za radius linazunguka$0.5 \text{rad/s}$. Je, ni kasi ya mstari$v$, kasi ya angular katika RPM, na kasi ya angular katika deg/s?

Jibu

$7$katika. /s,$4.77$ RPM,$28.65$ deg/s

62) CD ina kipenyo cha$120$ milimita. Wakati wa kucheza sauti, kasi ya angular inatofautiana ili kuweka kasi ya mstari mara kwa mara ambapo diski inasomwa. Wakati wa kusoma kando ya makali ya nje ya disc, kasi ya angular ni kuhusu$200$ RPM (mapinduzi kwa dakika). Pata kasi ya mstari.

63) Wakati wa kuchomwa moto kwenye gari la CD-R lililoandikwa, kasi ya angular ya CD mara nyingi ni kasi zaidi kuliko wakati wa kucheza sauti, lakini kasi ya angular bado inatofautiana ili kuweka kasi ya mstari mara kwa mara ambapo diski imeandikwa. Wakati wa kuandika kando ya makali ya nje ya disc, kasi ya angular ya gari moja ni kuhusu$4800$ RPM (mapinduzi kwa dakika). Pata kasi ya mstari ikiwa CD ina kipenyo cha$120$ milimita.

Jibu

$1,809,557.37 \text{ mm/min}=30.16 \text{ m/s}$

64) Mtu amesimama kwenye ikweta ya Dunia ($3960$maili ya radius). Je! Ni kasi gani ya mstari na ya angular?

65) Pata umbali pamoja na arc juu ya uso wa Dunia ambayo hupunguza pembe ya kati ya$5$ dakika$(1 \text{ minute}=\dfrac{1}{60} \text{ degree})$. Radi ya Dunia ni$3960$ maili.

Jibu

$5.76$maili

66) Pata umbali pamoja na arc juu ya uso wa Dunia ambayo hupunguza pembe ya kati ya$7$ dakika$(1 \text{ minute}=\dfrac{1}{60} \text{ degree})$. Radi ya Dunia ni$3960$ maili.

67) Fikiria saa na mkono wa saa na mkono wa dakika. Je! Ni kipimo gani cha angle ya dakika ya mkono wa$20$ dakika kwa dakika?

Jibu

$120°$

Upanuzi

68) Miji miwili ina longitude sawa. Latitude ya mji A ni$9.00$ digrii kaskazini na latitude ya mji B ni$30.00$ shahada kaskazini. Tuseme radius ya dunia ni$3960$ maili. Kupata umbali kati ya miji miwili.

69) Mji iko katika$40$ digrii kaskazini latitude. Fikiria radius ya dunia ni$3960$ maili na dunia inazunguka mara moja kila$24$ saa. Pata kasi ya mstari wa mtu anayeishi katika mji huu.

Jibu

$794$maili kwa saa

70) mji iko katika$75$ digrii kaskazini latitude. Fikiria radius ya dunia ni$3960$ maili na dunia inazunguka mara moja kila$24$ saa. Pata kasi ya mstari wa mtu anayeishi katika mji huu.

71) Pata kasi ya mstari wa mwezi ikiwa umbali wa wastani kati ya dunia na mwezi ni$239,000$ maili, kuchukua obiti ya mwezi ni mviringo na inahitaji kuhusu$28$ siku. Express jibu katika maili kwa saa.

Jibu

$2,234$maili kwa saa

72) Baiskeli ina magurudumu$28$ inchi katika kipenyo. Tachometer huamua kwamba magurudumu yanazunguka kwenye$180$ RPM (mapinduzi kwa dakika). Find kasi ya baiskeli ni kusafiri barabarani.

73) gari husafiri$3$ maili. Matairi yake hufanya$2640$ mapinduzi. Je, ni radius ya tairi katika inchi?

Jibu

$11.5$inchi

74) Gurudumu kwenye trekta ina kipenyo cha$24$ inchi. Je, gurudumu hufanya mapinduzi ngapi ikiwa trekta husafiri$4$ maili?

5.2: Mzunguko wa Kitengo - Kazi za Sine na Cosine

Maneno

1) Eleza mduara wa kitengo.

Jibu

Mduara wa kitengo ni mduara wa radius$1$ unaozingatia asili.

2) Je,$x$ - na$y$ -kuratibu ya pointi kwenye mduara wa kitengo inawakilisha nini?

3) Jadili tofauti kati ya angle ya coterminal na angle ya kumbukumbu.

Jibu

Pembe za Coterminal ni pembe zinazoshiriki upande huo wa terminal. Angle ya kumbukumbu ni ukubwa wa angle ndogo zaidi$t$, iliyoundwa na upande wa mwisho wa angle$t$ na mhimili usio na usawa.

4) Eleza jinsi cosine ya angle katika quadrant ya pili inatofautiana na cosine ya angle yake ya kumbukumbu katika mduara wa kitengo.

5) Eleza jinsi sine ya angle katika quadrant ya pili inatofautiana na sine ya angle yake ya kumbukumbu katika mduara wa kitengo.

Jibu

Maadili ya sine ni sawa.

Kialjebra

Kwa mazoezi 6-9, tumia ishara iliyotolewa ya kazi za sine na cosine ili kupata quadrant ambayo hatua ya mwisho imedhamiriwa na$t$ uongo.

6)$\sin (t)<0$ na$\cos (t)<0$

7)$\sin (t)>0$ na$\cos (t)>0$

Jibu

$\textrm{I}$

8)$\sin (t)>0$ na$\cos (t)<0$

9)$\sin (t)<0$ na$\cos (t)>0$

Jibu

$\textrm{IV}$

Kwa mazoezi 10-22, pata thamani halisi ya kila kazi ya trigonometric.

10)$\sin \dfrac{π}{2}$

11)$\sin \dfrac{π}{3}$

Jibu

$\dfrac{\sqrt{3}}{2}$

12)$\cos \dfrac{π}{2}$

13)$\cos \dfrac{π}{3}$

Jibu

$\dfrac{1}{2}$

14)$\sin \dfrac{π}{4}$

15)$\cos \dfrac{π}{4}$

Jibu

$\dfrac{\sqrt{2}}{2}$

16)$\sin \dfrac{π}{6}$

17)$\sin π$

Jibu

$0$

18)$\sin \dfrac{3π}{2}$

19)$\cos π$

Jibu

$−1$

20)$\cos 0$

21)$cos \dfrac{π}{6}$

Jibu

$\dfrac{\sqrt{3}}{2}$

22)$\sin 0$

Numeric

Kwa mazoezi 23-33, sema angle ya kumbukumbu kwa angle iliyotolewa.

23)$240°$

Jibu

$60°$

24)$−170°$

25)$100°$

Jibu

$80°$

26)$−315°$

27)$135°$

Jibu

$45°$

28)$\dfrac{5π}{4}$

29)$\dfrac{2π}{3}$

Jibu

$\dfrac{π}{3}$

30)$\dfrac{5π}{6}$

31)$−\dfrac{11π}{3}$

Jibu

$\dfrac{π}{3}$

32)$\dfrac{−7π}{4}$

33)$\dfrac{−π}{8}$

Jibu

$\dfrac{π}{8}$

Kwa mazoezi 34-49, tafuta angle ya kumbukumbu, quadrant ya upande wa terminal, na sine na cosine ya kila angle. Ikiwa angle sio moja ya pembe kwenye mduara wa kitengo, tumia calculator na pande zote hadi sehemu tatu za decimal.

34)$225°$

35)$300°$

Jibu

$60°$, Quadrant IV,$\sin (300°)=−\dfrac{\sqrt{3}}{2}, \cos (300°)=\dfrac{1}{2}$

36)$320°$

37)$135°$

Jibu

$45°$, Quadrant II,$\sin (135°)=\dfrac{\sqrt{2}}{2}, \cos (135°)=−\dfrac{\sqrt{2}}{2}$

38)$210°$

39)$120°$

Jibu

$60°$, Quadrant II$\sin (120°)=\dfrac{\sqrt{3}}{2}$,$\cos (120°)=−\dfrac{1}{2}$

40)$250°$

41)$150°$

Jibu

$30°$, Quadrant II$\sin (150°)=\frac{1}{2}$,$\cos(150°)=−\dfrac{\sqrt{3}}{2}$

42)$\dfrac{5π}{4}$

43)$\dfrac{7π}{6}$

Jibu

$\dfrac{π}{6}$, Quadrant III$\sin \left( \dfrac{7π}{6}\right )=−\dfrac{1}{2}$,$\cos \left (\dfrac{7π}{6} \right)=−\dfrac{\sqrt{3}}{2}$

44)$\dfrac{5π}{3}$

45)$\dfrac{3π}{4}$

Jibu

$\dfrac{π}{4}$, Quadrant II$\sin \left(\dfrac{3π}{4}\right)=\dfrac{\sqrt{2}}{2}$,$\cos\left(\dfrac{4π}{3}\right)=−\dfrac{\sqrt{2}}{2}$

46)$\dfrac{4π}{3}$

47)$\dfrac{2π}{3}$

Jibu

$\dfrac{π}{3}$, Quadrant II$\sin \left(\dfrac{2π}{3}\right)=\dfrac{\sqrt{3}}{2}$,$\cos \left(\dfrac{2π}{3}\right)=−\dfrac{1}{2}$

48)$\dfrac{5π}{6}$

49)$\dfrac{7π}{4}$

Jibu

$\dfrac{π}{4}$, Quadrant IV$\sin \left(\dfrac{7π}{4}\right)=−\dfrac{\sqrt{2}}{2}$,$\cos \left(\dfrac{7π}{4}\right)=\dfrac{\sqrt{2}}{2}$

Kwa mazoezi 50-59, pata thamani iliyoombwa.

50) Ikiwa$\cos (t)=\dfrac{1}{7}$ na$t$ iko katika$4^{th}$ roboduara, tafuta$\sin (t)$.

51) Ikiwa$\cos (t)=\dfrac{2}{9}$ na$t$ iko katika$1^{st}$ roboduara, tafuta$\sin (t)$.

Jibu

$\dfrac{\sqrt{77}}{9}$

52) Ikiwa$\sin (t)=\dfrac{3}{8}$ na$t$ iko katika$2^{nd}$ roboduara, tafuta$\cos (t)$.

53) Ikiwa$\sin (t)=−\dfrac{1}{4}$ na$t$ iko katika$3^{rd}$ roboduara, tafuta$\cos (t)$.

Jibu

$−\dfrac{\sqrt{15}}{4}$

54) Kupata kuratibu ya uhakika juu ya mduara na Radius$15$ sambamba na angle ya$220°$.

55) Kupata kuratibu ya uhakika juu ya mduara na Radius$20$ sambamba na angle ya$120°$.

Jibu

$(−10,10\sqrt{3})$

56) Kupata kuratibu ya uhakika juu ya mduara na Radius$8$ sambamba na angle ya$\dfrac{7π}{4}$.

57) Kupata kuratibu ya uhakika juu ya mduara na Radius$16$ sambamba na angle ya$\dfrac{5π}{9}$.

Jibu

$(–2.778,15.757)$

58) Weka uwanja wa kazi za sine na cosine.

59) Weka aina mbalimbali za kazi za sine na cosine.

Jibu

$[–1,1]$

Graphic

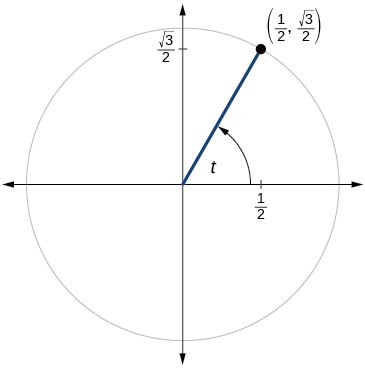
Kwa mazoezi 60-79, tumia hatua iliyotolewa kwenye mduara wa kitengo ili kupata thamani ya sine na cosine ya$t$.

60)

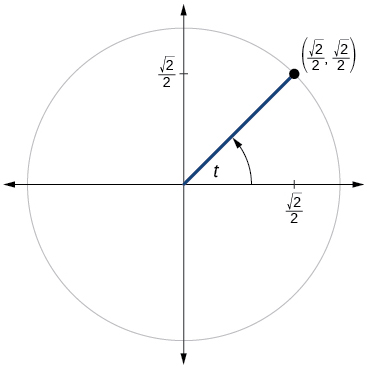
61)

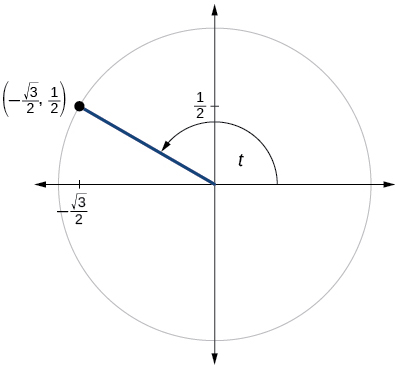
Jibu

$\sin t=\dfrac{1}{2}, \cos t=−\dfrac{\sqrt{3}}{2}$

62)

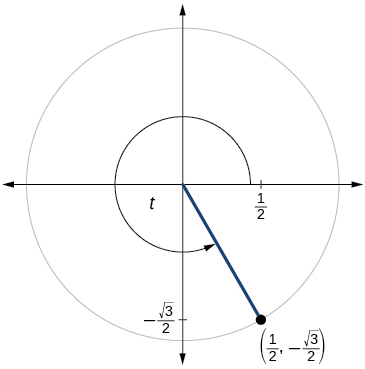
63)

Jibu

$\sin t=− \dfrac{\sqrt{2}}{2}, \cos t=−\dfrac{\sqrt{2}}{2}$

64)

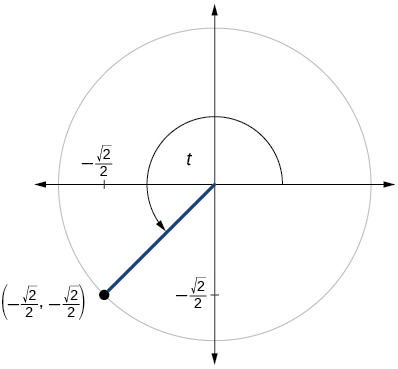
65)

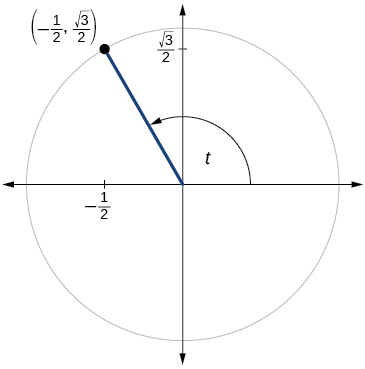
Jibu

$\sin t=\dfrac{\sqrt{3}}{2},\cos t=−\dfrac{1}{2}$

66)

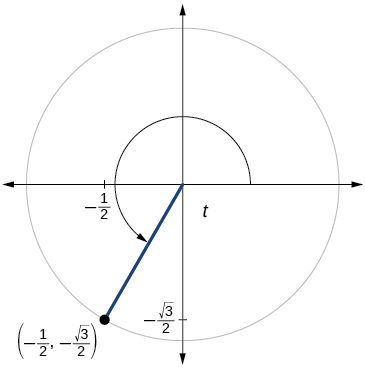
67)

Jibu

$\sin t=− \dfrac{\sqrt{2}}{2}, \cos t=\dfrac{\sqrt{2}}{2}$

68)

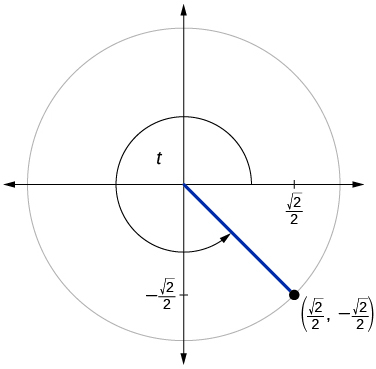
69)

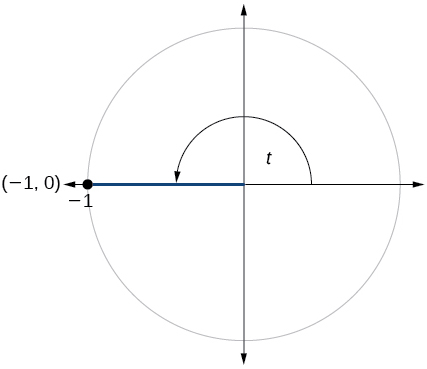
Jibu

$\sin t=0, \cos t=−1$

70)

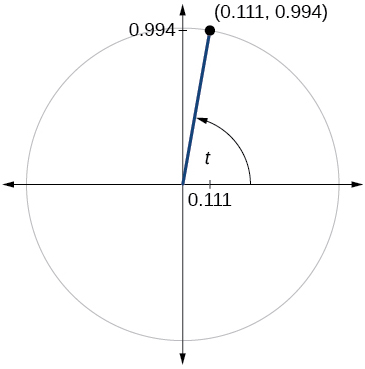
71)

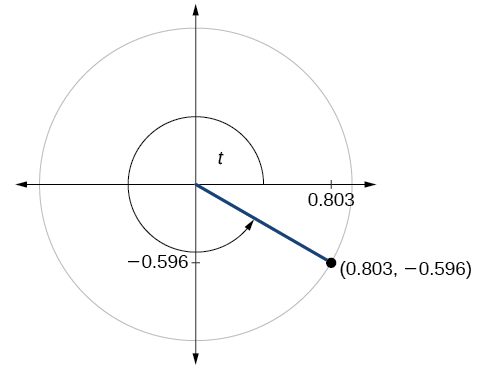
Jibu

$\sin t=−0.596, \cos t=0.803$

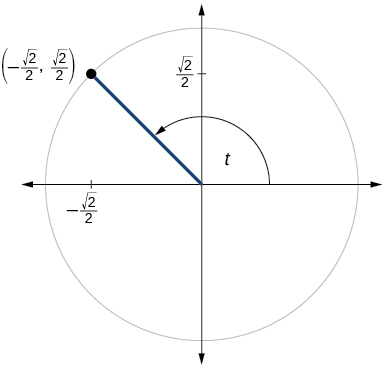
72)

73)

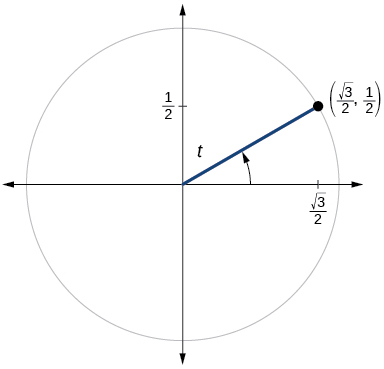
Jibu

$\sin t=\dfrac{1}{2}, \cos t= \dfrac{\sqrt{3}}{2}$

74)

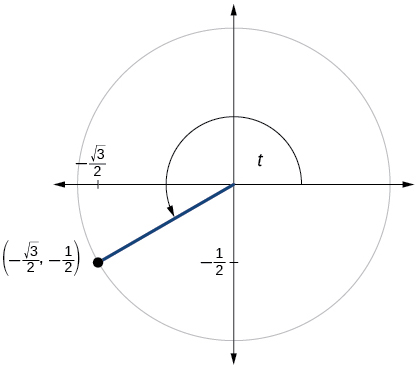
75)

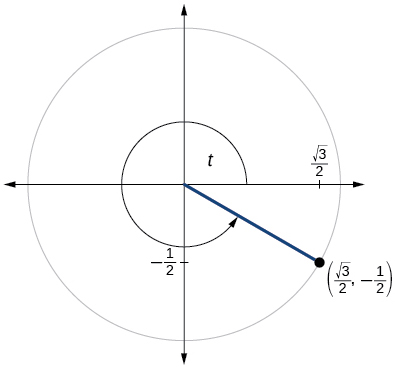
Jibu

$\sin t=−\dfrac{1}{2}, \cos t= \dfrac{\sqrt{3}}{2}$

76)

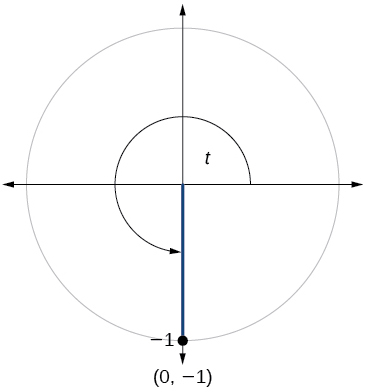
77)

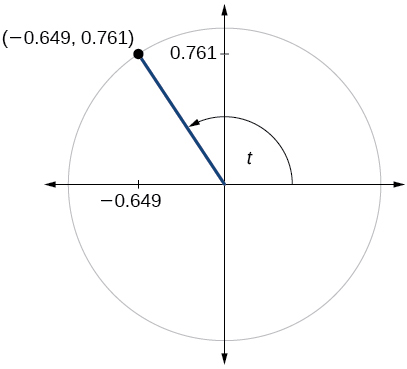
Jibu

$\sin t=0.761, \cos t=−0.649$

78)

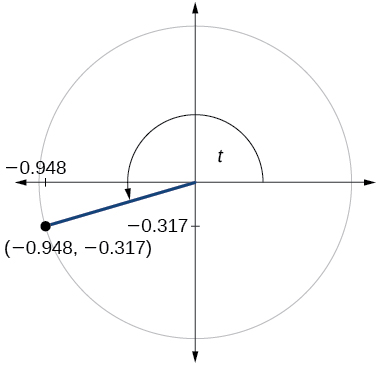
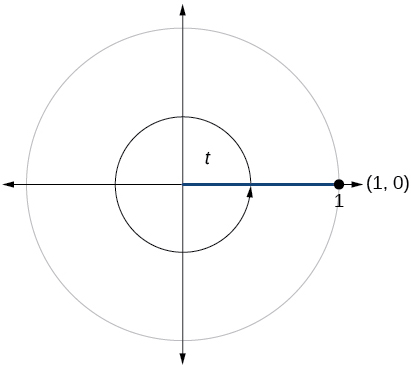
79)

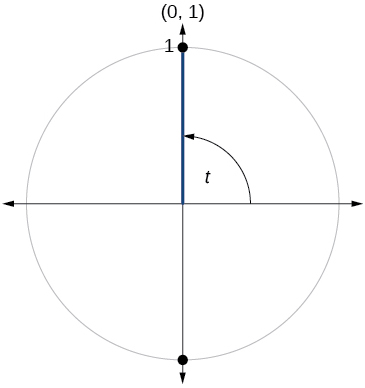
Jibu

$\sin t=1, \cos t=0$

Teknolojia

Kwa mazoezi 80-89, tumia calculator ya graphing kutathmini.

80)$\sin \dfrac{5π}{9}$

81)$cos \dfrac{5π}{9}$

Jibu

$−0.1736$

82)$\sin \dfrac{π}{10}$

83)$\cos \dfrac{π}{10}$

Jibu

$0.9511$

84)$\sin \dfrac{3π}{4}$

85)$\cos \dfrac{3π}{4}$

Jibu

$−0.7071$

86)$\sin 98°$

87)$\cos 98°$

Jibu

$−0.1392$

88)$\cos 310°$

89)$\sin 310°$

Jibu

$−0.7660$

Upanuzi

Kwa mazoezi 90-99, tathmini.

90)$\sin \left(\dfrac{11π}{3}\right) \cos \left(\dfrac{−5π}{6}\right)$

91)$\sin \left(\dfrac{3π}{4}\right) \cos \left(\dfrac{5π}{3}\right)$

Jibu

$\dfrac{\sqrt{2}}{4}$

92)$\sin \left(− \dfrac{4π}{3}\right) \cos \left(\dfrac{π}{2}\right)$

93)$\sin \left(\dfrac{−9π}{4}\right) \cos \left(\dfrac{−π}{6}\right)$

Jibu

$−\dfrac{\sqrt{6}}{4}$

94)$\sin \left(\dfrac{π}{6}\right) \cos \left(\dfrac{−π}{3}\right)$

95)$\sin \left(\dfrac{7π}{4}\right) \cos \left(\dfrac{−2π}{3}\right)$

Jibu

$\dfrac{\sqrt{2}}{4}$

96)$\cos \left(\dfrac{5π}{6}\right) \cos \left(\dfrac{2π}{3}\right)$

97)$\cos \left(\dfrac{−π}{3}\right) \cos \left(\dfrac{π}{4}\right)$

Jibu

$\dfrac{\sqrt{2}}{4}$

98)$\sin \left(\dfrac{−5π}{4}\right) \sin \left(\dfrac{11π}{6}\right)$

99)$\sin (π) \sin \left(\dfrac{π}{6}\right)$

Jibu

$0$

Real-World Matumizi

Kwa mazoezi 100-104, tumia hali hii: Mtoto huingia kwenye jukwa ambalo linachukua dakika moja ili kuzunguka mara moja. Mtoto huingia kwenye hatua$(0,1)$ hiyo, yaani, kwenye nafasi ya kaskazini. Tuseme jukwa inahusu counter clockwise.

100) Je, ni kuratibu gani za mtoto baada ya$45$ sekunde?

101) Je, ni kuratibu gani za mtoto baada ya$90$ sekunde?

Jibu

$(0,–1)$

102) Je, ni kuratibu gani za mtoto baada ya$125$ sekunde?

103) Mtoto atakuwa na kuratibu lini$(0.707,–0.707)$ ikiwa safari inakaribia$6$ dakika? (Kuna majibu mengi.)

Jibu

$37.5$sekunde,$97.5$$157.5$ sekunde,$217.5$ sekunde,$277.5$ sekunde,$337.5$ sekunde

104) Mtoto atakuwa na kuratibu lini$(−0.866,−0.5)$ ikiwa safari ya$6$ dakika ya mwisho?

5.3: Kazi nyingine za Trigonometric

Maneno

1) Katika muda wa$[ 0,2π )$, Je, maadili ya sine na cosine ya kipimo cha radian milele kuwa sawa? Ikiwa ndivyo, wapi?

Jibu

Ndiyo, wakati angle ya kumbukumbu ni$\dfrac{π}{4}$ na upande wa mwisho wa angle iko katika quadrants I na III. Hivyo, katika$x=\dfrac{π}{4},\dfrac{5π}{4}$, maadili ya sine na cosine ni sawa.

2) Je! Unakadiria nini cosine ya$\pi$ digrii kuwa? Eleza hoja zako.

3) Kwa pembe yoyote katika quadrant II, ikiwa ulijua sine ya angle, unawezaje kuamua cosine ya angle?

Jibu

Kuweka sine ya angle$y$ katika kwa Theorem ya Pythagorean$x^2+y^2=1$. Tatua$x$ na kuchukua suluhisho hasi.

4) Eleza kazi ya secant.

5) Tangent na cotangent na kipindi cha$π$. Hii inatuambia nini kuhusu pato la kazi hizi?

Jibu

Matokeo ya tangent na cotangent itarudia kila$π$ vitengo.

Kialjebra

Kwa mazoezi 6-17, pata thamani halisi ya kila kujieleza.

6)$\tan \dfrac{π}{6}$

7)$\sec \dfrac{π}{6}$

Jibu

$\dfrac{2\sqrt{3}}{3}$

8)$\csc \dfrac{π}{6}$

9)$\cot \dfrac{π}{6}$

Jibu

$\sqrt{3}$

10)$\tan \dfrac{π}{4}$

11)$\sec \dfrac{π}{4}$

Jibu

$\sqrt{2}$

12)$\csc \dfrac{π}{4}$

13)$\cot \dfrac{π}{4}$

Jibu

$1$

14)$\tan \dfrac{π}{3}$

15)$\sec \dfrac{π}{3}$

Jibu

$2$

16)$\csc \dfrac{π}{3}$

17)$\cot \dfrac{π}{3}$

Jibu

$\dfrac{\sqrt{3}}{3}$

Kwa mazoezi 18-48, tumia pembe za kumbukumbu ili kutathmini maneno.

18)$\tan \dfrac{5π}{6}$

19)$\sec \dfrac{7π}{6}$

Jibu

$−\dfrac{2\sqrt{3}}{3}$

20)$\csc \dfrac{11π}{6}$

21)$\cot \dfrac{13π}{6}$

Jibu

$\sqrt{3}$

22)$\tan \dfrac{7π}{4}$

23)$\sec \dfrac{3π}{4}$

Jibu

$−\sqrt{2}$

24)$\csc \dfrac{5π}{4}$

25)$\cot \dfrac{11π}{4}$

Jibu

$−1$

26)$\tan \dfrac{8π}{3}$

27)$\sec \dfrac{4π}{3}$

Jibu

$−2$

28)$\csc \dfrac{2π}{3}$

29)$\cot \dfrac{5π}{3}$

Jibu

$−\dfrac{\sqrt{3}}{3}$

30)$\tan 225°$

31)$\sec 300°$

Jibu

$2$

32)$\csc 150°$

33)$\cot 240°$

Jibu

$\dfrac{\sqrt{3}}{3}$

34)$\tan 330°$

35)$\sec 120°$

Jibu

$−2$

36)$\csc 210°$

37)$\cot 315°$

Jibu

$−1$

38) Kama$\sin t= \dfrac{3}{4}$, na$t$ ni katika roboduara II, kupata$\cos t, \sec t, \csc t, \tan t, \cot t$.

39) Ikiwa$\cos t=−\dfrac{1}{3},$ na$t$ iko katika quadrant III, tafuta$\sin t, \sec t, \csc t, \tan t, \cot t$.

Jibu

Kama$\sin t=−\dfrac{2\sqrt{2}}{3}, \sec t=−3, \csc t=−\csc t=−\dfrac{3\sqrt{2}}{4},\tan t=2\sqrt{2}, \cot t= \dfrac{\sqrt{2}}{4}$

40) Kama$\tan t=\dfrac{12}{5},$ na$0≤t< \dfrac{π}{2}$, kupata$\sin t, \cos t, \sec t, \csc t,$ na$\cot t$.

41) Kama$\sin t= \dfrac{\sqrt{3}}{2}$ na$\cos t=\dfrac{1}{2},$ kupata$\sec t, \csc t, \tan t,$ na$\cot t$.

Jibu

$\sec t=2, \csc t=\csc t=\dfrac{2\sqrt{3}}{3}, \tan t= \sqrt{3}, \cot t= \dfrac{\sqrt{3}}{3}$

42) Kama$\sin 40°≈0.643 \; \cos 40°≈0.766 \; \sec 40°,\csc 40°,\tan 40°, \text{ and } \cot 40°$.

43) Kama ni$\sin t= \dfrac{\sqrt{2}}{2},$ nini$\sin (−t)$?

Jibu

$−\dfrac{\sqrt{2}}{2}$

44) Kama ni$\cos t= \dfrac{1}{2},$ nini$\cos (−t)$?

45) Kama ni$\sec t=3.1,$ nini$\sec (−t)$?

Jibu

$3.1$

46) Kama ni$\csc t=0.34,$ nini$\csc (−t)$?

47) Kama ni$\tan t=−1.4,$ nini$\tan (−t)$?

Jibu

$1.4$

48) Kama ni$\cot t=9.23,$ nini$\cot (−t)$?

Graphic

Kwa mazoezi 49-51, tumia angle katika mduara wa kitengo ili kupata thamani ya kila kazi sita za trigonometric.

49)

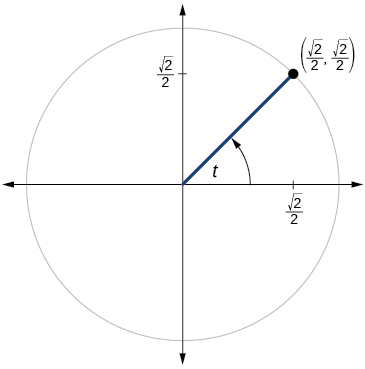
Jibu

$\sin t= \dfrac{\sqrt{2}}{2}, \cos t= \dfrac{\sqrt{2}}{2}, \tan t=1,\cot t=1,\sec t= \sqrt{2}, \csc t= \csc t= \sqrt{2}$

50)

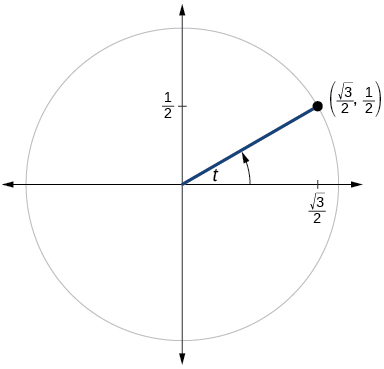
51)

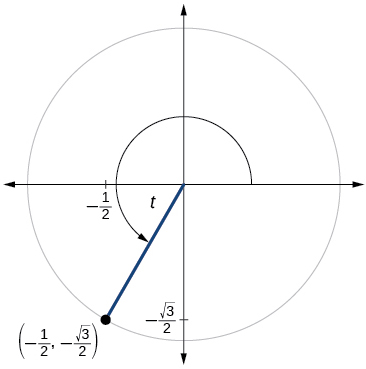
Jibu

$\sin t=−\dfrac{\sqrt{3}}{2}, \cos t=−\dfrac{1}{2}, \tan t=\sqrt{3}, \cot t= \dfrac{\sqrt{3}}{3}, \sec t=−2, \csc t=−\csc t=−\dfrac{2\sqrt{3}}{3}$

Teknolojia

Kwa mazoezi 52-61, tumia calculator ya graphing kutathmini.

52)$\csc \dfrac{5π}{9}$

53)$\cot \dfrac{4π}{7}$

Jibu

$–0.228$

54)$\sec \dfrac{π}{10}$

55)$\tan \dfrac{5π}{8}$

Jibu

$–2.414$

56)$\sec \dfrac{3π}{4}$

57)$\csc \dfrac{π}{4}$

Jibu

$1.414$

58)$\tan 98°$

59)$\cot 33°$

Jibu

$1.540$

60)$\cot 140°$

61)$\sec 310°$

Jibu

$1.556$

Upanuzi

Kwa mazoezi 62-69, tumia utambulisho kutathmini maneno.

62) Kama$\tan (t)≈2.7,$ na$\sin (t)≈0.94,$ kupata$\cos (t)$.

63) Kama$\tan (t)≈1.3,$ na$\cos (t)≈0.61$, kupata$\sin (t)$.

Jibu

$\sin (t)≈0.79$

64) Kama$\csc (t)≈3.2,$$\csc (t)≈3.2,$ na$\cos (t)≈0.95,$ kupata$\tan (t)$.

65) Kama$\cot (t)≈0.58,$ na$\cos (t)≈0.5,$ kupata$\csc (t)$.

Jibu

$\csc (t)≈1.16$

66) Kuamua kama kazi$f(x)=2 \sin x \cos x$ ni hata, isiyo ya kawaida, au wala.

67) Kuamua kama kazi$f(x)=3 \sin ^2 x \cos x + \sec x$ ni hata, isiyo ya kawaida, au wala.

Jibu

hata

68) Kuamua kama kazi$f(x)= \sin x −2 \cos ^2 x$ ni hata, isiyo ya kawaida, au wala.

69) Kuamua kama kazi$f(x)= \csc ^2 x+ \sec x$ ni hata, isiyo ya kawaida, au wala.

Jibu

hata

Kwa mazoezi 70-71, tumia utambulisho ili kurahisisha maneno.

70)$\csc t \tan t$

71)$\dfrac{\sec t}{ \csc t}$

Jibu

$\dfrac{ \sin t}{ \cos t}= \tan t$

Real-World Matumizi

72) Kiasi cha jua katika mji fulani kinaweza kuonyeshwa na kazi$h=15 \cos \left(\dfrac{1}{600}d\right),$ ambapo$h$ inawakilisha masaa ya jua, na$d$ ni siku ya mwaka. Tumia equation ili kupata masaa ngapi ya jua kuna Februari 10,$42^{nd}$ siku ya mwaka. Eleza kipindi cha kazi.

73) Kiasi cha jua katika mji fulani kinaweza kuonyeshwa na kazi$h=16 \cos \left(\dfrac{1}{500}d\right)$, ambapo$h$ inawakilisha masaa ya jua, na$d$ ni siku ya mwaka. Tumia equation ili kupata masaa ngapi ya jua kuna mnamo Septemba 24,$267^{th}$ siku ya mwaka. Eleza kipindi cha kazi.

Jibu

$13.77$masaa, kipindi:$1000π$

74) Equation$P=20 \sin (2πt)+100$ mifano ya shinikizo la damu,$P$, ambapo$t$ inawakilisha muda katika sekunde.

1. Pata shinikizo la damu baada ya$15$ sekunde.
2. Je! Ni shinikizo la juu na la chini la damu?

75) Urefu wa pistoni$h$, kwa inchi, unaweza kuonyeshwa na equation$y=2 \cos x+6,$ ambapo$x$ inawakilisha angle ya crank. Kupata urefu wa pistoni wakati angle crank ni$55°$.

Jibu

$7.73$inchi

76) Urefu wa pistoni$h$, kwa inchi, unaweza kuonyeshwa na equation$y=2 \cos x+5,$ ambapo$x$ inawakilisha angle ya crank. Kupata urefu wa pistoni wakati angle crank ni$55°$.

5.4: Trigonometry ya Triangle ya kulia

Maneno

1) Kwa pembetatu iliyotolewa, lebo upande wa karibu, upande wa pili, na hypotenuse kwa angle iliyoonyeshwa.

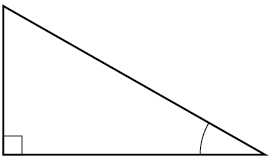
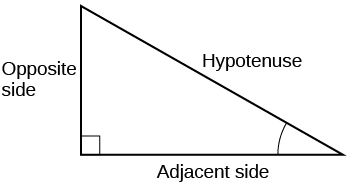
Jibu

2) Wakati pembetatu sahihi na hypotenuse ya$1$ imewekwa kwenye mduara wa kitengo, ni pande gani za pembetatu zinazohusiana na$x$ - na$y$ -kuratibu?

3) Tangent ya angle inalinganisha pande gani za pembetatu sahihi?

Jibu

Tangent ya angle ni uwiano wa upande wa pili na upande wa karibu.

4) Ni uhusiano gani kati ya pembe mbili za papo hapo katika pembetatu sahihi?

5) Eleza utambulisho wa cofunction.

Jibu

Kwa mfano, sine ya angle ni sawa na cosine ya inayosaidia yake; cosine ya angle ni sawa na sine ya inayosaidia.

Kialjebra

Kwa mazoezi 6-9, tumia cofunctions ya pembe za ziada.

6)$\cos (34°)= \sin (\_\_°)$

7)$\cos (\dfrac{π}{3})= \sin (\_\_\_)$

Jibu

$\dfrac{π}{6}$

8)$\csc (21°) = \sec (\_\_\_°)$

9)$\tan (\dfrac{π}{4})= \cot (\_\_)$

Jibu

$\dfrac{π}{4}$

Kwa mazoezi 10-16, tafuta urefu wa pande zilizopo ikiwa upande$a$ ni kinyume cha pembe$A$, upande$b$ ni kinyume cha pembe$B$, na upande$c$ ni hypotenuse.

10)$\cos B= \dfrac{4}{5},a=10$

11)$\sin B= \dfrac{1}{2}, a=20$

Jibu

$b= \dfrac{20\sqrt{3}}{3},c= \dfrac{40\sqrt{3}}{3}$

12)$\tan A= \dfrac{5}{12},b=6$

13)$\tan A=100,b=100$

Jibu

$a=10,000,c=10,000.5$

14)$\sin B=\dfrac{1}{\sqrt{3}}, a=2$

15)$a=5, ∡ A=60^∘$

Jibu

$b=\dfrac{5\sqrt{3}}{3},c=\dfrac{10\sqrt{3}}{3}$

16)$c=12, ∡ A=45^∘$

Graphic

Kwa mazoezi 17-22, tumia Kielelezo hapa chini ili kutathmini kila kazi ya trigonometric ya angle$A$.

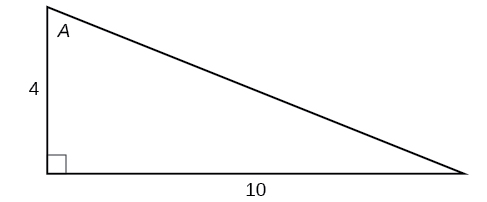
17)$\sin A$

Jibu

$\dfrac{5\sqrt{29}}{29}$

18)$\cos A$

19)$\tan A$

Jibu

$\dfrac{5}{2}$

20)$\csc A$

21)$\sec A$

Jibu

$\dfrac{\sqrt{29}}{2}$

22)$\cot A$

Kwa mazoezi 23-,28 tumia Kielelezo hapa chini ili kutathmini kila kazi ya trigonometric ya angle$A$.

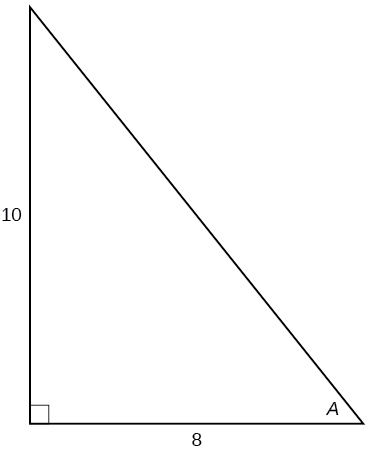
23)$\sin A$

Jibu

$\dfrac{5\sqrt{41}}{41}$

24)$\cos A$

25)$\tan A$

Jibu

$\dfrac{5}{4}$

26)$\csc A$

27)$\sec A$

Jibu

$\dfrac{\sqrt{41}}{4}$

28)$\cot A$

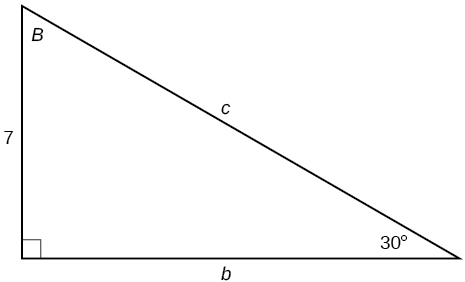
Kwa mazoezi 29-31, tatua kwa pande zisizojulikana za pembetatu iliyotolewa.

29)

Jibu

$c=14, b=7\sqrt{3}$

30)

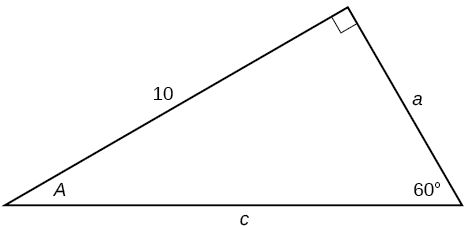
31)

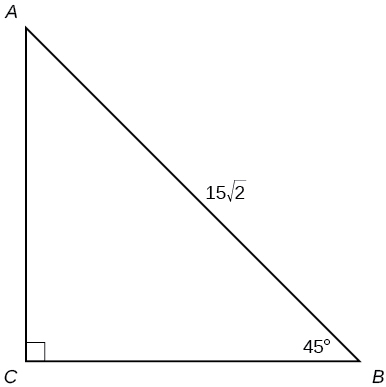
Jibu

$a=15, b=15$

Teknolojia

Kwa mazoezi 32-41, tumia calculator ili kupata urefu wa kila upande hadi sehemu nne za decimal.

32)

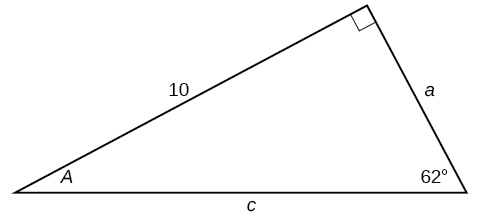
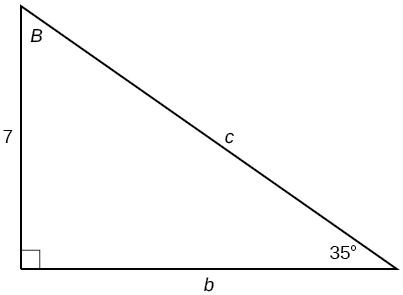
33)

Jibu

$b=9.9970, c=12.2041$

34)

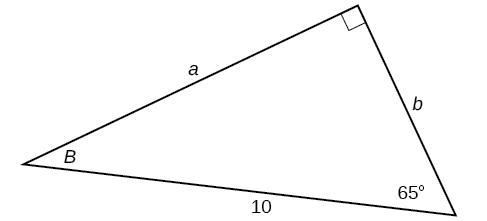
35)

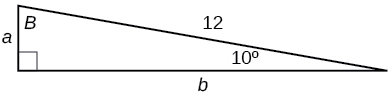
Jibu

$a=2.0838, b=11.8177$

36)

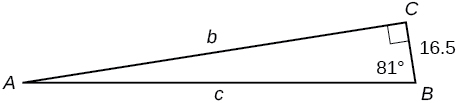
37)$b=15, ∡B=15^∘$

Jibu

$a=55.9808,c=57.9555$

38)$c=200, ∡B=5^∘$

39)$c=50, ∡B=21^∘$

Jibu

$a=46.6790,b=17.9184$

40)$a=30, ∡A=27^∘$

41)$b=3.5, ∡A=78^∘$

Jibu

$a=16.4662,c=16.8341$

Upanuzi

42) Tafuta$x$.

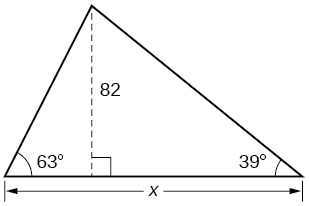
43) Tafuta$x$.

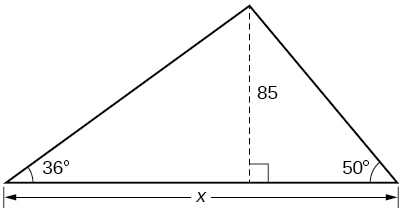
Jibu

$188.3159$

44) Kupata$x$.

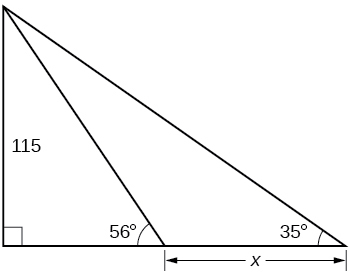
45) Kupata$x$.

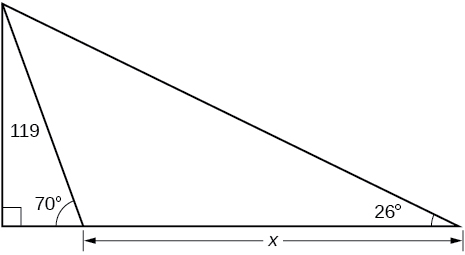
Jibu

$200.6737$

46) mnara wa redio iko$400$ miguu kutoka jengo. Kutoka dirisha ndani ya jengo, mtu anaamua kwamba angle ya mwinuko hadi juu ya mnara ni$36°$, na kwamba angle ya unyogovu chini ya mnara ni$23°$. Je, mnara ni mrefu sana?

47) mnara wa redio iko$325$ miguu kutoka jengo. Kutoka dirisha ndani ya jengo, mtu anaamua kwamba angle ya mwinuko hadi juu ya mnara ni$43°$, na kwamba angle ya unyogovu chini ya mnara ni$31°$. Je, mnara ni mrefu sana?

Jibu

$498.3471$ft

48) Monument mrefu wa$200$ mguu iko mbali. Kutoka dirisha katika jengo, mtu anaamua kwamba angle ya mwinuko hadi juu ya monument ni$15°$, na kwamba angle ya unyogovu chini ya mnara ni$2°$. Je! Mtu huyo ni mbali gani kutoka kwenye jiwe?

49) Monument mrefu wa$400$ mguu iko mbali. Kutoka dirisha katika jengo, mtu anaamua kwamba angle ya mwinuko hadi juu ya monument ni$18°$, na kwamba angle ya unyogovu chini ya monument ni$3°$. Je! Mtu huyo ni mbali gani kutoka kwenye jiwe?

Jibu

$1060.09$ft

50) Kuna antenna juu ya jengo. Kutoka eneo$300$ miguu kutoka msingi wa jengo, angle ya mwinuko hadi juu ya jengo ni kipimo kuwa$40°$. Kutoka eneo moja, angle ya mwinuko hadi juu ya antenna inapimwa kuwa$43°$. Pata urefu wa antenna.

51) Kuna fimbo ya umeme juu ya jengo. Kutoka eneo$500$ miguu kutoka msingi wa jengo, angle ya mwinuko hadi juu ya jengo ni kipimo kuwa$36°$. Kutoka eneo moja, angle ya mwinuko hadi juu ya fimbo ya umeme inapimwa kuwa$38°$. Pata urefu wa fimbo ya umeme.

Jibu

$27.372$ft

Real-World Matumizi

52) Ngazi$33$ -ft hutegemea jengo ili angle kati ya ardhi na ngazi ni$80°$. Je! Ngazi hiyo inafikia juu ya upande wa jengo?

53) Ngazi$23$ -ft hutegemea jengo ili angle kati ya ardhi na ngazi ni$80°$. Je! Ngazi hiyo inafikia juu ya upande wa jengo?

Jibu

$22.6506$ft

54) Angle ya mwinuko hadi juu ya jengo huko New York inapatikana kuwa$9$ digrii kutoka chini kwa umbali wa$1$ maili kutoka chini ya jengo hilo. Kutumia habari hii, pata urefu wa jengo.

55) Angle ya mwinuko hadi juu ya jengo huko Seattle inapatikana kuwa$2$ digrii kutoka chini kwa umbali wa$2$ maili kutoka chini ya jengo hilo. Kutumia habari hii, pata urefu wa jengo.

Jibu

$368.7633$ft

56) Kutokana kwamba$370$ -foot mrefu giant redwood kukua wima, kama mimi kutembea umbali fulani kutoka mti na kupima angle ya mwinuko hadi juu ya mti kuwa$60°$, jinsi mbali na msingi wa mti mimi?