13.3: Kazi nyingine za Trigonometric

Malengo ya kujifunza

• Kupata maadili halisi ya trigonometric kazi secant, cosecant, tangent, na cotangent ya\(\frac{\pi}{3}\),\(\frac{\pi}{4}\), na\(\frac{\pi}{6}\).
• Tumia pembe za kumbukumbu ili kutathmini kazi za trigonometric secant, tangent, na cotangent.
• Tumia mali ya kazi hata na isiyo ya kawaida ya trigonometric.
• Kutambua na kutumia utambulisho wa msingi.
• Tathmini kazi za trigonometric na calculator.

Njia ya magurudumu ambayo inakidhi viwango vya Sheria ya Wamarekani wenye ulemavu lazima ifanye angle na ardhi ambayo tangent ni\(\frac{1}{12}\) au chini, bila kujali urefu wake. Tangent inawakilisha uwiano, hivyo hii ina maana kwamba kwa kila inchi 1 ya kupanda, barabara lazima iwe na inchi 12 za kukimbia. Kazi za trigonometric zinatuwezesha kutaja maumbo na uwiano wa vitu huru na vipimo halisi. Tayari tumeelezea kazi za sine na cosine za angle. Ingawa sine na cosine ni kazi za trigonometric zinazotumiwa mara nyingi, kuna wengine wanne. Pamoja wao hufanya seti ya kazi sita za trigonometric. Katika sehemu hii, tutachunguza kazi zilizobaki.

Kutafuta Maadili halisi ya Kazi za Trigonometric Secant, Cosecant, Tangent, na Cotangent

Kufafanua kazi iliyobaki, sisi kwa mara nyingine tena kuteka kitengo mduara na uhakika\((x,y)\) sambamba na angle ya\(t\), kama inavyoonekana katika Kielelezo\(\PageIndex{1}\). Kama ilivyo na sine na cosine, tunaweza kutumia\((x,y)\) kuratibu ili kupata kazi nyingine.

Kielelezo\(\PageIndex{1}\)

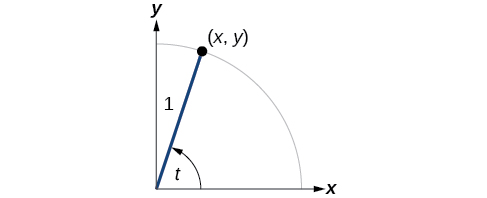
Kazi ya kwanza tutakayofafanua ni tangent. Tangent ya angle ni uwiano wa y -thamani kwa x -thamani ya uhakika sambamba kwenye mduara wa kitengo. Katika Kielelezo\(\PageIndex{1}\), tangent ya angle\(t\) ni sawa na\(\frac{y}{x},x≠0 \). Kwa sababu y -thamani ni sawa na sine ya\(t\), na x -value ni sawa na cosine ya\(t\), tangent ya angle pia\(t\) inaweza kuelezwa kama Kazi\( \frac{ \sin t}{ \cos t}, \cos t≠0.\) ya tangent inafupishwa kama\( \tan.\) Kazi tatu zilizobaki zinaweza kuelezwa kama kurudi kwa kazi ambazo tayari zimefafanuliwa.

• Kazi ya secant ni usawa wa kazi ya cosine. Katika Kielelezo\(\PageIndex{1}\), secant ya angle\(t\) ni sawa na\(\frac{1}{ \cos t} = \frac{1}{x},x≠0\). Kazi ya secant inafupishwa kama\( \sec \).
• Kazi ya cotangent ni usawa wa kazi ya tangent. Katika Kielelezo\(\PageIndex{1}\), cotangent ya angle\(t\) ni sawa na Kazi\( \frac{ \cos t}{ \sin t}= \frac{x}{y}, y≠0.\) ya cotangent inafupishwa kama\( \cot.\)
• Kazi ya cosecant ni usawa wa kazi ya sine. Katika Kielelezo\(\PageIndex{1}\), cosecant ya angle\(t\) ni sawa na Kazi\(\frac{1}{ \sin t}= \frac{1}{y},y≠0.\) ya cosecant inafupishwa kama\( \csc.\)

TANGENT, SECANT, COSECANT, NA COTANGENT KAZI

Ikiwa\(t\) ni namba halisi na\((x,y)\) ni hatua ambapo upande wa mwisho wa angle ya\(t\) radians huchukua mduara wa kitengo, basi

\[\begin{align} \tan t &= \frac{y}{x},x≠0 \\ \sec t & =\frac{1}{x},x≠0 \\ \csc t &=\frac{1}{y},y≠0 \\ \cot t &= \frac{x}{y},y≠0 \end{align}\]

Mfano\(\PageIndex{1}\): Finding Trigonometric Functions from a Point on the Unit Circle

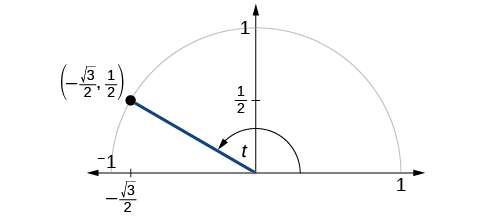
Hatua\((−\frac{\sqrt{3}}{2},\frac{1}{2})\) ni kwenye mduara wa kitengo, kama inavyoonekana kwenye Mchoro\(\PageIndex{2}\). Kupata\( \sin t, \cos t, \tan t, \sec t, \csc t,\) na\( \cot t\).

Kielelezo\(\PageIndex{2}\)

Suluhisho

Kwa sababu tunajua\((x,y)\) kuratibu za uhakika kwenye mduara wa kitengo unaonyeshwa kwa angle\(t\), tunaweza kutumia kuratibu hizo ili kupata kazi sita:

\[\begin{align*} \sin t &=y=\dfrac{1}{2} \\ \cos t &=x= −\dfrac{\sqrt{3}}{2} \\ \tan t &= \dfrac{y}{x}= \dfrac{\frac{1}{2}}{−\frac{\sqrt{3}}{2}}=\dfrac{1}{2}(−\dfrac{2}{\sqrt{3}})=−\dfrac{1}{\sqrt{3}}=−\dfrac{\sqrt{3}}{3} \\ \sec t &= \dfrac{1}{x}=\dfrac{1}{−\frac{\sqrt{3}}{2}}=−\dfrac{2}{\sqrt{3}}=−\dfrac{2\sqrt{3}}{3} \\ \csc t &= \dfrac{1}{y}=\dfrac{1}{\frac{1}{2}}=2 \\ \cot t &= \dfrac{x}{y}=\dfrac{−\frac{\sqrt{3}}{2}}{\frac{1}{2}}=−\dfrac{\sqrt{3}}{2}(\dfrac{2}{1})=−\sqrt{3} \end{align*}\]

Zoezi\(\PageIndex{1}\):

Hatua\((\frac{\sqrt{2}}{2},−\frac{\sqrt{2}}{2})\) ni kwenye mduara wa kitengo, kama inavyoonekana kwenye Mchoro\(\PageIndex{3}\). Kupata\( \sin t, \cos t, \tan t, \sec t, \csc t,\) na\( \cot t\).

Kielelezo\(\PageIndex{3}\)

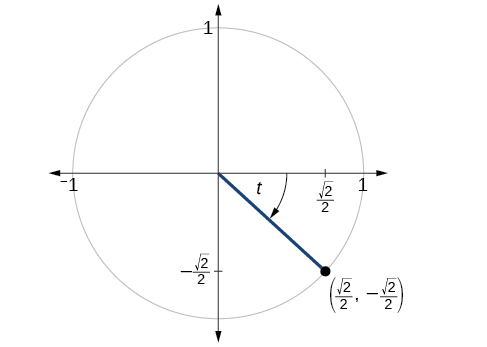
Suluhisho

\( \sin t=−\frac{\sqrt{2}}{2}, \cos t= \frac{\sqrt{2}}{2}, \tan t=−1, \sec t=\sqrt{2}, \csc t=−\sqrt{2}, \cot t=−1\)

Mfano\(\PageIndex{2}\): Finding the Trigonometric Functions of an Angle

Kupata\( \sin t, \cos t, \tan t, \sec t, \csc t, \) na\( \cot t\) wakati\(t=\frac{π}{6}\).

Suluhisho

Sisi hapo awali kutumika mali ya pembetatu equilateral kuonyesha kwamba\( \sin \frac{π}{6}=\frac{1}{2}\) na\( \cos \frac{π}{6}=\frac{\sqrt{3}}{2} \). Tunaweza kutumia maadili haya na ufafanuzi wa tangent, secant, cosecant, na cotangent kama kazi za sine na cosine ili kupata maadili ya kazi iliyobaki.

\[ \begin{align*} \tan \dfrac{π}{6} & = \dfrac{ \sin \frac{π}{6}}{\cos \frac{π}{6}} \\ & = \dfrac{\frac{1}{2} }{\frac{\sqrt{3}}{2}}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3} \\ \sec \dfrac{π}{6} &= \dfrac{1}{ \cos \frac{π}{6}} \\ & = \dfrac{1}{\frac{\sqrt{3}}{2}} = \dfrac{2}{\sqrt{3}}= \dfrac{2\sqrt{3}}{3} \\ \csc \dfrac{π}{6} &= \dfrac{1}{ \sin \frac{π}{6}}= \dfrac{1}{\frac{1}{2}}=2 \\ \cot \dfrac{π}{6} & = \dfrac{ \cos \frac{π}{6}}{ \sin \frac{π}{6}} \\ &= \dfrac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} =\sqrt{3} \end{align*}\]

Zoezi\(\PageIndex{2}\):

Pata\( \sin t, \cos t, \tan t, \sec t, \csc t,\) na\( \cot t\) lini\(t=\frac{π}{3}.\)

Suluhisho

\(\begin{align} \sin \frac{π}{3} & = \frac{\sqrt{3}}{2} \\ \cos \frac{π}{3} &=\frac{1}{2} \\ \tan \frac{π}{3} &= \sqrt{3} \\ \sec \frac{π}{3} &= 2 \\ \csc \frac{π}{3} &= \frac{2\sqrt{3}}{3} \\ \cot \frac{π}{3} &= \frac{\sqrt{3}}{3} \end{align}\)

Kwa sababu tunajua maadili ya sine na cosine kwa pembe ya kawaida ya kwanza ya roboduara, tunaweza kupata maadili mengine ya kazi kwa pembe hizo pia kwa kuweka x x sawa na cosine na y y sawa na sine na kisha kutumia ufafanuzi wa tangent, secant, cosecant, na cotangent. Matokeo yanaonyeshwa katika Jedwali\(\PageIndex{1}\).

Jedwali\(\PageIndex{1}\)

Angle	\(0\)	\(\frac{π}{6}, \text{ or } 30°\)	\(\frac{π}{4}, \text{ or } 45°\)	\(\frac{π}{3},\text{ or }60°\)	\(\frac{π}{2},\text{ or }90°\)
Cosine	\ (0\)” style="wima align:katikati; "> 1	\ (\ frac {π} {6},\ text {or} 30°\)” style="wima align:katikati; ">\(\frac{\sqrt{3}}{2}\)	\ (\ frac {π} {4},\ text {or} 45°\)” style="wima align:katikati; ">\(\frac{\sqrt{2}}{2}\)	\ (\ frac {π} {3},\ maandishi {or} 60°\)” style="wima align:katikati; ">\(\frac{1}{2}\)	\ (\ frac {π} {2},\ text {or} 90°\)” style="wima align:katikati; "> 0
Sine	\ (0\)” style="wima align:katikati; "> 0	\ (\ frac {π} {6},\ text {or} 30°\)” style="wima align:katikati; ">\(\frac{1}{2}\)	\ (\ frac {π} {4},\ text {or} 45°\)” style="wima align:katikati; ">\(\frac{\sqrt{2}}{2}\)	\ (\ frac {π} {3},\ maandishi {or} 60°\)” style="wima align:katikati; ">\(\frac{\sqrt{3}}{2}\)	\ (\ frac {π} {2},\ text {or} 90°\)” style="wima align:katikati; ">1
Tangent	\ (0\)” style="wima align:katikati; "> 0	\ (\ frac {π} {6},\ text {or} 30°\)” style="wima align:katikati; ">\(\frac{\sqrt{3}}{3}\)	\ (\ frac {π} {4},\ text {or} 45°\)” style="wima align:katikati; ">1	\ (\ frac {π} {3},\ maandishi {or} 60°\)” style="wima align:katikati; ">\(\sqrt{3}\)	\ (\ frac {π} {2},\ text {or} 90°\)” style="wima align:katikati; ">Haijafafanuliwa
Secant	\ (0\)” style="wima align:katikati; "> 1	\ (\ frac {π} {6},\ text {or} 30°\)” style="wima align:katikati; ">\(\frac{2\sqrt{3}}{3}\)	\ (\ frac {π} {4},\ text {or} 45°\)” style="wima align:katikati; ">\(\sqrt{2}\)	\ (\ frac {π} {3},\ text {or} 60°\)” style="wima align:katikati; "> 2	\ (\ frac {π} {2},\ text {or} 90°\)” style="wima align:katikati; ">Haijafafanuliwa
Cosecant	\ (0\)” style="wima align:katikati; "> Haijafafanuliwa	\ (\ frac {π} {6},\ text {or} 30°\)” style="wima align:katikati; "> 2	\ (\ frac {π} {4},\ text {or} 45°\)” style="wima align:katikati; ">\(\sqrt{2}\)	\ (\ frac {π} {3},\ maandishi {or} 60°\)” style="wima align:katikati; ">\(\frac{2\sqrt{3}}{3}\)	\ (\ frac {π} {2},\ text {or} 90°\)” style="wima align:katikati; ">1
Cotangent	\ (0\)” style="wima align:katikati; "> Haijafafanuliwa	\ (\ frac {π} {6},\ text {or} 30°\)” style="wima align:katikati; ">\(\sqrt{3}\)	\ (\ frac {π} {4},\ text {or} 45°\)” style="wima align:katikati; ">1	\ (\ frac {π} {3},\ maandishi {or} 60°\)” style="wima align:katikati; ">\(\frac{\sqrt{3}}{3}\)	\ (\ frac {π} {2},\ text {or} 90°\)” style="wima align:katikati; "> 0

Kutumia Angles za Kumbukumbu kutathmini Tangent, Secant, Cosecant, na Cotangent

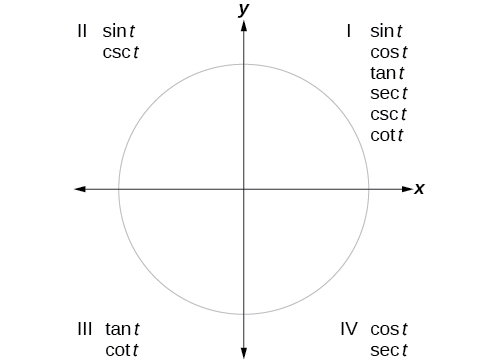
Tunaweza kutathmini kazi za trigonometric za pembe nje ya roboduara ya kwanza kwa kutumia pembe za kumbukumbu kama tulivyofanya na kazi za sine na cosine. Utaratibu huo ni sawa: Pata angle ya kumbukumbu iliyoundwa na upande wa mwisho wa angle iliyotolewa na mhimili usio na usawa. Maadili ya kazi ya trigonometric kwa angle ya awali yatakuwa sawa na yale ya angle ya kumbukumbu, isipokuwa kwa ishara nzuri au hasi, ambayo imedhamiriwa na x - na y -maadili katika roboduara ya awali. Kielelezo\(\PageIndex{4}\) kinaonyesha kazi ambazo ni chanya ambazo quadrant.

Ili kutusaidia kukumbuka ni kazi gani ya trigonometric sita ni chanya katika kila roboduara, tunaweza kutumia maneno ya mnemonic “Darasa la Smart Trig.” Kila moja ya maneno manne katika maneno yanafanana na moja ya quadrants nne, kuanzia na quadrant I na kupokezana kinyume chake. Katika quadrant I, ambayo ni “A,” kazi zote sita za trigonometric ni chanya. Katika quadrant II, “S mart,” tu kama faini na kazi yake ya usawa, cosecant, ni chanya. Katika quadrant III, “T pete,” tu kwa angent na kazi yake ya kurudi, mara kwa mara, ni chanya. Hatimaye, katika quadrant IV, “C lass,” tu c osine na kazi yake ya kurudi, secant, ni chanya.

Kielelezo\(\PageIndex{4}\)

HOWTO: Kutokana na angle si katika roboduara ya kwanza, tumia pembe za kumbukumbu ili kupata kazi zote sita za trigonometric

1. Pima angle iliyoundwa na upande wa mwisho wa angle iliyotolewa na mhimili usio na usawa. Hii ni angle ya kumbukumbu.
2. Tathmini kazi kwenye angle ya kumbukumbu.
3. Angalia quadrant ambapo upande wa mwisho wa angle ya awali iko. Kulingana na quadrant, onyesha kama pato ni chanya au hasi.

Mfano\(\PageIndex{3}\): Using Reference Angles to Find Trigonometric Functions

Matumizi pembe kumbukumbu ya kupata kazi zote sita trigonometric ya\(−\frac{5π}{6}\).

Suluhisho

Pembe kati ya upande huu wa terminal angle na x -axis ni\(\frac{π}{6}\), hivyo kwamba ni angle kumbukumbu. Kwa kuwa\(−\frac{5π}{6}\) ni katika roboduara ya tatu, ambapo wote wawili\(x\) na\(y\) ni hasi, cosine, sine, secant, na cosecant itakuwa hasi, wakati tangent na cotangent itakuwa chanya.

\[ \begin{align} \cos (−\dfrac{5π}{6}) &=−\dfrac{\sqrt{3}}{2}, \sin (−\dfrac{5π}{6})=−\dfrac{1}{2}, \tan (−\dfrac{5π}{6}) = \dfrac{\sqrt{3}}{3} \\ \sec (−\dfrac{5π}{6}) &=−\dfrac{2\sqrt{3}}{3}, \csc (−\dfrac{5π}{6})=−2, \cot (−\dfrac{5π}{6})=\sqrt{3} \end{align} \]

Zoezi\(\PageIndex{3}\)

Matumizi pembe kumbukumbu ya kupata kazi zote sita trigonometric ya\(−\frac{7π}{4}\).

Suluhisho

\( \sin (−\frac{7π}{4})= \frac{\sqrt{2}}{2}, \cos(\frac{−7π}{4})=\frac{\sqrt{2}}{2}, \tan (\frac{−7π}{4})=1,\)

\( \sec (\frac{−7π}{4})= \sqrt{2}, \csc (\frac{−7π}{4})= \sqrt{2}, \cot (\frac{−7π}{4})=1 \)

Kutumia Kazi Hata na isiyo ya kawaida ya Trigonometric

Ili tuweze kutumia kazi zetu sita za trigonometric kwa uhuru na pembejeo zenye chanya na hasi, tunapaswa kuchunguza jinsi kila kazi inachukua pembejeo hasi. Kama inageuka, kuna tofauti muhimu kati ya kazi katika suala hili.

Fikiria kazi\(f(x)=x^2\), iliyoonyeshwa kwenye Kielelezo\(\PageIndex{5}\). Grafu ya kazi ni ya kawaida kuhusu y -axis. Yote pamoja Curve, pointi zozote mbili na kinyume x -maadili na thamani sawa kazi. Hii inafanana na matokeo ya hesabu:\((4)^2=(−4)^2,(−5)^2=(5)^2\), na kadhalika. Hivyo\(f(x)=x^2\) ni hata kazi, kazi kama kwamba pembejeo mbili ambazo ni kinyume na pato sawa. Hiyo ina maana\(f(−x)=f(x)\).

Kielelezo\(\PageIndex{5}\): Kazi\(f(x)=x^2\) ni hata kazi.

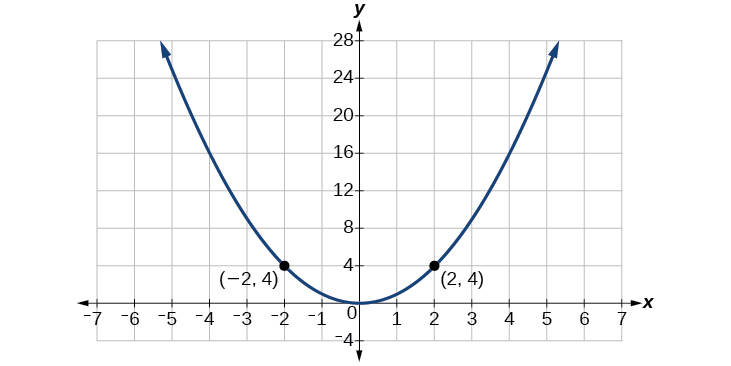
Sasa fikiria kazi\(f(x)=x^3\), iliyoonyeshwa kwenye Kielelezo\(\PageIndex{6}\). Grafu haipatikani kuhusu y -axis. Wote pamoja na grafu, pointi zozote mbili zilizo na maadili tofauti ya x pia zina kinyume na y -maadili. Hivyo\(f(x)=x^3\) ni kazi isiyo ya kawaida, moja kama kwamba pembejeo mbili ambazo ni kinyume na matokeo ambayo pia ni kinyume. Hiyo ina maana\(f(−x)=−f(x)\).

Kielelezo\(\PageIndex{6}\): Kazi\(f(x)=x^3\) ni kazi isiyo ya kawaida.

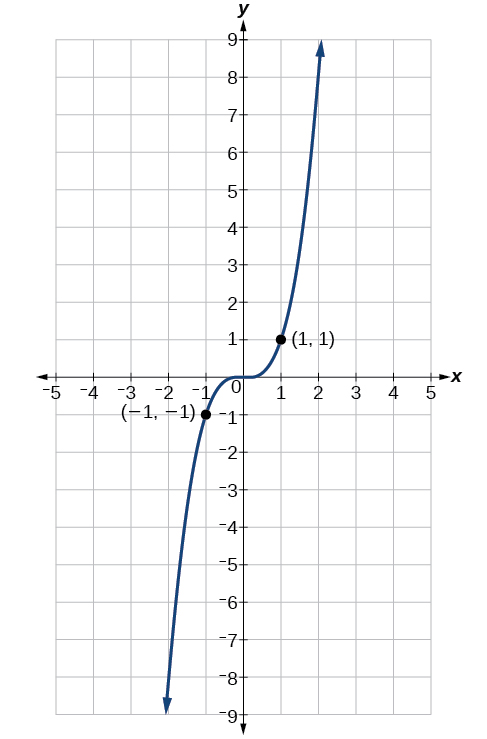
Tunaweza kupima kama kazi ya trigonometric ni hata au isiyo ya kawaida kwa kuchora mduara wa kitengo na angle nzuri na hasi, kama katika Kielelezo\(\PageIndex{7}\). Sine ya angle nzuri ni\(y\). Mstari wa angle hasi ni - y. Kazi ya sine, basi, ni kazi isiyo ya kawaida. Tunaweza kupima kila moja ya kazi sita za trigonometric kwa mtindo huu. Matokeo yanaonyeshwa katika Jedwali\(\PageIndex{2}\).

Kielelezo\(\PageIndex{7}\)

Jedwali\(\PageIndex{2}\)

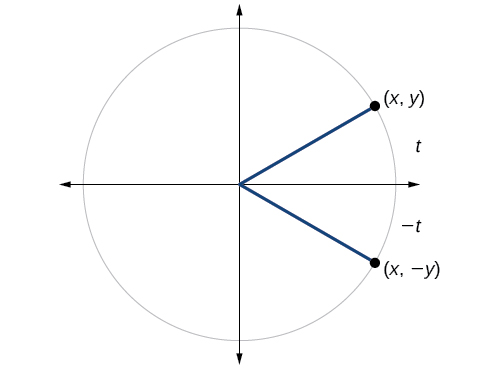
\(\begin{align} \sin t &=y \\ \sin (−t) &=−y \\ \sin t &≠sin(−t) \end{align}\)	\( \begin{align} \cos t &=x \\ \cos (−t)=x \\ \cos t &= \cos (−t) \end{align}\)	\(\begin{align} \tan (t) &= \frac{y}{x} \\ \tan (−t) &=−\frac{y}{x} \\ \tan t &≠ \tan (−t) \end{align}\)
\(\begin{align} \sec t &= \frac{1}{x} \\ \sec (−t) &= \frac{1}{x} \\ \sec t &= \sec (−t) \end{align}\)	\( \begin{align} \csc t &= \frac{1}{y} \\ \csc (−t) &= \frac{1}{−y} \\ \csc t &≠ \csc (−t) \end{align}\)	\( \begin{align} \cot t &= \frac{x}{y} \\ \cot (−t) &= \frac{x}{−y} \\ \cot t & ≠ \cot (−t) \end{align}\)

HATA NA ISIYO YA KAWAIDA KAZI TRIGONOMETRIC

• Kazi hata ni moja ambayo\(f(−x)=f(x)\).
• Kazi isiyo ya kawaida ni moja ambayo\(f(−x)=−f(x)\).

Cosine na secant ni hata:

\[ \begin{align} \cos (−t) &= \cos t \\ \sec (−t) &= \sec t \end{align}\]

Sine, tangent, cosecant, na cotangent ni isiyo ya kawaida:

\[\begin{align} \sin (−t) &=− \sin t \\ \tan (−t) &=−\tan t \\ \csc (−t) &=−\csc t \\ \cot (−t) &=−\cot t \end{align}\]

Mfano\(\PageIndex{4}\): Using Even and Odd Properties of Trigonometric Functions

Ikiwa secant ya angle ni 2, ni nini secant ya\(−t\)?

Suluhisho

Secant ni hata kazi. Sehemu ya pembe ni sawa na secant ya kinyume chake. Hivyo kama secant ya angle ni 2, secant ya pia\(−t\) ni 2.

Zoezi\(\PageIndex{4}\):

Kama cotangent ya angle\(t\) ni\(\sqrt{3}\), ni nini cotangent ya\(−t?\)

Suluhisho

\(−\sqrt{3}\)

Kutambua na Kutumia Utambulisho wa Msingi

Tumechunguza idadi ya mali ya kazi za trigonometric. Sasa, tunaweza kuchukua mahusiano hatua zaidi, na kupata baadhi ya utambulisho msingi. Utambulisho ni kauli ambazo ni za kweli kwa maadili yote ya pembejeo ambayo hufafanuliwa. Kawaida, utambulisho unaweza kupatikana kutokana na ufafanuzi na mahusiano tunayoyajua tayari. Kwa mfano, Identity ya Pythagorean tuliyojifunza mapema ilitokana na Theorem ya Pythagorean na ufafanuzi wa sine na cosine.

UTAMBULISHO WA MSINGI

Tunaweza kupata baadhi ya utambulisho muhimu kutoka kazi sita trigonometric. Kazi nyingine nne za trigonometric zinaweza kuhusishwa nyuma na kazi za sine na cosine kwa kutumia mahusiano haya ya msingi:

\[ \tan t= \dfrac{ \sin t}{ \cos t} \]

\[ \sec t= \dfrac{1}{\cos t}\]

\[ \csc t= \dfrac{1}{\sin t}\]

\[ \cot t= \dfrac{1}{ \tan t}= \dfrac{ \cos t}{ \sin t} \]

Mfano\(\PageIndex{5}\): Using Identities to Evaluate Trigonometric Functions

1. Kutokana\( \sin (45°)= \frac{\sqrt{2}}{2}, \cos (45°)= \frac{\sqrt{2}}{2}\), kutathmini\( \tan(45°).\)
2. Kutokana\( \sin (\frac{5π}{6})= \frac{1}{2}, \cos( \frac{5π}{6})=−\frac{\sqrt{3}}{2},\) kutathmini\(\sec (\frac{5π}{6})\).

Suluhisho

Kwa sababu tunajua maadili ya sine na cosine kwa pembe hizi, tunaweza kutumia utambulisho kutathmini kazi nyingine.

1. \[ \begin{align*} \tan(45°) &=\dfrac{ \sin(45°)}{ \cos (45°)} \\ &= \dfrac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} \\ & =1 \end{align*} \]
2. \[\begin{align*} \sec (\dfrac{5π}{6}) &= \dfrac{1}{ \cos (\frac{5π}{6})} \\ &= \dfrac{1}{−\frac{\sqrt{3}}{2}} \\ &= \dfrac{−2\sqrt{3}}{1} \\ &=\dfrac{−2}{\sqrt{3}} \\ &=−\dfrac{2\sqrt{3}}{3} \end{align*}\]

Zoezi\(\PageIndex{5}\)

Tathmini\(\csc (\frac{7π}{6}).\)

Suluhisho

\(−2\)

Mfano\(\PageIndex{6}\): Using Identities to Simplify Trigonometric Expressions

Kurahisisha\(\frac{ \sec t}{ \tan t}.\)

Suluhisho

Tunaweza kurahisisha hili kwa kuandika tena kazi zote mbili kwa suala la sine na cosine.

\[\begin{array}{lll} \dfrac{\sec t}{\tan t} & =\dfrac{1 / \cos t}{ \sin t / \cos t} & \text{To divide the functions, we multiply by the reciprocal.} \\ \text{} &= \dfrac{1}{\cos t} \dfrac{ \cos t}{\sin t} & \text{Divide out the cosines.} \\ \text{} & =\dfrac{1}{\sin t} & \text{Simplify and use the identity.} \\ \text{} & = \csc t \end{array}\]

Kwa kuonyesha kwamba\(\frac{ \sec t}{ \tan t}\) inaweza kuwa rahisi kwa\( \csc t\), tuna, kwa kweli, imara utambulisho mpya.

\[ \dfrac{ \sec t}{ \tan t}= \csc t \nonumber \]

Zoezi\(\PageIndex{6}\)

Kurahisisha\(( \tan t)( \cos t).\)

Suluhisho

\( \sin t \)

Aina mbadala za Identity ya Pythagorean

Tunaweza kutumia utambulisho huu wa msingi kupata aina mbadala ya Identity Pythagorean,\( \cos ^2 t+ \sin ^2 t=1\). Fomu moja inapatikana kwa kugawa pande zote mbili na\( \cos ^2 t:\)

\[ \begin{align} \dfrac{ \cos ^2 t}{ \cos ^2 t} + \dfrac{ \sin ^2 t}{ \cos ^2 t} & = \dfrac{1}{ \cos ^2 t} \\ 1+ \tan ^2 t & = \sec ^2 t \end{align}\]

Fomu nyingine inapatikana kwa kugawa pande zote mbili kwa\( \sin ^2 t\):

\[ \begin{align} \dfrac{ \cos ^2 t}{ \sin ^2 t}+ \dfrac{ \sin ^2 t}{ \sin ^2 t} &= \dfrac{1}{ \sin ^2 t} \\ \cot ^2 t+1 &= \csc ^2 t \end{align}\]

AINA MBADALA ZA UTAMBULISHO WA PYTHAGOREAN

\[1+ \tan ^2 t= \sec ^2 t \]

\[ \cot ^2 t+1= \csc ^2 t\]

Mfano\(\PageIndex{7}\): Using Identities to Relate Trigonometric Functions

Ikiwa cos (t) =1213 cos (t) =1213 na t t iko katika quadrant IV, kama inavyoonekana kwenye Mchoro\(\PageIndex{8}\), pata maadili ya kazi nyingine tano za trigonometric.

Kielelezo\(\PageIndex{8}\)

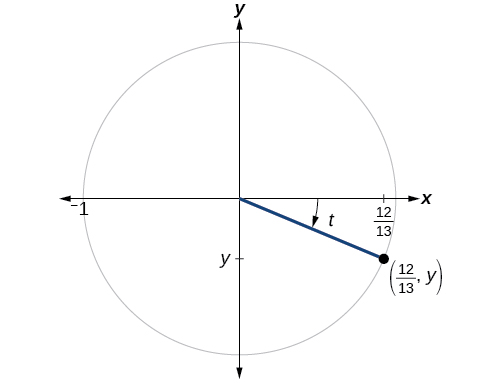
Suluhisho

Tunaweza kupata sine kwa kutumia Identity ya Pythagorean\( \cos ^2 t+ \sin ^2t=1 \),, na kazi iliyobaki kwa kuhusisha yao kwa sine na cosine.

\[ \begin{align} (\dfrac{12}{13})^2+ \sin ^2 t &= 1 \\ \sin ^2 t &=1−(\dfrac{12}{13})^2 \\ \sin ^2 t &=1− \dfrac{144}{169} \\ \sin ^2 t &= \dfrac{25}{169} \\ \sin t &=±\sqrt{\dfrac{25}{169}} \\ \sin t &=±\dfrac{\sqrt{25}}{\sqrt{169}} \\ \sin t &=± \dfrac{5}{13} \end{align} \]

Ishara ya sine inategemea y -maadili katika quadrant ambapo angle iko. Kwa kuwa angle iko katika quadrant IV, ambapo y -maadili ni hasi, sine yake ni hasi,\(−\frac{5}{13}\).

Kazi iliyobaki inaweza kuhesabiwa kwa kutumia utambulisho unaohusiana nao na sine na cosine.

\[ \begin{align} \tan t &= \dfrac{\sin t}{ \cos t}=\dfrac{−\frac{5}{13}}{\frac{12}{13}}=−\dfrac{5}{12} \\ \sec t &= \dfrac{1}{ \cos t}=\dfrac{1}{\frac{12}{13}}=\dfrac{13}{12} \\ \csc t &= \dfrac{1}{\sin t}=\dfrac{1}{−\frac{5}{13}} =−\dfrac{13}{5} \\ \cot t &= \dfrac{1}{ \tan t}=\dfrac{1}{−\frac{5}{12}}=−\dfrac{12}{5} \end{align} \]

Zoezi\(\PageIndex{7}\):

Ikiwa\( \sec (t)=− \frac{17}{8}\) na\(0<t<π,\) kupata maadili ya kazi nyingine tano.

Suluhisho

\( \cos t=−\frac{8}{17}, \sin t=\frac{15}{17}, \tan t=−\frac{15}{8}\)

\( \csc t= \frac{17}{15}, \cot t=−\frac{8}{15} \)

Kama tulivyojadiliwa katika ufunguzi wa sura, kazi ambayo hurudia maadili yake kwa vipindi vya kawaida inajulikana kama kazi ya mara kwa mara. Kazi ya trigonometric ni mara kwa mara. Kwa kazi nne za trigonometric, sine, cosine, cosecant na secant, mapinduzi ya mduara mmoja\(2π\), au, itasababisha matokeo sawa kwa kazi hizi. Na kwa tangent na cotangent, mapinduzi ya nusu tu yatasababisha matokeo sawa.

Kazi nyingine pia inaweza kuwa mara kwa mara. Kwa mfano, urefu wa miezi hurudia kila baada ya miaka minne. Ikiwa x x inawakilisha muda wa urefu, kipimo kwa miaka, na\(f(x)\) inawakilisha idadi ya siku mwezi Februari, basi\(f(x+4)=f(x)\). Mfano huu unarudia mara kwa mara na kwa wakati. Kwa maneno mengine, kila baada ya miaka minne, Februari imethibitishwa kuwa na idadi sawa ya siku kama ilivyofanya miaka 4 mapema. Nambari nzuri ya 4 ni nambari ndogo zaidi ambayo inatimiza hali hii na inaitwa kipindi hicho. Kipindi ni muda mfupi zaidi ambayo kazi inakamilisha mzunguko kamili-katika mfano huu, kipindi ni 4 na inawakilisha muda inachukua kwa sisi kuwa na uhakika Februari ina idadi sawa ya siku.

KIPINDI CHA KAZI

kipindi\(P\) cha kurudia kazi f f ni idadi anayewakilisha muda kama kwamba\(f(x+P)=f(x)\) kwa thamani yoyote ya\(x\).

Kipindi cha cosine, sine, secant, na cosecant kazi ni\(2π\).

Kipindi cha kazi za tangent na cotangent ni\(π\).

Mfano\(\PageIndex{8}\): Finding the Values of Trigonometric Functions

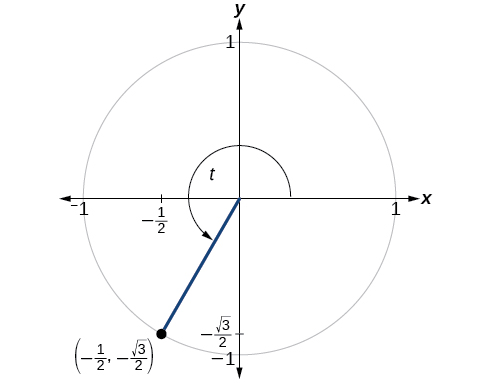
Pata maadili ya kazi sita za trigonometric za angle\(t\) kulingana na Kielelezo\(\PageIndex{9}\).

Kielelezo\(\PageIndex{9}\)

Suluhisho

\[\begin{align*} \sin t &= y=−\dfrac{\sqrt{3}}{2} \\ \cos t &=x =−\dfrac{1}{2} \\ \tan t &= \dfrac{ \sin t}{ \cos t}=\dfrac{−\frac{\sqrt{3}}{2}}{−\frac{1}{2}}= \sqrt{3} \\ \sec t &= \dfrac{1}{\cos t} = \dfrac{1}{−\frac{1}{2}}=−2 \\ \csc t &= \dfrac{1}{\sin t}= \dfrac{1}{−\frac{\sqrt{3}}{2}}=−\dfrac{2\sqrt{3}}{3} \\ \cot t &= \dfrac{1}{ \tan t}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3} \end{align*}\]

Zoezi\(\PageIndex{8}\)

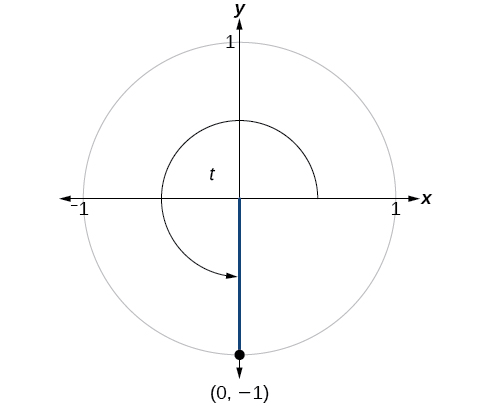
Pata maadili ya kazi sita za trigonometric za angle\(t\) kulingana na Kielelezo\(\PageIndex{10}\).

Kielelezo\(\PageIndex{10}\)

Suluhisho

\(\begin{align} \sin t &=−1, \cos t=0, \tan t= \text{Undefined} \\ \\sec t &= \text{Undefined}, \csc t=−1, \cot t=0 \end{align}\)

Mfano\(\PageIndex{9}\): Finding the Value of Trigonometric Functions

Ikiwa\( \sin(t)=−\frac{\sqrt{3}}{2}\) na\( \cos (t)=\frac{1}{2}\), tafuta\( \sec (t),\csc (t),\tan (t), \cot (t).\)

Suluhisho

\[ \begin{align} \sec t &= \dfrac{1}{ \cos t}= \dfrac{1}{\frac{1}{2}}=2 \\ \csc t &= \dfrac{1}{ \sin t}= \dfrac{1}{−\frac{\sqrt{3}}{2}}−\dfrac{2\sqrt{3}}{3} \\ \tan t &= \dfrac{\sin t}{\cos t}=\dfrac{−\frac{\sqrt{3}}{2}}{\frac{1}{2}}=−\sqrt{3} \\ \cot t &= \dfrac{1}{ \tan t}= \dfrac{1}{−\sqrt{3}}=−\dfrac{\sqrt{3}}{3} \end{align}\]

Zoezi\(\PageIndex{9}\):

Kama\(\sin (t)= \frac{\sqrt{2}}{2}\) na\(\cos (t)=\frac{\sqrt{2}}{2},\) kupata\( \sec (t), \csc (t),\tan (t),\) na\( \cot (t)\).

Suluhisho

\( \sec t= \sqrt{2},\csc t=\sqrt{2}, \tan t=1, \cot t=1\)

Kutathmini Kazi za Trigonometric na Calculator

Tumejifunza jinsi ya kutathmini kazi sita za trigonometric kwa pembe za kawaida za kwanza za quadrant na kuzitumia kama pembe za kumbukumbu kwa pembe katika quadrants nyingine. Ili kutathmini kazi za trigonometric za pembe nyingine, tunatumia calculator ya kisayansi au graphing au programu ya kompyuta. Ikiwa calculator ina mode ya shahada na mode ya radian, kuthibitisha hali sahihi imechaguliwa kabla ya kufanya hesabu.

Kutathmini kazi ya tangent na calculator ya kisayansi kinyume na calculator ya graphing au mfumo wa algebra ya kompyuta ni kama kutathmini sine au cosine: Ingiza thamani na bonyeza kitufe cha TAN. Kwa kazi za usawa, kunaweza kuwa na funguo yoyote ya kujitolea inayosema CSC, SEC, au COT. Katika hali hiyo, kazi inapaswa kupimwa kama usawa wa sine, cosine, au tangent.

Ikiwa tunahitaji kufanya kazi na digrii na calculator yetu au programu haina mode ya shahada, tunaweza kuingia digrii zilizoongezeka kwa sababu ya uongofu\(\frac{π}{180}\) ili kubadilisha digrii kwa radians. Ili kupata secant ya\( 30°\), tunaweza vyombo vya habari

\[\mathrm{(for \; a \; scientific \; calculator):\dfrac{1}{30×\frac{π}{180}}COS }\]

au

\[ \mathrm{(for \; a \; graphing \; calculator): \dfrac{1}{cos(\frac{30π}{180})} }\]

jinsi ya: Kutokana na kipimo cha angle katika radians, tumia calculator ya kisayansi ili kupata cosecant

1. Ikiwa calculator ina hali ya shahada na mode ya radian, kuiweka kwenye mode ya radian.
2. Ingiza:\(1 \; / \)
3. Ingiza thamani ya angle ndani ya mabano.
4. Bonyeza kitufe cha SIN.
5. Bonyeza kitufe cha =.

jinsi ya: Kutokana na kipimo cha angle katika radians, tumia matumizi ya graphing/calculator ili kupata cosecant

1. Ikiwa shirika la graphing lina mode ya shahada na mode ya radian, uiweka kwenye mode ya radian.
2. Ingiza:\(1 \; /\)
3. Bonyeza kitufe cha SIN.
4. Ingiza thamani ya angle ndani ya mabano.
5. Bonyeza kitufe cha ENTER.

Mfano\(\PageIndex{10}\): Evaluating the Cosecant Using Technology

Kutathmini cosecant ya\(\frac{5π}{7}\).

Suluhisho

Kwa calculator kisayansi, ingiza habari kama ifuatavyo:

\[ \mathrm{1 / ( 5 × π / 7 ) SIN =}\]

\[ \mathrm{ \csc (\dfrac{5π}{7})≈1.279} \]

Zoezi\(\PageIndex{10}\):

Kutathmini cotangent ya\(−\frac{π}{8}\).

\(≈−2.414\)

vyombo vya habari

Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na kazi nyingine za trigonometric.

• Kuamua Maadili ya Kazi ya Trig
• Mifano zaidi ya Kuamua Kazi za Trig
• Utambulisho wa Pythagorean
• Trig Kazi juu ya Calculator

Mlinganyo muhimu

Tangent kazi	\( \tan t= \frac{ \sin t}{\cos t}\)
Kazi ya secant	\( \sec t= \frac{1}{ \cos t}\)
Kazi ya Cosecant	\( \csc t= \frac{1}{ \sin t}\)
Kazi ya Cotangent	\( \cot t= \frac{1}{\tan t}= \frac{\cos t}{ \sin t}\)

Dhana muhimu

• Tangent ya angle ni uwiano wa y -thamani kwa x -thamani ya uhakika sambamba kwenye mduara wa kitengo.
• Ya secant, cotangent, na cosecant ni wote kurudi kwa kazi nyingine. Secant ni usawa wa kazi ya cosine, cotangent ni usawa wa kazi ya tangent, na cosecant ni usawa wa kazi ya sine.
• Kazi sita za trigonometric zinaweza kupatikana kutoka kwenye hatua kwenye mduara wa kitengo. Angalia Mfano.
• Kazi za trigonometric pia zinaweza kupatikana kutoka pembe. Angalia Mfano.
• Kazi za trigonometric za pembe nje ya quadrant ya kwanza zinaweza kuamua kutumia pembe za kumbukumbu. Angalia Mfano.
• kazi inasemekana kuwa hata kama\(f(−x)=f(x)\) na isiyo ya kawaida kama\(f(−x)=−f(x)\).
• Cosine na secant ni hata; sine, tangent, cosecant, na cotangent ni isiyo ya kawaida.
• Hata na mali isiyo ya kawaida inaweza kutumika kutathmini kazi za trigonometric. Angalia Mfano.
• Identity ya Pythagorean inafanya uwezekano wa kupata cosine kutoka sine au sine kutoka cosine.
• Utambulisho unaweza kutumika kutathmini kazi za trigonometric. Angalia Mfano na Mfano.
• Utambulisho wa msingi kama vile Identity ya Pythagorean unaweza kutumiwa algebraically kuzalisha utambulisho mpya. Angalia Mfano.
• Kazi za trigonometric hurudia kwa vipindi vya kawaida.
• Kipindi\(P\) cha kazi ya kurudia f f ni muda mdogo zaidi kama kwamba\(f(x+P)=f(x)\) kwa thamani yoyote ya\(x\).
• Maadili ya kazi ya trigonometric ya pembe maalum yanaweza kupatikana kwa uchambuzi wa hisabati.
• Kutathmini kazi za trigonometric za pembe nyingine, tunaweza kutumia calculator au programu ya kompyuta. Angalia Mfano.

faharasa

cosecant

usawa wa kazi ya sine: kwenye mduara wa kitengo,\( \csc t=\frac{1}{y},y≠0\)

cotangent

usawa wa kazi ya tangent: kwenye mduara wa kitengo,\( \cot t= \frac{x}{y},y≠0\)

vitambulisho

taarifa kwamba ni kweli kwa maadili yote ya pembejeo ambayo wao ni defined

kipindi

muda mdogo\(P\) wa kazi ya kurudia\(f\) kama vile\(f(x+P)=f(x)\)

sehemu

usawa wa kazi ya cosine: kwenye mduara wa kitengo,\( \sec t= \frac{1}{x},x≠0 \)

tangent

quotient ya sine na cosine: kwenye mduara wa kitengo,\( \tan t= \frac{y}{x},x≠0\)