11.7: Uwezekano
- Page ID
- 181140
- Kujenga mifano ya uwezekano.
- Compute probabilities ya matokeo sawa uwezekano.
- Compute probabilities ya muungano wa matukio mawili.
- Tumia utawala unaosaidia ili kupata uwezekano.
- Compute uwezekano kwa kutumia kuhesabu nadharia.
Wakazi wa Kusini Mashariki mwa Marekani wote pia ukoo na chati, inayojulikana kama mifano tambi, kama vile moja katika Kielelezo\(\PageIndex{1}\). Wao huchanganya mkusanyiko wa data ya hali ya hewa ili kutabiri njia inayowezekana zaidi ya kimbunga. Kila mstari wa rangi inawakilisha njia moja iwezekanavyo. Kikundi cha mistari ya squiggly inaweza kuanza kufanana na vipande vya tambi, kwa hiyo jina. Katika sehemu hii, tutachunguza mbinu za kufanya aina hizi za utabiri.
Kielelezo\(\PageIndex{1}\): Mfano wa “mfano wa tambi,” ambayo inaweza kutumika kutabiri njia zinazowezekana za dhoruba ya kitropiki. 1
Kujenga Mifano ya uwezekano
Tuseme tunapiga mchemraba wa namba sita. Rolling mchemraba namba ni mfano wa majaribio, au shughuli na matokeo inayoonekana. Idadi kwenye mchemraba ni matokeo iwezekanavyo, au matokeo, ya jaribio hili. Seti ya matokeo yote yanayowezekana ya jaribio inaitwa nafasi ya sampuli ya jaribio. Nafasi ya sampuli ya jaribio hili ni\(\{1,2,3,4,5,6 \}\). Tukio ni subset yoyote ya nafasi ya sampuli.
Uwezekano wa tukio unajulikana kama uwezekano. Uwezekano wa tukio pp ni idadi ambayo daima inatimiza\(0≤p≤1\), ambapo\(0\) inaonyesha tukio haliwezekani na\(1\) inaonyesha tukio fulani. mfano uwezekano ni maelezo ya hisabati ya majaribio listing matokeo yote iwezekanavyo na probabilities yao kuhusishwa. Kwa mfano, ikiwa kuna\(1\%\) nafasi ya kushinda bahati nasibu na\(99\%\) nafasi ya kupoteza bahati nasibu, mfano wa uwezekano utaonekana kama Jedwali\(\PageIndex{1}\).
| Matokeo | Uwezekano |
|---|---|
| Kushinda bahati nasibu | 1% |
| Kupoteza bahati nasibu | 99% |
Jumla ya probabilities waliotajwa katika mfano uwezekano lazima sawa\(1\), au\(100\%\).
- Tambua kila matokeo.
- Kuamua idadi ya matokeo iwezekanavyo.
- Linganisha kila matokeo kwa idadi ya matokeo iwezekanavyo.
Kujenga uwezekano mfano kwa rolling moja, haki kufa, na tukio kuwa idadi inavyoonekana kwenye kufa.
Suluhisho
Anza kwa kufanya orodha ya matokeo yote iwezekanavyo kwa jaribio. Matokeo iwezekanavyo ni namba ambazo zinaweza kuvingirwa:\(1\)\(2\),\(3\),\(4\),\(5\), na\(6\). Kuna matokeo sita yanayowezekana ambayo yanafanya nafasi ya sampuli.
Weka probabilities kwa kila matokeo katika nafasi ya sampuli kwa kuamua uwiano wa matokeo kwa idadi ya matokeo iwezekanavyo. Kuna moja ya kila moja ya namba sita kwenye mchemraba, na hakuna sababu ya kufikiri kwamba uso fulani una uwezekano mkubwa wa kuonekana kuliko nyingine yoyote, hivyo uwezekano wa kupiga namba yoyote ni\(16\).
| Matokeo | Roll ya 1 | Roll ya 2 | Roll ya 3 | Roll ya 4 | Roll ya 5 | Roll ya 6 |
|---|---|---|---|---|---|---|
| Uwezekano | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) |
Hapana. Probabilities inaweza kuelezwa kama sehemu ndogo, decimals, au percents. Uwezekano lazima daima kuwa idadi kati\(0\) na\(1\), umoja wa\(0\) na\(1\).
Probabilities ya Computing ya Matokeo Sawa uwezekano
Hebu\(S\) kuwa nafasi ya sampuli kwa jaribio. Wakati uchunguzi uwezekano, tukio ni subset yoyote ya\(S\). Wakati matokeo ya majaribio yote ni sawa uwezekano, tunaweza kupata uwezekano wa tukio kwa kugawa idadi ya matokeo katika tukio na idadi ya matokeo katika\(S\). Tuseme mchemraba wa namba umevingirwa, na tuna nia ya kupata uwezekano wa tukio hilo “kupiga namba chini ya au sawa na 4.” Kuna 4 matokeo iwezekanavyo katika tukio na 6 matokeo iwezekanavyo katika\(S\), hivyo uwezekano wa tukio ni\(\dfrac{4}{6}=\dfrac{2}{3}\).
Uwezekano wa tukio\(E\) katika jaribio la nafasi ya sampuli\(S\) na matokeo sawa yanatolewa na
\[P(E)=\dfrac{\text{number of elements in }E}{\text{number of elements in }S}=\dfrac{n(E)}{n(S)}\]
\(E\)ni subset ya\(S\), hivyo daima ni kweli kwamba\(0≤P(E)≤1\).
Mchemraba wa namba umevingirwa. Pata uwezekano wa kupiga idadi isiyo ya kawaida.
Suluhisho
Tukio “rolling idadi isiyo ya kawaida” ina matokeo matatu. Kuna matokeo\(6\) sawa katika nafasi ya sampuli. Gawanya ili kupata uwezekano wa tukio hilo.
\(P(E)=\dfrac{3}{6}=\dfrac{1}{2}\)
Mchemraba wa namba umevingirwa. Kupata uwezekano wa rolling idadi kubwa kuliko\(2\).
- Jibu
-
\(\dfrac{2}{3}\)
Computing Uwezekano wa Muungano wa Matukio mawili
Sisi ni mara nyingi nia ya kupata uwezekano kwamba moja ya matukio mbalimbali hutokea. Tuseme sisi ni kucheza mchezo kadi, na sisi kushinda kama kadi ya inayotolewa ni ama moyo au mfalme. Tutakuwa na nia ya kupata uwezekano wa kadi inayofuata kuwa moyo au mfalme. Muungano wa matukio mawili\(E\) na\(F\), yaliyoandikwa\(E\cup F\), ni tukio linalotokea ikiwa ama au matukio yote yanatokea.
\[P(E\cup F)=P(E)+P(F)−P(E\cap F)\]
Tuseme spinner katika Kielelezo\(\PageIndex{2}\) ni spun. Tunataka kupata uwezekano wa inazunguka machungwa au inazunguka a\(b\).
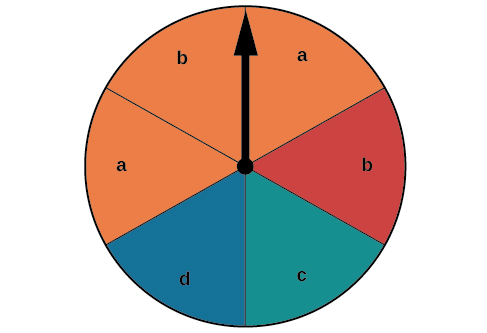
Kielelezo\(\PageIndex{2}\): Chati ya pie na chaguzi sita.
Kuna jumla ya\(6\) sehemu, na\(3\) kati yao ni machungwa. Hivyo uwezekano wa machungwa inazunguka ni\(\dfrac{3}{6}=\dfrac{1}{2}\). Kuna jumla ya\(6\) sehemu, na\(2\) wao wana\(b\). Hivyo uwezekano wa kuzunguka\(b\) ni\(\dfrac{2}{6}=\dfrac{1}{3}\). Kama sisi aliongeza probabilities hizi mbili, tutakuwa kuhesabu sekta hiyo ni ya machungwa na mara\(b\) mbili. Ili kupata uwezekano wa inazunguka machungwa au a\(b\), tunahitaji kuondoa uwezekano kwamba sekta ni ya machungwa na ina\(b\).
\(\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{6}=\dfrac{2}{3}\)
Uwezekano wa kuzunguka machungwa au\(b\) ni\(\dfrac{2}{3}\).
Uwezekano wa muungano wa matukio mawili\(E\) na\(F\) (imeandikwa\(E\cup F\)) ni sawa na jumla ya uwezekano wa\(E\) na uwezekano wa\(F\) kupunguza uwezekano wa\(E\) na\(F\) kutokea pamoja (ambayo inaitwa makutano ya\(E\) na\(F\) na imeandikwa kama\(E\cap F\)).
\[P(E\cup F)=P(E)+P(F)−P(E\cap F)\]
Kadi hutolewa kutoka kwenye staha ya kawaida. Pata uwezekano wa kuchora moyo au a\(7\).
Suluhisho
Staha ya kawaida ina idadi sawa ya mioyo, almasi, vilabu, na spades. Hivyo uwezekano wa kuchora moyo ni\(\dfrac{1}{4}\). Kuna nne\(7s\) katika staha kiwango, na kuna jumla ya\(52\) kadi. Hivyo uwezekano wa kuchora\(7\) ni\(\dfrac{1}{13}\).
kadi tu katika staha kwamba ni wote moyo na\(7\) ni\(7\) ya mioyo, hivyo uwezekano wa kuchora wote moyo na\(7\) ni\(\dfrac{1}{52}\). Mbadala\(P(H)=\dfrac{1}{4}\),\(P(7)=\dfrac{1}{13}\), na\(P(H\cap 7)=\dfrac{1}{52}\) katika formula.
\[\begin{align*} P(E\cup F) &=P(E)+P(F)−P(E\cap F) \\[4pt] &=\dfrac{1}{4}+\dfrac{1}{13}−\dfrac{1}{52} \\[4pt] &=\dfrac{4}{13} \end{align*}\]
Uwezekano wa kuchora moyo au\(7\) ni\(\dfrac{4}{13}\).
Kadi hutolewa kutoka kwenye staha ya kawaida. Pata uwezekano wa kuchora kadi nyekundu au ace.
- Jibu
-
\(\dfrac{7}{13}\)
Computing Uwezekano wa Matukio Pande Exclusive
Tuseme spinner katika Kielelezo\(\PageIndex{2}\) ni spun tena, lakini wakati huu sisi ni nia ya uwezekano wa inazunguka machungwa au a\(d\). Hakuna sekta ambayo ni ya machungwa na yana\(d\), hivyo matukio haya mawili hawana matokeo kwa pamoja. Matukio yanasemekana kuwa matukio ya kipekee wakati hawana matokeo sawa. Kwa sababu hakuna kuingiliana, hakuna kitu cha kuondoa, hivyo formula ya jumla ni
\[P(E\cap F)=P(E)+P(F)\]
Kumbuka kwamba kwa matukio ya kipekee, makutano ya\(E\) na\(F\) ni kuweka tupu. Uwezekano wa kuzunguka machungwa ni\(\dfrac{3}{6}=\dfrac{1}{2}\) na uwezekano wa kuzunguka\(d\) ni\(\dfrac{1}{6}\). Tunaweza kupata uwezekano wa inazunguka machungwa au\(d\) tu kwa kuongeza probabilities mbili.
\[\begin{align*} P(E\cap F)&=P(E)+P(F) \\[4pt] &=\dfrac{1}{2}+\dfrac{1}{6} \\ &=\dfrac{2}{3} \end{align*}\]
Uwezekano wa kuzunguka machungwa au\(d\) ni\(\dfrac{2}{3}\).
Uwezekano wa muungano wa matukio mawili ya kipekee\(E\) na\(F\) hutolewa na
\[P(E\cap F)=P(E)+P(F)\]
- Tambua idadi ya matokeo ya tukio la kwanza.
- Pata uwezekano wa tukio la kwanza.
- Tambua idadi ya matokeo ya tukio la pili.
- Pata uwezekano wa tukio la pili.
- Ongeza uwezekano.
Kadi hutolewa kutoka kwenye staha ya kawaida. Pata uwezekano wa kuchora moyo au jembe.
Suluhisho
Matukio ya “kuchora moyo” na “kuchora jembe” ni ya pekee kwa sababu hayawezi kutokea kwa wakati mmoja. Uwezekano wa kuchora moyo ni\(\dfrac{1}{4}\), na uwezekano wa kuchora jembe pia\(\dfrac{1}{4}\), hivyo uwezekano wa kuchora moyo au jembe ni
\(\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{2}\)
Kadi hutolewa kutoka kwenye staha ya kawaida. Pata uwezekano wa kuchora ace au mfalme.
- Jibu
-
\(\dfrac{2}{13}\)
Kutumia Kanuni inayosaidia ili kukokotoa probabilities
Tumejadili jinsi ya kuhesabu uwezekano kwamba tukio litatokea. Wakati mwingine, tuna nia ya kupata uwezekano kwamba tukio halitatokea. Msaidizi wa tukio\(E\), lililoashiria\(E′\), ni seti ya matokeo katika nafasi ya sampuli ambayo haipo\(E\). Kwa mfano, tuseme tuna nia ya uwezekano kwamba farasi itapoteza mbio. Ikiwa tukio\(W\) ni farasi kushinda mbio, basi msaidizi wa tukio\(W\) ni farasi kupoteza mbio.
Ili kupata uwezekano kwamba farasi hupoteza mbio, tunahitaji kutumia ukweli kwamba jumla ya uwezekano wote katika mfano wa uwezekano lazima iwe\(1\).
\[P(E′)=1−P(E)\]
Uwezekano wa kushinda farasi umeongezwa kwa uwezekano wa kupoteza farasi lazima iwe sawa na\(1\). Kwa hiyo, kama uwezekano wa farasi kushinda mbio ni\(\dfrac{1}{9}\), uwezekano wa farasi kupoteza mbio ni tu
\(1−\dfrac{1}{9}=\dfrac{8}{9}\)
Uwezekano kwamba msaidizi wa tukio litatokea hutolewa na
\[P(E′)=1−P(E)\]
Vipande viwili vya namba sita vimevingirwa.
- Kupata uwezekano kwamba jumla ya idadi akavingirisha ni chini ya au sawa na\(3\).
- Kupata uwezekano kwamba jumla ya idadi limekwisha ni kubwa kuliko\(3\).
Suluhisho
Hatua ya kwanza ni kutambua nafasi ya sampuli, ambayo ina matokeo yote iwezekanavyo. Kuna idadi mbili cubes, na kila mchemraba idadi ina matokeo sita iwezekanavyo. Kutumia Kanuni ya Kuzidisha, tunaona kwamba kuna\(6×6\), au matokeo ya\(36\) jumla yanayowezekana. Kwa hiyo, kwa mfano,\(1-1\) inawakilisha\(1\) limekwisha kwenye mchemraba kila namba.
| \(1-1\) | \(1-2\) | \(1-3\) | \(1-4\) | \(1-5\) | \(1-6\) |
| \(2-1\) | \(2-2\) | \(2-3\) | \(2-4\) | \(2-5\) | \(2-6\) |
| \(3-1\) | \(3-2\) | \(3-3\) | \(3-4\) | \(3-5\) | \(3-6\) |
| \(4-1\) | \(4-2\) | \(4-3\) | \(4-4\) | \(4-5\) | \(4-6\) |
| \(5-1\) | \(5-2\) | \(5-3\) | \(5-4\) | \(5-5\) | \(5-6\) |
| \(6-1\) | \(6-2\) | \(6-3\) | \(6-4\) | \(6-5\) | \(6-6\) |
- Tunahitaji kuhesabu idadi ya njia za kupakia jumla ya\(3\) au chini. Hizi zitajumuisha matokeo yafuatayo:\(1-1\)\(1-2\),, na\(2-1\). Kwa hiyo kuna njia tatu tu za kupakia jumla ya\(3\) au chini. Uwezekano ni
\(\dfrac{3}{36}=\dfrac{1}{12}\)
- Badala ya kuorodhesha uwezekano wote, tunaweza kutumia Sheria inayosaidia. Kwa sababu sisi tayari kupatikana uwezekano wa inayosaidia ya tukio hili, tunaweza tu Ondoa kwamba uwezekano kutoka\(1\) kupata uwezekano kwamba jumla ya idadi limekwisha ni kubwa kuliko\(3\).
\[\begin{align*} P(E')&=1-P(E)\\ &=1-\dfrac{1}{12}\\ &=\dfrac{11}{12} \end{align*}\]
Cubes mbili za namba zimevingirwa. Tumia Kanuni inayosaidia ili kupata uwezekano kwamba jumla ni chini ya\(10\).
- Jibu
-
\(\dfrac{5}{6}\)
Computing uwezekano Kutumia Hesabu Theory
Matatizo mengi ya kuvutia ya uwezekano yanahusisha kanuni za kuhesabu, vibali, na mchanganyiko. Katika matatizo haya, tutatumia vibali na mchanganyiko ili kupata idadi ya vipengele katika matukio na nafasi za sampuli. Matatizo haya yanaweza kuwa ngumu, lakini yanaweza kufanywa rahisi kwa kuvunja katika matatizo madogo ya kuhesabu.
Fikiria, kwa mfano, kwamba duka ina simu\(8\) za mkononi na ile\(3\) ya wale ni duni. Tunaweza kutaka kupata uwezekano kwamba wanandoa kununua\(2\) simu inapata\(2\) simu ambazo si defective. Ili kutatua tatizo hili, tunahitaji kuhesabu njia zote za kuchagua\(2\) simu ambazo hazina kasoro pamoja na njia zote za kuchagua\(2\) simu. Kuna\(5\) simu ambazo hazipatikani, kwa hiyo kuna\(C(5,2)\) njia za kuchagua\(2\) simu ambazo hazipatikani. Kuna\(8\) simu, kwa hiyo kuna\(C(8,2)\) njia za kuchagua\(2\) simu. Uwezekano wa kuchagua\(2\) simu ambazo hazipatikani ni:
\[ \begin{align*} \dfrac{\text{ways to select 2 phones that are not defective}}{\text{ways to select 2 phones}}&=\dfrac{C(5,2)}{C(8,2)} \\[4pt] &=\dfrac{10}{28} \\[4pt] &=\dfrac{5}{14} \end{align*}\]
Mtoto huchagua\(5\) vidole kutoka kwenye bin iliyo na\(3\) bunnies,\(5\) mbwa, na\(6\) huzaa.
- Pata uwezekano kwamba huzaa tu huchaguliwa.
- Pata uwezekano kwamba\(2\) huzaa na\(3\) mbwa huchaguliwa.
- Pata uwezekano kwamba angalau\(2\) mbwa huchaguliwa.
Suluhisho
- Tunahitaji kuhesabu idadi ya njia za kuchagua huzaa tu na idadi ya njia zinazowezekana za kuchagua\(5\) vidole. Kuna\(6\) huzaa, kwa hiyo kuna\(C(6,5)\) njia za kuchagua\(5\) huzaa. Kuna\(14\) vidole, kwa hiyo kuna\(C(14,5)\) njia za kuchagua\(5\) vidole vyovyote.
\(\dfrac{C(6,5)}{C(14,5)}=\dfrac{6}{2,002}=\dfrac{3}{1,001}\)
- Tunahitaji kuhesabu idadi ya njia za kuchagua\(2\) bears na\(3\) mbwa na idadi ya njia zinazowezekana za kuchagua\(5\) vidole. Kuna\(6\) huzaa, kwa hiyo kuna\(C(6,2)\) njia za kuchagua\(2\) huzaa. Kuna\(5\) mbwa, kwa hiyo kuna\(C(5,3)\) njia za kuchagua\(3\) mbwa. Kwa kuwa tunachagua bears na mbwa kwa wakati mmoja, tutatumia Kanuni ya Kuzidisha. Kuna\(C(6,2)⋅C(5,3)\) njia za kuchagua\(2\) huzaa na\(3\) mbwa. Tunaweza kutumia matokeo haya ili kupata uwezekano.
\(\dfrac{C(6,2)C(5,3)}{C(14,5)}=\dfrac{15⋅10}{2,002}=\dfrac{75}{1,001}\)
- Mara nyingi ni rahisi kutatua “angalau” matatizo kwa kutumia Kanuni inayosaidia. Tutaanza kwa kutafuta uwezekano kwamba wachache kuliko\(2\) mbwa huchaguliwa. Ikiwa chini ya\(2\) mbwa huchaguliwa, basi ama mbwa hakuna inaweza kuchaguliwa, au\(1\) mbwa inaweza kuchaguliwa.
Wakati hakuna mbwa huchaguliwa,\(5\) vidole vyote vinatoka kwenye\(9\) vidole ambavyo si mbwa. Kuna\(C(9,5)\) njia za kuchagua vidole kutoka kwenye\(9\) vidole ambavyo si mbwa. Kwa kuwa kuna\(14\) vidole, kuna\(C(14,5)\) njia za kuchagua\(5\) vidole kutoka kwenye vidole vyote.
\(\dfrac{C(9,5)}{C(14,5)}=\dfrac{63}{1,001}\)
Ikiwa kuna\(1\) mbwa aliyechaguliwa, basi\(4\) vidole vinapaswa kuja kutoka kwenye\(9\) vidole ambavyo si mbwa, na\(1\) lazima ziweke kutoka kwa\(5\) mbwa. Kwa kuwa tunachagua mbwa wote na vidole vingine kwa wakati mmoja, tutatumia Kanuni ya Kuzidisha. Kuna\(C(5,1)⋅C(9,4)\) njia za kuchagua\(1\) mbwa na toy\(1\) nyingine.
\(\dfrac{C(5,1)C(9,4)}{C(14,5)}=\dfrac{5⋅126}{2,002}=\dfrac{315}{1,001}\)
Kwa sababu matukio haya bila kutokea pamoja na kwa hiyo ni pande kipekee, sisi kuongeza probabilities kupata uwezekano kwamba wachache kuliko\(2\) mbwa ni kuchaguliwa.
\(\dfrac{63}{1,001}+\dfrac{315}{1,001}=\dfrac{378}{1,001}\)
Sisi kisha Ondoa kwamba uwezekano kutoka\(1\) kupata uwezekano kwamba angalau\(2\) mbwa ni kuchaguliwa.
\(1−\dfrac{378}{1,001}=\dfrac{623}{1,001}\)
mtoto nasibu kuchagua\(3\) gumballs kutoka chombo kufanya gumballs\(4\) zambarau, gumballs\(8\) njano, na gumballs\(2\) kijani.
- Kupata uwezekano kwamba\(3\) gumballs wote kuchaguliwa ni zambarau.
- Kupata uwezekano kwamba hakuna gumballs njano ni kuchaguliwa.
- Pata uwezekano kwamba angalau gumball ya\(1\) njano imechaguliwa.
- Jibu
-
\(\dfrac{1}{91}\)
- Jibu
-
\(\dfrac{5}{91}\)
- Jibu
-
\(\dfrac{86}{91}\)
Fikia rasilimali hizi mtandaoni kwa maelekezo ya ziada na mazoezi na uwezekano.
Ziara tovuti hii kwa maswali ya ziada mazoezi kutoka Learningpod.
Mlinganyo muhimu
| uwezekano wa tukio na matokeo sawa | \(P(E)=\dfrac{n(E)}{n(S)}\) |
| uwezekano wa umoja wa matukio mawili | \(P(E\cup F)=P(E)+P(F)−P(E\cap F)\) |
| uwezekano wa muungano wa matukio ya kipekee | \(P(E\cup F)=P(E)+P(F)\) |
| uwezekano wa msaidizi wa tukio | \(P(E')=1−P(E)\) |
Dhana muhimu
- Uwezekano daima ni idadi kati\(0\) na\(1\), ambapo\(0\) maana tukio haliwezekani na\(1\) ina maana tukio ni fulani.
- probabilities katika mfano uwezekano lazima jumla ya\(1\). Angalia Mfano\(\PageIndex{1}\).
- Wakati matokeo ya jaribio ni uwezekano wote sawa, tunaweza kupata uwezekano wa tukio kwa kugawa idadi ya matokeo katika tukio hilo na idadi ya matokeo katika nafasi ya sampuli kwa majaribio. Angalia Mfano\(\PageIndex{2}\).
- Ili kupata uwezekano wa muungano wa matukio mawili, tunaongeza uwezekano wa matukio mawili na kuondoa uwezekano kwamba matukio yote hutokea wakati huo huo. Angalia Mfano\(\PageIndex{3}\).
- Ili kupata uwezekano wa umoja wa matukio mawili ya kipekee, tunaongeza uwezekano wa kila matukio. Angalia Mfano\(\PageIndex{4}\).
- Uwezekano wa msaidizi wa tukio ni tofauti kati\(1\) na uwezekano kwamba tukio hutokea. Angalia Mfano\(\PageIndex{5}\).
- Katika matatizo mengine ya uwezekano, tunahitaji kutumia vibali na mchanganyiko ili kupata idadi ya vipengele katika matukio na nafasi za sampuli. Angalia Mfano\(\PageIndex{6}\).


