10.1: duaradufu

Malengo ya kujifunza

• Andika equations ya ellipses katika fomu ya kawaida.
• Grafu ellipses katikati katika asili.
• Grafu ellipses si katikati katika asili.
• Tatua matatizo yaliyotumika yanayohusisha ellipses.

Je, unaweza kufikiria kusimama kwenye mwisho mmoja wa chumba kikubwa na bado una uwezo wa kusikia whisper kutoka kwa mtu amesimama upande mwingine? National Statuary Hall katika Washington, D.C., inavyoonekana katika Kielelezo$\PageIndex{1}$, ni chumba kama. Ni chumba cha umbo la mviringo kinachoitwa chumba cha kunong'unika kwa sababu umbo hufanya iwezekanavyo kwa sauti kusafiri kando ya kuta. Katika sehemu hii, sisi kuchunguza sura ya chumba hiki na maombi yake halisi ya dunia, ikiwa ni pamoja na jinsi mbali mbali watu wawili katika Statuary Hall wanaweza kusimama na bado kusikia kila mmoja whisper.

Kielelezo$\PageIndex{1}$: Hall ya Taifa ya Statuary huko Washington, D.C. (mikopo: Greg Palmer, Flickr)

Kuandika equations ya ellipses katika Fomu ya Standard

Sehemu ya conic, au conic, ni sura inayotokana na kuingiliana koni ya mviringo sahihi na ndege. Pembe ambayo ndege inakabiliana na koni huamua sura, kama inavyoonekana kwenye Mchoro$\PageIndex{2}$.

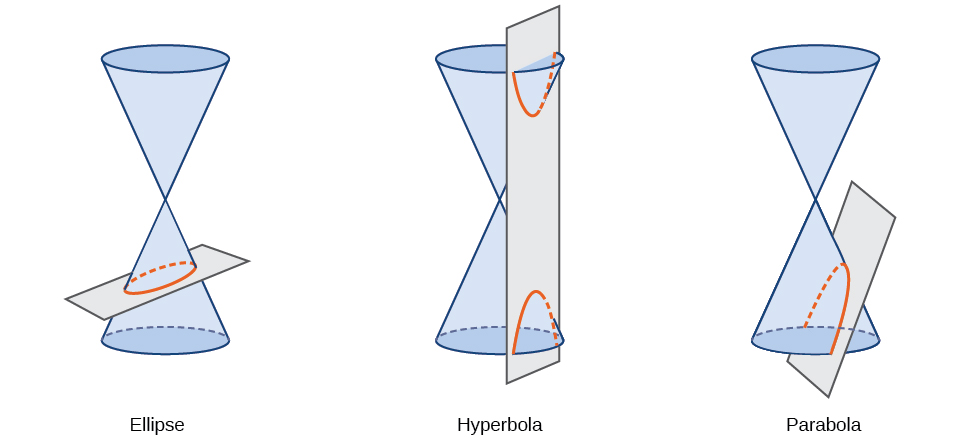
Kielelezo$\PageIndex{2}$

Sehemu za conic pia zinaweza kuelezewa na seti ya pointi katika ndege ya kuratibu. Baadaye katika sura hii, tutaona kwamba grafu ya equation yoyote quadratic katika vigezo mbili ni sehemu conic. Ishara za equations na coefficients ya maneno ya kutofautiana huamua sura. Sehemu hii inalenga katika tofauti nne za fomu ya kawaida ya equation kwa duaradufu. Ellipse ni seti ya pointi zote$(x,y)$ katika ndege kama vile jumla ya umbali wao kutoka pointi mbili fasta ni mara kwa mara. Kila hatua iliyowekwa inaitwa lengo (wingi: foci).

Tunaweza kuteka duaradufu kwa kutumia kipande cha kadibodi, thumbtacks mbili, penseli, na kamba. Weka thumbtacks kwenye kadi ili kuunda foci ya ellipse. Kata kipande cha kamba kwa muda mrefu kuliko umbali kati ya thumbtacks mbili (urefu wa kamba inawakilisha mara kwa mara katika ufafanuzi). Tack kila mwisho wa kamba kwa kadi, na kufuatilia Curve na kalamu uliofanyika taut dhidi ya kamba. Matokeo ni ellipse. Angalia Kielelezo$\PageIndex{3}$.

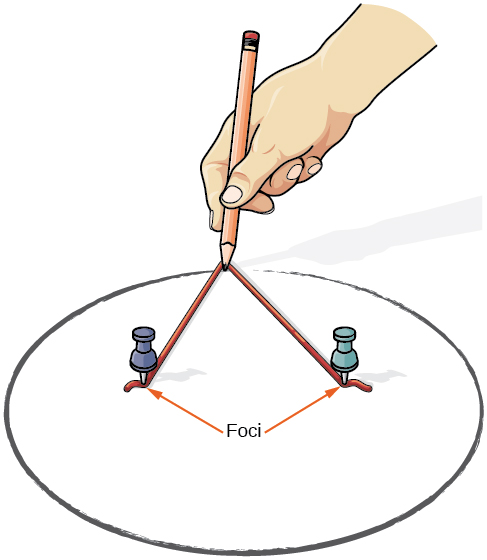
Kielelezo$\PageIndex{3}$

Kila duaradufu ina axes mbili za ulinganifu. Mhimili mrefu huitwa mhimili mkuu, na mhimili mfupi huitwa mhimili mdogo. Kila mwisho wa mhimili mkubwa ni vertex ya duaradufu (wingi: vertices), na kila mwisho wa mhimili mdogo ni ushirikiano vertex ya duaradufu. Katikati ya ellipse ni midpoint ya axes kuu na ndogo. Axes ni perpendicular katikati. Foci daima uongo juu ya mhimili mkubwa, na jumla ya umbali kutoka foci kwa hatua yoyote juu ya duaradufu (jumla ya mara kwa mara) ni kubwa kuliko umbali kati ya foci (Kielelezo$\PageIndex{4}$).

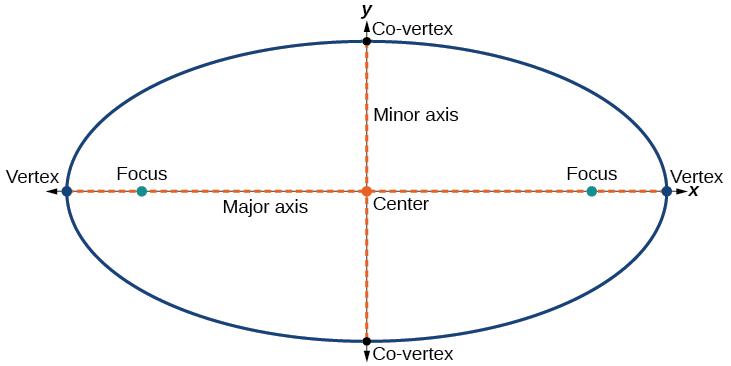
Kielelezo$\PageIndex{4}$

Katika sehemu hii, tunazuia ellipses kwa wale ambao wamewekwa kwa wima au usawa katika ndege ya kuratibu. Hiyo ni, axes itakuwa ama kulala au kuwa sawa na$x$ - na$y$ -axes. Baadaye katika sura, tutaona ellipses zinazozungushwa katika ndege ya kuratibu.

Kufanya kazi na ellipses ya usawa na wima katika ndege ya kuratibu, tunazingatia matukio mawili: yale ambayo yanazingatia asili na yale yanayotokana na hatua nyingine isipokuwa asili. Kwanza tutajifunza kupata equations ya ellipses, na kisha tutajifunza jinsi ya kuandika equations ya ellipses kwa fomu ya kawaida. Baadaye tutatumia kile tunachojifunza kuteka grafu.

Deriving Equation ya Ellipse unaozingatia katika Mwanzo

Ili kupata equation ya ellipse iliyozingatia asili, tunaanza na foci$(−c,0)$ na$(c,0)$. Dellipse ni seti ya pointi zote$(x,y)$ kama vile jumla ya umbali kutoka$(x,y)$ kwa foci ni mara kwa mara, kama inavyoonekana katika Kielelezo$\PageIndex{5}$.

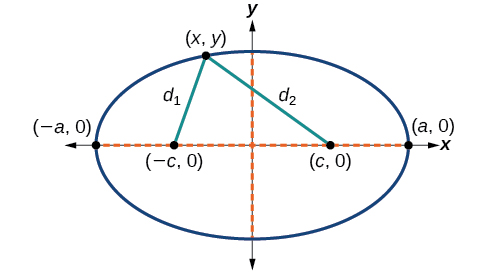
Kielelezo$\PageIndex{5}$

Ikiwa$(a,0)$ ni vertex ya ellipse, umbali kutoka$(−c,0)$ kwa$(a,0)$ ni$a−(−c)=a+c$. Umbali kutoka$(c,0)$ kwa$(a,0)$ ni$a−c$. Jumla ya umbali kutoka foci hadi vertex ni

$(a+c)+(a−c)=2a$

Ikiwa$(x,y)$ ni hatua juu ya duaradufu, basi tunaweza kufafanua vigezo vifuatavyo:

• $d_1=$umbali kutoka$(−c,0)$ kwa$(x,y)$
• $d_2=$umbali kutoka$(c,0)$ kwa$(x,y)$

Kwa ufafanuzi wa duaradufu,$d_1+d_2$ ni mara kwa mara kwa hatua yoyote$(x,y)$ juu ya duaradufu. Tunajua kwamba jumla ya umbali huu ni$2a$ kwa vertex$(a,0)$. Inafuata kwamba$d_1+d_2=2a$ kwa hatua yoyote juu ya ellipse. Tutaanza derivation kwa kutumia formula ya umbali. Wengine wa derivation ni algebraic.

$$\begin{align*} d_1+d_2&= 2a\\ \sqrt{{(x-(-c))}^2+{(y-0)}^2}+\sqrt{{(x-c)}^2+{(y-0)}^2}&=2a\qquad \text{Distance formula}\\ \sqrt{{(x+c)}^2+y^2}+\sqrt{{(x-c)}^2+y^2}&=2a\qquad \text{Simplify expressions.}\\ \sqrt{{(x+c)}^2+y^2}&=2a-\sqrt{{(x-c)}^2+y^2}\qquad \text{Move radical to opposite side.}\\ {(x+c)}^2+y^2&={\left[2a-\sqrt{{(x-c)}^2+y^2}\right]}^2\qquad \text{Square both sides.}\\ x^2+2cx+c^2+y^2&=4a^2-4a\sqrt{{(x-c)}^2+y^2}+{(x-c)}^2+y^2\qquad \text{Expand the squares.}\\ x^2+2cx+c^2+y^2&=4a^2-4a\sqrt{{(x-c)}^2+y^2}+x^2-2cx+c^2+y^2\qquad \text{Expand remaining squares.}\\ 2cx&=4a^2-4a\sqrt{{(x-c)}^2+y^2}-2cx\qquad \text{Combine like terms.}\\ 4cx-4a^2&=-4a\sqrt{{(x-c)}^2+y^2}\qquad \text{Isolate the radical.}\\ cx-a^2&=-a\sqrt{{(x-c)}^2+y^2}\qquad \text{Divide by 4.}\\ {\left[ cx-a^2\right]}^2&=a^2{\left[ \sqrt{{(x-c)}^2+y^2}\right] }^2\qquad \text{Square both sides.}\\ c^2x^2-2a^2cx+a^4&=a^2(x^2-2cx+c^2+y^2)\qquad \text{Expand the squares.}\\ c^2x^2-2a^2cx+a^4&=a^2x^2-2a^2cx+a^2c^2+a^2y^2\qquad \text{Distribute } a^2\\ a^2x^2-c^2x^2+a^2y^2&=a^4-a^2c^2\qquad \text{Rewrite.}\\ x^2(a^2-c^2)+a^2y^2&=a^2(a^2-c^2)\qquad \text{Factor common terms.}\\ x^2b^2+a^2y^2&=a^2b^2\qquad \text{Set } b^2=a^2-c^2\\ \dfrac{x^2b^2}{a^2b^2}+\dfrac{a^2y^2}{a^2b^2}&=\dfrac{a^2b^2}{a^2b^2}\qquad \text{Divide both sides by } a^2b^2\\ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}&=1\qquad \text{Simplify} \end{align*}$$

Hivyo, equation ya kiwango cha duaradufu$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ ni.Equation hii inafafanua duaradufu unaozingatia asili. Ikiwa$a>b$, ellipse imetambulishwa zaidi katika mwelekeo usio na usawa, na ikiwa$b>a$, ellipse imetambulishwa zaidi katika mwelekeo wa wima.

Kuandika Ulinganisho wa ellipses unaozingatia Mwanzo katika Fomu ya Standard

Aina za equations za kawaida zinatuambia kuhusu vipengele muhimu vya grafu. Kuchukua muda kukumbuka baadhi ya aina ya kiwango cha equations tumekuwa kazi na katika siku za nyuma: linear, quadratic, ujazo, kielelezo, logarithmic, na kadhalika. Kwa kujifunza kutafsiri aina ya kiwango cha usawa, tunaunganisha uhusiano kati ya uwakilishi wa algebraic na kijiometri wa matukio ya hisabati.

Makala muhimu ya ellipse ni kituo chake, vertices, co-vertices, foci, na urefu na nafasi za axes kuu na ndogo. Kama vile kwa equations nyingine, tunaweza kutambua yote ya makala haya tu kwa kuangalia fomu ya kiwango cha equation. Kuna tofauti nne za fomu ya kawaida ya ellipse. Tofauti hizi zinajumuishwa kwanza na eneo la kituo (asili au si asili), na kisha kwa nafasi (usawa au wima). Kila huwasilishwa pamoja na maelezo ya jinsi sehemu za equation zinahusiana na grafu. Kufafanua sehemu hizi inatuwezesha kuunda picha ya akili ya ellipse.

AINA YA KAWAIDA YA EQUATION YA DUARADUFU NA KATIKATI$(0,0)$

Aina ya kawaida ya equation ya ellipse na katikati$(0,0)$ na mhimili kuu kwenye$x$ -axis ni

$$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$$

wapi

• $a>b$
• urefu wa mhimili mkubwa ni$2a$
• kuratibu za vipeo ni$(\pm a,0)$
• urefu wa mhimili mdogo ni$2b$
• kuratibu ya vyeo vya ushirikiano ni$(0,\pm b)$
• kuratibu ya foci ni$(\pm c,0)$, wapi$c^2=a^2−b^2$. Angalia Kielelezo$\PageIndex{6a}$.

Aina ya kawaida ya equation ya ellipse na katikati$(0,0)$ na mhimili kuu kwenye$y$ -axis ni

$$\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1$$

wapi

• $a>b$
• urefu wa mhimili mkubwa ni$2a$
• kuratibu za vipeo ni$(0,\pm a)$
• urefu wa mhimili mdogo ni$2b$
• kuratibu ya vyeo vya ushirikiano ni$(\pm b,0)$
• kuratibu ya foci ni$(0,\pm c)$, wapi$c^2=a^2−b^2$. Angalia Kielelezo$\PageIndex{6b}$.

Kumbuka kwamba vertices, co-vertices, na foci ni kuhusiana na equation$c^2=a^2−b^2$. Tunapopewa kuratibu za foci na vipeo vya duaradufu, tunaweza kutumia uhusiano huu ili kupata equation ya duaradufu katika fomu ya kawaida.

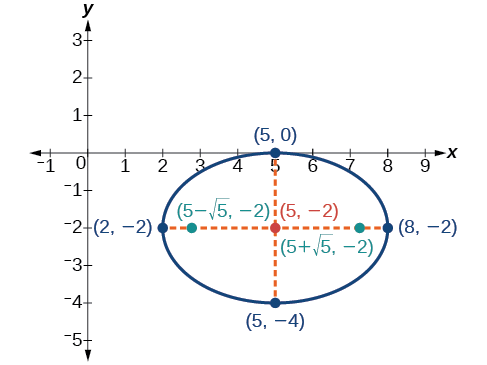
Kielelezo$\PageIndex{6}$: (a) ellipse ya usawa na kituo$(0,0)$ (b) duaradufu ya wima na kituo$(0,0)$

Jinsi ya: Kutokana na vertices na foci ya ellipse iliyozingatia asili, andika equation yake kwa fomu ya kawaida

1. Kuamua kama mhimili mkubwa uongo juu ya x - au y -axis.
   • Ikiwa kuratibu zilizopewa za vertices na foci zina fomu$(\pm a,0)$ na$(\pm c,0)$ kwa mtiririko huo, basi mhimili mkubwa ni x -axis. Tumia fomu ya kawaida$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$
   • Ikiwa kuratibu zilizopewa za vertices na foci zina fomu$(0,\pm a)$ na$(\pm c,0)$, kwa mtiririko huo, basi mhimili mkubwa ni y -axis. Tumia fomu ya kawaida$\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1$
2. Tumia equation$c^2=a^2−b^2$, pamoja na kuratibu zilizotolewa za vertices na foci, kutatua$b^2$.
3. Badilisha maadili kwa$a^2$ na$b^2$ ndani ya fomu ya kiwango cha equation iliyowekwa katika Hatua ya 1.

Mfano$\PageIndex{1}$: Writing the Equation of an Ellipse Centered at the Origin in Standard Form

Je, ni fomu ya kawaida ya equation ya ellipse ambayo ina vertices$(\pm 8,0)$ na foci$(\pm 5,0)$?

Suluhisho

Foci ni juu ya$x$ -axis, hivyo mhimili mkubwa ni$x$ -axis. Hivyo, equation itakuwa na fomu$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$

Vipeo ni$(\pm 8,0)$, hivyo$a=8$ na$a^2=64$.

Foci ni$(\pm 5,0)$, hivyo$c=5$ na$c^2=25$.

Tunajua kwamba vipeo na foci vinahusiana na equation$c^2=a^2−b^2$. Kutatua kwa$b^2$, tuna:

$$\begin{align*} c^2&=a^2-b^2\\ 25&=64-b^2\qquad \text{Substitute for } c^2 \text{ and } a^2\\ b^2&=39\qquad \text{Solve for } b^2 \end{align*}$$

Sasa tunahitaji tu mbadala$a^2=64$ na$b^2=39$ katika fomu ya kawaida ya equation. Equation ya duaradufu ni$\dfrac{x^2}{64}+\dfrac{y^2}{39}=1$.

Zoezi$\PageIndex{1}$

Je, ni fomu ya kawaida ya equation ya ellipse ambayo ina vertices$(0,\pm 4)$ na foci$(0,\pm \sqrt{15})$?

Jibu

$x^2+\dfrac{y^2}{16}=1$

Q & A

Je, tunaweza kuandika equation ya duaradufu unaozingatia katika asili kutokana kuratibu ya lengo moja tu na kipeo?

Ndiyo. Ellipses ni ya kawaida, hivyo kuratibu za vipeo vya duaradufu unaozunguka asili zitakuwa na fomu$(\pm a,0)$ au$(0, \pm a)$. Vile vile, kuratibu za foci zitakuwa na fomu$(\pm c,0)$ au$(0, \pm c)$. Kujua hili, tunaweza kutumia$a$ na$c$ kutoka kwa pointi zilizopewa, pamoja na equation$c^2=a^2−b^2$, kupata$b^2$.

Kuandika equations ya ellipses Si Centered katika Mwanzo

Kama grafu ya equations nyingine, grafu ya ellipse inaweza kutafsiriwa. Ikiwa duaradufu hutafsiriwa$h$$k$ vitengo kwa usawa na vitengo kwa wima, katikati ya ellipse itakuwa$(h,k)$. Matokeo tafsiri hii katika hali ya kawaida ya equation tuliona hapo awali, na$x$ kubadilishwa$(x−h)$ na y kubadilishwa na$(y−k)$.

AINA YA KAWAIDA YA EQUATION YA DUARADUFU NA KATIKATI$(H, K)$

Aina ya kawaida ya equation ya ellipse na katikati$(h, k)$ na mhimili kuu sambamba na$x$ -axis ni

$$\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1$$

wapi

• $a>b$
• urefu wa mhimili mkubwa ni$2a$
• kuratibu za vipeo ni$(h\pm a,k)$
• urefu wa mhimili mdogo ni$2b$
• kuratibu ya vyeo vya ushirikiano ni$(h,k\pm b)$
• kuratibu ya foci ni$(h\pm c,k)$, wapi$c^2=a^2−b^2$. Angalia Kielelezo$\PageIndex{7a}$.

Aina ya kawaida ya equation ya ellipse na katikati$(h,k)$ na mhimili kuu sambamba na$y$ -axis ni

$$\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1$$

wapi

• $a>b$
• urefu wa mhimili mkubwa ni$2a$
• kuratibu za vipeo ni$(h,k\pm a)$
• urefu wa mhimili mdogo ni$2b$
• kuratibu ya vyeo vya ushirikiano ni$(h\pm b,k)$
• kuratibu ya foci ni$(h,k\pm c)$, wapi$c^2=a^2−b^2$. Angalia Kielelezo$\PageIndex{7b}$.

Kama ilivyo na ellipses unaozingatia asili, ellipses ambazo zinakabiliwa na hatua$(h,k)$ zina vipeo, vyeo, na foci zinazohusiana na equation$c^2=a^2−b^2$. Tunaweza kutumia uhusiano huu pamoja na kanuni za midpoint na umbali ili kupata equation ya duaradufu katika fomu ya kawaida wakati vipeo na foci vinapewa.

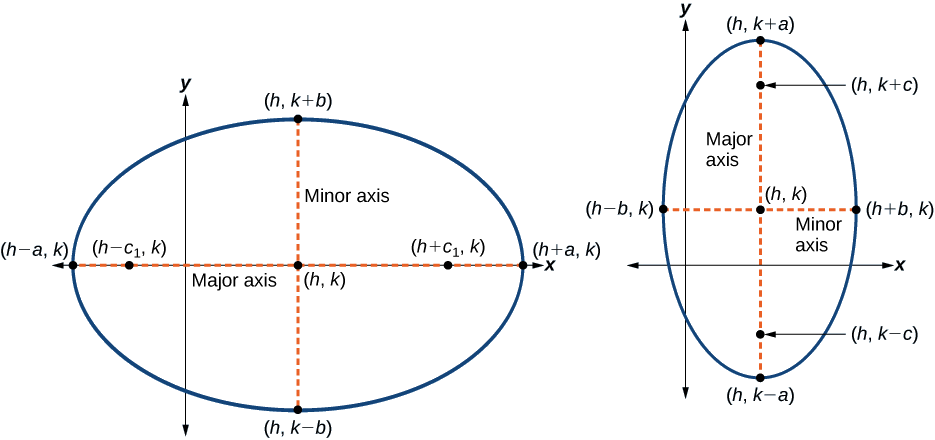
Kielelezo$\PageIndex{7}$: (a) ellipse ya usawa na kituo$(h,k)$ (b) duaradufu ya wima na kituo$(h,k)$

Jinsi ya: Kutokana na vertices na foci ya ellipse si katikati ya asili, kuandika equation yake katika fomu ya kawaida

1. Kuamua kama mhimili mkubwa ni sawa na$x$ - au$y$ -axis.
   • Ikiwa y -kuratibu ya vertices iliyotolewa na foci ni sawa, basi mhimili mkubwa ni sawa na$x$ -axis. Tumia fomu ya kawaida$\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1$
   • Ikiwa x -kuratibu ya vipeo vilivyopewa na foci ni sawa, basi mhimili mkubwa ni sawa na y -axis. Tumia fomu ya kawaida$\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1$
2. Tambua katikati ya ellipse$(h,k)$ kwa kutumia formula ya midpoint na kuratibu zilizopewa kwa vipeo.
3. Pata$a^2$ kwa kutatua urefu wa mhimili mkubwa$2a$, ambayo ni umbali kati ya vipeo vilivyopewa.
4. Pata$c^2$ kutumia$h$ na$k$, kupatikana katika Hatua ya 2, pamoja na kuratibu zilizopewa kwa foci.
5. Tatua kwa$b^2$ kutumia equation$c^2=a^2−b^2$.
6. Badilisha maadili kwa$h$,$k$$a^2$, na$b^2$ katika fomu ya kawaida ya equation iliyowekwa katika Hatua ya 1.

Mfano$\PageIndex{2}$: Writing the Equation of an Ellipse Centered at a Point Other Than the Origin

Je, ni fomu ya kawaida ya equation ya ellipse ambayo ina vertices$(−2,−8)$$(−2,2)$ na foci$(−2,−7)$ na$(−2,1)$?

Suluhisho

$x$Kuratibu -ya vertices na foci ni sawa, hivyo mhimili mkubwa ni sawa na$y$ -axis. Hivyo, equation ya ellipse itakuwa na fomu

$\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1 \nonumber$

Kwanza, tunatambua kituo,$(h,k)$. Kituo hicho ni nusu kati ya vipeo,$(−2,−8)$ na$(−2,2)$. Kutumia formula ya midpoint, tuna:

$$\begin{align} (h,k) &=\left(\dfrac{−2+(−2)}{2},\dfrac{−8+2}{2}\right) \nonumber \\ &=(−2,−3) \nonumber \end{align} \nonumber$$

Kisha, tunapata$a^2$. Urefu wa mhimili mkubwa$2a$, umefungwa na vertices. Sisi kutatua$a$ kwa kutafuta umbali kati ya y -kuratibu ya vertices.

$$\begin{align} 2a &=2−(−8) \nonumber \\ 2a &=10 \nonumber\\ a&=5 \nonumber \end{align} \nonumber$$

Hivyo$a^2=25$.

Sasa tunapata$c^2$. Foci hutolewa na$(h,k\pm c)$. Hivyo,$(h,k−c)=(−2,−7)$ na$(h,k+c)=(−2,1)$. Sisi badala ya$k=−3$ kutumia mojawapo ya pointi hizi kutatua kwa$c$.

$$\begin{align} k+c &=1 \nonumber \\ −3+c&=1 \nonumber \\ c&=4 \nonumber \end{align} \nonumber$$

Hivyo$c^2=16$.

Kisha, tunatatua kwa$b^2$ kutumia equation$c^2=a^2−b^2$.

$$\begin{align} c^2&=a^2−b^2 \nonumber \\ 16&=25−b^2 \nonumber \\ b^2&=9 \nonumber \end{align} \nonumber$$

Hatimaye, sisi badala ya maadili kupatikana kwa$h$,$k$$a^2$, na$b^2$ katika kiwango fomu equation kwa duaradufu:

$$\dfrac{{(x+2)}^2}{9}+\dfrac{{(y+3)}^2}{25}=1 \nonumber$$

Zoezi$\PageIndex{2}$

Je, ni fomu ya kawaida ya equation ya ellipse ambayo ina vertices$(−3,3)$$(5,3)$ na foci$(1−2\sqrt{3},3)$ na$(1+2\sqrt{3},3)$?

Jibu

$\dfrac{{(x−1)}^2}{16}+\dfrac{{(y−3)}^2}{4}=1 \nonumber$

Graphing ellipses Kuzingatia katika Mwanzo

Tu kama tunaweza kuandika equation kwa duaradufu kutokana grafu yake, tunaweza graph duaradufu kutokana equation yake. Ili grafu ya ellipses iliyozingatia asili, tunatumia fomu ya kawaida

$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1, a>b$kwa ellipses ya usawa

na

$\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1, a>b$kwa ellipses wima

Jinsi ya: Kutokana na fomu ya kiwango cha equation kwa duaradufu unaozingatia$(0, 0)$, sketch the graph.

1. Tumia aina za kawaida za equations ya ellipse ili kuamua mhimili mkubwa, vertices, co-vertices, na foci.
   • Ikiwa equation iko katika fomu$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$, wapi$a>b$, basi
     • mhimili kuu ni$x$ -axis
     • kuratibu za vipeo ni$(\pm a,0)$
     • kuratibu ya vyeo vya ushirikiano ni$(0,\pm b)$
     • kuratibu ya foci ni$(\pm c,0)$
   • Ikiwa equation iko katika fomu$x^2b^2+y^2a^2=1$, wapi$a>b$, basi
     • mhimili kuu ni$y$ -axis
     • kuratibu za vipeo ni$(0,\pm a)$
     • kuratibu ya vyeo vya ushirikiano ni$(\pm b,0)$
     • kuratibu ya foci ni$(0,\pm c)$
2. Tatua kwa$c$ kutumia equation$c^2=a^2−b^2$.
3. Panda katikati, vipeo, vyeo vya ushirikiano, na foci katika ndege ya kuratibu, na kuteka safu ya laini ili kuunda duaradufu.

Mfano$\PageIndex{3}$: Graphing an Ellipse Centered at the Origin

Grafu duaradufu iliyotolewa na equation,$\dfrac{x^2}{9}+\dfrac{y^2}{25}=1$. Tambua na uandike kituo hicho, vipeo, vyeo vya ushirikiano, na foci.

Suluhisho

Kwanza, tunaamua nafasi ya mhimili mkubwa. Kwa sababu$25>9$, mhimili mkubwa ni juu ya$y$ -axis. Kwa hiyo, equation iko katika fomu$\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1$, wapi$b^2=9$ na$a^2=25$. Inafuata kwamba:

• katikati ya ellipse ni$(0,0)$
• kuratibu za vipeo ni$(0,\pm a)=(0,\pm \sqrt{25})=(0,\pm 5)$
• kuratibu ya vyeo vya ushirikiano ni$(\pm b,0)=(\pm 9,0)=(\pm 3,0)$
• kuratibu ya foci ni$(0,\pm c)$, ambapo$c^2=a^2−b^2$ Kutatua kwa$c$, tuna:

$$\begin{align} c&=\pm \sqrt{a^2−b^2} \nonumber \\ &=\pm \sqrt{25−9} \nonumber\\ &=\pm \sqrt{16} \nonumber\\ &=\pm 4 \nonumber \end{align} \nonumber$$

Kwa hiyo, kuratibu za foci ni$(0,\pm 4)$.

Ifuatayo, tunapanga njama na kuandika kituo, vertices, co-vertices, na foci, na kuteka curve laini ili kuunda ellipse. Angalia Kielelezo$\PageIndex{8}$.

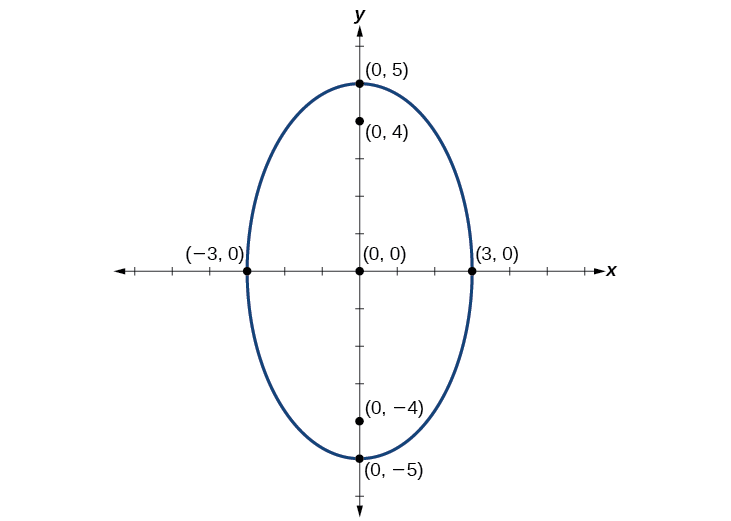
Kielelezo$\PageIndex{8}$

Zoezi$\PageIndex{3}$

Grafu duaradufu iliyotolewa na equation$\dfrac{x^2}{36}+\dfrac{y^2}{4}=1$. Tambua na uandike kituo hicho, vipeo, vyeo vya ushirikiano, na foci.

Jibu

kituo:$(0,0)$; vertices:$(\pm 6,0)$; ushirikiano vertices:$(0,\pm 2)$; foci:$(\pm 4\sqrt{2},0)$

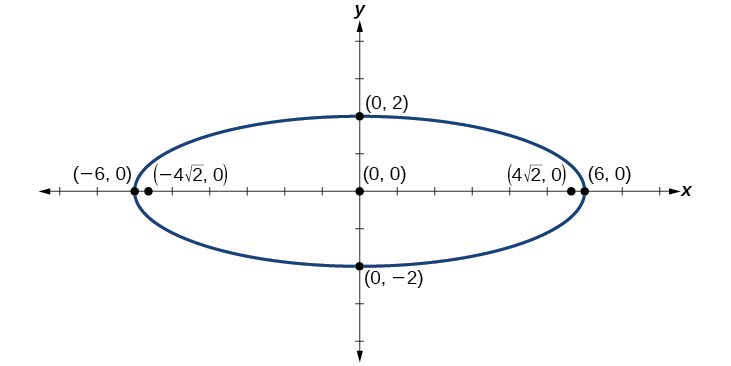
Kielelezo$\PageIndex{9}$

Mfano$\PageIndex{4}$: Graphing an Ellipse Centered at the Origin from an Equation Not in Standard Form

Grafu duaradufu iliyotolewa na equation$4x^2+25y^2=100$. Andika upya equation katika fomu ya kawaida. Kisha kutambua na uweke alama katikati, vertices, co-vertices, na foci.

Suluhisho

Kwanza, tumia algebra kuandika upya equation katika fomu ya kawaida.

$$\begin{align} 4x^2+25y^2&=100 \nonumber \\ \dfrac{4x^2}{100}+\dfrac{25y^2}{100}&=\dfrac{100}{100} \nonumber \\ \dfrac{x^2}{25}+\dfrac{y^2}{4}&=1 \nonumber \end{align} \nonumber$$

Kisha, tunaamua nafasi ya mhimili mkubwa. Kwa sababu$25>4$, mhimili mkubwa ni juu ya$x$ -axis. Kwa hiyo, equation iko katika fomu$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$, wapi$a^2=25$ na$b^2=4$. Inafuata kwamba:

• katikati ya ellipse ni$(0,0)$
• kuratibu za vipeo ni$(\pm a,0)=(\pm \sqrt{25},0)=(\pm 5,0)$
• kuratibu ya vyeo vya ushirikiano ni$(0,\pm b)=(0,\pm \sqrt{4})=(0,\pm 2)$
• kuratibu ya foci ni$(\pm c,0)$, wapi$c^2=a^2−b^2$. Kutatua kwa$c$, tuna:

$$\begin{align} c&=\pm \sqrt{a^2−b^2} \nonumber \\ &=\pm \sqrt{25−4} \nonumber \\ &=\pm \sqrt{21} \nonumber \end{align} \nonumber$$

Kwa hiyo, kuratibu za foci ni$(\pm \sqrt{21},0)$.

Ifuatayo, tunapanga njama na kuandika kituo, vertices, co-vertices, na foci, na kuteka curve laini ili kuunda ellipse.

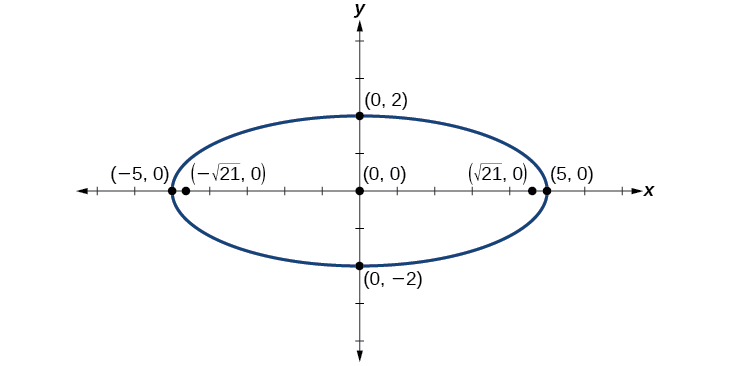
Kielelezo$\PageIndex{10}$

Zoezi$\PageIndex{4}$

Grafu duaradufu iliyotolewa na equation$49x^2+16y^2=784$. Andika upya equation katika fomu ya kawaida. Kisha kutambua na uweke alama katikati, vertices, co-vertices, na foci.

Jibu

Fomu ya kawaida:$\dfrac{x^2}{16}+\dfrac{y^2}{49}=1$; kituo cha:$(0,0)$; vertices:$(0,\pm 7)$; ushirikiano vertices:$(\pm 4,0)$; foci:$(0,\pm \sqrt{33})$

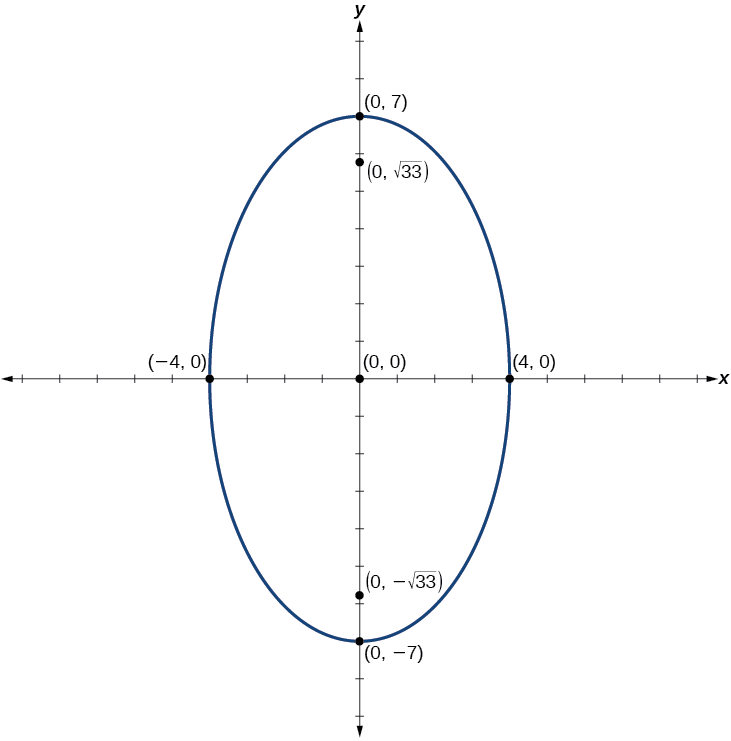
Kielelezo$\PageIndex{11}$

Graphing ellipses Si Centered katika Mwanzo

Wakati duaradufu haijawekwa katikati ya asili, bado tunaweza kutumia fomu za kawaida ili kupata vipengele muhimu vya grafu. Wakati duaradufu inazingatia wakati fulani$(h,k)$, tunatumia fomu za kawaida$\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1$,$a>b$ kwa ellipses ya usawa na$\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1$,$a>b$ kwa ellipses ya wima. Kutoka kwa equations hizi za kawaida, tunaweza kuamua kwa urahisi kituo, vertices, co-vertices, foci, na nafasi za axes kuu na ndogo.

Jinsi ya: Kutokana na fomu ya kiwango cha equation kwa duaradufu unaozingatia$(h, k)$, sketch the graph.

1. Tumia aina za kawaida za equations ya ellipse ili kuamua kituo, nafasi ya mhimili mkubwa, vertices, co-vertices, na foci.
   • Ikiwa equation iko katika fomu$\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1$, wapi$a>b$, basi
     • kituo hicho ni$(h,k)$
     • mhimili mkubwa ni sawa na$x$ -axis
     • kuratibu za vipeo ni$(h\pm a,k)$
     • kuratibu ya vyeo vya ushirikiano ni$(h,k\pm b)$
     • kuratibu ya foci ni$(h\pm c,k)$
   • Ikiwa equation iko katika fomu$\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1$, wapi$a>b$, basi
     • kituo hicho ni$(h,k)$
     • mhimili mkubwa ni sawa na$y$ -axis
     • kuratibu za vipeo ni$(h,k\pm a)$
     • kuratibu ya vyeo vya ushirikiano ni$(h\pm b,k)$
     • kuratibu ya foci ni$(h,k\pm c)$
2. Tatua kwa$c$ kutumia equation$c^2=a^2−b^2$.
3. Panda katikati, vipeo, vyeo vya ushirikiano, na foci katika ndege ya kuratibu, na kuteka safu ya laini ili kuunda duaradufu.

Mfano$\PageIndex{5}$: Graphing an Ellipse Centered at $(h, k)$

Grafu duaradufu iliyotolewa na equation,$\dfrac{{(x+2)}^2}{4}+\dfrac{{(y−5)}^2}{9}=1$. Tambua na uandike kituo hicho, vipeo, vyeo vya ushirikiano, na foci.

Suluhisho

Kwanza, tunaamua nafasi ya mhimili mkubwa. Kwa sababu$9>4$, mhimili mkubwa ni sawa na$y$ -axis. Kwa hiyo, equation iko katika fomu$\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1$, wapi$b^2=4$ na$a^2=9$. Inafuata kwamba:

• katikati ya ellipse ni$(h,k)=(−2,5)$
• kuratibu ya vipeo ni$(h,k\pm a)=(−2,5\pm \sqrt{9})=(−2,5\pm 3)$, au$(−2,2)$$(−2,8)$
• kuratibu ya vyeo vya ushirikiano ni$(h\pm b,k)=(−2\pm \sqrt{4},5)=(−2\pm 2,5)$, au$(−4,5)$$(0,5)$
• kuratibu ya foci ni$(h,k\pm c)$, wapi$c^2=a^2−b^2$. Kutatua kwa$c$, tuna:

$$\begin{align} c&=\pm \sqrt{a^2−b^2} \nonumber \\[4pt] &=\pm \sqrt{9−4} \nonumber \\[4pt] &=\pm \sqrt{5} \nonumber \end{align} \nonumber$$

Kwa hiyo, kuratibu za foci ni$(−2,5−\sqrt{5})$ na$(−2,5+\sqrt{5})$.

Ifuatayo, tunapanga njama na kuandika kituo, vertices, co-vertices, na foci, na kuteka curve laini ili kuunda ellipse.

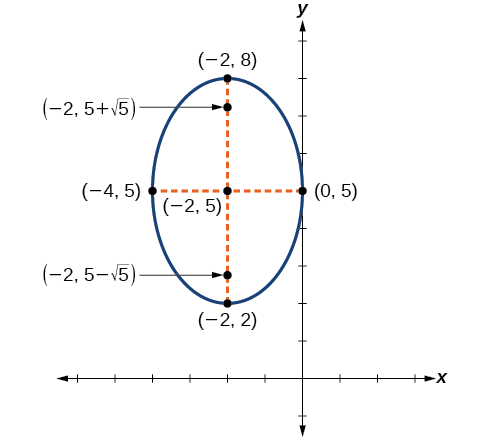
Kielelezo$\PageIndex{12}$

Zoezi$\PageIndex{5}$

Grafu duaradufu iliyotolewa na equation$\dfrac{{(x−4)}^2}{36}+\dfrac{{(y−2)}^2}{20}=1$. Tambua na uandike kituo hicho, vipeo, vyeo vya ushirikiano, na foci.

Jibu

Kituo:$(4,2)$; vertices:$(−2,2)$ na$(10,2)$; ushirikiano vertices:$(4,2−2\sqrt{5})$ na$(4,2+2\sqrt{5})$; foci:$(0,2)$ na$(8,2)$

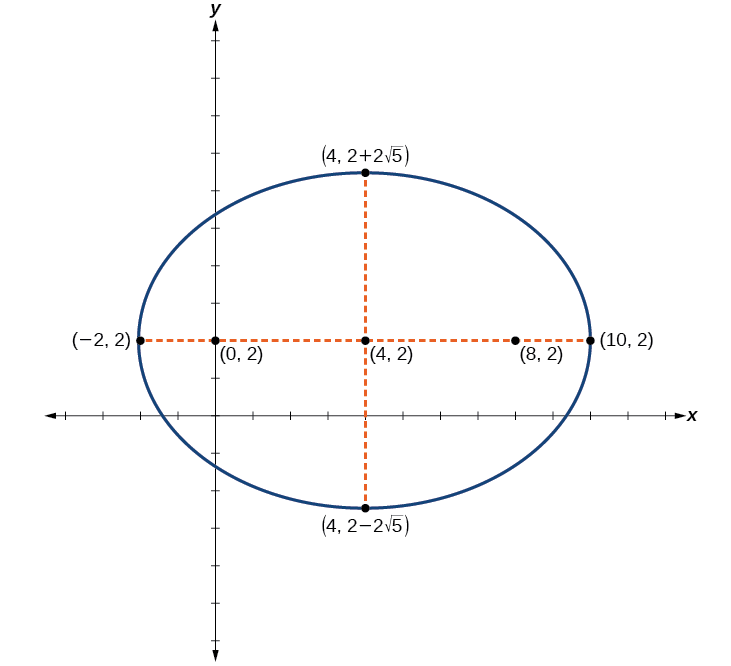
Kielelezo$\PageIndex{13}$

Jinsi ya: Kutokana na fomu ya jumla ya equation kwa duaradufu unaozingatia$(h, k)$, express the equation in standard form.

1. Tambua kwamba duaradufu iliyoelezwa na equation katika fomu$ax^2+by^2+cx+dy+e=0$ ni kwa fomu ya jumla.
2. Panga upya equation kwa maneno ya makundi ambayo yana variable sawa. Hoja muda wa mara kwa mara kwa upande wa pili wa equation.
3. Fanya nje ya coefficients ya$x^2$ na$y^2$ masharti katika maandalizi ya kukamilisha mraba.
4. Kukamilisha mraba kwa kila variable kuandika upya equation katika mfumo wa jumla ya mafungu ya binomials mbili squared kuweka sawa na mara kwa mara$m_1{(x−h)}^2+m_2{(y−k)}^2=m_3$, ambapo$m_1$,$m_2$, na$m_3$ ni constants.
5. Gawanya pande zote mbili za equation kwa muda wa mara kwa mara ili kuelezea equation katika fomu ya kawaida.

Mfano$\PageIndex{6}$: Graphing an Ellipse Centered at $(h, k)$ by First Writing It in Standard Form

Grafu duaradufu iliyotolewa na equation$4x^2+9y^2−40x+36y+100=0$. Tambua na uandike kituo hicho, vipeo, vyeo vya ushirikiano, na foci.

Suluhisho

Lazima tuanze kwa kuandika upya equation katika fomu ya kawaida.

$4x^2+9y^2−40x+36y+100=0$

Masharti ya kikundi ambayo yana variable sawa, na hoja ya mara kwa mara kwa upande wa pili wa equation.

$(4x^2−40x)+(9y^2+36y)=−100$

Fanya nje ya coefficients ya maneno ya mraba.

$4(x^2−10x)+9(y^2+4y)=−100$

Jaza mraba mara mbili. Kumbuka kusawazisha equation kwa kuongeza constants sawa kwa kila upande.

$4(x^2−10x+25)+9(y^2+4y+4)=−100+100+36$

Andika upya kama mraba kamilifu.

$4{(x−5)}^2+9{(y+2)}^2=36$

Gawanya pande zote mbili kwa muda wa mara kwa mara ili kuweka equation katika fomu ya kawaida.

$\dfrac{{(x−5)}^2}{9}+\dfrac{{(y+2)}^2}{4}=1$

Sasa kwa kuwa equation iko katika hali ya kawaida, tunaweza kuamua nafasi ya mhimili mkubwa. Kwa sababu$9>4$, mhimili mkubwa ni sawa na$x$ -axis. Kwa hiyo, equation iko katika fomu$\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1$, wapi$a^2=9$ na$b^2=4$. Inafuata kwamba:

• katikati ya ellipse ni$(h,k)=(5,−2)$
• kuratibu ya vipeo ni$(h\pm a,k)=(5\pm \sqrt{9},−2)=(5\pm 3,−2)$, au$(2,−2)$$(8,−2)$
• kuratibu ya vyeo vya ushirikiano ni$(h,k\pm b)=(5,−2\pm \sqrt{4})=(5,−2\pm 2)$, au$(5,−4)$$(5,0)$
• kuratibu ya foci ni$(h\pm c,k)$, wapi$c^2=a^2−b^2$. Kutatua kwa$c$, tuna:

$$\begin{align*} c&=\pm \sqrt{a^2-b^2}\\ &=\pm \sqrt{9-4}\\ &=\pm \sqrt{5} \end{align*}$$

Kwa hiyo, kuratibu za foci ni$(5−\sqrt{5},−2)$ na$(5+\sqrt{5},−2)$.

Kisha sisi njama na studio katikati, vertices, co-vertices, na foci, na kuteka curve laini ili kuunda duaradufu kama inavyoonekana katika Kielelezo$\PageIndex{14}$.

Kielelezo$\PageIndex{14}$

Zoezi$\PageIndex{6}$

Eleza equation ya duaradufu iliyotolewa katika fomu ya kawaida. Tambua kituo, vertices, vyeo vya ushirikiano, na foci ya ellipse.

$4x^2+y^2−24x+2y+21=0$

Jibu

$\dfrac{{(x−3)}^2}{4}+\dfrac{{(y+1)}^2}{16}=1$; katikati:$(3,−1)$; vertices:$(3,−5)$ na$(3,3)$; ushirikiano vertices:$(1,−1)$ na$(5,−1)$; foci:$(3,−1−2\sqrt{3})$ na$(3,−1+2\sqrt{3})$

Kutatua Matatizo yaliyotumika Kuhusisha Ellipses

Hali nyingi za ulimwengu halisi zinaweza kuwakilishwa na ellipses, ikiwa ni pamoja na njia za sayari, satelaiti, miezi na comets, na maumbo ya keels mashua, usukani, na baadhi ya mbawa za ndege. Kifaa cha kimatibabu kinachoitwa lithotripta kinatumia vielekezi vya duaradufu kuvunja mawe ya figo kwa kuzalisha mawimbi ya sauti. Baadhi ya majengo, aitwaye whispering vyumba, ni iliyoundwa na domes elliptical ili mtu whispering katika lengo moja kwa urahisi kusikilizwa na mtu amesimama katika lengo nyingine. Hii hutokea kwa sababu ya mali ya acoustic ya ellipse. Wakati wimbi la sauti linatoka kwenye lengo moja la chumba cha whispering, wimbi la sauti litaonekana mbali na dome ya elliptical na kurudi kwenye lengo lingine (Kielelezo$\PageIndex{15}$). Katika chumba cha whisper katika Makumbusho ya Sayansi na Viwanda huko Chicago, watu wawili wamesimama kwenye foci-kuhusu$43$ miguu mbali-wanaweza kusikia whisper kila mmoja.

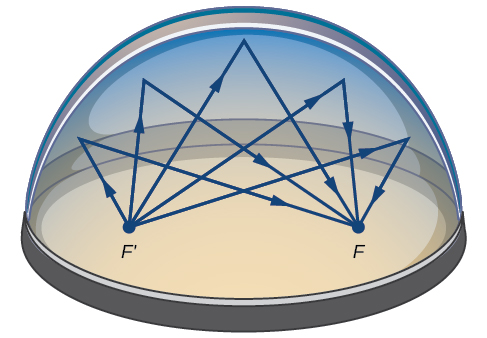
Kielelezo$\PageIndex{15}$: Mawimbi ya sauti yanajitokeza kati ya foci katika chumba cha elliptical, kinachoitwa chumba cha whispering.

Mfano$\PageIndex{7}$: Locating the Foci of a Whispering Chamber

Hall Statuary katika Capitol Building katika Washington, D.C. ni chumba whispering. Vipimo vyake ni$46$ miguu pana kwa$96$ miguu kwa muda mrefu kama inavyoonekana katika Kielelezo$\PageIndex{16}$.

1. Nini fomu ya kawaida ya equation ya ellipse inayowakilisha muhtasari wa chumba? Kidokezo: kudhani ellipse ya usawa, na basi katikati ya chumba iwe hatua$(0,0)$.
2. Ikiwa maseneta wawili wamesimama kwenye foci ya chumba hiki wanaweza kusikia whisper kila mmoja, ni mbali gani maseneta? Pande zote kwa mguu wa karibu.

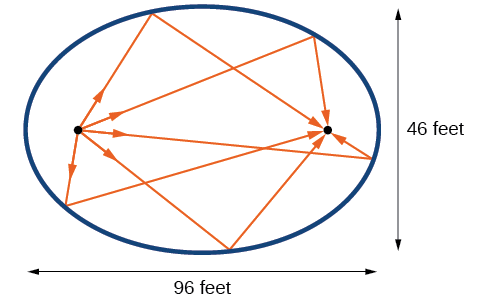
Kielelezo$\PageIndex{16}$

Suluhisho

1. Sisi ni kuchukua duaradufu usawa na kituo$(0,0)$, hivyo tunahitaji kupata equation ya fomu$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$, ambapo$a>b$. Tunajua kwamba urefu wa mhimili kuu,$2a$, ni mrefu kuliko urefu wa mhimili mdogo,$2b$. Hivyo urefu wa chumba, 96, unawakilishwa na mhimili mkubwa, na upana wa chumba, 46, unawakilishwa na mhimili mdogo.

   Kwa hiyo, equation ya duaradufu ni\ [(dfrac {x^2} {2304} +\ dfrac {y ^ 2} {529} =1\)

   • Kutatua kwa$a$, tuna$2a=96$, hivyo$a=48$, na$a^2=2304$.
   • Kutatua kwa$b$, tuna$2b=46$, hivyo$b=23$, na$b^2=529$.
2. Ili kupata umbali kati ya maseneta, tunapaswa kupata umbali kati ya foci$(\pm c,0)$, wapi$c^2=a^2−b^2$. Kutatua kwa$c$, tuna:

$$\begin{align*} c^2&=a^2-b^2\\ c^2&=2304-529\qquad \text{Substitute using the values found in part } (a)\\ c&=\pm \sqrt{2304-529}\qquad \text{Take the square root of both sides.}\\ c&=\pm \sqrt{1775}\qquad \text{Subtract.}\\ c&\approx \pm 42\qquad \text{Round to the nearest foot.} \end{align*}$$

Pointi$(\pm 42,0)$ zinawakilisha foci. Hivyo, umbali kati ya maseneta ni$2(42)=84$ miguu.

Zoezi$\PageIndex{7}$

Tuseme chumba cha whispering ni$480$ miguu ndefu na$320$ miguu pana.

1. Fomu ya kawaida ya equation ya ellipse inayowakilisha chumba ni nini? Kidokezo: kudhani ellipse ya usawa, na basi katikati ya chumba iwe hatua$(0,0)$.
2. Ikiwa watu wawili wamesimama kwenye foci ya chumba hiki na wanaweza kusikia whisper, ni mbali gani watu? Pande zote kwa mguu wa karibu.

Jibu

$\dfrac{x^2}{57,600}+\dfrac{y^2}{25,600}=1$

Jibu b

Watu wamesimama$358$ miguu mbali.

Media

Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na ellipses.

• sehemu conic: duaradufu
• Grafu ya Ellipse na Kituo cha Mwanzo
• Grafu ya Ellipse na Kituo Sio Mwanzo

Mlinganyo muhimu

ellipse ya usawa, katikati ya asili	$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$,$a>b$
ellipse ya wima, katikati ya asili	$\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1$,$a>b$
ellipse ya usawa, katikati$(h,k)$	$\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1$,$a>b$
ellipse ya wima, katikati$(h,k)$	$\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1$,$a>b$

Dhana muhimu

• Ellipse ni seti ya pointi zote$(x,y)$ katika ndege kama vile jumla ya umbali wao kutoka pointi mbili fasta ni mara kwa mara. Kila hatua iliyowekwa inaitwa lengo (wingi: foci).
• Tunapopewa kuratibu za foci na vipeo vya ellipse, tunaweza kuandika equation ya ellipse kwa fomu ya kawaida. Angalia Mfano$\PageIndex{1}$ na Mfano$\PageIndex{2}$.
• Wakati kupewa equation kwa duaradufu unaozingatia katika asili katika hali ya kawaida, tunaweza kutambua vipeo yake, ushirikiano vertices, foci, na urefu na nafasi ya shoka kuu na ndogo ili grafu duaradufu. Angalia Mfano$\PageIndex{3}$ na Mfano$\PageIndex{4}$.
• Wakati kupewa equation kwa duaradufu unaozingatia wakati fulani isipokuwa asili, tunaweza kutambua sifa zake muhimu na grafu duaradufu. Angalia Mfano$\PageIndex{5}$ na Mfano$\PageIndex{6}$.
• Hali halisi ya ulimwengu inaweza kutajwa kwa kutumia milinganyo ya kiwango cha ellipses na kisha tathmini ili kupata vipengele muhimu, kama vile urefu wa shoka na umbali kati ya foci. Angalia Mfano$\PageIndex{7}$.

Wachangiaji na Majina

• Template:ContribOpenStaxPreCalc