9.5: Matrices na Matrix Uendeshaji

Malengo ya kujifunza

• Pata jumla na tofauti ya matrices mbili.
• Pata makundi ya scalar ya tumbo.
• Pata bidhaa ya matrices mbili.

Timu mbili za klabu za soka, Wildcats na Paka za Mud, zina matumaini ya kupata vifaa vipya kwa msimu ujao. Jedwali$\PageIndex{1}$ linaonyesha mahitaji ya timu zote mbili.

Jedwali$\PageIndex{1}$

	paka mwitu	matope paka
Malengo	6	10
Mipira	30	24
Jerseys	14	20

Gharama za lengo$$300$; gharama za mpira$$10$; na gharama za jersey$$30$. Tunawezaje kupata gharama ya jumla ya vifaa vinavyohitajika kwa kila timu? Katika sehemu hii, tunagundua njia ambayo data katika meza ya vifaa vya soka inaweza kuonyeshwa na kutumika kwa kuhesabu habari zingine. Kisha, tutaweza kuhesabu gharama za vifaa.

Kielelezo$\PageIndex{1}$

Kupata Jumla na Tofauti ya Matrices Mbili

Ili kutatua tatizo kama ile iliyoelezwa kwa timu za soka, tunaweza kutumia tumbo, ambayo ni safu ya mstatili wa namba. Mstari katika tumbo ni seti ya namba ambazo zimeunganishwa kwa usawa. Safu katika tumbo ni seti ya namba ambazo zimeunganishwa kwa wima. Kila namba ni kuingia, wakati mwingine huitwa kipengele, cha tumbo. Matrices (wingi) hufungwa ndani ya [] au (), na kwa kawaida huitwa kwa herufi kubwa. Kwa mfano, matrices tatu aitwaye$A$$B$,, na$C$ ni hapa chini.

$$\begin{align*} A&=\begin{bmatrix} 1& 2 \\ 3 & 4 \\ \end{bmatrix} \\[4pt] B &=\begin{bmatrix} 1 & 2 & 7 \\ 0 & -5 & 6 \\ 7 & 8 & 2 \end{bmatrix} \\[4pt] C &=\begin{bmatrix} -1 & 3 \\ 0 & 2 \\ 3 & 1 \end{bmatrix} \end{align*}$$

Matrix mara nyingi hujulikana kwa ukubwa wake au vipimo:$m×n$ kuonyesha$m$ safu na$n$ nguzo. Maingizo ya Matrix hufafanuliwa kwanza kwa mstari na kisha kwa safu. Kwa mfano, ili kupata kuingia katika tumbo$A$ kutambuliwa kama$a_{ij}$, tunatafuta kuingia mfululizo$i$, safu$j$. Katika tumbo$A$, iliyoonyeshwa hapa chini, kuingia kwa safu$2$, safu$3$ ni$a_{23}$.

$$A=\begin{bmatrix} a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33} \end{bmatrix} \nonumber$$

• Matrix ya mraba ni tumbo yenye vipimo$n × n$, maana yake ina idadi sawa ya safu kama nguzo. $3×3$Matrix hapo juu ni mfano wa tumbo la mraba.
• Matrix ya mstari ni tumbo yenye mstari mmoja na vipimo$1 × n$. $$\begin{bmatrix} a_{11} & a_{12} & a_{13} \end{bmatrix} \nonumber$$
• Matrix ya safu ni tumbo yenye safu moja na vipimo$m × 1$. $$\begin{bmatrix} a_{11} \\ a_{21} \\a_{31} \end{bmatrix} \nonumber$$

Matrix inaweza kutumika kuwakilisha mfumo wa equations. Katika kesi hizi, namba zinawakilisha coefficients ya vigezo katika mfumo. Matrices mara nyingi hufanya mifumo ya kutatua equations rahisi kwa sababu haijatumiwa na vigezo. Tutachunguza wazo hili zaidi katika sehemu inayofuata, lakini kwanza tutaangalia shughuli za msingi za matrix.

Ufafanuzi: MATRICES

Matrix ni safu ya namba ya mstatili ambayo kwa kawaida huitwa kwa herufi kuu:$A$,$B$,$C$, na kadhalika. Kila kuingia katika tumbo ni inajulikana kama$a_{ij}$, kama kwamba$i$ inawakilisha mstari na$j$ inawakilisha safu. Matrices mara nyingi hujulikana kwa vipimo vyao:$m × n$ kuonyesha$m$ safu na$n$ nguzo.

Mfano$\PageIndex{1}$: Finding the Dimensions of the Given Matrix and Locating Entries

Kutokana na tumbo$A$:

1. Je! Ni vipimo gani vya matrix$A$?
2. Je, ni entries katika$a_{31}$ na$a_{22}$?

$$A=\begin{bmatrix} 2 & 1 & 0\\2 & 4 & 7\\3 & 1 & −2 \end{bmatrix} \nonumber$$

Suluhisho

1. Vipimo ni$3 \times 3$ kwa sababu kuna safu tatu na nguzo tatu.
2. Kuingia$a_{31}$ ni namba katika mstari wa 3, safu ya 1, yaani$3$. Kuingia$a_{22}$ ni namba katika mstari wa 2, safu ya 2, ambayo ni$4$. Kumbuka, mstari unakuja kwanza, kisha safu.

Kuongeza na Kutoa Matrices

Tunatumia matrices kuorodhesha data au kuwakilisha mifumo. Kwa sababu entries ni namba, tunaweza kufanya shughuli kwenye matrices. Tunaongeza au kuondoa matrices kwa kuongeza au kuondoa entries sambamba. Kwa kufanya hivyo, maingizo yanapaswa kuendana. Kwa hiyo, kuongeza na kuondoa matrices inawezekana tu wakati matrices yana vipimo sawa. Tunaweza kuongeza au Ondoa$3 \times 3$ tumbo na$3 \times 3$ tumbo jingine, lakini hatuwezi kuongeza au kuondoa$2 \times 3$ tumbo na tumbo kwa sababu baadhi ya entries katika tumbo moja haitakuwa na kuingia sambamba katika tumbo nyingine.$3 \times 3$

KUONGEZA NA KUONDOA MATRICES

Kutokana matrices$A$ na$B$ ya vipimo kama, kuongeza na kuondoa ya$A$ na$B$ kuzalisha tumbo$C$ au tumbo$D$ ya mwelekeo huo.

$$A+B=C$$

kama kwamba$a_{ij}+b_{ij}=c_{ij}$

$$A−B=D$$

kama kwamba$a_{ij}−b_{ij}=d_{ij}$

Matrix kuongeza ni commutative.

$$A+B=B+A$$

Pia ni associative.

$$(A+B)+C=A+(B+C)$$

Mfano$\PageIndex{2A}$: Finding the Sum of Matrices

Kupata jumla ya$A$ na$B$, kutokana

$$A=\begin{bmatrix}a & b\\c & d \end{bmatrix} \nonumber$$

na

$$B=\begin{bmatrix}e & f\\g & h\end{bmatrix} \nonumber$$

Suluhisho

Ongeza entries sambamba.

$$\begin{align} A+B &=\begin{bmatrix}a & b\\c & d\end{bmatrix}+\begin{bmatrix}e & f\\g & h\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}a+e & b+f\\c+g & d+h \end{bmatrix} \nonumber \end{align} \nonumber$$

Mfano$\PageIndex{2B}$: Adding Matrix $A$ and Matrix $B$

Kupata jumla ya$A$ na$B$.

$$A=\begin{bmatrix}4 &1\\3 & 2 \end{bmatrix} \nonumber$$

na

$$B=\begin{bmatrix}5 & 9\\0 & 7\end{bmatrix} \nonumber$$

Suluhisho

Ongeza entries sambamba. Ongeza kuingia katika mstari wa 1, safu ya 1$a_{11}$, ya Matrix$A$ kwa kuingia katika mstari wa 1, safu ya 1$b_{11}$, ya$B$. Endelea muundo mpaka maingizo yote yameongezwa.

$$\begin{align} A+B &=\begin{bmatrix}4&1\\3 &2\end{bmatrix}+\begin{bmatrix}5&9\\0&7\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}4+5&1+9\\3+0&2+7\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}9&10\\3&9\end{bmatrix} \nonumber \end{align} \nonumber$$

Mfano$\PageIndex{2C}$: Finding the Difference of Two Matrices

Kupata tofauti ya$A$ na$B$.

$A=\begin{bmatrix}−2&3\\0&1\end{bmatrix}$na$B=\begin{bmatrix}8&1\\5&4\end{bmatrix}$

Suluhisho

Tunaondoa entries sambamba za kila tumbo.

$$\begin{align} A−B &=\begin{bmatrix}−2&3\\0&1\end{bmatrix}−\begin{bmatrix}8&1\\5&4\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}−2−8&3−1\\0−5&1−4\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}−10&2\\−5&−3\end{bmatrix} \nonumber \end{align} \nonumber$$

Mfano$\PageIndex{2D}$: Finding the Sum and Difference of Two 3 x 3 Matrices

Kutokana$A$ na$B$:

1. Pata jumla.
2. Kupata tofauti.

$$A=\begin{bmatrix}2&−10&−2\\14&12&10\\4&−2&2\end{bmatrix} \nonumber$$

na

$$B=\begin{bmatrix}6&10&−2\\0&−12&−4\\−5&2&−2\end{bmatrix} \nonumber$$

Suluhisho

1. Ongeza entries sambamba.

$$\begin{align} A+B & =\begin{bmatrix} 2& −10& −2\\14 & 12 & 10\\4 & −2 & 2\end{bmatrix}+\begin{bmatrix}6 & 10 & −2\\0 & −12 & −4\\−5 & 2 & −2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}2+6 & −10+10 & −2−2\\14+0 & 12−12 & 10−4\\4−5 & −2+2 & 2−2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix} 8 & 0 & −4\\14 & 0 & 6\\−1 & 0 & 0\end{bmatrix} \nonumber \end{align} \nonumber$$

2. Ondoa entries sambamba.

$$\begin{align} A−B &=\begin{bmatrix}2&−10&−2\\14&12&10\\4&−2&2\end{bmatrix}−\begin{bmatrix}6&10&−2\\0&−12&−4\\−5&2&−2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}2−6 & −10−10 & −2+2\\14−0 & 12+12 & 10+4\\4+5 & −2−2 & 2+2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−4 & −20 & 0\\14 & 24 & 14\\9 & −4 & 4\end{bmatrix} \nonumber \end{align} \nonumber$$

Zoezi$\PageIndex{1}$

Ongeza tumbo$A$ na tumbo$B$.

$$A=\begin{bmatrix}2&6\\1&0\\1&−3\end{bmatrix} \nonumber$$

na

$$B=\begin{bmatrix}3&−2\\1&5\\−4&3\end{bmatrix} \nonumber$$

Jibu

$$\begin{align} A+B&=\begin{bmatrix}2&6\\ 1 &0\\1&−3\end{bmatrix}+\begin{bmatrix} 3&-2 \\1&5 \\-4&3\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}2+3&6+(−2)\\1+1&0+5\\1+(-4)&−3+3\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}5&4\\2&5\\-3&0\end{bmatrix} \nonumber \end{align} \nonumber$$

Kutafuta Mizigo ya Scalar ya Matrix

Mbali na kuongeza na kuondoa matrices nzima, kuna hali nyingi ambazo tunahitaji kuzidisha tumbo kwa mara kwa mara inayoitwa scalar. Kumbuka kwamba scalar ni idadi halisi ya idadi ambayo ina ukubwa, lakini si mwelekeo. Kwa mfano, wakati, joto, na umbali ni kiasi kikubwa. Mchakato wa kuzidisha kwa scalar unahusisha kuzidisha kila kuingia kwenye tumbo kwa scalar. Multiple scalar ni kuingia yoyote ya tumbo kwamba matokeo ya kuzidisha scalar.

Fikiria hali halisi ya ulimwengu ambapo chuo kikuu kinahitaji kuongeza kwenye hesabu yake ya kompyuta, meza za kompyuta, na viti katika maabara mawili ya chuo kutokana na kuongezeka kwa uandikishaji. Wanakadiria kuwa vifaa$15%$ vingi vinahitajika katika maabara yote mawili. Hesabu ya sasa ya shule inavyoonyeshwa kwenye Jedwali$\PageIndex{2}$.

Jedwali$\PageIndex{2}$

	Maabara A	Maabara B
Tarakilishi	15	27
Majedwali ya Kompyuta	16	34
Viti	16	34

Kubadili data kwenye tumbo, tuna

$$C_{2013}=\begin{bmatrix}15 & 27\\16&34\\16&34\end{bmatrix} \nonumber$$

Ili kuhesabu ni kiasi gani cha vifaa vya kompyuta vinavyohitajika, tunazidisha entries zote kwenye tumbo$C$ na$0.15$.

$$(0.15)C_{2013}=\begin{bmatrix}(0.15)15&(0.15)27\\(0.15)16&(0.15)34\\(0.15)16 &(0.15)34\end{bmatrix}=\begin{bmatrix}2.25 &4.05\\2.4&5.1\\2.4&5.1\end{bmatrix} \nonumber$$

Ni lazima pande zote hadi integer ijayo, hivyo kiasi cha vifaa vya mpya zinahitajika ni

$$\begin{bmatrix}3&5\\3&6\\3&6\end{bmatrix} \nonumber$$

Kuongeza matrices mbili kama inavyoonekana hapa chini, tunaona hesabu mpya kiasi.

$$\begin{bmatrix}15&27\\16&34\\16&34\end{bmatrix}+\begin{bmatrix}3&5\\3&6\\3&6\end{bmatrix}=\begin{bmatrix}18&32\\19&40\\19&40\end{bmatrix} \nonumber$$

Hii ina maana

$$C_{2014}=\begin{bmatrix}18&32\\19&40\\19&40\end{bmatrix} \nonumber$$

Hivyo, Lab A itakuwa na$18$ kompyuta, meza za$19$ kompyuta, na$19$ viti; Lab B itakuwa na$32$ kompyuta, meza za$40$ kompyuta, na$40$ viti.

KUZIDISHA SCALAR

Kuzidisha kwa scalar kunahusisha kutafuta bidhaa ya mara kwa mara kwa kila kuingia kwenye tumbo. Kutokana

$$A=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix} \nonumber$$

nyingi za scalar$cA$ ni

$$cA=c\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix} \nonumber$$

$$=\begin{bmatrix}ca_{11}&ca_{12}\\ca_{21}&ca_{22}\end{bmatrix} \nonumber$$

Kuzidisha kwa Scalar ni kusambaza. Kwa matrices$A$$B$,$C$ na kwa scalars$a$ na$b$,

$$a(A+B)=aA+aB$$

$$(a+b)A=aA+bA$$

Mfano$\PageIndex{3}$: Multiplying the Matrix by a Scalar

Kuzidisha tumbo$A$ kwa scalar$3$.

$$A=\begin{bmatrix}8&1\\5&4\end{bmatrix} \nonumber$$

Suluhisho

Panua kila kuingia$A$ kwa scalar$3$.

$$\begin{align} 3A&=3\begin{bmatrix}8&1\\5&4\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}3⋅8&3⋅1\\3⋅5&3⋅4\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}24&3\\15&12\end{bmatrix} \nonumber \end{align} \nonumber$$

Zoezi$\PageIndex{2}$

Kutokana na tumbo$B$, tafuta$−2B$ wapi

$$B=\begin{bmatrix}4&1\\3&2\end{bmatrix} \nonumber$$

Jibu

$$−2B=\begin{bmatrix}−8&−2\\−6&−4\end{bmatrix} \nonumber$$

Mfano$\PageIndex{4}$: Finding the Sum of Scalar Multiples

Pata jumla$3A+2B$.

$$A=\begin{bmatrix}1&−2&0\\0&−1&2\\4&3&−6\end{bmatrix} \nonumber$$

na

$$B=\begin{bmatrix}−1&2&1\\0&−3&2\\0&1&−4\end{bmatrix} \nonumber$$

Suluhisho

Kwanza, tafuta$3A$, basi$2B$.

$$\begin{align} 3A&=\begin{bmatrix}3⋅1&3(−2)&3⋅0\\3⋅0&3(−1)&3⋅2\\3⋅4&3⋅3&3(−6)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}3&−6&0\\0&−3&6\\12&9&−18\end{bmatrix}\nonumber \end{align} \nonumber$$

$$\begin{align} 2B&=\begin{bmatrix}2(−1)&2⋅2&2⋅1\\2⋅0&2(−3)&2⋅2\\2⋅0&2⋅1&2(−4)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−2&4&2\\0&−6&4\\0&2&−8\end{bmatrix}\nonumber \end{align} \nonumber$$

Sasa, ongeza$3A+2B$.

$$\begin{align} 3A+2B&=\begin{bmatrix}3&−6&0\\0&−3&6\\12&9&−18\end{bmatrix}+\begin{bmatrix}−2&4&2\\0&−6&4\\0&2&−8\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}3−2&−6+4&0+2\\0+0&−3−6&6+4\\12+0&9+2&−18−8\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}1& −2&2\\0&−9&10\\12&11&−26\end{bmatrix} \nonumber \end{align} \nonumber$$

Kutafuta Bidhaa ya Matrices Mbili

Mbali na kuzidisha tumbo kwa scalar, tunaweza kuzidisha matrices mbili. Kupata bidhaa ya matrices mbili inawezekana tu wakati vipimo vya ndani ni sawa, maana yake ni kwamba idadi ya nguzo za matrix ya kwanza ni sawa na idadi ya safu ya tumbo la pili. Ikiwa$A$ ni$m × r$ tumbo na$B$ ni$r × n$ tumbo, basi tumbo la bidhaa$AB$ ni$m × n$ tumbo. Kwa mfano, bidhaa$AB$ inawezekana kwa sababu idadi ya nguzo ndani$A$ ni sawa na idadi ya safu katika$B$. Ikiwa vipimo vya ndani havifanani, bidhaa haijafafanuliwa.

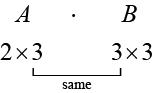
Sisi kuzidisha entries ya$A$ na entries ya$B$ kulingana na muundo maalum kama ilivyoainishwa hapa chini. Mchakato wa kuzidisha matrix inakuwa wazi wakati wa kufanya kazi tatizo na namba halisi.

Ili kupata entries mfululizo$i$ wa$AB$, sisi kuzidisha entries katika mstari$i$ wa$A$ na safu$j$ katika$B$ na kuongeza. Kwa mfano, kupewa matrices$A$ na$B$, ambapo vipimo vya$A$ ni$2 \times 3$ na vipimo vya$B$ ni$3 \times 3$, bidhaa ya$AB$ itakuwa$2 \times 3$ tumbo.

$$A=\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\end{bmatrix} \nonumber$$

na

$$B=\begin{bmatrix}b_{11}&b_{12}&b_{13}\\b_{21}&b_{22}&b_{23}\\b_{31}&b_{32}&b_{33}\end{bmatrix} \nonumber$$

Kuzidisha na kuongeza kama ifuatavyo ili kupata kuingia kwanza kwa tumbo la bidhaa$AB$.

1. Ili kupata kuingia katika mstari 1, safu 1 ya$AB$, kuzidisha mstari wa kwanza katika$A$ na safu ya kwanza katika$B$, na kuongeza.

   $$\begin{bmatrix}a_{11}&a_{12}&a_{13}\end{bmatrix} ⋅\begin{bmatrix}b_{11}\\b_{21}\\b_{31}\end{bmatrix}=a_{11}⋅b_{11}+a_{12}⋅b_{21}+a_{13}⋅b_{31} \nonumber$$

2. Ili kupata kuingia katika mstari 1, safu 2 ya$AB$, kuzidisha mstari wa kwanza wa$A$ kwa safu ya pili katika$B$, na kuongeza.

   $$\begin{bmatrix}a_{11}&a_{12}&a_{13}\end{bmatrix} ⋅\begin{bmatrix}b_{12}\\b_{22}\\b_{32}\end{bmatrix}=a_{11}⋅b_{12}+a_{12}⋅b_{22}+a_{13}⋅b_{32} \nonumber$$

3. Ili kupata kuingia katika mstari 1, safu 3 ya$AB$, kuzidisha mstari wa kwanza wa$A$ kwa safu ya tatu katika$B$, na kuongeza.

   $$\begin{bmatrix}a_{11}&a_{12}&a_{13}\end{bmatrix} ⋅\begin{bmatrix}b_{13}\\b_{23}\\b_{33}\end{bmatrix}=a_{11}⋅b_{13}+a_{12}⋅b_{23}+a_{13}⋅b_{33} \nonumber$$

Tunaendelea njia ile ile ya kupata mstari wa pili wa$AB$. Kwa maneno mengine, mstari 2 ya$A$ mara safu 1 ya$B$; mstari 2 ya$A$ mara safu 2 ya$B$; mstari 2 ya$A$ mara safu 3 ya$B$. Baada ya kukamilika, tumbo la bidhaa litakuwa

$$AB=\begin{bmatrix}a_{11}⋅b_{11}+a_{12}⋅b_{21}+a_{13}⋅b_{31} &a_{11}⋅b_{12}+a_{12}⋅b_{22}+a_{13}⋅b_{32}&a_{11}⋅b_{13}+a_{12}⋅b_{23}+a_{13}⋅b_{33} \\a_{21}⋅b_{11}+a_{22}⋅b_{21}+a_{23}⋅b_{31}&a_{21}⋅b_{12}+a_{22}⋅b_{22}+a_{23}⋅b_{32}&a_{21}⋅b_{13}+a_{22}⋅b_{23}+a_{23}⋅b_{33}\end{bmatrix} \nonumber$$

MALI YA KUZIDISHA MATRIX

Kwa matrice$A, B$, na mali$C$ zifuatazo zinashikilia.

• Uzidishaji wa Matrix ni ushirika: $$(AB)C=A(BC).$$
• Kuzidisha Matrix ni kusambaza: $$C(A+B)=CA+CB$$ $$(A+B)C=AC+BC.$$

Kumbuka kuwa kuzidisha matrix si commutative.

Mfano$\PageIndex{5A}$: Multiplying Two Matrices

Kuzidisha tumbo$A$ na tumbo$B$.

$$A=\begin{bmatrix}1&2\\3&4\end{bmatrix} \nonumber$$

na

$$B=\begin{bmatrix}5&6\\7&8\end{bmatrix} \nonumber$$

Suluhisho

Kwanza, tunaangalia vipimo vya matrices. Matrix$A$ ina vipimo$2 × 2$ na tumbo$B$ ina vipimo$2 × 2$. Vipimo vya ndani ni sawa ili tuweze kufanya kuzidisha. Bidhaa itakuwa na vipimo$2 × 2$.

Tunafanya shughuli zilizotajwa hapo awali.

Mfano$\PageIndex{5B}$: Multiplying Two Matrices

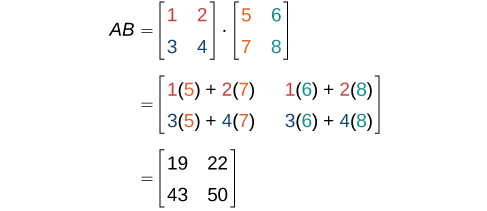
Kutokana$A$ na$B$:

1. Kupata$AB$.
2. Kupata$BA$.

$$A=\begin{bmatrix}−1&2&3\\ 4&0&5\end{bmatrix} \nonumber$$

na

$$B=\begin{bmatrix}5&−1\\-4&0\\2&3\end{bmatrix} \nonumber$$

Suluhisho

1. Kama vipimo vya$A$ ni$2 \times 3$ na vipimo vya$B$ ni$3 \times 2$, matrices hizi zinaweza kuzidishwa pamoja kwa sababu idadi ya nguzo$A$ inafanana na idadi ya safu ndani$B$. Bidhaa hiyo itakuwa$2 \times 2$ matrix, idadi ya safu ndani$A$ na idadi ya nguzo ndani$B$.

$$\begin{align}AB&=\begin{bmatrix}−1&2&3\\4&0&5\end{bmatrix} \begin{bmatrix}5&−1\\−4&0\\2&3\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−1(5)+2(−4)+3(2)&−1(−1)+2(0)+3(3)\\4(5)+0(−4)+5(2)&4(−1)+0(0)+5(3)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−7&10\\30&11\end{bmatrix} \nonumber \end{align} \nonumber$$

2. Vipimo vya$B$ ni$3 \times 2$ na vipimo vya$A$ ni$2 \times 3$. Vipimo vya ndani vinafanana hivyo bidhaa hufafanuliwa na itakuwa$3 \times 3$ tumbo.

$$\begin{align}BA&=\begin{bmatrix}5&−1\\−4&0\\2&3\end{bmatrix} \begin{bmatrix} −1&2&3\\4&0&5\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}5(−1)+−1(4)&5(2)+−1(0)&5(3)+−1(5)\\−4(−1)+0(4)&−4(2)+0(0)&−4(3)+0(5)\\2(−1)+3(4)& 2(2)+3(0)&2(3)+3(5)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−9&10&10\\4&−8&−12\\10&4&21\end{bmatrix} \nonumber \end{align} \nonumber$$

Uchambuzi

Kumbuka kwamba bidhaa$AB$ na$BA$ si sawa.

$$AB=\begin{bmatrix}−7&10\\30&11\end{bmatrix}≠ \begin{bmatrix}−9&10&10\\4&−8&−12\\10&4&21\end{bmatrix}=BA \nonumber$$

Hii inaonyesha ukweli kwamba kuzidisha kwa tumbo sio kubadilisha.

Q & A: Je, inawezekana kwa AB kufafanuliwa lakini si BA?

Ndiyo, fikiria tumbo$A$ na mwelekeo$3 × 4$ na tumbo$B$ na mwelekeo$4 × 2$. Kwa bidhaa vipimo$AB$ vya ndani ni$4$ na bidhaa hufafanuliwa, lakini kwa bidhaa vipimo$BA$ vya ndani ni$2$ na$3$ hivyo bidhaa haijulikani.

Mfano$\PageIndex{6}$: Using Matrices in Real-World Problems

Hebu kurudi kwenye tatizo lililowasilishwa wakati wa ufunguzi wa sehemu hii. Tuna Jedwali$\PageIndex{3}$, anayewakilisha mahitaji ya vifaa vya timu mbili za soka.

Jedwali$\PageIndex{3}$

	paka mwitu	matope paka
Malengo	6	10
Mipira	30	24
Jerseys	14	20

Pia tunapewa bei za vifaa, kama inavyoonekana katika Jedwali$\PageIndex{4}$.

Jedwali$\PageIndex{4}$

Lengo	$300
Mpira	$10
Jersey	$30

Tutabadilisha data kwa matrices. Hivyo, matrix haja ya vifaa imeandikwa kama

$$E=\begin{bmatrix}6&10\\30&24\\14&20\end{bmatrix} \nonumber$$

Matrix ya gharama imeandikwa kama

$$C=\begin{bmatrix}300&10&30\end{bmatrix} \nonumber$$

Tunafanya kuzidisha matrix ili kupata gharama za vifaa.

$$\begin{align} CE&=\begin{bmatrix}300&10&30\end{bmatrix}⋅\begin{bmatrix}6&10\\30&24\\14&20\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}300(6)+10(30)+30(14)&300(10)+10(24)+30(20)\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}2,520&3,840\end{bmatrix} \nonumber \end{align} \nonumber$$

gharama ya jumla kwa ajili ya vifaa kwa ajili ya Wildcats ni$$2,520$, na gharama ya jumla kwa ajili ya vifaa kwa ajili ya matope Cats ni$$3,840$.

Jinsi ya: Kutokana na operesheni ya tumbo, tathmini kutumia calculator

1. Hifadhi kila tumbo kama variable Matrix$[A], [B], [C],...$
2. Ingiza operesheni ndani ya calculator, wito up kila variable Matrix kama inahitajika.
3. Ikiwa operesheni inafafanuliwa, calculator itawasilisha tumbo la suluhisho; ikiwa operesheni haijulikani, itaonyesha ujumbe wa kosa.

Mfano$\PageIndex{7}$: Using a Calculator to Perform Matrix Operations

Kupata$AB−C$ aliyopewa

$A=\begin{bmatrix}−15&25&32\\41&−7&−28\\10&34&−2\end{bmatrix}$,$B=\begin{bmatrix}45&21&−37\\−24&52&19\\6&−48&−31\end{bmatrix}$, na$C=\begin{bmatrix}−100&−89&−98\\25&−56&74\\−67&42&−75\end{bmatrix}$

Suluhisho

Kwenye ukurasa wa tumbo wa calculator, tunaingia tumbo$A$ hapo juu kama variable ya tumbo$[ A ]$, tumbo$B$ hapo juu kama kutofautiana kwa tumbo$[ B ]$, na tumbo$C$ hapo juu kama kutofautiana kwa tumbo$[ C ]$.

Kwenye skrini ya nyumbani ya calculator, tunaandika tatizo na tutaita kila variable ya tumbo kama inahitajika.

$$[A]×[B]−[C] \nonumber$$

Calculator inatupa tumbo zifuatazo.

$$\begin{bmatrix}−983&−462&136\\1,820&1,897&−856\\−311&2,032&413\end{bmatrix} \nonumber$$

vyombo vya habari

Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na matrices na shughuli za matrix.

• Vipimo vya Matrix
• Matrix kuongeza na Ondoa
• Uendeshaji wa Matrix
• Matrix kuzidisha

Dhana muhimu

• Matrix ni safu ya mstatili wa namba. Maingizo yanapangwa katika safu na nguzo.
• Vipimo vya tumbo hutaja idadi ya safu na idadi ya nguzo. $3×2$Matrix ina safu tatu na nguzo mbili. Angalia Mfano$\PageIndex{1}$.
• Sisi kuongeza na kuondoa matrices ya vipimo sawa kwa kuongeza na kuondoa entries sambamba ya kila tumbo. Angalia Mfano$\PageIndex{2}$, Mfano$\PageIndex{3}$, Mfano$\PageIndex{4}$, na Mfano$\PageIndex{5}$.
• Kuzidisha kwa scalar kunahusisha kuzidisha kila kuingia kwenye tumbo kwa mara kwa mara. Angalia Mfano$\PageIndex{6}$.
• Kuzidisha kwa scalar mara nyingi huhitajika kabla ya kuongeza au kuondoa kunaweza kutokea. Angalia Mfano$\PageIndex{7}$.
• Kuongezeka kwa matrices kunawezekana wakati vipimo vya ndani ni sawa-idadi ya nguzo katika tumbo la kwanza lazima ifanane na idadi ya safu katika pili.
• bidhaa ya matrices mbili,$A$ na$B$, ni kupatikana kwa kuzidisha kila kuingia katika mstari 1 ya$A$ kwa kila kuingia katika safu 1 ya$B$; kisha kuzidisha kila kuingia ya mstari 1 ya$A$ kwa kila kuingia katika nguzo 2 ya$B$, na kadhalika. Angalia Mfano$\PageIndex{8}$ na Mfano$\PageIndex{9}$.
• Matatizo mengi ya ulimwengu halisi yanaweza kutatuliwa mara nyingi kwa kutumia matrices. Angalia Mfano$\PageIndex{10}$.
• Tunaweza kutumia calculator kufanya shughuli matrix baada ya kuokoa kila tumbo kama variable Matrix. Angalia Mfano$\PageIndex{11}$.