8.R: Matumizi zaidi ya Trigonometry (Tathmini)

Last updated
Save as PDF

Page ID: 181006

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

8.1: Pembetatu zisizo za haki: Sheria ya Sines

Kwa ajili ya mazoezi 1-5 kudhani$\alpha $ ni upande kinyume$a$,$\beta $ ni upande kinyume$b$, na$\gamma $ ni upande kinyume$c$. Tatua kila pembetatu, ikiwa inawezekana. Pande kila jibu kwa kumi ya karibu.

1)$\beta =50^{\circ}, a=105, b=45$

Jibu: Haiwezekani

2)$\alpha =43.1^{\circ}, a=184.2, b=242.8$

3) Tatua pembetatu.

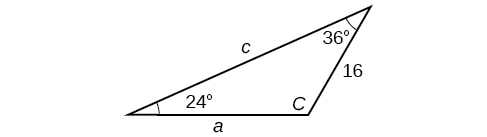
$Ex 8R 8.1.3.png$

Jibu: $C=120^{\circ}, a=23.1, c=34.1$

4) Pata eneo la pembetatu.

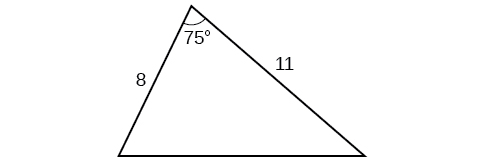
5) Majaribio ni kuruka juu ya barabara kuu moja kwa moja. Yeye huamua pembe ya unyogovu kwa posts maili mbili$2.1$ km mbali kuwa$25^{\circ}$ na$49^{\circ}$, kama inavyoonekana katika takwimu hapa chini. Pata umbali wa ndege kutoka hatua$A$ na mwinuko wa ndege.

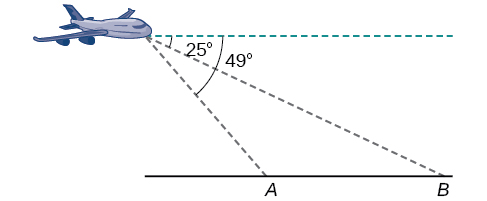
$Ex 8R 8.1.5.png$

Jibu: umbali wa ndege kutoka$A:2.2$ kilomita kilomita, mwinuko wa ndege:$1.6$ km

8.2: Pembetatu zisizo za haki - Sheria ya Cosines

1) Tatua pembetatu, ukizunguka hadi kumi ya karibu, ukichukua$\alpha $ ni kinyume upande$a$,$\beta $ ni kinyume upande$b$, na$\gamma $ s upande kinyume$c: a=4, b=6,c=8$.

2) Tatua pembetatu kwenye Kielelezo hapa chini, ukizunguka hadi kumi ya karibu.

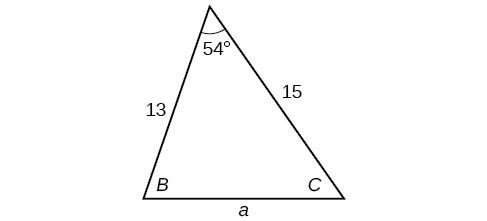
$Ex 8R 8.2.2.png$

Jibu: $B=71.0^{\circ},C=55.0^{\circ},a=12.8$

3) Pata eneo la pembetatu na pande za urefu$8.3$,$6.6$, na$9.1$.

4) Ili kupata umbali kati ya miji miwili, satellite huhesabu umbali na angle iliyoonyeshwa kwenye Mchoro hapa chini (sio kiwango). Pata umbali kati ya miji. Majibu ya pande zote kwa kumi ya karibu.

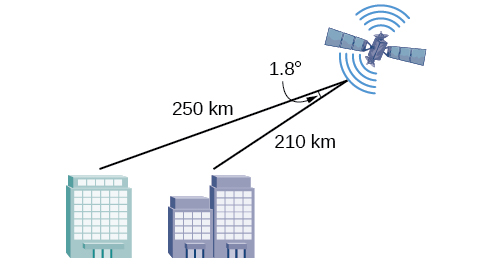
$Ex 8R 8.2.4.png$

Jibu: $40.6$km

8.3: Kuratibu Polar

1) Panda hatua na kuratibu polar$\left ( 3,\dfrac{\pi }{6} \right )$.

2) Panda hatua na kuratibu polar$\left ( 5,\dfrac{-2\pi }{3} \right )$.

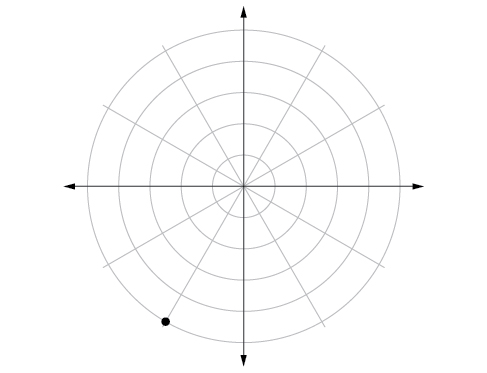
Jibu: $Ex 8R 8.3.2.png$

3) Badilisha kwenye$\left ( 6,\dfrac{-3\pi }{4} \right )$ kuratibu za mstatili.

4) Badilisha kwenye$\left ( -2,\dfrac{3\pi }{2} \right )$ kuratibu za mstatili.

Jibu: $(0,2)$

5) Badilisha kwenye$(7,-2)$ kuratibu za polar.

6) Badilisha kwenye$(-9,-4)$ kuratibu za polar.

Jibu: $(9.8489,203.96^{\circ})$

Kwa mazoezi 7-9, kubadilisha equation ya Cartesian iliyotolewa kwa equation polar.

7)$x=-2$

8)$x^2+y^2=64$

Jibu: $r=8$

9)$x^2+y^2=-2y$

Kwa mazoezi 10-11, kubadilisha equation ya polar iliyotolewa kwa equation ya Cartesian.

10)$r=7\cos \theta$

Jibu: $x^2+y^2=7x$

11)$r=\dfrac{-2}{4\cos \theta +\sin \theta }$

Kwa mazoezi 12-13, kubadilisha fomu ya mstatili na grafu.

12)$\theta =\dfrac{3\pi }{4}$

Jibu

$y=-x$

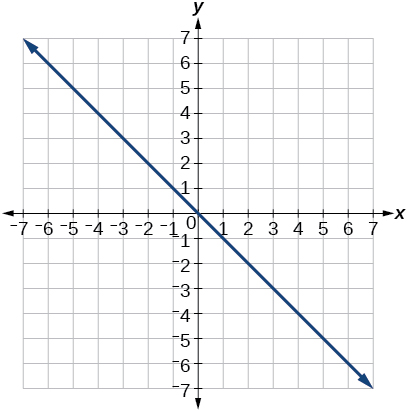
$Ex 8R 8.3.12.png$

13)$r=5\sec \theta$

8.4: Kuratibu Polar - Grafu

Kwa mazoezi 1-5, jaribu kila equation kwa ulinganifu.

1)$r=4+4\sin \theta$

Jibu: ulinganifu kwa heshima na mstari$\theta =\dfrac{\pi }{2}$

2)$r=7$

3) Mchoro grafu ya equation polar$r=1-5\sin \theta$. Weka alama ya mhimili.

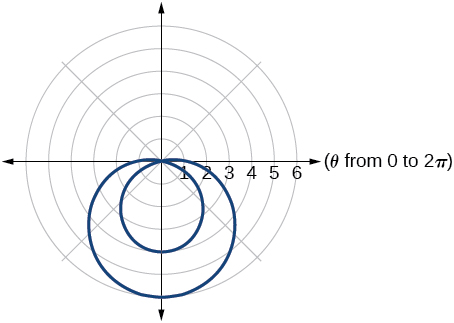
Jibu: $Ex 8R 8.4.3.png$

4) Mchoro grafu ya equation polar$r=5\sin (7\theta )$.

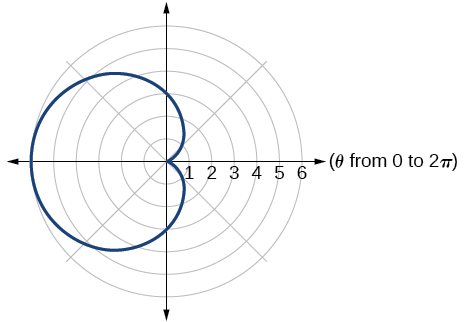
5) Mchoro grafu ya equation ya polar$r=3-3\cos \theta$

Jibu: $Ex 8R 8.4.5.png$

8.5: Fomu ya Polar ya Hesabu Complex

Kwa mazoezi 1-2, pata thamani kamili ya kila nambari tata.

1)$-2+6i$

2)$4-3i$

Jibu: $5$

Andika namba tata katika fomu ya polar.

3)$5+9i$

4)$\dfrac{1}{2}-\dfrac{\sqrt{3}}{2}i$

Jibu: $\mathrm{cis}\left (-\dfrac{\pi }{3} \right )$

Kwa mazoezi 5-6, kubadilisha namba tata kutoka polar hadi fomu ya mstatili.

5)$z=5\mathrm{cis}\left (\dfrac{5\pi }{6} \right )$

6)$z=3\mathrm{cis}(40^{\circ})$

Jibu: $2.3+1.9i$

Kwa mazoezi 7-8, pata bidhaa$z_1 z_2$ katika fomu ya polar.

7)$\begin{align*} z_1 &= 2\mathrm{cis}(89^{\circ})\\ z_2 &= 5\mathrm{cis}(23^{\circ}) \end{align*}$

8)$\begin{align*} z_1 &= 10\mathrm{cis}\left ( \dfrac{\pi }{6} \right )\\ z_2 &= 6\mathrm{cis}\left ( \dfrac{\pi }{3} \right ) \end{align*}$

Jibu: $60\mathrm{cis}\left ( \dfrac{\pi }{2} \right )$

Kwa mazoezi 9-10, pata quotient$\dfrac{z_1}{z_2}$ katika fomu ya polar.

9)$\begin{align*} z_1 &= 12\mathrm{cis}(55^{\circ})\\ z_2 &= 3\mathrm{cis}(18^{\circ}) \end{align*}$

10)$\begin{align*} z_1 &= 27\mathrm{cis}\left ( \dfrac{5\pi }{3} \right )\\ z_2 &= 9\mathrm{cis}\left ( \dfrac{\pi }{3} \right ) \end{align*}$

Jibu: $3\mathrm{cis}\left ( \dfrac{4\pi }{3} \right )$

Kwa mazoezi 11-12, pata nguvu za kila nambari tata katika fomu ya polar.

11) Pata$z^4$ wakati$z=2\mathrm{cis}(70^{\circ})$

12) Pata$z^2$ wakati$z=5\mathrm{cis}\left ( \dfrac{3\pi }{4} \right )$

Jibu: $25\mathrm{cis}\left ( \dfrac{3\pi }{2} \right )$

Kwa mazoezi 13-14, tathmini kila mizizi.

13) Tathmini mizizi ya mchemraba wa$z$ wakati$z=64\mathrm{cis}(210^{\circ})$.

14) Tathmini mizizi ya mraba ya$z$ wakati$z=25\mathrm{cis}\left ( \dfrac{3\pi }{2} \right )$.

Jibu: $5\mathrm{cis}\left ( \dfrac{3\pi }{4} \right )$,$5\mathrm{cis}\left ( \dfrac{7\pi }{4} \right )$

Kwa mazoezi 15-16, njama namba tata katika ndege tata.

15)$6-2i$

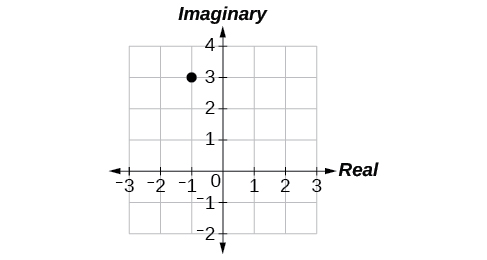
16)$-1+3i$

Jibu: $Ex 8R 8.5.16.png$

8.6: Ulinganifu wa parametric

1)$\begin{cases} & x(t)= 3t-1\\ & y(t)= \sqrt{t} \end{cases}$

2)$\begin{cases} & x(t)= -\cos t\\ & y(t)= 2\sin ^2t \end{cases}$

Jibu: $x^2+\dfrac{1}{2}y=1$

3) Parameterize (kuandika equation parametric kwa) kila equation Cartesian kwa kutumia$x(t)=a\cos t$ na$y(t)=b\sin t$ kwa$\dfrac{x^2}{25}+\dfrac{y^2}{16}=1$.

4) Parameterize mstari kutoka kwa$(-2,3)$$(4,7)$ ili mstari$(-2,3)$ ulipo$t=0$ na$(4,7)$ saa$t=1$.

Jibu: $\begin{cases} & x(t)= -2+6t\\ & y(t)= 3+4t \end{cases}$

8.7: Ulinganifu wa parametric - Grafu

Kwa mazoezi 1-, fanya meza ya maadili kwa kila seti ya equations parametric, grafu equations, na ni pamoja na mwelekeo; kisha kuandika equation Cartesian.

1)$\begin{cases} & x(t)= 3t^2\\ & y(t)= 2t-1 \end{cases}$

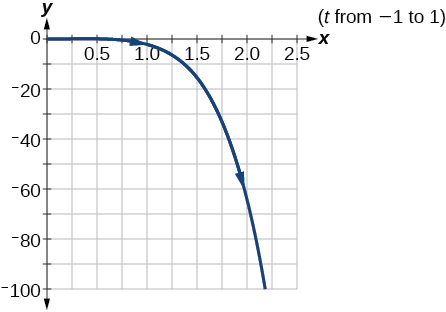
2)$\begin{cases} & x(t)= e^t\\ & y(t)= -2e^{5t} \end{cases}$

Jibu

$y=-2x^5$

$Ex 8R 8.7.2.png$

3)$\begin{cases} & x(t)= 3\cos t\\ & y(t)= 2\sin t \end{cases}$

4) mpira ni ilizinduliwa kwa kasi ya awali ya$80$ miguu kwa pili kwa pembe ya$40^{\circ}$ kwa usawa. Mpira hutolewa kwa urefu wa$4$ miguu juu ya ardhi.

Wapi mpira baada ya$3$ sekunde?
Je! Mpira ni muda gani?

Jibu

$\begin{cases} & x(t)= (80\cos (40^{\circ}))t\\ & y(t)= -16t^2+(80\sin (40^{\circ}))t+4 \end{cases}$
Mpira una urefu wa futi 14 na futi 184 kutoka ambapo ulizinduliwa.
$3.3$sekunde

8.8: Vectors

Kwa mazoezi 1-2, onyesha kama vectors mbili,$\vecs u$ na$\vecs v$, ni sawa, ambapo$\vecs u$ ina hatua ya awali$P_1$ na hatua ya mwisho$P_2$, na$\vecs v$ ina hatua ya awali$P_3$ na hatua ya mwisho$P_4$.

1)$P_1=(-1,4), P_2=(3,1), P_3=(5,5), P_4=(9,2)$

2)$P_1=(6,11), P_2=(-2,8), P_3=(0,-1), P_4=(-8,2)$

Jibu: si sawa

Kwa mazoezi 3-4, tumia vectors$\vecs u=2\hat{\mathbf{i}}-\hat{\mathbf{j}}$,$\vecs v=4\hat{\mathbf{i}}-3\hat{\mathbf{j}}$, na$\vecs w=-2\hat{\mathbf{i}}+5\hat{\mathbf{j}}$ kutathmini maneno.

3)$ \vecs u-\vecs v $

4)$ 2\vecs v-\vecs u+\vecs w $

Jibu: $4\hat{\mathbf{i}}$

Kwa mazoezi 5-6, pata vector kitengo katika mwelekeo sawa na vector iliyotolewa.

5)$\vecs a=8\hat{\mathbf{i}}-6\hat{\mathbf{j}}$

6)$\vecs b=-3\hat{\mathbf{i}}-\hat{\mathbf{j}}$

Jibu: $-\dfrac{3\sqrt{10}}{10}\hat{\mathbf{i}}-\dfrac{\sqrt{10}}{10}\hat{\mathbf{j}}$

Kwa mazoezi 7-11, mahesabu$\vecs u\cdot \vecs v$

7)$\vecs u=-2\hat{\mathbf{i}}+\hat{\mathbf{j}}$ na$\vecs v=3\hat{\mathbf{i}}+7\hat{\mathbf{j}}$

8)$\vecs u=\hat{\mathbf{i}}+4\hat{\mathbf{j}}$ na$\vecs v=4\hat{\mathbf{i}}+3\hat{\mathbf{j}}$

Jibu: $16$

9) Kutokana na$\vecs v=\left \langle -3,4 \right \rangle$ kuteka$\vecs v$$2\vecs v$,, na$\dfrac{1}{2}\vecs v$.

10) Kutokana na wadudu inavyoonekana katika Kielelezo hapa chini, mchoro$\vecs u + \vecs v$,$\vecs u − \vecs v$ na$3\vecs v$.

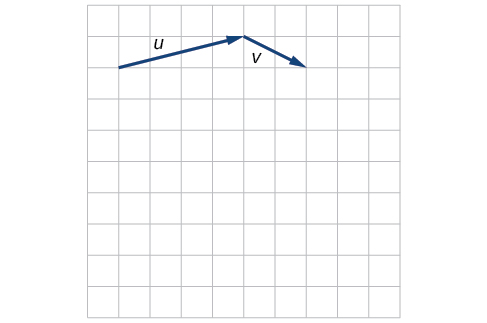
$Ex 8R 8.8.10.png$

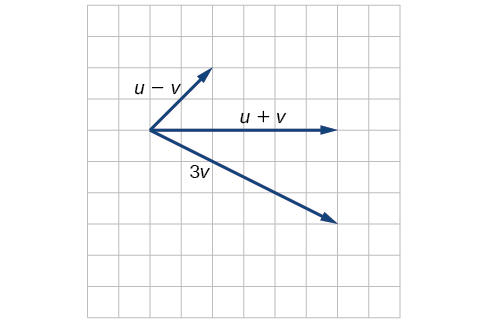
Jibu: $Ex 8R 8.8.10 sol.png$

11) Kutokana$P_1=(3,2)$ na hatua ya awali na hatua ya mwisho$P_2=(-5,-1)$, kuandika vector$\vecs v$ katika suala la$\hat{\mathbf{i}}$ na$\hat{\mathbf{j}}$. Chora pointi na vector kwenye grafu.

Mazoezi mtihani

1)$\alpha $ Kudhani ni kinyume upande$a$,$\beta $ ni kinyume upande$b$, na$\gamma $ ni kinyume upande$c$. Tatua pembetatu, ikiwa inawezekana, na pande zote jibu kwa kumi ya karibu, iliyotolewa$\beta =68^{\circ},b=21,c=16$.

Jibu: $\alpha =67.1^{\circ}, \gamma =44.9^{\circ}, a=20.9$

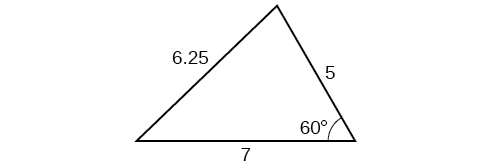
2) Pata eneo la pembetatu kwenye Kielelezo hapa chini. Pande kila jibu kwa kumi ya karibu.

$Ex 8rp.2.png$

3) Jaribio linaruka kwa njia moja kwa moja kwa$2$ masaa. Kisha hufanya marekebisho ya kozi,$15^{\circ}$ akielekea haki ya kozi yake ya awali, na nzi$1$ saa katika mwelekeo mpya. Ikiwa anaendelea kasi ya$575$ maili kwa saa, ni mbali gani kutoka nafasi yake ya kuanzia?

Jibu: $1712$maili

4) Badilisha$(2,2)$ kwa kuratibu polar, na kisha njama uhakika.

5) Badilisha kwenye$\left ( 2,\dfrac{\pi }{3} \right )$ kuratibu za mstatili.

Jibu: $(1,\sqrt{3})$

6) Badilisha equation ya polar kwa equation ya Cartesian:$x^2+y^2=5y$.

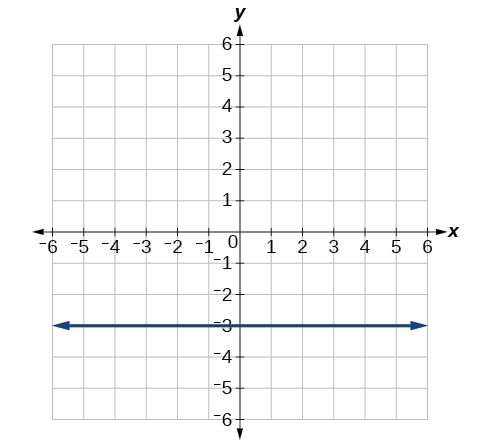
7) Badilisha fomu ya mstatili na grafu:$r=-3\csc θ$.

Jibu

$y=-3$

$Kutoka 8rp.7.png$

8) Mtihani equation kwa ulinganifu:$r=-4\sin(2\theta )$.

9) Grafu$r=3+3\cos \theta$.

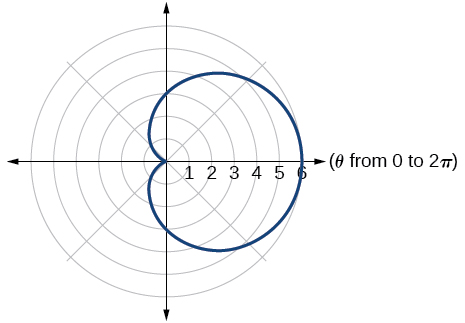
Jibu: $Ex 8rp.9.png$

10) Grafu$r=3-5\sin \theta$.

11) Pata thamani kamili ya idadi tata$5-9i$.

Jibu: $\sqrt{106}$

12) Andika namba tata katika fomu ya polar:$4+i$.

13) Badilisha idadi tata kutoka polar hadi fomu ya mstatili:$z=5\mathrm{cis}\left ( \dfrac{2\pi }{3} \right )$

Jibu: $\dfrac{-5}{2}+i\dfrac{5\sqrt{3}}{2}$

14)$z_1 z_2$

15)$\dfrac{z_1}{z_2}$

Jibu: $4\mathrm{cis}(21^{\circ})$

16)$(z_2)^3$

17)$\sqrt{z_1}$

Jibu: $2\sqrt{2}\mathrm{cis}(18^{\circ}), 2\sqrt{2}\mathrm{cis}(198^{\circ})$

18) Plot idadi tata$-5-i$ katika ndege tata.

19) Ondoa parameter$t$ kuandika upya equations zifuatazo parametric kama equation Cartesian:$\begin{cases} & x(t)= t+1\\ & y(t)= 2t^2 \end{cases}$

Jibu: $y=2(x-1)^2$

20) Parameterize (kuandika equation parametric kwa) zifuatazo Cartesian equation kwa kutumia$x(t)=a\cos t$ na$y(t)=b\sin t : \dfrac{x^2}{36}+\dfrac{y^2}{100}=1$

21) Grafu seti ya equations parametric na kupata equation Cartesian:$\begin{cases} & x(t)= -2\sin t\\ & y(t)= 5\cos t \end{cases}$

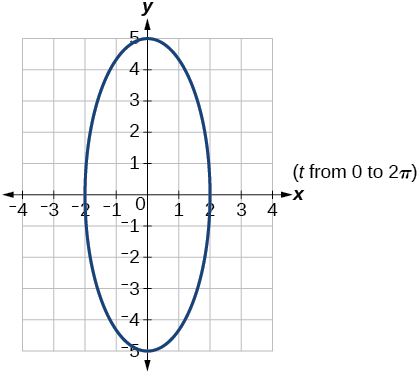
Jibu: $Kutoka 8rp.21.png$

22) mpira ni ilizinduliwa kwa kasi ya awali ya$95$ miguu kwa pili kwa pembe ya$52^{\circ}$ kwa usawa. Mpira hutolewa kwa urefu wa$3.5$ miguu juu ya ardhi.

Wapi mpira baada ya$2$ sekunde?
Je! Mpira ni muda gani?

Kwa mazoezi 23-26, tumia vectors$\vecs u = \hat{\mathbf{i}} − 3\hat{\mathbf{j}}$ na$\vecs v = 2\hat{\mathbf{i}} + 3\hat{\mathbf{j}}$.

23) Kupata$2\vecs u − 3\vecs v$.

Jibu: $-4\hat{\mathbf{i}}-15\hat{\mathbf{j}}$

24) Tumia hesabu$\vecs u\cdot \vecs v$.

25) Kupata kitengo vector katika mwelekeo sawa na$\vecs v$.

Jibu: $\dfrac{2\sqrt{3}}{13}\hat{\mathbf{i}}+\dfrac{3\sqrt{3}}{13}\hat{\mathbf{j}}$

26) Kutokana na vector$\vecs v$ ina hatua ya awali$P_1=(2,2)$ na hatua ya mwisho$P_2=(-1,0)$, kuandika vector$\vecs u\cdot \vecs v$.

Wachangiaji na Majina

Template:OpenStaxPreCalc