8.E: Matumizi zaidi ya Trigonometry (Mazoezi)

8.1: Pembetatu zisizo za haki: Sheria ya Sines

Maneno

1) Eleza urefu wa pembetatu.

Jibu

Urefu unatoka kwenye vertex yoyote hadi upande wa pili au kwenye mstari ulio na upande wa pili kwa$90^{\circ}$ pembe.

2) Linganisha pembetatu sahihi na pembetatu za oblique.

3) Wakati gani unaweza kutumia Sheria ya Sines kupata angle kukosa?

Jibu

Wakati maadili inayojulikana ni upande kinyume na angle kukosa na upande mwingine na angle yake kinyume.

4) Katika Sheria ya Sines, ni uhusiano gani kati ya angle katika nambari na upande katika denominator?

5) Ni aina gani ya pembetatu inayosababisha kesi isiyofaa?

Jibu

Pembetatu yenye pande mbili zilizopewa na angle isiyojumuishwa.

Kialjebra

Kwa mazoezi 6-10, kudhani$\alpha$ ni upande wa pili$a$,$\beta$ ni upande wa pili$b$, na$\gamma$ ni upande wa pili$c$. Tatua kila pembetatu, ikiwa inawezekana. Pande kila jibu kwa karibu kumi.

6)$\alpha =43^{\circ}, \gamma =69^{\circ}, a=20$

7)$\alpha =35^{\circ}, \gamma =73^{\circ}, c=20$

Jibu

$\beta =72^{\circ}, a\approx 12.0, b\approx 19.9$

8)$\alpha =60^{\circ}, \beta =60^{\circ}, \gamma =60^{\circ}$

9)$a=4, \alpha =60^{\circ}, \beta =100^{\circ}$

Jibu

$\gamma =20^{\circ}, b\approx 4.5, c\approx 1.6$

10)$b=10, \beta =95^{\circ}, \gamma =30^{\circ}$

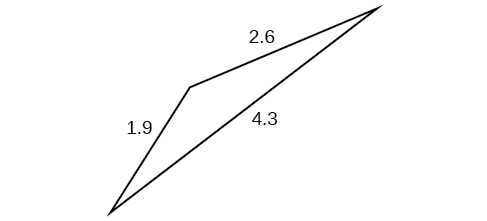
11) Pata upande$b$ wakati$A=37^{\circ}, B=49^{\circ}, c=5$

Jibu

$b\approx 3.78$

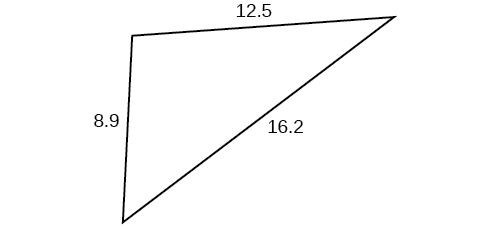
12) Pata upande$a$ wakati$A=132^{\circ}, C=23^{\circ}, b=10$

13) Pata upande$c$ wakati$B=37^{\circ}, C=21^{\circ}, b=23$

Jibu

$c\approx 13.70$

Kwa mazoezi 14-23, kudhani$\alpha$ ni upande wa pili$a$,$\beta$ ni upande wa pili$b$, na$\gamma$ ni upande wa pili$c$. Kuamua kama hakuna pembetatu, pembetatu moja, au pembetatu mbili. Kisha kutatua kila pembetatu, ikiwa inawezekana. Pande kila jibu kwa karibu kumi.

14)$\alpha =119^{\circ}, a=14, b=26$

15)$\gamma =113^{\circ}, b=10, c=32$

Jibu

pembetatu moja,$\alpha \approx 50.3^{\circ}, \beta \approx 16.7^{\circ}, a\approx 26.7$

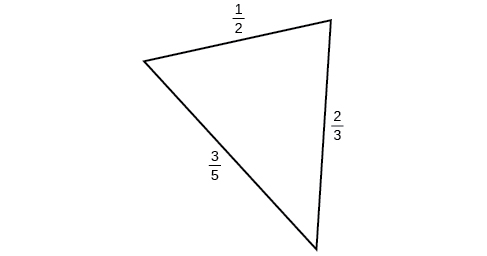
16)$b=3.5, c=5.3, \gamma =80^{\circ}$

17)$a=12, c=17, \alpha =35^{\circ}$

Jibu

pembetatu mbili,$\gamma \approx 54.3^{\circ}, \beta \approx 90.7^{\circ}, b\approx 20.9$ au$\gamma '\approx 125.7^{\circ}, \beta '\approx 19.3^{\circ}, b'\approx 6.9$

18)$a=20.5, b=35.0, \beta =25^{\circ}$

19)$a=7, c=9, \alpha =43^{\circ}$

Jibu

pembetatu mbili,$\beta \approx 75.7^{\circ}, \gamma \approx 61.3^{\circ}, b\approx 9.9$ au$\beta '\approx 18.3^{\circ}, \gamma '\approx 118.7^{\circ}, b'\approx 3.2$

20)$a=7, b=3, \beta =24^{\circ}$

21)$b=13, c=5, \gamma =10^{\circ}$

Jibu

pembetatu mbili,$\alpha \approx 143.2^{\circ}, \beta \approx 26.8^{\circ}, a\approx 17.3$ au$\alpha '\approx 16.8^{\circ}, \beta '\approx 153.2^{\circ}, a'\approx 8.3$

22)$a=2.3, c=1.8, \gamma =28^{\circ}$

23)$\beta =119^{\circ}, b=8.2, a=11.3$

Jibu

hakuna pembetatu iwezekanavyo

Kwa mazoezi 24-26, tumia Sheria ya Sines ili kutatua, ikiwa inawezekana, upande usiopotea au angle kwa kila pembetatu au pembetatu katika kesi isiyofaa. Pande kila jibu kwa karibu kumi.

24) Pata angle$A$ wakati$a=24, b=5, B=22^{\circ}$

25) Pata angle$A$ wakati$a=13, b=6, B=20^{\circ}$

Jibu

$A\approx 47.8^{\circ}$au$A'\approx 132.2^{\circ}$

26) Pata angle$B$ wakati$A=12^{\circ}, a=2, b=9$

Kwa mazoezi 27-30, tafuta eneo la pembetatu na vipimo vilivyopewa. Pande kila jibu kwa karibu kumi.

27)$a=5, c=6, \beta =35^{\circ}$

Jibu

$8.6$

28)$b=11, c=8, \alpha =28^{\circ}$

29)$a=32, b=24, \gamma =75^{\circ}$

Jibu

$370.9$

30)$a=7.2, b=4.5, \gamma =43^{\circ}$

Graphic

Kwa mazoezi 31-36, pata urefu wa upande$x$. Pande zote hadi kumi ya karibu.

31)

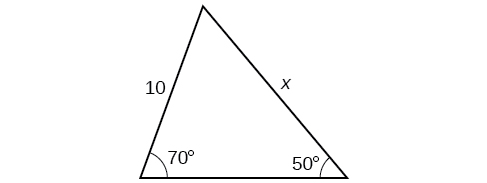
Jibu

$12.3$

32)

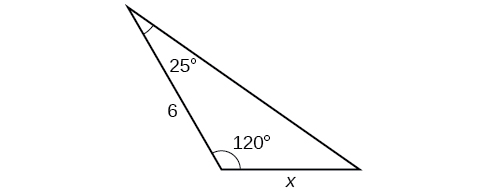
33)

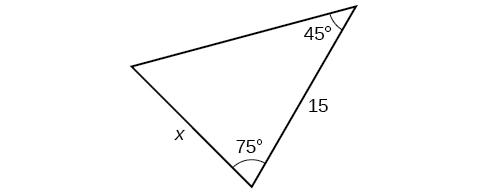
Jibu

$12.2$

34)

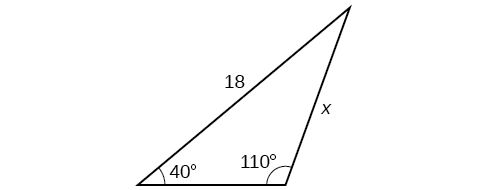
35)

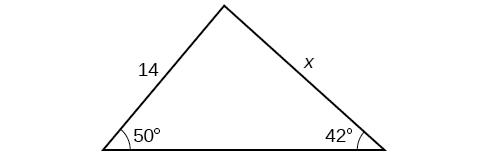
Jibu

$16.0$

36)

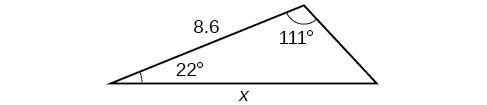
Kwa mazoezi 37-,42 kupata kipimo cha angle$x$, ikiwa inawezekana. Pande zote hadi kumi ya karibu.

37)

Jibu

$29.7^{\circ}$

38)

39)

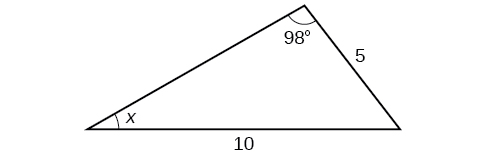
Jibu

$x=76.9^{\circ}$au$x=103.1^{\circ}$

40)

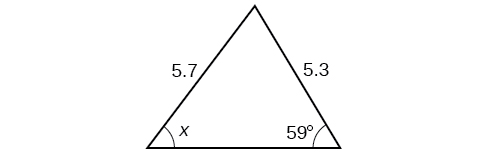
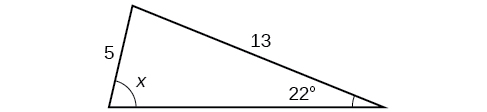
41) Taarifa kwamba$x$ ni angle obtuse.

Jibu

$110.6^{\circ}$

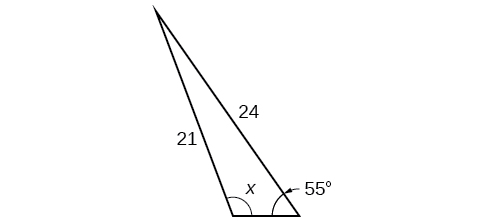
42)

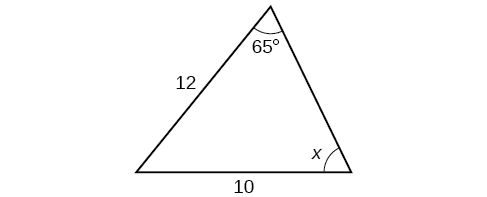
Kwa mazoezi 43-49, tafuta eneo la kila pembetatu. Pande kila jibu kwa karibu kumi.

43)

Jibu

$A\approx 39.4, C\approx 47.6, BC\approx 20.7$

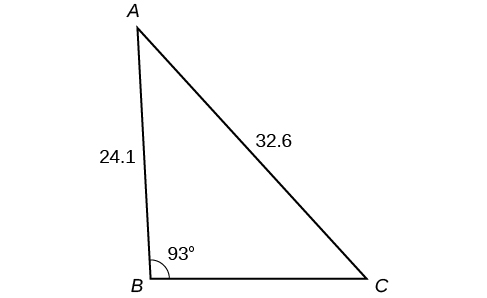
44)

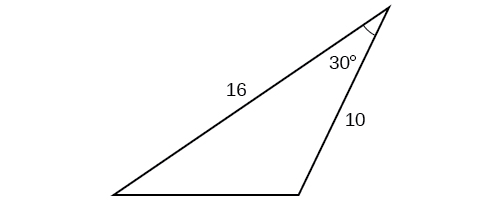
45)

Jibu

$57.1$

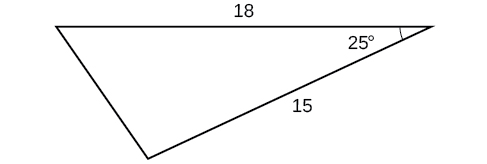
46)

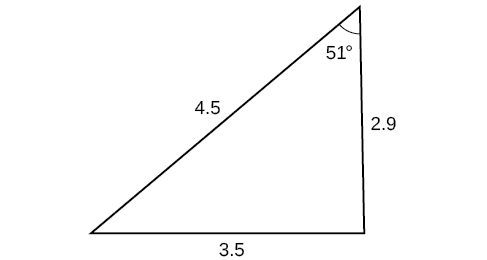
47)

Jibu

$42.0$

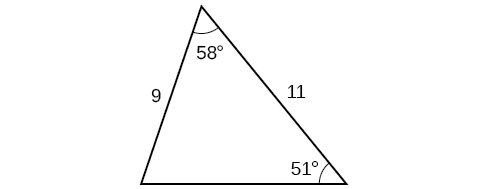
48)

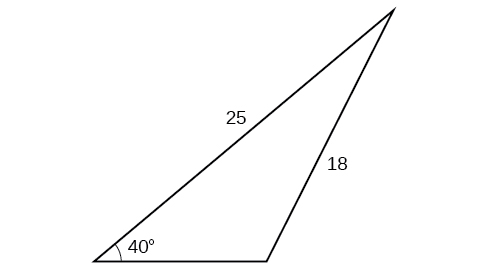
49)

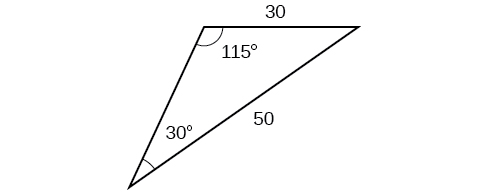
Jibu

$430.2$

Upanuzi

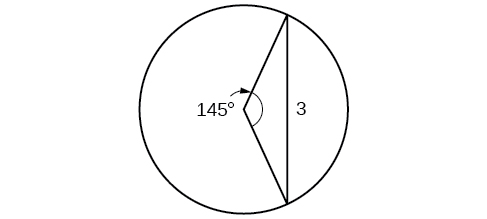
50) Pata radius ya mduara kwenye Kielelezo hapa chini. Pande zote hadi kumi ya karibu.

Kielelezo 50.

51) Pata kipenyo cha mduara kwenye Kielelezo hapa chini. Pande zote hadi kumi ya karibu.

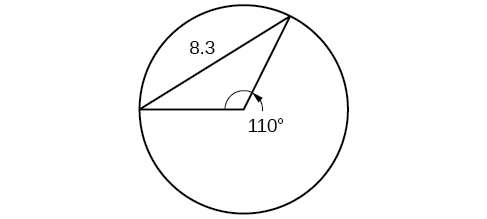
Jibu

$10.1$

52) Pata$m\angle ADC$ katika Kielelezo hapa chini. Pande zote hadi kumi ya karibu.

Kielelezo 52.

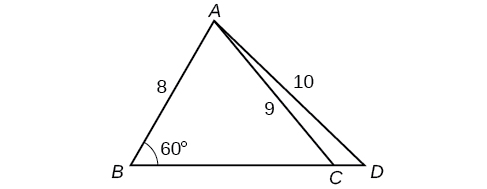
53) Pata upande$AD$ katika Kielelezo hapa chini. Pande zote hadi kumi ya karibu.

Jibu

$AD\approx 13.8$

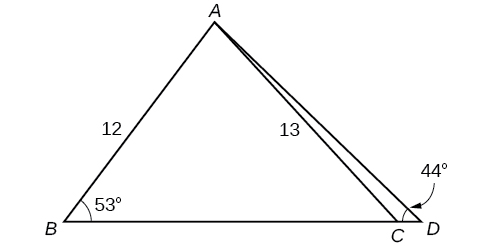
54) Tatua pembetatu zote mbili katika Kielelezo hapa chini. Pande kila jibu kwa karibu kumi.

Kielelezo 54.

55) Pata upande$AB$ katika parallelogram iliyoonyeshwa hapa chini. Pande zote hadi kumi ya karibu.

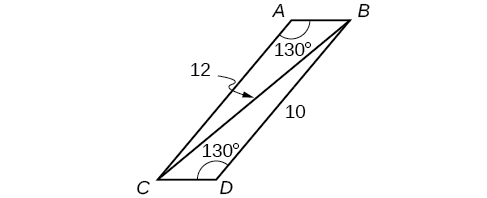
Jibu

$AB\approx 2.8$

56) Tatua pembetatu katika Kielelezo hapa chini. (kidokezo: Chora perpendicular kutoka$H$ kwa$JK$. Pande kila jibu kwa karibu kumi.

Kielelezo 56.

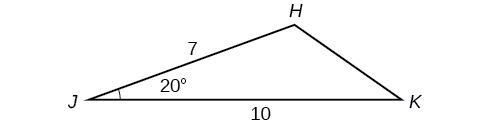
57) Tatua pembetatu katika Kielelezo hapa chini. (kidokezo: Chora perpendicular kutoka$N$ kwa$LM$. Pande kila jibu kwa karibu kumi.

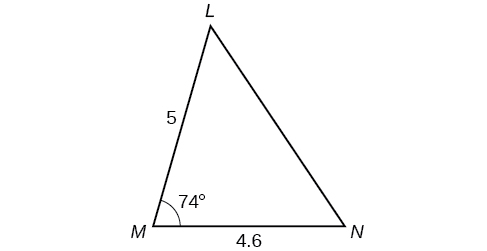
Jibu

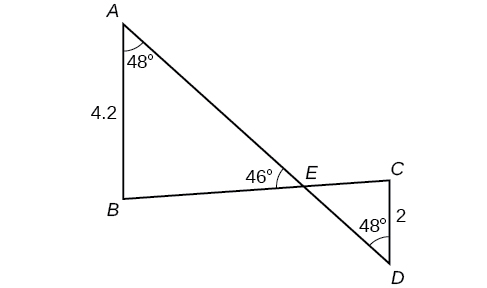
$L\approx 49.7 ^{\circ} , N\approx 56.3 ^{\circ} , LN\approx 5.8$

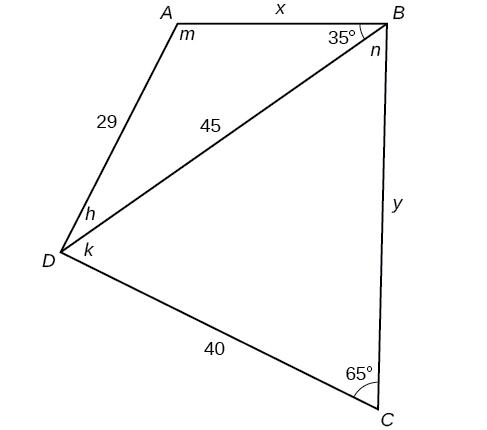
58) Katika Kielelezo hapa chini,$ABCD$ sio parallelogram. $\angle m$ni butu. Tatua pembetatu zote mbili. Pande kila jibu kwa karibu kumi.

Real-World Matumizi

59) pole leans mbali na jua kwa pembe ya$7^{\circ}$ wima, kama inavyoonekana katika Kielelezo hapa chini. Wakati mwinuko wa jua ni$55^{\circ}$, pole hupiga$42$ miguu ya kivuli kwa muda mrefu kwenye ardhi ya ngazi. Je! Pole ni muda gani? Pindua jibu kwa kumi ya karibu.

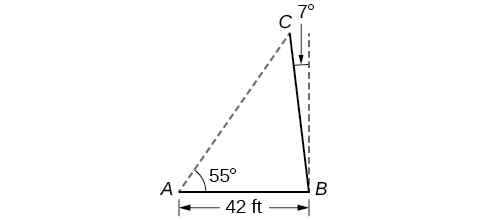
Jibu

$51.4$ft

60) Kuamua jinsi mbali mashua ni kutoka pwani, vituo viwili rada$500$ miguu mbali kupata pembe nje ya mashua, kama inavyoonekana katika Kielelezo hapa chini. Kuamua umbali wa mashua kutoka kituo$A$ na umbali wa mashua kutoka pwani. Pindua majibu yako kwa mguu mzima wa karibu.

Kielelezo 60.

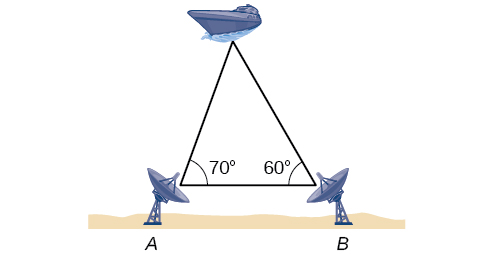
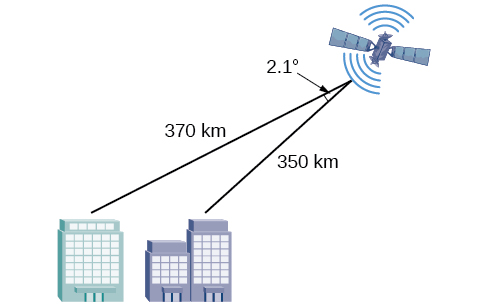
61) Kielelezo hapa chini kinaonyesha satellite inayozunguka Dunia. satellite hupita moja kwa moja juu ya vituo vya kufuatilia mbili$A$ na$B$, ambayo ni$69$ maili mbali. Wakati satellite iko upande mmoja wa vituo viwili, pembe za mwinuko kwenye$A$ na$B$ zinapimwa kuwa$86.2^{\circ}$ na$83.9^{\circ}$ mtawalia. Jinsi mbali ni satellite kutoka kituo$A$ na jinsi ya juu ni satellite juu ya ardhi? Round majibu kwa karibu maili nzima.

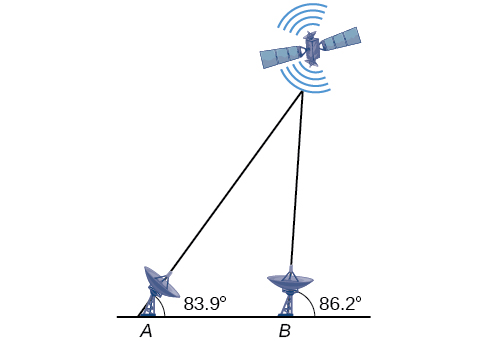
Jibu

Umbali kutoka satelaiti hadi kituo$A$ ni takriban$1716$ maili. Satellite iko takriban$1706$ maili juu ya ardhi.

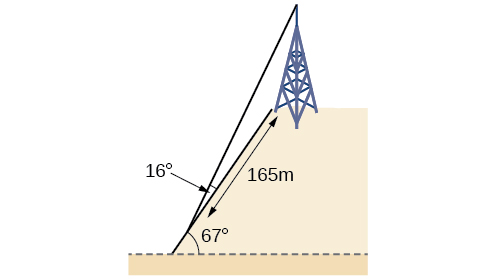
62) Mnara wa mawasiliano iko juu ya kilima cha mwinuko, kama inavyoonekana kwenye Mchoro hapa chini. Pembe ya mwelekeo wa kilima ni$67^{\circ}$. Waya wa guy ni kushikamana juu ya mnara na chini,$165$ mita kuteremka kutoka chini ya mnara. Pembe iliyoundwa na waya wa guy na kilima ni$16^{\circ}$. Pata urefu wa cable inahitajika kwa waya wa guy kwa mita nzima ya karibu.

Kielelezo 62.

63) Paa la nyumba ni$20^{\circ}$ pembe. Jopo la jua la$8$ mguu linapaswa kuwekwa juu ya paa na inapaswa kuwa angled$38^{\circ}$ jamaa na usawa kwa matokeo bora. (Angalia Kielelezo hapa chini). Je! Msaada wa wima unashikilia nyuma ya jopo unahitaji kuwa muda gani? Pande zote hadi kumi ya karibu.

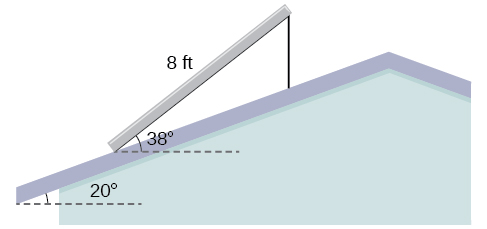
Jibu

$2.6$ft

64) Sawa na angle ya mwinuko, angle ya unyogovu ni angle ya papo hapo inayoundwa na mstari usio na usawa na mstari wa kuona kwa kitu chini ya usawa. Jaribio linaruka juu ya barabara kuu moja kwa moja. Yeye huamua pembe ya unyogovu kwa mileposts mbili,$6.6$ km mbali, kuwa$37^{\circ}$ na$44^{\circ}$ kama inavyoonekana katika Kielelezo hapa chini. Pata umbali wa ndege kutoka hatua$A$ hadi karibu ya kumi ya kilomita.

Kielelezo 64.

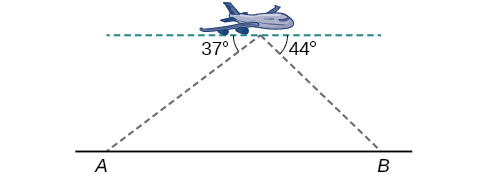
65) Majaribio ni kuruka juu ya barabara kuu moja kwa moja. Yeye huamua pembe ya unyogovu kwa mileposts mbili,$4.3$ km mbali, kuwa$32^{\circ}$ na$56^{\circ}$, kama inavyoonekana katika Kielelezo hapa chini. Pata umbali wa ndege kutoka hatua$A$ hadi karibu ya kumi ya kilomita.

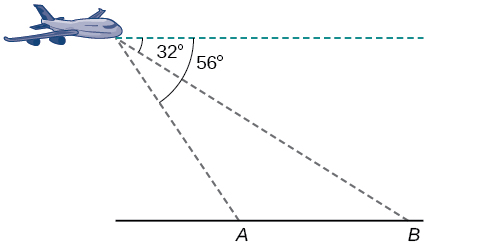
Jibu

$5.6$km

66) Ili kukadiria urefu wa jengo, wanafunzi wawili wanasimama umbali fulani kutoka jengo kwenye ngazi ya barabara. Kutoka hatua hii, wanapata angle ya mwinuko kutoka mitaani hadi juu ya jengo kuwa$39^{\circ}$. Kisha hoja$300$ miguu karibu na jengo na kupata angle ya mwinuko kuwa$50^{\circ}$. Kwa kuzingatia kwamba barabara ni ngazi, tathmini urefu wa jengo kwa mguu wa karibu.

67) Ili kukadiria urefu wa jengo, wanafunzi wawili wanasimama umbali fulani kutoka jengo kwenye ngazi ya barabara. Kutoka hatua hii, wanapata angle ya mwinuko kutoka mitaani hadi juu ya jengo kuwa$35^{\circ}$. Kisha hoja$250$ miguu karibu na jengo na kupata angle ya mwinuko kuwa$53^{\circ}$. Kwa kuzingatia kwamba barabara ni ngazi, tathmini urefu wa jengo kwa mguu wa karibu.

Jibu

$371$ft

68) Pointi$A$ na$B$ ni pande tofauti za ziwa. Point$C$ ni$97$ mita kutoka$A$. Kipimo cha$\angle BAC$ imedhamiriwa kuwa$101^{\circ}$, na kipimo cha$\angle ACB$ imedhamiriwa kuwa$53^{\circ}$. Umbali ni nini kutoka$A$ kwa$B$, mviringo kwa mita karibu nzima?

69) Mwanamume na mwanamke wamesimama$3\dfrac{1}{2}$ maili mbali hupiga puto ya hewa ya moto kwa wakati mmoja. Ikiwa angle ya mwinuko kutoka kwa mtu hadi kwenye puto ni$27^{\circ}$, na angle ya mwinuko kutoka kwa mwanamke hadi kwenye puto ni$41^{\circ}$, pata urefu wa puto kwa mguu wa karibu.

Jibu

$5936$ft

70) Timu mbili za utafutaji zinaona climber iliyopigwa kwenye mlima. Timu ya kwanza ya utafutaji ni$0.5$ maili kutoka timu ya pili ya utafutaji, na timu zote mbili ziko kwenye urefu wa$1$ maili. Pembe ya mwinuko kutoka kwa timu ya kwanza ya utafutaji hadi mchezaji aliyepigwa ni$15^{\circ}$. Pembe ya mwinuko kutoka kwa timu ya pili ya utafutaji hadi mchezaji ni$22^{\circ}$. Je! Ni urefu gani wa mchezaji? Pande zote kwa karibu kumi ya maili.

71) Mwanga wa barabara umewekwa kwenye pole. Mtu$6$ mrefu wa mguu amesimama mitaani umbali mfupi kutoka kwa pigo, akitoa kivuli. Pembe ya mwinuko kutoka ncha ya kivuli cha mtu hadi juu ya kichwa chake cha$28^{\circ}$. Mwanamke$6$ mwenye urefu wa mguu amesimama kwenye barabara moja upande wa pili wa pole kutoka kwa mtu huyo. Pembe ya mwinuko kutoka ncha ya kivuli chake hadi juu ya kichwa chake ni$28^{\circ}$. Ikiwa mwanamume na mwanamke ni$20$ miguu mbali, ni mbali gani mwanga wa barabara kutoka ncha ya kivuli cha kila mtu? Pande umbali wa kumi ya karibu ya mguu.

Jibu

$24.1$ft

72) Miji mitatu$A$,$B$,$C$, na, ziko ili mji huo$A$ ni kutokana mashariki ya mji$B$. Kama mji$C$ iko$35^{\circ}$ magharibi ya kaskazini kutoka mji$B$ na ni$100$ maili kutoka mji$A$ na$70$ maili kutoka mji$B$, jinsi mbali ni mji$A$ na mji$B$? Pande zote umbali wa kumi ya karibu ya maili.

73) Mitaa miwili hukutana kwa$80^{\circ}$ pembe. Kwenye kona, hifadhi inajengwa kwa sura ya pembetatu. Pata eneo la hifadhi ikiwa, kando ya barabara moja, hifadhi hupima$180$ miguu, na kando ya barabara nyingine, hifadhi hiyo inachukua$215$ miguu.

Jibu

$19,056$futi ²

74) Nyumba ya Brian iko kwenye kona nyingi. Pata eneo la yadi ya mbele ikiwa mipaka ya kupima$40$ na$56$ miguu, kama inavyoonekana kwenye Mchoro hapa chini.

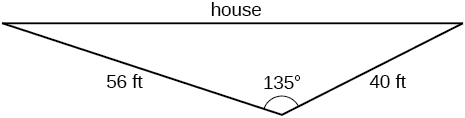
75) Pembetatu ya Bermuda ni kanda ya Bahari ya Atlantiki inayounganisha Bermuda, Florida, na Pwetoriko. Pata eneo la pembetatu ya Bermuda ikiwa umbali kutoka Florida hadi Bermuda ni$1030$ maili, umbali kutoka Puerto Rico hadi Bermuda ni$980$ maili, na angle iliyoundwa na umbali huo mbili ni$62^{\circ}$.

Jibu

$445,624$maili mraba

76) mavuno ishara hatua$30$ inches pande zote tatu. Eneo la ishara ni nini?

77) Naomi alinunua meza ya kisasa ya dining ambayo juu yake iko katika sura ya pembetatu. Pata eneo la juu ya meza ikiwa pande mbili zinapima$4$ miguu na$4.5$ miguu, na pembe ndogo hupima$32^{\circ}$ na$42^{\circ}$, kama inavyoonekana kwenye Kielelezo hapa chini.

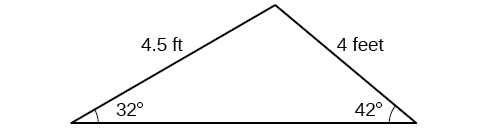
Jibu

$8.65$futi ²

8.2: Pembetatu zisizo za haki - Sheria ya Cosines

Maneno

1) Ikiwa unatafuta upande usiopotea wa pembetatu, unahitaji kujua nini wakati unatumia Sheria ya Cosines?

Jibu

pande mbili na angle kinyume upande kukosa.

2) Ikiwa unatafuta angle ya kukosa ya pembetatu, unahitaji kujua nini wakati unatumia Sheria ya Cosines?

3) Eleza kile$s$ kinachowakilisha katika formula ya Heron.

Jibu

$s$ni nusu ya mzunguko, ambayo ni nusu ya mzunguko wa pembetatu.

 

4) Eleza uhusiano kati ya Theorem ya Pythagorean na Sheria ya Cosines.

5) Ni lazima utumie wakati gani Sheria ya Cosines badala ya Theorem ya Pythagorean?

Jibu

Sheria ya Cosines inapaswa kutumika kwa pembetatu yoyote ya oblique (isiyo ya kulia).

Kialjebra

Kwa mazoezi 6-15, kudhani$\alpha$ ni upande wa pili$a$,$\beta$ ni upande wa pili$b$, na$\gamma$ ni upande wa pili$c$. Ikiwezekana, tatua kila pembetatu kwa upande usiojulikana. Pande zote hadi kumi ya karibu.

6)$\gamma =41.2^{\circ}, a=2.49, b=3.13$

7)$\alpha =120^{\circ}, b=6, c=7$

Jibu

$11.3$

8)$\beta =58.7^{\circ}, a=10.6, c=15.7$

9)$\alpha =115^{\circ}, a=18, b=23$

Jibu

$34.7$

10)$\alpha =119^{\circ}, a=26, b=14$

11)$\gamma =113^{\circ}, b=10, c=32$

Jibu

$26.7$

12)$\beta =67^{\circ}, a=49, b=38$

13)$\alpha =43.1^{\circ}, a=184.2, b=242.8$

Jibu

$257.4$

14)$\alpha =36.6^{\circ}, a=186.2, b=242.2$

15)$\beta =50^{\circ}, a=105, b=45$

Jibu

haiwezekani

Kwa mazoezi 16-20, tumia Sheria ya Cosines kutatua kwa angle ya kukosa ya pembetatu ya oblique. Pande zote hadi kumi ya karibu.

16)$a=42, b=19, c=30$; pata angle$A$.

17)$a=14, b=13, c=20$; pata angle$C$.

Jibu

$95.5^{\circ}$

18)$a=16, b=31, c=20$; pata angle$B$.

19)$a=13, b=22, c=28$; pata angle$A$.

Jibu

$26.9^{\circ}$

20)$a=108, b=132, c=160$; pata angle$C$.

Kwa mazoezi 21-26, tatua pembetatu. Pande zote hadi kumi ya karibu.

21)$A=35^{\circ}, b=8, c=11$

Jibu

$B\approx 45.9^{\circ}, C\approx 99.1^{\circ}, a\approx 6.4$

22)$B=88^{\circ}, a=4.4, c=5.2$

23)$C=121^{\circ}, a=21, b=37$

Jibu

$A\approx 20.6^{\circ}, B\approx 38.4^{\circ}, c\approx 51.1$

24)$a=13, b=11, c=15$

25)$a=3.1, b=3.5, c=5$

Jibu

$A\approx 37.8^{\circ}, B\approx 43.8^{\circ}, C\approx 98.4$

26)$a=51, b=25, c=29$

Kwa mazoezi 27-,31 tumia formula ya Heron ili kupata eneo la pembetatu. Pande zote hadi karibu na mia moja.

27) Pata eneo la pembetatu na pande za urefu$18$ ndani,$21$ ndani, na$32$ ndani. Pande zote hadi kumi ya karibu.

Jibu

$177.56$katika ²

28) Pata eneo la pembetatu na pande za urefu wa$20$ cm,$26$ cm, na$37$ cm. Pande zote hadi kumi ya karibu.

29)$a=\dfrac{1}{2}$ m,$b=\dfrac{1}{3}$ m,$c=\dfrac{1}{4}$ m

Jibu

$0.04$m ²

30)$a=12.4$ ft,$b=13.7$ ft,$c=20.2$ ft

31)$a=1.6$ yd,$b=2.6$ yd,$c=4.1$ yd

Jibu

$0.91$yd ²

Picha

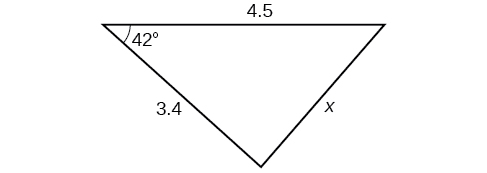
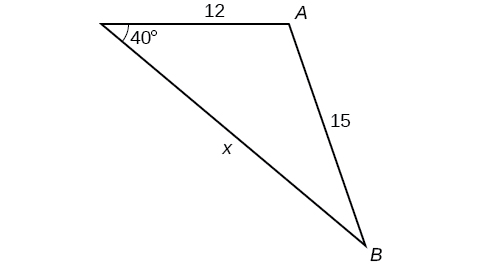
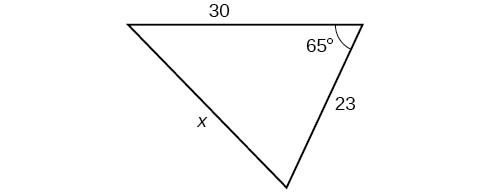
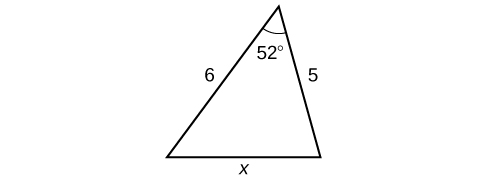
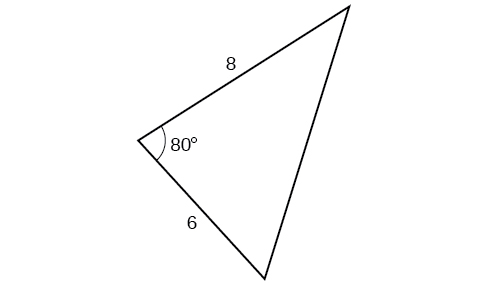
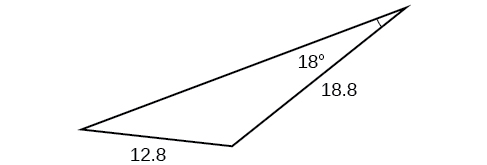
Kwa mazoezi 32-37, pata urefu wa upande$x$. Pande zote hadi kumi ya karibu.

32)

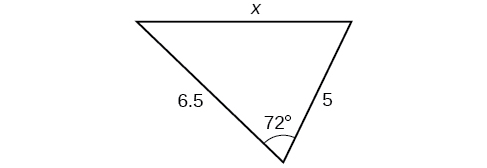
33)

Jibu

$3.0$

34)

35)

Jibu

$29.1$

36)

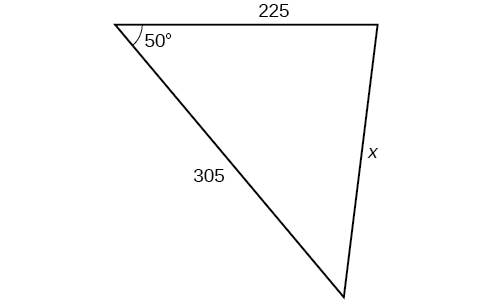
37)

Jibu

$0.5$

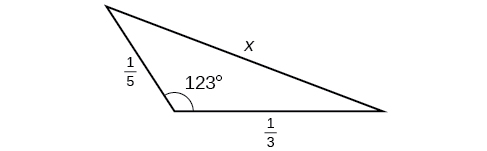
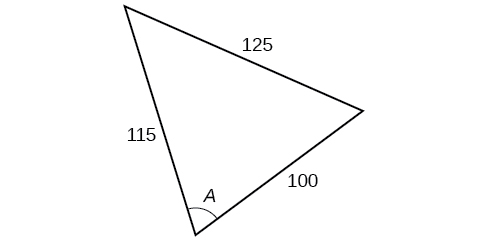
Kwa mazoezi 38-41, pata kipimo cha angle$A$

38)

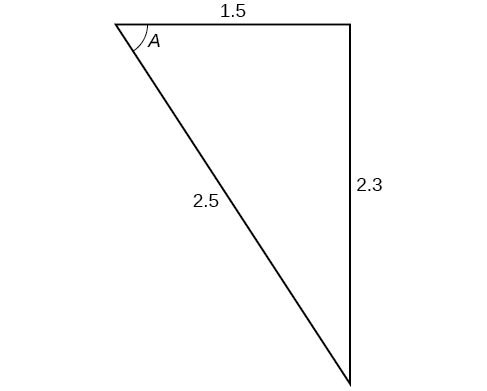
39)

Jibu

$70.7^{\circ}$

40)

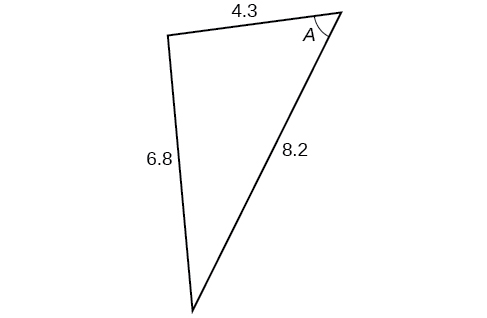
41)

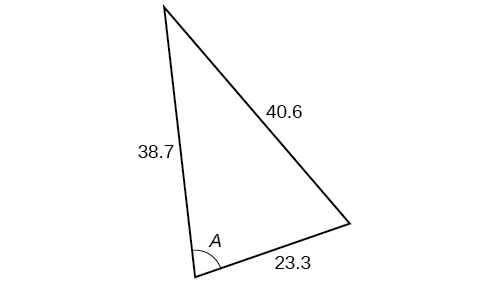
Jibu

$77.4^{\circ}$

42) Pata kipimo cha kila angle katika pembetatu iliyoonyeshwa kwenye Kielelezo hapa chini. Pande zote hadi kumi ya karibu.

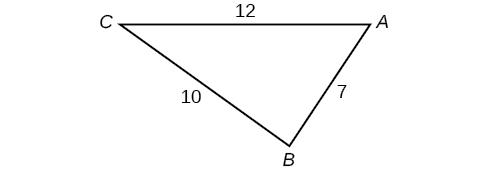
Kwa mazoezi 43-46, tatua kwa upande usiojulikana. Pande zote hadi kumi ya karibu.

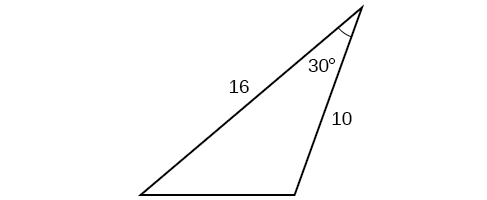
43)

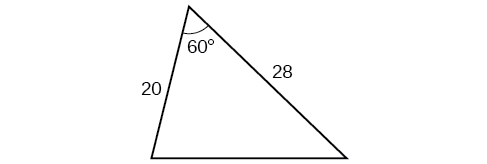
Jibu

$25.0$

44)

45)

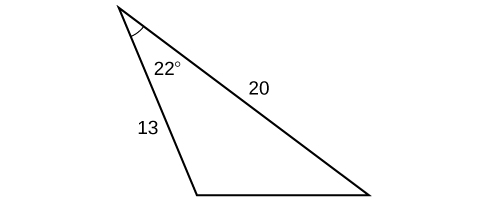
Jibu

$9.3$

46)

Kwa mazoezi 47-51, tafuta eneo la pembetatu. Pande zote hadi karibu na mia moja.

47)

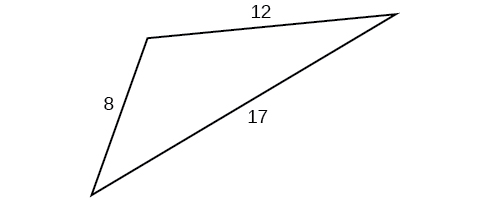
Jibu

$43.52$

48)

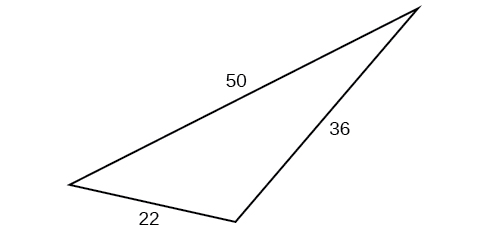
49)

Jibu

$1.41$

50)

51)

Jibu

$0.14$

Upanuzi

52) Parallelogram ina pande za$16$ vitengo vya urefu na$10$ vitengo. Ulalo mfupi ni$12$ vitengo. Pata kipimo cha diagonal ndefu.

53) Pande za parallelogram ni$11$ miguu na$17$ miguu. Ulalo mrefu ni$22$ miguu. Pata urefu wa diagonal mfupi.

Jibu

$18.3$

54) Pande za parallelogram ni$28$ sentimita na$40$ sentimita. Kipimo cha angle kubwa ni$100^{\circ}$. Pata urefu wa diagonal mfupi.

55) Octagon ya kawaida imeandikwa kwenye mduara na radius ya$8$ inchi. (Angalia Kielelezo hapa chini.) Pata mzunguko wa octagon.

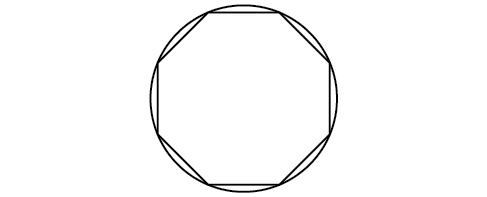
Jibu

$48.98$

56) Pentagon ya kawaida imeandikwa katika mduara wa$12$ cm radius. (Angalia Kielelezo hapa chini.) Pata mzunguko wa pentagon. Pande zote hadi kumi ya karibu ya sentimita.

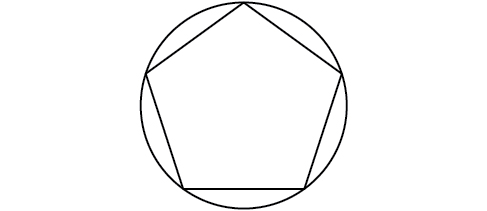
Kwa mazoezi 57-58, tuseme kwamba$x^2=25+36-60\cos(52)$ inawakilisha uhusiano wa pande tatu za pembetatu na cosine ya angle.

57) Chora pembetatu.

Jibu

58) Pata urefu wa upande wa tatu.

Kwa mazoezi 59-61, tafuta eneo la pembetatu.

59)

Jibu

$7.62$

60)

61)

Jibu

$85.1$

Real-World Matumizi

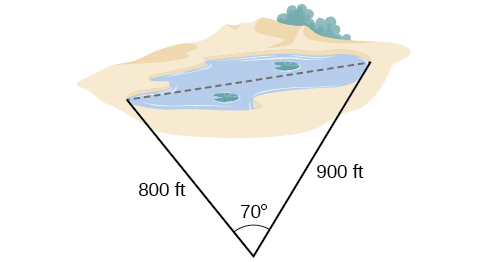
62) Mtafiti amechukua vipimo vilivyoonyeshwa kwenye Kielelezo hapa chini. Kupata umbali katika ziwa. Majibu ya pande zote kwa kumi ya karibu.

Kielelezo hapa chini (si kwa kiwango). Kupata umbali kati ya miji miwili. Majibu ya pande zote kwa kumi ya karibu.

Jibu

$24.0$km

64) Ndege inaruka$220$ maili na kichwa cha$40^{\circ}$, na kisha nzi$180$ maili na kichwa cha$170^{\circ}$. Ndege ni mbali gani kutoka mwanzo wake, na ni nini kinachoongoza? Majibu ya pande zote kwa kumi ya karibu.

65)$113$ Mnara wa mguu iko kwenye kilima ambacho kinakabiliwa$34^{\circ}$ na usawa, kama inavyoonekana kwenye Mchoro hapa chini. Wire-guy ni kuwa masharti ya juu ya mnara na nanga katika hatua$98$ miguu kupanda kutoka msingi wa mnara. Pata urefu wa waya unahitajika.

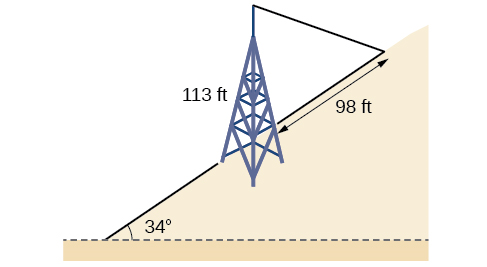
Jibu

$99.9$ft

66) Meli mbili ziliondoka bandari kwa wakati mmoja. Meli moja alisafiri kwa kasi ya$18$ maili kwa saa katika kichwa cha$320^{\circ}$. Meli nyingine alisafiri kwa kasi ya$22$ maili kwa saa katika kichwa cha$194^{\circ}$. Find umbali kati ya meli mbili baada ya$10$ masaa ya kusafiri.

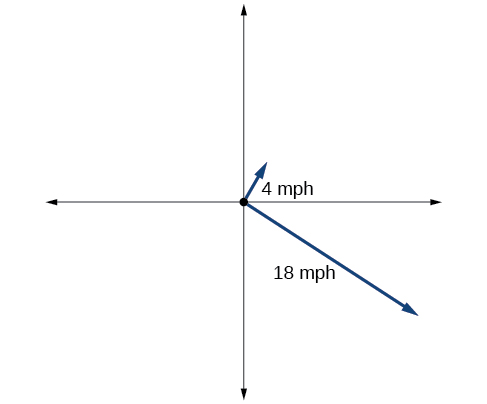
67) Grafu katika Kielelezo hapa chini inawakilisha boti mbili zinazoondoka kwa wakati mmoja kutoka kwenye kiwanja hicho. mashua ya kwanza ni kusafiri katika$18$ maili kwa saa katika kichwa cha$327^{\circ}$ na mashua ya pili ni kusafiri katika$4$ maili kwa saa katika kichwa cha$60^{\circ}$. Find umbali kati ya boti mbili baada ya$2$ masaa.

Jibu

$37.3$maili

68) Pwani ya kuogelea ya triangular inachukua$40$$65$ miguu upande mmoja na miguu upande mwingine. Pande hizi huunda angle inayopima$50^{\circ}$. Je, upande wa tatu ni muda gani (kwa kumi ya karibu)?

69) Majaribio inaruka kwa njia moja kwa moja kwa$30$ dakika ya$1$ saa. Kisha hufanya marekebisho ya kozi,$10^{\circ}$ akielekea haki ya kozi yake ya awali, na kuruka$2$ masaa katika mwelekeo mpya. Kama yeye ana kasi ya mara kwa mara ya$680$ maili kwa saa, ni mbali gani yeye kutoka nafasi yake kuanzia?

Jibu

$2371$maili

70) Los Angeles ni$1,744$ maili kutoka Chicago, Chicago ni$714$ maili kutoka New York, na New York ni$2,451$ maili kutoka Los Angeles. Chora pembetatu kuunganisha miji hii mitatu, na kupata pembe katika pembetatu.

71) Philadelphia ni$140$ maili kutoka Washington, DC, Washington, DC ni$442$ maili kutoka Boston, na Boston ni$315$ maili kutoka Philadelphia. Chora pembetatu kuunganisha miji hii mitatu na kupata pembe katika pembetatu.

Jibu

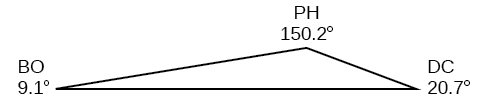
72) Ndege mbili zinatoka uwanja wa ndege huo huo kwa wakati mmoja. Mmoja anaruka$20^{\circ}$ mashariki mwa kaskazini kwa$500$ maili kwa saa. Ya pili inaruka$30^{\circ}$ mashariki mwa kusini kwa$600$ maili kwa saa. Ni mbali gani ndege baada ya$2$ masaa?

73) Ndege mbili zinaondoka kwa njia tofauti. Moja husafiri$300$ mph kutokana magharibi na nyingine husafiri$25^{\circ}$ kaskazini ya magharibi katika$420$ mph. Baada ya$90$ dakika, ni mbali sana, wakidhani wanaruka kwenye urefu sawa?

Jibu

$599.8$maili

74) Parallelogram ina pande za$15.4$ vitengo vya urefu na$9.8$ vitengo. Eneo lake ni vitengo vya$72.9$ mraba. Pata kipimo cha diagonal ndefu.

75) Pande nne za mfululizo wa quadrilateral zina urefu$4.5$ cm,$7.9$ cm,$9.4$ cm, na$12.9$ cm. Pembe kati ya pande mbili ndogo ni$117^{\circ}$. Eneo la quadrilateral hii ni nini?

Jibu

$65.4$cm ²

76) Pande nne za mfululizo wa quadrilateral zina urefu$5.7$ cm,$7.2$ cm,$9.4$ cm, na$12.8$ cm. Pembe kati ya pande mbili ndogo ni$106^{\circ}$. Eneo la quadrilateral hii ni nini?

77) Pata eneo la kipande cha ardhi cha triangular ambacho$30$ kinapima miguu upande mmoja na$42$ miguu kwa mwingine; hatua za angle zilizojumuishwa$132^{\circ}$. Pande zote kwa karibu nzima mraba mguu.

Jibu

$468$futi ²

78) Pata eneo la kipande cha ardhi cha triangular ambacho$110$ kinapima miguu upande mmoja na$250$ miguu kwa mwingine; hatua za angle zilizojumuishwa$85^{\circ}$. Pande zote kwa karibu nzima mraba mguu.

8.3: Kuratibu Polar

Maneno

1) Je! Kuratibu za polar zinatofautiana na kuratibu za mstatili?

Jibu

Kwa kuratibu polar, hatua katika ndege inategemea angle kutoka kwa$x$ mhimili mzuri na umbali kutoka kwa asili, wakati katika kuratibu za Cartesian, hatua inawakilisha umbali wa usawa na wima kutoka kwa asili. Kwa kila hatua katika ndege ya kuratibu, kuna uwakilishi mmoja, lakini kwa kila hatua katika ndege ya polar, kuna uwakilishi usio na kipimo

2) Je, pembe za polar zinatofautiana na$x$ - na$y$ -axes ya ndege ya Cartesian?

3) Eleza jinsi kuratibu polar ni graphed.

Jibu

Kuamua$\theta$ kwa uhakika, kisha uondoe$r$ vitengo kutoka kwenye pole ili kupanga njama. Kama$r$ ni hasi, hoja$r$ vitengo kutoka pole katika mwelekeo kinyume lakini pamoja pembe moja. Hatua ni umbali wa$r$ mbali na asili kwa pembe ya$\theta$ kutoka mhimili wa polar.

4) Vipi ni pointi$\left ( 3,\dfrac{\pi }{2} \right )$ na$\left ( -3,\dfrac{\pi }{2} \right )$ kuhusiana?

5) Eleza kwa nini pointi$\left ( -3,\dfrac{\pi }{2} \right )$ na$\left ( 3,-\dfrac{\pi }{2} \right )$ ni sawa.

Jibu

Hatua$\left ( -3,\dfrac{\pi }{2} \right )$ ina angle chanya lakini radius hasi na imepangwa kwa kuhamia pembe ya$\dfrac{\pi }{2}$ na kisha kusonga$3$ vitengo katika mwelekeo hasi. Hii inaweka$3$ vitengo uhakika chini hasi$y$ -axis. Hatua$\left ( 3,-\dfrac{\pi }{2} \right )$ ina angle hasi na radius chanya na imepangwa kwa kuhamia kwanza kwa angle ya$-\dfrac{\pi }{2}$ na kisha kusonga$3$ vitengo chini, ambayo ni mwelekeo chanya kwa angle hasi. uhakika pia$3$ vitengo chini hasi$y$ -axis.

Kialjebra

6)$\left ( 7,\dfrac{7\pi }{6} \right )$

7)$(5,\pi )$

Jibu

$(-5,0)$

8)$\left ( 6,-\dfrac{\pi }{4} \right )$

9)$\left ( -3,\dfrac{\pi }{6} \right )$

Jibu

$\left ( -\dfrac{3\sqrt{3}}{2},-\dfrac{3}{2} \right )$

10)$\left ( 4,\dfrac{7\pi }{4} \right )$

Kwa mazoezi 11-15, kubadilisha kuratibu za Cartesian zilizopewa kwa kuratibu polar$r>0$ na$0\leq \theta \leq 2\pi$. Kumbuka kuzingatia quadrant ambayo hatua iliyotolewa iko.

11)$(4,2)$

Jibu

$(2\sqrt{5},0.464)$

12)$(-4,6)$

13)$(3,-5)$

Jibu

$(\sqrt{34},5.253)$

14)$(-10,-13)$

15)$(8,8)$

Jibu

$\left(8\sqrt{2},\dfrac{\pi }{4}\right)$

Kwa mazoezi 16-27, kubadilisha equation ya Cartesian iliyotolewa kwa equation polar.

16)$x=3$

17)$y=4$

Jibu

$r=4\csc \theta$

18)$y=4x^2$

19)$y=2x^4$

Jibu

$r=\sqrt[3]{\dfrac{\sin \theta }{2\cos ^4\theta }}$

20)$x^2 + y^2 = 4y$

21)$x^2 + y^2 = 3x$

Jibu

$r=3\cos \theta$

22)$x^2 - y^2 = x$

23)$x^2 - y^2 = 3y$

Jibu

$r=\dfrac{3\sin \theta }{\cos (2\theta )}$

24)$x^2 + y^2 = 9$

25)$x^2 = 9y$

Jibu

$r=\dfrac{9\sin \theta }{\cos ^2\theta }$

26)$y^2 = 9x$

27)$9xy = 1$

Jibu

$r=\sqrt{\dfrac{1}{9\cos \theta \sin \theta }}$

Kwa mazoezi 28-39, kubadilisha equation ya polar iliyopewa kwa equation ya Cartesian. Andika kwa fomu ya kawaida ya conic ikiwa inawezekana, na utambue sehemu ya conic iliyowakilishwa.

28)$r=3\sin \theta$

29)$r=4\cos \theta$

Jibu

$x^2 + y^2 =4x$au$\dfrac{(x-2)^2}{4} + \dfrac{y^2}{4} = 1$; mduara

30)$r = \dfrac{4}{\sin \theta +7\cos \theta }$

31)$r = \dfrac{6}{\cos \theta +3\sin \theta }$

Jibu

$3y+x=6$; mstari

32)$r=2\sec \theta$

33)$r=3\csc \theta$

Jibu

$y=3$; mstari

34)$r = \sqrt{r\cos \theta +2}$

35)$r^2 = 4\sec \theta \csc \theta$

Jibu

$xy=4$; hyperbola

36)$r =4$

37)$r^2 = 4$

Jibu

$x^2 + y^2 =4$; mduara

38)$r = \dfrac{1}{4\cos \theta - 3\sin \theta }$

39)$r = \dfrac{3}{\cos \theta - 5\sin \theta }$

Jibu

$x-5y=3$; mstari

Picha

Kwa mazoezi 40-44, tafuta kuratibu za polar za uhakika.

40)

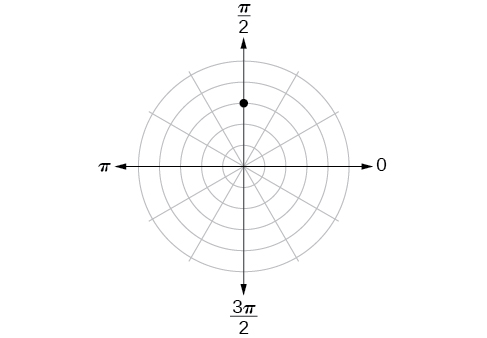
41)

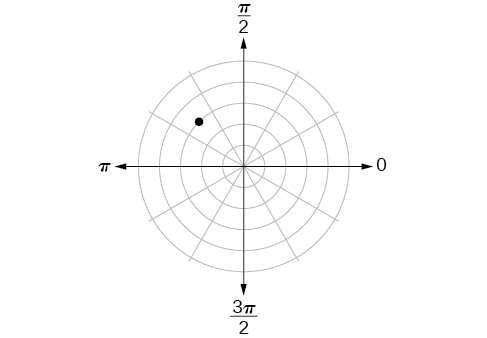
Jibu

$\left (3,\dfrac{3\pi }{4} \right )$

42)

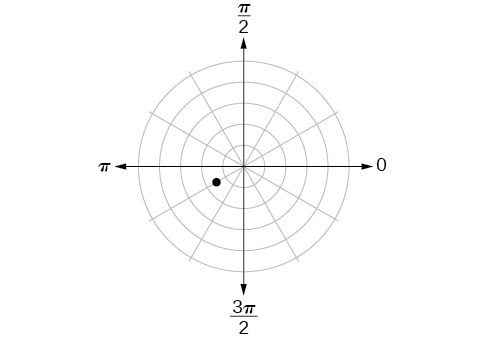
43)

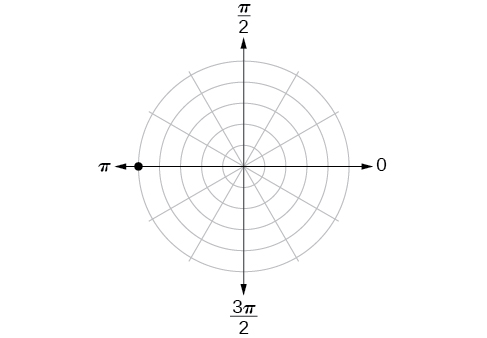
Jibu

$(5,\pi )$

44)

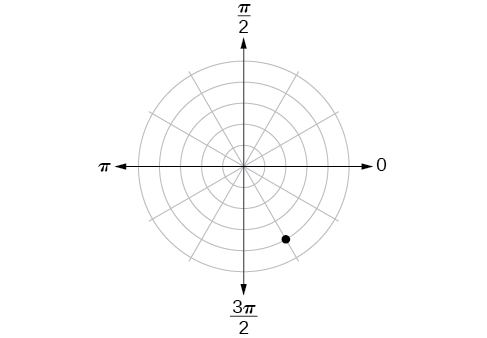
Kwa mazoezi 45-54, njama pointi.

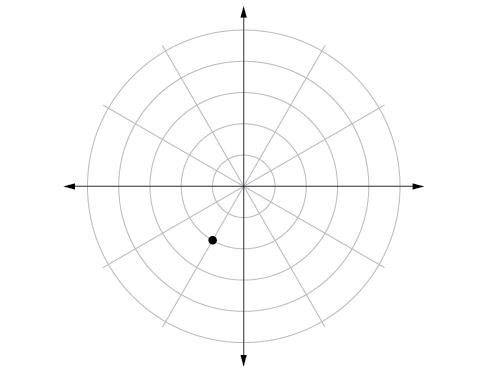
45)$\left (-2,\dfrac{\pi }{3} \right )$

Jibu

46)$\left (-1,-\dfrac{\pi }{2} \right )$

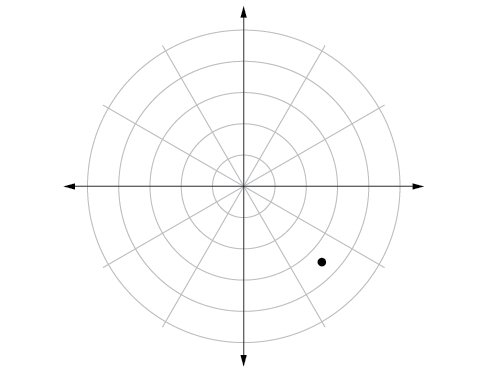
47)$\left (3.5,\dfrac{7\pi }{4} \right )$

Jibu

48)$\left (-4,\dfrac{\pi }{3} \right )$

49)$\left (5,\dfrac{\pi }{2} \right )$

Jibu

50)$\left (4,\dfrac{-5\pi }{4} \right )$

51)$\left (3,\dfrac{5\pi }{6} \right )$

Jibu

52)$\left (-1.5,\dfrac{7\pi }{6} \right )$

53)$\left (-2,\dfrac{\pi }{4} \right )$

Jibu

54)$\left (1,\dfrac{3\pi }{2} \right )$

Kwa mazoezi 55-61, kubadilisha equation kutoka mstatili hadi fomu ya polar na grafu kwenye mhimili wa polar.

55)$5x-y = 6$

Jibu

$r = \dfrac{6}{5\cos \theta - \sin \theta }$

56)$2x + 7y = -3$

57)$x^2 + (y-1)^2 = 1$

Jibu

$r = 2\sin \theta$

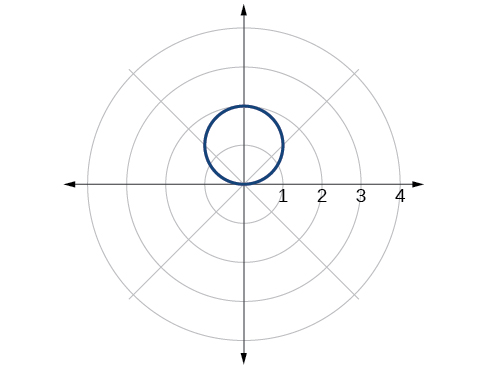
58)$(x+2)^2+(y+3)^2=13$

59)$x = 2$

Jibu

$r = \dfrac{2}{\cos \theta }$

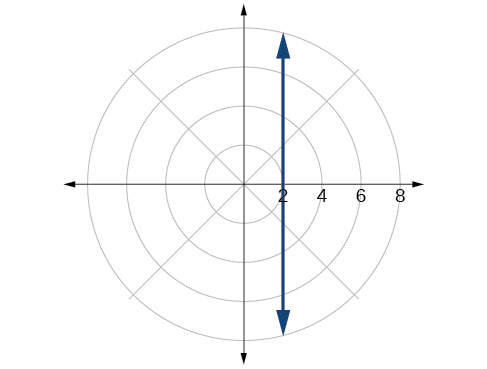
60)$x^2 + y^2 =5y$

61)$x^2 + y^2 =3x$

Jibu

$r = 3\cos \theta$

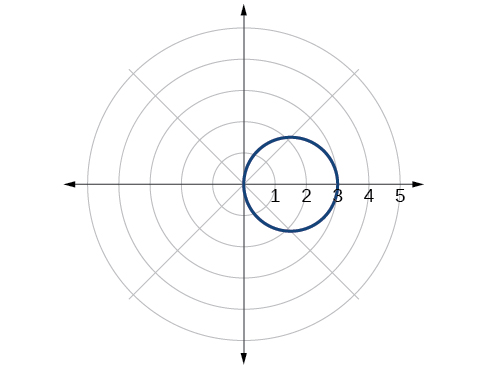
Kwa mazoezi 62-68, kubadilisha equation kutoka polar hadi fomu ya mstatili na grafu kwenye ndege ya mstatili.

62)$r = 6$

63)$r = -4$

Jibu

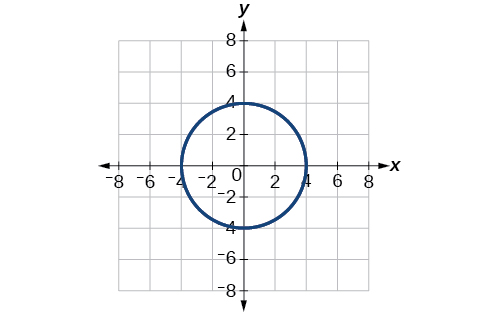
$x^2 + y^2 =16$

64)$\theta = -\dfrac{2\pi }{3}$

65)$\theta = \dfrac{\pi }{4}$

Jibu

$y=x$

66)$r = \sec \theta$

67)$r = -10\sin \theta$

Jibu

$x^2 + (y+5)^2 = 25$

68)$r = 3\cos \theta$

Teknolojia

69) Tumia calculator ya graphing kupata kuratibu mstatili wa$\left (2,-\dfrac{\pi }{5} \right )$. Pande zote kwa elfu ya karibu.

Jibu

$(1.618,-1.176)$

70) Matumizi graphing calculator kupata kuratibu mstatili wa$\left (-3,\dfrac{3\pi }{7} \right )$. Pande zote kwa elfu ya karibu.

71) Tumia calculator ya graphing ili kupata kuratibu za$(-7,8)$ polar za digrii. Pande zote kwa elfu ya karibu.

Jibu

$(10.630,131.186^{\circ})$

72) Tumia calculator ya graphing ili kupata kuratibu za$(3,-4)$ polar za digrii. Pande zote hadi karibu na mia moja.

73) Tumia calculator ya graphing ili kupata kuratibu za$(-2,0)$ polar za digrii. Pande zote hadi karibu na mia moja.

Jibu

$(2,3.14)$au$(2,\pi )$

Upanuzi

74) Eleza grafu ya$r=a\sec \theta$;$a>0$.

75) Eleza grafu ya$r=a\sec \theta$;$a<0$.

Jibu

Mstari wa wima na$a$ vitengo vya kushoto vya$y$ -axis.

76) Eleza grafu ya$r=a\csc \theta$;$a>0$.

77) Eleza grafu ya$r=a\csc \theta$;$a<0$.

Jibu

Mstari wa usawa na$a$ vitengo chini ya$x$ -axis.

78) Nini milinganyo ya polar itatoa mstari wa oblique?

Kwa mazoezi 79-84, grafu usawa wa polar.

79)$r<4$

Jibu

80)$0\leq \theta \leq \dfrac{\pi }{4}$

81)$\theta = \dfrac{\pi }{4}, r\geq 2$

Jibu

82)$\theta = \dfrac{\pi }{4}, r\geq -3$

83)$0\leq \theta \leq \dfrac{\pi }{3}, r<2$

Jibu

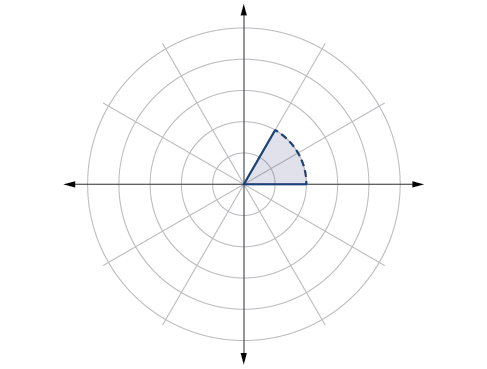
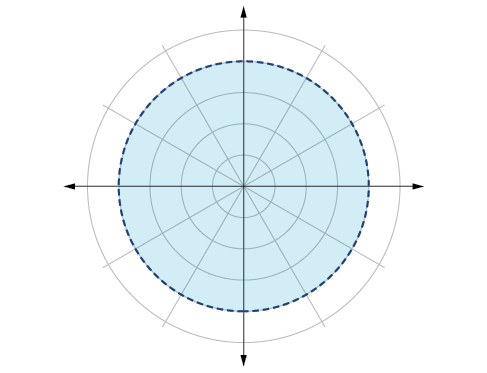
84)\(\dfrac{-\pi }{6} < \theta \leq \dfrac{\pi }{3}, -3<2\)>< span="">/span>

8.4: Kuratibu Polar - Grafu

Maneno

1) Eleza aina tatu za ulinganifu katika grafu za polar, na ulinganishe na ulinganifu wa ndege ya Cartesian.

Jibu

Ulinganifu kuhusiana na mhimili wa polar ni sawa na ulinganifu kuhusu$x$ -axis, ulinganifu kuhusiana na pole ni sawa na ulinganifu kuhusu asili, na ulinganifu kuhusiana na mstari$\theta = \dfrac{\pi }{2}$ ni sawa na ulinganifu kuhusu$y$ -axis.

2) Ni ipi kati ya aina tatu za ulinganifu wa grafu za polar zinazohusiana na ulinganifu kwa heshima na$x$ -axis,$y$ -axis, na asili?

3) Ni hatua gani za kufuata wakati wa kuchora usawa wa polar?

Jibu

Mtihani kwa ulinganifu; kupata zero, intercepts, na maxima; fanya meza ya maadili. Chagua aina ya jumla ya grafu, cardioid, limaçon, lemniscate, nk, kisha njama pointi$\theta = 0$$\dfrac{\pi }{2}$$\pi$,,$\dfrac{3\pi }{2}$ na mchoro grafu.

4) Eleza maumbo ya grafu ya cardioids, limaçons, na lemniscates.

5) Ni sehemu gani ya equation huamua sura ya grafu ya equation polar?

Jibu

Sura ya grafu ya polar imedhamiriwa na ikiwa ni pamoja na sine, cosine, na mara kwa mara katika equation.

Picha

Kwa mazoezi 6-15, jaribu equation kwa ulinganifu.

6)$r=5\cos 3\theta$

7)$r=3-3\cos \theta$

Jibu

ulinganifu kwa heshima na mhimili wa polar

8)$r=3+2\sin \theta$

9)$r=3\sin 2\theta$

Jibu

ulinganifu kwa heshima na mhimili Polar, ulinganifu kwa heshima na mstari$\theta = \dfrac{\pi }{2}$,ulinganifu kwa heshima na pole

10)$r=4$

11)$r=2\theta$

Jibu

hakuna ulinganifu

12)$r=4\cos \dfrac{\theta }{2}$

13)$r=\dfrac{2}{\theta }$

Jibu

hakuna ulinganifu

14)$r=3\sqrt{1-\cos ^2\theta }$

15)$r=\sqrt{5\sin 2\theta }$

Jibu

ulinganifu kwa heshima na pole

Kwa mazoezi 16-43, grafu equation polar. Tambua jina la sura.

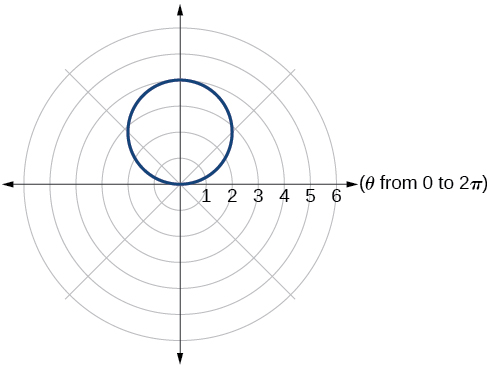
16)$r=3\cos \theta$

17)$r=4\sin \theta$

Jibu

mduara

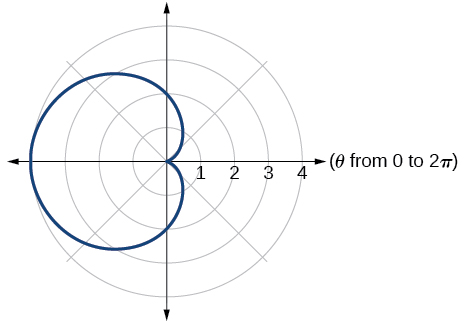
18)$r=2+2\cos \theta$

19)$r=2-2\cos \theta$

Jibu

cardioid

20)$r=5-5\sin \theta$

21)$r=3+3\sin \theta$

Jibu

cardioid

22)$r=3+2\sin \theta$

23)$r=7+4\sin \theta$

Jibu

loop/dimpled limaçon

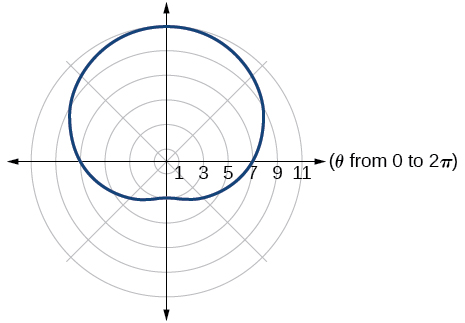
24)$r=4+3\cos \theta$

25)$r=5+4cos \theta$

Jibu

loop/dimpled limaçon

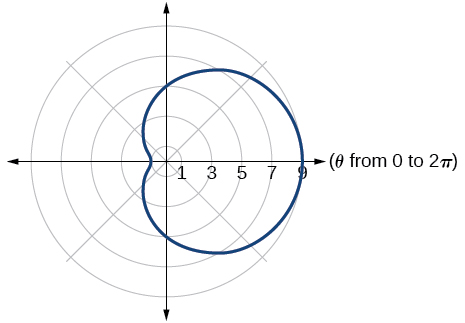
26)$r=10+9\cos \theta$

27)$r=1+3\sin \theta$

Jibu

kitanzi cha ndani/limaçon mbili kitanzi

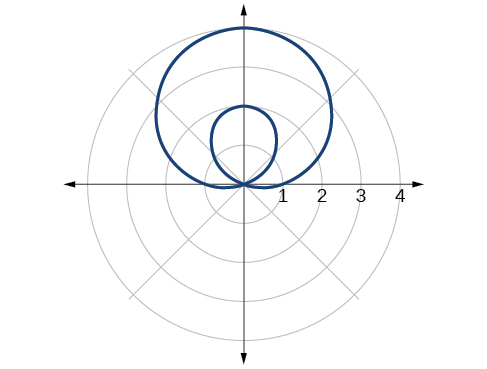
28)$r=2+5\sin \theta$

29)$r=5+7\sin \theta$

Jibu

kitanzi cha ndani/limaçon mbili kitanzi

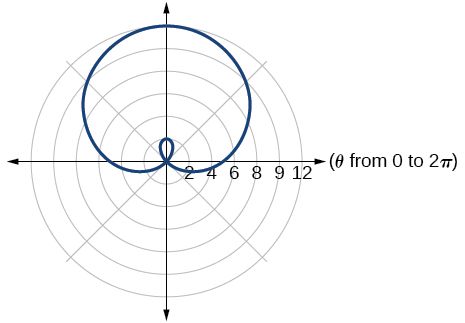
30)$r=2+4\cos \theta$

31)$r=5+6\cos \theta$

Jibu

kitanzi cha ndani/limaçon mbili kitanzi

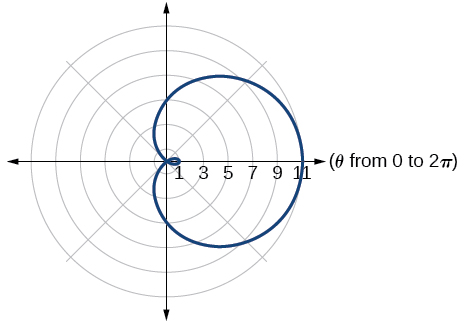
32)$r^2=36\cos (2\theta )$

33)$r^2=10\cos (2\theta )$

Jibu

kuondoa

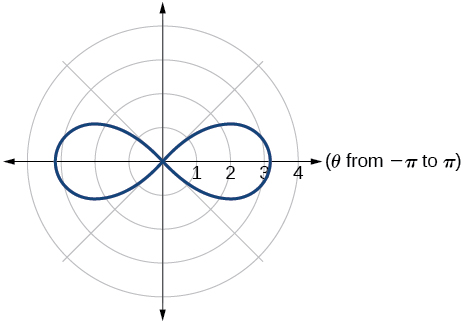
34)$r^2=4\sin (2\theta )$

35)$r^2=10\sin (2\theta )$

Jibu

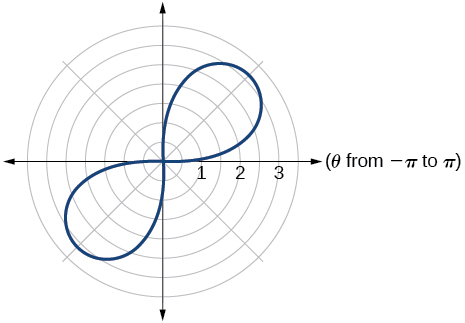
kuondoa

36)$r=3\sin (2\theta )$

37)$r=3\cos (2\theta )$

Jibu

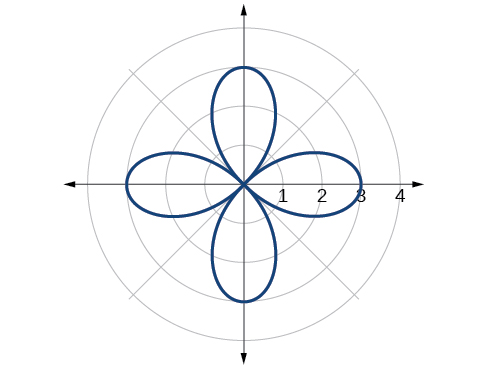
rose Curve

38)$r=5\sin (3\theta )$

39)$r=4\sin (4\theta )$

Jibu

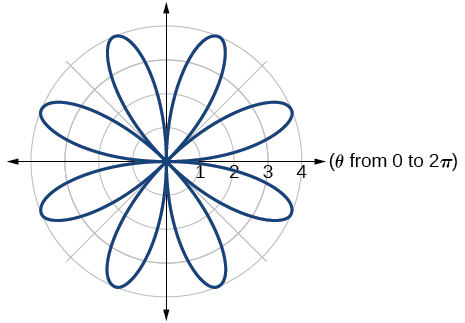
rose Curve

40)$r=4\sin (5\theta )$

41)$r=-\theta$

Jibu

Archimedes 'ond

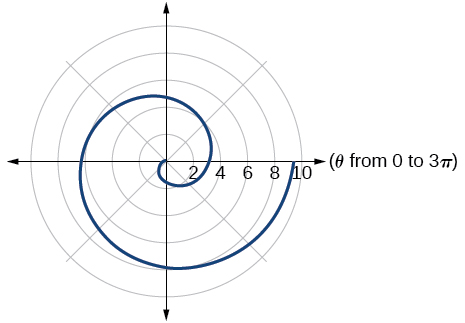
42)$r=2\theta$

43)$r=-3\theta$

Jibu

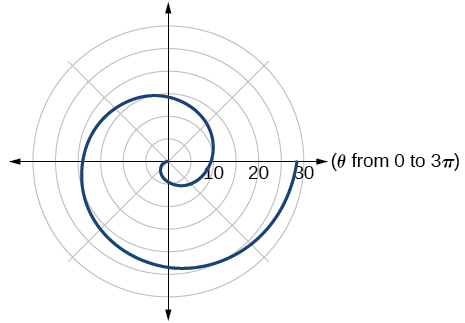
Archimedes 'ond

Teknolojia

Kwa mazoezi 44-53, tumia calculator ya graphing ili mchoro wa grafu ya equation ya polar.

44)$r=\dfrac{1}{\theta }$

45)$r=\dfrac{1}{\sqrt{\theta }}$

Jibu

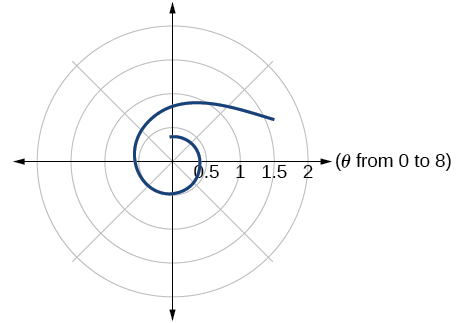
46)$r=2\sin \theta \tan \theta$, cissoid

47)$r=2\sqrt{1-\sin ^2\theta }$, kiboko

Jibu

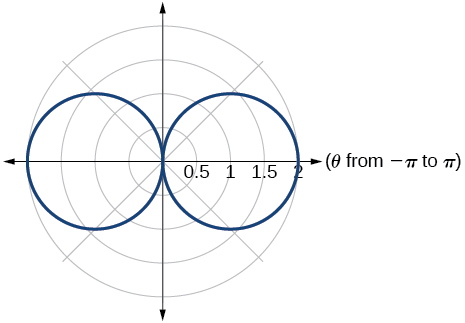
48)$r=5+\cos (4\theta )$

49)$r=2-\sin (2\theta )$

Jibu

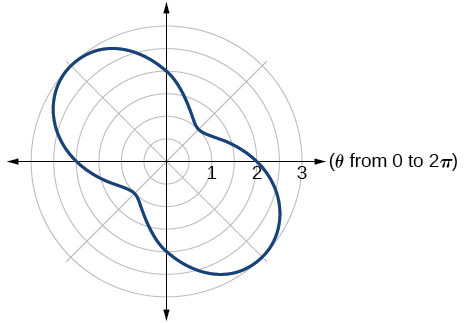
50)$r=\theta ^2$

51)$r=\theta +1$

Jibu

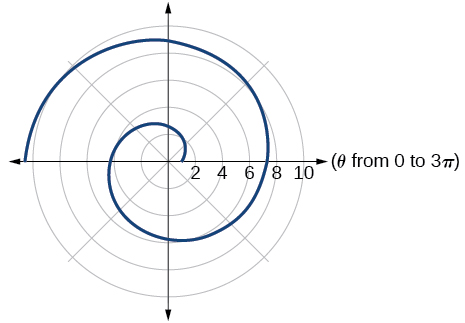
52)$r=\theta \sin \theta$

53)$r=\theta \cos \theta$

Jibu

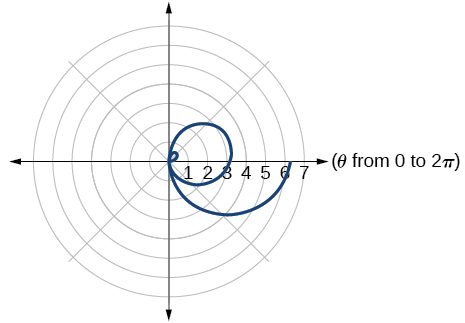
Kwa mazoezi 54-63, tumia matumizi ya graphing kwa grafu kila jozi ya milinganyo ya polar kwenye uwanja wa$[0,4\pi ]$ na kisha kuelezea tofauti zilizoonyeshwa kwenye grafu.

54)$r=\theta ,r=-\theta$

55)$r=\theta ,r=\theta +\sin \theta$

Jibu

Wote wawili ni spirals, lakini si sawa kabisa.

56)$r=\sin \theta +\theta ,r=\sin \theta -\theta$

57)$r=2\sin \left (\dfrac{\theta }{2} \right ),r=\theta \sin \left (\dfrac{\theta }{2} \right )$

Jibu

Grafu zote mbili ni curves na$2$ loops. Equation na mgawo wa$\theta$ ina loops mbili upande wa kushoto, equation na mgawo wa$2$ ina loops mbili upande kwa upande. Grafu hizi kutoka$0$$4\pi$ kwa kupata picha bora.

58)$r=\sin (\cos (3\theta )),r=\sin (3\theta )$

59) Katika matumizi ya graphing, grafu$r=\sin \left (\dfrac{16}{5}\theta \right )$ juu$[0,4\pi ]$,$[0,8\pi ]$,$[0,12\pi ]$ na$[0,16\pi ]$. Eleza athari za kuongeza upana wa kikoa.

Jibu

Wakati upana wa kikoa umeongezeka, petals zaidi ya maua huonekana.

60) Katika matumizi ya graphing, grafu na mchoro$r=\sin \theta + \left(\sin \left(\dfrac{5}{2}\theta \right) \right)^3$ juu ya$[0,4\pi ]$.

61) Katika matumizi ya graphing, grafu kila equation polar. Eleza kufanana na tofauti unazozingatia kwenye grafu. $$\begin{align*} r_1 &= 3\sin(3\theta )\\ r_2 &= 2\sin(3\theta )\\ r_3 &= \sin(3\theta ) \end{align*}$$

Jibu

Grafu ni tatu-petal, rose curves. Mgawo mkubwa, umbali mkubwa wa pembe kutoka kwa pole.

62) Katika matumizi ya graphing, grafu kila equation polar. Eleza kufanana na tofauti unazozingatia kwenye grafu. $$\begin{align*} r_1 &= 3+3\cos(\theta )\\ r_2 &= 2+2\cos(\theta )\\ r_3 &= 1+\cos(\theta ) \end{align*}$$

63) Katika matumizi ya graphing, grafu kila equation polar. Eleza kufanana na tofauti unazozingatia kwenye grafu. $$\begin{align*} r_1 &= 3\theta \\ r_2 &= 2\theta \\ r_3 &= \theta \end{align*}$$

Jibu

Grafu ni spirals. Mgawo mdogo, unaimarisha ond.

Upanuzi

Kwa mazoezi 64-72, futa kila equation ya polar kwenye seti sawa ya shaba za polar, na upate pointi za makutano.

64)$r_1=3+2\sin \theta , r_2=2$

65)$r_1=6-4\cos \theta , r_2=4$

Jibu

$\left ( 4,\dfrac{\pi }{3} \right ), \left ( 4,\dfrac{5\pi }{3} \right )$

66)$r_1=1+\sin \theta , r_2=3\sin \theta$

67)$r_1=1+\cos \theta , r_2=3\cos \theta$

Jibu

$\left ( \dfrac{3}{2},\dfrac{\pi }{3} \right ), \left ( \dfrac{3}{2},\dfrac{5\pi }{3} \right )$

68)$r_1=\cos (2\theta ), r_2=\sin (2\theta )$

69)$r_1=\sin ^2(2\theta ), r_2=1-\cos (4\theta )$

Jibu

$\left ( 0,\dfrac{\pi }{2} \right ), (0,\pi ), \left ( 0,\dfrac{3\pi }{2} \right ), (0,2\pi )$

70)$r_1=\sqrt{3}, r_2=2\sin (\theta )$

71)$r_1^2=\sin \theta , r_2^2=\cos \theta$

Jibu

$\left ( \dfrac{\sqrt[4]{8}}{2},\dfrac{\pi }{4} \right )$$\left ( \dfrac{\sqrt[4]{8}}{2},\dfrac{5\pi }{4} \right )$, na saa$\theta =\dfrac{3\pi }{4}$,$\dfrac{7\pi }{4}$ tangu$r$ ni mraba

72)$r_1=1+\cos \theta , r_2=1-\sin \theta$

8.5: Fomu ya Polar ya Hesabu Complex

Maneno

1) Idadi tata ni$a+bi$. Eleza kila sehemu.

Jibu

$a$ni sehemu halisi,$b$ ni sehemu imaginary, na$i=\sqrt{-1}$

2) Thamani kamili ya nambari tata inawakilisha nini?

3) Nambari tata inabadilishaje kuwa fomu ya polar?

Jibu

Fomu ya polar inabadilisha sehemu halisi na ya kufikiri ya idadi tata katika fomu ya polar kutumia$x=r\cos \theta$ na$y=r\sin \theta$.

4) Tunawezaje kupata bidhaa ya namba mbili ngumu?

5) Theorem ya De Moivre ni nini na hutumiwa nini?

Jibu

$z^n=r^n(\cos (n\theta )+i\sin (n\theta ))$

Inatumika kurahisisha fomu ya polar wakati idadi imefufuliwa kwa nguvu.

Kialjebra

Kwa mazoezi 6-11, pata thamani kamili ya nambari tata iliyotolewa.

6)$5+3i$

7)$-7+i$

Jibu

$5\sqrt{2}$

8)$-3-3i$

9)$\sqrt{2}-6i$

Jibu

$\sqrt{38}$

10)$2i$

11)$2.2-3.1i$

Jibu

$\sqrt{14.45}$

Kwa mazoezi 12-16, weka namba tata katika fomu ya polar.

12)$2+2i$

13)$8-4i$

Jibu

$4\sqrt{5}\mathbf{cis}(333.4^{\circ})$

14)$-\dfrac{1}{2}-\dfrac{1}{2}i$

15)$\sqrt{3}+i$

Jibu

$2\mathbf{cis}\left ( \dfrac{\pi }{6} \right )$

16)$3i$

Kwa mazoezi 17-22, kubadilisha namba tata kutoka polar hadi fomu ya mstatili.

17)$z=7\mathbf{cis}\left ( \dfrac{\pi }{6} \right )$

Jibu

$\dfrac{7\sqrt{3}}{2}+i\dfrac{7}{2}$

18)$z=2\mathbf{cis}\left ( \dfrac{\pi }{3} \right )$

19)$z=4\mathbf{cis}\left ( \dfrac{7\pi }{6} \right )$

Jibu

$-2\sqrt{3}-2i$

20)$z=7\mathbf{cis}(25^{\circ})$

21)$z=3\mathbf{cis}(240^{\circ})$

Jibu

$-1.5-i\dfrac{3\sqrt{3}}{2}$

22)$z=\sqrt{2}\mathbf{cis}(100^{\circ})$

Kwa mazoezi 23-28, pata$z_1 z_2$ fomu ya polar.

23)$z_1=2\sqrt{3}\mathbf{cis}(116^{\circ}); z_2=2\mathbf{cis}(82^{\circ})$

Jibu

$4\sqrt{3}\mathbf{cis}(198^{\circ})$

24)$z_1=\sqrt{2}\mathbf{cis}(205^{\circ}); z_2=2\sqrt{2}\mathbf{cis}(118^{\circ})$

25)$z_1=3\mathbf{cis}(120^{\circ}); z_2=\dfrac{1}{4}\mathbf{cis}(60^{\circ})$

Jibu

$\dfrac{3}{4}\mathbf{cis}(180^{\circ})$

26)$z_1=3\mathbf{cis} \left(\dfrac{\pi }{4} \right); z_2=5\mathbf{cis}\left(\dfrac{\pi }{6} \right)$

27)$z_1=\sqrt{5}\mathbf{cis} \left(\dfrac{5\pi }{8} \right); z_2=\sqrt{15}\mathbf{cis}\left(\dfrac{\pi }{12} \right)$

Jibu

$5\sqrt{3}\mathbf{cis} \left(\dfrac{17\pi }{24} \right)$

28)$z_1=4\mathbf{cis} \left(\dfrac{\pi }{2} \right); z_2=2\mathbf{cis}\left(\dfrac{\pi }{4} \right)$

Kwa mazoezi 29-,34 hupata$\dfrac{z_1}{z_2}$ fomu ya polar.

29)$z_1=21\mathbf{cis}(135^{\circ}); z_2=3\mathbf{cis}(65^{\circ})$

Jibu

$7\mathbf{cis}(70^{\circ})$

30)$z_1=\sqrt{2}\mathbf{cis}(90^{\circ}); z_2=2\mathbf{cis}(60^{\circ})$

31)$z_1=15\mathbf{cis}(120^{\circ}); z_2=3\mathbf{cis}(40^{\circ})$

Jibu

$5\mathbf{cis}(80^{\circ})$

32)$z_1=6\mathbf{cis} \left(\dfrac{\pi }{3} \right); z_2=2\mathbf{cis}\left(\dfrac{\pi }{4} \right)$

33)$z_1=5\sqrt{2}\mathbf{cis} (\pi ); z_2=\sqrt{2}\mathbf{cis}\left(\dfrac{2\pi }{3} \right)$

Jibu

$5\mathbf{cis} \left(\dfrac{\pi }{3} \right)$

34)$z_1=2\mathbf{cis} \left(\dfrac{3\pi }{5} \right); z_2=3\mathbf{cis}\left(\dfrac{\pi }{4} \right)$

Kwa mazoezi 35-40, pata nguvu za kila nambari tata katika fomu ya polar.

35) Kupata$z^3$ wakati$z=5\mathbf{cis} (45^{\circ})$.

Jibu

$125\mathbf{cis} (135^{\circ})$

36) Kupata$z^4$ wakati$z=2\mathbf{cis} (70^{\circ})$.

37) Kupata$z^2$ wakati$z=3\mathbf{cis} (120^{\circ})$.

Jibu

$9\mathbf{cis} (240^{\circ})$

38) Kupata$z^2$ wakati$z=4\mathbf{cis}\left(\dfrac{\pi }{4} \right)$.

39) Kupata$z^4$ wakati$z=\mathbf{cis}\left(\dfrac{3\pi }{16} \right)$.

Jibu

$\mathbf{cis}\left(\dfrac{3\pi }{4} \right)$

40) Kupata$z^3$ wakati$z=3\mathbf{cis}\left(\dfrac{5\pi }{3} \right)$.

Kwa mazoezi 41-45, tathmini kila mizizi.

41) Tathmini mizizi ya mchemraba wa$z$ wakati$z=27\mathbf{cis} (240^{\circ})$.

 

Jibu

$3\mathbf{cis}(80^{\circ}), 3\mathbf{cis}(200^{\circ}), 3\mathbf{cis}(320^{\circ})$

42) Tathmini mizizi ya mraba ya$z$ wakati$z=16\mathbf{cis} (100^{\circ})$.

43) Tathmini mizizi ya mchemraba wa$z$ wakati$z=32\mathbf{cis} \left(\dfrac{2\pi }{3} \right)$.

Jibu

$2\sqrt[3]{4}\mathbf{cis} \left(\dfrac{2\pi }{9} \right), 2\sqrt[3]{4}\mathbf{cis} \left(\dfrac{8\pi }{9} \right), 2\sqrt[3]{4}\mathbf{cis} \left(\dfrac{14\pi }{9} \right)$

44) Tathmini mizizi ya mraba ya$z$ wakati$z=32\mathbf{cis} (\pi )$.

45) Tathmini mizizi ya mchemraba wa$z$ wakati$z=8\mathbf{cis} \left(\dfrac{7\pi }{4} \right)$.

Jibu

$2\sqrt{2}\mathbf{cis} \left(\dfrac{7\pi }{8} \right), 2\sqrt{2}\mathbf{cis} \left(\dfrac{15\pi }{8} \right)$

Picha

Kwa mazoezi 46-55, njama namba tata katika ndege tata.

46)$2+4i$

47)$-3-3i$

Jibu

48)$5-4i$

49)$-1-5i$

Jibu

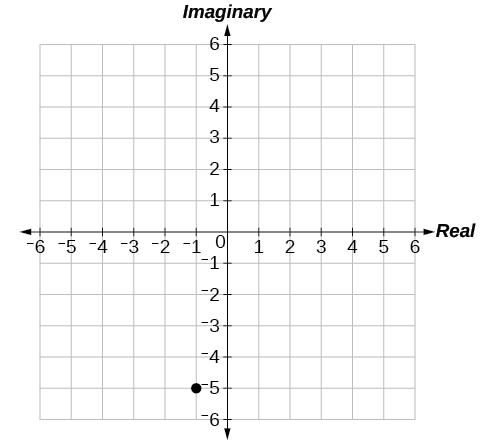
50)$3+2i$

51)$2i$

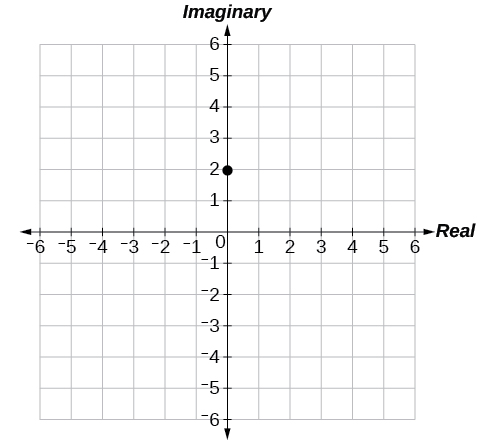
Jibu

52)$-4$

53)$6-2i$

Jibu

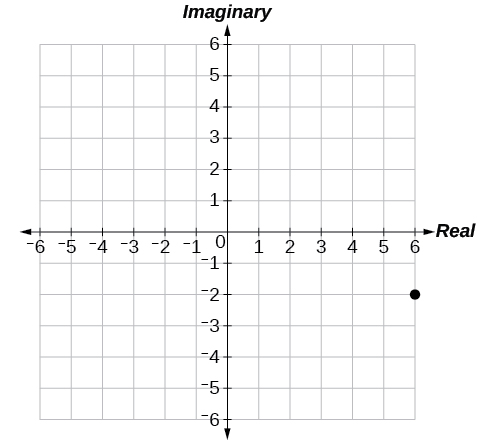
54)$-2+i$

55)$1-4i$

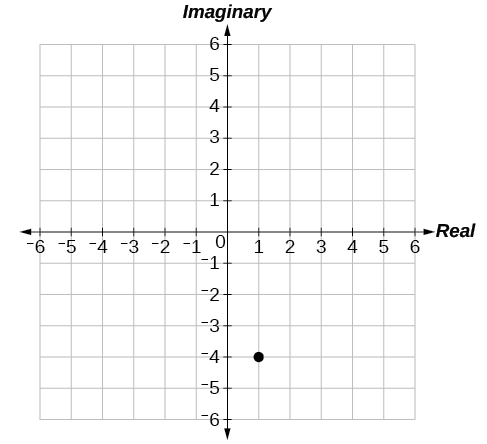
Jibu

Teknolojia

Kwa mazoezi 56-, pata majibu yote yaliyozunguka kwa karibu mia moja.

56) Tumia mstatili kwa kipengele cha polar kwenye calculator ya graphing$5+5i$ kubadili fomu ya polar.

57) Tumia mstatili kwa kipengele cha polar kwenye calculator ya graphing$3-2i$ kubadili fomu ya polar.

Jibu

$3.61e^{-0.59i}$

58) Tumia mstatili kwa kipengele cha polar kwenye calculator ya graphing$-3-8i$ kubadili fomu ya polar.

59) Tumia kipengele cha polar kwa mstatili kwenye calculator ya graphing kubadili fomu ya$4\mathbf{cis} (120^{\circ})$ mstatili.

Jibu

$-2+3.46i$

60) Tumia kipengele cha polar kwa mstatili kwenye calculator ya graphing kubadili fomu ya$2\mathbf{cis} (45^{\circ})$ mstatili.

61) Tumia kipengele cha polar kwa mstatili kwenye calculator ya graphing kubadili fomu ya$5\mathbf{cis} (210^{\circ})$ mstatili.

Jibu

$-4.33-2.50i$

8.6: Ulinganifu wa parametric

Maneno

1) Mfumo wa usawa wa parametric ni nini?

Jibu

Jozi ya kazi ambayo inategemea sababu ya nje. Kazi mbili zimeandikwa kwa mujibu wa parameter sawa. Kwa mfano,$x=f(t)$ na$y=f(t)$.

2) Baadhi ya mifano ya parameter ya tatu ni wakati, urefu, kasi, na kiwango. Eleza wakati unatumiwa kama parameter.

3) Eleza jinsi ya kuondoa parameter iliyotolewa seti ya equations parametric.

Jibu

Chagua equation moja kutatua kwa$t$, mbadala katika equation nyingine na kurahisisha.

4) Ni faida gani ya kuandika mfumo wa equations parametric kama equation Cartesian?

5) Ni faida gani ya kutumia equations parametric?

Jibu

Baadhi ya milinganyo haiwezi kuandikwa kama kazi, kama duara. Hata hivyo, wakati imeandikwa kama equations mbili parametric, tofauti equations ni kazi.

6) Kwa nini kuna seti nyingi za milinganyo ya parametric kuwakilisha kwenye kazi ya Cartesian?

Kialjebra

Kwa mazoezi 7-25, ondoa parameter$t$ ili uandike upya equation ya parametric kama equation ya Cartesian.

7)$\begin{cases} & x(t)= 5-t\\ & y(t)= 8-2t \end{cases}$

Jibu

$y=-2+2x$

8)$\begin{cases} & x(t)= 6-3t\\ & y(t)= 10-t \end{cases}$

9)$\begin{cases} & x(t)= 2t+1\\ & y(t)= 3\sqrt{t} \end{cases}$

Jibu

$y=3\sqrt{\dfrac{x-1}{2}}$

10)$\begin{cases} & x(t)= 3t-1\\ & y(t)= 2t^2 \end{cases}$

11)$\begin{cases} & x(t)= 2e^t\\ & y(t)= 1-5t \end{cases}$

Jibu

$x=2e^{\tfrac{1-y}{5}}$au$y=1-5\ln \left ( \dfrac{x}{2} \right )$

12)$\begin{cases} & x(t)= e^{-2t}\\ & y(t)= 2e^{-t} \end{cases}$

13)$\begin{cases} & x(t)= 4\log (t)\\ & y(t)= 3+2t \end{cases}$

Jibu

$x=4\log \left ( \dfrac{y-3}{2} \right )$

14)$\begin{cases} & x(t)= \log (2t)\\ & y(t)= \sqrt{t-1} \end{cases}$

15)$\begin{cases} & x(t)= t^3-t\\ & y(t)= 2t \end{cases}$

Jibu

$x=\left ( \dfrac{y}{2} \right )^3-\dfrac{y}{2}$

16)$\begin{cases} & x(t)= t-t^4\\ & y(t)= t+2 \end{cases}$

17)$\begin{cases} & x(t)= e^{2t}\\ & y(t)= e^{6t} \end{cases}$

Jibu

$y=x^3$

18)$\begin{cases} & x(t)= t^{5}\\ & y(t)= t^{10} \end{cases}$

19)$\begin{cases} & x(t)= 4\cos t\\ & y(t)= 5\sin t \end{cases}$

Jibu

$\left ( \dfrac{x}{4} \right )^2+\left ( \dfrac{y}{5} \right )^2=1$

20)$\begin{cases} & x(t)= 3\sin t\\ & y(t)= 6\cos t \end{cases}$

21)$\begin{cases} & x(t)= 2\cos ^2t\\ & y(t)= -\sin t \end{cases}$

Jibu

$y^2=1-\dfrac{1}{2}x$

22)$\begin{cases} & x(t)= \cos t+4\\ & y(t)= 2\sin ^2t \end{cases}$

23)$\begin{cases} & x(t)= t-1\\ & y(t)= t^2 \end{cases}$

Jibu

$y=x^2+2x+1$

24)$\begin{cases} & x(t)= -t\\ & y(t)= t^3+1 \end{cases}$

25)$\begin{cases} & x(t)= 2t-1\\ & y(t)= t^3-2 \end{cases}$

Jibu

$y=\left ( \dfrac{x+1}{2} \right )^3 - 2$

Kwa mazoezi 26-29, andika upya equation parametric kama equation Cartesian kwa kujenga$x-y$ meza.

26)$\begin{cases} & x(t)= 2t-1\\ & y(t)= t+4 \end{cases}$

27)$\begin{cases} & x(t)= 4-t\\ & y(t)= 3t+2 \end{cases}$

Jibu

$y=-3x+14$

28)$\begin{cases} & x(t)= 2t-1\\ & y(t)= 5t \end{cases}$

29)$\begin{cases} & x(t)= 4t-1\\ & y(t)= 4t+2 \end{cases}$

Jibu

$y=x+3$

Kwa mazoezi 30-33, parameterize (kuandika equations parametric kwa) kila equation Cartesian kwa kuweka$x(t)=t$ au kwa kuweka$y(t)=t$.

30)$y(x)=3x^2 + 3$

31)$y(x)=2\sin x + 1$

Jibu

$\begin{cases} & x(t)= t\\ & y(t)= 2\sin t + 1 \end{cases}$

32)$x(y)=3\log (y)+y$

33)$x(y)=\sqrt{y}+2y$

Jibu

$\begin{cases} & x(t)= \sqrt{t}+2t\\ & y(t)= t \end{cases}$

Kwa mazoezi 34-41, parameterize (kuandika equations parametric kwa) kila equation Cartesian kwa kutumia$x(t)=a\cos t$ na$y(t)=b\sin t$. Tambua Curve.

34)$\dfrac{x^2}{4}+\dfrac{x^2}{9}=1$

35)$\dfrac{x^2}{16}+\dfrac{x^2}{36}=1$

Jibu

$\begin{cases} & x(t)= 4\cos t\\ & y(t)= 6\sin t \end{cases}; \text{Ellipse}$

36)$x^2 + y^2 = 16$

37)$x^2 + y^2 = 10$

Jibu

$\begin{cases} & x(t)= \sqrt{10}\cos t\\ & y(t)= \sqrt{10}\sin t \end{cases}; \text{Circle}$

38) Parameterize mstari kutoka kwa$(3,0)$$(-2,-5)$ ili mstari$(3,0)$ ulipo$t=0$, na$(-2,-5)$ saa$t=1$.

39) Parameterize mstari kutoka kwa$(-1,0)$$(3,-2)$ ili mstari$(-1,0)$ ulipo$t=0$, na$(3,-2)$ saa$t=1$.

Jibu

$\begin{cases} & x(t)= -1+4t\\ & y(t)= -2t \end{cases}$

40) Parameterize mstari kutoka kwa$(-1,5)$$(2,3)$ ili mstari$(-1,5)$ ulipo$t=0$, na$(2,3)$ saa$t=1$.

41) Parameterize mstari kutoka kwa$(4,1)$$(6,-2)$ ili mstari$(4,1)$ ulipo$t=0$, na$(6,-2)$ saa$t=1$.

Jibu

$\begin{cases} & x(t)= 4+2t\\ & y(t)= 1-3t \end{cases}$

Teknolojia

Kwa mazoezi 42-43, tumia kipengele cha meza katika calculator ya graphing ili uone kama grafu zinaingiliana.

42)$\begin{cases} & x_1(t)= 3t\\ & y_1(t)= 2t-1 \end{cases}\; \; \text{and}\; \; \begin{cases} & x_2(t)= t+3\\ & y_2(t)= 4t-4 \end{cases}$

43)$\begin{cases} & x_1(t)= t^2\\ & y_1(t)= 2t-1 \end{cases}\; \; \text{and}\; \; \begin{cases} & x_2(t)= -t+6\\ & y_2(t)= t+1 \end{cases}$

Jibu

ndiyo, katika$t=2$

Kwa mazoezi 44-46, tumia calculator ya graphing kukamilisha meza ya maadili kwa kila seti ya equations parametric.

44)$\begin{cases} & x_1(t)= 3t^2-3t+7\\ & y_1(t)= 2t+3 \end{cases}$

$t$	$x$	$y$
\ (t\) ">-1	\ (x\) ">	\ (y\) ">
\ (t\) "> 0	\ (x\) ">	\ (y\) ">
\ (t\) ">1	\ (x\) ">	\ (y\) ">

45)$\begin{cases} & x_1(t)= t^2-4\\ & y_1(t)= 2t^2-1 \end{cases}$

$t$	$x$	$y$
\ (t\)” style="background-attachment:kitabu; background-clip:sanduku la mpaka; picha ya background:hakuna; asili ya asili: sanduku la padding; background-msimamo-x: 0%; background-kurudia:kurudia; background-ukubwa: auto; mpaka chini-rangi: rgb (204, 204, 204); mpaka chini-style: dashed; mpaka wa chini-upana: 1px; mpaka -picha-outset: 0; mpakana-picha-kurudia: kunyoosha; mpaka-picha-kipande: 100%; mpaka picha-upana-upana: 1; mpaka-kushoto-rangi: rgb (204, 204, 204); mpaka-kushoto-style: dashed; - upana wa kulia:1px; mpako-juu-rangi: rgb (204, 204 , 204); Mpaka-juu-style: dashed; upana-juu-upana:1px; ukubwa wa sanduku: sanduku la mpaka; padding-chini-chini: 16px; padding-kulia: 16px; padding-juu-juu: 16px; maandishi-align: katikati; wima align: juu; neno wrap: kuvunja-neno; "> 1	\ (x\)” style="background-attachment:kitabu; background-clip:sanduku la mpaka; picha ya background:hakuna; asili ya asili: sanduku la padding; background-msimamo-x: 0%; background-kurudia:kurudia; background-ukubwa: auto; mpaka chini-rangi: rgb (204, 204, 204); mpaka chini-style: dashed; mpaka wa chini-upana: 1px; mpaka -picha-outset: 0; mpakana-picha-kurudia: kunyoosha; mpaka-picha-kipande: 100%; mpaka picha-upana-upana: 1; mpaka-kushoto-rangi: rgb (204, 204, 204); mpaka-kushoto-style: dashed; - upana wa kulia:1px; mpako-juu-rangi: rgb (204, 204 , 204); mpako-juu-style: dashed; upana-juu-upana: 1px; sanduku-sizing: sanduku la mpaka; padding-chini-chini: 16px; padding-kulia: 16px; padding-juu-juu: 16px; maandishi-align: katikati; wima align: juu; neno-wrap: kuvunja-neno; ">	\ (y\)” style="background-attachment:kitabu; background-clip:sanduku la mpaka; picha ya background:hakuna; asili ya asili: sanduku la padding; background-msimamo-x: 0%; background-kurudia:kurudia; background-ukubwa: auto; mpaka chini-rangi: rgb (204, 204, 204); mpaka chini-style: dashed; mpaka wa chini-upana: 1px; mpaka -picha-outset: 0; mpakana-picha-kurudia: kunyoosha; mpaka-picha-kipande: 100%; mpaka picha-upana-upana: 1; mpaka-kushoto-rangi: rgb (204, 204, 204); mpaka-kushoto-style: dashed; - upana wa kulia:1px; mpako-juu-rangi: rgb (204, 204 , 204); mpako-juu-style: dashed; upana-juu-upana: 1px; sanduku-sizing: sanduku la mpaka; padding-chini-chini: 16px; padding-kulia: 16px; padding-juu-juu: 16px; maandishi-align: katikati; wima align: juu; neno-wrap: kuvunja-neno; ">
\ (t\)” style="background-attachment:kitabu; background-clip:sanduku la mpaka; rangi ya background: rgb (239, 239, 239); picha ya background:hakuna; asili ya asili:sanduku; background-msimamo-x: 0%; background-kurudia: kurudia; background-sage: auto; mpaka chini-rangi: rgb: rgb (204, 204, 204); Mpaka-chini-style: dashed; mpaka-chini-upana: 1px; mpaka-picha-outset: 0; mpaka-picha-kurudia: kunyoosha; mpaka-picha-kipande: 100%; mpako-picha-upana: 1; mpaka-kushoto-rangi: rgb (204, 204); mpaka-kushoto-style: dashed; mpaka-kushoto-upana: 1px; mpaka-haki-rangi: rgb (204, 204), 204); mpaka-haki-style: dashed; mpaka-haki- upana: 1px; mpaka-juu-rangi: rgb (204, 204, 204); mpako-juu-style: dashed; upana-upana-upana: 1px; sanduku-sizing: sanduku mpaka; padding-chini: 16px; padding-juu-juu: 16px; Nakala-align: juu; neno-wrap: kuvunja neno; ">2	\ (x\)” style="background-attachment:kitabu; background-clip:sanduku la mpaka; rangi ya background: rgb (239, 239, 239); picha ya background:hakuna; asili ya asili:sanduku; background-msimamo-x: 0%; background-kurudia: kurudia; background: auto; mpaka chini-rangi: rgb (204, 204, 204); Mpaka-chini-style: dashed; mpaka-chini-upana: 1px; mpaka-picha-outset: 0; mpaka-picha-kurudia: kunyoosha; mpaka-picha-kipande: 100%; mpako-picha-upana: 1; mpaka-kushoto-rangi: rgb (204, 204); mpaka-kushoto-style: dashed; mpaka-kushoto-upana: 1px; mpaka-haki-rangi: rgb (204, 204), 204); mpaka-haki-style: dashed; mpaka-haki- upana: 1px; mpaka-juu-rangi: rgb (204, 204, 204); mpako-juu-style: dashed; upana-upana-upana: 1px; sanduku-sizing: sanduku mpaka; padding-chini: 16px; padding-juu-juu: 16px; Nakala-align: juu; neno-wrap: kuvunja neno; ">	\ (y\)” style="background-attachment:kitabu; background-clip:sanduku la mpaka; rangi ya background: rgb (239, 239, 239); picha ya background:hakuna; asili-asili-sanduku; background-msimamo-x: 0%; background-kurudia: kurudia; background-sage: auto; mpaka chini-rangi: rgb: rgb (204, 204, 204); Mpaka-chini-style: dashed; mpaka-chini-upana: 1px; mpaka-picha-outset: 0; mpaka-picha-kurudia: kunyoosha; mpaka-picha-kipande: 100%; mpako-picha-upana: 1; mpaka-kushoto-rangi: rgb (204, 204); mpaka-kushoto-style: dashed; mpaka-kushoto-upana: 1px; mpaka-haki-rangi: rgb (204, 204), 204); mpaka-haki-style: dashed; mpaka-haki- upana: 1px; mpaka-juu-rangi: rgb (204, 204, 204); mpako-juu-style: dashed; upana-upana-upana: 1px; sanduku-sizing: sanduku mpaka; padding-chini: 16px; padding-juu-juu: 16px; Nakala-align: juu; neno-wrap: kuvunja neno; ">
\ (t\)” style="background-attachment:kitabu; background-clip:sanduku la mpaka; picha ya background:hakuna; asili ya asili: sanduku la padding; background-msimamo-x: 0%; background-kurudia:kurudia; background-ukubwa: auto; mpaka chini-rangi: rgb (204, 204, 204); mpaka chini-style: dashed; mpaka wa chini-upana: 1px; mpaka -picha-outset: 0; mpakana-picha-kurudia: kunyoosha; mpaka-picha-kipande: 100%; mpaka picha-upana-upana: 1; mpaka-kushoto-rangi: rgb (204, 204, 204); mpaka-kushoto-style: dashed; - upana wa kulia:1px; mpako-juu-rangi: rgb (204, 204 , 204); Mpaka-juu-style: dashed; upana-juu-upana:1px; ukubwa wa sanduku: sanduku la mpaka; padding-chini-chini: 16px; padding-kulia: 16px; padding-juu-juu: 16px; maandishi-align: katikati; wima align: juu; neno wrap: kuvunja-neno; "> 3	\ (x\)” style="background-attachment:kitabu; background-clip:sanduku la mpaka; picha ya background:hakuna; asili ya asili: sanduku la padding; background-msimamo-x: 0%; background-kurudia:kurudia; background-ukubwa: auto; mpaka chini-rangi: rgb (204, 204, 204); mpaka chini-style: dashed; mpaka wa chini-upana: 1px; mpaka -picha-outset: 0; mpakana-picha-kurudia: kunyoosha; mpaka-picha-kipande: 100%; mpaka picha-upana-upana: 1; mpaka-kushoto-rangi: rgb (204, 204, 204); mpaka-kushoto-style: dashed; - upana wa kulia:1px; mpako-juu-rangi: rgb (204, 204 , 204); mpako-juu-style: dashed; upana-juu-upana: 1px; sanduku-sizing: sanduku la mpaka; padding-chini-chini: 16px; padding-kulia: 16px; padding-juu-juu: 16px; maandishi-align: katikati; wima align: juu; neno-wrap: kuvunja-neno; ">	\ (y\)” style="background-attachment:kitabu; background-clip:sanduku la mpaka; picha ya background:hakuna; asili ya asili: sanduku la padding; background-msimamo-x: 0%; background-kurudia:kurudia; background-ukubwa: auto; mpaka chini-rangi: rgb (204, 204, 204); mpaka chini-style: dashed; mpaka wa chini-upana: 1px; mpaka -picha-outset: 0; mpakana-picha-kurudia: kunyoosha; mpaka-picha-kipande: 100%; mpaka picha-upana-upana: 1; mpaka-kushoto-rangi: rgb (204, 204, 204); mpaka-kushoto-style: dashed; - upana wa kulia:1px; mpako-juu-rangi: rgb (204, 204 , 204); mpako-juu-style: dashed; upana-juu-upana: 1px; sanduku-sizing: sanduku la mpaka; padding-chini-chini: 16px; padding-kulia: 16px; padding-juu-juu: 16px; maandishi-align: katikati; wima align: juu; neno-wrap: kuvunja-neno; ">

Jibu

$t$	$x$	$y$
\ (t\) ">1	\ (x\) ">-3	\ (y\) ">1
\ (t\) "> 2	\ (x\) "> 0	\ (y\) ">7
\ (t\) ">3	\ (x\) "> 5	\ (y\) ">17

46)$\begin{cases} & x_1(t)= t^4\\ & y_1(t)= t^3+4 \end{cases}$

$t$	$x$	$y$
\ (t\)” style="background-attachment:kitabu; background-clip:sanduku la mpaka; picha ya background:hakuna; asili ya asili: sanduku la padding; background-msimamo-x: 0%; background-kurudia:kurudia; background-ukubwa: auto; mpaka chini-rangi: rgb (204, 204, 204); mpaka chini-style: dashed; mpaka wa chini-upana: 1px; mpaka -picha-outset: 0; mpakana-picha-kurudia: kunyoosha; mpaka-picha-kipande: 100%; mpaka picha-upana-upana: 1; mpaka-kushoto-rangi: rgb (204, 204, 204); mpaka-kushoto-style: dashed; - upana wa kulia:1px; mpako-juu-rangi: rgb (204, 204 , 204); mpako-juu-style: dashed; upana-juu-upana:1px; ukubwa wa sanduku: sanduku la mpaka; padding-chini-chini: 16px; padding-kulia: 16px; padding-juu-juu: 16px; maandishi-align: katikati; wima align: juu; neno wrap: kuvunja-neno; "> -1	\ (x\)” style="background-attachment:kitabu; background-clip:sanduku la mpaka; picha ya background:hakuna; asili ya asili: sanduku la padding; background-msimamo-x: 0%; background-kurudia:kurudia; background-ukubwa: auto; mpaka chini-rangi: rgb (204, 204, 204); mpaka chini-style: dashed; mpaka wa chini-upana: 1px; mpaka -picha-outset: 0; mpakana-picha-kurudia: kunyoosha; mpaka-picha-kipande: 100%; mpaka picha-upana-upana: 1; mpaka-kushoto-rangi: rgb (204, 204, 204); mpaka-kushoto-style: dashed; - upana wa kulia:1px; mpako-juu-rangi: rgb (204, 204 , 204); mpako-juu-style: dashed; upana-juu-upana: 1px; sanduku-sizing: sanduku la mpaka; padding-chini-chini: 16px; padding-kulia: 16px; padding-juu-juu: 16px; maandishi-align: katikati; wima align: juu; neno-wrap: kuvunja-neno; ">	\ (y\)” style="background-attachment:kitabu; background-clip:sanduku la mpaka; picha ya background:hakuna; asili ya asili: sanduku la padding; background-msimamo-x: 0%; background-kurudia:kurudia; background-ukubwa: auto; mpaka chini-rangi: rgb (204, 204, 204); mpaka chini-style: dashed; mpaka wa chini-upana: 1px; mpaka -picha-outset: 0; mpakana-picha-kurudia: kunyoosha; mpaka-picha-kipande: 100%; mpaka picha-upana-upana: 1; mpaka-kushoto-rangi: rgb (204, 204, 204); mpaka-kushoto-style: dashed; - upana wa kulia:1px; mpako-juu-rangi: rgb (204, 204 , 204); mpako-juu-style: dashed; upana-juu-upana: 1px; sanduku-sizing: sanduku la mpaka; padding-chini-chini: 16px; padding-kulia: 16px; padding-juu-juu: 16px; maandishi-align: katikati; wima align: juu; neno-wrap: kuvunja-neno; ">
\ (t\)” style="background-attachment:kitabu; background-clip:sanduku la mpaka; rangi ya background: rgb (239, 239, 239); picha ya background:hakuna; asili ya asili:sanduku; background-msimamo-x: 0%; background-kurudia: kurudia; background-sage: auto; mpaka chini-rangi: rgb: rgb (204, 204, 204); Mpaka-chini-style: dashed; mpaka-chini-upana: 1px; mpaka-picha-outset: 0; mpaka-picha-kurudia: kunyoosha; mpaka-picha-kipande: 100%; mpako-picha-upana: 1; mpaka-kushoto-rangi: rgb (204, 204); mpaka-kushoto-style: dashed; mpaka-kushoto-upana: 1px; mpaka-haki-rangi: rgb (204, 204), 204); mpaka-haki-style: dashed; mpaka-haki- upana: 1px; mpaka-juu-rangi: rgb (204, 204, 204); mpako-juu-style: dashed; upana-upana-upana: 1px; sanduku-sizing: sanduku mpaka; padding-chini: 16px; padding-juu-juu: 16px; Nakala-align: juu; neno-wrap: kuvunja neno; ">0	\ (x\)” style="background-attachment:kitabu; background-clip:sanduku la mpaka; rangi ya background: rgb (239, 239, 239); picha ya background:hakuna; asili ya asili:sanduku; background-msimamo-x: 0%; background-kurudia: kurudia; background: auto; mpaka chini-rangi: rgb (204, 204, 204); Mpaka-chini-style: dashed; mpaka-chini-upana: 1px; mpaka-picha-outset: 0; mpaka-picha-kurudia: kunyoosha; mpaka-picha-kipande: 100%; mpako-picha-upana: 1; mpaka-kushoto-rangi: rgb (204, 204); mpaka-kushoto-style: dashed; mpaka-kushoto-upana: 1px; mpaka-haki-rangi: rgb (204, 204), 204); mpaka-haki-style: dashed; mpaka-haki- upana: 1px; mpaka-juu-rangi: rgb (204, 204, 204); mpako-juu-style: dashed; upana-upana-upana: 1px; sanduku-sizing: sanduku mpaka; padding-chini: 16px; padding-juu-juu: 16px; Nakala-align: juu; neno-wrap: kuvunja neno; ">	\ (y\)” style="background-attachment:kitabu; background-clip:sanduku la mpaka; rangi ya background: rgb (239, 239, 239); picha ya background:hakuna; asili-asili-sanduku; background-msimamo-x: 0%; background-kurudia: kurudia; background-sage: auto; mpaka chini-rangi: rgb: rgb (204, 204, 204); Mpaka-chini-style: dashed; mpaka-chini-upana: 1px; mpaka-picha-outset: 0; mpaka-picha-kurudia: kunyoosha; mpaka-picha-kipande: 100%; mpako-picha-upana: 1; mpaka-kushoto-rangi: rgb (204, 204); mpaka-kushoto-style: dashed; mpaka-kushoto-upana: 1px; mpaka-haki-rangi: rgb (204, 204), 204); mpaka-haki-style: dashed; mpaka-haki- upana: 1px; mpaka-juu-rangi: rgb (204, 204, 204); mpako-juu-style: dashed; upana-upana-upana: 1px; sanduku-sizing: sanduku mpaka; padding-chini: 16px; padding-juu-juu: 16px; Nakala-align: juu; neno-wrap: kuvunja neno; ">
\ (t\)” style="background-attachment:kitabu; background-clip:sanduku la mpaka; picha ya background:hakuna; asili ya asili: sanduku la padding; background-msimamo-x: 0%; background-kurudia:kurudia; background-ukubwa: auto; mpaka chini-rangi: rgb (204, 204, 204); mpaka chini-style: dashed; mpaka wa chini-upana: 1px; mpaka -picha-outset: 0; mpakana-picha-kurudia: kunyoosha; mpaka-picha-kipande: 100%; mpaka picha-upana-upana: 1; mpaka-kushoto-rangi: rgb (204, 204, 204); mpaka-kushoto-style: dashed; - upana wa kulia:1px; mpako-juu-rangi: rgb (204, 204 , 204); Mpaka-juu-style: dashed; upana-juu-upana:1px; ukubwa wa sanduku: sanduku la mpaka; padding-chini-chini: 16px; padding-kulia: 16px; padding-juu-juu: 16px; maandishi-align: katikati; wima align: juu; neno wrap: kuvunja-neno; "> 1	\ (x\)” style="background-attachment:kitabu; background-clip:sanduku la mpaka; picha ya background:hakuna; asili ya asili: sanduku la padding; background-msimamo-x: 0%; background-kurudia:kurudia; background-ukubwa: auto; mpaka chini-rangi: rgb (204, 204, 204); mpaka chini-style: dashed; mpaka wa chini-upana: 1px; mpaka -picha-outset: 0; mpakana-picha-kurudia: kunyoosha; mpaka-picha-kipande: 100%; mpaka picha-upana-upana: 1; mpaka-kushoto-rangi: rgb (204, 204, 204); mpaka-kushoto-style: dashed; - upana wa kulia:1px; mpako-juu-rangi: rgb (204, 204 , 204); mpako-juu-style: dashed; upana-juu-upana: 1px; sanduku-sizing: sanduku la mpaka; padding-chini-chini: 16px; padding-kulia: 16px; padding-juu-juu: 16px; maandishi-align: katikati; wima align: juu; neno-wrap: kuvunja-neno; ">	\ (y\)” style="background-attachment:kitabu; background-clip:sanduku la mpaka; picha ya background:hakuna; asili ya asili: sanduku la padding; background-msimamo-x: 0%; background-kurudia:kurudia; background-ukubwa: auto; mpaka chini-rangi: rgb (204, 204, 204); mpaka chini-style: dashed; mpaka wa chini-upana: 1px; mpaka -picha-outset: 0; mpakana-picha-kurudia: kunyoosha; mpaka-picha-kipande: 100%; mpaka picha-upana-upana: 1; mpaka-kushoto-rangi: rgb (204, 204, 204); mpaka-kushoto-style: dashed; - upana wa kulia:1px; mpako-juu-rangi: rgb (204, 204 , 204); mpako-juu-style: dashed; upana-juu-upana: 1px; sanduku-sizing: sanduku la mpaka; padding-chini-chini: 16px; padding-kulia: 16px; padding-juu-juu: 16px; maandishi-align: katikati; wima align: juu; neno-wrap: kuvunja-neno; ">
\ (t\)” style="background-attachment:kitabu; background-clip:sanduku la mpaka; picha ya background:hakuna; asili ya asili: sanduku la padding; background-msimamo-x: 0%; background-kurudia:kurudia; background-ukubwa: auto; mpaka chini-rangi: rgb (204, 204, 204); mpaka chini-style: dashed; mpaka wa chini-upana: 1px; mpaka -picha-outset: 0; mpakana-picha-kurudia: kunyoosha; mpaka-picha-kipande: 100%; mpaka picha-upana-upana: 1; mpaka-kushoto-rangi: rgb (204, 204, 204); mpaka-kushoto-style: dashed; - upana wa kulia:1px; mpako-juu-rangi: rgb (204, 204 , 204); Mpaka-juu-style: dashed; upana-juu-upana:1px; ukubwa wa sanduku: sanduku la mpaka; padding-chini-chini: 16px; padding-kulia: 16px; padding-juu-juu: 16px; maandishi-align: katikati; wima align: juu; neno wrap: kuvunja-neno; "> 2	\ (x\)” style="background-attachment:kitabu; background-clip:sanduku la mpaka; picha ya background:hakuna; asili ya asili: sanduku la padding; background-msimamo-x: 0%; background-kurudia:kurudia; background-ukubwa: auto; mpaka chini-rangi: rgb (204, 204, 204); mpaka chini-style: dashed; mpaka wa chini-upana: 1px; mpaka -picha-outset: 0; mpakana-picha-kurudia: kunyoosha; mpaka-picha-kipande: 100%; mpaka picha-upana-upana: 1; mpaka-kushoto-rangi: rgb (204, 204, 204); mpaka-kushoto-style: dashed; - upana wa kulia:1px; mpako-juu-rangi: rgb (204, 204 , 204); mpako-juu-style: dashed; upana-juu-upana: 1px; sanduku-sizing: sanduku la mpaka; padding-chini-chini: 16px; padding-kulia: 16px; padding-juu-juu: 16px; maandishi-align: katikati; wima align: juu; neno-wrap: kuvunja-neno; ">	\ (y\)” style="background-attachment:kitabu; background-clip:sanduku la mpaka; picha ya background:hakuna; asili ya asili: sanduku la padding; background-msimamo-x: 0%; background-kurudia:kurudia; background-ukubwa: auto; mpaka chini-rangi: rgb (204, 204, 204); mpaka chini-style: dashed; mpaka wa chini-upana: 1px; mpaka -picha-outset: 0; mpakana-picha-kurudia: kunyoosha; mpaka-picha-kipande: 100%; mpaka picha-upana-upana: 1; mpaka-kushoto-rangi: rgb (204, 204, 204); mpaka-kushoto-style: dashed; - upana wa kulia:1px; mpako-juu-rangi: rgb (204, 204 , 204); mpako-juu-style: dashed; upana-juu-upana: 1px; sanduku-sizing: sanduku la mpaka; padding-chini-chini: 16px; padding-kulia: 16px; padding-juu-juu: 16px; maandishi-align: katikati; wima align: juu; neno-wrap: kuvunja-neno; ">

Upanuzi

47) Kupata seti mbili tofauti ya milinganyo parametric kwa$y=(x+1)^2$.

Jibu

majibu inaweza kutofautiana:$\begin{cases} & x(t)= t-1\\ & y(t)= t^2 \end{cases}\; \; \text{and}\; \; \begin{cases} & x(t)= t+1\\ & y(t)= (t+2)^2 \end{cases}$

48) Kupata seti mbili tofauti ya milinganyo parametric kwa$y=3x-2$.

49) Kupata seti mbili tofauti ya milinganyo parametric kwa$y=x^2-4x+4$.

Jibu

majibu inaweza kutofautiana:$\begin{cases} & x(t)= t\\ & y(t)= t^2-4t+4 \end{cases}\; \; \text{and}\; \; \begin{cases} & x(t)= t+2\\ & y(t)= t^2 \end{cases}$

8.7: Ulinganifu wa parametric - Grafu

Maneno

1) Ni njia gani mbili zinazotumiwa kwa usawa wa parametric?

Jibu

kupanga njama na mshale wa mwelekeo na calculator ya graphing

2) Ni tofauti gani moja katika usawa wa parametric wa uhakika ikilinganishwa na equations ya Cartesian?

3) Kwa nini baadhi ya grafu inayotolewa na mishale?

Jibu

Mishale inaonyesha mwelekeo, mwelekeo wa mwendo kulingana na kuongezeka kwa maadili ya$t$.

4) Jina aina chache za kawaida za grafu za equations parametric.

5) Kwa nini grafu za parametric muhimu katika kuelewa mwendo wa projectile?

Jibu

Ulinganisho wa parametric unaonyesha mwendo tofauti wa wima na usawa kwa muda.

Picha

Kwa mazoezi 6-11, grafu kila seti ya equations parametric kwa kufanya meza ya maadili. Jumuisha mwelekeo kwenye grafu.

6)$\begin{cases} & x(t)= t\\ & y(t)= t^2-1 \end{cases}$

$t$	$x$	$y$
\ (t\) ">-3	\ (x\) ">	\ (y\) ">
\ (t\) ">-2	\ (x\) ">	\ (y\) ">
\ (t\) ">-1	\ (x\) ">	\ (y\) ">
\ (t\) "> 0	\ (x\) ">	\ (y\) ">
\ (t\) ">1	\ (x\) ">	\ (y\) ">
\ (t\) "> 2	\ (x\) ">	\ (y\) ">
\ (t\) ">3

7)$\begin{cases} & x(t)= t-1\\ & y(t)= t^2 \end{cases}$

$t$	-3	-2	-1	0	1	2
$x$
$y$

Jibu

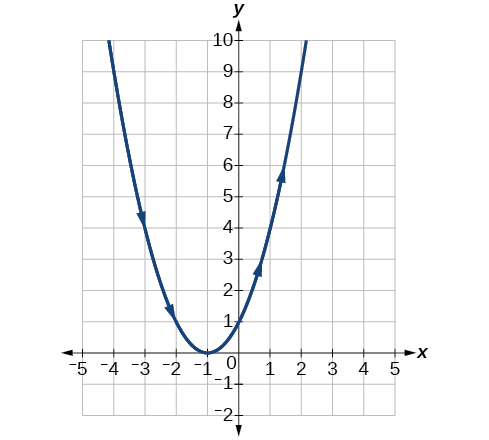
8)$\begin{cases} & x(t)= 2+t\\ & y(t)= 3-2t \end{cases}$

$t$	-2	-1	0	1	2	3
$x$
$y$

9)$\begin{cases} & x(t)= -2-2t\\ & y(t)= 3+t \end{cases}$

$t$	-3	-2	-1	0	1
$x$
$y$

Jibu

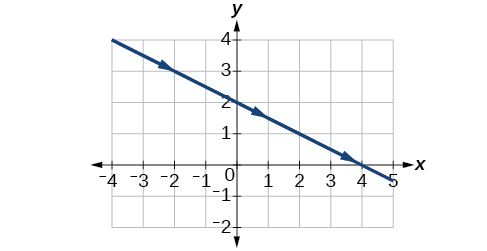
10)$\begin{cases} & x(t)= t^3\\ & y(t)= t+2 \end{cases}$

$t$	-2	-1	0	1	2
$x$
$y$

11)$\begin{cases} & x(t)= t^2\\ & y(t)= t+3 \end{cases}$

$t$	-2	-1	0	1	2
$x$
$y$

Jibu

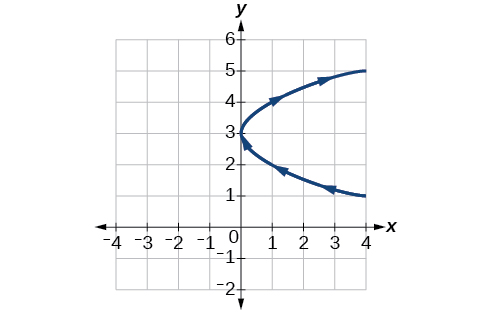
Kwa mazoezi 12-22, mchoro mchoro na ujumuishe mwelekeo.

12)$\begin{cases} & x(t)= t\\ & y(t)= \sqrt{t} \end{cases}$

13)$\begin{cases} & x(t)= -\sqrt{t}\\ & y(t)= t \end{cases}$

Jibu

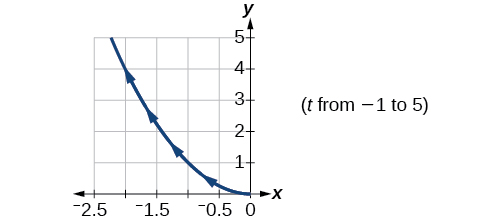
14)$\begin{cases} & x(t)= 5-\left | t \right |\\ & y(t)= t+2 \end{cases}$

15)$\begin{cases} & x(t)= -t+2\\ & y(t)= 5-\left | t \right | \end{cases}$

Jibu

16)$\begin{cases} & x(t)= 4\sin t\\ & y(t)= 2\cos t \end{cases}$

17)$\begin{cases} & x(t)= 2\sin t\\ & y(t)= 4\cos t \end{cases}$

Jibu

18)$\begin{cases} & x(t)= 3\cos ^2t\\ & y(t)= -3\sin t \end{cases}$

19)$\begin{cases} & x(t)= 3\cos ^2t\\ & y(t)= -3\sin ^2t \end{cases}$

Jibu

20)$\begin{cases} & x(t)= \sec t\\ & y(t)= \tan t \end{cases}$

21)$\begin{cases} & x(t)= \sec t\\ & y(t)= \tan ^2t \end{cases}$

Jibu

22)$\begin{cases} & x(t)= \dfrac{1}{e^{2t}}\\ & y(t)= e^{-t} \end{cases}$

Kwa mazoezi 23-27, grafu equation na ni pamoja na mwelekeo. Kisha, andika equation ya Cartesian.

23)$\begin{cases} & x(t)= t-1\\ & y(t)= -t^2 \end{cases}$

Jibu

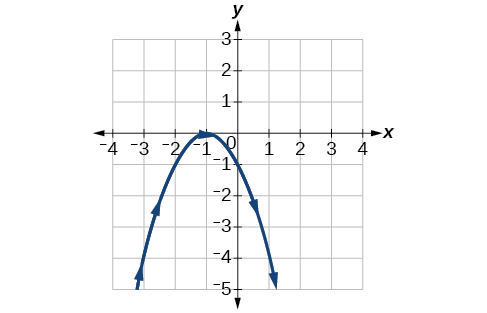
24)$\begin{cases} & x(t)= t^3\\ & y(t)= t+3 \end{cases}$

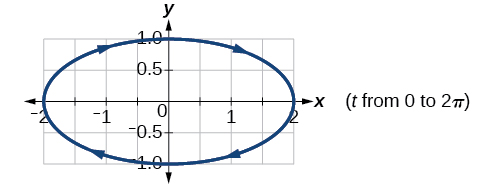
25)$\begin{cases} & x(t)= 2\cos t\\ & y(t)= -\sin t \end{cases}$

Jibu

26)$\begin{cases} & x(t)= 7\cos t\\ & y(t)= 7\sin t \end{cases}$

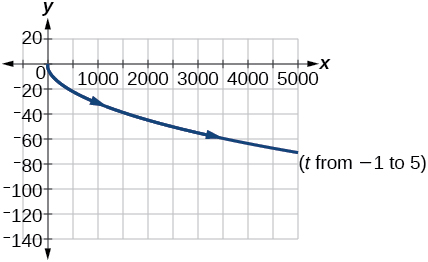
27)$\begin{cases} & x(t)= e^{2t}\\ & y(t)= -e^{t} \end{cases}$

Jibu

Kwa mazoezi 28-33, grafu equation na ni pamoja na mwelekeo.

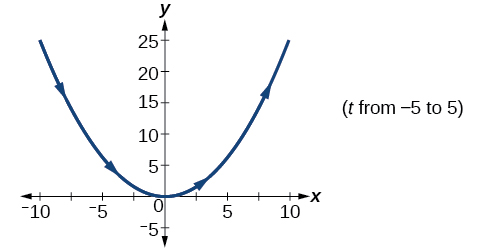
28)$x=t^2, y = 3t, 0\leq t\leq 5$

29)$x=2t, y = t^2, -5\leq t\leq 5$

Jibu

30)\(x=t, y=\sqrt{25-t^2}, 0<t\leq>

31)$x(t)=-t,y(t)=\sqrt{t}, t\geq 0$

Jibu

32)$x=-2\cos t, y=6\sin t, 0\leq t\leq \pi$

33)$x=-\sec t, y=\tan t, -\dfrac{\pi }{2}< t< \dfrac{\pi }{2}$

Jibu

Kwa mazoezi 34-41, tumia usawa wa parametric kwa integers$a$ na$b$: $$\begin{align*} x(t) &= a\cos ((a+b)t)\\ y(t) &= a\cos ((a-b)t) \end{align*} \nonumber$$

34) Grafu kwenye uwanja$[-\pi ,0]$, wapi$a=2$ na$b=1$, na ujumuishe mwelekeo.

35) Grafu kwenye uwanja$[-\pi ,0]$, wapi$a=3$ na$b=2$, na ujumuishe mwelekeo.

Jibu

36) Grafu kwenye uwanja$[-\pi ,0]$, wapi$a=4$ na$b=3$, na ujumuishe mwelekeo.

37) Grafu kwenye uwanja$[-\pi ,0]$, wapi$a=5$ na$b=4$, na ujumuishe mwelekeo.

Jibu

38) Ikiwa$a$ ni$1$ zaidi ya$b$, kuelezea athari maadili ya$a$ na$b$ kuwa kwenye grafu ya equations parametric.

 

39) Eleza grafu ikiwa$a=100$ na$b=99$.

Jibu

Kutakuwa na mwendo$100$ wa kurudi nyuma.

40) Nini kinatokea ikiwa$b$ ni$1$ zaidi ya$a$? Eleza grafu.

41) Kama equations parametric$x(t)=t^2$ na$y(t)=6-3t$ kuwa na grafu ya usawa parabola kufungua kwa haki, nini kubadilisha mwelekeo wa Curve?

Jibu

Chukua kinyume cha$x(t)$ equation.

Kwa mazoezi 42-46, kuelezea grafu ya seti ya equations parametric.

42)$x(t)=-t^2$ na$y(t)$ ni mstari

43)$y(t)=t^2$ na$x(t)$ ni mstari

Jibu

Parabola inafungua.

44)$y(t)=-t^2$ na$x(t)$ ni mstari

45) Andika equations parametric ya mduara na kituo$(0,0)$,radius$5$, na mwelekeo kinyume chake.

Jibu

$\begin{cases} & x(t)= 5\cos t\\ & y(t)= 5\sin t \end{cases}$

46) Andika equations parametric ya ellipse na kituo$(0,0)$,mhimili mkubwa wa urefu$10$, mhimili mdogo wa urefu$6$, na mwelekeo wa kinyume chake.

 

Kwa mazoezi 47-52, tumia matumizi ya graphing kwenye grafu kwenye dirisha$[-3,3]$ na$[-3,3]$ kwenye uwanja$[0,2\pi )$ kwa maadili yafuatayo ya $a$na$b$, na ujumuishe mwelekeo. $$\begin{cases} & x(t)= \sin (at)\\ & y(t)= \sin (bt) \end{cases} \nonumber$$

47)$a=1,b=2$

Jibu

48)$a=2, b=1$

49)$a=3, b=3$

Jibu

50)$a=5, b=5$

51)$a=2, b=5$

Jibu

52)$a=5, b=2$

Teknolojia

Kwa mazoezi 53-56, angalia grafu zilizoundwa na usawa wa parametric wa fomu $$\begin{cases} & x(t)= a\cos (bt)\\ & y(t)= c\sin (dt) \end{cases} \nonumber$$ Tumia mode ya parametric kwenye calculator ya graphing ili kupata maadili ya$a, b, c$, na$d$ kufikia kila grafu.

53)

Jibu

$a=4, b=3, c=6, d=1$

54)

55)

Jibu

$a=4, b=2, c=3, d=3$

56)

Kwa mazoezi 57-62, tumia matumizi ya graphing kwa grafu ya usawa wa parametric iliyotolewa.

$$\begin{cases} & x(t)= \cos t-1\\ & y(t)= \sin t+t \end{cases} \nonumber$$

$$\begin{cases} & x(t)= \cos t+t\\ & y(t)= \sin t-1 \end{cases} \nonumber$$

$$\begin{cases} & x(t)= t-\sin t\\ & y(t)= \cos t-1 \end{cases} \nonumber$$

57) Grafu seti zote tatu za equations parametric kwenye uwanja$[0,2\pi ]$.

Jibu

58) Grafu seti zote tatu za equations parametric kwenye uwanja$[0,4\pi]$.

59) Grafu seti zote tatu za equations parametric kwenye uwanja$[-4\pi ,6\pi]$.

Jibu

60) Grafu ya kila seti ya equations parametric inaonekana “huenda” pamoja na moja ya axes. Ni udhibiti gani ambao mhimili wa grafu huenda pamoja?

61) Eleza athari kwenye grafu ya equation parametric wakati sisi switched$\sin t$ na$\cos t$.

Jibu

Mabadiliko$y$ -intercept.

62) Eleza athari kwenye grafu ya equation ya parametric wakati tulibadilisha kikoa.

Upanuzi

63) Kitu kinatupwa hewa na kasi ya wima ya$20$ ft/s na kasi ya usawa wa$15$ ft/s. urefu wa kitu inaweza kuwa ilivyoelezwa na equation$y(t)=-16t^2+20t$, wakati kitu hatua sambamba na kasi ya mara kwa mara$15$ ft/s Andika milinganyo parametric kwa kitu nafasi, na kisha kuondoa muda wa kuandika urefu kama kazi ya nafasi ya usawa.

Jibu

$y(x)=-16\left ( \dfrac{x}{15} \right )^2+20\left ( \dfrac{x}{15} \right )$

64) Skateboarder wanaoendesha juu ya uso wa ngazi kwa kasi ya mara kwa mara ya$9$ ft/s inatupa mpira hewa, urefu ambao unaweza kuelezewa na equation$y(t)=-16t^2+10t+5$. Andika equations parametric kwa nafasi ya mpira, na kisha kuondoa muda wa kuandika urefu kama kazi ya nafasi ya usawa.

Kwa mazoezi 65-69, tumia hali hii: dart inatupwa juu na kasi ya awali ya$65$ ft/s kwa pembe ya mwinuko wa$52^{\circ}$. Fikiria nafasi ya dart wakati wowote$t$. Puuza upinzani wa hewa.

65) Pata equations parametric kwamba mfano hali ya tatizo.

Jibu

$\begin{cases} & x(t)= 64t\cos (52^{\circ})\\ & y(t)= -16t^2+64t\sin (52^{\circ}) \end{cases}$

66) Kupata maadili yote iwezekanavyo ya$x$ kwamba kuwakilisha hali hiyo.

67) Dart itapiga lini chini?

Jibu

takriban$3.2$ sekunde

68) Pata urefu wa juu wa dart.

69) Wakati gani dart itafikia urefu wa juu?

Jibu

$1.6$sekunde

Kwa mazoezi 70-73, angalia grafu za kila moja ya milinganyo minne ya parametric. Ingawa wanaonekana isiyo ya kawaida na nzuri, ni ya kawaida sana kuwa wana majina, kama ilivyoonyeshwa katika kila zoezi. Tumia matumizi ya graphing kwa grafu kila kwenye uwanja ulioonyeshwa.

70)$\text{An epicycloid}\begin{cases} & x(t)= 14\cos t-\cos (14t)\\ & y(t)= 14\sin t+\sin (14t) \end{cases}\; \; \text{on the domain }[0,2\pi ]$

71)$\text{An hypocycloid}\begin{cases} & x(t)= 6\sin t+2\sin (6t)\\ & y(t)= 6\cos t-2\cos (6t) \end{cases}\; \; \text{on the domain }[0,2\pi ]$

Jibu

72)$\text{An hypotrochoid}\begin{cases} & x(t)= 2\sin t+5\cos (6t)\\ & y(t)= 5\cos t-2\sin (6t) \end{cases}\; \; \text{on the domain }[0,2\pi ]$

73)$\text{A rose}\begin{cases} & x(t)= 5\sin (2t)\sin t\\ & y(t)= 5\sin (2t)\cos t \end{cases}\; \; \text{on the domain }[0,2\pi ]$

Jibu

8.8: Vectors

Maneno

1) Ni sifa gani za barua ambazo hutumiwa kuwakilisha wadudu?

Jibu

chini, barua ya ujasiri, kwa kawaida$u, v, w$

2) Je, vector ni maalum zaidi kuliko sehemu ya mstari?

3) Ni nini$i$ na$j$, na wanawakilisha nini?

Jibu

Wao ni vectors kitengo. Wao hutumiwa kuwakilisha vipengele vya usawa na wima vya vector. Kila mmoja ana ukubwa wa$1$.

4) Fomu ya sehemu ni nini?

5) Wakati vector kitengo ni walionyesha kama barua$\left \langle a,b \right \rangle$ ambayo ni mgawo wa$i$ na ambayo$j$?

Jibu

Nambari ya kwanza daima inawakilisha mgawo wa$i$ na pili inawakilisha$j$.

Kialjebra

6) Kutokana na vector na hatua ya awali$(5,2)$ na hatua ya mwisho$(-1,-3)$, pata vector sawa ambayo hatua ya awali ni$(0,0)$. Andika vector katika fomu ya sehemu$\left \langle a,b \right \rangle$.

7) Kutokana na vector na hatua ya awali$(-4,2)$ na hatua ya mwisho$(3,-3)$, kupata vector sawa ambao hatua ya awali ni$(0,0)$. Andika vector katika fomu ya sehemu$\left \langle a,b \right \rangle$.

Jibu

$\left \langle 7,-5 \right \rangle$

8) Kutokana na vector na hatua ya awali$(7,-1)$ na hatua ya mwisho$(-1,-7)$, kupata vector sawa ambao hatua ya awali ni$(0,0)$. Andika vector katika fomu ya sehemu$\left \langle a,b \right \rangle$.

Kwa mazoezi 9-15, onyesha kama vectors mbili$u$ na$v$ ni sawa, ambapo$u$ ina hatua ya awali$P_1$ na hatua ya mwisho$P_2$ na$v$ ina hatua ya awali$P_3$ na hatua ya mwisho$P_4$.

9)$P_1=(5,1), P_2=(3,-2), P_3=(-1,3), P4=(9,−4)$

Jibu

si sawa

10)$P_1=(2,-3), P_2=(5,1), P_3=(6,-1), P_4=(9,3)$

11)$P_1=(-1,-1), P_2=(-4,5), P_3=(-10,6), P_4=(-13,12)$

Jibu

sawa

12)$P_1=(3,7), P_2=(2,1), P_3=(1,2), P_4=(-1,-4)$

13)$P_1=(8,3), P_2=(6,5), P_3=(11,8), P4=(9,10)$

Jibu

sawa

14) Kutokana$P_1=(-3,1)$ na hatua ya awali na hatua ya mwisho$P_2=(5,2)$, weka vector$v$ kwa suala la$i$ na$j$.

15) Kutokana$P_1=(6,0)$ na hatua ya awali na hatua ya mwisho$P_2=(-1,-3)$, kuandika vector$v$ kwa suala la$i$ na$j$.

Jibu

$7i-3j$

Kwa mazoezi 16-17, tumia vectors$u = i+5j, v = -2i-3j, w = 4i-j$

16) Pata$u+(v-w)$

17) Kupata$4v+2u$

Jibu

$-6i-2j$

Kwa mazoezi 18-21, tumia wadudu waliopewa kukokotoa$u + v, u - v, 2u - 3v$

18)$u=\left \langle 2,-3 \right \rangle, v=\left \langle 1,5 \right \rangle$

1 9)$u=\left \langle -3,4 \right \rangle, v=\left \langle -2,1 \right \rangle$

Jibu

$u+v=\left \langle -5,5 \right \rangle,u-v=\left \langle -1,3 \right \rangle,2u-3v=\left \langle 0,5 \right \rangle$

20) Hebu$v = -4i + 3j$. Kupata vector kwamba ni nusu urefu na pointi katika mwelekeo huo kama$v$.

21) Hebu$v = 5i + 2j$. Kupata vector kwamba ni mara mbili ya urefu na pointi katika mwelekeo kinyume kama$v$.

Jibu

$-10i-4j$

Kwa mazoezi 22-27, pata vector kitengo katika mwelekeo sawa na vector iliyotolewa.

22)$a = 3i + 4j$

23)$b = -2i + 5j$

Jibu

$-\dfrac{2\sqrt{29}}{29}i+\dfrac{5\sqrt{29}}{29}j$

24)$c = 10i - j$

25)$d=-\dfrac{1}{3}i+\dfrac{5}{2}j$

Jibu

$-\dfrac{2\sqrt{229}}{229}i+\dfrac{15\sqrt{229}}{229}j$

26)$u = 100i + 200j$

27)$u = -14i + 2j$

Jibu

$-\dfrac{7\sqrt{2}}{10}i+\dfrac{\sqrt{2}}{10}j$

 

Kwa mazoezi 28-35, pata ukubwa na mwelekeo wa vector,$0\leq \theta < 2\pi$.

28)$\left \langle 0,4 \right \rangle$

29)$\left \langle 6,5 \right \rangle$

Jibu

$\left | v \right |=7.810, \theta =39.806^{\circ}$

30)$\left \langle 2,-5 \right \rangle$

31)$\left \langle -4,-6 \right \rangle$

Jibu

$\left | v \right |=7.211, \theta =236.310^{\circ}$

32) Kutokana$u = 3i − 4j$ na$v = −2i + 3j$, mahesabu$u\cdot v$.

33) Kutokana$u = −i − j$ na$v = i + 5j$, mahesabu$u\cdot v$.

Jibu

$-6$

34) Kutokana$u=\left \langle -2,4 \right \rangle$ na$v=\left \langle -3,1 \right \rangle$, hesabu$u\cdot v$.

35) Kutokana$u=\left \langle -1,6 \right \rangle$ na$v=\left \langle 6,-1 \right \rangle$,hesabu$u\cdot v$.

Jibu

$-12$

Picha

Kwa mazoezi 36-,38 iliyotolewa$v$, kuteka$v$,$3v$, na$\dfrac{1}{2}v$.

36)$\left \langle 2,-1 \right \rangle$

37)$\left \langle -1,4 \right \rangle$

Jibu

38)$\left \langle -3,-2 \right \rangle$

Kwa mazoezi 39-41, tumia vectors zilizoonyeshwa kwa mchoro$u + v$,$u − v$, na$2u$.

39)

Jibu

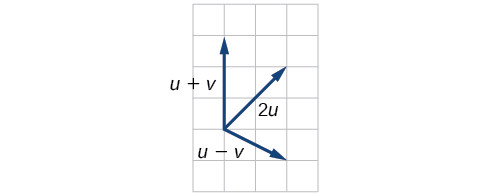
40)

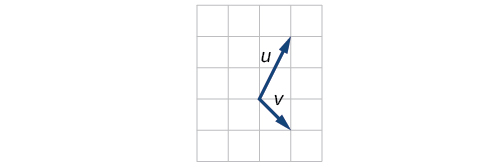
41)

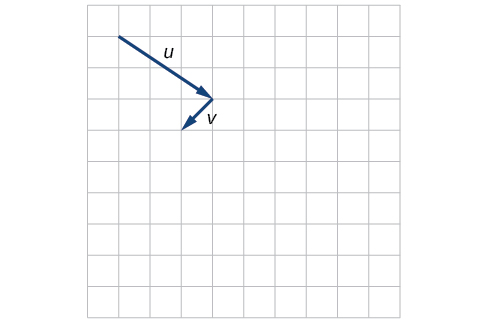
Jibu

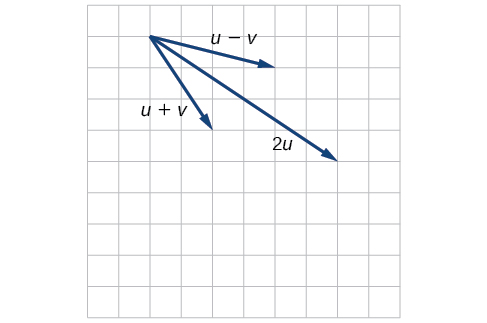
Kwa mazoezi 42-43, tumia vectors zilizoonyeshwa kwa mchoro$2u + v$.

42)

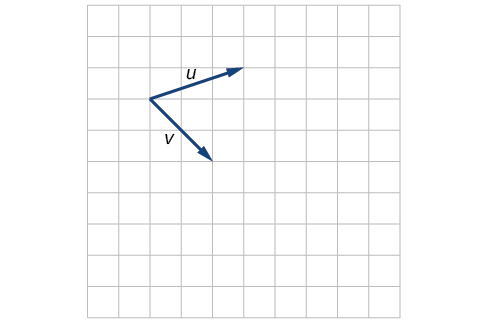
43)

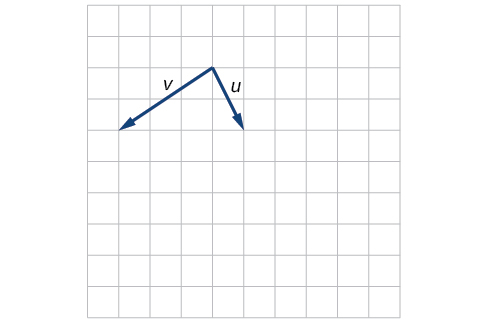
Jibu

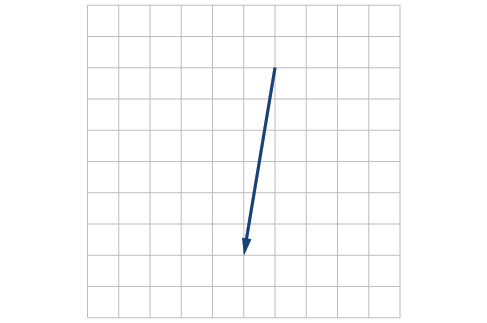
Kwa mazoezi 44-45, tumia vectors zilizoonyeshwa kwa mchoro$u − 3v$.

44)

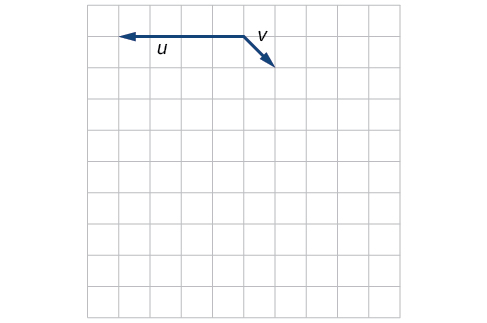
45)

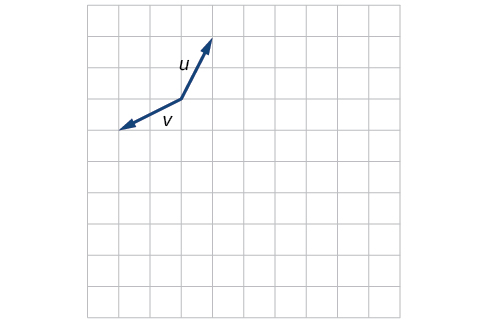
Jibu

Kwa mazoezi 46-47, weka vector iliyoonyeshwa katika fomu ya sehemu.

46)

47)

Jibu

$\left \langle 4,1 \right \rangle$

48) Kutokana$P_1=(2,1$ na hatua ya awali na hatua ya mwisho$P_2=(-1,2)$, kuandika vector$v$ katika suala la$i$ na$j$, kisha kuteka vector kwenye grafu.

49) Kutokana$P_1=(4,-1$ na hatua ya awali na hatua ya mwisho$P_2=(-3,2)$, weka vector$v$ kwa suala la$i$ na$j$. Chora pointi na vector kwenye grafu.

Jibu

$v=-7i+3j$

50) Kutokana$P_1=(3,3$ na hatua ya awali na hatua ya mwisho$P_2=(-3,3)$, weka vector$v$ kwa suala la$i$ na$j$. Chora pointi na vector kwenye grafu.

Upanuzi

Kwa mazoezi 51-54, tumia ukubwa uliopewa na mwelekeo katika nafasi ya kawaida, andika vector katika fomu ya sehemu.

51)$\left | v \right |=6, \theta =45^{\circ}$

Jibu

$3\sqrt{2}i+3\sqrt{2}j$

52)$\left | v \right |=8, \theta =220^{\circ}$

53)$\left | v \right |=2, \theta =300^{\circ}$

Jibu

$i-\sqrt{3}j$

54)$\left | v \right |=5, \theta =135^{\circ}$

55)$60$ Sanduku la pound linapumzika kwenye barabara inayoelekezwa$12^{\circ}$. Kuzunguka kwa kumi ya karibu,

1. Pata ukubwa wa sehemu ya kawaida (perpendicular) ya nguvu.
2. Pata ukubwa wa sehemu ya nguvu inayofanana na barabara.

Jibu

1. $58.7$
2. $12.5$

56)$25$ Sanduku la pound linapumzika kwenye barabara inayoelekezwa$8^{\circ}$. Kuzunguka kwa kumi ya karibu,

1. Pata ukubwa wa sehemu ya kawaida (perpendicular) ya nguvu.
2. Pata ukubwa wa sehemu ya nguvu inayofanana na barabara.

57) Pata ukubwa wa vipengele vya usawa na wima vya vector na$8$ paundi za ukubwa zilizoelekezwa katika mwelekeo wa$27^{\circ}$ juu ya usawa. Pande zote hadi karibu na mia moja.

Jibu

$x=7.13$paundi,$y=3.63$ paundi

58) Pata ukubwa wa vipengele vya usawa na wima vya vector na$4$ paundi za ukubwa zilizoelekezwa katika mwelekeo wa$127^{\circ}$ juu ya usawa. Pande zote hadi karibu na mia moja.

59) Pata ukubwa wa vipengele vya usawa na wima vya vector na$5$ paundi za ukubwa zilizoelekezwa katika mwelekeo wa$55^{\circ}$ juu ya usawa. Pande zote hadi karibu na mia moja.

Jibu

$x=2.87$paundi,$y=4.10$ paundi

60) Kupata ukubwa wa vipengele usawa na wima ya vector na$1$ pound ukubwa alisema katika mwelekeo wa$8^{\circ}$ juu usawa. Pande zote hadi karibu na mia moja.

Real-World Matumizi

61) Mwanamke huondoka nyumbani na anatembea$3$ maili magharibi, kisha$2$ maili kusini magharibi. Jinsi mbali na nyumbani ni yeye, na katika mwelekeo gani lazima atembee kwenda kichwa moja kwa moja nyumbani?

Jibu

$4.635$maili,$17.764^{\circ}$ N ya E

62) mashua majani marina na sails$6$ maili kaskazini, kisha$2$ maili kaskazini. Jinsi mbali na marina ni mashua, na katika mwelekeo gani lazima kusafiri kwa kichwa moja kwa moja nyuma marina?

63) Mtu anaanza kutembea kutoka nyumbani na anatembea$4$ maili mashariki, maili kusini,$2$ maili kusini,$5$ maili kusini magharibi, na$2$ maili mashariki.$4$ Jinsi mbali yeye kutembea? Ikiwa alitembea moja kwa moja nyumbani, angeweza kutembea mbali?

Jibu

$17$maili,$10.318$ maili

64) Mwanamke anaanza kutembea kutoka nyumbani na anatembea$4$ maili mashariki, maili kusini,$7$ maili kusini,$6$$5$ maili kusini magharibi, na$3$ maili mashariki. Jinsi mbali yeye kutembea? Ikiwa yeye alitembea moja kwa moja nyumbani, angeweza kutembea kwa mbali?

65) Mtu anaanza kutembea kutoka nyumbani na anatembea$3$ maili$20^{\circ}$ kaskazini mwa magharibi, halafu$5$ maili upande wa$10^{\circ}$ magharibi wa kusini, halafu$4$ maili$15^{\circ}$ kaskazini mwa mashariki. Ikiwa alitembea moja kwa moja nyumbani, angekuwa na umbali gani wa kutembea, na katika mwelekeo gani?

Jibu

Umbali:$2.868$, Mwelekeo:$86.474^{\circ}$ Kaskazini ya Magharibi, au$3.526^{\circ}$ Magharibi ya Kaskazini

66) Mwanamke anaanza kutembea kutoka nyumbani na kutembea$6$ maili$40^{\circ}$ kaskazini mwa mashariki, halafu$2$ maili upande wa$15^{\circ}$ mashariki mwa kusini, halafu$5$ maili$30^{\circ}$ kusini mwa magharibi. Ikiwa yeye alitembea moja kwa moja nyumbani, angeweza kutembea mbali, na kwa upande gani?

67) Ndege inaelekea kaskazini kwa kasi ya hewa ya$600$ km/hr, lakini kuna upepo unaopiga kutoka kusini magharibi saa$80$ km/hr. Ndege ngapi bila shaka itaishia kuruka, na kasi ya ndege inahusiana na ardhi?

Jibu

$4.924^{\circ}$, 659 km/h

68) Ndege inaelekea kaskazini kwa kasi ya hewa ya$500$ km/hr, lakini kuna upepo unaopiga kutoka kaskazini magharibi saa$50$ km/hr. Ndege ngapi bila shaka itaishia kuruka, na kasi ya ndege inahusiana na ardhi?

69) Ndege inahitaji kichwa kutokana kaskazini, lakini kuna upepo unaopiga kutoka kusini magharibi saa$60$ km/hr. Ndege inaruka kwa kasi ya$550$ km/hr. Ili kuishia kuruka kaskazini, ngapi digrii magharibi mwa kaskazini itakuwa majaribio haja ya kuruka ndege?

Jibu

$4.424^{\circ}$

70) Ndege inahitaji kichwa kutokana kaskazini, lakini kuna upepo unaopiga kutoka kaskazini magharibi saa$80$ km/hr. Ndege inaruka kwa kasi ya$500$ km/hr. Ili kuishia kuruka kaskazini, ngapi digrii magharibi mwa kaskazini itakuwa majaribio haja ya kuruka ndege?

71) Kama sehemu ya mchezo wa video, hatua$(5,7)$ ni kuzungushwa kinyume chake kuhusu asili kupitia angle ya\(35^{\circ}\). Kupata kuratibu mpya ya hatua hii.

Jibu

$(0.081,8.602)$

72) Kama sehemu ya mchezo video, uhakika$(7,3)$ ni kuzungushwa kinyume chake kuhusu asili kwa njia ya pembe ya$40^{\circ}$. Pata kuratibu mpya za hatua hii.

73) Watoto wawili wanatupa mpira na kurudi moja kwa moja kwenye kiti cha nyuma cha gari. mpira ni kuwa kutupwa$10$ mph jamaa na gari, na gari ni kusafiri$25$ mph barabarani. Ikiwa mtoto mmoja hawezi kukamata mpira, na hutoka nje ya dirisha, ni mwelekeo gani mpira unaruka (kupuuza upinzani wa upepo)?

Jibu

$21.801^{\circ}$, kuhusiana na mwelekeo wa mbele wa gari

74) Watoto wawili wanatupa mpira na kurudi moja kwa moja kwenye kiti cha nyuma cha gari. mpira ni kuwa kutupwa$8$ mph jamaa na gari, na gari ni kusafiri$45$ mph barabarani. Ikiwa mtoto mmoja hawezi kukamata mpira, na hutoka nje ya dirisha, ni mwelekeo gani mpira unaruka (kupuuza upinzani wa upepo)?

75) Kitu cha$50$ pound kinakaa kwenye barabara inayoelekezwa$19^{\circ}$. Pata ukubwa wa vipengele vya nguvu vinavyolingana na na perpendicular kwa (kawaida) barabara hadi kumi ya karibu ya pound.

Jibu

sambamba:$16.28$, perpendicular:$47.28$ paundi

76) Tuseme mwili una nguvu ya$10$ paundi inayofanya juu yake kwa haki,$25$ paundi zinazofanya juu yake juu, na$5$ paundi zinazofanya$45^{\circ}$ kutoka usawa. Nguvu gani moja ni nguvu inayosababisha mwili?

77) Tuseme mwili una nguvu ya$10$ paundi inayofanya juu yake kwa haki,$25$ paundi zinazofanya juu yake ─$135^{\circ}$ kutoka usawa, na$5$ paundi zinazofanya juu yake iliyoongozwa$150^{\circ}$ kutoka usawa. Nguvu gani moja ni nguvu inayosababisha mwili?

Jibu

$19.35$paundi,$231.54^{\circ}$ kutoka usawa

78) Hali ya usawa ni wakati jumla ya nguvu zinazofanya mwili ni vector sifuri. Tuseme mwili una nguvu ya$2$ paundi inayofanya juu yake kwa haki,$5$ paundi zinazofanya juu yake juu, na$3$ paundi zinafanya$45^{\circ}$ kutoka usawa. Ni nguvu gani inayohitajika ili kuzalisha hali ya usawa kwenye mwili?

79) Tuseme mwili una nguvu ya$3$ paundi inayofanya juu yake kwa upande wa kushoto,$4$ paundi zinazofanya juu yake juu, na$2$ paundi zinazofanya\(30^{\circ}\) kutoka usawa. Ni nguvu gani inayohitajika ili kuzalisha hali ya usawa kwenye mwili? Chora vector.

Jibu

$5.1583$paundi,$75.8^{\circ}$ kutoka usawa

Wachangiaji na Majina

• Template:OpenStaxPreCalc