8.7: Ulinganifu wa parametric - Grafu
- Page ID
- 181015
- Graph ndege curves ilivyoelezwa na equations parametric na pointi njama.
- Grafu milinganyo ya parametric.
Ni chini ya inning tisa, na mitumbwi miwili na watu wawili juu ya msingi. Timu ya nyumbani inapoteza kwa kukimbia mbili. Batter swings na hits baseball kwa\(140\) miguu kwa pili na kwa pembe ya takriban\(45°\) kwa usawa. Je! Mpira utasafiri mbali gani? Je, ni wazi uzio kwa ajili ya mchezo kushinda nyumbani kukimbia? Matokeo yanaweza kutegemea sehemu juu ya mambo mengine (kwa mfano, upepo), lakini wanahisabati wanaweza kuiga njia ya projectile na kutabiri takriban umbali gani utakavyosafiri kwa kutumia milinganyo ya parametric. Katika sehemu hii, tutaweza kujadili milinganyo parametric na baadhi ya maombi ya kawaida, kama vile matatizo projectile mwendo.

Kielelezo\(\PageIndex{1}\): Ulinganifu wa parametric unaweza kuiga njia ya projectile. (mikopo: Paul Kreher, Flickr)
Graphing Ulinganifu wa Parametric na Pointi za kupanga
Badala ya calculator ya graphing au programu ya graphing ya kompyuta, pointi za kupanga mipango ya kuwakilisha grafu ya equation ni njia ya kawaida. Muda mrefu kama sisi ni makini katika kuhesabu maadili, njama ya uhakika inategemea sana.
- Jenga meza na nguzo tatu:\(t\),\(x(t)\), na\(y(t)\).
- Tathmini\(x\) na\(y\) kwa maadili ya tt juu ya muda ambao kazi zinafafanuliwa.
- Panda jozi zinazosababisha\((x,y)\).
Mchoro grafu ya equations parametric\(x(t)=t^2+1\),\( y(t)=2+t\).
Suluhisho
Kujenga meza ya maadili kwa\(t\),\(x(t)\), na\(y(t)\), kama katika Jedwali\(\PageIndex{1}\), na njama pointi katika ndege.
| \(t\) | \(x(t)=t^2+1\) | \(y(t)=2+t\) |
|---|---|---|
| \(−5\) | \(26\) | \(−3\) |
| \(−4\) | \(17\) | \(−2\) |
| \(−3\) | \(10\) | \(−1\) |
| \(−2\) | \(5\) | \(0\) |
| \(−1\) | \(2\) | \(1\) |
| \(0\) | \(1\) | \(2\) |
| \(1\) | \(2\) | \(3\) |
| \(2\) | \(5\) | \(4\) |
| \(3\) | \(10\) | \(5\) |
| \(4\) | \(17\) | \(6\) |
| \(5\) | \(26\) | \(7\) |
Grafu ni parabola na vertex kwa uhakika\((1,2)\), kufungua kwa haki. Angalia Kielelezo\(\PageIndex{2}\).
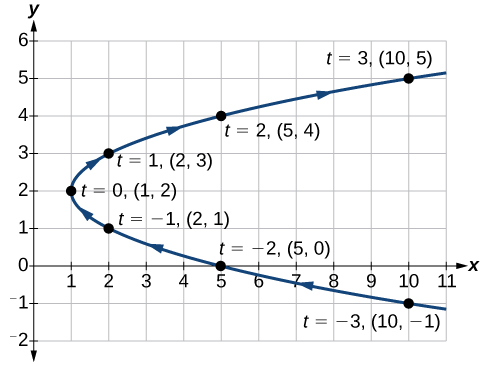
Kielelezo\(\PageIndex{2}\)
Uchambuzi
Kama maadili ya\(t\) maendeleo katika mwelekeo mzuri kutoka\(0\) kwa\(5\), pointi zilizopangwa zinafuatilia nusu ya juu ya parabola. Kama maadili ya laini kuwa hasi, wao hufuatilia nusu ya chini ya parabola. Hakuna vikwazo kwenye kikoa. Mishale zinaonyesha mwelekeo kulingana na kuongezeka kwa maadili ya\(t\). Grafu haiwakilishi kazi, kwani itashindwa mtihani wa mstari wa wima. Grafu hutolewa katika sehemu mbili: maadili mazuri\(t\), na maadili hasi kwa\(t\).
Mchoro grafu ya equations parametric\(x=\sqrt{t}\),\( y=2t+3\),\(0≤t≤3\).
- Jibu
-
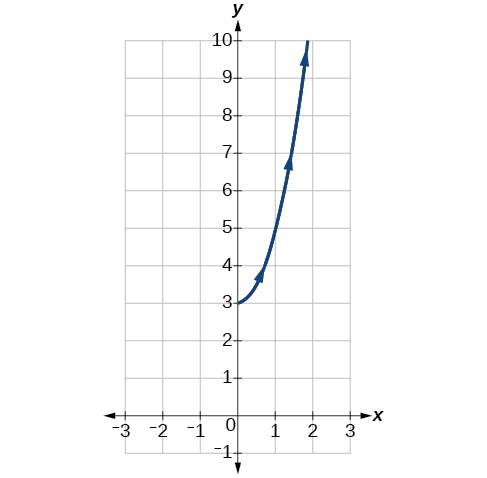
Kielelezo\(\PageIndex{3}\)
Kujenga meza ya maadili kwa equations parametric iliyotolewa na mchoro grafu:
\(x=2 \cos t\)
\(y=4 \sin t\)
Suluhisho
Kujenga meza kama ile katika Jedwali\(\PageIndex{2}\) kwa kutumia angle kipimo katika radians kama pembejeo kwa\(t\), na kutathmini\(x\) na\(y\). Kwa kutumia pembe na inayojulikana sine na cosine maadili kwa\(t\) hufanya mahesabu rahisi.
| \(t\) | \(x=2 \cos t\) | \(y=4 \sin t\) |
|---|---|---|
| \(0\) | \(x=2 \cos(0)=2\) | \(y=4 \sin(0)=0\) |
| \(\dfrac{\pi}{6}\) | \(x=2 \cos(\dfrac{\pi}{6})=\sqrt{3}\) | \(y=4 \sin(\dfrac{π}{6})=2\) |
| \(\dfrac{\pi}{3}\) | \(x=2 \cos(\dfrac{\pi}{3})=1\) | \(y=4 \sin(\dfrac{\pi}{3})=2\sqrt{3}\) |
| \(\dfrac{\pi}{2}\) | \(x=2 \cos(\dfrac{\pi}{2})=0\) | \(y=4 \sin(\dfrac{\pi}{2})=4\) |
| \(\dfrac{2\pi}{3}\) | \(x=2 \cos(\dfrac{2\pi}{3})=−1\) | \(y=4 \sin(\dfrac{2\pi}{3})=2\sqrt{3}\) |
| \(\dfrac{5\pi}{6}\) | \(x=2 \cos(\dfrac{5\pi}{6})=−\sqrt{3}\) | \(y=4 \sin(\dfrac{5\pi}{6})=2\) |
| \(\pi\) | \(x=2 \cos(\pi)=−2\) | \(y=4 \sin(\pi)=0\) |
| \(\dfrac{7\pi}{6}\) | \(x=2 \cos(\dfrac{7\pi}{6})=−\sqrt{3}\) | \(y=4 \sin(\dfrac{7\pi}{6})=−2\) |
| \(\dfrac{4\pi}{3}\) | \(x=2 \cos(\dfrac{4\pi}{3})=−1\) | \(y=4 \sin(\dfrac{4\pi}{3})=−2\sqrt{3}\) |
| \(\dfrac{3\pi}{2}\) | \(x=2 \cos(\dfrac{3\pi}{2})=0\) | \(y=4 \sin(\dfrac{3\pi}{2})=−4\) |
| \(\dfrac{5\pi}{3}\) | \(x=2 \cos(\dfrac{5\pi}{3})=1\) | \(y=4 \sin(\dfrac{5\pi}{3})=−2\sqrt{3}\) |
| \(\dfrac{11\pi}{6}\) | \(x=2 \cos(\dfrac{11\pi}{6})=\sqrt{3}\) | \(y=4 \sin(\dfrac{11\pi}{6})=−2\) |
| \(2\pi\) | \(x=2 \cos(2\pi)=2\) | \(y=4 \sin(2\pi)=0\) |
Kielelezo\(\PageIndex{4}\) kinaonyesha grafu.
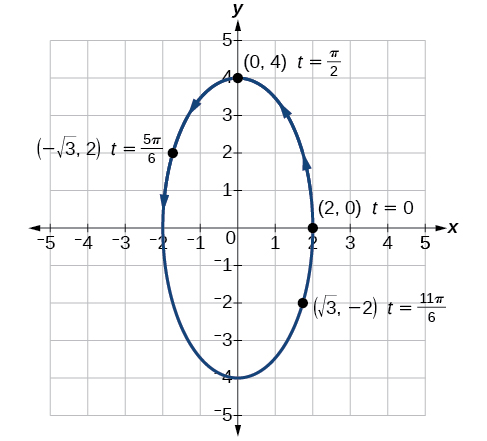
Kielelezo\(\PageIndex{4}\)
Kwa ulinganifu ulioonyeshwa katika maadili ya\(x\) na\(y\), tunaona kwamba equations parametric inawakilisha ellipse. duaradufu ni ramani katika mwelekeo kinyume chake kama inavyoonekana na mishale kuonyesha\(t\) maadili kuongezeka.
Uchambuzi
Tumeona kwamba equations parametric inaweza graphed na pointi njama. Hata hivyo, calculator ya graphing itaokoa muda na kufunua nuances katika grafu ambayo inaweza kuwa mbaya sana kugundua kutumia mahesabu ya mkono tu. Hakikisha kubadilisha mode kwenye calculator kwa parametric (PAR). Ili kuthibitisha,\(Y=\) dirisha linapaswa kuonyesha
\[\begin{align*} X_{1T} &= \\ Y_{1T} &= \end{align*}\]
badala ya\(Y_1=\).
Grafu milinganyo ya parametric:\(x=5 \cos t\),\(y=3 \sin t\).
- Jibu
-
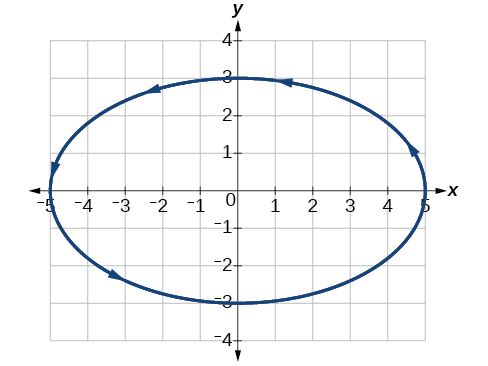
Kielelezo\(\PageIndex{5}\)
Grafu milinganyo ya parametric\(x=5 \cos t\) na\(y=2 \sin t\). Kwanza, jenga grafu kwa kutumia pointi za data zinazozalishwa kutoka kwa fomu ya parametric. Kisha grafu fomu ya mstatili wa equation. Linganisha grafu mbili.
Suluhisho
Kujenga meza ya maadili kama ile katika Jedwali\(\PageIndex{3}\).
| \(t\) | \(x=5 \cos t\) | \(y=2 \sin t\) |
|---|---|---|
| \(0\) | \(x=5 \cos(0)=5\) | \(y=2 \sin(0)=0\) |
| \(1\) | \(x=5 \cos(1)≈2.7\) | \(y=2 \sin(1)≈1.7\) |
| \(2\) | \(x=5 \cos(2)≈−2.1\) | \(y=2 \sin(2)≈1.8\) |
| \(3\) | \(x=5 \cos(3)≈−4.95\) | \(y=2 \sin(3)≈0.28\) |
| \(4\) | \(x=5 \cos(4)≈−3.3\) | \(y=2 \sin(4)≈−1.5\) |
| \(5\) | \(x=5 \cos(5)≈1.4\) | \(y=2 \sin(5)≈−1.9\) |
| \(−1\) | \(x=5 \cos(−1)≈2.7\) | \(y=2 \sin(−1)≈−1.7\) |
| \(−2\) | \(x=5 \cos(−2)≈−2.1\) | \(y=2 \sin(−2)≈−1.8\) |
| \(−3\) | \(x=5 \cos(−3)≈−4.95\) | \(y=2 \sin(−3)≈−0.28\) |
| \(−4\) | \(x=5 \cos(−4)≈−3.3\) | \(y=2 \sin(−4)≈1.5\) |
| \(−5\) | \(x=5 \cos(−5)≈1.4\) | \(y=2 \sin(−5)≈1.9\) |
Panda\((x,y)\) maadili kutoka meza (Kielelezo\(\PageIndex{6}\)).
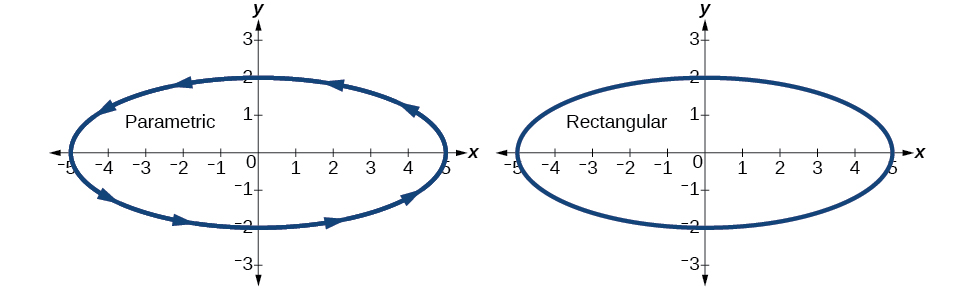
Kielelezo\(\PageIndex{6}\)
Kisha, tafsiri usawa wa parametric kwa fomu ya mstatili. Ili kufanya hivyo, sisi kutatua\(t\) kwa aidha\(x(t)\) au\(y(t)\), na kisha badala ya kujieleza kwa\(t\) katika equation nyingine. Matokeo yake itakuwa kazi\(y(x)\) kama kutatua kwa\(t\) kama kazi ya\(x\), au\(x(y)\) kama kutatua kwa\(t\) kama kazi ya\(y\).
\[\begin{align*} x &= 5 \cos t \\ \dfrac{x}{5} &= \cos t \end{align*}\]
Kutatua kwa\(\cos t\).
\(y=2 \sin t\)
Kutatua kwa\(\sin t\).
\(\dfrac{y}{2}=\sin t\)
Kisha, tumia Theorem ya Pythagorean.
\[\begin{align*} {\cos}^2 t+{\sin}^2 t &=1 \\ {\left(\dfrac{x}{5}\right)}^2+{\left(\dfrac{y}{2}\right)}^2 &= 1 \\ \dfrac{x^2}{25}+\dfrac{y^2}{4} &=1 \end{align*}\]
Uchambuzi
Katika Kielelezo\(\PageIndex{7}\), data kutoka kwa usawa wa parametric na equation ya mstatili hupangwa pamoja. Equations parametric ni njama katika bluu; grafu kwa equation mstatili ni inayotolewa juu ya parametric katika style dashed rangi nyekundu. Kwa wazi, fomu zote mbili zinazalisha grafu sawa.
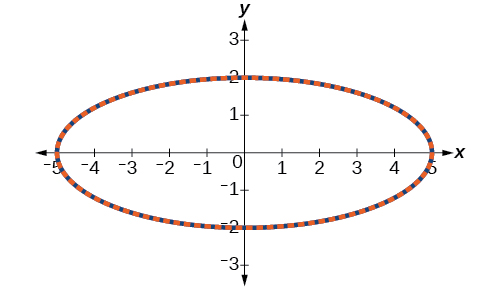
Kielelezo\(\PageIndex{7}\)
Graph equations parametric\(x=t+1\) na\(y=\sqrt{t}\)\(t≥0\),, na sawa mstatili\(y=\sqrt{x−1}\) kwenye mfumo huo kuratibu.
Suluhisho
Kujenga meza ya maadili kwa equations parametric, kama tulivyofanya katika mfano uliopita, na grafu\(y=\sqrt{t}\),\(t≥0\) kwenye gridi hiyo, kama katika Kielelezo\(\PageIndex{8}\).
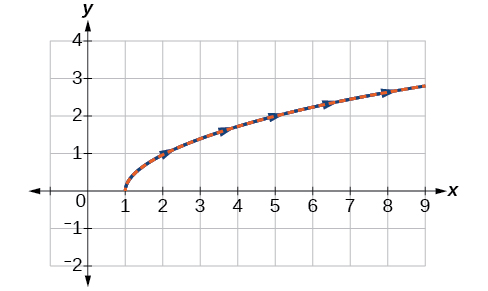
Kielelezo\(\PageIndex{8}\)
Uchambuzi
Pamoja na uwanja juu ya\(t\) vikwazo, sisi tu njama maadili chanya ya\(t\). Data ya parametric imewekwa katika bluu na grafu ya equation ya mstatili imepigwa nyekundu. Mara nyingine tena, tunaona kwamba aina mbili zinaingiliana.
Mchoro grafu ya equations parametric\(x=2 \cos \theta\) na\(y=4 \sin \theta\), pamoja na equation mstatili kwenye gridi hiyo.
- Jibu
-
Grafu ya equations parametric ni nyekundu na grafu ya equation mstatili hutolewa katika dots bluu juu ya equations parametric.
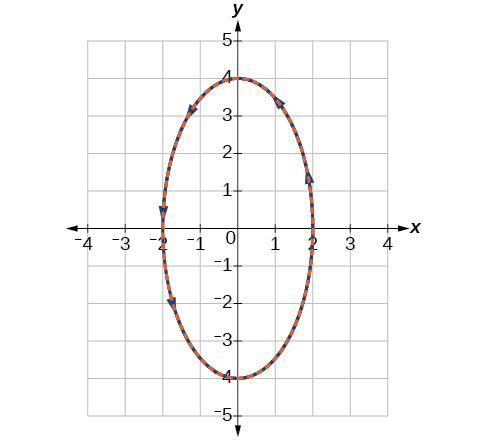
Kielelezo\(\PageIndex{9}\)
Matumizi ya Equations Parametric
Faida nyingi za equations parametric kuwa dhahiri wakati kutumika kutatua matatizo halisi ya dunia. Ingawa milinganyo ya mstatili ndani\(x\) na\(y\) kutoa picha ya jumla ya njia ya kitu, hazifunua nafasi ya kitu kwa wakati fulani. Equations parametric, hata hivyo, kuonyesha jinsi maadili ya\(x\) na\(y\) mabadiliko kulingana na\(t\), kama eneo la kitu kusonga kwa wakati fulani.
Matumizi ya kawaida ya equations parametric ni kutatua matatizo yanayohusisha mwendo wa projectile. Katika aina hii ya mwendo, kitu kinachukuliwa mbele katika mwelekeo wa juu na kutengeneza angle ya\(\theta\) usawa, na kasi ya awali ya\(v_0\), na kwa urefu\(h\) juu ya usawa.
Njia ya kitu kilichotembea kwa mwelekeo wa\(\theta\) usawa, na kasi ya awali\(v_0\), na kwa urefu\(h\) juu ya usawa, hutolewa na
\[\begin{align*} x &= (v_0 \cos \theta)t \\ y &= −\dfrac{1}{2}gt^2+(v_0 \sin \theta)t+h \end{align*}\]
ambapo\(g\) akaunti kwa ajili ya madhara ya mvuto na\(h\) ni urefu wa awali wa kitu. Kulingana na vitengo kushiriki katika tatizo, kutumia\(g=32 ft / s^2\) au\(g=9.8 m / s^2\). equation kwa\(x\) anatoa umbali usawa, na equation kwa\(y\) anatoa umbali wima.
- Umbali wa usawa hutolewa na\(x=(v_0 \cos \theta)t\). Badilisha kasi ya awali ya kitu kwa\(v_0\).
- Maneno\(\cos \theta\) yanaonyesha angle ambayo kitu kinaendeshwa. Mbadala kwamba angle katika digrii kwa\(\cos \theta\).
- Umbali wa wima hutolewa na formula\(y=−\dfrac{1}{2}gt^2+(v_0 \sin \theta)t+h\). Neno\(−\dfrac{1}{2}gt^2\) linawakilisha athari za mvuto. Kulingana na vitengo kushiriki, kutumia\(g=32 ft/s^2\) au\(g=9.8 m/s^2\). Tena, badala ya kasi ya awali kwa\(v_0\), na urefu ambao kitu kilichotolewa\(h\).
- Endelea kwa kuhesabu kila neno ili kutatua\(t\).
Tatua tatizo lililowasilishwa mwanzoni mwa sehemu hii. Je, kugonga hit mchezo kushinda nyumbani kukimbia? Kudhani kwamba mpira ni hit na kasi ya awali ya\(140\) miguu kwa sekunde\(45°\) kwa pembeni ya kwa usawa, kufanya mawasiliano\(3\) miguu juu ya ardhi.
- Find equations parametric kwa mfano njia ya baseball.
- Wapi mpira baada ya\(2\) sekunde?
- Je! Mpira ni muda gani?
- Je, ni kukimbia nyumbani?
Suluhisho
1. Tumia formula ili kuanzisha equations. Msimamo wa usawa unapatikana kwa kutumia equation ya parametric kwa\(x\). Hivyo,
\[\begin{align*} x &= (v_0 \cos \theta)t \\ x &= (140 \cos(45°))t \end{align*}\]
Msimamo wa wima unapatikana kwa kutumia equation ya parametric kwa\(y\). Hivyo,
\[\begin{align*} y &=−16t^2+(v_0 \sin \theta)t+h \\ y &= −16t^2+(140 \sin(45°))t+3 \end{align*}\]
2. \(2\)Kuingiza katika equations kupata nafasi usawa na wima ya mpira.
\[\begin{align*} x &= (140 \cos(45°))(2) \\ x &= 198\space feet \\ y &= −16{(2)}^2+(140 \sin(45°))(2)+3 \\ y &=137\space feet \end{align*}\]
Baada ya\(2\) sekunde, mpira ni\(198\) miguu mbali na sanduku la batter na\(137\) miguu juu ya ardhi.
3. Kuhesabu muda gani mpira ni katika hewa, tuna kujua wakati itakuwa hit chini, au wakati\(y=0\). Hivyo,
\[\begin{align*} y &= −16t^2+(140\sin(45∘))t+3 \\ y &=0 \text{ Set }y(t)=0 \text{ and solve the quadratic.} \\ t &= 6.2173 \end{align*}\]
Wakati\(t=6.2173\) sekunde, mpira umepiga ardhi. (Equation quadratic inaweza kutatuliwa kwa njia mbalimbali, lakini tatizo hili lilitatuliwa kwa kutumia programu ya hesabu ya kompyuta.)
4. Hatuwezi kuthibitisha kwamba hit ilikuwa kukimbia nyumbani bila kuzingatia ukubwa wa outfield, ambayo inatofautiana kutoka shamba hadi shamba. Hata hivyo, kwa ajili ya unyenyekevu, hebu tufikiri kwamba ukuta wa nje ni\(400\) miguu kutoka sahani ya nyumbani katika sehemu ya kina kabisa ya hifadhi. Hebu pia tufikiri kwamba ukuta ni\(10\) miguu ya juu. Ili kuamua kama mpira unafuta ukuta, tunahitaji kuhesabu jinsi mpira ulivyo juu wakati\(x = 400\) miguu. Hivyo sisi kuweka\(x = 400\), kutatua kwa\(t\), na pembejeo tt katika\(y\).
\[\begin{align*} x &= (140 \cos(45°))t \\ 400 &= (140 \cos(45°))t \\ t &= 4.04 \\ y &= −16{(4.04)}^2+(140 \sin(45°))(4.04)+3 \\ y &= 141.8 \end{align*}\]
Mpira ni\(141.8\) miguu katika hewa wakati inapoongezeka nje ya ballpark. Ilikuwa kweli kukimbia nyumbani. Angalia Kielelezo\(\PageIndex{10}\).

Kielelezo\(\PageIndex{10}\)
Fikia rasilimali zifuatazo za mtandaoni kwa maelekezo ya ziada na mazoezi na grafu za usawa wa parametric.
Dhana muhimu
- Wakati kuna variable ya tatu, parameter ya tatu ambayo\(x\) na\(y\) inategemea, equations parametric inaweza kutumika.
- Ili grafu ya usawa wa parametric kwa pointi za kupanga, fanya meza na nguzo tatu zilizoandikwa\(t\)\(x(t)\),, na\(y(t)\). Chagua maadili fort t ili kuongeza. Plot nguzo mbili za mwisho kwa\(x\) na\(y\). Angalia Mfano\(\PageIndex{1}\) na Mfano\(\PageIndex{2}\).
- Wakati wa kuchora safu ya parametric kwa pointi za kupanga njama, angalia maadili ya t yanayohusiana na kuonyesha mishale kwenye grafu inayoonyesha mwelekeo wa curve. Angalia Mfano\(\PageIndex{3}\) na Mfano\(\PageIndex{4}\).
- Ulinganisho wa parametric kuruhusu mwelekeo au mwelekeo wa curve kuonyeshwa kwenye grafu. Equations ambayo si kazi inaweza graphed na kutumika katika maombi mengi kuwashirikisha mwendo. Angalia Mfano\(\PageIndex{5}\).
- Mwendo wa projectile unategemea equations mbili parametric:\(x=(v_0 \cos \theta)t\) na\(y=−16t^2+(v_0 \sin \theta)t+h\). Kasi ya awali inaashiria kama\(v_0\). \(\theta\)inawakilisha angle ya awali ya kitu wakati wa kutupwa, na\(h\) inawakilisha urefu ambao kitu kinaendeshwa.


