8.6: Ulinganifu wa parametric

Malengo ya kujifunza

• Parameterize Curve.
• Ondoa parameter.
• Kupata equation mstatili kwa Curve defined parametrically.
• Kupata milinganyo parametric kwa curves inavyoelezwa na milinganyo mstatili

Fikiria njia ya mwezi ifuatavyo kama inavyozunguka sayari, ambayo wakati huo huo huzunguka jua, kama inavyoonekana kwenye Mchoro\(\PageIndex{1}\). Wakati wowote, mwezi iko kwenye doa fulani kuhusiana na sayari. Lakini tunaandikaje na kutatua equation kwa nafasi ya mwezi wakati umbali kutoka sayari, kasi ya obiti ya mwezi karibu na sayari, na kasi ya mzunguko kuzunguka jua yote haijulikani? Tunaweza kutatua tu kwa variable moja kwa wakati mmoja.

Kielelezo\(\PageIndex{1}\)

Katika sehemu hii, tutazingatia seti ya equations iliyotolewa\(x(t)\) na\(y(t)\) wapi\(t\) tofauti ya muda. Tunaweza kutumia equations hizi parametric katika idadi ya maombi wakati sisi ni kuangalia kwa si tu nafasi fulani lakini pia mwelekeo wa harakati. Kama sisi kuwaeleza nje maadili mfululizo wa\(t\), mwelekeo wa Curve inakuwa wazi. Hii ni moja ya faida za msingi za kutumia equations parametric: tunaweza kufuatilia harakati ya kitu kando ya njia kulingana na wakati. Tunaanza sehemu hii kwa kuangalia vipengele vya msingi vya equations parametric na nini maana ya parameterize curve. Kisha sisi kujifunza jinsi ya kuondoa parameter, kutafsiri equations ya Curve defined parametrically katika equations mstatili, na kupata equations parametric kwa curves defined na equations mstatili.

Parameterizing Curve

Wakati kitu kinachotembea kando ya njia ya curve-au curvilinear-katika mwelekeo fulani na kwa kiasi fulani cha muda, nafasi ya kitu katika ndege hutolewa na\(x\) - kuratibu na\(y\) - kuratibu. Hata hivyo, wote\(x\) na\(y\) kutofautiana baada ya muda na hivyo ni kazi ya muda. Kwa sababu hii, tunaongeza variable nyingine, parameter, ambayo wote wawili\(x\) na\(y\) ni tegemezi kazi. Katika mfano katika kopo ya sehemu, parameter ni wakati,\(t\). \(x\)Msimamo wa mwezi kwa wakati\(t\), unawakilishwa kama kazi\(x(t)\), na\(y\) nafasi ya mwezi kwa wakati\(t\), inawakilishwa kama kazi\(y(t)\). Pamoja,\(x(t)\) na\(y(t)\) huitwa equations parametric, na kuzalisha jozi kuamuru\((x(t), y(t))\). Ulinganifu wa parametric hasa huelezea mwendo na mwelekeo.

Wakati sisi parameterize Curve, sisi ni kutafsiri equation moja katika vigezo mbili\(y\), kama vile\(x\) na, katika jozi sawa ya milinganyo katika vigezo tatu\(x\),\(y\), na\(t\). Moja ya sababu sisi parameterize Curve ni kwa sababu milinganyo parametric mavuno habari zaidi: hasa, mwelekeo wa mwendo wa kitu baada ya muda.

Wakati sisi graph milinganyo parametric, tunaweza kuchunguza tabia ya mtu binafsi ya\(x\) na ya\(y\). Kuna idadi ya maumbo ambayo hayawezi kuwakilishwa katika fomu\(y=f(x)\), maana yake ni kwamba si kazi. Kwa mfano, fikiria grafu ya mduara, iliyotolewa kama\(r^2=x^2+y^2\). Kutatua kwa\(y\) anatoa\(y=\pm \sqrt{r^2−x^2}\), au milinganyo mbili:\(y_1=\sqrt{r^2−x^2}\) na\(y_2=−\sqrt{r^2−x^2}\). Ikiwa sisi grafu\(y_1\) na\(y_2\) pamoja, grafu haitapita mtihani wa mstari wa wima, kama inavyoonekana kwenye Mchoro\(\PageIndex{2}\). Hivyo, equation kwa grafu ya mduara sio kazi.

Kielelezo\(\PageIndex{2}\)

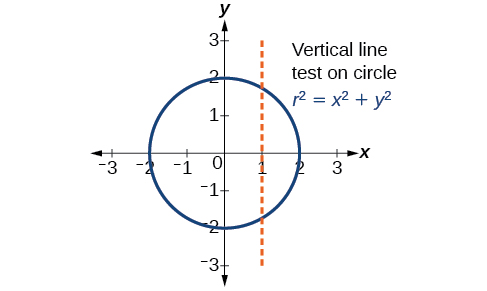
Hata hivyo, kama tulikuwa na grafu kila equation peke yake, kila mmoja bila kupita wima line mtihani na kwa hiyo ingekuwa kuwakilisha kazi. Katika baadhi ya matukio, dhana ya kuvunja equation kwa mduara katika kazi mbili ni sawa na dhana ya kujenga equations parametric, kama sisi kutumia kazi mbili kuzalisha yasiyo ya kazi. Hii itakuwa wazi kama sisi kusonga mbele.

MILINGANYO YA PARAMETRI

Tuseme\(t\) ni idadi ya muda,\(I\). Seti ya jozi zilizoamriwa\((x(t), y(t))\), wapi\(x=f(t)\) na\(y=g(t)\), huunda safu ya ndege kulingana na parameter\(t\). Equations\(x=f(t)\) na\(y=g(t)\) ni equations parametric.

Mfano\(\PageIndex{1}\): Parameterizing a Curve

Parameterize Curve\(y=x^2−1\) kuruhusu\(x(t)=t\). Grafu equations zote mbili.

Suluhisho

Kama\(x(t)=t\), basi kupata\(y(t)\) sisi kuchukua nafasi ya variable\(x\) na kujieleza iliyotolewa katika\(x(t)\). Kwa maneno mengine,\(y(t)=t^2−1\) .Fanya meza ya maadili sawa na Jedwali\(\PageIndex{1}\), na mchoro grafu.

Jedwali\(\PageIndex{1}\)

\(t\)	\(x(t)\)	\(y(t)\)
\ (t\) ">\(−4\)	\ (x (t)\) ">\(−4\)	\ (y (t)\) ">\(y(−4)={(−4)}^2−1=15\)
\ (t\) ">\(−3\)	\ (x (t)\) ">\(−3\)	\ (y (t)\) ">\(y(−3)={(−3)}^2−1=8\)
\ (t\) ">\(−2\)	\ (x (t)\) ">\(−2\)	\ (y (t)\) ">\(y(−2)={(−2)}^2−1=3\)
\ (t\) ">\(−1\)	\ (x (t)\) ">\(−1\)	\ (y (t)\) ">\(y(−1)={(−1)}^2−1=0\)
\ (t\) ">\(0\)	\ (x (t)\) ">\(0\)	\ (y (t)\) ">\(y(0)={(0)}^2−1=−1\)
\ (t\) ">\(1\)	\ (x (t)\) ">\(1\)	\ (y (t)\) ">\(y(1)={(1)}^2−1=0\)
\ (t\) ">\(2\)	\ (x (t)\) ">\(2\)	\ (y (t)\) ">\(y(2)={(2)}^2−1=3\)
\ (t\) ">\(3\)	\ (x (t)\) ">\(3\)	\ (y (t)\) ">\(y(3)={(3)}^2−1=8\)
\ (t\) ">\(4\)	\ (x (t)\) ">\(4\)	\ (y (t)\) ">\(y(4)={(4)}^2−1=15\)

Angalia grafu katika Kielelezo\(\PageIndex{3}\). Inaweza kuwa na manufaa kwa kutumia TRACE kipengele cha calculator graphing kuona jinsi pointi ni yanayotokana kama\(t\) ongezeko.

Kielelezo\(\PageIndex{3}\): (a) Parametric\(y(t)=t^2−1\) (b) Rectangular\(y=x^2−1\)

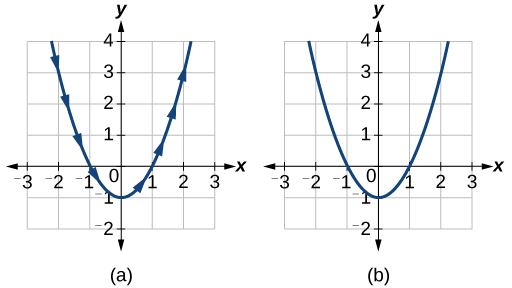
Uchambuzi

Mishale inaonyesha mwelekeo ambao curve huzalishwa. Taarifa Curve ni sawa na Curve ya\(y=x^2−1\).

Zoezi\(\PageIndex{1}\)

Kujenga meza ya maadili na njama equations parametric:\(x(t)=t−3\),\(y(t)=2t+4\);\(−1≤t≤2\).

Jibu

\(t\)	\(x(t)\)	\(y(t)\)
\ (t\) ">\(-1\)	\ (x (t)\) ">\(-4\)	\ (y (t)\) ">\(2\)
\ (t\) ">\(0\)	\ (x (t)\) ">\(-3\)	\ (y (t)\) ">\(4\)
\ (t\) ">\(1\)	\ (x (t)\) ">\(-2\)	\ (y (t)\) ">\(6\)
\ (t\) ">\(2\)	\ (x (t)\) ">\(-1\)	\ (y (t)\) ">\(8\)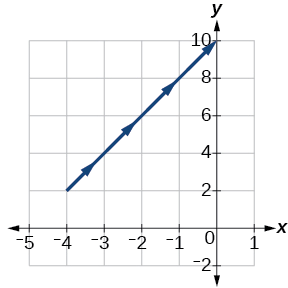

Kielelezo\(\PageIndex{4}\)

Mfano\(\PageIndex{2}\): Finding a Pair of Parametric Equations

Kupata jozi ya equations parametric kwamba mifano grafu ya\(y=1−x^2\), kwa kutumia parameter\(x(t)=t\). Panda pointi fulani na mchoro grafu.

Suluhisho

Ikiwa\(x(t)=t\) na sisi badala\(t\) ya\(x\) ndani ya\(y\) equation, basi\(y(t)=1−t^2\). Jozi yetu ya equations parametric ni

\[\begin{align*} x(t) &=t \\ y(t) &= 1−t^2 \end{align*}\]

Kwa grafu equations, kwanza sisi kujenga meza ya maadili kama kwamba katika Jedwali\(\PageIndex{2}\). Tunaweza kuchagua maadili karibu\(t=0\), kutoka\(t=−3\) kwa\(t=3\). Maadili katika\(x(t)\) safu yatakuwa sawa na yale yaliyo kwenye\(t\) safu kwa sababu\(x(t)=t\). Tumia maadili kwa safu\(y(t)\).

Jedwali\(\PageIndex{2}\)

\ (t)	\(x(t)=t\)	\(y(t)=1−t^2\)
\ (t) ">\ (-3\)	\ (x (t) =t\) ">\(−3\)	\ (y (t) =1,1t^2\) ">\(y(−3)=1−{(−3)}^2=−8\)
\ (t) ">\ (-2\)	\ (x (t) =t\) ">\(−2\)	\ (y (t) =1,1t^2\) ">\(y(−2)=1−{(−2)}^2=−3\)
\ (t) ">\ (-1\)	\ (x (t) =t\) ">\(−1\)	\ (y (t) =1,1t^2\) ">\(y(−1)=1−{(−1)}^2=0\)
\ (t) ">\ (0\)	\ (x (t) =t\) ">\(0\)	\ (y (t) =1,1t^2\) ">\(y(0)=1−0=1\)
\ (t) ">\ (1\)	\ (x (t) =t\) ">\(1\)	\ (y (t) =1,1t^2\) ">\(y(1)=1−{(1)}^2=0\)
\ (t) ">\ (2\)	\ (x (t) =t\) ">\(2\)	\ (y (t) =1,1t^2\) ">\(y(2)=1−{(2)}^2=−3\)
\ (t) ">\ (3\)	\ (x (t) =t\) ">\(3\)	\ (y (t) =1,1t^2\) ">\(y(3)=1−{(3)}^2=−8\)

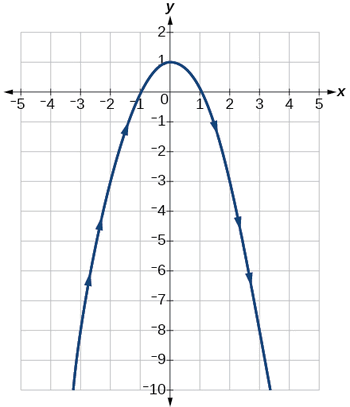
Grafu ya\(y=1−t^2\) ni parabola inakabiliwa chini, kama inavyoonekana katika Kielelezo\(\PageIndex{5}\). Sisi mapped Curve juu ya muda\([−3, 3]\), umeonyesha kama mstari imara na mishale kuonyesha mwelekeo wa Curve kulingana na\(t\). Mwelekeo inahusu njia kufuatiliwa pamoja Curve katika suala la kuongeza maadili ya\(t\). Kama parabola hii inalinganishwa na heshima na mstari\(x=0\), maadili ya\(x\) yanajitokeza kwenye y -axis.

Kielelezo\(\PageIndex{5}\)

Zoezi\(\PageIndex{2}\)

Parameterize Curve iliyotolewa na\(x=y^3−2y\).

Jibu

\(x(t)=t^3−2t\)

\(y(t)=t\)

Mfano\(\PageIndex{3}\): Finding Parametric Equations That Model Given Criteria

Kitu kinasafiri kwa kiwango cha kutosha kwenye njia moja kwa moja\((−5, 3)\)\((3, −1)\) kwenda kwenye ndege moja kwa sekunde nne. Kuratibu hupimwa kwa mita. Pata usawa wa parametric kwa nafasi ya kitu.

Suluhisho

Ulinganisho wa parametric ni maneno rahisi ya mstari, lakini tunahitaji kuona tatizo hili kwa mtindo wa hatua kwa hatua. Thamani ya x ya kitu huanza saa\(−5\) mita na inakwenda\(3\) mita. Hii ina maana umbali\(x\) umebadilika kwa\(8\) mita katika\(4\) sekunde, ambayo ni kiwango cha\(\dfrac{8\space m}{4\space s}\), au\(2\space m/s\). Tunaweza kuandika x -kuratibu kama kazi linear kwa heshima na wakati kama\(x(t)=2t−5\). Katika template linear kazi\(y=mx+b\),\(2t=mx\) na\(−5=b\).

Vile vile,\(y\) thamani ya kitu huanza\(3\) na inakwenda\(−1\), ambayo ni mabadiliko katika umbali\(y\) wa\(−4\) mita kwa\(4\) sekunde, ambayo ni kiwango cha\(\dfrac{−4\space m}{4\space s}\), au\(−1\space m/s\). Tunaweza pia kuandika y -kuratibu kama kazi linear\(y(t)=−t+3\). Pamoja, haya ni equations parametric kwa nafasi ya kitu, wapi\(x\) na\(y\) ni walionyesha katika mita na\(t\) inawakilisha wakati:

\[\begin{align*} x(t) &= 2t−5 \\ y(t) &= −t+3 \end{align*}\]

Kutumia equations hizi, tunaweza kujenga meza ya maadili kwa\(t\),\(x\), na\(y\) (tazama Jedwali\(\PageIndex{3}\)). Katika mfano huu, sisi mdogo maadili ya\(t\) idadi zisizo hasi. Kwa ujumla, thamani yoyote ya\(t\) inaweza kutumika.

Jedwali\(\PageIndex{3}\)

\(t\)	\(x(t)=2t−5\)	\(y(t)=−t+3\)
\ (t\) ">\(0\)	\ (x (t) =2t-5\) ">\(x=2(0)−5=−5\)	\ (y (t) =-t+3\) ">\(y=−(0)+3=3\)
\ (t\) ">\(1\)	\ (x (t) =2t-5\) ">\(x=2(1)−5=−3\)	\ (y (t) =-t+3\) ">\(y=−(1)+3=2\)
\ (t\) ">\(2\)	\ (x (t) =2t-5\) ">\(x=2(2)−5=−1\)	\ (y (t) =-t+3\) ">\(y=−(2)+3=1\)
\ (t\) ">\(3\)	\ (x (t) =2t-5\) ">\(x=2(3)−5=1\)	\ (y (t) =-t+3\) ">\(y=−(3)+3=0\)
\ (t\) ">\(4\)	\ (x (t) =2t-5\) ">\(x=2(4)−5=3\)	\ (y (t) =-t+3\) ">\(y=−(4)+3=−1\)

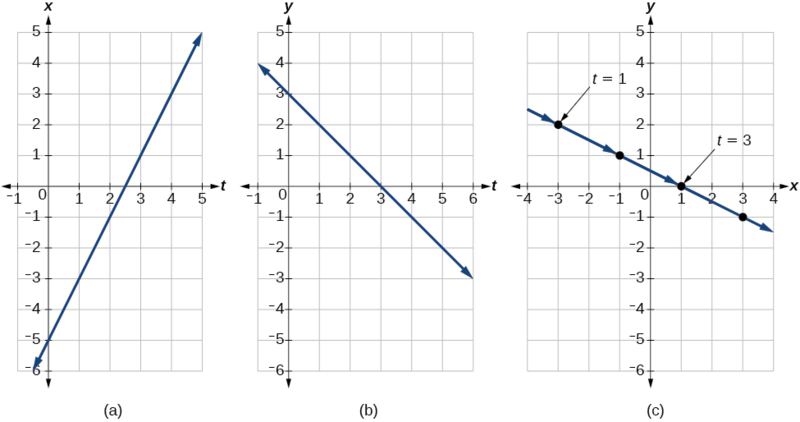
Kutoka meza hii, tunaweza kuunda grafu tatu, kama inavyoonekana kwenye Kielelezo\(\PageIndex{6}\).

Kielelezo\(\PageIndex{6}\): (a) Grafu ya\(x\) vs.\(t\), inayowakilisha nafasi ya usawa kwa muda. (b) Grafu ya\(y\) vs.\(t\), inayowakilisha nafasi ya wima kwa muda. (c) Grafu ya\(y\) vs.\(x\), inayowakilisha nafasi ya kitu katika ndege kwa wakati\(t\).

Uchambuzi

Tena, tunaona kwamba, katika Kielelezo\(\PageIndex{6}\) (c), wakati parameter inawakilisha wakati, tunaweza kuonyesha harakati ya kitu kando ya njia na mishale.

Kuondoa Parameter

Mara nyingi, tunaweza kuwa na jozi ya milinganyo parametric lakini kupata kwamba ni rahisi kuteka Curve kama equation inahusisha vigezo mbili tu, kama vile\(x\) na\(y\). Kuondoa parameter ni njia ambayo inaweza kufanya graphing baadhi curves rahisi. Hata hivyo, ikiwa tuna wasiwasi na ramani ya equation kulingana na wakati, basi itakuwa muhimu kuonyesha mwelekeo wa curve pia. Kuna mbinu mbalimbali za kuondoa parameter\(t\) kutoka kwa seti ya equations parametric; si kila njia inafanya kazi kwa kila aina ya equation. Hapa tutaangalia njia za aina za kawaida za equations.

Kuondoa Parameter kutoka kwa Ulinganisho wa Polynomial, Kielelezo, na Logarithmic

Kwa milinganyo ya polynomial, kielelezo, au logarithmic iliyoelezwa kama milinganyo miwili ya parametric, tunachagua equation ambayo ni rahisi zaidi manipulated na kutatua kwa\(t\). Sisi badala ya kujieleza kusababisha kwa\(t\) katika equation pili. Hii inatoa equation moja katika\(x\) na\(y\).

Mfano\(\PageIndex{4}\): Eliminating the Parameter in Polynomials

Kutokana\(x(t)=t^2+1\) na\(y(t)=2+t\), kuondoa parameter, na kuandika equations parametric kama equation Cartesian.

Suluhisho

Tutaanza na equation kwa\(y\) sababu equation linear ni rahisi kutatua kwa\(t\).

\[\begin{align*} y &= 2+t \\ y−2 &=t \end{align*}\]

Next, mbadala\(y−2\) kwa ajili ya\(t\) katika\(x(t)\).

\[\begin{align*} x &= t^2+1 \\ x &= {(y−2)}^2+1 \;\;\;\;\;\;\;\; \text{Substitute the expression for }t \text{ into }x. \\ x &= y^2−4y+4+1 \\ x &= y^2−4y+5 \\ x &= y^2−4y+5 \end{align*}\]

Fomu ya Cartesian ni\(x=y^2−4y+5\).

Uchambuzi

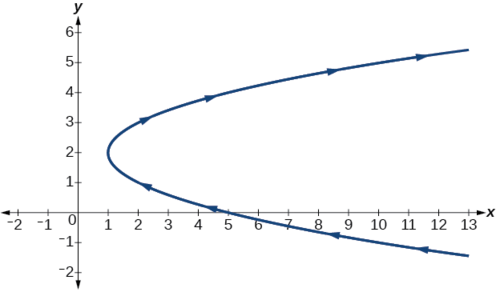
Hii ni equation kwa parabola ambayo, kwa maneno ya mstatili,\(x\) inategemea\(y\). Kutoka vertex ya Curve saa\((1,2)\), graph sweeps nje ya haki. Angalia Kielelezo\(\PageIndex{7}\). Katika sehemu hii, tunazingatia seti ya equations iliyotolewa\(x(t)\) na kazi na\(y(t)\), wapi\(t\) tofauti tofauti ya muda. Taarifa, wote\(x\) na\(y\) ni kazi ya muda; hivyo\(y\) kwa ujumla si kazi ya\(x\).

Kielelezo\(\PageIndex{7}\)

Zoezi\(\PageIndex{3}\)

Kutokana milinganyo chini, kuondoa parameter na kuandika kama equation mstatili kwa\(y\) kama kazi ya\(x\).

\[\begin{align*} x(t) &= 2t^2+6 \\ y(t) &= 5−t \end{align*}\]

Jibu

\(y=5−\sqrt{\frac{1}{2}x−3}\)

Mfano\(\PageIndex{5}\): Eliminating the Parameter in Exponential Equations

Ondoa parameter na uandike kama equation ya Cartesian:\(x(t)=e^{−t}\) na\(y(t)=3e^t\),\(t>0\).

Suluhisho

Kutenga\(e^t\).

\[\begin{align*} x &=e^{−t} \\ e^t &= \dfrac{1}{x} \end{align*}\]

Badilisha maneno katika\(y(t)\).

\[\begin{align*} y &= 3e^t \\ y &= 3 \left(\dfrac{1}{x}\right) \\ y &= \dfrac{3}{x} \end{align*}\]

Fomu ya Cartesian ni\(y=\dfrac{3}{x}\).

Uchambuzi

Grafu ya equation ya parametric inavyoonekana kwenye Kielelezo\(\PageIndex{8a}\). Uwanja huo umezuiwa\(t>0\). Equation Cartesian,\(y=\dfrac{3}{x}\) inavyoonekana katika Kielelezo\(\PageIndex{8b}\) na ina kizuizi kimoja tu kwenye uwanja,\(x≠0\).

0, na grafu ya equation hiyo ya parametric katika kuratibu polar na uwanja tu vikwazo kwa x si sawa na 0. Toleo la kuratibu la Cartesian lina tafakari ya ziada ya kazi katika asili katika Q 3 (awali ilikuwa tu katika Q 1)." src="https://math.libretexts.org/@api/dek...3487926125.png">

Kielelezo\(\PageIndex{8}\)

Mfano\(\PageIndex{6}\): Eliminating the Parameter in Logarithmic Equations

Ondoa parameter na uandike kama equation ya Cartesian:\(x(t)=\sqrt{t}+2\) na\(y(t)=\log(t)\).

Suluhisho

Kutatua equation kwanza kwa\(t\).

\[\begin{align*} x &= \sqrt{t}+2 \\ x−2 &= \sqrt{t} \\ {(x−2)}^2 &= t \;\;\;\;\;\;\;\; \text{Square both sides.} \end{align*}\]

Kisha, badala ya kujieleza kwa\(t\) katika\(y\) equation.

\[\begin{align*} y &= \log(t) \\ y &= \log{(x−2)}^2 \end{align*}\]

Fomu ya Cartesian ni\(y=\log{(x−2)}^2\).

Uchambuzi

Ili kuhakikisha kwamba equations parametric ni sawa na equation Cartesian, angalia domains. equations parametric kuzuia uwanja juu\(x=\sqrt{t}+2\) ya\(t>0\); sisi kuzuia uwanja juu\(x\) ya\(x>2\). Domain kwa equation parametric\(y=\log(t)\) ni vikwazo kwa\(t>0\); sisi kikomo kikoa juu\(y=\log{(x−2)}^2\) ya\(x>2\).

Zoezi\(\PageIndex{4}\)

Ondoa parameter na uandike kama equation ya mstatili.

\[\begin{align*} x(t) &= t^2 \\ y(t) &= \ln t\text{, } t>0 \end{align*}\]

Jibu

\(y=\ln \sqrt{x}\)

Kuondoa Parameter kutoka kwa Ulinganisho wa Trigonometric

Kuondoa parameter kutoka equations trigonometric ni badala ya moja kwa moja. Tunaweza kutumia chache cha utambulisho wa trigonometric na Theorem ya Pythagorean.

Kwanza, tunatumia utambulisho:

\[\begin{align*} x(t) &= a \cos t \\ y(t) &= b \sin t \end{align*}\]

Kutatua kwa\(\cos t\) na\(\sin t\), tuna

\[\begin{align*} \dfrac{x}{a} &= \cos t \\ \dfrac{y}{b} &= \sin t \end{align*}\]

Kisha, tumia Theorem ya Pythagorean:

\({\cos}^2 t+{\sin}^2 t=1\)

Kubadilisha anatoa

\({\cos}^2 t+{\sin}^2 t={\left(\dfrac{x}{a}\right)}^2+{\left(\dfrac{y}{b}\right)}^2=1\)

Mfano\(\PageIndex{7}\): Eliminating the Parameter from a Pair of Trigonometric Parametric Equations

Ondoa parameter kutoka kwa jozi iliyotolewa ya equations trigonometric ambapo\(0≤t≤2\pi\) na mchoro grafu.

\[\begin{align*} x(t) &=4 \cos t \\ y(t) &=3 \sin t \end{align*}\]

Suluhisho

Kutatua kwa\(\cos t\) na\(\sin t\), tuna

\[\begin{align*} x &=4 \cos t \\ \dfrac{x}{4} &= \cos t \\ y &=3 \sin t \\ \dfrac{y}{3} &= \sin t \end{align*}\]

Kisha, tumia utambulisho wa Pythagorean na ufanye mbadala.

\[\begin{align*} {\cos}^2 t+{\sin}^2 t &= 1 \\ {\left(\dfrac{x}{4}\right)}^2+{\left(\dfrac{y}{3}\right)}^2 &=1 \\ \dfrac{x^2}{16}+\dfrac{y^2}{9} &=1 \end{align*}\]

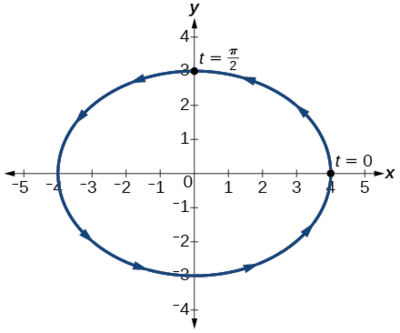
Grafu ya equation inavyoonekana kwenye Kielelezo\(\PageIndex{9}\).

Kielelezo\(\PageIndex{9}\)

Uchambuzi

Kutumia equations jumla kwa ajili ya sehemu conic (kuletwa katika Analytic Jiometri, tunaweza kutambua\(\dfrac{x^2}{16}+\dfrac{y^2}{9}=1\) kama duaradufu unaozingatia katika\((0,0)\). Kumbuka kwamba wakati\(t=0\) kuratibu ni\((4,0)\), na wakati\(t=\dfrac{\pi}{2}\) kuratibu ni\((0,3)\). Hii inaonyesha mwelekeo wa Curve na kuongeza maadili ya\(t\).

Zoezi\(\PageIndex{5}\)

Ondoa parameter kutoka kwa jozi iliyotolewa ya equations parametric na kuandika kama equation Cartesian:\(x(t)=2 \cos t\) na\(y(t)=3 \sin t\).

Jibu

\(\dfrac{x^2}{4}+\dfrac{y^2}{9}=1\)

Kupata Equations Cartesian kutoka Curves Defined Parametrically

Wakati sisi ni kupewa seti ya equations parametric na haja ya kupata sawa Cartesian equation, sisi ni kimsingi “kuondoa parameter.” Hata hivyo, kuna mbinu mbalimbali tunaweza kutumia kuandika upya seti ya milinganyo parametric kama equation Cartesian. Njia rahisi ni kuweka equation moja sawa na parameter, kama vile\(x(t)=t\). Katika kesi hii,\(y(t)\) inaweza kuwa maneno yoyote. Kwa mfano, fikiria jozi zifuatazo za equations.

\[\begin{align*} x(t) &=t \\ y(t) &= t^2−3 \end{align*}\]

Kuandika upya seti hii ya equations parametric ni suala la kubadili\(x\)\(t\). Hivyo, equation Cartesian ni\(y=x^2−3\).

Mfano\(\PageIndex{8}\): Finding a Cartesian Equation Using Alternate Methods

Tumia mbinu mbili tofauti ili kupata equation ya Cartesian sawa na seti iliyotolewa ya milinganyo ya parametric.

\[\begin{align*} x(t) &= 3t−2 \\ y(t) &= t+1 \end{align*}\]

Suluhisho

Njia ya 1. Kwanza, hebu kutatua\(x\) equation kwa\(t\). Kisha tunaweza kubadilisha matokeo katika\(y\) equation.

\[\begin{align*} x &= 3t−2 \\ x+2 &= 3t \\ \dfrac{x+2}{3} &= t \end{align*}\]

Sasa badala ya kujieleza kwa\(t\) ndani ya\(y\) equation.

\[\begin{align*} y &= t+1 \\ y & = \left(\dfrac{x+2}{3}\right)+1 \\ y &= \dfrac{x}{3}+\dfrac{2}{3}+1 \\ y &= \dfrac{1}{3}x+\dfrac{5}{3} \end{align*}\]

Njia ya 2. Kutatua\(y\) equation kwa\(t\) na mbadala maneno haya katika\(x\) equation.

\[\begin{align*} y &= t+1 \\ y−1 &=t \end{align*}\]

Fanya badala na kisha utatue\(y\).

\[\begin{align*} x &= 3(y−1)−2 \\ x &= 3y−3−2 \\ x &= 3y−5 \\ x+5 &= 3y \\ \dfrac{x+5}{3} &= y \\ y &= \dfrac{1}{3}x+\dfrac{5}{3} \end{align*}\]

Zoezi\(\PageIndex{6}\)

Andika equations parametric iliyotolewa kama equation Cartesian:\(x(t)=t^3\) na\(y(t)=t^6\).

Jibu

\(y=x^2\)

Kutafuta equations Parametric kwa Curves Inafafanuliwa na Equations

Ingawa tumeonyesha tu kwamba kuna njia moja tu ya kutafsiri seti ya milinganyo ya parametric kama equation mstatili, kuna njia nyingi za kutafsiri equation mstatili kama seti ya milinganyo parametric. Mkakati wowote tunaweza kutumia ili kupata milinganyo parametric ni halali kama inazalisha equivalency. Kwa maneno mengine, kama sisi kuchagua kujieleza kuwakilisha\(x\), na kisha badala yake katika\(y\) equation, na inazalisha grafu sawa juu ya uwanja huo kama equation mstatili, basi seti ya milinganyo parametric ni halali. Ikiwa uwanja unazuia katika seti ya usawa wa parametric, na kazi hairuhusu maadili sawa\(x\) kama uwanja wa equation mstatili, basi grafu zitakuwa tofauti.

Mfano\(\PageIndex{9}\): Finding a Set of Parametric Equations for Curves Defined by Rectangular Equations

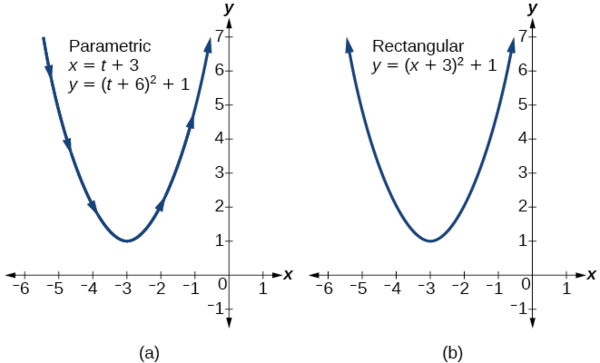
Kupata seti ya sawa parametric milinganyo kwa\(y={(x+3)}^2+1\).

Suluhisho

Uchaguzi dhahiri itakuwa kuruhusu\(x(t)=t\). Kisha\(y(t)={(t+3)}^2+1\). Lakini hebu jaribu kitu cha kuvutia zaidi. Nini kama sisi basi\(x=t+3\)? Kisha tuna

\[\begin{align*} y &= {(x+3)}^2+1 \\ y &= {((t+3)+3)}^2+1 \\ y &= {(t+6)}^2+1 \end{align*}\]

Seti ya equations parametric ni

\[\begin{align*} x(t) &= t+3 \\ y(t) &= {(t+6)}^2+1 \end{align*}\]

Angalia Kielelezo\(\PageIndex{10}\).

Kielelezo\(\PageIndex{10}\)

Media

Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na usawa wa parametric.

• Utangulizi wa Equations Parametric
• Kubadilisha Ulinganisho wa Parametric kwa Fomu ya

Dhana muhimu

• Parameterizing Curve inahusisha kutafsiri equation mstatili katika vigezo mbili\(y\),\(x\) na, katika equations mbili katika vigezo tatu\(x\),\(y\),, na\(t\). Mara nyingi, habari zaidi hupatikana kutoka kwa seti ya equations parametric. Angalia Mfano\(\PageIndex{1}\), Mfano\(\PageIndex{2}\), na Mfano\(\PageIndex{3}\).
• Wakati mwingine equations ni rahisi kwa grafu wakati imeandikwa katika fomu ya mstatili. Kwa kuondoa\(t\), equation katika\(x\) na\(y\) ni matokeo.
• Kuondoa\(t\), kutatua moja ya equations kwa\(t\), na badala ya kujieleza katika equation ya pili. Angalia Mfano\(\PageIndex{4}\), Mfano\(\PageIndex{5}\), Mfano\(\PageIndex{6}\), na Mfano\(\PageIndex{7}\).
• Kupata equation mstatili kwa Curve defined parametrically kimsingi ni sawa na kuondoa parameter. Kutatua kwa\(t\) katika moja ya equations, na badala ya kujieleza katika equation pili. Angalia Mfano\(\PageIndex{8}\).
• Kuna idadi isiyo na kipimo ya njia za kuchagua seti ya milinganyo ya parametric kwa safu inayofafanuliwa kama equation ya mstatili.
• Pata maelezo kwa\(x\) vile uwanja wa seti ya equations parametric bado sawa na equation ya awali ya mstatili. Angalia Mfano\(\PageIndex{9}\).

Wachangiaji

• Template:ContribOpenStaxPreCalc