6.3: Kazi za Trigonometric Inverse

Malengo ya kujifunza

• Kuelewa na kutumia sine inverse, cosine, na kazi tangent.
• Pata thamani halisi ya maneno yanayohusisha sine inverse, cosine, na kazi za tangent.
• Tumia calculator kutathmini kazi inverse trigonometric.
• Pata maadili halisi ya kazi za composite na kazi za trigonometric inverse.

Kwa pembetatu yoyote ya kulia, kutokana na angle nyingine na urefu wa upande mmoja, tunaweza kujua nini pembe nyingine na pande ni. Lakini vipi ikiwa tunapewa pande mbili tu za pembetatu sahihi? Tunahitaji utaratibu unaotuongoza kutoka uwiano wa pande hadi pembe. Hii ndio ambapo dhana ya inverse kwa kazi ya trigonometric inakuja. Katika sehemu hii, tutachunguza kazi za trigonometric inverse.

Kuelewa na Kutumia Sine Inverse, Cosine, na Kazi za Tangent

Ili kutumia kazi za trigonometric inverse, tunahitaji kuelewa kwamba kazi ya trigonometric inverse “hupunguza” kile kazi ya awali ya trigonometric “inafanya,” kama ilivyo kwa kazi nyingine yoyote na inverse yake. Kwa maneno mengine, uwanja wa kazi inverse ni aina mbalimbali ya kazi ya awali, na kinyume chake, kama ilivyofupishwa katika Kielelezo$\PageIndex{1}$.

Kielelezo$\PageIndex{1}$

Kwa mfano, kama$f(x)=\sin\space x$, basi tunataka kuandika$f^{−1}(x)={\sin}^{−1}x$. Kuwa na ufahamu kwamba${\sin}^{−1}x$ haina maana$\dfrac{1}{\sin\space x}$. Mifano zifuatazo zinaonyesha kazi za trigonometric inverse:

• Tangu$\sin\left(\dfrac{\pi}{6}\right)=\dfrac{1}{2}$, basi$\dfrac{\pi}{6}={\sin}^{−1}\left(\dfrac{1}{2}\right)$.
• Tangu$\cos(\pi)=−1$, basi$\pi={\cos}^{−1}(−1)$.
• Tangu$\tan\left (\dfrac{\pi}{4}\right )=1$, basi$\dfrac{\pi}{4}={\tan}^{−1}(1)$.

Katika sehemu zilizopita, tulipima kazi za trigonometric kwa pembe mbalimbali, lakini wakati mwingine tunahitaji kujua ni angle gani itazalisha sine maalum, cosine, au thamani ya tangent. Kwa hili, tunahitaji kazi za inverse. Kumbuka kwamba, kwa kazi moja kwa moja, ikiwa$f(a)=b$, basi kazi ya inverse ingeweza kukidhi$f^{−1}(b)=a$.

Kumbuka kwamba kazi za sine, cosine, na tangent sio kazi moja kwa moja. Grafu ya kila kazi ingeweza kushindwa mtihani wa mstari usio na usawa. Kwa kweli, hakuna kazi ya mara kwa mara inaweza kuwa moja kwa moja kwa sababu kila pato katika aina yake inalingana na pembejeo angalau moja katika kila kipindi, na kuna idadi isiyo na kipimo cha vipindi. Kama ilivyo na kazi nyingine ambazo si moja kwa moja, tutahitaji kuzuia uwanja wa kila kazi ili kutoa kazi mpya ambayo ni moja kwa moja. Sisi kuchagua uwanja kwa kila kazi ambayo ni pamoja na idadi 0. Kielelezo$\PageIndex{2}$ inaonyesha grafu ya kazi sine mdogo$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$ na grafu ya kazi cosine mdogo kwa$[ 0,\pi ]$.

Kielelezo$\PageIndex{2}$: (a) Sine kazi kwenye uwanja vikwazo ya$\left[ −\dfrac{\pi}{2}, \dfrac{\pi}{2} \right]$; (b) Cosine kazi kwenye uwanja vikwazo wa$[ 0,\pi ]$

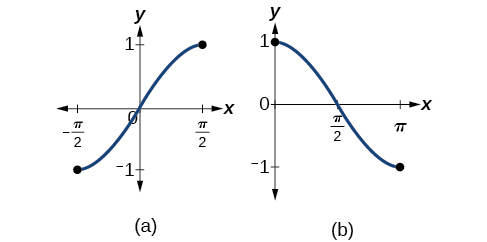
Kielelezo$\PageIndex{3}$ inaonyesha grafu ya kazi tangent mdogo kwa$\left(−\dfrac{\pi}{2},\dfrac{\pi}{2}\right)$.

Kielelezo$\PageIndex{3}$: Tangent kazi kwenye uwanja vikwazo wa$\left (−\dfrac{\pi}{2},\dfrac{\pi}{2}\right )$

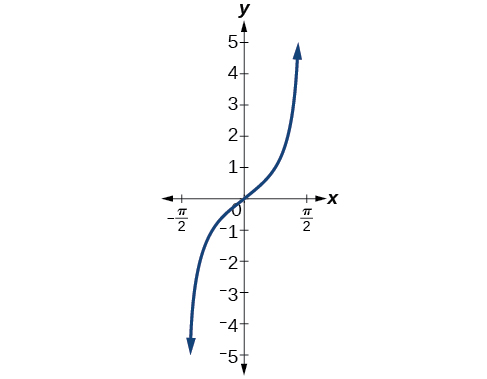
Uchaguzi huu wa kawaida kwa uwanja uliozuiliwa ni kiasi kikubwa, lakini wana sifa muhimu, zinazosaidia. Kila kikoa kinajumuisha asili na maadili mazuri, na muhimu zaidi, kila matokeo katika kazi moja kwa moja ambayo haiwezi kushindwa. Uchaguzi wa kawaida kwa kikoa kilichozuiliwa cha kazi ya tangent pia ina mali muhimu ambayo inatokana na asymptote moja ya wima hadi ijayo badala ya kugawanywa katika sehemu mbili na asymptote.

Katika nyanja hizi vikwazo, tunaweza kufafanua kazi inverse trigonometric.

• Inverse sine kazi$y={\sin}^{−1}x$ ina maana$x=\sin\space y$. Kazi ya sine inverse wakati mwingine huitwa kazi ya arcsine, na imeelezwa$\arcsin\space x$.

  $y={\sin}^{−1}x$ina uwanja$[−1,1]$ na upeo$\left[−\frac{\pi}{2},\frac{\pi}{2}\right]$

• Kazi ya cosine inverse$y={\cos}^{−1}x$ ina maana$x=\cos\space y$. Kazi ya cosine inverse wakati mwingine huitwa kazi ya arccosine, na imetajwa$\arccos\space x$.

  $y={\cos}^{−1}x$ina uwanja$[−1,1]$ na upeo$[0,π]$

• Kazi ya tangent inverse$y={\tan}^{−1}x$ ina maana$x=\tan\space y$. Kazi ya tangent inverse wakati mwingine huitwa kazi ya arctangent, na imetajwa$\arctan\space x$.

  $y={\tan}^{−1}x$ina uwanja$(−\infty,\infty)$ na upeo$\left(−\frac{\pi}{2},\frac{\pi}{2}\right)$

Grafu ya kazi inverse ni inavyoonekana katika Takwimu$\PageIndex{4}$ -$\PageIndex{6}$. Angalia kwamba pato la kila moja ya kazi hizi za inverse ni namba, angle katika kipimo cha radian. Tunaona kwamba${\sin}^{−1}x$ ina kikoa$[ −1,1 ]$ na upeo$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$,${\cos}^{−1}x$ ina uwanja$[ −1,1 ]$ na upeo$[0,\pi]$, na${\tan}^{−1}x$ ina uwanja wa namba zote halisi na upeo$\left(−\dfrac{\pi}{2},\dfrac{\pi}{2}\right)$. Ili kupata uwanja na aina mbalimbali za kazi za trigonometric inverse, kubadili kikoa na aina mbalimbali za kazi za awali. Kila grafu ya kazi ya trigonometric inverse ni mfano wa grafu ya kazi ya awali kuhusu mstari$y=x$.

Kielelezo$\PageIndex{4}$: kazi ya mgongo na kazi ya mgongo (au arcsine)

Kielelezo$\PageIndex{5}$: Kazi ya cosine na cosine inverse (au arccosine) kazi

Kielelezo$\PageIndex{6}$: kazi tangent na inverse tangent (au arctangent) kazi

MAHUSIANO KWA SINE INVERSE, COSINE, NA KAZI TANGENT

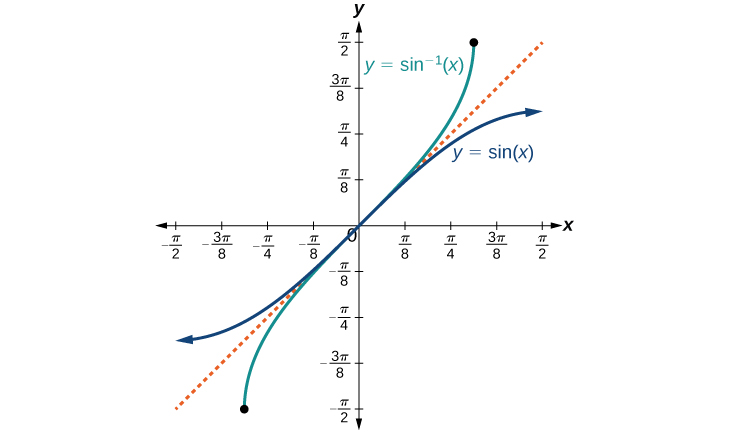
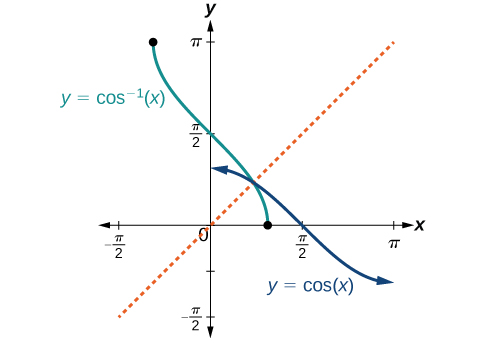
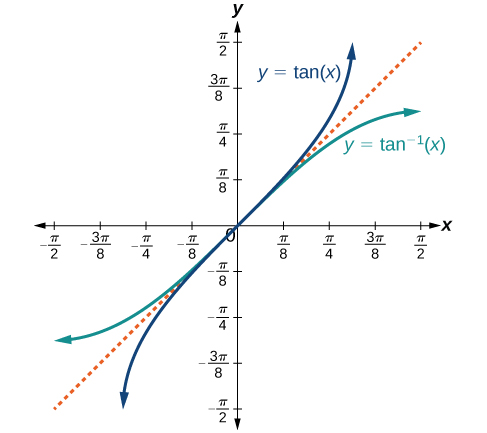
Kwa pembe katika kipindi$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$, ikiwa$\sin y=x$, basi${\sin}^{−1}x=y$.

Kwa pembe katika kipindi$[ 0,\pi ]$, ikiwa$\cos y=x$, basi${\cos}^{−1}x=y$.

Kwa pembe katika kipindi$\left(−\dfrac{\pi}{2},\dfrac{\pi}{2}\right )$, ikiwa$\tan y=x$, basi${\tan}^{−1}x=y$.

Mfano$\PageIndex{1}$: Writing a Relation for an Inverse Function

kutokana$\sin\left(\dfrac{5\pi}{12}\right)≈0.96593$, kuandika uhusiano kuwashirikisha sine inverse.

Suluhisho

Tumia uhusiano kwa sine inverse. Ikiwa$\sin y=x$, basi${\sin}^{−1}x=y$.

Katika tatizo hili,$x=0.96593$, na$y=\dfrac{5\pi}{12}$.

${\sin}^{−1}(0.96593)≈\dfrac{5\pi}{12}$

Zoezi$\PageIndex{1}$

Kutokana$\cos(0.5)≈0.8776$, kuandika uhusiano unaohusisha cosine inverse.

Jibu

$\arccos(0.8776)≈0.5$

Kutafuta Thamani halisi ya Maneno Kuhusisha Sine Inverse, Cosine, na Kazi za Tangent

Sasa kwa kuwa tunaweza kutambua kazi za kinyume, tutajifunza kutathmini. Kwa maadili mengi katika nyanja zao, tunapaswa kutathmini kazi za trigonometric inverse kwa kutumia calculator, kutafsiri kutoka meza, au kutumia mbinu nyingine za namba. Kama tulivyofanya na kazi za awali za trigonometric, tunaweza kutoa maadili halisi kwa kazi za inverse tunapotumia pembe maalum, hasa$\dfrac{\pi}{6}$ (30°),$\dfrac{\pi}{4}$ (45°), na$\dfrac{\pi}{3}$ (60°), na tafakari zao katika quadrants nyingine.

Kutokana na thamani ya pembejeo “maalum”, tathmini kazi ya trigonometric inverse.

1. Pata angle$x$ ambayo kazi ya awali ya trigonometric ina pato sawa na pembejeo iliyotolewa kwa kazi ya trigonometric inverse.
2. Ikiwa$x$ sio katika upeo ulioelezwa wa inverse, pata pembe nyingine$y$ iliyo katika upeo ulioelezwa na ina sine sawa, cosine, au tangent kama$x$, kulingana na ambayo inalingana na kazi iliyopewa inverse.

Mfano$\PageIndex{2}$: Evaluating Inverse Trigonometric Functions for Special Input Values

Tathmini kila moja ya yafuatayo.

1. ${\sin}^{−1}\left(\dfrac{1}{2}\right)$
2. ${\sin}^{−1}\left(−\dfrac{\sqrt{2}}{2}\right)$
3. ${\cos}^{−1}\left(−\dfrac{\sqrt{3}}{2}\right)$
4. ${\tan}^{−1}(1)$

Suluhisho

1. Kutathmini${\sin}^{−1}\left(\dfrac{1}{2}\right)$ ni sawa na kuamua angle ambayo ingekuwa na thamani sine ya$\dfrac{1}{2}$. Kwa maneno mengine, ni angle gani$x$ ingeweza kukidhi$\sin(x)=\dfrac{1}{2}$? Kuna maadili mengi ambayo yanaweza kukidhi uhusiano huu, kama vile$\dfrac{\pi}{6}$ na$\dfrac{5\pi}{6}$, lakini tunajua tunahitaji angle katika kipindi$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$, hivyo jibu litakuwa${\sin}^{−1}\left (\dfrac{1}{2}\right)=\dfrac{\pi}{6}$. Kumbuka kwamba inverse ni kazi, hivyo kwa kila pembejeo, tutapata pato moja hasa.
2. Kutathmini${\sin}^{−1}\left(−\dfrac{\sqrt{2}}{2}\right)$, tunajua kwamba$\dfrac{5\pi}{4}$ na$\dfrac{7\pi}{4}$ wote wana thamani sine ya$-\dfrac{\sqrt{2}}{2}$, lakini wala ni katika muda$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$. Kwa hiyo, tunahitaji angle hasi coterminal na$\dfrac{7\pi}{4}$:${\sin}^{−1}\left(−\dfrac{\sqrt{2}}{2}\right)=−\dfrac{\pi}{4}$.
3. Kutathmini${\cos}^{−1}\left(−\dfrac{\sqrt{3}}{2}\right)$, tunatafuta angle katika kipindi$[ 0,\pi ]$ na thamani ya cosine ya$-\dfrac{\sqrt{3}}{2}$. Pembe ambayo inatimiza hii ni${\cos}^{−1}\left(−\dfrac{\sqrt{3}}{2}\right)=\dfrac{5\pi}{6}$.
4. Kutathmini${\tan}^{−1}(1)$, tunatafuta angle katika kipindi$\left(−\dfrac{\pi}{2},\dfrac{\pi}{2}\right)$ na thamani ya tangent ya$1$. Pembe sahihi ni${\tan}^{−1}(1)=\dfrac{\pi}{4}$.

Zoezi$\PageIndex{2}$

Tathmini kila moja ya yafuatayo.

1. ${\sin}^{−1}(−1)$
2. ${\tan}^{−1}(−1)$
3. ${\cos}^{−1}(−1)$
4. ${\cos}^{−1}\left(\dfrac{1}{2}\right)$

Jibu

$-\dfrac{\pi}{2}$

Jibu b

$-\dfrac{\pi}{4}$

Jibu c

$\pi$

Jibu d

$\dfrac{\pi}{3}$

Kutumia Calculator Kutathmini Inverse Trigonometric Kazi

Ili kutathmini kazi za trigonometric ambazo hazihusishi pembe maalum zilizojadiliwa hapo awali, tutahitaji kutumia calculator au aina nyingine ya teknolojia. Wengi calculators kisayansi na maombi calculator-emulating na funguo maalum au vifungo kwa inverse sine, cosine, na kazi tangent. Hizi zinaweza kuitwa, kwa mfano, SIN-1, ARCSIN, au ASIN.

Katika sura iliyotangulia, tulifanya kazi na trigonometry kwenye pembetatu sahihi ili kutatua kwa pande za pembetatu iliyotolewa upande mmoja na angle ya ziada. Kutumia kazi za trigonometric inverse, tunaweza kutatua kwa pembe za pembetatu ya kulia iliyotolewa pande mbili, na tunaweza kutumia calculator kupata maadili kwa maeneo kadhaa ya decimal.

Katika mifano hii na mazoezi, majibu yatafsiriwa kama pembe na tutatumia$\theta$ kama tofauti ya kujitegemea. Thamani iliyoonyeshwa kwenye calculator inaweza kuwa katika digrii au radians, hivyo hakikisha kuweka mode inayofaa kwa programu.

Mfano$\PageIndex{3}$: Evaluating the Inverse Sine on a Calculator

Tathmini${\sin}^{−1}(0.97)$ kutumia calculator.

Suluhisho

Kwa sababu pato la kazi inverse ni angle, calculator itatupa thamani ya shahada ikiwa katika hali ya shahada na thamani ya radian ikiwa katika hali ya radian. Wahesabu pia hutumia vikwazo vya kikoa sawa kwenye pembe kama tunavyotumia.

Katika hali ya radian,${\sin}^{−1}(0.97)≈1.3252$. Katika hali ya shahada,${\sin}^{−1}(0.97)≈75.93°$. Kumbuka kuwa katika calculus na zaidi tutatumia radians karibu na matukio yote.

Zoezi$\PageIndex{3}$

Tathmini${\cos}^{−1}(−0.4)$ kutumia calculator.

Jibu

$1.9823$au$113.578^{\circ}$

Kutokana na pande mbili za pembetatu sahihi kama ile iliyoonyeshwa kwenye Mchoro 8.4.7, pata angle.

Kielelezo$\PageIndex{7}$

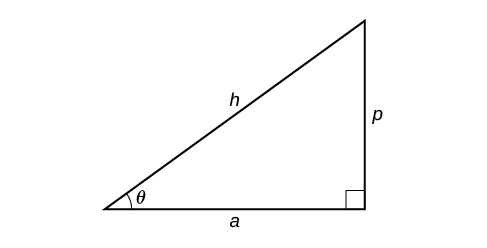
1. Ikiwa upande mmoja uliopewa ni hypotenuse ya urefu$h$ na upande wa urefu$a$ karibu na angle inayotakiwa hutolewa, tumia equation$\theta={\cos}^{−1}\left(\dfrac{a}{h}\right)$.
2. Ikiwa upande mmoja uliopewa ni hypotenuse ya urefu$h$ na upande wa urefu$p$ kinyume na angle inayotakiwa hutolewa, tumia equation$\theta={\sin}^{−1}\left(\dfrac{p}{h}\right)$.
3. Ikiwa miguu miwili (pande karibu na pembe ya kulia) hutolewa, kisha utumie equation$\theta={\tan}^{−1}\left(\dfrac{p}{a}\right)$.

Mfano$\PageIndex{4}$: Applying the Inverse Cosine to a Right Triangle

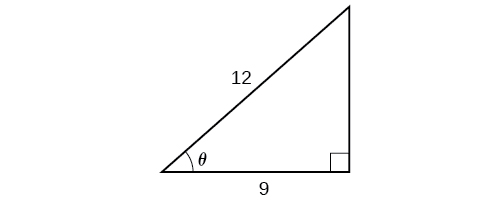
Tatua pembetatu katika Kielelezo$\PageIndex{8}$ kwa angle$\theta$.

Kielelezo$\PageIndex{8}$

Suluhisho

Kwa sababu tunajua hypotenuse na upande karibu na angle, ni busara kwetu kutumia kazi ya cosine.

$$\begin{align*} \cos \theta&= \dfrac{9}{12}\\ \theta&= {\cos}^{-1}\left(\dfrac{9}{12}\right)\qquad \text{Apply definition of the inverse}\\ \theta&\approx 0.7227\qquad \text{or about } 41.4096^{\circ} \text{ Evaluate} \end{align*}$$

Zoezi$\PageIndex{4}$

Tatua pembetatu katika Kielelezo$\PageIndex{9}$ kwa angle$\theta$.

Kielelezo$\PageIndex{9}$

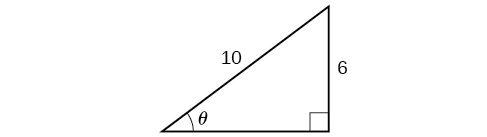
Jibu

${\sin}^{−1}(0.6)=36.87°=0.6435$radiani

Kutafuta Maadili halisi ya Kazi za Composite na Kazi za Trigonometric Inverse

Kuna nyakati ambapo tunahitaji kutunga kazi ya trigonometric na kazi ya trigonometric inverse. Katika kesi hizi, tunaweza kupata maadili halisi kwa maneno yaliyotokana bila kutumia calculator. Hata wakati pembejeo kwa kazi Composite ni variable au kujieleza, tunaweza mara nyingi kupata kujieleza kwa pato. Ili kusaidia kutatua kesi tofauti, basi$f(x)$ na$g(x)$ uwe na kazi mbili tofauti za trigonometric za kuweka {$\sin(x)$,$\cos(x)$,$\tan(x)$} na basi$f^{-1}(y)$ na$g^{-1}(y)$ uwe inverses yao.

Kutathmini Maandishi ya Fomu$f(f^{-1}(y))$ na$f^{-1}(f(x))$

Kwa kazi yoyote ya trigonometric,$f(f^{-1}(y))=y$ kwa wote$y$ katika uwanja sahihi kwa kazi iliyotolewa. Hii ifuatavyo kutokana na ufafanuzi wa inverse na kutokana na ukweli kwamba mbalimbali ya$f$ ilifafanuliwa kuwa sawa na uwanja wa$f^{−1}$. Hata hivyo, tunapaswa kuwa makini zaidi na maneno ya fomu$f^{-1}(f(x))$.

NYIMBO ZA KAZI YA TRIGONOMETRIC NA INVERSE YAKE

$$\begin{align*} \sin({\sin}^{-1}x)&= x\qquad \text{for } -1\leq x\leq 1\\ \cos({\cos}^{-1}x)&= x\qquad \text{for } -1\leq x\leq 1\\ \tan({\tan}^{-1}x)&= x\qquad \text{for } -\infty<x<\infty\\ {\sin}^{-1}(\sin x)&= x\qquad \text{only for } -\dfrac{\pi}{2}\leq x\leq \dfrac{\pi}{2}\\ {\cos}^{-1}(\cos x)&= x\qquad \text{only for } 0\leq x\leq \pi\\ {\tan}^{-1}(\tan x)& =x\qquad \text{only for } -\dfrac{\pi}{2}< x< \dfrac{\pi}{2} \end{align*}$$

Q & A

Je, ni sahihi kwamba${\sin}^{−1}(\sin x)=x$?

Hapana. Equation hii ni sahihi kama x ni ya kikoa vikwazo$\left[−\dfrac{\pi}{2},\dfrac{\pi}{2}\right]$, lakini sine hufafanuliwa kwa maadili yote ya pembejeo halisi, na kwa$x$ nje ya muda vikwazo, equation si sahihi kwa sababu inverse yake daima anarudi thamani katika$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$. Hali hiyo ni sawa kwa cosine na tangent na inverses yao. Kwa mfano,${\sin}^{−1}\left(\sin\left(\dfrac{3\pi}{4}\right)\right)=\dfrac{\pi}{4}$.

Kutokana na usemi wa fomu$f^{-1}(f(\theta))$ where $f(\theta)=\sin \theta$, $\cos \theta$, or $\tan \theta$, evaluate.

1. Kama$\theta$ ni katika uwanja vikwazo ya$f$, kisha$f^{−1}(f(\theta))=\theta$.
2. Ikiwa sio, basi pata angle$\phi$ ndani ya kikoa kilichozuiliwa mbali na hivyo$f(\phi)=f(\theta)$. Kisha$f^{−1}(f(\theta))=\phi$.

Mfano$\PageIndex{5}$: Using Inverse Trigonometric Functions

Tathmini zifuatazo:

1. ${\sin}^{−1}\left (\sin \left(\dfrac{\pi}{3}\right )\right )$
2. ${\sin}^{−1}\left (\sin \left(\dfrac{2\pi}{3}\right )\right )$
3. ${\cos}^{−1}\left (\cos \left (\dfrac{2\pi}{3}\right )\right )$
4. ${\cos}^{−1}\left (\cos \left (−\dfrac{\pi}{3}\right )\right )$

Suluhisho

1. $\dfrac{\pi}{3}$ni katika$\left[−\dfrac{\pi}{2},\dfrac{\pi}{2}\right]$, hivyo${\sin}^{−1}\left(\sin\left(\dfrac{\pi}{3}\right)\right)=\dfrac{\pi}{3}$.
2. $\dfrac{2\pi}{3}$si katika$\left[−\dfrac{\pi}{2},\dfrac{\pi}{2}\right]$, lakini$sin\left(\dfrac{2\pi}{3}\right)=sin\left(\dfrac{\pi}{3}\right)$, hivyo${\sin}^{−1}\left(\sin\left(\dfrac{2\pi}{3}\right)\right)=\dfrac{\pi}{3}$.
3. $\dfrac{2\pi}{3}$ni katika$[ 0,\pi ]$, hivyo${\cos}^{−1}\left(\cos\left(\dfrac{2\pi}{3}\right)\right)=\dfrac{2\pi}{3}$.
4. $-\dfrac{\pi}{3}$si katika$[ 0,\pi ]$, lakini$\cos\left(−\dfrac{\pi}{3}\right)=\cos\left(\dfrac{\pi}{3}\right)$ kwa sababu cosine ni hata kazi. $\dfrac{\pi}{3}$ni katika$[ 0,\pi ]$, hivyo${\cos}^{−1}\left(\cos\left(−\dfrac{\pi}{3}\right)\right)=\dfrac{\pi}{3}$.

Zoezi$\PageIndex{5}$

Tathmini${\tan}^{−1}\left(\tan\left(\dfrac{\pi}{8}\right)\right)$ na${\tan}^{−1}\left(\tan\left(\dfrac{11\pi}{9}\right)\right)$.

Jibu

$\dfrac{\pi}{8}$;$\dfrac{2\pi}{9}$

Kutathmini Maandishi ya Fomu$f^{-1}(g(x))$

Sasa kwa kuwa tunaweza kutunga kazi ya trigonometric na inverse yake, tunaweza kuchunguza jinsi ya kutathmini muundo wa kazi ya trigonometric na inverse ya kazi nyingine ya trigonometric. Tutaanza na nyimbo za fomu$f^{-1}(g(x))$. Kwa maadili maalum ya$x$, tunaweza hasa kutathmini kazi ya ndani na kisha nje, kazi inverse. Hata hivyo, tunaweza kupata mbinu ya jumla zaidi kwa kuzingatia uhusiano kati ya pembe mbili za papo hapo za pembetatu sahihi ambapo moja ni$\theta$, na kufanya$\dfrac{\pi}{2}−\theta$ nyingine.Fikiria sine na cosine ya kila pembe ya pembetatu sahihi katika Kielelezo$\PageIndex{10}$.

Kielelezo$\PageIndex{10}$: Pembetatu ya kulia inayoonyesha mahusiano ya cofunction

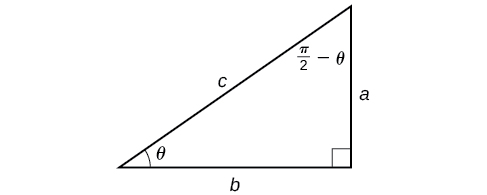
Kwa sababu$\cos \theta=\dfrac{b}{c}=sin\left(\dfrac{\pi}{2}−\theta\right)$, tuna${\sin}^{−1}(\cos \theta)=\dfrac{\pi}{2}−\theta$ kama$0≤\theta≤\pi$. Kama$\theta$ si katika uwanja huu, basi tunahitaji kupata angle nyingine ambayo ina cosine sawa$\theta$ na haina mali ya uwanja vikwazo; sisi kisha Ondoa angle hii$\dfrac{\pi}{2}$ kutoka.Vile vile$\sin \theta=\dfrac{a}{c}=\cos\left(\dfrac{\pi}{2}−\theta\right)$, hivyo${\cos}^{−1}(\sin \theta)=\dfrac{\pi}{2}−\theta$ kama$−\dfrac{\pi}{2}≤\theta≤\dfrac{\pi}{2}$. Hizi ni mahusiano tu ya kazi-cofunction iliyotolewa kwa njia nyingine.

Kutokana na kazi za fomu${\sin}^{−1}(\cos x)$ and ${\cos}^{−1}(\sin x)$, evaluate them.

1. Ikiwa$x$ iko$[ 0,\pi ]$, basi${\sin}^{−1}(\cos x)=\dfrac{\pi}{2}−x$.
2. Ikiwa$x$ haipo$[ 0,\pi ]$, basi pata angle nyingine$y$ katika$[ 0,\pi ]$ vile vile$\cos y=\cos x$.

   $${\sin}^{−1}(\cos x)=\dfrac{\pi}{2}−y$$

3. Ikiwa$x$ iko$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$, basi${\cos}^{−1}(\sin x)=\dfrac{\pi}{2}−x$.
4. Ikiwa$x$ haipo$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$, basi pata angle nyingine$y$ katika$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$ vile vile$\sin y=\sin x$.

   $${\cos}^{−1}(\sin x)=\dfrac{\pi}{2}−y$$

Mfano$\PageIndex{6}$: Evaluating the Composition of an Inverse Sine with a Cosine

Tathmini${\sin}^{−1}\left(\cos\left(\dfrac{13\pi}{6}\right)\right)$

1. na tathmini ya moja kwa moja.
2. kwa njia iliyoelezwa hapo awali.

Suluhisho

1. Hapa, tunaweza kutathmini moja kwa moja ndani ya muundo. $$\begin{align*} \cos\left(\dfrac{13\pi}{6}\right)&= \cos\left (\dfrac{\pi}{6}+2\pi\right )\\ &= \cos\left (\dfrac{\pi}{6}\right )\\ &= \dfrac{\sqrt{3}}{2} \end{align*}$$ Sasa, tunaweza kutathmini kazi inverse kama tulivyofanya mapema. $${\sin}^{−1}\left (\dfrac{\sqrt{3}}{2}\right )=\dfrac{\pi}{3}$$
2. Tuna$x=\dfrac{13\pi}{6}$,$y=\dfrac{\pi}{6}$, na $$\begin{align*} {\sin}^{-1}\left (\cos \left (\dfrac{13\pi}{6} \right ) \right )&= \dfrac{\pi}{2}-\dfrac{\pi}{6}\\ &= \dfrac{\pi}{3} \end{align*}$$

Zoezi$\PageIndex{6}$

Tathmini${\cos}^{−1}\left (\sin\left (−\dfrac{11\pi}{4}\right )\right )$.

Jibu

$\dfrac{3\pi}{4}$

Kutathmini Maandishi ya Fomu$f(g^{−1}(x))$

Kutathmini nyimbo za fomu$f(g^{−1}(x))$, wapi$f$ na$g$ ni mbili yoyote ya kazi sine, cosine, au tangent na$x$ ni pembejeo yoyote katika uwanja wa$g^{−1}$, tuna formula halisi, kama vile$\sin({\cos}^{−1}x)=\sqrt{1−x^2}$. Tunapohitaji kuitumia, tunaweza kupata fomu hizi kwa kutumia mahusiano ya trigonometric kati ya pembe na pande za pembetatu sahihi, pamoja na matumizi ya uhusiano wa Pythagoras kati ya urefu wa pande. Tunaweza kutumia utambulisho wa Pythagorean${\sin}^2 x+{\cos}^2 x=1$, kutatua kwa moja wakati unapopewa nyingine. Tunaweza pia kutumia kazi inverse trigonometric kupata nyimbo kuwashirikisha maneno algebraic.

Mfano$\PageIndex{7}$: Evaluating the Composition of a Sine with an Inverse Cosine

Kupata thamani halisi kwa ajili ya$\sin\left({\cos}^{−1}\left(\dfrac{4}{5}\right)\right)$.

Suluhisho

Kuanzia na ndani, tunaweza kusema kuna pembe kama hiyo$\theta={\cos}^{−1}\left (\dfrac{4}{5}\right )$, ambayo ina maana$\cos \theta=\dfrac{4}{5}$, na tunatafuta$\sin \theta$. Tunaweza kutumia utambulisho wa Pythagorean kufanya hivyo.

$$\begin{align*} {\sin}^2 \theta+{\cos}^2 \theta&= 1\qquad \text{Use our known value for cosine}\\ {\sin}^2 \theta+{\left (\dfrac{4}{5} \right )}^2&= 1\qquad \text{Solve for sine}\\ {\sin}^2 \theta&= 1-\dfrac{16}{25}\\ \sin \theta&=\pm \dfrac{9}{25}\\ &= \pm \dfrac{3}{5} \end{align*}$$

Tangu$\theta={\cos}^{−1}\left (\dfrac{4}{5}\right )$ ni katika quadrant mimi,$\sin \theta$ lazima kuwa chanya, hivyo ufumbuzi ni$35$. Angalia Kielelezo$\PageIndex{11}$.

Kielelezo$\PageIndex{11}$: Right pembetatu kuonyesha kwamba kama$\cos \theta=\dfrac{4}{5}$, basi$\sin \theta=\dfrac{3}{5}$

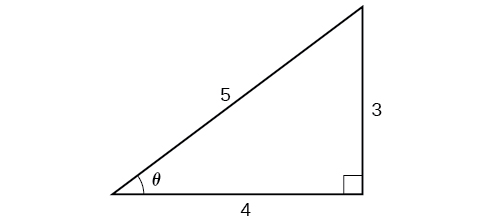
Tunajua kwamba cosine inverse daima inatoa angle juu ya muda$[ 0,\pi ]$, hivyo tunajua kwamba sine ya angle hiyo lazima kuwa chanya; kwa hiyo$\sin \left ({\cos}^{−1}\left (\dfrac{4}{5} \right ) \right )=\sin \theta=\dfrac{3}{5}$.

Zoezi$\PageIndex{7}$

Tathmini$\cos \left ({\tan}^{−1} \left (\dfrac{5}{12} \right ) \right )$.

Jibu

$\frac{12}{13}$

Mfano$\PageIndex{8}$: Evaluating the Composition of a Sine with an Inverse Tangent

Kupata thamani halisi kwa ajili ya$\sin\left({\tan}^{−1}\left(\dfrac{7}{4}\right)\right)$.

Suluhisho

Wakati tunaweza kutumia mbinu sawa kama katika Mfano$\PageIndex{6}$, tutaonyesha mbinu tofauti hapa. Kutoka ndani, tunajua kuna angle kama hiyo$\tan \theta=\dfrac{7}{4}$. Tunaweza kuona hii kama pande kinyume na karibu juu ya pembetatu haki, kama inavyoonekana katika Kielelezo$\PageIndex{12}$.

Kielelezo$\PageIndex{12}$: pembetatu haki na pande mbili inayojulikana

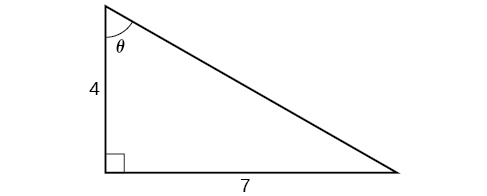
Kutumia Theorem ya Pythagorean, tunaweza kupata hypotenuse ya pembetatu hii.

\ [\ kuanza {align*}
4^2+7^2&= {hypotenuse} ^2\\
hypotenuse&=\ sqrt {65}\
\ maandishi {Sasa, tunaweza kutathmini sine ya angle kama upande wa pili umegawanyika na hypotenuse.} \\ sin
\ theta&=\ dfrac {7} {\ sqrt {65}}\
\ Nakala {Hii inatupa utungaji wetu uliotaka.} \
\ dhambi\ kushoto ({\ tan} ^ {-1}\ kushoto (\ dfrac {7} {4}\ kulia) &=\ dhambi\ theta\\
&=\ dfrac {7} {\ sqrt {65}}\\
&=\ dfrac {7\ sqrt {65}
\ mwisho {align*}\]

Zoezi$\PageIndex{8}$

Tathmini$\cos\left({\sin}^{−1}\left(\dfrac{7}{9}\right)\right)$.

Jibu

$\dfrac{4\sqrt{2}}{9}$

Mfano$\PageIndex{9}$: Finding the Cosine of the Inverse Sine of an Algebraic Expression

Kupata kujieleza rahisi kwa$\cos\left({\sin}^{−1}\left(\dfrac{x}{3}\right)\right)$ ajili ya$−3≤x≤3$.

Suluhisho

Tunajua kuna angle$\theta$ kama hiyo$\sin \theta=\dfrac{x}{3}$.

$$\begin{align*} {\sin}^2 \theta+{\cos}^2 \theta&= 1\qquad \text{Use the Pythagorean Theorem}\\ {\left (\dfrac{x}{3}\right )}^2+{\cos}^2 \theta&= 1\qquad \text{Solve for cosine}\\ {\cos}^2 \theta&= 1-\dfrac{x^2}{9}\\ \cos \theta &= \pm \sqrt{\dfrac{9-x^2}{9}}\\ &= \pm \sqrt{\dfrac{9-x^2}{3}} \end{align*}$$

Kwa sababu tunajua kwamba sine inverse lazima kutoa angle juu ya muda$[ −\dfrac{\pi}{2},\dfrac{\pi}{2} ]$, tunaweza kutambua kwamba cosine ya angle hiyo lazima kuwa chanya.

$cos\left({\sin}^{−1}\left(\dfrac{x}{3}\right)\right)=\sqrt{\dfrac{9-x^2}{3}}$

Zoezi$\PageIndex{9}$

Pata maelezo rahisi$\sin({\tan}^{−1}(4x))$ for $−\dfrac{1}{4}≤x≤\dfrac{1}{4}$.

Jibu

$\dfrac{4x}{\sqrt{16x^2+1}}$

Media

Fikia rasilimali hii ya mtandaoni kwa maelekezo ya ziada na mazoezi na kazi za trigonometric inverse.

• Kutathmini Maneno Kuhusisha Inverse Trigonometric Kazi

Ziara tovuti hii kwa maswali ya ziada mazoezi kutoka Learningpod.

Dhana muhimu

• Kazi ya inverse ni moja ambayo “hupunguza” kazi nyingine. Kikoa cha kazi ya inverse ni aina ya kazi ya awali na kazi mbalimbali ya inverse ni uwanja wa kazi ya awali.
• Kwa sababu kazi za trigonometric sio moja kwa moja kwenye nyanja zao za asili, kazi za trigonometric inverse zinafafanuliwa kwa vikoa vikwazo.
• Kwa kazi yoyote ya trigonometric$f(x)$, ikiwa$x=f^{−1}(y)$, basi$f(x)=y$. Hata hivyo,$f(x)=y$ tu ina maana$x=f^{−1}(y)$ kama$x$ ni katika uwanja vikwazo ya$f$. Angalia Mfano$\PageIndex{1}$.
• Pembe maalum ni matokeo ya kazi za trigonometric inverse kwa maadili maalum ya pembejeo; kwa mfano,$\frac{\pi}{4}={\tan}^{−1}(1)$ na$\frac{\pi}{6}={\sin}^{−1}(\frac{1}{2})$ .Angalia Mfano$\PageIndex{2}$.
• Calculator itarudi angle ndani ya kikoa kilichozuiliwa cha kazi ya awali ya trigonometric. Angalia Mfano$\PageIndex{3}$.
• Kazi za inverse zinatuwezesha kupata angle wakati tunapopewa pande mbili za pembetatu sahihi. Angalia Mfano$\PageIndex{4}$.
• Katika utungaji wa kazi, ikiwa kazi ya ndani ni kazi ya trigonometric inverse, basi kuna maneno halisi; kwa mfano,$\sin({\cos}^{−1}(x))=\sqrt{1−x^2}$. Angalia Mfano$\PageIndex{5}$.
• Ikiwa kazi ya ndani ni kazi ya trigonometric, basi mchanganyiko pekee unaowezekana ni${\sin}^{−1}(\cos x)=\frac{\pi}{2}−x$ kama$0≤x≤\pi$ na${\cos}^{−1}(\sin x)=\frac{\pi}{2}−x$ ikiwa$−\frac{\pi}{2}≤x≤\frac{\pi}{2}$. Angalia Mfano$\PageIndex{6}$ na Mfano$\PageIndex{7}$.
• Wakati wa kutathmini muundo wa kazi ya trigonometric na kazi ya trigonometric inverse, futa pembetatu ya kumbukumbu ili kusaidia katika kuamua uwiano wa pande zinazowakilisha pato la kazi ya trigonometric. Angalia Mfano$\PageIndex{8}$.
• Wakati wa kutathmini muundo wa kazi ya trigonometric na kazi ya trigonometric inverse, unaweza kutumia utambulisho wa trig ili kusaidia katika kuamua uwiano wa pande. Angalia Mfano$\PageIndex{9}$.