4.3: Kazi za Logarithmic
- Page ID
- 181251
- Badilisha kutoka kwa logarithmic hadi fomu ya kielelezo.
- Badilisha kutoka kwa kielelezo hadi fomu ya logarithmic.
- Tathmini logarithms.
- Tumia logarithms ya kawaida.
- Tumia logarithms ya asili.
Mwaka 2010, tetemeko kubwa la ardhi lilipiga Haiti, kuharibu au kuharibu nyumba zaidi ya 285,000. Mwaka mmoja baadaye, mwingine, nguvu tetemeko la ardhi ukiwa Honshu, Japan, kuharibu au kuharibu zaidi ya 332,000 majengo, kama wale inavyoonekana katika Kielelezo\(\PageIndex{1}\). Ingawa wote wawili walisababisha uharibifu mkubwa, tetemeko la ardhi mwaka 2011 lilikuwa na nguvu mara 100 kuliko tetemeko la ardhi nchini Haiti. Tunajuaje? Ukubwa wa matetemeko ya ardhi hupimwa kwa kiwango kinachojulikana kama Richter Scale. Tetemeko la ardhi la Haiti lilijiandikisha 7.0 kwenye Richter Scale wakati tetemeko la ardhi la Kijapani liliandikisha

Kielelezo\(\PageIndex{1}\): Uharibifu wa Machi 11, 2011 tetemeko la ardhi huko Honshu, Japan. (mikopo: Daniel Pierce).
Kiwango cha Richter ni kiwango cha msingi cha kumi cha logarithmic. Kwa maneno mengine, tetemeko la ardhi la ukubwa\(8\) sio mara mbili kubwa kama tetemeko la ardhi la ukubwa\(4\). Ni
\[10^{8−4}=10^4=10,000 \nonumber\]
mara kama kubwa! Katika somo hili, tutachunguza hali ya Richter Scale na kazi ya msingi kumi ambayo inategemea.
Kubadilisha kutoka Logarithmic hadi Fomu ya Kielelezo
Ili kuchambua ukubwa wa matetemeko ya ardhi au kulinganisha ukubwa wa matetemeko mawili tofauti, tunahitaji kuwa na uwezo wa kubadili kati ya fomu ya logarithmic na ya kielelezo. Kwa mfano, tuseme kiasi cha nishati iliyotolewa kutokana na tetemeko moja ilikuwa mara 500 zaidi kuliko kiasi cha nishati iliyotolewa kutoka kwa mwingine. Tunataka kuhesabu tofauti katika ukubwa. equation kwamba inawakilisha tatizo hili ni\(10^x=500\), ambapo\(x\) inawakilisha tofauti katika magnitudes juu ya Richter Scale. Jinsi gani sisi kutatua kwa\(x\)?
Hatujajifunza njia ya kutatua usawa wa kielelezo. Hakuna zana yoyote ya algebraic iliyojadiliwa hadi sasa inatosha kutatua\(10^x=500\). Tunajua kwamba\({10}^2=100\) na\({10}^3=1000\), hivyo ni wazi kwamba\(x\) lazima baadhi ya thamani kati ya 2 na 3, tangu\(y={10}^x\) ni kuongeza. Tunaweza kuchunguza grafu, kama katika Kielelezo\(\PageIndex{1}\), ili kukadiria vizuri suluhisho.
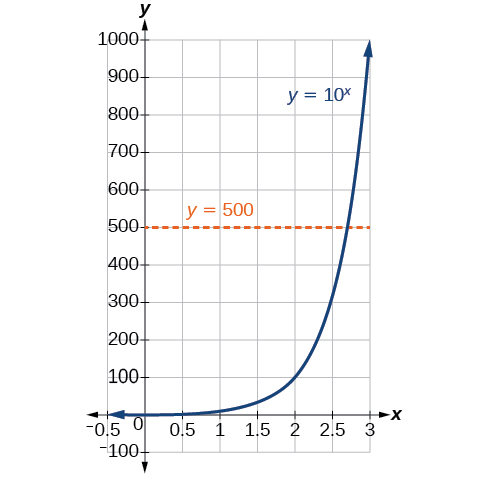
Kielelezo\(\PageIndex{2}\)
Kukadiria kutoka kwenye grafu, hata hivyo, ni sahihi. Ili kupata suluhisho la algebraic, lazima tuanze kazi mpya. Angalia kwamba grafu katika Kielelezo\(\PageIndex{2}\) hupita mtihani wa mstari usio na usawa. Kazi ya kielelezo\(y=b^x\) ni moja kwa moja, hivyo inverse yake, pia\(x=b^y\) ni kazi. Kama ilivyo kwa kazi zote inverse, sisi tu\(x\)\(y\) interchange na kutatua\(y\) kwa kupata kazi inverse. Kuwakilisha\(y\) kama kazi ya\(x\), tunatumia kazi logarithmic ya fomu\(y={\log}_b(x)\). \(b\)Logarithm msingi ya idadi ni exponent ambayo ni lazima kuongeza\(b\) kupata idadi hiyo.
Tunasoma kujieleza logarithmic kama, “Logarithm na msingi\(b\) wa\(x\) ni sawa na\(y\),” au, kilichorahisishwa, “logi msingi\(b\) wa\(x\) ni\(y\).” Pia tunaweza kusema, “\(b\)kukulia kwa nguvu ya\(y\) sisi\(x\),” kwa sababu magogo ni exponents. Kwa mfano, msingi\(2\) logarithm ya\(32\) ni\(5\), kwa sababu\(5\) ni exponent ni lazima\(2\) kuomba kwa kupata\(32\). Tangu\(2^5=32\), tunaweza kuandika\({\log}_232=5\). Tunasoma hii kama “logi msingi\(2\) wa\(32\) ni\(5\).”
Tunaweza kueleza uhusiano kati ya fomu ya logarithmic na fomu yake inayofanana ya kielelezo kama ifuatavyo:
\[\begin{align} \log_b(x)=y\Leftrightarrow b^y=x, b> 0, b\neq 1 \end{align}\]
Kumbuka kuwa msingi daima\(b\) ni chanya.
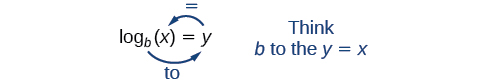
Kwa sababu logarithm ni kazi, ni sahihi zaidi imeandikwa kama\(\log_b(x)\), kwa kutumia mabano kuashiria kazi tathmini, kama sisi ingekuwa na\(f(x)\). Hata hivyo, wakati pembejeo ni variable moja au idadi, ni jambo la kawaida kuona mabano imeshuka na kujieleza imeandikwa bila mabano, kama\(\log_bx\). Kumbuka kuwa calculators wengi zinahitaji mabano karibu\(x\).
Tunaweza kuonyesha notation ya logarithms kama ifuatavyo:

Kumbuka kwamba, kulinganisha kazi ya logarithm na kazi ya kielelezo, pembejeo na pato hubadilishwa. Hii ina maana\(y={\log}^b(x)\) na\(y=b^x\) ni kazi inverse.
Msingi wa logarithm\(b\) wa nambari nzuri\(x\) hutimiza ufafanuzi wafuatayo.
Kwa\(x>0\),\(b>0\),\(b≠1\),
\[\begin{align} y={\log}_b(x)\text{ is equivalent to } b^y=x \end{align}\]
wapi,
- tunasoma\({\log}_b(x)\) kama, “logarithm na msingi\(b\) wa\(x\)” au “logi msingi\(b\) wa\(x\).”
- logarithm\(y\) ni exponent ambayo\(b\) lazima kukulia kupata\(x\).
Pia, tangu kazi za logarithmic na za kielelezo zinabadili\(x\) na\(y\) maadili, uwanja na upeo wa kazi ya kielelezo hubadilishana kwa kazi ya logarithmic. Kwa hiyo,
- uwanja wa kazi ya logarithm na msingi\(b\) ni\((0,\infty)\).
- aina mbalimbali ya kazi ya logarithm na msingi\(b\) ni\((−\infty,\infty)\).
Hapana. Kwa sababu msingi wa kazi kielelezo daima ni chanya, hakuna nguvu ya msingi kwamba unaweza milele kuwa hasi. Hatuwezi kamwe kuchukua logarithm ya idadi hasi. Pia, hatuwezi kuchukua logarithm ya sifuri. Wahesabu wanaweza kuzalisha logi ya nambari hasi wakati wa hali ngumu, lakini logi ya nambari hasi sio namba halisi.
- Kuchunguza equation\(y={\log}_bx\) na kutambua\(b\),\(y\), na\(x\).
- Andika upya\({\log}_bx=y\) kama\(b^y=x\).
Andika equations zifuatazo za logarithmic katika fomu ya kielelezo.
- \({\log}_6(\sqrt{6})=\dfrac{1}{2}\)
- \({\log}_3(9)=2\)
Suluhisho
Kwanza, tambua maadili ya\(b\),\(y\), na\(x\). Kisha, andika equation katika fomu\(b^y=x\).
- \({\log}_6(\sqrt{6})=\dfrac{1}{2}\)
Hapa,\(b=6\),\(y=\dfrac{1}{2}\), na\(x=\sqrt{6}\). Kwa hiyo, equation\({\log}_6(\sqrt{6})=\dfrac{1}{2}\) ni sawa na
\(6^{\tfrac{1}{2}}=\sqrt{6}\)
- \({\log}_3(9)=2\)
Hapa,\(b=3\),\(y=2\), na\(x=9\). Kwa hiyo, equation\({\log}_3(9)=2\) ni sawa na
\(3^2=9\)
Andika equations zifuatazo za logarithmic katika fomu ya kielelezo.
- \({\log}_{10}(1,000,000)=6\)
- \({\log}_5(25)=2\)
- Jibu
-
\({\log}_{10}(1,000,000)=6\)ni sawa na\({10}^6=1,000,000\)
- Jibu b
-
\({\log}_5(25)=2\)ni sawa na\(5^2=25\)
Kubadilisha kutoka Kielelezo hadi Fomu ya Logarithmic
Ili kubadilisha kutoka kwa watazamaji hadi logarithms, tunafuata hatua sawa katika reverse. Sisi kutambua msingi\(b\), exponent\(x\), na pato\(y\). Kisha tunaandika\(x={\log}_b(y)\).
Andika equations zifuatazo za kielelezo katika fomu ya logarithmic.
- \(2^3=8\)
- \(5^2=25\)
- \({10}^{−4}=\dfrac{1}{10,000}\)
Suluhisho
Kwanza, tambua maadili ya\(b\),\(y\), na\(x\). Kisha, andika equation katika fomu\(x={\log}_b(y)\).
- \(2^3=8\)
Hapa,\(b=2\),\(x=3\), na\(y=8\). Kwa hiyo, equation\(2^3=8\) ni sawa na\({\log}_2(8)=3\).
- \(5^2=25\)
Hapa,\(b=5\),\(x=2\), na\(y=25\). Kwa hiyo, equation\(5^2=25\) ni sawa na\({\log}_5(25)=2\).
- \({10}^{−4}=\dfrac{1}{10,000}\)
Hapa,\(b=10\),\(x=−4\), na\(y=\dfrac{1}{10,000}\). Kwa hiyo, equation\({10}^{−4}=\dfrac{1}{10,000}\) ni sawa na\({\log}_{10} \left (\dfrac{1}{10,000} \right )=−4\).
Andika equations zifuatazo za kielelezo katika fomu ya logarithmic.
- \(3^2=9\)
- \(5^3=125\)
- \(2^{−1}=\dfrac{1}{2}\)
- Jibu
-
\(3^2=9\)ni sawa na\({\log}_3(9)=2\)
- Jibu b
-
\(5^3=125\)ni sawa na\({\log}_5(125)=3\)
- Jibu c
-
\(2^{−1}=\dfrac{1}{2}\)ni sawa na\({\log}_2 \left (\dfrac{1}{2} \right )=−1\)
Kutathmini Logarithms
Kujua mraba, cubes, na mizizi ya namba inatuwezesha kutathmini logarithms nyingi kiakili. Kwa mfano, fikiria\({\log}_28\). Tunauliza, “Kwa nini exponent\(2\) lazima kukulia ili kupata 8?” Kwa sababu tunajua tayari\(2^3=8\), inafuata hiyo\({\log}_28=3\).
Sasa fikiria kutatua\({\log}_749\) na\({\log}_327\) kiakili.
- Tunauliza, “Kwa nini exponent\(7\) lazima kufufuliwa ili kupata\(49\)?” Tunajua\(7^2=49\). Kwa hiyo,\({\log}_749=2\)
- Tunauliza, “Kwa nini exponent\(3\) lazima kufufuliwa ili kupata\(27\)?” Tunajua\(3^3=27\). Kwa hiyo,\(\log_{3}27=3\)
Hata baadhi ya logarithms inayoonekana ngumu zaidi inaweza kupimwa bila calculator. Kwa mfano, hebu tathmini\(\log_{\ce{2/3}} \frac{4}{9}\) kiakili.
- Tunauliza, “Kwa nini exponent\(\ce{2/3}\) lazima kufufuliwa ili kupata\(\ce{4/9}\)? ” Tunajua\(2^2=4\) na\(3^2=9\), hivyo\[{\left(\dfrac{2}{3} \right )}^2=\dfrac{4}{9}. \nonumber\] kwa hiyo,\[{\log}_{\ce{2/3}} \left (\dfrac{4}{9} \right )=2. \nonumber\]
- Andika upya hoja\(x\) kama nguvu ya\(b\):\(b^y=x\).
- Tumia ujuzi uliopita wa mamlaka ya\(b\) kutambua\(y\) kwa kuuliza, “Kwa nini exponent\(b\) lazima kukulia ili kupata\(x\)?”
Tatua\(y={\log}_4(64)\) bila kutumia calculator.
Suluhisho
Kwanza tunaandika upya logarithm kwa fomu ya kielelezo:\(4^y=64\). Kisha, tunauliza, “Kwa nini exponent\(4\) lazima kukulia ili kupata\(64\)?”
Tunajua
\(4^3=64\)
Kwa hiyo,
\({\log}_4(64)=3\)
Tatua\(y={\log}_{121}(11)\) bila kutumia calculator.
- Jibu
-
\({\log}_{121}(11)=\dfrac{1}{2}\)(akikumbuka kwamba\(\sqrt{121}={(121)}^{\tfrac{1}{2}}=11)\)
Tathmini\(y={\log}_3 \left (\dfrac{1}{27} \right )\) bila kutumia calculator.
Suluhisho
Kwanza tunaandika upya logarithm kwa fomu ya kielelezo:\(3^y=\dfrac{1}{27}\). Kisha, tunauliza, “Kwa nini exponent\(3\) lazima kukulia ili kupata\(\dfrac{1}{27}\)?”
Tunajua\(3^3=27\), lakini ni lazima tufanye nini ili kupata usawa,\(\dfrac{1}{27}\)? Kumbuka kutoka kufanya kazi na exponents kwamba\(b^{−a}=\dfrac{1}{b^a}\). Tunatumia maelezo haya kuandika
\[\begin{align*} 3^{-3}&= \dfrac{1}{3^3}\\ &= \dfrac{1}{27} \end{align*}\]
Kwa hiyo,\({\log}_3 \left (\dfrac{1}{27} \right )=−3\).
Tathmini\(y={\log}_2 \left (\dfrac{1}{32} \right )\) bila kutumia calculator.
- Jibu
-
\({\log}_2 \left (\dfrac{1}{32} \right )=−5\)
Kutumia Logarithms ya kawaida
Wakati mwingine tunaweza kuona logarithm iliyoandikwa bila msingi. Katika kesi hii, tunadhani kwamba msingi ni\(10\). Kwa maneno mengine,\(\log(x)\) maana ya maneno\({\log}_{10}(x)\). Tunaita\(-10\) logarithm ya msingi ya logarithm ya kawaida. Logarithms ya kawaida hutumiwa kupima Kiwango cha Richter kilichotajwa mwanzoni mwa sehemu hiyo. Mizani ya kupima mwangaza wa nyota na pH ya asidi na besi pia hutumia logarithimu ya kawaida.
Logarithm ya kawaida ni logarithm yenye msingi\(10\). Tunaandika\({\log}_{10}(x)\) tu kama\(\log(x)\). Logarithm ya kawaida ya nambari nzuri\(x\) inatimiza ufafanuzi wafuatayo.
Kwa\(x>0\),
\[\begin{align} y={\log}(x)\text{ is equivalent to } {10}^y=x \end{align}\]
Tunasoma\(\log(x)\) kama, “logarithm na msingi\(10\) wa\(x\)” au “logi msingi\(10\) wa\(x\).”
Logarithm\(y\) ni exponent ambayo\(10\) inapaswa kuinuliwa kupata\(x\).
- Andika upya hoja\(x\) kama nguvu ya\(10\):\({10}^y=x\).
- Tumia maarifa ya awali ya mamlaka ya\(10\) kutambua\(y\) kwa kuuliza, “Kwa nini exponent\(10\) lazima kukulia ili kupata\(x\)?”
Tathmini\(y=\log(1000)\) bila kutumia calculator.
Suluhisho
Kwanza tunaandika upya logarithm kwa fomu ya kielelezo:\({10}^y=1000\). Kisha, tunauliza, “Kwa nini exponent\(10\) lazima kukulia ili kupata\(1000\)?” Tunajua
\({10}^3=1000\)
Kwa hiyo,\(\log(1000)=3\).
Tathmini\(y=\log(1,000,000)\).
- Jibu
-
\(\log(1,000,000)=6\)
- Waandishi wa habari [LOG].
- Ingiza thamani iliyotolewa kwa\(x\), ikifuatiwa na [)].
- Waandishi wa habari [INGIZA].
Tathmini\(y=\log(321)\) kwa maeneo manne ya decimal kwa kutumia calculator.
Suluhisho
- Waandishi wa habari [LOG].
- Ingiza 321, ikifuatiwa na [)].
- Waandishi wa habari [INGIZA].
Kuzunguka kwa maeneo manne ya decimal,\(\log(321)≈2.5065\).
Uchambuzi
Kumbuka kwamba\({10}^2=100\) na kwamba\({10}^3=1000\). Kwa kuwa\(321\) ni kati\(100\) na\(1000\), tunajua kwamba\(\log(321)\) lazima iwe kati\(\log(100)\) na\(\log(1000)\). Hii inatupa yafuatayo:
\(100<321<1000\)
\(2<2.5065<3\)
Tathmini\(y=\log(123)\) kwa maeneo manne ya decimal kwa kutumia calculator.
- Jibu
-
\(\log(123)≈2.0899\)
Kiasi cha nishati iliyotolewa kutokana na tetemeko moja ilikuwa\(500\) mara kubwa zaidi kuliko kiasi cha nishati iliyotolewa kutoka kwa mwingine. Equation\({10}^x=500\) inawakilisha hali hii, ambapo\(x\) ni tofauti katika ukubwa juu ya Richter Scale. Kwa elfu ya karibu, ilikuwa tofauti gani katika ukubwa?
Suluhisho
Tunaanza kwa kuandika upya equation ya kielelezo katika fomu ya logarithmic.
\({10}^x=500\)
\(\log(500)=x\)Tumia ufafanuzi wa logi ya kawaida.
Halafu tunatathmini logarithm kwa kutumia calculator:
- Waandishi wa habari [LOG].
- Ingiza\(500\), ikifuatiwa na [)].
- Waandishi wa habari [INGIZA].
- Kwa karibu elfu,\(\log(500)≈2.699\).
Tofauti katika ukubwa ilikuwa karibu\(2.699\).
Kiasi cha nishati iliyotolewa kutokana na tetemeko moja ilikuwa\(8,500\) mara kubwa zaidi kuliko kiasi cha nishati iliyotolewa kutoka kwa mwingine. Equation\({10}^x=8500\) inawakilisha hali hii, ambapo\(x\) ni tofauti katika ukubwa juu ya Richter Scale. Kwa elfu ya karibu, ilikuwa tofauti gani katika ukubwa?
- Jibu
-
Tofauti katika ukubwa ilikuwa karibu\(3.929\).
Kutumia Logarithms Asili
Msingi unaotumiwa mara kwa mara kwa logarithms ni\(e\). \(e\)Logarithms ya msingi ni muhimu katika calculus na baadhi ya maombi ya kisayansi; huitwa logarithms asili. \(e\)Logarithm ya msingi\({\log}_e(x)\), ina alama yake mwenyewe,\(\ln(x)\). Maadili mengi ya\(\ln(x)\) yanaweza kupatikana tu kwa kutumia calculator. Mbali kubwa ni kwamba, kwa sababu logarithm ya daima\(1\) ni\(0\) katika msingi wowote,\(\ln1=0\). Kwa logarithms nyingine za asili, tunaweza kutumia\(\ln\) ufunguo ambao unaweza kupatikana kwenye mahesabu mengi ya kisayansi. Tunaweza pia kupata logarithm ya asili ya nguvu yoyote ya\(e\) kutumia mali inverse ya logarithms.
Logarithm ya asili ni logarithm yenye msingi\(e\). Tunaandika\({\log}_e(x)\) tu kama\(\ln(x)\). Logarithm ya asili ya nambari nzuri\(x\) inatimiza ufafanuzi wafuatayo.
Kwa\(x>0\),
\(y=\ln(x)\)ni sawa na\(e^y=x\)
Tunasoma\(\ln(x)\) kama, “logarithm na msingi\(e\) wa\(x\)” au “logarithm asili ya\(x\).”
Logarithm\(y\) ni exponent ambayo\(e\) inapaswa kuinuliwa kupata\(x\).
Tangu kazi\(y=e^x\) na\(y=\ln(x)\) ni kazi inverse,\(\ln(e^x)=x\) kwa wote\(x\) na\(e^{\ln (x)}=x\) kwa\(x>0\).
- Waandishi wa habari [LN].
- Ingiza thamani iliyotolewa kwa\(x\), ikifuatiwa na [)].
- Waandishi wa habari [INGIZA].
Tathmini\(y=\ln(500)\) kwa maeneo manne ya decimal kwa kutumia calculator.
Suluhisho
- Waandishi wa habari [LN].
- Ingiza\(500\), ikifuatiwa na [)].
- Waandishi wa habari [INGIZA].
Kuzunguka kwa sehemu nne za decimal,\(\ln(500)≈6.2146\)
Tathmini\(\ln(−500)\).
- Jibu
-
Haiwezekani kuchukua logarithm ya idadi hasi katika seti ya namba halisi.
Fikia rasilimali hii ya mtandaoni kwa maelekezo ya ziada na mazoezi na logarithms.
Mlinganyo muhimu
| Ufafanuzi wa kazi ya logarithmic | Kwa\(x>0\),\(b>0\),\(b≠1\),\(y={\log}_b(x)\) kama na tu kama\(b^y=x\). |
| Ufafanuzi wa logarithm ya kawaida | Kwa\(x>0\),\(y=\log(x)\) kama na tu kama\({10}^y=x\). |
| Ufafanuzi wa logarithm ya asili | Kwa\(x>0\),\(y=\ln(x)\) kama na tu kama\(e^y=x\). |
Dhana muhimu
- Inverse ya kazi ya kielelezo ni kazi ya logarithmic, na inverse ya kazi ya logarithmic ni kazi ya kielelezo.
- Ulinganisho wa Logarithmic unaweza kuandikwa kwa fomu sawa ya kielelezo, kwa kutumia ufafanuzi wa logarithm. Angalia Mfano\(\PageIndex{1}\).
- Ulinganifu wa kielelezo unaweza kuandikwa katika fomu yao sawa ya logarithmic kwa kutumia ufafanuzi wa logarithm Angalia Mfano\(\PageIndex{2}\).
- Kazi za Logarithmic na msingi\(b\) zinaweza kupimwa kiakili kwa kutumia ujuzi wa awali wa nguvu za\(b\). Angalia Mfano\(\PageIndex{3}\) na Mfano\(\PageIndex{4}\).
- Logarithms ya kawaida inaweza kupimwa kiakili kwa kutumia maarifa ya awali ya mamlaka ya\(10\). Angalia Mfano\(\PageIndex{5}\).
- Wakati logarithimu za kawaida haziwezi kutathminiwa kiakili, kikokotoo kinaweza kutumika. Angalia Mfano\(\PageIndex{6}\).
- Matatizo halisi ya ulimwengu wa kielelezo na msingi\(10\) yanaweza kuandikwa upya kama logarithm ya kawaida na kisha tathmini kwa kutumia calculator. Angalia Mfano\(\PageIndex{7}\).
- Logarithms za asili zinaweza kutathminiwa kwa kutumia Mfano wa calculator\(\PageIndex{8}\).


