4.1: Kazi za kielelezo
- Page ID
- 181236
- Tathmini kazi za kielelezo.
- Pata equation ya kazi ya kielelezo.
- Tumia fomu za riba za kiwanja.
- Tathmini kazi za kielelezo na msingi\(e\).
Uhindi ni nchi ya pili yenye wakazi wengi duniani ikiwa na idadi ya watu\(1.25\) wapatao bilioni mwaka 2013. Idadi ya watu inakua kwa kiwango cha karibu\(.2\%\) kila mwaka. Kama kiwango hiki kinaendelea, idadi ya watu wa India itazidi idadi ya watu wa China kufikia mwaka 2031. Wakati watu wanapokua kwa kasi, mara nyingi tunasema kuwa ukuaji ni “kielelezo,” maana yake ni kwamba kitu kinakua kwa kasi sana. Kwa mtaalamu wa hisabati, hata hivyo, neno ukuaji wa kielelezo lina maana maalum sana. Katika sehemu hii, tutaangalia kazi za kielelezo, ambazo zinaonyesha aina hii ya ukuaji wa haraka.
Wakati wa kuchunguza ukuaji wa mstari, tuliona kiwango cha mara kwa mara cha mabadiliko-idadi ya mara kwa mara ambayo pato limeongezeka kwa kila ongezeko la kitengo katika pembejeo. Kwa mfano, katika equation\(f(x)=3x+4\), mteremko inatuambia ongezeko la pato kwa\(3\) kila wakati pembejeo huongezeka kwa\(1\). Hali katika mfano wa idadi ya watu wa India ni tofauti kwa sababu tuna mabadiliko ya asilimia kwa wakati wa kitengo (badala ya mabadiliko ya mara kwa mara) katika idadi ya watu.
Kufafanua Kazi ya Kielelezo
Utafiti uligundua kuwa asilimia ya wakazi ambao ni vegans nchini Marekani mara mbili kutoka 2009 hadi 2011. Mwaka 2011, kati\(2.5\%\) ya wakazi walikuwa vegan, wakiambatana na chakula ambacho hakijumuishi bidhaa zozote za mnyama—hakuna nyama, kuku, samaki, maziwa, au mayai. Kama kiwango hiki kinaendelea, vegans itakuwa na idadi\(10\%\) ya watu wa Marekani katika 2015,\(40\%\) katika 2019, na\(80\%\) katika 2050.
Nini hasa ina maana ya kukua exponentially? Je, neno mara mbili linalofanana na ongezeko la asilimia? Watu hutupa maneno haya karibu sana. Je! Maneno haya yanatumiwa kwa usahihi? Maneno hakika yanaonekana mara kwa mara katika vyombo vya habari.
- Mabadiliko ya asilimia inahusu mabadiliko kulingana na asilimia ya kiasi cha awali.
- Ukuaji wa kielelezo unahusu ongezeko kulingana na kiwango cha mara kwa mara cha kuzidisha mabadiliko juu ya nyongeza sawa za muda, yaani, ongezeko la asilimia ya kiasi cha awali baada ya muda.
- Uozo wa kielelezo unamaanisha kupungua kulingana na kiwango cha mara kwa mara cha kuzidisha cha mabadiliko juu ya nyongeza sawa za muda, yaani, kupungua kwa asilimia ya kiasi cha awali baada ya muda.
Kwa sisi kupata uelewa wazi wa ukuaji wa kielelezo, hebu tufananishe ukuaji wa kielelezo na ukuaji wa mstari. Tutajenga kazi mbili. Kazi ya kwanza ni ya kielelezo. Tutaanza na pembejeo ya\(0\), na kuongeza kila pembejeo kwa\(1\). Sisi mara mbili matokeo sambamba mfululizo. Kazi ya pili ni ya mstari. Tutaanza na pembejeo ya\(0\), na kuongeza kila pembejeo kwa\(1\). Tutaongeza matokeo\(2\) ya mfululizo yanayofanana (Jedwali\(\PageIndex{1}\)).
Kutoka Jedwali\(\PageIndex{1}\) tunaweza kudai kwamba kwa ajili ya kazi hizi mbili, kielelezo ukuaji dwarfs linear ukuaji.
- Ukuaji wa kielelezo unahusu thamani ya awali kutoka kwa ongezeko la aina kwa asilimia sawa juu ya nyongeza sawa zilizopatikana katika uwanja.
- Ukuaji wa mstari unahusu thamani ya awali kutoka kwa ongezeko la aina kwa kiasi sawa juu ya nyongeza sawa zilizopatikana katika uwanja.
| \(x\) | \(f(x)=2^x\) | \(g(x)=2x\) |
|---|---|---|
| \ (x\)” style="wima align:katikati; "> 0 | \ (f (x) =2^x\)” style="wima align:katikati; "> 1 | \ (g (x) =2x\)” style="wima align:katikati; "> 0 |
| \ (x\)” style="wima align:katikati; "> 1 | \ (f (x) =2^x\)” style="wima align:katikati; "> 2 | \ (g (x) =2x\)” style="wima align:katikati; "> 2 |
| \ (x\)” style="wima align:katikati; "> 2 | \ (f (x) =2^x\)” style="wima align:katikati; "> 4 | \ (g (x) =2x\)” style="wima align:katikati; "> 4 |
| \ (x\)” style="wima align:katikati; "> 3 | \ (f (x) =2^x\)” style="wima align:katikati; "> 8 | \ (g (x) =2x\)” style="wima align:katikati; "> 6 |
| \ (x\)” style="wima align:katikati; "> 4 | \ (f (x) =2^x\)” style="wima align:katikati; "> 16 | \ (g (x) =2x\)” style="wima align:katikati; "> 8 |
| \ (x\)” style="wima align:katikati; "> 5 | \ (f (x) =2^x\)” style="wima align:katikati; "> 32 | \ (g (x) =2x\)” style="wima align:katikati; "> 10 |
| \ (x\)” style="wima align:katikati; "> 6 | \ (f (x) =2^x\)” style="wima align:katikati; "> 64 | \ (g (x) =2x\)” style="wima align:katikati; "> 12 |
Inaonekana, tofauti kati ya “asilimia sawa” na “kiasi sawa” ni muhimu sana. Kwa ukuaji wa kielelezo, juu ya nyongeza sawa, kiwango cha mara kwa mara cha mabadiliko kilisababisha mara mbili pato wakati wowote pembejeo iliongezeka kwa moja. Kwa ukuaji wa mstari, kiwango cha kuongezea mara kwa mara cha mabadiliko juu ya nyongeza sawa\(2\) kilisababisha kuongeza pato wakati wowote pembejeo iliongezeka kwa moja.
Fomu ya jumla ya kazi ya kielelezo ni\(f(x)=ab^x\), wapi\(a\) nambari yoyote isiyo ya zero,\(b\) ni nambari halisi isiyo sawa na\(1\).
- Ikiwa\(b>1\), kazi inakua kwa kiwango sawa na ukubwa wake.
- Kama\(0<b<1\), kazi kuoza kwa kiwango sawia na ukubwa wake.
Hebu tuangalie kazi\(f(x)=2^x\) kutoka kwa mfano wetu. Tutaunda meza (Jedwali\(\PageIndex{2}\)) ili kuamua matokeo yanayofanana juu ya muda katika uwanja kutoka\(−3\) kwa\(3\).
| \(x\) | \(−3\) | \(−2\) | \(−1\) | \(0\) | \(1\) | \(2\) | \(3\) |
|---|---|---|---|---|---|---|---|
| \(f(x)=2^x\) | \(2^{−3}=\dfrac{1}{8}\) | \(2^{−2}=\dfrac{1}{4}\) | \(2^{−1}=\dfrac{1}{2}\) | \(2^0=1\) | \(2^1=2\) | \(2^2=4\) | \(2^3=8\) |
Hebu tuchunguze grafu ya\(f\) kwa kupanga njama zilizoamriwa kutoka Jedwali\(\PageIndex{2}\) na kisha tufanye uchunguzi machache\(\PageIndex{1}\).
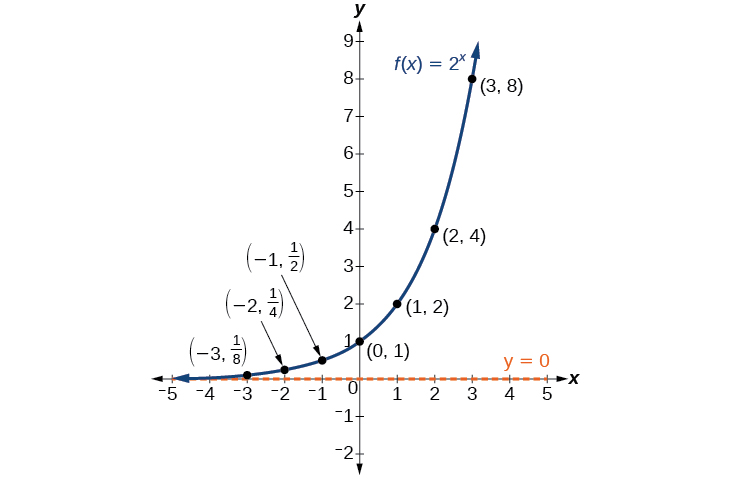
Hebu tufafanue tabia ya grafu ya kazi ya kielelezo\(f(x)=2^x\) na uonyeshe baadhi ya sifa zake muhimu.
- uwanja ni\((−\infty,\infty)\),
- mbalimbali ni\((0,\infty)\),
- kama\(x\rightarrow \infty\),\(f(x)\rightarrow \infty\),
- kama\(x\rightarrow −\infty\),\(f(x)\rightarrow 0\),
- \(f(x)\)daima inaongezeka,
- graph ya\(f(x)\) kamwe kugusa x -axis kwa sababu msingi mbili kukulia kwa exponent yoyote kamwe ina matokeo ya sifuri.
- \(y=0\)ni asymptote ya usawa.
- y -intercept ni\(1\).
Kwa idadi yoyote halisi\(x\), kazi ya kielelezo ni kazi na fomu
\[f(x)=ab^x\]
wapi
- \(a\)ni nambari isiyo ya sifuri halisi inayoitwa thamani ya awali na
- \(b\)ni yoyote chanya halisi idadi hiyo\(b≠1\).
- uwanja wa\(f\) ni namba zote halisi.
- mbalimbali ya\(f\) ni chanya idadi halisi kama\(a>0\).
- mbalimbali ya\(f\) ni namba zote hasi halisi kama\(a<0\).
- Y-intercept ni\((0,a)\), na asymptote ya usawa ni\(y=0\).
Ni ipi kati ya milinganyo ifuatayo sio kazi za kielelezo?
- \(f(x)=4^{3(x−2)}\)
- \(g(x)=x^3\)
- \(h(x)=\left(\dfrac{1}{3}\right)^x\)
- \(j(x)=(−2)^x\)
Suluhisho
Kwa ufafanuzi, kazi ya kielelezo ina mara kwa mara kama msingi na kutofautiana kwa kujitegemea kama kielelezo. Hivyo,\(g(x)=x^3\) haina kuwakilisha kazi kielelezo kwa sababu msingi ni variable huru. Kwa kweli,\(g(x)=x^3\) ni kazi ya nguvu.
Kumbuka kwamba msingi wa kazi\(b\) ya kielelezo daima ni mara kwa mara chanya, na\(b≠1\). Hivyo,\(j(x)={(−2)}^x\) haina kuwakilisha kazi kielelezo kwa sababu msingi,\(−2\), ni chini ya\(0\).
Ni ipi kati ya milinganyo ifuatayo inayowakilisha kazi za kielelezo?
- \(f(x)=2x^2−3x+1\)
- \(g(x)={0.875}^x\)
- \(h(x)=1.75x+2\)
- \(j(x)={1095.6}^{−2x}\)
- Jibu
-
\(g(x)={0.875}^x\)na\(j(x)={1095.6}^{−2x}\) kuwakilisha kazi za kielelezo.
Kutathmini Kazi za Kielelezo
Kumbuka kwamba msingi wa kazi exponential lazima chanya halisi idadi zaidi\(1\) ya.Kwa nini sisi kikomo bb msingi kwa maadili chanya? Ili kuhakikisha kwamba matokeo yatakuwa namba halisi. Angalia kinachotokea ikiwa msingi sio chanya:
- Hebu\(b=−9\) na\(x=\dfrac{1}{2}\). Kisha\(f(x)=f\left(\dfrac{1}{2}\right)={(−9)}^{\dfrac{1}{2}}=\sqrt{−9}\), ambayo si idadi halisi.
Kwa nini tunapunguza msingi kwa maadili mazuri zaidi ya\(1\)? Kwa sababu\(1\) matokeo ya msingi katika kazi ya mara kwa mara. Angalia kinachotokea ikiwa msingi ni\(1\):
- Hebu\(b=1\). Kisha\(f(x)=1^x=1\) kwa thamani yoyote ya\(x\).
Ili kutathmini kazi ya kielelezo na fomu\(f(x)=b^x\), tunabadilisha\(x\) tu thamani iliyotolewa, na kuhesabu nguvu inayosababisha. Kwa mfano:
Hebu\(f(x)=2^x\). Ni nini\(f(3)\)?
\[\begin{align*} f(x)&= 2^x\\ f(3)&= 2^3 \qquad \text{Substitute } x=3\\ &= 8 \qquad \text{Evaluate the power} \end{align*}\]
Ili kutathmini kazi ya kielelezo na fomu nyingine isipokuwa fomu ya msingi, ni muhimu kufuata utaratibu wa shughuli. Kwa mfano:
Hebu\(f(x)=30{(2)}^x\). Ni nini\(f(3)\)?
\[\begin{align*} f(x)&= 30{(2)}^x\\ f(3)&= 30{(2)}^3 \qquad \text{Substitute } x=3\\ &= 30(8) \qquad \text{Simplify the power first}\\ &= 240 \qquad \text{Multiply} \end{align*}\]
Kumbuka kwamba ikiwa utaratibu wa shughuli haukufuatiwa, matokeo hayatakuwa sahihi:
\[f(3)=30{(2)}^3≠{60}^3=216,000 \nonumber\]
Hebu\(f(x)=5{(3)}^{x+1}\). Tathmini\(f(2)\) bila kutumia calculator.
Suluhisho
Fuata utaratibu wa shughuli. Hakikisha uangalie mabano.
\[\begin{align*} f(x)&= 5{(3)}^{x+1}\\ f(2)&= 5{(3)}^{2+1} \qquad \text{Substitute } x=2\\ &= 5{(3)}^3 \qquad \text{Add the exponents}\\ &= 5(27) \qquad \text{Simplify the power}\\ &= 135 \qquad \text{Multiply} \end{align*}\]
Hebu\(f(x)=8{(1.2)}^{x−5}\). Tathmini\(f(3)\) kutumia calculator. Pande zote hadi sehemu nne za decimal.
- Jibu
-
\(5.5556\)
Kufafanua ukuaji wa kielelezo
Kwa sababu pato la kazi za kielelezo huongezeka kwa kasi sana, neno “ukuaji wa kielelezo” hutumiwa mara nyingi katika lugha ya kila siku kuelezea chochote kinachokua au kinaongezeka haraka. Hata hivyo, ukuaji wa kielelezo unaweza kuelezwa kwa usahihi kwa maana ya hisabati. Kama kiwango cha ukuaji ni sawia na kiasi sasa, kazi mifano ukuaji kielelezo.
kazi kwamba mifano ukuaji kielelezo kukua kwa kiwango sawia na kiasi sasa. Kwa idadi yoyote halisi\(x\) na idadi yoyote nzuri halisi\(a\) na\(b\) vile kwamba\(b≠1\), kazi ya ukuaji wa kielelezo ina fomu
\[f(x)=ab^x\]
wapi
- \(a\)ni thamani ya awali au ya kuanzia ya kazi.
- \(b\)ni sababu ya ukuaji au ukuaji multiplier kwa kitengo\(x\).
Kwa maneno zaidi ya jumla, tuna kazi ya kielelezo, ambayo msingi wa mara kwa mara unafufuliwa kwa kielelezo cha kutofautiana. Ili kutofautisha kati ya kazi za mstari na za kielelezo, hebu tuchunguze makampuni mawili, A na B. kampuni A ina\(100\) maduka na huongeza kwa kufungua maduka\(50\) mapya kwa mwaka, hivyo ukuaji wake unaweza kuwakilishwa na kazi\(A(x)=100+50x\). Kampuni B ina\(100\) maduka na huongeza kwa kuongeza idadi ya maduka kwa\(50\%\) kila mwaka, hivyo ukuaji wake unaweza kuwakilishwa na kazi\(B(x)=100{(1+0.5)}^x\).
Miaka michache ya ukuaji kwa makampuni haya ni mfano katika Jedwali\(\PageIndex{3}\).
| Mwaka,\(x\) | Maduka, Kampuni A | Maduka, Kampuni B |
|---|---|---|
| \ (x\) ">\(0\) | \(100+50(0)=100\) | \(100{(1+0.5)}^0=100\) |
| \ (x\) ">\(1\) | \(100+50(1)=150\) | \(100{(1+0.5)}^1=150\) |
| \ (x\) ">\(2\) | \(100+50(2)=200\) | \(100{(1+0.5)}^2=225\) |
| \ (x\) ">\(3\) | \(100+50(3)=250\) | \(100{(1+0.5)}^3=337.5\) |
| \ (x\) ">\(x\) | \(A(x)=100+50x\) | \(B(x)=100{(1+0.5)}^x\) |
Grafu kulinganisha idadi ya maduka kwa kila kampuni zaidi ya kipindi cha miaka mitano ni inavyoonekana katika Kielelezo\(\PageIndex{2}\). Tunaweza kuona kwamba, kwa ukuaji wa kielelezo, idadi ya maduka huongezeka kwa kasi zaidi kuliko ukuaji wa mstari.
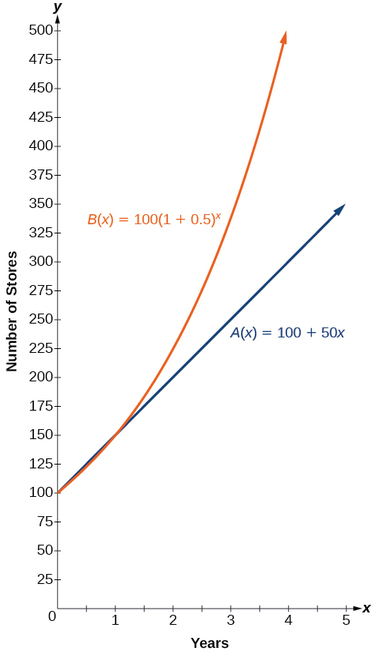
Angalia kwamba uwanja wa kazi zote mbili ni\([0,\infty)\), na upeo wa kazi zote mbili ni\([100,\infty)\). Baada ya mwaka 1, Kampuni B daima ina maduka zaidi kuliko Kampuni A.
Sasa tutageuka mawazo yetu kwa kazi inayowakilisha idadi ya maduka kwa Kampuni\(B\),\(B(x)=100{(1+0.5)}^x\). Katika kazi hii kielelezo,\(100\) inawakilisha idadi ya awali ya maduka,\(0.50\) inawakilisha kiwango cha ukuaji, na\(1+0.5=1.5\) inawakilisha sababu ya ukuaji. Generalizing zaidi, tunaweza kuandika kazi hii kama\(B(x)=100{(1.5)}^x\), ambapo\(100\) ni thamani ya awali,\(1.5\) inaitwa msingi, na\(x\) inaitwa exponent.
Mwanzoni mwa sehemu hii, tulijifunza kwamba idadi ya watu wa India ilikuwa karibu\(1.25\) bilioni mwaka 2013, na kiwango cha ukuaji wa kila mwaka wa karibu\(1.2\%\). Hali hii inawakilishwa na kazi ya ukuaji\(P(t)=1.25{(1.012)}^t\), ambapo\(t\) ni idadi ya miaka tangu 2013. Kwa elfu ya karibu, idadi ya watu wa India itakuwa nini mwaka 2031?
Suluhisho
Ili kukadiria idadi ya watu mwaka 2031, tunatathmini mifano ya\(t=18\), kwa sababu 2031 ni\(18\) miaka baada ya 2013. Kuzunguka kwa elfu ya karibu,
\[P(18)=1.25{(1.012)}^{18}≈1.549 \nonumber\]
Kutakuwa na watu\(1.549\) bilioni nchini India mwaka 2031.
Idadi ya wakazi wa China ilikuwa karibu\(1.39\) bilioni mwaka 2013, na kiwango cha ukuaji wa kila mwaka wa karibu\(0.6\%\). Hali hii inawakilishwa na kazi ya ukuaji\(P(t)=1.39{(1.006)}^t\), wapi\(t\) idadi ya miaka tangu 2013.Kwa elfu ya karibu, idadi ya watu wa China itakuwa nini kwa mwaka 2031? Je, hii inalinganishaje na utabiri wa idadi ya watu tuliyoifanya kwa India katika Mfano\(\PageIndex{3}\)?
- Jibu
-
\(1.548\)Takriban watu bilioni; kufikia mwaka 2031, idadi ya watu India itazidi China kwa karibu\(0.001\) bilioni, au watu\(1\) milioni.
Kutafuta Ulinganisho wa Kazi za Kielelezo
Katika mifano ya awali, tulipewa kazi kielelezo, ambayo sisi kisha tathmini kwa pembejeo fulani. Wakati mwingine tunapewa taarifa kuhusu kazi ya kielelezo bila kujua kazi wazi. Tunapaswa kutumia habari ili kwanza kuandika fomu ya kazi, kisha tambua mara kwa mara\(a, a\) na\(b, b\), na tathmini kazi.
- Ikiwa moja ya pointi za data ina fomu\((0,a)\), basi\(a\) ni thamani ya awali. Kwa kutumia\(a\), badala ya hatua ya pili katika equation\(f(x)=a{(b)}^x\), na kutatua kwa\(b\).
- Ikiwa hakuna pointi za data zina fomu\((0,a)\), badala ya pointi zote mbili katika milinganyo miwili na fomu\(f(x)=a{(b)}^x\). Tatua mfumo unaozalishwa wa equations mbili katika haijulikani mbili kupata\(a\) na\(b\).
- Kutumia\(a\) na\(b\) kupatikana katika hatua zilizo juu, andika kazi ya kielelezo katika fomu\(f(x)=a{(b)}^x\).
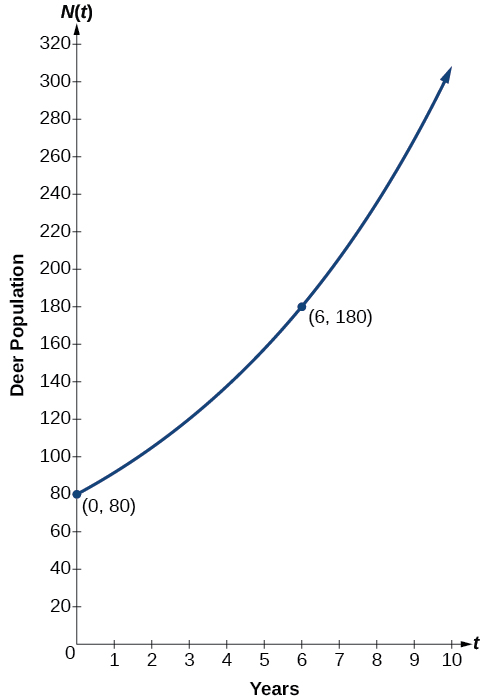
Mwaka 2006,\(80\) kulungu waliletwa katika kimbilio la wanyamapori. Kufikia mwaka 2012, idadi ya watu ilikuwa imeongezeka kwa\(180\) kulungu. Idadi ya watu ilikuwa inakua exponentially. Andika kazi ya algebraic\(N(t)\) inayowakilisha idadi\((N)\) ya kulungu baada ya muda\(t\).
Suluhisho
Tunaruhusu kutofautiana yetu ya kujitegemea\(t\) kuwa idadi ya miaka baada ya 2006. Hivyo, taarifa iliyotolewa katika tatizo inaweza kuandikwa kama jozi za pembejeo-pato: (0, 80) na (6, 180). Kumbuka kwamba kwa kuchagua pembejeo yetu variable kupimwa kama miaka baada ya 2006, tumetoa wenyewe thamani ya awali kwa ajili ya kazi,\(a=80\). Sasa tunaweza kubadilisha hatua ya pili katika equation\(N(t)=80b^t\) kupata\(b\):
\[\begin{align*} N(t)&= 80b^t\\ 180&= 80b^6 \qquad \text{Substitute using point } (6, 180)\\ \dfrac{9}{4}&= b^6 \qquad \text{Divide and write in lowest terms}\\ b&= {\left (\dfrac{9}{4} \right )}^{\tfrac{1}{6}} \qquad \text{Isolate b using properties of exponents}\\ b&\approx 1.1447 \qquad \text{Round to 4 decimal places} \end{align*}\]
Isipokuwa ilivyoelezwa vinginevyo, usizunguze mahesabu yoyote ya kati. Kisha pande zote jibu la mwisho kwa maeneo manne kwa salio la sehemu hii.
Mfano wa kielelezo kwa idadi ya watu wa kulungu ni\(N(t)=80{(1.1447)}^t\). (Kumbuka kuwa mfano huu wa kazi ya kielelezo ukuaji wa muda mfupi. Kama pembejeo inapata kubwa, pato litazidi kuongezeka, kiasi kwamba mfano hauwezi kuwa na manufaa kwa muda mrefu.)
Tunaweza graph mfano wetu kuchunguza ukuaji wa idadi ya kulungu katika kimbilio baada ya muda. Kumbuka kwamba grafu katika Kielelezo\(\PageIndex{3}\) hupita kupitia pointi za awali zilizotolewa katika tatizo,\((0, 80)\) na\((6, 180)\). Tunaweza pia kuona kwamba uwanja kwa ajili ya kazi ni\([0,\infty)\), na mbalimbali kwa ajili ya kazi ni\([80,\infty)\).
Idadi ya mbwa mwitu inakua kwa kiasi kikubwa. Mwaka 2011,\(129\) mbwa mwitu zilihesabiwa. Kufikia mwaka 2013, idadi ya watu ilikuwa imefikia\(236\) mbwa mwitu. Nini pointi mbili zinaweza kutumika hupata equation kielelezo modeling hali hii? Andika equation inayowakilisha idadi ya\(N\) mbwa mwitu baada ya muda\(t\).
- Jibu
-
\((0,129)\)na\((2,236)\);\(N(t)=129{(1.3526)}^t\)
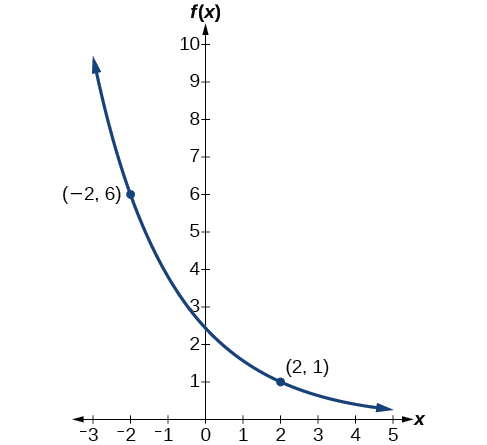
Kupata kazi kielelezo kwamba hupita kwa njia ya pointi\((−2,6)\) na\((2,1)\).
Suluhisho
Kwa sababu hatuna thamani ya awali, sisi badala pointi zote mbili katika equation ya fomu\(f(x)=ab^x\), na kisha kutatua mfumo kwa\(a\) na\(b\).
- Kubadilisha\((−2,6)\) anatoa\(6=ab^{−2}\)
- Kubadilisha\((2,1)\) anatoa\(1=ab^2\)
Tumia equation ya kwanza kutatua\(a\) kwa suala la\(b\):
\[\begin{align*} 6&= ab^{-2}\\ \dfrac{6}{b^{-2}}&= a \qquad \text{Divide}\\ a&= 6b^2 \qquad \text{Use properties of exponents to rewrite the denominator} \end{align*}\]
Mbadala a katika equation pili, na kutatua kwa\(b\):
\[\begin{align*} 1&= ab^{2}\\ 1&= 6b^2 b^2\\ &= 6b^4 \qquad \text{Substitute a}\\ b&= \left (\dfrac{1}{6} \right )^{\tfrac{1}{4}} \qquad \text{Round 4 decimal places rewrite the denominator}\\ b&\approx 0.6389 \end{align*}\]
Tumia thamani ya\(b\) katika equation kwanza kutatua kwa thamani ya\(a\):
\[\begin{align*} a&= 6b^{2}\\ &\approx 6(0.6389)^2 \\ &\approx 2.4492 \end{align*}\]
Hivyo, equation ni\(f(x)=2.4492{(0.6389)}^x\).
Tunaweza graph mfano wetu kuangalia kazi yetu. Kumbuka kwamba grafu katika Kielelezo\(\PageIndex{4}\) hupita kupitia pointi za awali zilizotolewa katika tatizo,\((−2, 6)\) na\((2, 1)\). Grafu ni mfano wa kazi ya kuoza kwa ufafanuzi.
Kutokana\((1,3)\) na pointi mbili na\((2,4.5)\), kupata equation ya kazi kielelezo kwamba hupita kwa njia ya pointi hizi mbili.
- Jibu
-
\(f(x)=2{(1.5)}^x\)
Ndiyo, zinazotolewa pointi mbili ni ama juu ya x-axis au wote chini ya x-axis na kuwa na tofauti x-kuratibu. Lakini kukumbuka kwamba tunahitaji pia kujua kwamba grafu ni, kwa kweli, kazi ya kielelezo. Si kila grafu ambayo inaonekana kielelezo kweli ni kielelezo. Tunahitaji kujua grafu ni msingi mfano kwamba inaonyesha sawa asilimia ukuaji na kila ongezeko kitengo katika\(x\), ambayo katika kesi nyingi ulimwengu halisi inahusisha muda.
- Kwanza, tambua pointi mbili kwenye grafu. Chagua\(y\) -intercept kama moja ya pointi mbili wakati wowote iwezekanavyo. Jaribu kuchagua pointi ambazo ni mbali mbali iwezekanavyo ili kupunguza kosa la pande zote.
- Ikiwa moja ya pointi za data ni\(y\) -intercept\((0,a)\), basi\(a\) ni thamani ya awali. Kutumia\(a\), badala ya hatua ya pili katika equation\(f(x)=a{(b)}^x\), na kutatua kwa\(b\)
- Ikiwa hakuna pointi za data zina fomu\((0,a)\), badala ya pointi zote mbili katika milinganyo miwili na fomu\(f(x)=a{(b)}^x\). Tatua mfumo unaozalishwa wa equations mbili katika haijulikani mbili kupata\(a\) na\(b\).
- Andika kazi ya kielelezo,\(f(x)=a{(b)}^x\).
Kupata equation kwa ajili ya kazi kielelezo graphed katika Kielelezo\(\PageIndex{5}\).
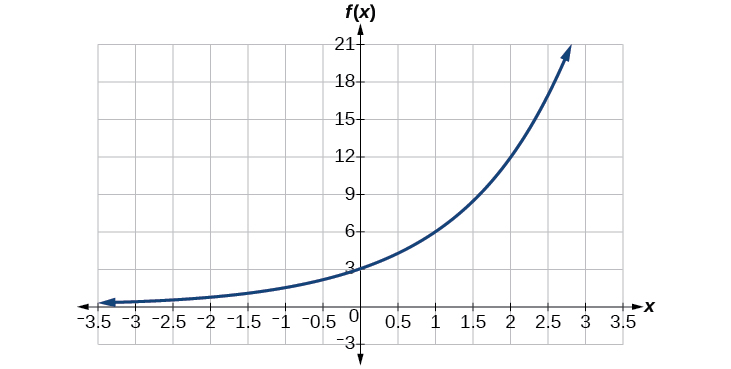
Suluhisho
Tunaweza kuchagua \(y\)-intercept ya grafu\((0,3)\), kama hatua yetu ya kwanza. Hii inatupa thamani ya awali,\(a=3\). Next, kuchagua uhakika juu ya Curve baadhi umbali mbali na\((0,3)\) kwamba ina kuratibu integer. Jambo moja ni\((2,12)\).
\[\begin{align*} y&= ab^x \qquad \text{Write the general form of an exponential equation}\\ y&= 3b^x \qquad \text{Substitute the initial value } 3 \text{ for } a\\ 12&= 3b^2 \qquad \text{Substitute in 12 for } y \text{ and } 2 \text{ for } x\\ 4&= b^2 \qquad \text{Divide by }3\\ b&= \pm 2 \qquad \text{Take the square root} \end{align*}\]
Kwa sababu sisi kuzuia wenyewe kwa maadili chanya ya\(b\), tutatumia\(b=2\). Mbadala\(a\) na\(b\) katika fomu ya kawaida ili kuzalisha equation\(f(x)=3{(2)}^x\).
Kupata equation kwa ajili ya kazi kielelezo graphed katika Kielelezo\(\PageIndex{6}\).
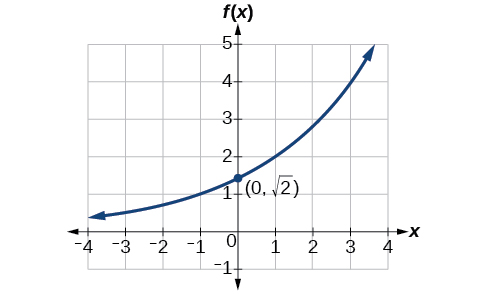
- Jibu
-
\(f(x)=\sqrt{2}{(\sqrt{2})}^x\). Majibu yanaweza kutofautiana kutokana na hitilafu ya pande zote. Jibu linapaswa kuwa karibu sana\(1.4142{(1.4142)}^x\).
- Vyombo vya habari [STAT].
- Futa entries yoyote zilizopo katika nguzo L1 au L2.
- Katika L1, ingiza kuratibu x zilizopewa.
- Katika L2, ingiza y sambamba -kuratibu.
- Press [STAT] tena. Cursor haki ya CALC, kitabu chini kwa Expreg (Kielelezo regression), na waandishi wa habari [ENTER].
- Screen inaonyesha maadili ya a na b katika equation exponential\(y=a⋅b^x\).
Tumia calculator graphing kupata equation kielelezo kuwa ni pamoja\((2,24.8)\) na pointi na\((5,198.4)\).
Suluhisho
Fuata miongozo hapo juu. Kwanza vyombo vya habari [STAT], [HARIRI], [1: Hariri...], na wazi orodha L1 na L2. Kisha, katika safu ya L1, ingiza\(x\) -kuratibu,\(2\) na\(5\). Fanya sawa katika safu ya L2 kwa\(y\) kuratibu,\(24.8\) na\(198.4\).
Sasa waandishi wa habari [STAT], [CALC], [0: ExPreg] na waandishi wa habari [ENTER]. Maadili\(a=6.2\) na\(b=2\) itaonyeshwa. equation kielelezo ni\(y=6.2⋅2^x\).
Tumia calculator graphing kupata equation kielelezo kuwa ni pamoja\((3, 75.98)\) na pointi na\((6, 481.07)\).
- Jibu
-
\(y≈12⋅{1.85}^x\)
Kutumia Mfumo wa Maslahi ya Kiwanja
Vyombo vya akiba ambavyo mapato yanaendelea kurejeshwa tena, kama vile fedha za kuheshimiana na akaunti za kustaafu, tumia riba ya kiwanja. Neno linamaanisha maslahi ya chuma sio tu kwa thamani ya awali, lakini kwa thamani ya kusanyiko ya akaunti.
Kiwango cha asilimia ya kila mwaka (Aprili) ya akaunti, pia huitwa kiwango cha nominella, ni kiwango cha riba cha kila mwaka kilichopatikana na akaunti ya uwekezaji. Neno la jina linatumiwa wakati mchanganyiko hutokea mara kadhaa zaidi ya mara moja kwa mwaka. Kwa kweli, wakati riba imezungukwa zaidi ya mara moja kwa mwaka, kiwango cha riba cha ufanisi kinaishia kuwa kikubwa kuliko kiwango cha majina! Hii ni chombo chenye nguvu cha kuwekeza.
Tunaweza kuhesabu maslahi ya kiwanja kwa kutumia fomu ya riba ya kiwanja, ambayo ni kazi ya kielelezo ya wakati wa vigezo\(t\)\(P\)\(APR\)\(r\), mkuu, na idadi ya vipindi vya kuchanganya kwa mwaka\(n\):
\[A(t)=P{\left (1+\dfrac{r}{n} \right )}^{nt} \nonumber\]
Kwa mfano, angalia Jedwali\(\PageIndex{4}\), ambayo inaonyesha matokeo ya kuwekeza\($1,000\)\(10\%\) kwa mwaka mmoja. Angalia jinsi thamani ya akaunti inavyoongezeka kama mzunguko unavyoongezeka.
| Marudio | Thamani baada ya\(1\) mwaka |
|---|---|
| Kila mwaka | \ (1\) mwaka">\($1100\) |
| Semikila mwaka | \ (1\) mwaka">\($1102.50\) |
| Robo | \ (1\) mwaka">\($1103.81\) |
| Kila mwezi | \ (1\) mwaka">\($1104.71\) |
| Daily | \ (1\) mwaka">\($1105.16\) |
Maslahi ya kiwanja yanaweza kuhesabiwa kwa kutumia formula
\[A(t)=P{\left (1+\dfrac{r}{n} \right )}^{nt}\]
wapi
- \(A(t)\)ni thamani ya akaunti,
- \(t\)hupimwa kwa miaka,
- \(P\)ni kiasi cha kuanzia cha akaunti, mara nyingi huitwa mkuu, au thamani zaidi ya sasa,
- \(r\)ni kiwango cha asilimia ya kila mwaka (Aprili) walionyesha kama decimal, na
- \(n\)ni idadi ya vipindi vya kuchanganya katika mwaka mmoja.
Kama sisi kuwekeza\($3,000\) katika akaunti ya uwekezaji kulipa\(3\%\) riba imezungukwa robo mwaka, ni kiasi gani akaunti kuwa na thamani katika\(10\) miaka?
Suluhisho
Kwa sababu tunaanza na\($3,000\),\(P=3000\). Kiwango cha riba yetu ni\(3\%\), hivyo\(r = 0.03\). Kwa sababu sisi ni compounding robo mwaka, sisi ni compounding\(4\) mara kwa mwaka, hivyo\(n=4\). Tunataka kujua thamani ya akaunti katika\(10\) miaka, kwa hiyo tunatafuta\(A(10)\), thamani wakati\(t = 10\).
\[\begin{align*} A(t)&= P{\left (1+\dfrac{r}{n} \right )}^{nt} \qquad \text{Use the compound interest formula}\\ A(10)&= 3000{\left (1+\dfrac{0.03}{4} \right )}^{(4)\cdot (10)} \qquad \text{Substitute using given values}\\ &\approx \$4045.05 \qquad \text{Round to two decimal places} \end{align*}\]
Akaunti itakuwa ya thamani kuhusu\($4,045.05\)\(10\) miaka.
Uwekezaji wa awali wa\($100,000\)\(12\%\) maslahi ni umezungukwa kila\(52\) wiki (kutumia wiki kwa mwaka). Uwekezaji utakuwa na thamani gani katika\(30\) miaka?
- Jibu
-
kuhusu\($3,644,675.88\)
Mpango wa 529 ni mpango wa akiba ya chuo ambayo inaruhusu jamaa kuwekeza pesa kulipia masomo ya chuo ya baadaye ya mtoto; akaunti inakua bila kodi. Lily anataka kuanzisha akaunti ya 529 kwa mjukuu wake mpya na anataka akaunti kukua hadi\($40,000\) zaidi ya\(18\) miaka. Yeye anaamini akaunti kulipwa\(6\%\) imezungukwa nusu mwaka (mara mbili kwa mwaka). Kwa dola ya karibu, ni kiasi gani Lily atahitaji kuwekeza katika akaunti sasa?
Suluhisho
Kiwango cha riba cha nominella ni\(6\%\), hivyo\(r=0.06\). Maslahi ni umezungukwa mara mbili kwa mwaka, hivyo\(k=2\).
Tunataka kupata uwekezaji wa awali\(P\),, zinahitajika ili thamani ya akaunti itakuwa na thamani\($40,000\) katika\(18\) miaka. Badilisha maadili yaliyotolewa katika formula ya maslahi ya kiwanja, na kutatua\(P\).
\[\begin{align*} A(t)&= P{\left (1+\dfrac{r}{n} \right )}^{nt} \qquad \text{Use the compound interest formula}\\ 40,000&= P{\left (1+\dfrac{0.06}{2} \right )}^{2(18)} \qquad \text{Substitute using given values } A, r, n, t\\ 40,000&= P{(1.03)}^{36} \qquad \text{Simplify}\\ \dfrac{40,000}{ {(1.03)}^{36} }&= P \qquad \text{Isolate } P\\ P&\approx \$13,801 \qquad \text{Divide and round to the nearest dollar} \end{align*}\]
Lily haja ya\($13,801\) kuwekeza kuwa\($40,000\) katika\(18\) miaka.
Rejea Mfano\(\PageIndex{9}\). Kwa dola ya karibu, ni kiasi gani Lily haja ya kuwekeza kama akaunti imezungukwa robo mwaka?
- Jibu
-
\($13,693\)
Kutathmini Kazi na Msingi\(e\)
Kama tulivyoona hapo awali, kiasi kilichopatikana kwenye akaunti kinaongezeka kama kuongezeka kwa mzunguko unaoongezeka. Jedwali\(\PageIndex{5}\) linaonyesha kwamba ongezeko kutoka kwa kila mwaka hadi nusu ya kila mwaka ni kubwa zaidi kuliko ongezeko kutoka kila mwezi hadi kila siku. Hii inaweza kutuongoza kuuliza kama muundo huu utaendelea.
Kuchunguza thamani ya\($1\) imewekeza katika\(100\%\) riba kwa\(1\) mwaka, imezungukwa katika masafa mbalimbali, waliotajwa katika Jedwali\(\PageIndex{5}\).
| Marudio | \(A(t)={\left (1+\dfrac{1}{n} \right )}^n\) | Thamani |
|---|---|---|
| Kila mwaka | \ (A (t) = {\ kushoto (1+\ dfrac {1} {n}\ haki)} ^n\)” style="wima align:katikati; ">\({\left (1+\dfrac{1}{1} \right )}^1\) | \($2\) |
| Semikila mwaka | \ (A (t) = {\ kushoto (1+\ dfrac {1} {n}\ haki)} ^n\)” style="wima align:katikati; ">\({\left (1+\dfrac{1}{2} \right )}^2\) | \($2.25\) |
| Robo | \ (A (t) = {\ kushoto (1+\ dfrac {1} {n}\ haki)} ^n\)” style="wima align:katikati; ">\({\left (1+\dfrac{1}{4} \right )}^4\) | \($2.441406\) |
| Kila mwezi | \ (A (t) = {\ kushoto (1+\ dfrac {1} {n}\ haki)} ^n\)” style="wima align:katikati; ">\({\left (1+\dfrac{1}{12} \right )}^{12}\) | \($2.613035\) |
| Daily | \ (A (t) = {\ kushoto (1+\ dfrac {1} {n}\ haki)} ^n\)” style="wima align:katikati; ">\({\left (1+\dfrac{1}{365} \right )}^{365}\) | \($2.714567\) |
| Kila saa | \ (A (t) = {\ kushoto (1+\ dfrac {1} {n}\ haki)} ^n\)” style="wima align:katikati; ">\({\left (1+\dfrac{1}{8760} \right )}^{8760}\) | \($2.718127\) |
| Mara moja kwa dakika | \ (A (t) = {\ kushoto (1+\ dfrac {1} {n}\ haki)} ^n\)” style="wima align:katikati; ">\({\left (1+\dfrac{1}{525600} \right )}^{525600}\) | \($2.718279\) |
| Mara moja kwa sekunde | \ (A (t) = {\ kushoto (1+\ dfrac {1} {n}\ haki)} ^n\)” style="wima align:katikati; ">\({\left (1+\dfrac{1}{31536000} \right )}^{31536000}\) | \($2.718282\) |
Maadili haya yanaonekana kuwa inakaribia kikomo kama\(n\) ongezeko bila kufungwa. Kwa kweli, kama\(n\) anapata kubwa na kubwa, kujieleza\({\left (1+\dfrac{1}{n} \right )}^n\) mbinu idadi kutumika hivyo mara nyingi katika hisabati kwamba ina jina lake mwenyewe: barua\(e\). Thamani hii ni namba isiyo na maana, ambayo ina maana kwamba upanuzi wake wa decimal unaendelea milele bila kurudia. Makadirio yake kwa maeneo sita ya decimal ni hapa chini.
Barua\(e\) inawakilisha nambari isiyo na maana
\[{\left (1+\dfrac{1}{n} \right )}^n\]
kama\(n\) ongezeko bila kufungwa
Barua\(e\) hutumiwa kama msingi kwa mifano mingi ya ulimwengu halisi. Kufanya kazi na msingi\(e\), tunatumia makadirio,\(e≈2.718282\). Mara kwa mara iliitwa na mwanahisabati wa Uswisi Leonhard Euler (1707—1783) aliyechunguza kwanza na kugundua mali zake nyingi.
Tumia\(e^{3.14}\). Pande zote hadi maeneo tano ya decimal.
Suluhisho
Kwenye calculator, bonyeza kitufe kinachoitwa\([e^x]\). Dirisha inaonyesha\([e {}^( ]\). \(3.14\)Andika na kisha karibu na mabano,\([)]\). Waandishi wa habari [INGIZA]. Kuzunguka kwa maeneo ya\(5\) decimal,\(e^{3.14}≈23.10387\). Tahadhari: Wahesabu wengi wa kisayansi wana kifungo cha “Exp”, ambacho hutumiwa kuingia namba katika nukuu za kisayansi. Haitumiwi kupata nguvu za\(e\).
Tumia calculator kupata\(e^{−0.5}\). Pande zote hadi maeneo tano ya decimal.
- Jibu
-
\(e^{−0.5}≈0.60653\)
Kuchunguza ukuaji wa kuendelea
Hadi sasa tumefanya kazi na misingi ya busara kwa kazi za kielelezo. Kwa matukio mengi ya ulimwengu halisi, hata hivyo,\(e\) hutumiwa kama msingi wa kazi za kielelezo. Mifano ya kielelezo ambayo hutumia\(e\) kama msingi huitwa ukuaji wa kuendelea au mifano ya kuoza. Tunaona mifano hii katika fedha, sayansi ya kompyuta, na sayansi nyingi, kama vile fizikia, toxicology, na mienendo ya maji.
Kwa namba zote halisi\(t\), na namba zote nzuri\(a\) na\(r\), ukuaji wa kuendelea au kuoza huwakilishwa na formula
\[A(t)=ae^{rt}\]
wapi
- \(a\)ni thamani ya awali,
- \(r\)ni kiwango cha ukuaji wa kuendelea kwa wakati kitengo,
- \(t\)ni wakati uliopita.
Ikiwa\(r>0\), basi formula inawakilisha ukuaji wa kuendelea. Ikiwa\(r<0\), basi formula inawakilisha kuoza kwa kuendelea.
Kwa ajili ya maombi ya biashara, formula ya ukuaji wa kuendelea inaitwa formula inayoendelea inayoendelea na inachukua fomu
\[A(t)=Pe^{rt}\]
wapi
- \(P\)ni mkuu au ya awali imewekeza,
- \(r\)ni ukuaji au kiwango cha riba kwa wakati kitengo,
- \(t\)ni kipindi au muda wa uwekezaji.
- Tumia habari katika tatizo kuamua\(a\), thamani ya awali ya kazi.
- Tumia habari katika tatizo ili kuamua kiwango cha ukuaji\(r\).
- Ikiwa tatizo linamaanisha ukuaji wa kuendelea, basi\(r>0\).
- Ikiwa tatizo linamaanisha kuoza kwa kuendelea, basi\(r<0\).
- Tumia habari katika tatizo ili ueleze wakati\(t\).
- Badilisha taarifa iliyotolewa katika fomu ya ukuaji wa kuendelea na kutatua\(A(t)\).
Mtu aliyewekeza\($1,000\) katika akaunti akipata jina la majina\(10\%\) kwa mwaka linajumuishwa kwa kuendelea. Ni kiasi gani kilichokuwa katika akaunti mwishoni mwa mwaka mmoja?
Suluhisho
Kwa kuwa akaunti inakua kwa thamani, hii ni tatizo linaloendelea la kuchanganya na kiwango cha ukuaji\(r=0.10\). Uwekezaji wa awali ulikuwa\($1,000\), hivyo\(P=1000\). Tunatumia formula inayoendelea inayoendelea ili kupata thamani baada ya\(t=1\) mwaka:
\[\begin{align*} A(t)&= Pe^{rt} \qquad \text{Use the continuous compounding formula}\\ &= 1000{(e)}^{0.1} \qquad \text{Substitute known values for } P, r, t\\ &\approx 1105.17 \qquad \text{Use a calculator to approximate} \end{align*}\]
Akaunti ni\($1,105.17\) ya thamani baada ya mwaka mmoja.
Mtu huwekeza\($100,000\) kwa\(12\%\) maslahi ya nominella kwa mwaka imezungukwa kuendelea. Nini itakuwa thamani ya uwekezaji katika\(30\) miaka?
- Jibu
-
\($3,659,823.44\)
\(Radon-222\)kuoza kwa kiwango cha kuendelea\(17.3\%\) kwa siku. Ni kiasi gani\(100 mg\) cha\(Radon-222\) kuoza kwa\(3\) siku?
Suluhisho
Tangu dutu hii inaoza, kiwango,\(17.3\%\), ni hasi. Kwa hiyo,\(r = −0.173\). Kiasi cha awali cha\(Radon-222\) ilikuwa\(100\) mg, hivyo\(a=100\). Tunatumia fomu ya kuoza inayoendelea ili kupata thamani baada ya\(t=3\) siku:
\[\begin{align*} A(t)&= ae^{rt} \qquad \text{Use the continuous growth formula}\\ &= 100e6{-0.173(3)} \qquad \text{Substitute known values for } a, r, t\\ &\approx 59.5115 \qquad \text{Use a calculator to approximate} \end{align*}\]
Hivyo\(59.5115\) mg ya\(Radon-222\) kubaki.
Kutumia data katika Mfano\(\PageIndex{12}\), ni kiasi gani\(Radon-222\) kitabaki baada ya mwaka mmoja?
- Jibu
-
\(3.77E-26\)(Hii ni calculator nukuu kwa idadi iliyoandikwa kama\(3.77×10^{−26}\) katika nukuu ya kisayansi. Wakati pato la kazi kielelezo ni kamwe sifuri, idadi hii ni karibu na sifuri kwamba kwa madhumuni yote ya vitendo tunaweza kukubali sifuri kama jibu.)
Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na kazi za kielelezo.
- Kazi ya ukuaji wa kielelezo
- Kiwanja maslahi
Mlinganyo muhimu
| ufafanuzi wa kazi ya kielelezo | \(f(x)=b^x\), wapi\(b>0\),\(b≠1\) |
| ufafanuzi wa ukuaji wa kielelezo | \(f(x)=ab^x\), wapi\(a>0\)\(b>0\),\(b≠1\) |
| kiwanja riba formula |
\(A(t)=P{(1+\dfrac{r}{n})}^{nt}\), \(A(t)\)wapi thamani ya akaunti kwa wakati\(t\) \(t\)ni idadi ya miaka \(P\)ni uwekezaji wa awali, mara nyingi huitwa mkuu \(r\)ni kiwango cha asilimia ya kila mwaka (Aprili), au kiwango cha nominella \(n\)ni idadi ya vipindi vya kuchanganya katika mwaka mmoja |
| formula ya ukuaji wa kuendelea | \(A(t)=ae^{rt}\), wapi\(t\) idadi ya vipindi vya wakati wa kitengo cha ukuaji\(a\) ni kiasi cha kuanzia (katika formula inayoendelea ya kuchanganya a inabadilishwa na\(P\), mkuu)\(e\) ni mara kwa mara ya hisabati,\(e≈2.718282\) |
Dhana muhimu
- kazi kielelezo hufafanuliwa kama kazi na mara kwa mara chanya zaidi ya\(1\) kukulia kwa exponent variable. Angalia Mfano.
- Kazi ni tathmini kwa kutatua kwa thamani maalum. Angalia Mfano na Mfano.
- Mfano wa kielelezo unaweza kupatikana wakati kiwango cha ukuaji na thamani ya awali hujulikana. Angalia Mfano.
- Mfano wa kielelezo unaweza kupatikana wakati pointi mbili za data kutoka kwa mfano zinajulikana. Angalia Mfano.
- Mfano wa kielelezo unaweza kupatikana kwa kutumia pointi mbili za data kutoka kwenye grafu ya mfano. Angalia Mfano.
- Mfano wa kielelezo unaweza kupatikana kwa kutumia pointi mbili za data kutoka kwenye grafu na calculator. Angalia Mfano.
- Thamani ya akaunti wakati wowote\(t\) inaweza kuhesabiwa kwa kutumia formula ya riba ya kiwanja wakati mkuu, kiwango cha riba ya kila mwaka, na vipindi vya kuchanganya vinajulikana. Angalia Mfano.
- Uwekezaji wa awali wa akaunti unaweza kupatikana kwa kutumia fomu ya riba ya kiwanja wakati thamani ya akaunti, kiwango cha riba ya kila mwaka, vipindi vya kuchanganya, na muda wa maisha ya akaunti hujulikana. Angalia Mfano.
- Nambari\(e\) ni mara kwa mara ya hisabati mara nyingi hutumiwa kama msingi wa ukuaji wa kielelezo wa dunia halisi na mifano ya kuoza. Makadirio yake ya decimal ni\(e≈2.718282\).
- Scientific na graphing calculators na ufunguo\([ex]\) au\([exp(x)]\) kwa ajili ya kuhesabu nguvu ya\(e\). Angalia Mfano.
- Ukuaji unaoendelea au mifano ya kuoza ni mifano ya kielelezo ambayo hutumia\(e\) kama msingi. Ukuaji unaoendelea na mifano ya kuoza inaweza kupatikana wakati thamani ya awali na ukuaji au kiwango cha kuoza kinajulikana. Angalia Mfano na Mfano.


