1.1: Kazi na Uthibitishaji wa Kazi
- Page ID
- 181141
Malengo ya kujifunza
- Kuamua kama uhusiano inawakilisha kazi.
- Kupata thamani ya kazi.
- Kuamua kama kazi ni moja kwa moja.
- Tumia mtihani wa mstari wa wima ili kutambua kazi.
- Grafu kazi zilizoorodheshwa kwenye maktaba ya kazi.
Jetliner inabadilisha urefu kama umbali wake kutoka mwanzo wa ndege huongezeka. Uzito wa mtoto anayekua huongezeka kwa wakati. Katika kila kesi, kiasi kimoja kinategemea mwingine. Kuna uhusiano kati ya kiasi mbili ambazo tunaweza kuelezea, kuchambua, na kutumia kufanya utabiri. Katika sehemu hii, tutachambua mahusiano hayo.
Kuamua Kama Uhusiano Inawakilisha Kazi
Uhusiano ni seti ya jozi zilizoamriwa. Seti ya vipengele vya kwanza vya kila jozi iliyoamriwa inaitwa kikoa na seti ya vipengele vya pili vya kila jozi iliyoamriwa inaitwa upeo. Fikiria seti zifuatazo za jozi zilizoamriwa. Nambari za kwanza katika kila jozi ni namba tano za kwanza za asili. Nambari ya pili katika kila jozi ni mara mbili ya kwanza.
\[\{(1, 2), (2, 4), (3, 6), (4, 8), (5, 10)\}\tag{1.1.1}\]
Kikoa ni\(\{1, 2, 3, 4, 5\}\). Mipangilio ni\(\{2, 4, 6, 8, 10\}\).
Kumbuka kwamba kila thamani katika uwanja pia inajulikana kama thamani ya pembejeo, au kutofautiana kwa kujitegemea, na mara nyingi huandikwa na barua ya chini\(x\). Kila thamani katika upeo pia inajulikana kama thamani ya pato, au kutofautiana kwa tegemezi, na mara nyingi huitwa barua ya chini\(y\).
Kazi\(f\) ni uhusiano unaoweka thamani moja katika upeo kwa kila thamani katika kikoa. Kwa maneno mengine, hakuna\(x\) maadili yanarudiwa. Kwa mfano wetu kwamba inahusiana kwanza tano namba ya asili kwa idadi mara mbili ya maadili yao, uhusiano huu ni kazi kwa sababu kila kipengele katika uwanja, {1, 2, 3, 4, 5}, ni paired na hasa kipengele moja katika mbalimbali,\(\{2, 4, 6, 8, 10\}\).
Sasa hebu tuchunguze seti ya jozi zilizoamriwa zinazohusiana na maneno “hata” na “isiyo ya kawaida” kwa namba tano za kwanza za asili. Inaweza kuonekana kama
\[\mathrm{\{(odd, 1), (even, 2), (odd, 3), (even, 4), (odd, 5)\}} \tag{1.1.2}\]
Angalia kwamba kila kipengele katika uwanja, {hata, isiyo ya kawaida} haijaunganishwa na kipengele kimoja hasa katika upeo,\(\{1, 2, 3, 4, 5\}\). Kwa mfano, neno “isiyo ya kawaida” linalingana na maadili matatu kutoka kwa upeo,\(\{1, 3, 5\},\) na neno “hata” linalingana na maadili mawili kutoka kwa upeo,\(\{2, 4\}\). Hii inakiuka ufafanuzi wa kazi, hivyo uhusiano huu si kazi.
Kielelezo\(\PageIndex{1}\) kulinganisha mahusiano ambayo ni kazi na si kazi.
![[Mahusiano matatu ambayo yanaonyesha nini hufanya kazi.]](https://math.libretexts.org/@api/deki/files/861/CNX_Precalc_Figure_01_01_001.jpg)
Kazi
Kazi ni uhusiano ambao kila thamani ya pembejeo inayowezekana inaongoza kwa thamani moja ya pato. Tunasema “pato ni kazi ya pembejeo.”
Maadili ya pembejeo yanafanya kikoa, na maadili ya pato hufanya upeo.
Jinsi ya: Kutokana na uhusiano kati ya kiasi mbili, kuamua kama uhusiano ni kazi
- Tambua maadili ya pembejeo.
- Tambua maadili ya pato.
- Ikiwa kila thamani ya pembejeo inaongoza kwa thamani moja tu ya pato, weka uhusiano kama kazi. Ikiwa thamani yoyote ya pembejeo inaongoza kwa matokeo mawili au zaidi, usifanye uhusiano kama kazi.
Mfano\(\PageIndex{1}\): Determining If Menu Price Lists Are Functions
kahawa duka menu, inavyoonekana katika Kielelezo\(\PageIndex{2}\) lina vitu na bei zao.
- Je, bei ni kazi ya bidhaa?
- Je, bidhaa ni kazi ya bei?

Suluhisho
- Hebu tuanze kwa kuzingatia pembejeo kama vitu kwenye menyu. Maadili ya pato ni basi bei. Angalia Kielelezo\(\PageIndex{3}\).
![[Orodha ya bei za donut kutoka duka la kahawa ambapo donut wazi ni $1.49 na donut ya jelly na donut ya chokoleti ni $1.99.]](https://math.libretexts.org/@api/deki/files/865/CNX_Precalc_Figure_01_01_027.v2.jpg)
Kila kitu kwenye menyu kina bei moja tu, hivyo bei ni kazi ya kipengee.
- Vipengee viwili kwenye menyu vina bei sawa. Ikiwa tunazingatia bei kuwa maadili ya pembejeo na vitu kuwa pato, basi thamani sawa ya pembejeo inaweza kuwa na pato zaidi ya moja inayohusishwa nayo. Angalia Kielelezo\(\PageIndex{4}\).
![[Chama cha bei kwa donuts.]](https://math.libretexts.org/@api/deki/files/866/CNX_Precalc_Figure_01_01_028.jpg)
Kwa hiyo, bidhaa ni si kazi ya bei.
Mfano\(\PageIndex{2}\): Determining If Class Grade Rules Are Functions
Katika darasa fulani la hesabu, daraja la jumla la asilimia linalingana na wastani wa kiwango cha daraja. Je daraja uhakika wastani kazi ya asilimia daraja? Je asilimia daraja kazi ya wastani daraja uhakika? Jedwali\(\PageIndex{1}\) linaonyesha utawala unaowezekana wa kugawa pointi za daraja.
| Asilimia daraja | 0—56 | 57—61 | 62—66 | 67—71 | 72—77 | 78—86 | 87—91 | 92—100 |
| Wastani wa kiwango cha daraja | 0.0 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Suluhisho
Kwa asilimia yoyote daraja chuma, kuna kuhusishwa daraja uhakika wastani, hivyo daraja uhakika wastani ni kazi ya asilimia daraja. Kwa maneno mengine, kama sisi pembejeo asilimia daraja, pato ni maalum daraja uhakika wastani.
Katika mfumo grading kutokana, kuna aina mbalimbali ya asilimia darasa kwamba yanahusiana na kiwango sawa daraja uhakika wastani. Kwa mfano, wanafunzi wanaopata wastani wa kiwango cha daraja la 3.0 wanaweza kuwa na aina mbalimbali za asilimia darasa kuanzia 78 njia yote hadi 86. Hivyo, asilimia daraja si kazi ya wastani daraja uhakika.
Zoezi\(\PageIndex{2}\)
Meza\(\PageIndex{2}\) orodha tano kubwa wachezaji baseball wa wakati wote katika utaratibu wa cheo.
| Mchezaji | Cheo |
|---|---|
| mtoto Ruth | 1 |
| Willie Mays | 2 |
| Ty Cobb | 3 |
| Walter Johnson | 4 |
| Hank Haruni | 5 |
- Je cheo kazi ya jina mchezaji?
- Je mchezaji jina kazi ya cheo?
- Jibu
-
Ndio
- Jibu b
-
ndiyo. (Kumbuka: Ikiwa wachezaji wawili walikuwa wamefungwa, sema, nafasi ya 4, basi jina halikuwa kazi ya cheo.)
Kutumia Uthibitishaji wa Kazi
Mara baada ya kuamua kuwa uhusiano ni kazi, tunahitaji kuonyesha na kufafanua mahusiano ya kazi ili tuweze kuelewa na kuitumia, na wakati mwingine pia ili tuweze kuzipanga kwenye kompyuta. Kuna njia mbalimbali za kuwakilisha kazi. Uthibitishaji wa kazi ya kawaida ni uwakilishi mmoja unaowezesha kufanya kazi na kazi.
Kuwakilisha “urefu ni kazi ya umri,” tunaanza kwa kutambua vigezo vya maelezo\(h\) kwa urefu na\(a\) kwa umri. Barua\(f\),\(g\), na mara nyingi\(h\) hutumiwa kuwakilisha kazi kama tunavyotumia\(x\),\(y\), na\(z\) kuwakilisha namba na\(A\),\(B\), na\(C\) kuwakilisha seti.
\[\begin{array}{ll} h \text{ is } f \text{ of }a \;\;\;\;\;\; & \text{We name the function }f \text{; height is a function of age.} \\ h=f(a) & \text{We use parentheses to indicate the function input.} \\ f(a) & \text{We name the function }f \text{ ; the expression is read as “ }f \text{ of }a \text{.”}\end{array}\]
Kumbuka, tunaweza kutumia barua yoyote kwa jina kazi; nukuu\(h(a)\) inaonyesha sisi kwamba\(h\) inategemea\(a\). Thamani\(a\) lazima iingizwe katika kazi\(h\) ili kupata matokeo. Mabano yanaonyesha kwamba umri ni pembejeo katika kazi; hawaonyeshi kuzidisha.
Pia tunaweza kutoa kujieleza algebraic kama pembejeo kwa kazi. Kwa mfano\(f(a+b)\) ina maana “kwanza kuongeza\(a\) na\(b\), na matokeo ni pembejeo kwa ajili ya kazi\(f\).” Shughuli lazima zifanyike kwa utaratibu huu ili kupata matokeo sahihi.
Uthibitishaji wa Kazi
Nukuu\(y=f(x)\) inafafanua kazi inayoitwa\(f\). Hii ni kusoma kama “\(y\)ni kazi ya\(x\).” Barua\(x\) inawakilisha thamani ya pembejeo, au kutofautiana kwa kujitegemea. Barua\(y\), au\(f(x)\), inawakilisha thamani ya pato, au kutofautiana kwa tegemezi.
Mfano\(\PageIndex{3}\): Using Function Notation for Days in a Month
Tumia uthibitisho wa kazi ili kuwakilisha kazi ambayo pembejeo yake ni jina la mwezi na pato ni idadi ya siku katika mwezi huo.
Suluhisho
Kutumia Uthibitishaji wa Kazi kwa Siku kwa Mwezi
Tumia uthibitisho wa kazi ili kuwakilisha kazi ambayo pembejeo yake ni jina la mwezi na pato ni idadi ya siku katika mwezi huo.
Idadi ya siku katika mwezi ni kazi ya jina la mwezi, hivyo kama sisi jina kazi\(f\), sisi kuandika\(\text{days}=f(\text{month})\) au\(d=f(m)\). Jina la mwezi ni pembejeo kwa “utawala” unaohusisha nambari maalum (pato) na kila pembejeo.
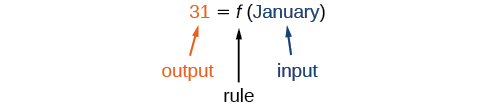
Kwa mfano,\(f(\text{March})=31\), kwa sababu Machi ina siku 31. Uthibitisho\(d=f(m)\) unatukumbusha kwamba idadi ya siku,\(d\) (pato), inategemea jina la mwezi,\(m\) (pembejeo).
Uchambuzi
Kumbuka kuwa pembejeo za kazi hazipaswi kuwa namba; pembejeo za kazi zinaweza kuwa majina ya watu, maandiko ya vitu vya kijiometri, au kipengele kingine chochote kinachoamua aina fulani ya pato. Hata hivyo, kazi nyingi tutakazofanya kazi nazo katika kitabu hiki zitakuwa na idadi kama pembejeo na matokeo.
Mfano\(\PageIndex{3B}\): Interpreting Function Notation
kazi\(N=f(y)\) inatoa idadi ya maafisa wa polisi\(N\),, katika mji katika mwaka\(y\). \(f(2005)=300\)Inawakilisha nini?
Suluhisho
Tunaposoma\(f(2005)=300\), tunaona kwamba mwaka wa pembejeo ni 2005. Thamani ya pato, idadi ya maafisa wa polisi\((N)\), ni 300. Kumbuka,\(N=f(y)\). Taarifa hiyo\(f(2005)=300\) inatuambia kuwa katika mwaka 2005 kulikuwa na maafisa wa polisi 300 mjiani.
Zoezi\(\PageIndex{3}\)
Tumia uthibitisho wa kazi ili kueleza uzito wa nguruwe kwa paundi kama kazi ya umri wake kwa siku\(d\).
- Jibu
-
\(w=f(d)\)
Q & A
Badala ya nukuu kama vile\(y=f(x)\), tunaweza kutumia alama sawa kwa pato kama kwa kazi, kama vile\(y=y(x)\), maana “\(y\)ni kazi ya\(x\)?”
Ndiyo, hii mara nyingi hufanyika, hasa katika masomo yaliyotumika ambayo hutumia hesabu ya juu, kama vile fizikia na uhandisi. Hata hivyo, katika kuchunguza hesabu yenyewe tunapenda kudumisha tofauti kati ya kazi kama vile\(f\), ambayo ni utawala au utaratibu, na y pato sisi kupata kwa kutumia\(f\) kwa pembejeo fulani\(x\). Hii ni kwa nini sisi kawaida kutumia nukuu kama vile\(y=f(x),P=W(d)\), na kadhalika.
Kuwakilisha Kazi Kutumia Majedwali
Njia ya kawaida ya kuwakilisha kazi ni katika fomu ya meza. Safu za meza au nguzo zinaonyesha maadili ya pembejeo na pato linalofanana. Wakati mwingine, maadili haya yanawakilisha yote tunayoyajua kuhusu uhusiano; wakati mwingine, meza hutoa mifano michache ya kuchagua kutoka kwa uhusiano kamili zaidi.
Jedwali\(\PageIndex{3}\) linaorodhesha namba ya pembejeo ya kila mwezi (\(\text{January}=1\)\(\text{February}=2\),, na kadhalika) na thamani ya pato la idadi ya siku katika mwezi huo. Taarifa hii inawakilisha yote tunayoyajua kuhusu miezi na siku kwa mwaka uliopewa (hiyo sio mwaka wa leap). Kumbuka kwamba, katika meza hii, sisi kufafanua siku-katika-mwezi kazi\(f\) ambapo\(D=f(m)\) kubainisha miezi kwa integer badala ya kwa jina.
| Nambari ya mwezi,\(m\) (pembejeo) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Siku kwa mwezi,\(D\) (pato) | 31 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
Jedwali\(\PageIndex{4}\) amefafanua kazi\(Q=g(n)\) Kumbuka, nukuu hii inatuambia kwamba\(g\) ni jina la kazi ambayo inachukua pembejeo\(n\) na anatoa pato\(Q\).
| \(n\) | 1 | 2 | 3 | 4 | 5 |
| \(Q\) | 8 | 6 | 7 | 6 | 8 |
Jedwali\(\PageIndex{5}\) linaonyesha umri wa watoto kwa miaka na urefu wao unaofanana. Jedwali hili linaonyesha baadhi tu ya data zinazopatikana kwa urefu na umri wa watoto. Tunaweza kuona mara moja kwamba meza hii haina kuwakilisha kazi kwa sababu thamani sawa pembejeo, miaka 5, ina maadili mawili tofauti pato, 40 katika. na 42 katika.
| Umri katika miaka,\(a\) (pembejeo) | 5 | 5 | 6 | 7 | 8 | 9 | 10 |
| Urefu katika inchi,\(h\) (pato) | 40 | 42 | 44 | 47 | 50 | 52 | 54 |
Jinsi ya: Kutokana na meza ya maadili ya pembejeo na pato, onyesha kama meza inawakilisha kazi
- Tambua maadili ya pembejeo na pato.
- Angalia ili uone ikiwa kila thamani ya pembejeo imeunganishwa na thamani moja tu ya pato. Ikiwa ndivyo, meza inawakilisha kazi.
Mfano\(\PageIndex{5}\): Identifying Tables that Represent Functions
Ni meza gani, Jedwali\(\PageIndex{6}\), Jedwali\(\PageIndex{7}\)\(\PageIndex{8}\), au Jedwali, inawakilisha kazi (kama ipo)?
| Ingiza | Pato |
|---|---|
| 2 | 1 |
| 5 | 3 |
| 8 | 6 |
| Ingiza | Pato |
|---|---|
| -3 | 5 |
| 0 | 1 |
| 4 | 5 |
| Ingiza | Pato |
|---|---|
| 1 | 0 |
| 5 | 2 |
| 5 | 4 |
Suluhisho
Jedwali\(\PageIndex{6}\) na Jedwali\(\PageIndex{7}\) hufafanua kazi. Katika wote wawili, kila thamani ya pembejeo inalingana na thamani moja ya pato. Jedwali\(\PageIndex{8}\) halifafanua kazi kwa sababu thamani ya pembejeo ya 5 inalingana na maadili mawili tofauti ya pato.
Wakati meza inawakilisha kazi, maadili sambamba pembejeo na pato pia inaweza maalum kwa kutumia kazi nukuu.
Kazi iliyowakilishwa na Jedwali\(\PageIndex{6}\) inaweza kusimamishwa kwa kuandika
\[f(2)=1\text{, }f(5)=3\text{, and }f(8)=6 \nonumber\]
Vile vile, kauli
\[g(−3)=5\text{, }g(0)=1\text{, and }g(4)=5 \nonumber\]
kuwakilisha kazi katika Jedwali\(\PageIndex{7}\).
Jedwali\(\PageIndex{8}\) haliwezi kuonyeshwa kwa namna hiyo kwa sababu haiwakilishi kazi.
Zoezi\(\PageIndex{5}\)
Je, Jedwali\(\PageIndex{9}\) linawakilisha kazi?
| Ingiza | Pato |
|---|---|
| 1 | 10 |
| 2 | 100 |
| 3 | 1000 |
- Jibu
-
ndiyo
Kutafuta Maadili ya Pembejeo na Pato la Kazi
Tunapojua thamani pembejeo na wanataka kuamua sambamba thamani pato kwa ajili ya kazi, sisi kutathmini kazi. Kutathmini daima kuzalisha matokeo moja kwa sababu kila thamani pembejeo ya kazi sambamba na hasa thamani moja pato.
Wakati sisi kujua thamani pato na wanataka kuamua maadili pembejeo ambayo kuzalisha kwamba thamani pato, sisi kuweka pato sawa na formula kazi ya na kutatua kwa pembejeo. Kutatua kunaweza kuzalisha suluhisho zaidi ya moja kwa sababu maadili tofauti ya pembejeo yanaweza kuzalisha thamani sawa ya pato.
Tathmini ya Kazi katika Fomu za Algebraic
Wakati tuna kazi katika fomu formula, ni kawaida jambo rahisi kutathmini kazi. Kwa mfano, kazi\(f(x)=5−3x^2\) inaweza kupimwa kwa kuzingatia thamani ya pembejeo, kuongezeka kwa 3, na kisha kuondoa bidhaa kutoka 5.
jinsi ya: Kutokana formula kwa ajili ya kazi, kutathmini.
Kutokana formula kwa ajili ya kazi, kutathmini.
- Badilisha nafasi ya pembejeo katika formula na thamani iliyotolewa.
- Tumia matokeo.
Mfano\(\PageIndex{6A}\): Evaluating Functions at Specific Values
1. Tathmini\(f(x)=x^2+3x−4\) katika
- \(2\)
- \(a\)
- \(a+h\)
- Tathmini\(\frac{f(a+h)−f(a)}{h}\)
Suluhisho
Badilisha nafasi ya x katika kazi na kila thamani maalum.
a Kwa sababu thamani pembejeo ni idadi, 2, tunaweza kutumia algebra rahisi kurahisisha.
\[\begin{align*}f(2)&=2^2+3(2)−4\\&=4+6−4\\ &=6\end{align*}\]
b Katika kesi hii, thamani ya pembejeo ni barua hivyo hatuwezi kurahisisha jibu lolote zaidi.
\[f(a)=a^2+3a−4\nonumber\]
c. pamoja na thamani ya pembejeo ya\(a+h\), ni lazima kutumia mali ya usambazaji.
\[\begin{align*}f(a+h)&=(a+h)^2+3(a+h)−4\\&=a^2+2ah+h^2+3a+3h−4 \end{align*}\]
d Katika kesi hii, tunatumia maadili ya pembejeo kwa kazi zaidi ya mara moja, na kisha kufanya shughuli za algebraic kwenye matokeo. Tayari tumegundua kwamba
\[f(a+h)=a^2+2ah+h^2+3a+3h−4\nonumber\]
na tunajua kwamba
\[f(a)=a^2+3a−4 \nonumber\]
Sasa tunachanganya matokeo na kurahisisha.
\[\begin{align*}\dfrac{f(a+h)−f(a)}{h}&=\dfrac{(a^2+2ah+h^2+3a+3h−4)−(a^2+3a−4)}{h}\\ &=\dfrac{(2ah+h^2+3h)}{h} \\ &=\dfrac{h(2a+h+3)}{h} & &\text{Factor out h.}\\ &=2a+h+3 & & \text{Simplify.}\end{align*}\]
Mfano\(\PageIndex{6B}\): Evaluating Functions
Kutokana na kazi\(h(p)=p^2+2p\), tathmini\(h(4)\).
Suluhisho
Kutathmini\(h(4)\), sisi badala ya thamani 4 kwa pembejeo variable p katika kazi iliyotolewa.
\[\begin{align*}h(p)&=p^2+2p\\h(4)&=(4)^2+2(4)\\ &=16+8\\&=24\end{align*}\]
Kwa hiyo, kwa pembejeo ya 4, tuna pato la 24.
Zoezi\(\PageIndex{6}\)
Kutokana na kazi\(g(m)=\sqrt{m−4}\), tathmini\(g(5)\).
- Jibu
-
\(g(5)=1\)
Mfano\(\PageIndex{7}\): Solving Functions
Kutokana na kazi\(h(p)=p^2+2p\), tatua\(h(p)=3\).
Suluhisho
\[\begin{array}{rl} h(p)=3\\p^2+2p=3 & \text{Substitute the original function}\\ p^2+2p−3=0 & \text{Subtract 3 from each side.}\\(p+3)(p−1)=0&\text{Factor.}\end{array} \nonumber \]
Kama\((p+3)(p−1)=0\), ama\((p+3)=0\) au\((p−1)=0\) (au wote wawili sawa\(0\)). Tutaweka kila sababu sawa\(0\) na kutatua\(p\) kwa kila kesi.
\[(p+3)=0,\; p=−3 \nonumber \]
\[(p−1)=0,\, p=1 \nonumber\]
Hii inatupa ufumbuzi mbili. Pato\(h(p)=3\) wakati pembejeo ni ama\(p=1\) au\(p=−3\). Tunaweza pia kuthibitisha kwa graphing kama katika Kielelezo\(\PageIndex{6}\). Grafu inathibitisha kwamba\(h(1)=h(−3)=3\) na\(h(4)=24\).
![[Grafu ya parabola yenye alama zilizoandikwa (-3, 3), (1, 3), na (4, 24).]](https://math.libretexts.org/@api/deki/files/868/CNX_Precalc_Figure_01_01_006.jpg)
Zoezi\(\PageIndex{7}\)
Kutokana na kazi\(g(m)=\sqrt{m−4}\), tatua\(g(m)=2\).
- Jibu
-
\(m=8\)
Kutathmini Kazi zilizoelezwa katika Fomu
Baadhi ya kazi hufafanuliwa na sheria za hisabati au taratibu zilizoelezwa katika fomu ya equation. Ikiwa inawezekana kueleza pato la kazi na formula inayohusisha wingi wa pembejeo, basi tunaweza kufafanua kazi katika fomu ya algebraic. Kwa mfano, equation\(2n+6p=12\) inaonyesha uhusiano wa kazi kati\(n\) na\(p\). Tunaweza kuandika upya kuamua kama\(p\) ni kazi ya\(n\).
Jinsi ya: Kutokana na kazi katika fomu equation, kuandika formula yake algebraic.
- Kutatua equation kutenganisha variable pato upande mmoja wa ishara sawa, na upande mwingine kama kujieleza kwamba inahusisha tu pembejeo variable.
- Tumia mbinu zote za kawaida za algebraic za kutatua equations, kama vile kuongeza au kuondoa kiasi sawa au kutoka pande zote mbili, au kuzidisha au kugawa pande zote mbili za equation kwa kiasi sawa.
Mfano\(\PageIndex{8A}\): Finding an Equation of a Function
Eleza uhusiano\(2n+6p=12\) kama kazi\(p=f(n)\), ikiwa inawezekana.
Suluhisho
Ili kuelezea uhusiano katika fomu hii, tunahitaji kuwa na uwezo wa kuandika uhusiano ambapo\(p\) ni kazi ya\(n\), ambayo ina maana kuandika kama\(p=[\text{expression involving }n]\).
\[\begin{align*}2n+6p&=12 \\ 6p&=12−2n && \text{Subtract 2n from both sides.} \\ p&=\dfrac{12−2n}{6} & &\text{Divide both sides by 6 and simplify.} \\ p&=\frac{12}{6}−\frac{2n}{6} \\ p&=2−\frac{1}{3}n\end{align*}\]
Kwa hiyo,\(p\) kama kazi ya\(n\) imeandikwa kama
\[p=f(n)=2−\frac{1}{3}n \nonumber\]
Uchambuzi
Ni muhimu kutambua kwamba si kila uhusiano ulioonyeshwa na equation unaweza pia kuelezwa kama kazi na formula.
Mfano\(\PageIndex{8B}\): Expressing the Equation of a Circle as a Function
Je, equation\(x^2+y^2=1\) inawakilisha kazi na\(x\) kama pembejeo na\(y\) kama pato? Ikiwa ndivyo, onyesha uhusiano kama kazi\(y=f(x)\).
Suluhisho
Kwanza tunaondoa\(x^2\) kutoka pande zote mbili.
\[y^2=1−x^2 \nonumber\]
Sasa tunajaribu kutatua\(y\) kwa equation hii.
\[y=\pm\sqrt{1−x^2} \nonumber\]
\[\text{so, }y=\sqrt{1−x^2}\;\text{and}\;y = −\sqrt{1−x^2} \nonumber\]
Sisi kupata matokeo mawili sambamba na pembejeo huo, hivyo uhusiano huu hauwezi kuwakilishwa kama kazi moja\(y=f(x)\).
Zoezi\(\PageIndex{8}\)
Kama\(x−8y^3=0\), kueleza\(y\) kama kazi ya\(x\).
- Jibu
-
\(y=f(x)=\dfrac{\sqrt[3]{x}}{2}\)
Q & A
Je, kuna mahusiano yaliyotolewa na equation kwamba kufanya kuwakilisha kazi lakini ambayo bado haiwezi kuwakilishwa na formula algebraic?
Ndiyo, hii inaweza kutokea. Kwa mfano, kutokana na equation\(x=y+2^y\), kama tunataka kueleza y kama kazi ya x, hakuna rahisi algebraic formula kuwashirikisha tu\(x\) kwamba sawa\(y\). Hata hivyo, kila mmoja\(x\) anaamua thamani ya kipekee kwa\(y\), na kuna taratibu za hisabati ambazo\(y\) zinaweza kupatikana kwa usahihi wowote uliotaka. Katika kesi hii, sisi kusema kwamba equation anatoa thabiti (alisema) utawala kwa ajili ya\(y\) kama kazi ya\(x\), hata kama formula haiwezi kuandikwa wazi.
Kutathmini Kazi iliyotolewa katika Fomu ya Tabular
Kama tulivyoona hapo juu, tunaweza kuwakilisha kazi katika meza. Kinyume chake, tunaweza kutumia habari katika meza kuandika kazi, na tunaweza kutathmini kazi kwa kutumia meza. Kwa mfano, wanyama wetu wanakumbuka vizuri kumbukumbu ambazo tunazoshiriki nao? Kuna hadithi ya miji kwamba goldfish ina kumbukumbu ya sekunde 3, lakini hii ni hadithi tu. Goldfish inaweza kukumbuka hadi miezi 3, wakati samaki ya beta ina kumbukumbu ya hadi miezi 5. Na wakati kumbukumbu ya puppy si zaidi ya sekunde 30, mbwa wazima anaweza kukumbuka kwa dakika 5. Hii ni mdogo ikilinganishwa na paka, ambao kumbukumbu yake huchukua muda wa masaa 16.
Kazi inayohusiana na aina ya pet kwa muda wa kumbukumbu yake ya kumbukumbu inaonekana kwa urahisi na matumizi ya meza (Jedwali\(\PageIndex{10}\)).
| pet kumbukumbu | span katika masaa |
|---|---|
| Puppy | 0.008 |
| Mbwa wazima | 0.083 |
| Paka | 3 |
| Samaki wa dhahabu | 2160 |
| beta samaki | 3600 |
Wakati mwingine, kutathmini kazi katika fomu ya meza inaweza kuwa muhimu zaidi kuliko kutumia equations. Hapa hebu wito kazi\(P\). Kikoa cha kazi ni aina ya pet na upeo ni nambari halisi inayowakilisha idadi ya masaa ya kumbukumbu ya pet inachukua. Tunaweza kutathmini kazi kwa thamani ya\(P\) pembejeo ya “goldfish.” Tungeandika\(P(goldfish)=2160\). Kumbuka kwamba, kutathmini kazi katika fomu ya meza, tunatambua thamani ya pembejeo na thamani ya pato inayofanana kutoka kwenye mstari muhimu wa meza. Fomu ya tabular ya kazi P inaonekana inafaa kwa kazi hii, zaidi ya kuandika katika aya au fomu ya kazi.
Jinsi ya: Kutokana na kazi iliyowakilishwa na meza, kutambua maadili maalum ya pato na pembejeo
1. Pata pembejeo iliyotolewa katika mstari (au safu) ya maadili ya pembejeo.
2. Tambua thamani ya pato inayoendana na thamani ya pembejeo.
3. Pata maadili ya pato yaliyotolewa katika mstari (au safu) ya maadili ya pato, akibainisha kila wakati thamani ya pato inaonekana.
4. Tambua thamani ya pembejeo inayohusiana na thamani ya pato iliyotolewa.
Mfano\(\PageIndex{9}\): Evaluating and Solving a Tabular Function
Kutumia Jedwali\(\PageIndex{11}\),
a. kutathmini\(g(3)\).
b. kutatua\(g(n)=6\).
| \(n\) | 1 | 2 | 3 | 4 | 5 |
| \(g(n)\) | 8 | 6 | 7 | 6 | 8 |
Suluhisho
a. kutathmini\(g(3)\) njia kuamua thamani ya pato la kazi\(g\) kwa thamani ya pembejeo ya\(n=3\). Thamani ya pato la meza inalingana\(n=3\) na ni 7, hivyo\(g(3)=7\).
b. kutatua\(g(n)=6\) maana kutambua maadili pembejeo, n, kwamba kuzalisha thamani pato la 6. Jedwali\(\PageIndex{12}\) linaonyesha ufumbuzi mbili: 2 na 4.
| \(n\) | 1 | 2 | 3 | 4 | 5 |
| \(g(n)\) | 8 | 6 | 7 | 6 | 8 |
Tunapoingiza 2 katika kazi\(g\), pato letu ni 6. Wakati sisi pembejeo 4 katika kazi\(g\), pato yetu pia ni 6.
Zoezi\(\PageIndex{1}\)
Kutumia Jedwali\(\PageIndex{12}\), tathmini\(g(1)\).
- Jibu
-
\(g(1)=8\)
Kutafuta Maadili ya Kazi kutoka Grafu
Kutathmini kazi kwa kutumia grafu pia inahitaji kupata thamani ya pato inayofanana kwa thamani ya pembejeo iliyotolewa, tu katika kesi hii, tunapata thamani ya pato kwa kuangalia grafu. Kutatua equation ya kazi kwa kutumia grafu inahitaji kutafuta matukio yote ya thamani ya pato iliyotolewa kwenye grafu na kuzingatia thamani ya pembejeo inayofanana.
Mfano\(\PageIndex{10}\): Reading Function Values from a Graph
Kutokana na grafu katika Kielelezo\(\PageIndex{7}\),
- Tathmini\(f(2)\).
- Kutatua\(f(x)=4\).
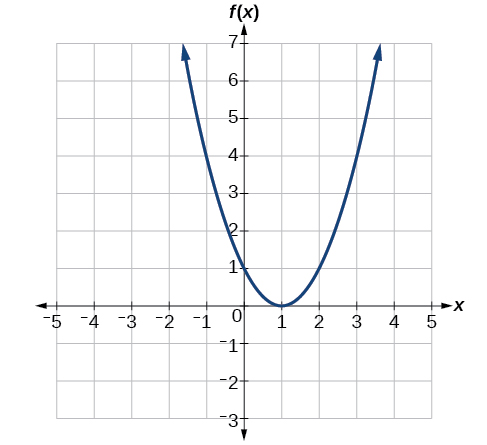
Suluhisho
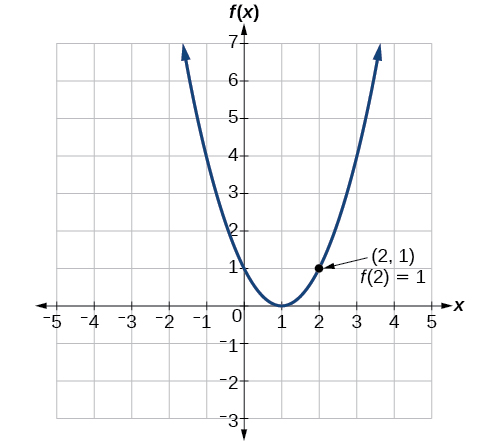
Kutathmini\(f(2)\), Machapisho uhakika juu ya Curve ambapo\(x=2\), kisha kusoma y-kuratibu ya hatua hiyo. Hatua ina kuratibu\((2,1)\), hivyo\(f(2)=1\). Angalia Kielelezo\(\PageIndex{8}\).
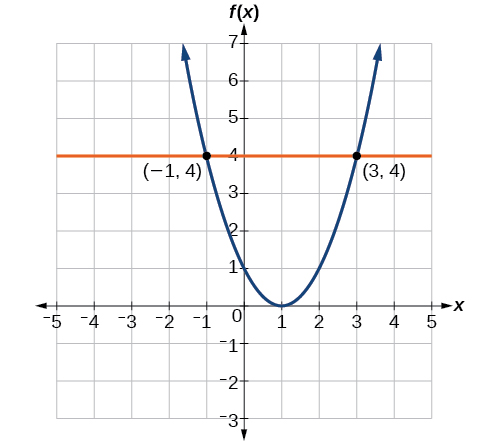
Ili kutatua\(f(x)=4\), tunapata thamani ya pato 4 kwenye mhimili wima. Kuhamia usawa kando ya mstari\(y=4\), tunapata pointi mbili za pembe na thamani ya pato 4:\((−1,4)\) na\((3,4)\). Hizi pointi kuwakilisha ufumbuzi mbili kwa\(f(x)=4\): -1 au 3. Hii ina maana\(f(−1)=4\) na\(f(3)=4\), au wakati pembejeo ni -1 au 3, pato ni 4. Angalia Kielelezo\(\PageIndex{9}\).
Zoezi\(\PageIndex{10}\)
Kutokana na grafu katika Kielelezo\(\PageIndex{7}\), tatua\(f(x)=1\).
- Jibu
-
\(x=0\)au\(x=2\)
Kuamua Kama Kazi ni moja kwa moja
Kazi zingine zina thamani ya pato iliyotolewa ambayo inalingana na maadili mawili au zaidi ya pembejeo. Kwa mfano, katika chati ya hisa iliyoonyeshwa kwenye Kielelezo mwanzoni mwa sura hii, bei ya hisa ilikuwa $1000 kwenye tarehe tano tofauti, maana yake ni kwamba kulikuwa na maadili tano tofauti ya pembejeo ambayo yote yalisababisha thamani sawa ya pato la $1000.
Hata hivyo, baadhi ya kazi zina thamani moja tu ya pembejeo kwa kila thamani ya pato, pamoja na kuwa na pato moja tu kwa kila pembejeo. Tunaita kazi hizi kazi moja kwa moja. Kwa mfano, fikiria shule ambayo inatumia darasa la barua tu na viwango vya decimal, kama ilivyoorodheshwa kwenye Jedwali\(\PageIndex{13}\).
| Barua Daraja | Daraja la Kiwango Wastani |
|---|---|
| A | 4.0 |
| B | 3.0 |
| C | 2.0 |
| D | 1.0 |
Mfumo huu wa grading inawakilisha kazi moja kwa moja, kwa sababu kila pembejeo ya barua huzaa pato moja la wastani wa daraja na kila wastani wa kiwango cha daraja inalingana na barua moja ya pembejeo.
Ili kutazama dhana hii, hebu tuangalie tena kazi mbili rahisi zilizopigwa katika Takwimu\(\PageIndex{1a}\) na\(\PageIndex{1b}\). Kazi katika sehemu (a) inaonyesha uhusiano ambao sio kazi moja kwa moja kwa sababu pembejeo\(q\) na\(r\) zote mbili hutoa pato\(n\). Kazi katika sehemu (b) inaonyesha uhusiano ambao ni kazi moja kwa moja kwa sababu kila pembejeo inahusishwa na pato moja.
Kazi moja kwa moja
Kazi moja kwa moja ni kazi ambayo kila thamani ya pato inalingana na thamani moja ya pembejeo.
Mfano\(\PageIndex{11}\): Determining Whether a Relationship Is a One-to-One Function
Je! Eneo la mduara ni kazi ya radius yake? Kama ndiyo, ni kazi moja kwa moja?
Suluhisho
Mduara wa radius\(r\) ina kipimo cha eneo la kipekee\(A={\pi}r^2\) kilichotolewa na, hivyo kwa pembejeo yoyote\(r\), kuna pato moja tu,\(A\). Eneo hilo ni kazi ya radius\(r\).
Ikiwa kazi ni moja kwa moja, thamani ya pato, eneo hilo, lazima iwe sawa na thamani ya pembejeo ya kipekee, radius. Kipimo chochote cha eneo\(A\) kinatolewa na formula\(A={\pi}r^2\). Kwa sababu maeneo na radii ni idadi nzuri, kuna suluhisho moja hasa:\(\sqrt{\frac{A}{\pi}}\). Hivyo eneo la mduara ni kazi moja kwa moja ya radius ya mduara.
Zoezi\(\PageIndex{11A}\)
- Je, usawa ni kazi ya nambari ya akaunti ya benki?
- Je, nambari ya akaunti ya benki ni kazi ya usawa?
- Je, usawa ni kazi moja kwa moja ya nambari ya akaunti ya benki?
- Jibu
-
a. ndiyo, kwa sababu kila akaunti ya benki ina usawa mmoja wakati wowote;
b. hapana, kwa sababu idadi kadhaa ya akaunti ya benki inaweza kuwa na usawa sawa;
c. hapana, kwa sababu pato sawa linaweza kuendana na pembejeo zaidi ya moja.
Zoezi\(\PageIndex{11B}\)
Tathmini zifuatazo:
- Kama kila daraja asilimia chuma katika kozi tafsiri ya daraja moja barua, ni barua daraja kazi ya daraja asilimia?
- Kama ni hivyo, ni kazi moja kwa moja?
- Jibu
-
Ndiyo, daraja la barua ni kazi ya daraja la asilimia;
b. hapana, sio moja kwa moja. Kuna 100 tofauti asilimia idadi tunaweza kupata lakini tu kuhusu tano inawezekana herufi darasa, hivyo hawezi kuwa na asilimia moja tu idadi kwamba sambamba na kila daraja herufi.
Kutumia Mtihani wa mstari wa Wima
Kama tulivyoona katika baadhi ya mifano hapo juu, tunaweza kuwakilisha kazi kwa kutumia grafu. Grafu zinaonyesha jozi nyingi za pembejeo-pato katika nafasi ndogo. Maelezo ya kuona ambayo hutoa mara nyingi hufanya mahusiano iwe rahisi kuelewa. Kwa mkataba, grafu hujengwa kwa maadili ya pembejeo pamoja na mhimili usio na usawa na maadili ya pato pamoja na mhimili wima.
grafu ya kawaida jina thamani pembejeo\(x\) na pato\(y\), na sisi kusema\(y\) ni kazi ya\(x\), au\(y=f(x)\) wakati kazi ni jina lake\(f\). Grafu ya kazi ni seti ya pointi zote\((x,y)\) katika ndege ambayo inatimiza equation\(y=f(x)\). Ikiwa kazi inaelezwa kwa maadili machache tu ya pembejeo, basi grafu ya kazi ni pointi chache tu, ambapo kuratibu x-ya kila hatua ni thamani ya pembejeo na kuratibu y ya kila hatua ni thamani ya pato inayofanana. Kwa mfano, dots nyeusi kwenye grafu katika Kielelezo\(\PageIndex{10}\) kutuambia kwamba\(f(0)=2\) na\(f(6)=1\). Hata hivyo, seti ya pointi zote\((x,y)\)\(y=f(x)\) zinazotosheleza ni safu. Curve inavyoonekana ni pamoja\((0,2)\) na, na\((6,1)\) kwa sababu Curve hupita kupitia pointi hizo
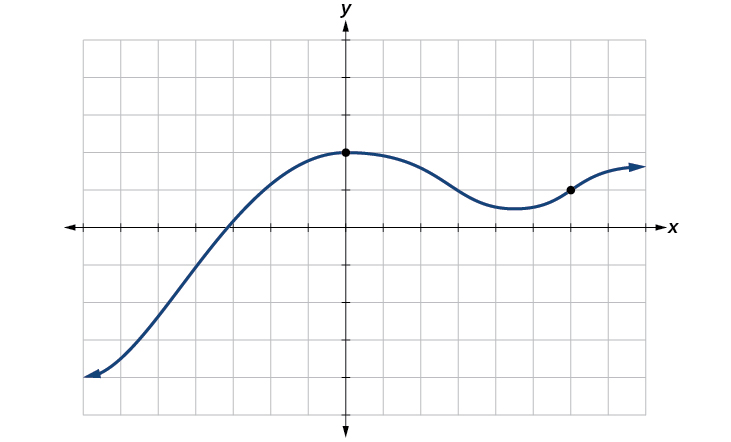
Mtihani wa mstari wa wima unaweza kutumika kuamua kama grafu inawakilisha kazi. Ikiwa tunaweza kuteka mstari wowote wa wima unaozunguka grafu zaidi ya mara moja, basi grafu haina kufafanua kazi kwa sababu kazi ina thamani moja tu ya pato kwa kila thamani ya pembejeo. Angalia Kielelezo\(\PageIndex{11}\).
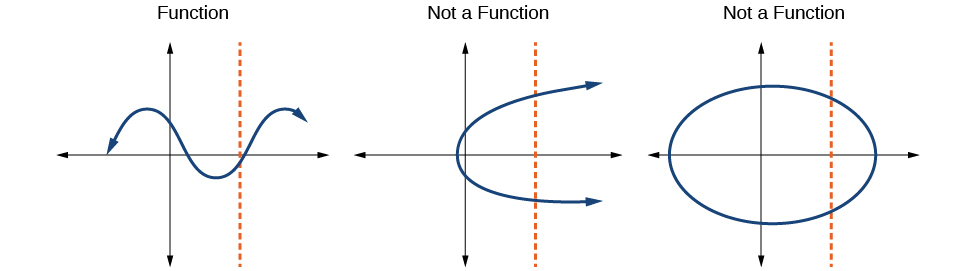
Howto: Kutokana na grafu, tumia mtihani wa mstari wa wima ili uone kama grafu inawakilisha kazi
- Kukagua grafu kuona kama mstari wowote wima inayotolewa bila intersect Curve zaidi ya mara moja.
- Ikiwa kuna mstari wowote kama huo, onyesha kwamba grafu haiwakilishi kazi.
Mfano\(\PageIndex{12}\): Applying the Vertical Line Test
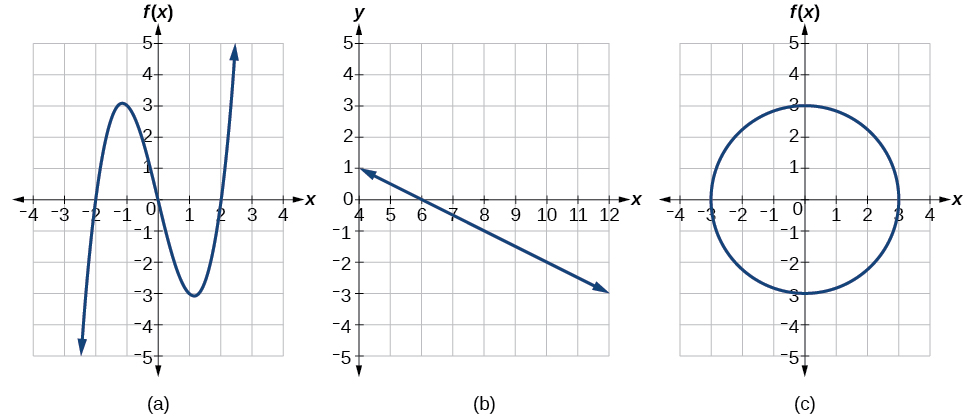
Ni ipi kati ya grafu katika Kielelezo\(\PageIndex{12}\) inawakilisha (s) kazi\(y=f(x)\)?
Suluhisho
Ikiwa mstari wowote wa wima unaingilia grafu zaidi ya mara moja, uhusiano unaowakilishwa na grafu sio kazi. Kumbuka kwamba mstari wowote wima bila kupita katika hatua moja tu ya grafu mbili inavyoonekana katika sehemu (a) na (b) ya Kielelezo\(\PageIndex{12}\). Kutoka hili tunaweza kuhitimisha kwamba grafu hizi mbili zinawakilisha kazi. Grafu ya tatu haiwakilishi kazi kwa sababu, kwa zaidi ya x-maadili, mstari wa wima ungeweza kuingiliana grafu kwa hatua zaidi ya moja, kama inavyoonekana kwenye Kielelezo\(\PageIndex{13}\).
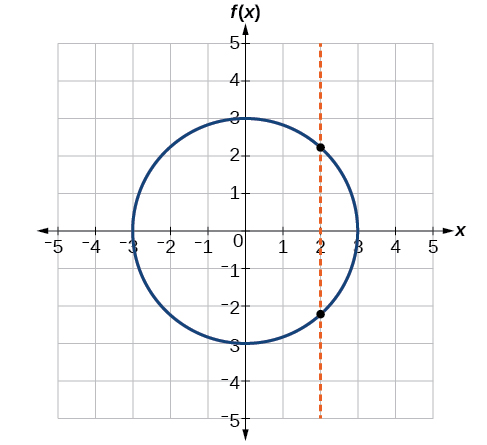
Zoezi\(\PageIndex{12}\)
Je, grafu katika Kielelezo\(\PageIndex{14}\) inawakilisha kazi?
![[Kazi kamili f (x) =|x|.]](https://math.libretexts.org/@api/deki/files/885/CNX_Precalc_Figure_01_02_013.jpg)
- Jibu
-
ndiyo
Kutumia Mtihani wa Line ya Ulalo
Mara baada ya kuamua kwamba grafu inafafanua kazi, njia rahisi ya kuamua ikiwa ni kazi moja kwa moja ni kutumia mtihani wa mstari wa usawa. Chora mistari ya usawa kupitia grafu. Ikiwa mstari wowote wa usawa unaingilia grafu zaidi ya mara moja, basi grafu haiwakilishi kazi moja kwa moja.
Howto: Kutokana na grafu ya kazi, tumia mtihani wa mstari wa usawa ili uone kama grafu inawakilisha kazi moja kwa moja
- Kagua grafu ili uone kama mstari wowote ulio na usawa ungeweza kuingiliana kwa kasi zaidi ya mara moja.
- Ikiwa kuna mstari wowote huo, onyesha kwamba kazi sio moja kwa moja.
Mfano\(\PageIndex{13}\): Applying the Horizontal Line Test
Fikiria kazi zilizoonyeshwa kwenye Kielelezo\(\PageIndex{12a}\) na Kielelezo\(\PageIndex{12b}\). Je, ni kazi moja kwa moja?
Suluhisho
Kazi katika Kielelezo\(\PageIndex{12a}\) sio moja kwa moja. Mstari wa usawa unaoonyeshwa kwenye Mchoro\(\PageIndex{15}\) unaingilia grafu ya kazi kwa pointi mbili (na tunaweza hata kupata mistari ya usawa inayoingiliana kwa pointi tatu.)
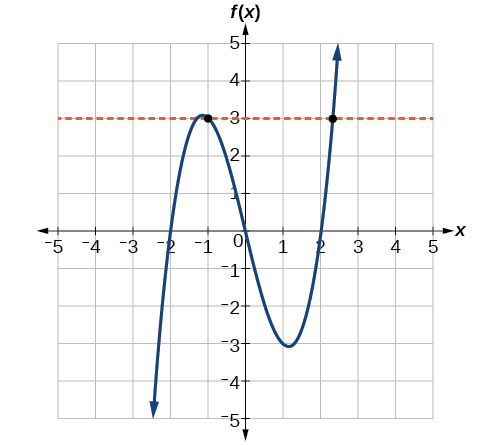
Kazi katika Kielelezo\(\PageIndex{12b}\) ni moja kwa moja. Mstari wowote wa usawa utaingiliana mstari wa diagonal mara moja.
Zoezi\(\PageIndex{13}\)
Je! Grafu imeonyeshwa kwenye Kielelezo\(\PageIndex{13}\) moja kwa moja?
- Jibu
-
Hapana, kwa sababu haipiti mtihani wa mstari usio na usawa.
Kutambua Kazi za Msingi za Toolkit
Katika maandishi haya, tutachunguza kazi-maumbo ya grafu zao, sifa zao za kipekee, kanuni zao za algebraic, na jinsi ya kutatua matatizo nao. Wakati wa kujifunza kusoma, tunaanza na alfabeti. Wakati wa kujifunza kufanya hesabu, tunaanza na namba. Wakati wa kufanya kazi na kazi, ni sawa na manufaa kuwa na seti ya msingi ya vipengele vya kuzuia jengo. Tunaita hizi “kazi za toolkit”, ambazo huunda seti ya kazi za msingi ambazo tunajua grafu, formula, na mali maalum. Baadhi ya kazi hizi zimewekwa kwa vifungo vya mtu binafsi kwenye mahesabu mengi. Kwa ufafanuzi huu tutatumia x kama variable pembejeo na\(y=f(x)\) kama variable pato.
Tutaona kazi hizi za toolkit, mchanganyiko wa kazi za toolkit, grafu zao, na mabadiliko yao mara kwa mara katika kitabu hiki. Itakuwa na manufaa sana ikiwa tunaweza kutambua kazi hizi za toolkit na vipengele vyake haraka kwa jina, formula, grafu, na mali ya msingi ya meza. Grafu na maadili ya meza ya sampuli yanajumuishwa na kila kazi iliyoonyeshwa kwenye Jedwali\(\PageIndex{14}\).
| Jina | Kazi | Grafu |
|---|---|---|
| Mara kwa mara | \(f(x)=c\)wapi\(c\) mara kwa mara | 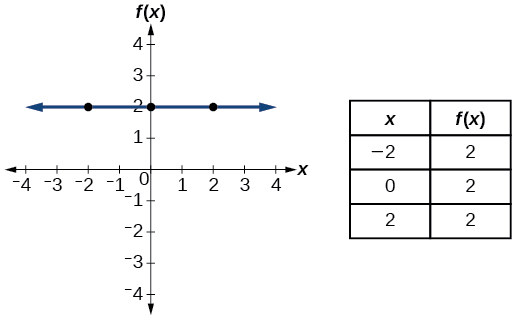 |
| Identity | \(f(x)=x\) | 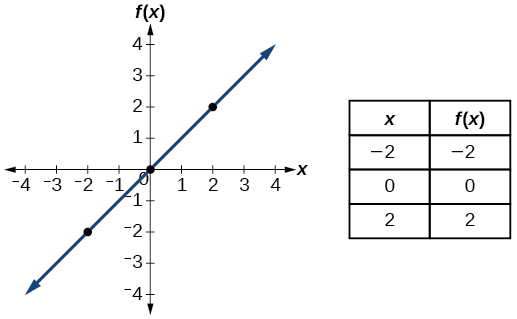 |
| Thamani kamili | \(f(x)=|x|\) | 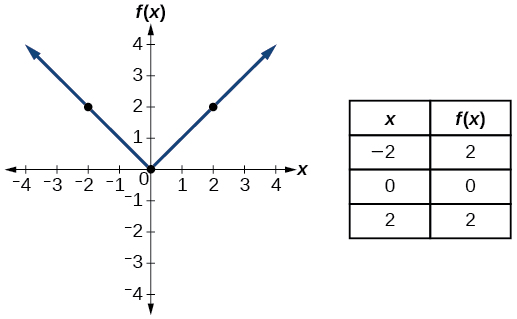 |
| Quadratic | \(f(x)=x^2\) | 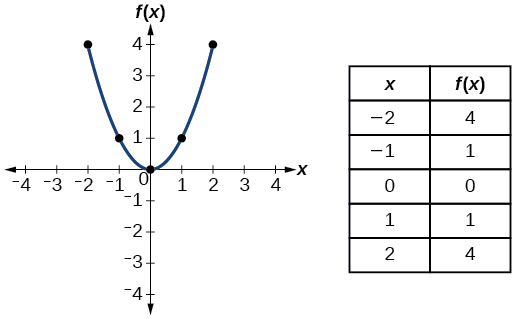 |
| Cubic | \(f(x)=x^3\) | 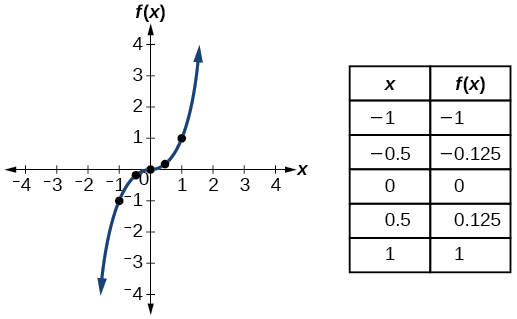 |
| kurudisha nyuma | \(f(x)=\dfrac{1}{x}\) | 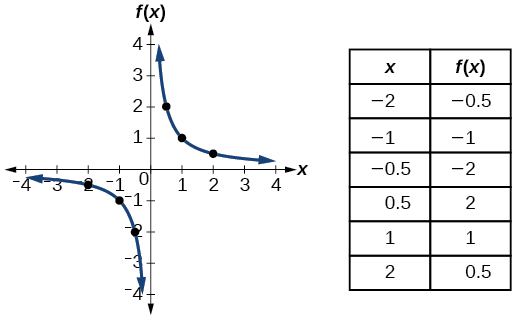 |
| Mraba ya kurudisha | \(f(x)=\dfrac{1}{x^2}\) | 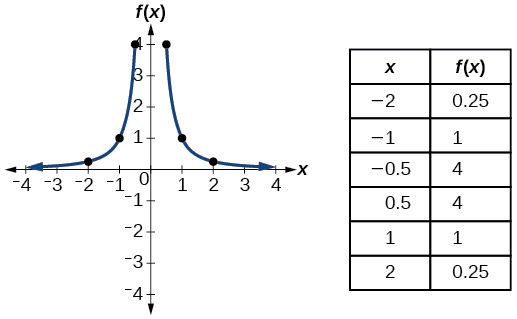 |
| Mizizi ya mraba | \(f(x)=\sqrt{x}\) | 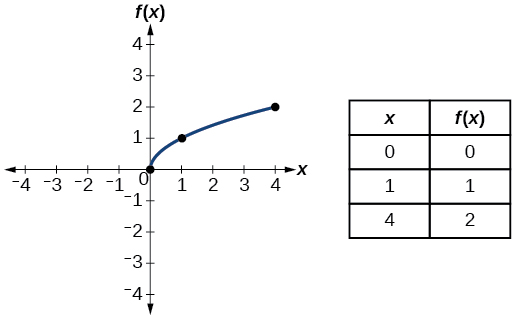 |
| Cube mizizi | \(f(x)=\sqrt[3]{x}\) | 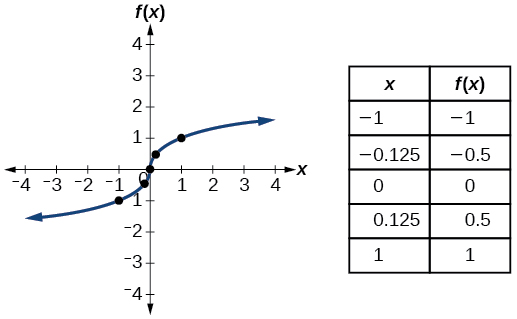 |
Mlinganyo muhimu
- Kazi ya mara kwa mara\(f(x)=c\), ambapo\(c\) ni mara kwa mara
- Kazi ya utambulisho\(f(x)=x\)
- Kazi kamili ya thamani\(f(x)=|x|\)
- Kazi ya Quadratic\(f(x)=x^2\)
- Kazi za ujazo\(f(x)=x^3\)
- Kazi ya kurudisha\(f(x)=\dfrac{1}{x}\)
- Kazi ya mraba ya usawa\(f(x)=\frac{1}{x^2}\)
- Kazi ya mizizi ya mraba\(f(x)=\sqrt{x}\)
- Kazi ya mizizi ya mchemraba\(f(x)=3\sqrt{x}\)
Dhana muhimu
- Uhusiano ni seti ya jozi zilizoamriwa. Kazi ni aina maalum ya uhusiano ambayo kila thamani ya kikoa, au pembejeo, inaongoza kwa thamani moja ya aina, au pato.
- Uthibitishaji wa kazi ni njia ya shorthand ya kuhusisha pembejeo kwa pato kwa fomu\(y=f(x)\).
- Katika fomu ya tabular, kazi inaweza kuwakilishwa na safu au nguzo zinazohusiana na maadili ya pembejeo na pato.
- Ili kutathmini kazi, tunaamua thamani ya pato kwa thamani ya pembejeo inayofanana. Aina za algebraic za kazi zinaweza kutathminiwa kwa kuchukua nafasi ya kutofautiana kwa thamani iliyotolewa.
- Ili kutatua thamani maalum ya kazi, tunaamua maadili ya pembejeo yanayotoa thamani maalum ya pato.
- Aina ya algebraic ya kazi inaweza kuandikwa kutoka kwa equation.
- Maadili ya pembejeo na pato ya kazi yanaweza kutambuliwa kutoka meza.
- Kuhusiana na maadili ya pembejeo kwa maadili ya pato kwenye grafu ni njia nyingine ya kutathmini kazi.
- Kazi ni moja kwa moja ikiwa kila thamani ya pato inalingana na thamani moja tu ya pembejeo.
- Grafu inawakilisha kazi ikiwa mstari wowote wa wima unaotolewa kwenye grafu huingilia grafu bila zaidi ya hatua moja.
- Grafu ya kazi moja kwa moja hupita mtihani wa mstari usio na usawa.
maelezo ya chini
1 http://www.baseball-almanac.com/lege... /lisn 100.shtml. kupatikana 3/24/2014.
2 www.kgbanswers.com/jinsi-long-i... y-span/4221590. kupatikana 3/24/2014.
faharasa
variable tegemezi
variable pato
domain seti ya maadili yote inawezekana pembejeo kwa uhusiano
kazi
uhusiano ambapo kila thamani pembejeo mavuno ya kipekee pato thamani
mtihani wa mstari
wa usawa njia ya kupima ikiwa kazi ni moja kwa moja kwa kuamua kama mstari wowote wa usawa unaingilia grafu zaidi ya mara moja
variable huru variable
pembejeo
pembejeo
kila kitu au thamani katika uwanja unaohusiana na kitu kingine au thamani kwa uhusiano unaojulikana kama kazi
kazi
moja kwa moja - kazi ambayo kila thamani ya pato inahusishwa na thamani ya pembejeo ya kipekee
pato
kila kitu au thamani katika upeo unaozalishwa wakati thamani ya pembejeo imeingia kwenye kazi
aina
ya seti ya maadili ya pato yanayotokana na maadili ya pembejeo katika uhusiano
kuhusiana
na seti ya jozi zilizoamriwa
mtihani
wa mstari wa wima - njia ya kupima kama grafu inawakilisha kazi kwa kuamua kama mstari wa wima unaingilia grafu si zaidi ya mara moja.


