B: Misingi ya hisabati
- Page ID
- 174934
Mraba na Mamlaka nyingine
Mtazamaji, au nguvu, ni shorthand ya hisabati kwa kuzidisha mara kwa mara. Kwa mfano, exponent “2” ina maana ya kuzidisha msingi kwa kuwa exponent yenyewe (katika mfano hapa, msingi ni “5"):
\[5^2=5×5=25\]
Mtazamaji ni “2" na msingi ni namba “5.” Maneno haya (kuzidisha namba yenyewe) pia huitwa mraba. Nambari yoyote iliyoinuliwa kwa nguvu ya 2 ni kuwa mraba. Nambari yoyote iliyoinuliwa kwa nguvu ya 3 ni kuwa cubed:
\[5^3=5×5×5=125\]
Nambari iliyoinuliwa hadi nguvu ya nne ni sawa na namba hiyo inayoongezeka yenyewe mara nne, na kadhalika kwa mamlaka ya juu. Kwa ujumla:
\[n^x=n×n^{x−1}\]
Kuhesabu asilimia
Asilimia ni njia ya kuonyesha kiasi cha sehemu ya kitu kwa kutumia nzima imegawanywa katika sehemu 100. Asilimia ni uwiano ambao denominator yake ni 100. Tunatumia alama ya asilimia,%, ili kuonyesha asilimia. Hivyo, 25% ina maana uwiano wa\(\frac{25}{100}\), 3% ina maana uwiano wa\(\frac{3}{100}\), na asilimia 100% ina maana\(\frac{100}{100}\), au kwa ujumla.
Kubadilisha asilimia
Asilimia inaweza kubadilishwa kuwa sehemu kwa kuandika thamani ya asilimia kama sehemu na denominator ya 100 na kurahisisha sehemu iwezekanavyo.
\[25\%=\dfrac{25}{100}=\dfrac{1}{4}\]
Asilimia inaweza kubadilishwa kuwa decimal kwa kuandika thamani ya asilimia kama sehemu yenye denominator ya 100 na kugawa namba kwa denominator.
\[10\%=\dfrac{10}{100}=0.10\]
Ili kubadilisha decimal kwa asilimia, andika decimal kama sehemu. Ikiwa denominator ya sehemu sio 100, ubadilishe kwa sehemu na denominator ya 100, na kisha uandike sehemu kama asilimia.
\[0.833=\dfrac{833}{1000}=\dfrac{83.3}{100}=83.3\%\]
Ili kubadilisha sehemu kwa asilimia, kwanza kubadilisha sehemu kwa decimal, na kisha ubadili decimal kwa asilimia.
\[\dfrac{3}{4}=0.75=\dfrac{75}{100}=75\%\]
Tuseme mtafiti anaona kwamba wanafunzi 15 kati ya 23 katika darasa ni flygbolag ya Neisseria meningitides. Ni asilimia gani ya wanafunzi ni flygbolag? Ili kupata thamani hii, kwanza onyesha namba kama sehemu.
\[\mathrm{\dfrac{carriers}{total\: students}}=\dfrac{15}{23}\]
Kisha ugawanye nambari na denominator.
\[\dfrac{15}{23}=15\div 23 \approx 0.65\]
Hatimaye, kubadili decimal kwa asilimia, kuzidisha kwa 100.
\[0.65 \times 100=65\%\]
Asilimia ya wanafunzi ambao ni flygbolag ni 65%.
Unaweza pia kupata data juu ya tukio na yasiyo ya tukio; kwa mfano, katika sampuli ya wanafunzi, 9 majaribio chanya kwa ajili ya kingamwili Toxoplasma, wakati 28 majaribio hasi. Ni asilimia gani ya wanafunzi wa seropositive? Hatua ya kwanza ni kuamua “nzima,” ambayo wanafunzi wazuri ni sehemu. Kwa kufanya hivyo, jumla ya vipimo vyema na hasi.
\[\mathrm{positive+negative=9+28=37}\]
Sampuli nzima ilikuwa na wanafunzi 37. Sehemu ya chanya ni:
\[\mathrm{\dfrac{positive}{total\: students}=\dfrac{9}{37}}\]
Ili kupata asilimia ya wanafunzi ambao ni flygbolag, kugawanya nambari na denominator na kuzidi kwa 100.
\ [dfrac {9} {37} =9\ div 37\ takriban 0.24\\
0.24\ nyakati 100=24\%\]
Asilimia ya wanafunzi chanya ni takriban 24%.
Njia nyingine ya kufikiri juu ya kuhesabu asilimia ni kuanzisha sehemu sawa, moja ambayo ni sehemu na 100 kama denominator, na kuzidisha msalaba. Mfano uliopita utaelezwa kama:
\[\dfrac{9}{37}=\dfrac{x}{100}\]
Sasa, msalaba kuzidisha na kutatua kwa haijulikani:
\ [kuanza {align}
9\ mara 100 &=37 x & &\ nonumber\\ [5pt]
\ Frac {9\ mara 100} {37} &=x & &\ maandishi {Gawanya pande zote mbili kwa 37}\ nonumber\\ [5pt]
\ Frac {900} {37} &= x &\ maandishi {Kuzidisha}\ nonumber\\ [5pt]
24 & x wastani & &\ maandishi {Gawanya}\ nonumber
\ mwisho {align}\]
Jibu, lililozunguka, ni sawa.
Kuzidisha na Kugawa kwa Makumi
Katika nyanja nyingi, hasa katika sayansi, ni kawaida kuzidisha decimals kwa nguvu ya 10. Hebu angalia nini kinatokea wakati sisi kuzidisha 1.9436 na baadhi ya nguvu ya 10.
\ [kuanza {align}
1.9436 (10) &=19.436\ hakuna idadi\\
1.9436 (100) &=194.36\ hakuna idadi\\
1.9436 (1000) &=1943.6\ hakuna idadi
\ mwisho {align}\]
Idadi ya maeneo ambayo hatua ya decimal inakwenda ni sawa na idadi ya zero katika nguvu ya kumi. \(\PageIndex{1}\)Jedwali linafupisha matokeo.
| Kuzidisha kwa | Zeros | Hatua ya decimal hatua. |
|---|---|---|
| 10 | 1 | 1 mahali pa kulia |
| 100 | 2 | Sehemu 2 kwa haki |
| 1,000 | 3 | Sehemu 3 kwa haki |
| 10,000 | 4 | 4 maeneo ya haki |
Tunaweza kutumia ruwaza hii kama njia ya mkato ili kuzidisha kwa nguvu za kumi badala ya kuzidisha kwa kutumia muundo wa wima. Tunaweza kuhesabu zero katika nguvu ya 10 na kisha hoja uhakika decimal kwamba idadi sawa ya maeneo ya haki.
Kwa hiyo, kwa mfano, kuzidisha 45.86 na 100, fanya sehemu ya decimal 2 mahali pa kulia.
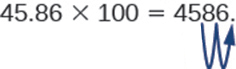
Wakati mwingine tunahitaji kusonga hatua ya decimal, hakuna maeneo ya kutosha ya decimal. Katika hali hiyo, tunatumia zero kama mahali placeholders. Kwa mfano, hebu tuzidishe 2.4 na 100. Tunahitaji kuhamisha sehemu ya decimal 2 kwa haki. Kwa kuwa kuna tarakimu moja tu kwa haki ya hatua ya decimal, lazima tuandike 0 katika sehemu ya hundredths.
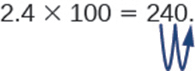
Wakati kugawa kwa nguvu ya 10, tu kuchukua mbinu kinyume na hoja decimal upande wa kushoto na idadi ya zero katika nguvu ya kumi.
Hebu angalia nini kinatokea wakati sisi kugawanya 1.9436 na baadhi ya mamlaka ya 10.
\ [kuanza {align}
1.9436\ div 10&= 0.19436\ namba\\
1.9436\ div 100&= 0.019436\ nambari\\
1.9436\ div 1000&= 0.0019436\ hakuna idadi
\ mwisho {align}\]
Ikiwa kuna tarakimu za kutosha kuhamisha decimal, ongeza zero ili uunda maeneo.
Nukuu ya kisayansi
Nukuu ya kisayansi hutumiwa kueleza namba kubwa sana na ndogo sana kama bidhaa ya namba mbili. Nambari ya kwanza ya bidhaa, neno la tarakimu, kwa kawaida ni idadi isiyo chini ya 1 na si zaidi ya 10. Nambari ya pili ya bidhaa, neno la ufafanuzi, imeandikwa kama 10 na kielelezo. Baadhi ya mifano ya nukuu ya kisayansi hutolewa katika Jedwali\(\PageIndex{2}\).
| Standard Nukuu | Nukuu ya kisayansi |
|---|---|
| 1000 | 1 × 10 3 |
| 100 | 1 × 10 2 |
| 10 | 1 × 10 1 |
| 1 | 1 × 10 0 |
| 0.1 | 1 × 10 -1 |
| 0.01 | 1 × 10 -2 |
Nukuu ya kisayansi ni nukuu muhimu sana kwa idadi kubwa sana na ndogo sana, kama vile 1,230,000,000 = 1.23 × 10 9, na 0.00000000036 = 3.6 × 10 -10.
Kueleza Hesabu katika Nukuu ya kisayansi
Kubadili nambari yoyote kwa notation ya kisayansi ni moja kwa moja. Hesabu idadi ya maeneo inahitajika kuhamisha decimal karibu na tarakimu ya kushoto isiyo ya sifuri: yaani, kufanya namba kati ya 1 na 10. Kisha kuzidisha idadi hiyo kwa 10 kukulia kwa idadi ya maeneo uliyohamisha decimal. Mtazamaji ni chanya ikiwa umehamisha decimal upande wa kushoto na hasi ikiwa umehamisha decimal kwenda kulia. Hivyo
\[2386=2.386\times1000=2.386\times10^3\]
na
\[0.123=1.23\times0.1=1.23\times10^{-1}\]
Nguvu (exponent) ya 10 ni sawa na idadi ya maeneo ambayo decimal inabadilishwa.
Logarithms
Logarithm ya kawaida (logi) ya namba ni nguvu ambayo 10 inapaswa kuinuliwa ili sawa na idadi hiyo. Kwa mfano, logarithm ya kawaida ya 100 ni 2, kwa sababu 10 inapaswa kuinuliwa kwa nguvu ya pili ili sawa 100. Mifano ya ziada iko katika Jedwali\(\PageIndex{3}\).
| Idadi | Fomu ya kielelezo | Logarithm ya kawaida |
|---|---|---|
| 1000 | 10 3 | 3 |
| 10 | 10 1 | 1 |
| 1 | 10 0 | 0 |
| 0.1 | 10 -1 | -1 |
| 0.001 | 10-3 | 1-3 |
Ili kupata logarithm ya kawaida ya namba nyingi, utahitaji kutumia kifungo cha LOG kwenye calculator.
Mzunguko na tarakimu muhimu
Katika kuripoti data za namba zilizopatikana kupitia vipimo, tunatumia takwimu nyingi muhimu kama usahihi wa vibali vya kipimo. Kwa mfano, tuseme microbiologist kutumia counter kiini automatiska huamua kuwa kuna seli za bakteria 525,341 katika sampuli moja ya lita moja ya maji ya mto. Hata hivyo, anarekodi mkusanyiko huo kama seli 525,000 kwa lita na hutumia namba hii iliyozunguka ili kukadiria idadi ya seli ambazo zinaweza kupatikana katika lita 10 za maji ya mto. Katika mfano huu, tarakimu tatu za mwisho za kiasi kilichopimwa hazizingatiwi kuwa muhimu. Wao ni mviringo kwa akaunti kwa tofauti katika idadi ya seli ambazo zinaweza kutokea ikiwa sampuli zaidi zilipimwa.
Umuhimu wa takwimu muhimu liko katika maombi yao kwa hesabu ya msingi. Kwa kuongeza na kutoa, jumla au tofauti inapaswa kuwa na tarakimu nyingi kwa haki ya decimal kama kwamba katika angalau fulani (imeonyeshwa kwa kusisitiza katika mfano wafuatayo) ya namba zilizotumiwa katika hesabu.
Tuseme microbiologist anataka kuhesabu molekuli jumla ya sampuli mbili za agar.
\ [kuanza {safu} {l}
4.38\ kusisitiza {3}\ maandishi {g}\\ kusisitiza {3.002
\ kusisitiza {1}}\ maandishi {g}\
7.38\ kusisitiza {5}\ Nakala {5}\ maandishi {g}
\ mwisho {safu}\]
Baadhi ya watu wawili wana sehemu tatu za decimal, hivyo jumla lazima iwe na maeneo matatu ya decimal.
Katika kuzidisha na mgawanyiko, bidhaa au quotient haipaswi kuwa na tarakimu zaidi kuliko katika sababu iliyo na idadi ndogo ya takwimu muhimu. Tuseme microbiologist angependa kuhesabu kiasi gani cha reagent kitakuwapo katika 6.6 mL ikiwa mkusanyiko ni 0.638 g/ml.
\[\mathrm{0.63\underline{8}\:\dfrac{g}{mL}\times6.\underline{6}\:mL=4.1\:g}\]
Tena, jibu lina sehemu moja tu ya decimal kwa sababu hii ni usahihi wa idadi sahihi zaidi katika hesabu.
Wakati namba za mzunguko, ongeze tarakimu iliyohifadhiwa na 1 ikiwa inafuatiwa na namba kubwa kuliko 5 (“pande zote”). Usibadilishe tarakimu iliyohifadhiwa ikiwa tarakimu zinazofuata ni chini ya 5 (“pande zote chini”). Ikiwa tarakimu iliyohifadhiwa inafuatiwa na 5, pande zote ikiwa tarakimu iliyobaki ni isiyo ya kawaida, au pande zote chini ikiwa ni hata (baada ya kuzunguka, tarakimu iliyohifadhiwa itakuwa hivyo daima kuwa hata).
Muda wa kizazi
Inawezekana kuandika equation kuhesabu namba za seli wakati wowote ikiwa idadi ya seli za kuanzia na wakati wa mara mbili hujulikana, kwa muda mrefu kama seli zinagawanyika kwa kiwango cha mara kwa mara. Tunafafanua N 0 kama idadi ya mwanzo ya bakteria, idadi kwa wakati t = 0. N i ni idadi ya bakteria wakati t = i, wakati wa kiholela katika siku zijazo. Hatimaye sisi kuweka j sawa na idadi ya vizazi, au idadi ya mara idadi ya seli mara mbili wakati wa kipindi cha muda. Kisha tuna,
\[N_i=N_0\times2^j\]
Equation hii ni usemi wa ukuaji na fission binary.
Katika mfano wetu, N 0 = 4, idadi ya vizazi, j, ni sawa na 3 baada ya dakika 90 kwa sababu wakati wa kizazi ni dakika 30. Idadi ya seli zinaweza kuhesabiwa kutoka kwa usawa wafuatayo:
\ [kuanza {align}
n_i & = N_0\ mara 2 ^ j\ nambari\\
N_ {90} &= 4\ mara 2 ^ 3\
n_ {90} &=4\ mara 8 = 32\ nambari
\ mwisho {align}\]
Idadi ya seli baada ya dakika 90 ni 32.
Idadi inayowezekana zaidi
Jedwali katika Kielelezo\(\PageIndex{1}\) lina maadili yaliyotumiwa kuhesabu mfano wa idadi inayowezekana zaidi iliyotolewa katika Jinsi Microbes Kukua.