Skip to main content
Global

30.8: Hesabu na Kanuni za Quantum

  1. Last updated
  2. Save as PDF
  • Page ID
    182938

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Eleza idadi ya quantum.
    • Tumia angle ya vector ya kasi ya angular na mhimili.
    • Kufafanua spin quantum idadi.

    Tabia za kimwili ambazo zinahesabiwa - kama nishati, malipo, na kasi ya angular - zina umuhimu sana kwamba majina na alama hupewa. Maadili ya vyombo vya kupima yanaonyeshwa kwa mujibu wa idadi ya quantum, na sheria zinazosimamia ni za umuhimu mkubwa katika kuamua ni asili gani na inafanya. Sehemu hii inashughulikia baadhi ya namba muhimu zaidi za quantum na sheria-zote ambazo zinatumika katika kemia, sayansi ya vifaa, na mbali zaidi ya eneo la fizikia ya atomiki, ambapo waligunduliwa kwanza. Mara nyingine tena, tunaona jinsi fizikia inavyofanya uvumbuzi ambao huwezesha mashamba mengine kukua.

    Nchi za nishati za mifumo iliyofungwa zinahesabiwa, kwa sababu wavelength ya chembe inaweza kuingia katika mipaka ya mfumo kwa njia fulani tu. Hii ilifafanuliwa kwa atomi ya hidrojeni, ambayo nguvu za kuruhusiwa zinaelezwa kama

    \[E_{n} \propto \frac{1}{n^{2}},\label{30.9.1}\]

    wapi\(n = 1,2,3, \cdot \cdot \cdot\). Tunafafanua\(n\) kuwa namba kuu ya quantum inayoandika majimbo ya msingi ya mfumo. Hali ya chini ya nishati ina\(n = 1\), hali ya kwanza ya msisimko ina\(n=2\), na kadhalika. Hivyo, maadili ya kuruhusiwa kwa idadi kuu ya quantum ni:

    \[n = 1, 2, 3, ...\label{30.9.2}\]

    Hii ni zaidi ya mpango wa kuhesabu, kwani nishati ya mfumo, kama vile atomi ya hidrojeni, inaweza kuelezwa kama kazi fulani ya\(n\), kama vile sifa nyingine (kama vile radii orbital ya atomi ya hidrojeni).

    Ukweli kwamba ukubwa wa kasi ya angular ni quantized mara ya kwanza kutambuliwa na Bohr kuhusiana na atomi ya hidrojeni; sasa inajulikana kuwa kweli kwa ujumla. Pamoja na maendeleo ya mechanics ya quantum, iligundua kuwa ukubwa wa kasi ya angular\(L\) inaweza tu kuwa na maadili

    \[L = \sqrt{l \left( l+1 \right) } \frac{h}{2\pi} \left(l = 0, 1, 2, ..., n-1\right), \label{30.9.3}\]

    ambapo\(l\) ni defined kuwa angular kasi quantum idadi. Utawala wa atomi hutolewa katika mabano.\(l\) Kutokana\(n\), thamani\(l\) inaweza kuwa integer yoyote kutoka sifuri hadi\(n-1\). Kwa mfano, ikiwa\(n = 4\), basi\(l\) inaweza kuwa 0, 1, 2, au 3.

    Kumbuka kwamba kwa\(n = 1\),\(l\) inaweza tu kuwa sifuri. Hii ina maana kwamba kasi ya angular ya ardhi kwa hidrojeni ni kweli sifuri, si\(h/2\pi\) kama Bohr alipendekeza. Picha ya mzunguko wa mviringo si halali, kwa sababu kutakuwa na kasi ya angular kwa obiti yoyote ya mviringo. Picha halali zaidi ni wingu la uwezekano unaoonyeshwa kwa hali ya ardhi ya hidrojeni katika kiungo hiki. Kwa kweli elektroni hutumia muda ndani na karibu na kiini. Sababu elektroni haibaki katika kiini inahusiana na kanuni ya kutokuwa na uhakika wa Heisenberg — nishati ya elektroni ingekuwa kubwa mno ili ifunge kwenye nafasi ndogo ya kiini. Sasa hali ya kwanza ya msisimko wa hidrojeni ina\(n=2\), hivyo kwamba\(l\) inaweza kuwa ama 0 au 1, kulingana na utawala katika Equation\(\ref{30.9.3}\). Vile vile\(n =3\), kwa,\(l\) inaweza kuwa 0, 1, au 2. Mara nyingi ni rahisi zaidi kusema thamani ya\(l\), integer rahisi, badala ya kuhesabu thamani ya\(L\) kutoka Equation\(\ref{30.9.3}\). Kwa mfano, kwa\(l = 2\), tunaona kwamba

    \[L = \sqrt{l \left( l+1 \right) } \frac{h}{2\pi} = \sqrt{6} \frac{h}{2 \pi} = 0.390 h = 2.58 \times 10^{-34} J \cdot s.\]

    Ni rahisi sana kusema\(l = 2\). Kama kutambuliwa katika athari ya Zeeman, mwelekeo wa kasi ya angular ni quantized. Sasa tunajua hii ni kweli katika hali zote. Inapatikana kuwa sehemu ya kasi ya angular pamoja na mwelekeo mmoja katika nafasi, kwa kawaida huitwa -axis, inaweza kuwa na maadili fulani tu ya\(L_{z}\). Mwelekeo katika nafasi lazima uwe na uhusiano na kitu cha kimwili, kama vile mwelekeo wa shamba la magnetic mahali hapo. Hii ni kipengele cha relativity. Mwelekeo hauna maana kama hakuna kitu ambacho hutofautiana na mwelekeo, kama inavyofanya nguvu ya magnetic. Maadili ya kuruhusiwa\(L_{z}\)\(L_{z}\) ni\[L_{z} = m_{l} \frac{h}{2\pi} \left( m_{l} = -l, -l + 1, ..., -1, 0, 1, ... l-1, l\right),\label{30.9.4}\] wapi z-sehemu ya kasi ya angular na\(m_{l}\) ni angular kasi makadirio quantum idadi. Utawala katika mabano kwa maadili ya\(m_{l}\) ni kwamba inaweza kuanzia\(-l\) hadi\(l\) katika hatua za moja. Kwa mfano, kama\(l = 2\), basi\(m_{l}\) unaweza kuwa na maadili tano - 2, -1, 0, 1, na 2. Kila\(m_{l}\) inalingana na nishati tofauti mbele ya shamba la magnetic, ili waweze kuhusishwa na kugawanyika kwa mistari ya spectral katika sehemu za kipekee, kama ilivyojadiliwa katika sehemu iliyotangulia. Ikiwa\(z\) - sehemu ya kasi ya angular inaweza kuwa na maadili fulani tu, basi kasi ya angular inaweza kuwa na maelekezo fulani tu, kama ilivyoonyeshwa kwenye Mchoro 30.9.1.

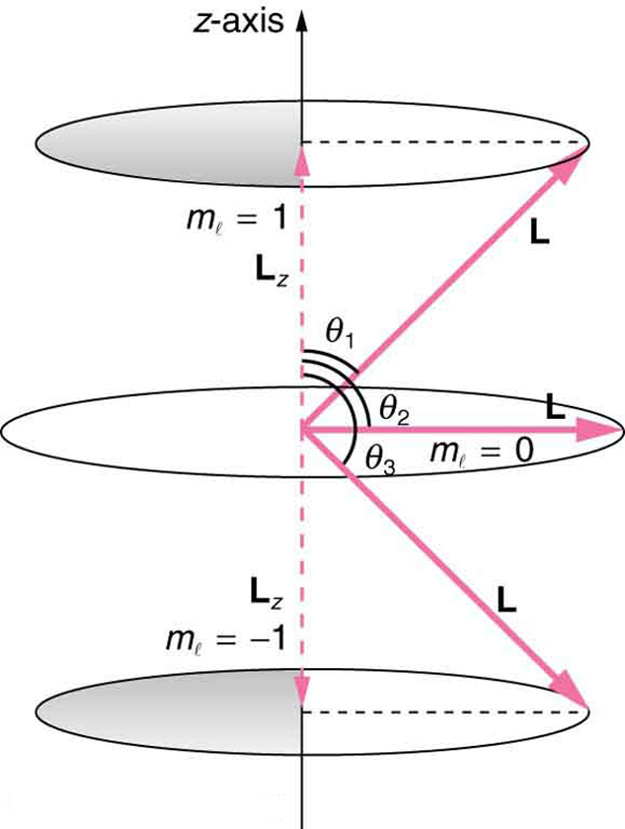
    Picha inaonyesha maadili mawili iwezekanavyo ya sehemu ya kasi ya angular iliyotolewa pamoja na mhimili wa z. Moja mviringo obiti juu ya awali mviringo obiti ni umeonyesha kwa m ndogo l thamani ya pamoja moja. Mwingine obiti mviringo chini ya awali mviringo obiti ni umeonyesha kwa m ndogo l thamani ya bala moja. Vector ya kasi ya angular kwa obiti ya juu ya mviringo hufanya angle ya theta ndogo moja na mhimili wima. Vector ya kasi ya angular ya usawa katika obiti ya awali ya mviringo hufanya angle ya theta ndogo mbili na mhimili wima. Vector ya kasi ya angular kwa obiti ya chini ya mviringo hufanya angle ya theta ndogo tatu na mhimili wima.
    Kielelezo\(\PageIndex{1}\). Sehemu ya kasi ya angular iliyopewa kando ya mhimili wa z (inayoelezwa na mwelekeo wa shamba la magnetic) inaweza kuwa na maadili fulani tu; hizi zinaonyeshwa hapa\(l =1\), kwa hiyo\(m_{l} = -1, 0, and +1\). Mwelekeo wa\(L\) ni quantized kwa maana kwamba inaweza kuwa na pembe fulani tu kuhusiana na z-axis.

    Mfano\(\PageIndex{1}\): What are the Allowed Directions?

    Tumia pembe ambazo vector ya kasi ya angular\(L\) inaweza kufanya na mhimili wa z-kwa\(l = 1\), kama ilivyoonyeshwa kwenye Mchoro 30.9.1.

    Mkakati:

    Kielelezo 30.9.1. inawakilisha vectors\(L\) na\(L_{z}\) kama kawaida, na mishale sawia na ukubwa wao na akizungumzia katika maelekezo sahihi. \(L\)na\(L_{z}\) kuunda pembetatu sahihi, na\(L\) kuwa hypotenuse na upande\(L_{z}\) wa karibu. Hii ina maana kwamba uwiano wa\(L_{z}\) to\(L\) ni cosine ya angle ya riba. Tunaweza kupata\(L\) na\(L_{z}\) kutumia\(L = \sqrt{l\left(l + 1\right)}\frac{h}{2\pi}\) na\(L_{z} = m \frac{h}{2\pi}\).

    Suluhisho

    Sisi ni kutoa\(l = 1\), hivyo kwamba\(m_{l}\) inaweza kuwa =1, 0, au -1. Hivyo\(L\) ina thamani iliyotolewa na\(L = \sqrt{l\left(l + 1\right)}\frac{h}{2\pi}\).

    \[L = \frac{\sqrt{l\left(l + 1\right)}h}{2\pi} = \frac{\sqrt{2}h}{2\pi} \label{30.9.5}\]

    \(L_{z}\)inaweza kuwa na maadili matatu, iliyotolewa na\(L_{z} = m_{l} \frac{h}{2\pi}\). \[L_{z} = m_{l} \frac{h}{2\pi} = \begin{cases} \frac{h}{2\pi}, ~ m_{l} = +1 \\[2ex] 0, ~ m_{l} = 0 \\[2ex] \frac{h}{2\pi}, ~ m_{l} = -1 \end{cases} \label{30.9.6}\]

    Kama inavyoonekana katika Kielelezo\(\cos{\theta} = L_{z}/L\), na hivyo\(m_{l} \pm 1\), tuna\[\cos{\theta_{1}} = \frac{L_{z}}{L} = \frac{\frac{h}{2\pi}}{\frac{\sqrt{2}h}{2\pi}} = \frac{1}{\sqrt{2}} = -.707.\label{30.9.7}\]

    Hivyo,

    \[\theta_{1} = \cos{0.707}^{-1} = 45.0 ^{\circ}.\label{30.9.8}\]

    Vile vile\(m_{l} = 0\), kwa, tunaona\(\cos_{2} = 0\); hivyo,

    \[\theta_{2} = \cos{0}^{-1} = 90.0. ^{\circ} \label{30.9.9}\]

    Na kwa ajili ya\(m_{l} = -1\),

    \[\cos{\theta_{3}} = \frac{L_{z}}{L} = \frac{-\frac{h}{2\pi}}{\frac{\sqrt{2}h}{2\pi}} = -\frac{1}{\sqrt{2}} = -0.707, \label{30.9.10}\]

    ili

    \[\theta_{3} = \cos{\left(-0.707\right)}^{-1} = 135.0^{\circ}.\label{30.9.11}\]

    Majadiliano:

    Pembe ni sawa na takwimu. Tu angle jamaa na z-axis ni quantized. \(L\)inaweza kuelekeza katika mwelekeo wowote kwa muda mrefu kama inafanya angle sahihi na mhimili wa z. Hivyo vectors angular kasi uongo juu ya mbegu kama ilivyoonyeshwa. Tabia hii haionyeshi kwa kiwango kikubwa. Kuona jinsi kanuni ya mawasiliano inashikilia hapa, fikiria kwamba angle ndogo (\(\theta_{1}\)katika mfano) ni kwa thamani ya juu ya\(m_{l} = 0\), yaani\(m_{l} = l\). Kwa kuwa angle ndogo,

    \[\cos{\theta} = \frac{L_{z}}{L} = \frac{l}{\sqrt{l\left(l + 1 \right) }},\label{30.9.12}\]

    ambayo inakaribia 1 kama\(l\) inakuwa kubwa sana. Ikiwa\(\cos{\theta} = 1\), basi\(\theta = 0^{\circ}\). Zaidi ya hayo\(l\), kwa kubwa, kuna maadili mengi ya\(m_{l}\), ili pembe zote kuwa inawezekana kama\(l\) anapata kubwa sana.

    Intrinsic Spin Angular Moment Ni Quantized katika Ukubwa na Mwelekeo

    Kuna idadi mbili zaidi ya quantum ya wasiwasi wa haraka. Wote wawili walikuwa kwanza aligundua kwa elektroni kwa kushirikiana na muundo faini katika spectra atomiki. Sasa imara kuwa elektroni na chembe nyingine za msingi zina spin ya ndani, takribani sawa na sayari inayozunguka kwenye mhimili wake. Spin hii ni tabia ya msingi ya chembe, na ukubwa mmoja tu wa spin ya ndani inaruhusiwa kwa aina fulani ya chembe. Intrinsic angular kasi ni quantized kwa kujitegemea ya orbital angular kasi. Zaidi ya hayo, mwelekeo wa spin pia hupimwa. Imekuwa kupatikana kwamba ukubwa wa ndani (ndani) spin kasi angular,\(S\), ya elektroni hutolewa na

    \[S = \sqrt{s\left(s+1\right)}\frac{h}{2\pi} \left( s = 1/2 ~ for ~ electrons\right), \label{30.9.13}\]

    ambapo\(s\) hufafanuliwa kuwa idadi ya quantum ya spin. Hii ni sawa na quantization ya\(L\) kutolewa katika\(L = \sqrt{l\left(l+1\right)}\frac{h}{2\pi}\), isipokuwa kwamba thamani tu kuruhusiwa\(s\) kwa elektroni ni 1/2.

    Mwelekeo wa spin ya ndani ni quantized, kama vile mwelekeo wa kasi ya angular orbital. Mwelekeo wa kasi ya angular ya spin pamoja na mwelekeo mmoja katika nafasi, tena inayoitwa z-axis, inaweza kuwa na maadili tu

    \[s_{z} = m_{s} \frac{h}{2\pi} \left( m_{s} = -\frac{1}{2}, +\frac{1}{2} \right) \label{30.9.14}\]

    kwa elektroni. \(s_{z}\0 is the z-component of spin angular momentum and \(m_{s}\)ni spin makadirio quantum idadi. Kwa elektroni,\(s\) inaweza tu 1/2, na\(m_{s}\) inaweza kuwa ama +1/2 au —1/2. Spin makadirio\(m_{s} = + 1/2\) inajulikana kama spin up, ambapo\(m_{s} = -1/2\) inaitwa\(m_{s} = - 1/2\) inaitwa spin chini. Hizi zinaonyeshwa katika kiungo hiki.

    SPIN YA NDANI

    Katika sura za baadaye, tutaona kwamba spin ya ndani ni tabia ya chembe zote za subatomic. Kwa baadhi ya chembe\(s\) ni nusu-muhimu, ambapo kwa wengine\(s\) ni muhimu - kuna tofauti muhimu kati ya chembe nusu-muhimu spin na chembe muhimu spin. Protoni na nyutroni, kama elektroni, zina\(s = 1/2\), ambapo fotoni zina\(s = 1\), na chembe nyingine zinazoitwa pioni zina\(s = 0\), na kadhalika.

    Kwa muhtasari, hali ya mfumo, kama vile asili sahihi ya elektroni katika atomi, imedhamiriwa na namba zake za quantum. Hizi zinaonyeshwa kwa fomu\(n, l, m_{l}, m_{s}\) — tazama Jedwali Kwa elektroni katika atomi, nambari kuu ya quantum inaweza kuwa na maadili\(n = 1, 2, 3, ...\). Mara baada\(n\) ya kujulikana, maadili ya idadi ya kasi ya angular ya quantum ni mdogo\(l = 1, 2, 3, ..., n-1\). Kwa thamani fulani ya\(l\), angular kasi makadirio quantum idadi inaweza kuwa tu maadili\(m_{l} = -l, -l + 1, ..., -1, 0, 1, ..., l-1, l\). Electron spin ni huru ya\(n\),\(l\), na\(m_{l}\), daima kuwa na\(s = 1/2\). Nambari ya quantum ya kupima spin inaweza kuwa na maadili mawili. \(m_{s} = 1/2 ~ or ~ -1/2\).

    Jina Mkono Maadili ya kuruhusiwa
    Nambari kuu ya quantum \(n\) \(1,2,3,...\)
    Kasi ya angular \(l\) \(0, 1, 2, ... n-1\)
    Makadirio ya kasi ya pembe \(m_{l}\) \(-l, -l+1, ..., -1, 0, 1, ..., l-1, l \left(or ~ 0, \pm 1, \pm 2, ..., \pm l \right)\)
    Spin \(s\) \(1/2 \left(electrons\right)\)
    Spin makadirio \(m_{s}\) \(\pm 1/2\)

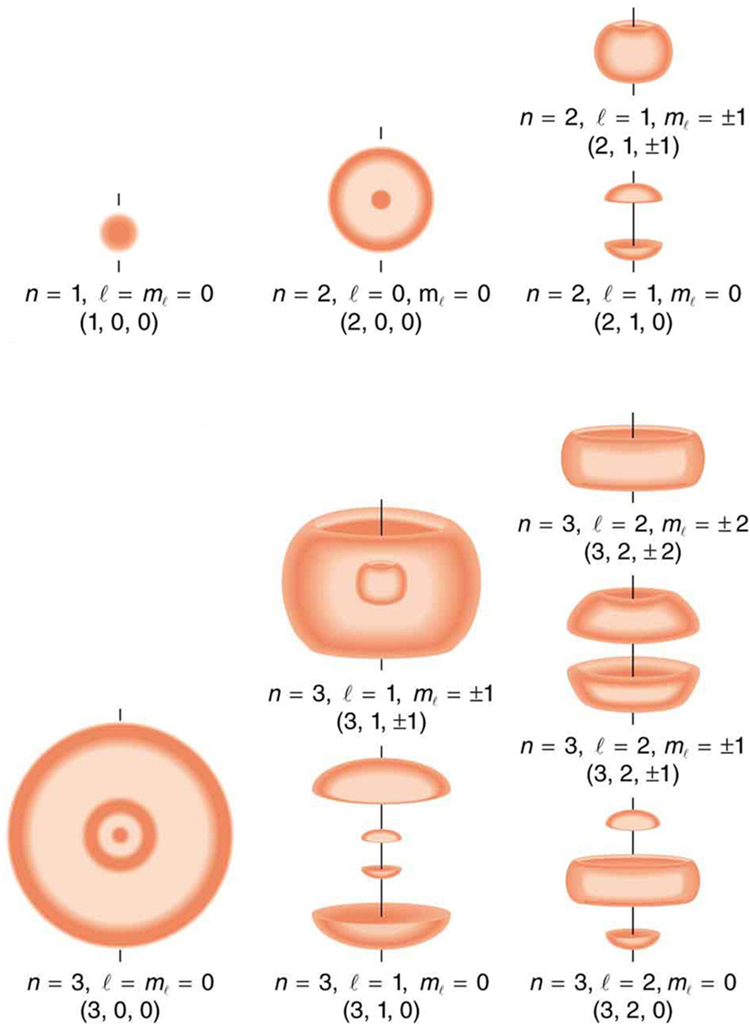
    Kielelezo 30.9.2. inaonyesha majimbo kadhaa ya hidrojeni yanayohusiana na seti tofauti za namba za quantum. Kumbuka kwamba mawingu haya ya uwezekano ni maeneo ya elektroni kama ilivyoainishwa kwa kufanya vipimo mara kwa mara - kila kipimo hupata elektroni katika eneo la uhakika, likiwa na nafasi kubwa ya kupata elektroni mahali fulani badala ya nyingine. Kwa vipimo vya mara kwa mara, mfano wa uwezekano unaoonyeshwa kwenye takwimu hujitokeza. Mawingu ya uwezekano hayaonekani kama wala yanahusiana na njia za classical. Kanuni ya kutokuwa na uhakika kweli inatuzuia sisi na asili tusijue jinsi elektroni inapata kutoka sehemu moja hadi nyingine, na hivyo obiti kweli haipo kama vile. Hali kwa kiwango kidogo ni tofauti sana na ile kwa kiwango kikubwa.

    Picha inaonyesha uwezekano wa mawingu kwa elektroni katika hali ya ardhi na majimbo kadhaa ya msisimko wa hidrojeni. Seti ya idadi quantum kutolewa kama n l m Subscript l ni umeonyesha kwa kila hali. Hali ya ardhi ni sifuri sifuri sifuri. Uwezekano wa kupata elektroni unaonyeshwa na kivuli cha rangi.
    Kielelezo\(\PageIndex{2}\). Mawingu ya uwezekano kwa elektroni katika hali ya ardhi na majimbo kadhaa ya msisimko wa hidrojeni. Hali ya majimbo haya imedhamiriwa na seti zao za namba za quantum, hapa imetolewa kama\(n, l, m_{l}\). Hali ya ardhi ni (0, 0, 0); moja ya uwezekano wa hali ya pili ya msisimko ni (3, 2, 1). Uwezekano wa kupata elektroni unaonyeshwa na kivuli cha rangi; giza kuchorea nafasi kubwa ya kupata elektroni.

    Tutaona kwamba idadi ya quantum iliyojadiliwa katika sehemu hii ni halali kwa aina mbalimbali za chembe na mifumo mingine, kama vile nuclei. Baadhi ya idadi quantum, kama vile spin ndani, ni kuhusiana na uainishaji wa msingi wa chembe subatomic, na wao kutii sheria ambayo itatupa ufahamu zaidi katika substructure ya suala na mwingiliano wake.

    PHET EXPLORATIONS: STERN-GERLACH MAJARIBIO

    classic Stern-Gerlach majaribio inaonyesha kwamba atomi na mali iitwayo spin. Spin ni aina ya kasi ya angular ya ndani, ambayo haina mwenzake wa kawaida. Wakati sehemu ya z-ya spin inapimwa, moja hupata moja ya maadili mawili: spin up au spin chini.

    PhET_Icon.png
    Kielelezo\(\PageIndex{3}\): Majaribio ya Stern-Gerlach

    Muhtasari

    • Nambari za quantum hutumiwa kuelezea maadili ya kuruhusiwa ya vyombo vya kupima. Nambari kuu ya\(n\) quantum inaandika majimbo ya msingi ya mfumo na hutolewa na\(n = 1, 2, 3, ... \)
    • Ukubwa wa kasi ya angular hutolewa na\(L = \sqrt{l \left( l+1 \right) } \frac{h}{2\pi} \left(l = 0, 1, 2, ..., n-1\right),\) wapi\(l\) idadi ya angular kasi ya quantum. Mwelekeo wa kasi ya angular ni quantized, kwa kuwa sehemu yake pamoja na mhimili inavyoelezwa na shamba magnetic, aitwaye z-mhimili hutolewa na\(L_{z} = m_{l} \frac{h}{2\pi} ~ \left(m_{l} = -l, -l+1, ..., -1, 0, 1, ... l-1, l\right),\) wapi\(L_{z}\) z-sehemu ya kasi ya angular na\(m_{l}\) ni angular kasi makadirio quantum idadi. Vile vile, kasi ya elektroni ya ndani ya spin angular\(S\) hutolewa na\(S = \sqrt{s\left(s+1\right)}\frac{h}{2\pi} ~ \left(s = 1/2 ~ for ~ electrons \right),\) wapi\(S_{z}\) sehemu ya z-ya kasi ya angular na\(m_{s}\) ni namba ya quantum ya makadirio ya spin. Spin makadirio\(m_{s} = +1/2\) inajulikana kama spin up, ambapo\(m_{s} = -1/2\) inaitwa spin chini. Jedwali linafupisha idadi ya quantum ya atomiki na maadili yao ya kuruhusiwa.