2.7: Kuanguka vitu

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Eleza madhara ya mvuto juu ya vitu katika mwendo.
• Eleza mwendo wa vitu ambavyo viko katika kuanguka kwa bure.
• Tumia nafasi na kasi ya vitu katika kuanguka kwa bure.

vitu kuanguka

Vitu vya kuanguka huunda darasa la kuvutia la matatizo ya mwendo. Kwa mfano, tunaweza kukadiria kina cha shimoni la mgodi wima kwa kuacha mwamba ndani yake na kusikiliza mwamba kugonga chini. Kwa kutumia kinematics zilizotengenezwa hadi sasa kwa vitu vya kuanguka, tunaweza kuchunguza hali zenye kuvutia na kujifunza mengi kuhusu mvuto katika mchakato.

Mvuto

Ukweli wa ajabu zaidi na usiotarajiwa juu ya vitu vya kuanguka ni kwamba, ikiwa upinzani wa hewa na msuguano hauna maana, basi katika eneo fulani vitu vyote vinaanguka kuelekea katikati ya Dunia na kuongeza kasi ya mara kwa mara, bila kujitegemea kwa wingi wao. Ukweli huu wa majaribio haukutarajiwa, kwa sababu tumezoea madhara ya upinzani wa hewa na msuguano ambao tunatarajia vitu vidogo kuanguka polepole kuliko nzito.

Kielelezo\(\PageIndex{1}\): Nyundo na manyoya zitaanguka kwa kuongeza kasi ya mara kwa mara ikiwa upinzani wa hewa unachukuliwa kuwa duni. Hii ni tabia ya jumla ya mvuto si ya kipekee kwa Dunia, kama mwanaanga David R. Scott alionyesha juu ya Mwezi mwaka 1971, ambapo kasi kutokana na mvuto ni tu. 67 m/s 2.

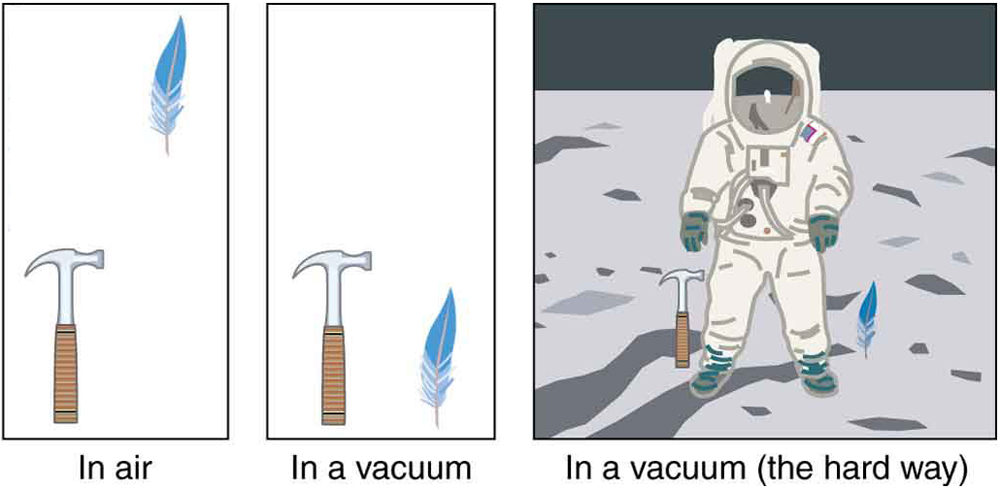
Katika ulimwengu wa kweli, upinzani wa hewa unaweza kusababisha kitu nyepesi kuanguka polepole kuliko kitu kikubwa cha ukubwa sawa. Mpira wa tenisi utafikia chini baada ya baseball ngumu imeshuka kwa wakati mmoja. (Huenda ikawa vigumu kuchunguza tofauti ikiwa urefu si mkubwa.) Upinzani wa hewa unapinga mwendo wa kitu kupitia hewa, huku msuguano kati ya vitu—kama vile kati ya nguo na chute ya kufulia au kati ya jiwe na bwawa ambalo linashuka-pia hupinga mwendo baina yao. Kwa hali nzuri ya sura hizi chache za kwanza, kitu kinachoanguka bila upinzani wa hewa au msuguano kinaelezwa kuwa katika kuanguka kwa bure.

Nguvu ya mvuto husababisha vitu kuanguka kuelekea katikati ya Dunia. Kwa hiyo kuongeza kasi ya vitu vya kuanguka bure huitwa kuongeza kasi kutokana na mvuto. Kuongezeka kwa sababu ya mvuto ni mara kwa mara, ambayo inamaanisha tunaweza kutumia equations ya kinematics kwa kitu chochote cha kuanguka ambapo upinzani wa hewa na msuguano ni duni. Hii inafungua darasa pana la hali ya kuvutia kwetu. Kuongezeka kwa sababu ya mvuto ni muhimu sana kwamba ukubwa wake unapewa ishara yake mwenyewe,. Ni mara kwa mara katika eneo lolote duniani na ina thamani ya wastani

\[g=9.80 m/s^2.\]

Ingawa inatofautiana kutoka. 78 m/s 2 hadi 9.83 m/s2, kulingana na latitude, urefu, miundo ya msingi ya kijiolojia, na topografia ya ndani, thamani ya wastani ya 9.80 m/s2 itatumika katika maandishi haya isipokuwa vinginevyo maalum. Mwelekeo wa kuongeza kasi kutokana na mvuto ni chini (kuelekea katikati ya Dunia). Kwa kweli, mwelekeo wake unafafanua kile tunachokiita wima. Kumbuka kwamba kama kuongeza kasi katika equations kinematic ina thamani +g au -g inategemea jinsi tunavyofafanua mfumo wetu wa kuratibu. Ikiwa tunafafanua mwelekeo wa juu kama hasi, basi a=-g=-9.80 m/s2, na ikiwa tunafafanua mwelekeo wa chini kama chanya, basi = g = 9. 80 m/s 2.

Mwendo mmoja wa mwelekeo unaohusisha Mvuto

Njia bora ya kuona vipengele vya msingi vya mwendo unaohusisha mvuto ni kuanza na hali rahisi na kisha kuendelea kuelekea ngumu zaidi. Kwa hiyo tunaanza kwa kuzingatia mwendo wa moja kwa moja juu na chini bila upinzani wa hewa au msuguano. Dhana hizi zinamaanisha kwamba kasi (ikiwa kuna yoyote) ni wima. Ikiwa kitu kimeshuka, tunajua kasi ya awali ni sifuri. Mara baada ya kitu kushoto kuwasiliana na chochote uliofanyika au kurusha, kitu ni katika free-kuanguka. Chini ya hali hizi, mwendo ni moja-dimensional na ina kasi ya mara kwa mara ya ukubwa g.Tutawakilisha pia uhamisho wima na ishara y na kutumia x kwa makazi ya usawa.

MILINGANISHO YA KINEMATIC KWA VITU KATIKA KUANGUKA KWA BURE AMBAPO KUONGEZA KASI = -G

\(v=v_0−gt\)

\(y=y_0+v_0t−\frac{1}{2}gt^2\)

\(v^2=v^2_0−2g(y−y_0)\)

Mfano\(\PageIndex{1}\): Calculating Position and Velocity of a Falling Object: A Rock Thrown Upward

Mtu amesimama kando ya mwamba wa juu hutupa mwamba moja kwa moja na kasi ya awali ya 13.0 m/s. Mwamba hukosa makali ya mwamba unapoanguka nyuma duniani. Tumia nafasi na kasi ya mwamba 1.00 s, 2.00 s, na 3.00 s baada ya kutupwa, kukataa madhara ya upinzani wa hewa.

Mkakati

Chora mchoro.

Kielelezo\(\PageIndex{2}\)

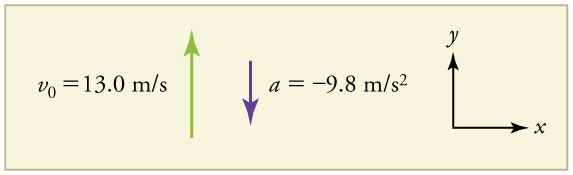
Tunaulizwa kuamua msimamo\(y\) kwa nyakati mbalimbali. Ni busara kuchukua nafasi ya kwanza\(y_0\) kuwa sifuri. Tatizo hili linahusisha mwendo mmoja wa mwelekeo katika mwelekeo wa wima. Sisi kutumia pamoja na minus ishara kuonyesha mwelekeo, na hadi kuwa chanya na chini hasi. Kwa kuwa up ni chanya, na mwamba unatupwa juu, kasi ya awali lazima iwe chanya pia. Kuharakisha kutokana na mvuto ni chini, hivyo ni hasi. Ni muhimu kwamba kasi ya awali na kuongeza kasi kutokana na mvuto ina ishara tofauti. Ishara za kinyume zinaonyesha kuwa kasi kutokana na mvuto inapinga mwendo wa awali na itapunguza na hatimaye kuirudisha.

Kwa kuwa sisi ni aliuliza kwa ajili ya maadili ya nafasi na kasi kwa mara tatu, sisi kutaja haya kama\(y_1\) na\(v_1; y_2\) na\(v_2\); na\(y_3\) na\(v_3\).

Suluhisho kwa Nafasi\(y_1\)

1. Tambua maarifa. Tunajua kwamba\(y_0=0; v_0=13.0 m/s; a=−g=−9.80 m/s^2\), na\(t=1.00 s.\)

2. Kutambua equation bora ya kutumia. Tutatumia\(y=y_0+v_0t+\frac{1}{2}at^2\) kwa sababu inajumuisha haijulikani moja tu\(y_1\),\(y\) (au, hapa), ambayo ni thamani tunayotaka kupata.

3. Plug katika maadili inayojulikana na kutatua kwa\(y_1\).

\(y_1=0+(13.0 m/s)(1.00 s)+\frac{1}{2}(−9.80m/s^2)(1.00 s)^2=8.10m\)

Majadiliano

Mwamba ni 8.10 m juu ya hatua yake ya kuanzia saa\(t=1.00 s\), tangu\(y_1>y_0\). Inaweza kusonga juu au chini; njia pekee ya kuwaambia ni kuhesabu\(v_1\) na kujua kama ni chanya au hasi.

Suluhisho la Velocity\(v_1\)

1. Tambua maarifa. Tunajua kwamba\(y_0=0; v_0=13.0 m/s; a=−g=−9.80 m/s^2\); na\(t=1.00 s\). Tunajua pia kutokana na suluhisho hapo juu\(y_1=8.10 m.\)

2. Kutambua equation bora ya kutumia. Moja kwa moja ni\(v=v_0−gt\) (kutoka\(v=v_0+at\), wapi a=kasi ya mvuto =-g).

3. Plug katika knowns na kutatua.

\(v_1=v_0−gt=13.0 m/s−(9.80 m/s^2)(1.00 s)=3.20 m/s\)

Majadiliano

Thamani chanya kwa\(v_1\) maana kwamba mwamba bado inaelekea juu\(t=1.00s\). Hata hivyo, imepungua kutoka 13.0 m/s yake ya awali, kama inavyotarajiwa.

Suluhisho kwa Nyakati zilizobaki

Taratibu za kuhesabu nafasi na kasi na\(3.00 s\) ni sawa\(t=2.00s\) na zile zilizo juu. Matokeo ni muhtasari katika Jedwali na mfano katika Kielelezo.

Matokeo

Muda, t	Nafasi, y	Velocity, v	Kuharakisha,
. 00 s	. 10 m	. 20 m/s\)	9. 80 m/s^ 2\)
. 00 s	. 40 m	6. 60 m/s\)	9. 80 m/s^ 2\)
. 00 s	5. 10 m	16. 4 m/s\)	9. 80 m/s^ 2\)

Graphing data inatusaidia kuelewa ni wazi zaidi.

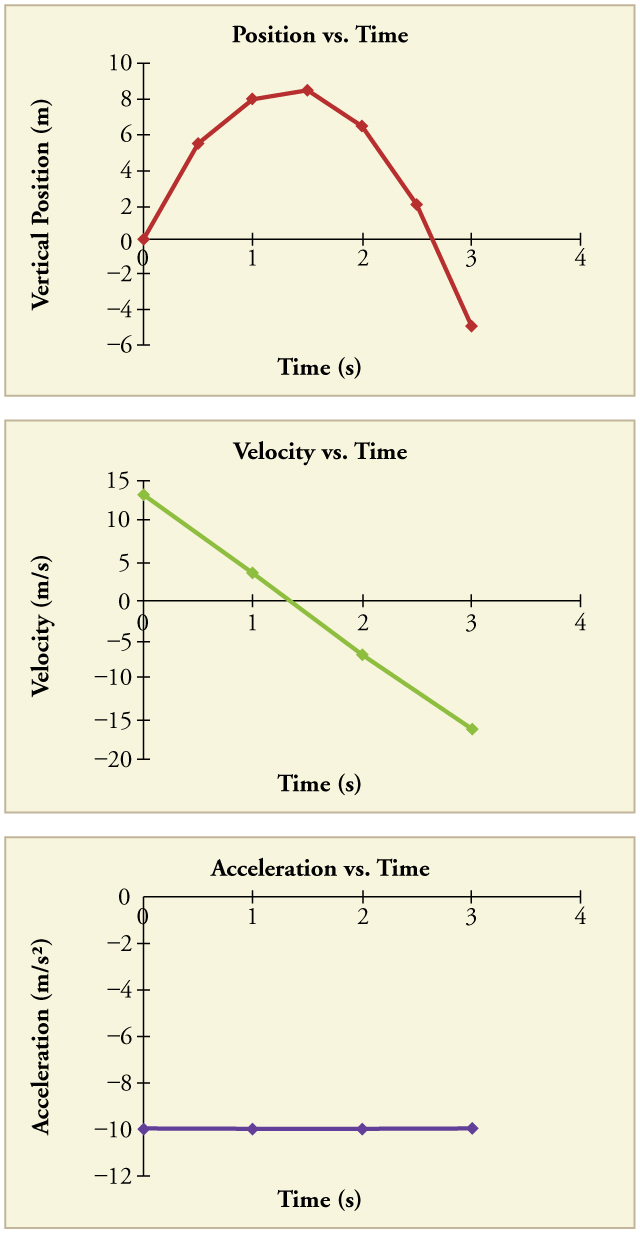
\(PageIndex{3}\): msimamo wima, kasi wima, na kuongeza kasi wima vs. wakati kwa ajili ya mwamba kutupwa wima juu katika makali ya mwamba. Kumbuka kwamba kasi mabadiliko linearly na wakati na kwamba kuongeza kasi ni mara kwa mara. Potofu Alert! Kumbuka kwamba msimamo vs wakati grafu inaonyesha msimamo wima tu. Ni rahisi kupata hisia kwamba grafu inaonyesha mwendo wa usawa - sura ya grafu inaonekana kama njia ya projectile. Lakini hii sio kesi; mhimili usio na usawa ni wakati, sio nafasi. Njia halisi ya mwamba angani ni sawa juu, na sawa chini.

Majadiliano

Tafsiri ya matokeo haya ni muhimu. Katika 1.00 s mwamba ni juu ya hatua yake ya kuanzia na kuelekea juu, tangu\(y_1\) and \(v_1\) are both positive. At 2.00 s, the rock is still above its starting point, but the negative velocity means it is moving downward. At 3.00 s, both \(y_3\) and \(v_3\) are negative, meaning the rock is below its starting point and continuing to move downward. Notice that when the rock is at its highest point (at 1.5 s), its velocity is zero, but its acceleration is still \(−9.80 m/s^2\). Its acceleration is \(−9.80 m/s^2\) for the whole trip—while it is moving up and while it is moving down. Note that the values for y are the positions (or displacements) of the rock, not the total distances traveled. Finally, note that free-fall applies to upward motion as well as downward. Both have the same acceleration—the acceleration due to gravity, which remains constant the entire time. Astronauts training in the famous Vomit Comet, for example, experience free-fall while arcing up as well as down, as we will discuss in more detail later.The interpretation of these results is important. At 1.00 s the rock is above its starting point and heading upward, since y1 and v1 are both positive. At 2.00 s, the rock is still above its starting point, but the negative velocity means it is moving downward. At 3.00 s, both y3 and v3 are negative, meaning the rock is below its starting point and continuing to move downward. Notice that when the rock is at its highest point (at 1.5 s), its velocity is zero, but its acceleration is still −9.80 m/s2. Its acceleration is −9.80 m/s2 for the whole trip—while it is moving up and while it is moving down. Note that the values for y are the positions (or displacements) of the rock, not the total distances traveled. Finally, note that free-fall applies to upward motion as well as downward. Both have the same acceleration—the acceleration due to gravity, which remains constant the entire time. Astronauts training in the famous Vomit Comet, for example, experience free-fall while arcing up as well as down, as we will discuss in more detail later.

MAKING CONNECTIONS: TAKE-HOME EXPERIMENT—REACTION TIME

A simple experiment can be done to determine your reaction time. Have a friend hold a ruler between your thumb and index finger, separated by about 1 cm. Note the mark on the ruler that is right between your fingers. Have your friend drop the ruler unexpectedly, and try to catch it between your two fingers. Note the new reading on the ruler. Assuming acceleration is that due to gravity, calculate your reaction time. How far would you travel in a car (moving at 30 m/s) if the time it took your foot to go from the gas pedal to the brake was twice this reaction time?

Example \(\PageIndex{2}\):Calculating Velocity of a Falling Object: A Rock Thrown Down

What happens if the person on the cliff throws the rock straight down, instead of straight up? To explore this question, calculate the velocity of the rock when it is 5.10 m below the starting point, and has been thrown downward with an initial speed of 13.0 m/s.

Strategy

Draw a sketch.

Figure \(\PageIndex{4}\)

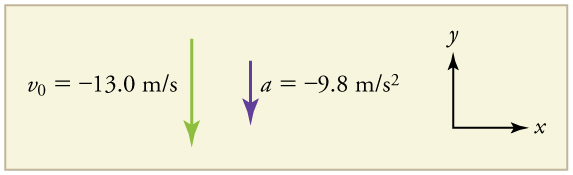
Since up is positive, the final position of the rock will be negative because it finishes below the starting point at \(y_0=0\). Similarly, the initial velocity is downward and therefore negative, as is the acceleration due to gravity. We expect the final velocity to be negative since the rock will continue to move downward.

Solution

1. Identify the knowns. \(y_0=0; y_1=−5.10 m; v_0=−13.0 m/s; a=−g=−9.80 m/s^2\).

2. Choose the kinematic equation that makes it easiest to solve the problem. The equation \(v^2=v^2_0+2a(y−y_0)\) works well because the only unknown in it is \(v\). (We will plug \(y_1\) in for \(y\).)

3. Enter the known values

\(v^2=(−13.0 m/s)^2+2(−9.80 m/s^2)(−5.10 m−0 m)=268.96 m^2/s^2,\)

where we have retained extra significant figures because this is an intermediate result.

Taking the square root, and noting that a square root can be positive or negative, gives

\(v=±16.4 m/s.\)

The negative root is chosen to indicate that the rock is still heading down. Thus,

\(v=−16.4 m/s.\)

Discussion

Note that this is exactly the same velocity the rock had at this position when it was thrown straight upward with the same initial speed. (See Example and Figure(a).) This is not a coincidental result. Because we only consider the acceleration due to gravity in this problem, the speed of a falling object depends only on its initial speed and its vertical position relative to the starting point. For example, if the velocity of the rock is calculated at a height of 8.10 m above the starting point (using the method from Example) when the initial velocity is 13.0 m/s straight up, a result of \(±3.20 m/s\) is obtained. Here both signs are meaningful; the positive value occurs when the rock is at 8.10 m and heading up, and the negative value occurs when the rock is at 8.10 m and heading back down. It has the same speed but the opposite direction.

Figure \(PageIndex{5}\): (a) A person throws a rock straight up, as explored in Example. The arrows are velocity vectors at 0, 1.00, 2.00, and 3.00 s. (b) A person throws a rock straight down from a cliff with the same initial speed as before, as in Example. Note that at the same distance below the point of release, the rock has the same velocity in both cases.

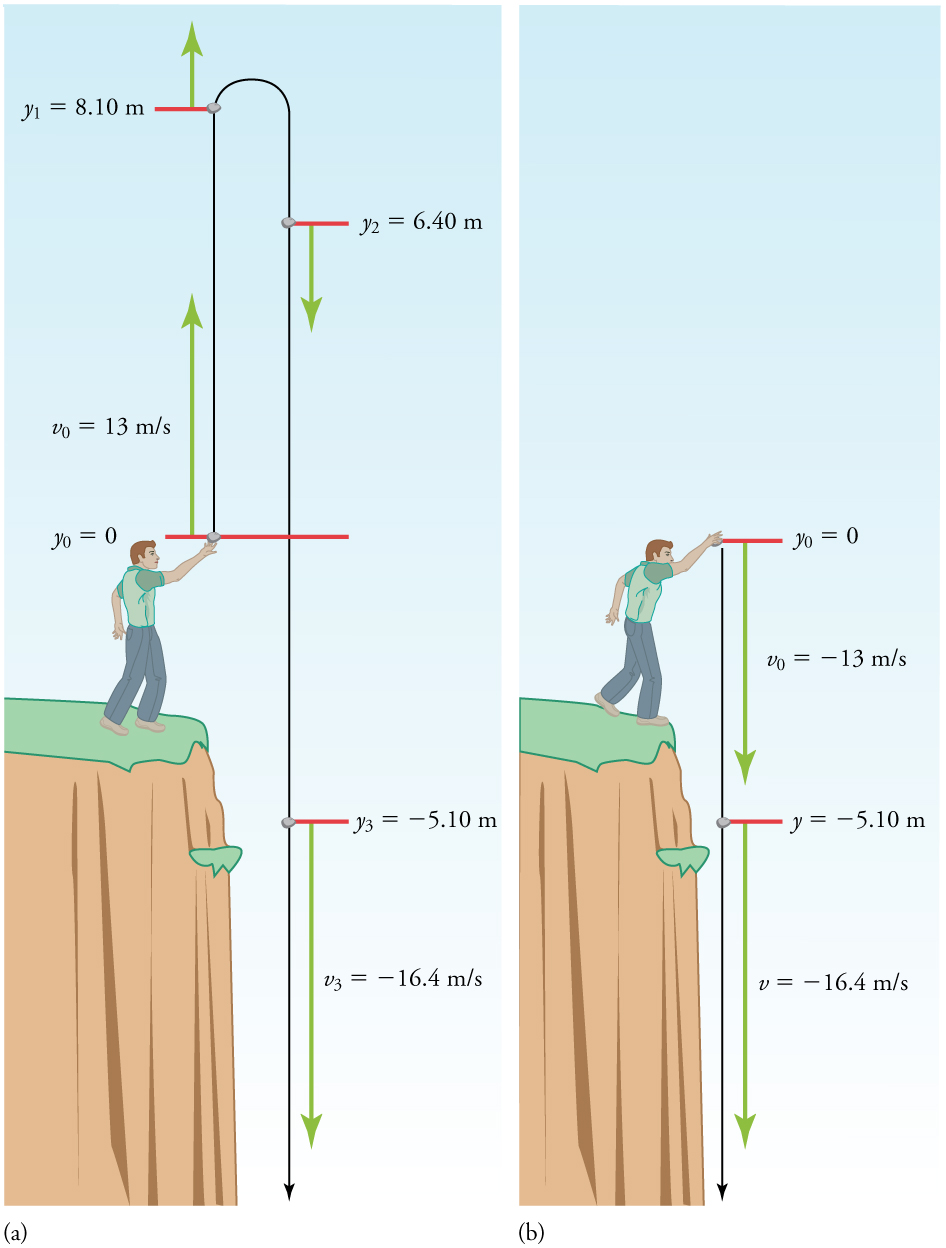
Another way to look at it is this: In Example, the rock is thrown up with an initial velocity of \(13.0 m/s\). It rises and then falls back down. When its position is \(y=0\) on its way back down, its velocity is \(−13.0 m/s\). That is, it has the same speed on its way down as on its way up. We would then expect its velocity at a position of \(y=−5.10\) m to be the same whether we have thrown it upwards at \(+13.0 m/s\) or thrown it downwards at \(−13.0 m/s\). The velocity of the rock on its way down from \(y=0\) is the same whether we have thrown it up or down to start with, as long as the speed with which it was initially thrown is the same.

Example \(\PageIndex{3}\):Find g from Data on a Falling Object

The acceleration due to gravity on Earth differs slightly from place to place, depending on topography (e.g., whether you are on a hill or in a valley) and subsurface geology (whether there is dense rock like iron ore as opposed to light rock like salt beneath you.) The precise acceleration due to gravity can be calculated from data taken in an introductory physics laboratory course. An object, usually a metal ball for which air resistance is negligible, is dropped and the time it takes to fall a known distance is measured. See, for example, Figure. Very precise results can be produced with this method if sufficient care is taken in measuring the distance fallen and the elapsed time.

Figure \(\PageIndex{6}\): Positions and velocities of a metal ball released from rest when air resistance is negligible. Velocity is seen to increase linearly with time while displacement increases with time squared. Acceleration is a constant and is equal to gravitational acceleration.

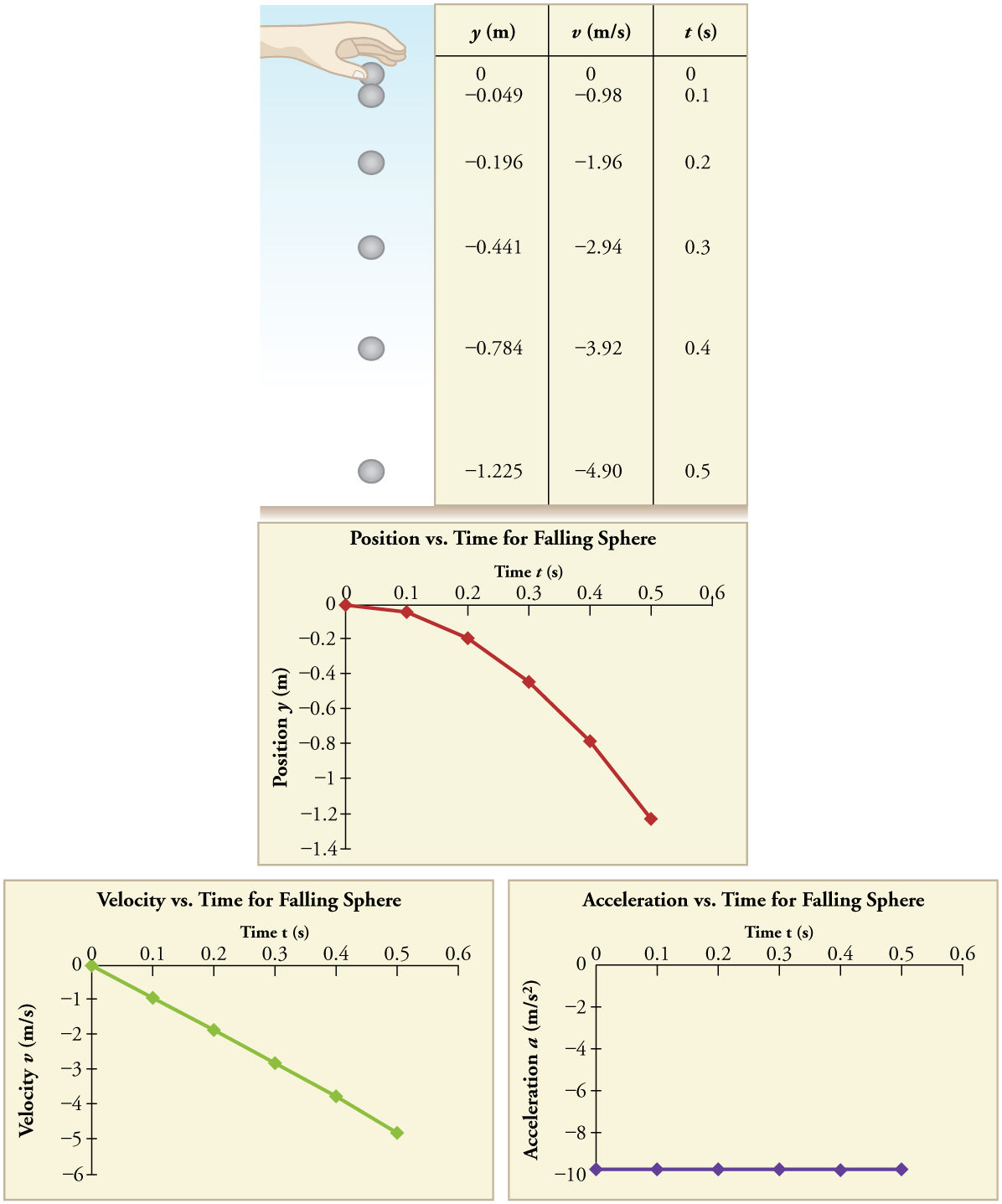
Suppose the ball falls 1.0000 m in 0.45173 s. Assuming the ball is not affected by air resistance, what is the precise acceleration due to gravity at this location?

Strategy

Draw a sketch.

Figure \(\PageIndex{7}\):

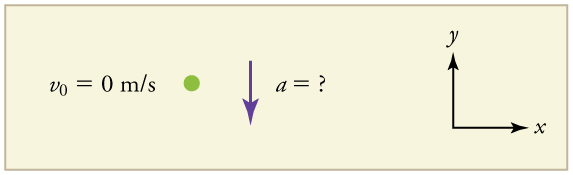
We need to solve for acceleration \(a.\) Note that in this case, displacement is downward and therefore negative, as is acceleration.

Solution

1. Identify the knowns. \(y_0=0; y=–1.0000 m; t=0.45173; v_0=0.\)

2. Choose the equation that allows you to solve for \(a\) using the known values.

\(y=y_0+v_0t+\frac{1}{2}at^2\)

3. Substitute 0 for \(v_0\) and rearrange the equation to solve for \(a\). Substituting 0 for \(v_0\)yields

\(y=y_0+\frac{1}{2}at^2\).

Solving for \(a\) gives

\(a=\frac{2(y−y_0)}{t^2}\).

4. Substitute known values yields

\(a=\frac{2(−1.0000 m – 0)}{(0.45173 s)^2}=−9.8010 m/s^2,\)

so, because \(a=−g\) with the directions we have chosen,

\(g=9.8010 m/s^2.\)

Discussion

The negative value for a indicates that the gravitational acceleration is downward, as expected. We expect the value to be somewhere around the average value of \(9.80 m/s^2\), so \(9.8010 m/s^2\) makes sense. Since the data going into the calculation are relatively precise, this value for g is more precise than the average value of \(9.80 m/s%2\); it represents the local value for the acceleration due to gravity.

Exercise \(\PageIndex{1}\)

A chunk of ice breaks off a glacier and falls 30.0 meters before it hits the water. Assuming it falls freely (there is no air resistance), how long does it take to hit the water?

Answer

We know that initial position \(y_0=0\), final position \(y=−30.0 m\), and \(a=−g=−9.80 m/s^2\). We can then use the equation \(y=y_0+v_0t+\frac{1}{2}at^2\) to solve for \(t\). Inserting \(a=−g\), we obtain

\(y=0+0−\frac{1}{2}gt^2\)

\(t^2=\frac{2y}{−g}\)

\(t=±\sqrt{\frac{2y}{−g}}=±\sqrt{\frac{2(−30.0 m)}{−9.80 m/s^2}}=±\sqrt{6.12s^2}=2.47 s≈2.5 s\)

where we take the positive value as the physically relevant answer. Thus, it takes about 2.5 seconds for the piece of ice to hit the water.

PHET EXPLORATIONS: EQUATION GRAPHER

Learn about graphing polynomials. The shape of the curve changes as the constants are adjusted. View the curves for the individual terms (e.g. \(y=bx\)) to see how they add to generate the polynomial curve.

Figure \(\PageIndex{8}\): Equation Grapher

Summary

• An object in free-fall experiences constant acceleration if air resistance is negligible.
• On Earth, all free-falling objects have an acceleration due to gravity \(g\), which averages

\(g=9.80 m/s^2\).

• Whether the acceleration a should be taken as \(+g\) or \(−g\) is determined by your choice of coordinate system. If you choose the upward direction as positive, \(a=−g=−9.80 m/s^2\) is negative. In the opposite case, \(a=+g=9.80 m/s^2\) is positive. Since acceleration is constant, the kinematic equations above can be applied with the appropriate \(+g\) or \(−g\) substituted for a.
• For objects in free-fall, up is normally taken as positive for displacement, velocity, and acceleration.

Glossary

free-fall

the state of movement that results from gravitational force only

acceleration due to gravity

acceleration of an object as a result of gravity