Skip to main content
Global

2.5: Ulinganisho wa mwendo kwa Kuharakisha Mara kwa mara katika Kipimo kimoja

  1. Last updated
  2. Save as PDF
  • Page ID
    183176

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Tumia uhamisho wa kitu ambacho hakiharakisha, kutokana na nafasi ya awali na kasi.
    • Tumia kasi ya mwisho ya kitu cha kuharakisha, kilichopewa kasi ya awali, kuongeza kasi, na wakati.
    • Tumia uhamisho na nafasi ya mwisho ya kitu cha kuharakisha, kilichopewa nafasi ya awali, kasi ya awali, wakati, na kuongeza kasi.

    Tunaweza kujua kwamba zaidi ya kuongeza kasi ya, kusema, gari kusonga mbali na ishara ya kuacha, zaidi makazi yao katika muda fulani. Lakini sisi si maendeleo equation maalum kwamba inahusiana kuongeza kasi na makazi yao. Katika sehemu hii, tunaendeleza equations rahisi kwa mahusiano ya kinematic, kuanzia ufafanuzi wa uhamisho, kasi, na kuongeza kasi tayari imefunikwa.

    Watu wanne racing up mto katika kayaks yao.
    Kielelezo\(\PageIndex{1}\): equations Kinematic inaweza kutusaidia kuelezea na kutabiri mwendo wa kusonga vitu kama vile hizi kayaks racing katika Newbury, England. (mikopo: Barry Skeates, Flickr)

    Uthibitisho: t, x, v, a

    Kwanza, hebu tufanye baadhi ya kurahisisha katika notation. Kuchukua muda wa awali kuwa sifuri, kama wakati unapimwa na stopwatch, ni kurahisisha sana. Tangu muda uliopita ni\(\displaystyle Δt=t_f−t_0\), kuchukua\(\displaystyle t_0=0\) ina maana kwamba\(\displaystyle Δt=t_f\), wakati wa mwisho juu ya stopwatch. Wakati wa awali unachukuliwa kuwa sifuri, tunatumia usajili 0 ili kutaja maadili ya awali ya nafasi na kasi. Hiyo ni,\(\displaystyle x_0\) ni nafasi ya kwanza na\(\displaystyle v_0\) ni kasi ya awali. Sisi kuweka hakuna subscripts juu ya maadili ya mwisho. Hiyo ni,\(\displaystyle t\) ni mara ya mwisho,\(\displaystyle x\) ni nafasi ya mwisho, na\(\displaystyle v\) ni kasi ya mwisho. Hii inatoa kujieleza rahisi kwa muda uliopita - sasa,\(\displaystyle Δt=t\). Pia simplifies kujieleza kwa ajili ya makazi yao, ambayo ni sasa\(\displaystyle Δx=x−x_0\). Pia, inaeleza maneno ya mabadiliko katika kasi, ambayo sasa ni\(\displaystyle Δv=v−v_0\). Kwa muhtasari, kwa kutumia notation kilichorahisishwa, na wakati wa awali kuchukuliwa kuwa sifuri,

    \(\displaystyle Δt=t\)
    \(\displaystyle Δx=x−x_0\)
    \(\displaystyle Δv=v−v_0\)

    ambapo usajili 0 unaashiria thamani ya awali na ukosefu wa usajili unaashiria thamani ya mwisho katika mwendo wowote unaozingatiwa.

    Sasa tunafanya dhana muhimu kwamba kasi ni mara kwa mara. Dhana hii inatuwezesha kuepuka kutumia calculus ili kupata kasi ya haraka. Kwa kuwa kasi ni mara kwa mara, kasi ya wastani na instantaneous ni sawa. Hiyo ni,

    \[\bar{a}=a=constant,\]

    hivyo sisi kutumia ishara kwa ajili ya kuongeza kasi wakati wote. Kutokana na kuongeza kasi ya kuwa mara kwa mara haina kikomo kwa umakini hali tunaweza kujifunza wala kuharibu usahihi wa matibabu yetu. Kwa jambo moja, kuongeza kasi ni mara kwa mara katika idadi kubwa ya hali. Zaidi ya hayo, katika hali nyingine nyingi tunaweza kuelezea kwa usahihi mwendo kwa kuchukua kasi ya mara kwa mara sawa na kuongeza kasi ya wastani kwa mwendo huo. Hatimaye, katika mwendo ambapo kasi inabadilika kwa kasi, kama vile gari kuharakisha kasi ya juu na kisha kusimama kwa kuacha, mwendo unaweza kuchukuliwa katika sehemu tofauti, ambayo kila mmoja ina kasi yake ya mara kwa mara.

    Kutatua kwa makazi yao (Δx) na nafasi ya mwisho (x) Kutoka wastani wa kasi wakati kasi (a) ni mara kwa mara

    Ili kupata equations yetu ya kwanza mbili mpya, tunaanza na ufafanuzi wa kasi ya wastani:

    \[\displaystyle \bar{v}=\frac{Δx}{Δt}\]

    Kubadilisha notation kilichorahisishwa kwa\(\displaystyle Δx\) na\(\displaystyle Δt\) mavuno

    \[\displaystyle \bar{v}=\frac{x−x_0}{t}.\]

    Kutatua kwa\(\displaystyle x\) mavuno

    \[\displaystyle x=x_0+\bar{v}t,\]

    ambapo kasi ya wastani ni

    \[\displaystyle \bar{v}=\frac{v_0+v}{2} \label{eq5}\]

    na mara kwa mara\(a\).

    Equation\ ref {eq5} inaonyesha ukweli kwamba, wakati kuongeza kasi\(v\) ni mara kwa mara, ni wastani tu ya kasi ya awali na ya mwisho. Kwa mfano, ikiwa unaongeza kasi yako (yaani, kwa kuongeza kasi ya mara kwa mara) kutoka 30 hadi 60 km/h, basi kasi yako ya wastani wakati wa ongezeko hili la kutosha ni 45 km/h.\(\displaystyle \bar{v}=\frac{v_0+v}{2}\)

    \(\displaystyle \bar{v}=\frac{v_0+v}{2}=\frac{30 km/h+60 km/h}{2}=45 km/h,\)

    ambayo inaonekana mantiki.

    Mfano\(\PageIndex{1}\): Calculating Displacement - How Far does the Jogger Run?

    Jogger anaendesha chini ya kunyoosha moja kwa moja ya barabara na kasi ya wastani ya 4.00 m/s kwa 2.00 min. Nini nafasi yake ya mwisho, kuchukua nafasi yake ya kwanza kuwa sifuri?

    Mkakati

    Chora mchoro.

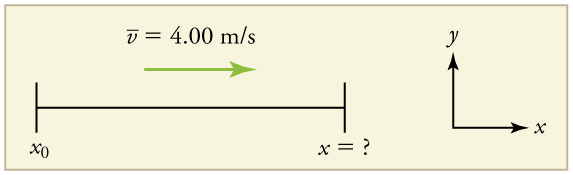
    Velocity vector mshale kinachoitwa v sawa 4 uhakika sifuri mita zero kwa sekunde juu ya x mhimili kuonyesha nafasi ya awali na ya mwisho. Nafasi ya mwisho ni kinachoitwa x sawa alama ya swali.
    Kielelezo\(\PageIndex{2}\)

    Msimamo wa mwisho hutolewa na equation

    \(\displaystyle x=x_0+\bar{v}t\).

    Ili kupata\(\displaystyle x\), sisi kutambua maadili ya\(\displaystyle x_0, \bar{v}\), na\(\displaystyle t\) kutoka taarifa ya tatizo na badala yao katika equation.

    Suluhisho

    1. Tambua maarifa. \(\displaystyle \bar{v}=4.00 m/s, Δt=2.00 min\), na\(\displaystyle x_0=0 m\).
    2. Ingiza maadili inayojulikana katika equation.
    \(\displaystyle x=x_0+\bar{v}t=0+(4.00 m/s)(120 s)=480 m\)

    Majadiliano

    Uhamisho wa kasi na uhamisho wa mwisho ni chanya, ambayo inamaanisha kuwa ni katika mwelekeo huo.

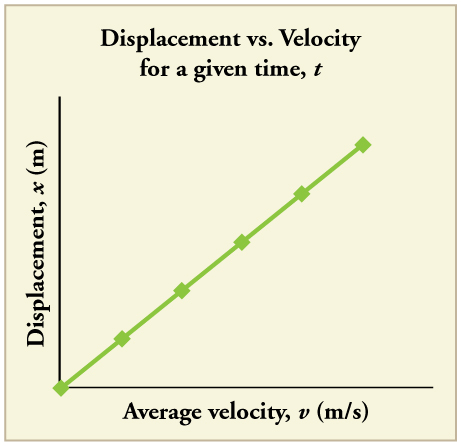
    Equation\(\displaystyle x=x_0+\bar{v}t\) inatoa ufahamu katika uhusiano kati ya makazi yao, kasi ya wastani, na wakati. Inaonyesha, kwa mfano, kwamba uhamisho ni kazi ya mstari wa kasi ya wastani. (Kwa kazi linear, tunamaanisha kuwa makazi yao inategemea\(\displaystyle \bar{v}\) badala ya\(\displaystyle \bar{v}\) kukulia kwa nguvu nyingine, kama vile\(\displaystyle \bar{v}^2\). Wakati wa kuchora, kazi za mstari zinaonekana kama mistari ya moja kwa moja na mteremko wa mara kwa mara.) Katika safari ya gari, kwa mfano, tutapata mara mbili kwa wakati uliopangwa ikiwa tuna wastani wa 90 km/h kuliko ikiwa wastani wa kilomita 45 km/h.

    Grafu ya mstari inayoonyesha uhamisho katika mita dhidi ya kasi ya wastani katika mita kwa sekunde. Mstari ni sawa na mteremko mzuri. Uhamisho x huongezeka linearly na ongezeko la kasi ya wastani v.
    Kielelezo\(\PageIndex{3}\): Kuna uhusiano wa mstari kati ya uhamisho na kasi ya wastani. Kwa muda fulani\(\displaystyle t\), an object moving twice as fast as another object will move twice as far as the other object.

    KUTATUA KWA KASI YA MWISHO

    Tunaweza kupata equation nyingine muhimu kwa kuendesha ufafanuzi wa kuongeza kasi.

    \(\displaystyle a=\frac{Δv}{Δt}\)

    Kubadilisha nukuu kilichorahisishwa kwa\(\displaystyle Δv\) na\(\displaystyle Δt\) inatupa

    \[\displaystyle a=\frac{v−v_0}{t}\](mara kwa mara a).

    Kutatua kwa\(\displaystyle v\) mavuno

    \[\displaystyle v=v_0+at\](constanta).

    Mfano\(\PageIndex{2}\):Calculating Final Velocity: An Airplane Slowing Down after Landing

    Ndege inashuka kwa kasi ya awali ya 70.0 m/s na kisha hupungua\(\displaystyle 1.50 m/s^2\) kwa 40.0 s. kasi yake ya mwisho ni nini?

    Mkakati

    Chora mchoro. Sisi kuteka vector kuongeza kasi katika mwelekeo kinyume vector kasi kwa sababu ndege ni decelerating.

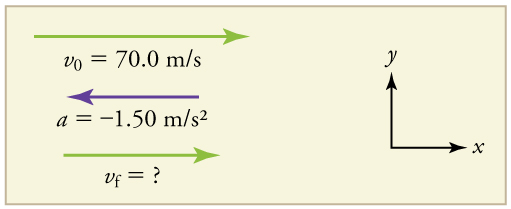
    Velocity vector mshale akizungumzia kuelekea haki katika chanya x mwelekeo. Kasi ya awali inalingana na mita sabini kwa pili. Mwisho kasi sawa alama ya swali. kuongeza kasi vector mshale akizungumzia upande wa kushoto kinachoitwa sawa hasi 1 pointi 50 mita kwa mraba pili.
    Kielelezo\(\PageIndex{4}\)

    Suluhisho

    1. Tambua maarifa. \(\displaystyle v_0=70.0 m/s, a=−1.50 m/s^2, t=40.0s.\)

    2. Tambua haijulikani. Katika kesi hii, ni kasi ya mwisho,\(\displaystyle v_f\).

    3. Tambua ni equation gani ya kutumia. Tunaweza kuhesabu kasi ya mwisho kwa kutumia equation\(\displaystyle v=v_0+at\).

    4. Plug katika maadili inayojulikana na kutatua.

    \(\displaystyle v=v_0+at=70.0 m/s+(−1.50 m/s^2)(40.0 s)=10.0 m/s\)

    Majadiliano

    Kasi ya mwisho ni ndogo sana kuliko kasi ya awali, kama inavyotakiwa wakati unapunguza kasi, lakini bado ni chanya. Pamoja na inji za ndege, reverse traction inaweza kudumishwa kwa muda mrefu wa kutosha kuacha ndege na kuanza kusonga nyuma. Hiyo itaonyeshwa kwa kasi mbaya ya mwisho, ambayo sio hapa.

    Ndege inayohamia kuelekea kulia kwa pointi mbili kwa wakati. Wakati sawa 0 kasi vector mshale pointi kuelekea haki na ni kinachoitwa mita sabini kwa sekunde. Mshale wa vector wa kasi unaelekea upande wa kushoto na umeandikwa hasi 1 kumweka mita 5 kwa mraba wa pili. Kwa wakati sawa na sekunde arobaini, mshale wa kasi ni mfupi, unaelekea upande wa kulia, na umeandikwa mita kumi kwa pili. kuongeza kasi vector mshale bado akizungumzia upande wa kushoto na ni kinachoitwa sawa hasi 1 uhakika 5 mita kwa mraba pili.
    Kielelezo\(\PageIndex{5}\): Ndege inashuka kwa kasi ya awali ya 70.0 m/s na hupungua hadi kasi ya mwisho ya 10.0 m/s kabla ya kuelekea terminal. Kumbuka kuwa kasi ni hasi kwa sababu mwelekeo wake ni kinyume na kasi yake, ambayo ni chanya.

    Mbali na kuwa na manufaa katika kutatua tatizo, equation\(\displaystyle v=v_0+at\) inatupa ufahamu katika mahusiano kati ya kasi, kuongeza kasi, na wakati. Kutoka humo tunaweza kuona, kwa mfano, kwamba

    • kasi ya mwisho inategemea jinsi kubwa kuongeza kasi ni na kwa muda gani unaendelea
    • ikiwa kasi ni sifuri, basi kasi ya mwisho inalingana na kasi ya awali (\(\displaystyle v=v_0\)), kama inavyotarajiwa (yaani, kasi ni mara kwa mara)
    • ikiwa ni hasi, basi kasi ya mwisho ni chini ya kasi ya awali

    (Uchunguzi huu wote unafaa intuition yetu, na daima ni muhimu kuchunguza equations msingi katika mwanga wa Intuition yetu na uzoefu kuangalia kwamba wao kweli kuelezea asili kwa usahihi.)

    KUFANYA UHUSIANO: UHUSIANO HALISI WA

    Nafasi kuhamisha ulipuaji mbali usiku.
    Kielelezo\(\PageIndex{6}\): Nafasi Shuttle Endeavor blasts mbali na Kennedy Space Center Februari (mikopo: Mathayo Simantov, Flickr)

    Kombora ya mabara ya ballistic (ICBM) ina kasi kubwa ya wastani kuliko Kuhamisha Nafasi na kufikia kasi kubwa katika dakika ya kwanza au mbili ya kukimbia (mara halisi ya kuchoma ICBM ni classified-muda kuchoma makombora ni ngumu zaidi kwa adui kuharibu). Lakini Space Shuttle inapata kasi kubwa ya mwisho, ili iweze obiti dunia badala ya kuja moja kwa moja nyuma chini kama ICBM gani. Kuhamisha Nafasi hufanya hivyo kwa kuharakisha kwa muda mrefu.

    KUTATUA KWA NAFASI YA MWISHO WAKATI KASI SI MARA KWA MARA (A0)

    Tunaweza kuchanganya equations hapo juu ili kupata equation ya tatu ambayo inaruhusu sisi kuhesabu nafasi ya mwisho ya kitu inakabiliwa na kasi ya mara kwa mara. Tunaanza na

    \(\displaystyle v=v_0+at.\)

    Kuongeza\(\displaystyle v_0\) kwa kila upande wa equation hii na kugawa kwa 2 anatoa

    \(\displaystyle \frac{v_0+v}{2}=v_0+\frac{1}{2}at\).

    Tangu\\ frac {(v_0+v} {2} =\ bar {v}\) kwa kuongeza kasi ya mara kwa mara, basi

    \(\displaystyle \bar{v}=v_0+\frac{1}{2}at\).

    Sasa sisi badala ya kujieleza hii kwa\(\displaystyle \bar{v}\) katika equation kwa makazi yao\(\displaystyle x=x_0+\bar{v}t\), kujitoa

    \(\displaystyle x=x_0+v_0t+\frac{1}{2}at^2\)(mara kwa mara a).

    Mfano\(\PageIndex{3}\): Calculating Displacement of an Accelerating Object - Dragsters

    Dragsters unaweza kufikia kasi ya wastani wa\(\displaystyle 26.0 m/s^2\). Suppose such a dragster accelerates from rest at this rate for 5.56 s. How far does it travel in this time?

    Dragster kuongeza kasi ya chini kufuatilia mashindano.
    Kielelezo\(\PageIndex{7}\): Jeshi la Marekani Top Mafuta majaribio Tony “Sarge” Schumacher huanza mbio na burnout kudhibitiwa. (mikopo: Luteni Col. William Thurmond. Picha kwa hisani ya Jeshi la Marekani)

    Mkakati

    Chora mchoro.

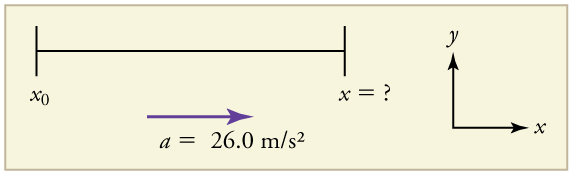
    Kuongeza kasi vector arrow akizungumzia upande wa kulia katika chanya x mwelekeo, kinachoitwa sawa na ishirini na sita uhakika 0 mita kwa mraba pili. x nafasi graph na nafasi ya awali katika mwisho wa kushoto wa grafu. Mwisho wa kulia wa grafu umeandikwa x sawa na alama ya swali.
    Kielelezo\(\PageIndex{8}\)

    Sisi ni aliuliza kupata makazi yao, ambayo ni\(\displaystyle x\) if we take \(\displaystyle x_0\) to be zero. (Think about it like the starting line of a race. It can be anywhere, but we call it 0 and measure all other positions relative to it.) We can use the equation \(\displaystyle x=x_0+v_0t+\frac{1}{2}at^2\) once we identify \(\displaystyle v_0, a,\) and \(\displaystyle t\) from the statement of the problem.

    Suluhisho

    1. Tambua maarifa. Kuanzia kupumzika ina maana kwamba\(\displaystyle v_0=0, a\) is given as \(\displaystyle 26.0m/s^2\) and t is given as 5.56 s.

    2. Plug maadili inayojulikana katika equation kutatua kwa x haijulikani:

    \(\displaystyle x=x_0+v_0t+\frac{1}{2}at^2\).

    Kwa kuwa msimamo wa awali na kasi ni sifuri, hii inaeleza

    \(\displaystyle x=\frac{1}{2}at^2\).

    Kubadilisha maadili yaliyotambuliwa ya a na t inatoa

    \(\displaystyle x=\frac{1}{2}(26.0 m/s^2)(5.56 s)^2\),

    kujitoa

    \(\displaystyle x=402 m.\)

    Majadiliano

    Kama sisi kubadilisha 402 m kwa maili, tunaona kwamba umbali kufunikwa ni karibu sana na robo moja ya maili, umbali kiwango kwa ajili ya racing Drag. Hivyo jibu ni busara. Hii ni makazi ya kuvutia katika 5.56 s tu, lakini dragsters juu-notch wanaweza kufanya robo maili katika muda hata kidogo kuliko hii.

    Nini kingine tunaweza kujifunza kwa kuchunguza equation\(\displaystyle x=x_0+v_0t+\frac{1}{2}at^2\)? Tunaona kwamba:

    • uhamisho hutegemea mraba wa muda uliopita wakati kasi sio sifuri. Katika Mfano, dragster inashughulikia moja tu ya nne ya umbali wa jumla katika nusu ya kwanza ya muda uliopita
    • ikiwa kuongeza kasi ni sifuri, basi kasi ya awali ni sawa na kasi ya wastani (\(\displaystyle v_0=\bar{v}\)) na\(\displaystyle x=x_0+v_0t+\frac{1}{2}at^2\) inakuwa\(\displaystyle x=x_0+v_0t\)

    KUTATUA KWA KASI YA MWISHO WAKATI KASI SI MARA KWA MARA (A0)

    Equation ya nne muhimu inaweza kupatikana kutoka kwa uharibifu mwingine wa algebraic wa equations uliopita.

    Kama sisi kutatua\(\displaystyle v=v_0+at\) kwa\(\displaystyle t\), sisi kupata

    \(\displaystyle t=\frac{v−v_0}{a}\).

    Kubadilisha hii na\(\displaystyle \bar{v}=\frac{v_0+v}{2}\) ndani\(\displaystyle x=x_0+\bar{v}t\), tunapata

    \(\displaystyle v^2=v^2_0+2a(x−x_0)\)(mara kwa mara a).

    Mfano\(\PageIndex{4}\): Calculating Final Velocity: Dragsters

    Tumia kasi ya mwisho ya dragster katika Mfano\(\PageIndex{3}\) bila kutumia taarifa kuhusu wakati.

    Mkakati

    Chora mchoro.

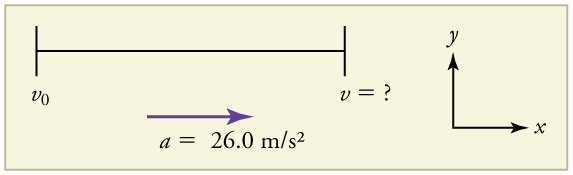
    Kuongeza kasi vector mshale akizungumzia kuelekea haki, kinachoitwa ishirini na sita pointi sifuri mita kwa pili mraba. Awali kasi sawa 0. Mwisho kasi sawa alama ya swali.
    Kielelezo\(\PageIndex{9}\)

    Equation\(\displaystyle v^2=v^2_0+2a(x−x_0)\) ni walau inafaa kwa kazi hii kwa sababu inahusiana kasi, kuongeza kasi, na makazi yao, na hakuna taarifa wakati inahitajika.

    Suluhisho

    1. Tambua maadili inayojulikana. Tunajua kwamba\(\displaystyle v_0=0\), tangu dragster huanza kutoka kupumzika. Kisha tunaona kwamba\(\displaystyle x−x_0=402 m\) (hii ndiyo jibu katika Mfano). Hatimaye, kuongeza kasi ya wastani ilitolewa kuwa\(\displaystyle a=26.0 m/s^2\).

    2. Plug knowns katika equation\(\displaystyle v^2=v^2_0+2a(x−x_0)\) na kutatua kwa\(\displaystyle v\).

    \(\displaystyle v^2=0+2(26.0 m/s^2)(402 m).\)

    Hivyo

    \(\displaystyle v^2=2.09×10^4m^2/s^2.\)

    Ili kupata\(\displaystyle v\), tunachukua mizizi ya mraba:

    \(\displaystyle v=\sqrt{2.09×10^4m^2/s^2}=145 m/s\).

    Majadiliano

    145 m/s ni kuhusu 522 km/h au kuhusu 324 mi/h, lakini hata kasi hii breakneck ni mfupi wa rekodi ya robo maili. Pia, kumbuka kuwa mizizi ya mraba ina maadili mawili; tulichukua thamani nzuri ili kuonyesha kasi katika mwelekeo sawa na kuongeza kasi.

    Uchunguzi wa equation\(\displaystyle v^2=v^2_0+2a(x−x_0)\) unaweza kuzalisha ufahamu zaidi katika mahusiano ya jumla kati ya wingi wa kimwili:

    • Kasi ya mwisho inategemea jinsi kasi ya kasi ni kubwa na umbali juu ya ambayo hufanya
    • Kwa deceleration fasta, gari kwamba ni kwenda mara mbili kwa haraka haina tu kuacha katika mara mbili umbali - inachukua mengi zaidi kuacha. (Hii ndiyo sababu tumepunguza maeneo ya kasi karibu na shule.)

    Kuweka equations Pamoja

    Katika mifano ifuatayo, sisi zaidi kuchunguza mwendo moja-dimensional, lakini katika hali zinazohitaji kidogo zaidi algebraic kudanganywa. Mifano pia hutoa ufahamu katika mbinu za kutatua matatizo. Sanduku hapa chini hutoa rejea rahisi kwa equations zinazohitajika.

    MUHTASARI WA MILINGANISHO YA KINEMATIC (MARA KWA MARA A)

    \(\displaystyle x=x_0+\bar{v}t\)

    \(\displaystyle \bar{v}=\frac{v_0+v}{2}\)

    \(\displaystyle v=v_0+at\)

    \(\displaystyle x=x_0+v_0t+\frac{1}{2}at^2\)

    \(\displaystyle v^2=v^2_0+2a(x−x_0)\)

    Mfano\(\PageIndex{5}\):Calculating Displacement: How Far Does a Car Go When Coming to a Halt?

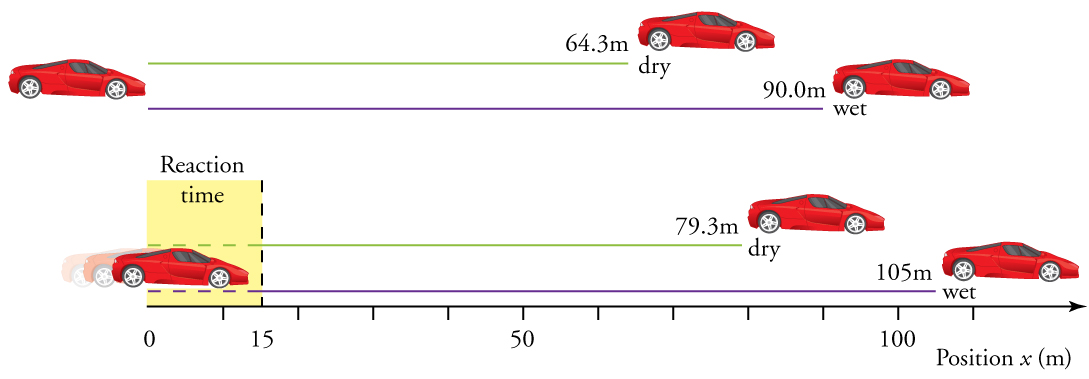
    Juu ya saruji kavu, gari linaweza kupungua kwa kiwango cha\(7.00 m/s^2\), wakati juu ya saruji ya mvua inaweza kupungua kwa tu\(5.00 m/s^2\). Pata umbali unaohitajika kuacha gari kusonga saa 30.0 m/s (kuhusu 110 km/h)

    1. juu ya saruji kavu na
    2. juu ya saruji ya mvua.
    3. Kurudia mahesabu yote, kutafuta uhamisho kutoka mahali ambapo dereva anaona mwanga wa trafiki kugeuka nyekundu, akizingatia muda wake wa majibu ya 0.500 s ili kupata mguu wake juu ya kuvunja.

    Mkakati

    Chora mchoro.

    Kasi ya awali ni sawa na mita thelathini kwa pili. Mwisho kasi sawa 0. Kuharakisha kavu sawa na hasi 7 kumweka sifuri mita sifuri kwa pili squared. Kuharakisha mvua sawa na hasi 5 kumweka sifuri mita sifuri kwa pili squared.
    Kielelezo\(\PageIndex{10}\)

    Ili kuamua ni equations gani bora kutumia, tunahitaji kuandika maadili yote inayojulikana na kutambua hasa kile tunachohitaji kutatua. Tutafanya hivyo wazi katika mifano kadhaa ijayo, kwa kutumia meza kuwaweka mbali.

    Suluhisho kwa (a)

    1. Tambua ujuzi na kile tunachotaka kutatua. Tunajua kwamba\(\displaystyle v_0=30.0 m/s; v=0; a=−7.00m/s^2\) (\(\displaystyle a\)ni hasi kwa sababu ni katika mwelekeo kinyume na kasi). Tunachukua\(\displaystyle x_0\) kuwa\(\displaystyle 0\). Sisi ni kuangalia kwa ajili ya makazi yao\(\displaystyle Δx\), au\(\displaystyle x−x_0\).

    2. Tambua equation ambayo itasaidia kutatua tatizo. Equation bora kutumia ni

    \(\displaystyle v^2=v^2_0+2a(x−x_0)\).

    equation Hii ni bora kwa sababu ni pamoja na haijulikani moja tu,\(\displaystyle x\). Tunajua maadili ya vigezo vingine vyote katika equation hii. (Kuna milinganyo mengine ambayo itatuwezesha kutatua\(\displaystyle x\), lakini yanahitaji sisi kujua wakati wa kuacha\(\displaystyle t\), ambayo hatujui. Tunaweza kuitumia lakini ingeweza kuhusisha mahesabu ya ziada.)

    3. Panga upya equation kutatua kwa\(\displaystyle x\).

    \(\displaystyle x−x_0=\frac{v^2−v^2_0}{2a}\)

    4. Ingiza maadili inayojulikana.

    \(\displaystyle x−0=\frac{0^2−(30.0 m/s)^2}{2(−7.00 m/s^2)}\)

    Hivyo,

    \(\displaystyle x=64.3 m\)juu ya saruji kavu.

    Suluhisho kwa (b)

    Sehemu hii inaweza kutatuliwa kwa njia sawa na Sehemu ya A. tofauti tu ni kwamba deceleration ni\(\displaystyle –5.00 m/s^2\). Matokeo yake ni

    \(\displaystyle x_{wet}=90.0 m\)juu ya saruji mvua.

    Suluhisho kwa (c)

    Mara baada ya dereva kuguswa, umbali wa kuacha ni sawa na ulivyo katika Sehemu za A na B kwa saruji kavu na mvua. Ili kujibu swali hili, tunahitaji kuhesabu jinsi gari linasafiri wakati wa majibu, na kisha kuongeza hiyo wakati wa kuacha. Ni busara kudhani kwamba kasi inabakia mara kwa mara wakati wa majibu ya dereva.

    1. Tambua ujuzi na kile tunachotaka kutatua. Tunajua kwamba\(\displaystyle \bar{v}=30.0 m/s; t_{reaction}=0.500s; a_{reaction}=0\). Tunachukua\(\displaystyle x_{0−reaction}\) kuwa 0. Tunatafuta\(\displaystyle x_{reaction}\).

    2. Kutambua equation bora ya kutumia.

    \(\displaystyle x=x_0+\bar{v}t\)kazi vizuri kwa sababu tu haijulikani thamani ni\(\displaystyle x\), ambayo ni nini tunataka kutatua kwa.

    3. Plug katika knowns kutatua equation.

    \(\displaystyle x=0+(30.0 m/s)(0.500 s)=15.0 m.\)

    Hii inamaanisha gari linasafiri 15.0 m huku dereva anajitikia, na kufanya uhamisho wa jumla katika kesi mbili za saruji kavu na mvua 15.0 m kubwa kuliko kama alijibu mara moja.

    4. Ongeza uhamisho wakati wa majibu ya uhamisho wakati wa kusonga.

    \(\displaystyle x_{braking}+x_{reaction}=x_{total}\)

    a. 64.3 m + 15.0 m = 79.3 m wakati kavu
    b. 90.0 m + 15.0 m = 105 m wakati mvua

    Mchoro unaonyesha umbali mbalimbali wa kusimama muhimu kwa kuacha gari. Kwa wakati wowote wa majibu unaozingatiwa, umbali wa kusimama ni mita 64 za mita 3 kwenye uso kavu na mita 90 kwenye uso wa mvua. Kwa wakati wa majibu ya sekunde 0 500, umbali wa kusimama ni 79 kumweka mita 3 kwenye uso kavu na mita 105 kwenye uso wa mvua.
    Kielelezo\(\PageIndex{11}\): umbali muhimu kuacha gari hutofautiana sana, kulingana na hali ya barabara na wakati wa majibu ya dereva. Inavyoonekana hapa ni umbali wa kusimama kwa lami kavu na mvua, kama ilivyohesabiwa katika mfano huu, kwa gari awali kusafiri saa 30.0 m/s Pia umeonyesha umbali jumla alisafiri kutoka mahali ambapo dereva kwanza anaona mwanga kugeuka nyekundu, kuchukua 0.500 s majibu wakati.

    Majadiliano

    Mahamisho yaliyopatikana katika mfano huu yanaonekana kuwa ya busara kwa kuacha gari linalohamia haraka. Inapaswa kuchukua muda mrefu kuacha gari kwenye mvua badala ya lami kavu. Inashangaza kwamba wakati wa majibu huongeza kwa kiasi kikubwa kwa uhamisho. Lakini muhimu zaidi ni mbinu ya jumla ya kutatua matatizo. Sisi kutambua knowns na kiasi kuamua na kisha kupata equation sahihi. Kuna mara nyingi zaidi ya njia moja ya kutatua tatizo. Sehemu mbalimbali za mfano huu zinaweza kutatuliwa kwa njia nyingine, lakini ufumbuzi uliowasilishwa hapo juu ni mfupi zaidi.

    Mfano\(\PageIndex{5}\): Calculating Time - A Car Merges into Traffic

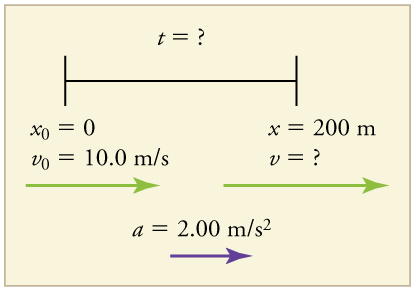
    Tuseme gari linaunganisha kwenye trafiki ya barabara kuu kwenye barabara ya urefu wa 200 m. Ikiwa kasi yake ya awali ni 10.0 m/s na inaharakisha saa\(\displaystyle .00 m/s^2\), inachukua muda gani kusafiri 200 m juu ya barabara? (Taarifa hiyo inaweza kuwa na manufaa kwa mhandisi wa trafiki.)

    Mkakati

    Chora mchoro.

    sehemu line na mwisho kinachoitwa x subs sifuri sawa sifuri na x = mia mbili. Juu ya sehemu ya mstari, equation t sawa na alama ya swali inaonyesha kwamba wakati haijulikani. Vectors tatu, wote akizungumzia katika mwelekeo wa x sawa na 200, kuwakilisha knowns nyingine na haijulikani. Wao ni kinachoitwa v ndogo zero sawa kumi pointi sifuri mita kwa sekunde, v sawa alama ya kuuliza, na sawa mbili pointi sifuri mita sifuri kwa pili mraba.
    Kielelezo\(\PageIndex{12}\): Tunaulizwa kutatua kwa wakati\(t\). Kama hapo awali, tunatambua kiasi kinachojulikana ili kuchagua uhusiano rahisi wa kimwili (yaani, equation na haijulikani,\(t\)).

    Suluhisho

    1. Tambua ujuzi na kile tunachotaka kutatua. Tunajua kwamba\(\displaystyle v_0=10 m/s; a=2.00 m/s^2\); and \(\displaystyle x=200 m.\)

    2. Tunahitaji kutatua kwa t Chagua equation bora. \(\displaystyle x=x_0+v_0t+\frac{1}{2}at^2\) works best because the only unknown in the equation is the variable t for which we need to solve.

    3. Tutahitaji kupanga upya equation kutatua\(t\). In this case, it will be easier to plug in the knowns first.

    \(\displaystyle 200 m=0 m+(10.0 m/s)t+\frac{1}{2}(2.00 m/s^2)t^2\)

    4. Kurahisisha equation. Vitengo vya mita (m) vinafuta kwa sababu viko katika kila muda. Tunaweza kupata vitengo ya sekunde (s) kufuta kwa kuchukua\(\displaystyle t=ts\), where \(\displaystyle t\) is the magnitude of time and s is the unit. Doing so leaves

    \(\displaystyle 200=10t+t^2.\)

    5. Tumia formula ya quadratic kutatua\(\displaystyle t\).

    (a) Panga upya equation kupata 0 upande mmoja wa equation.

    \(\displaystyle t^2+10t−200=0\)

    Hii ni equation quadratic ya fomu

    \(\displaystyle at^2+bt+c=0,\)

    ambapo constants ni\(\displaystyle a=1.00,b=10.0\),and \(\displaystyle c=−200.\)

    (b) Ufumbuzi wake hutolewa na formula ya quadratic:

    \(\displaystyle t=\frac{−b±\sqrt{b^2−4ac}}{2a}\).

    Hii mavuno ufumbuzi mbili kwa\(\displaystyle t\), which are

    \(\displaystyle t=10.0\) and \(\displaystyle −20.0\).

    Katika kesi hiyo, basi, wakati ni\(\displaystyle t=t\) in seconds, or

    \(\displaystyle t=10.0s\) and \(\displaystyle −20.0s\).

    Thamani hasi kwa muda ni ya maana, kwani ingekuwa na maana kwamba tukio hilo lilitokea 20 s kabla ya mwendo kuanza. Tunaweza kuondokana na ufumbuzi huo. Hivyo,

    \(\displaystyle t=10.0s.\)

    Majadiliano

    Wakati wowote equation ina mraba haijulikani, kutakuwa na ufumbuzi mbili. Katika matatizo mengine ufumbuzi wote ni wa maana, lakini kwa wengine, kama vile hapo juu, suluhisho moja tu ni busara. the 10.0 s jibu inaonekana busara kwa kawaida freeway on-njia panda.

    Kwa misingi ya kinematics imara, tunaweza kuendelea na mifano mingine mingi ya kuvutia na maombi. Katika mchakato wa kuendeleza kinematics, tumeelezea pia mbinu ya jumla ya kutatua matatizo ambayo hutoa majibu sahihi na ufahamu katika mahusiano ya kimwili. Misingi ya kutatua matatizo inazungumzia misingi ya kutatua matatizo na inaonyesha mbinu ambayo itasaidia kufanikiwa katika kazi hii muhimu sana.

    KUFANYA UHUSIANO: CHUKUA-NYUMBANI MAJARIBI-KUVUNJA HABARI

    Tumekuwa tukitumia vitengo vya mita za SI kwa kila mraba wa pili kuelezea baadhi ya mifano ya kuongeza kasi au kupungua kwa magari, wakimbiaji, na treni. Ili kufikia kujisikia vizuri kwa namba hizi, mtu anaweza kupima kupungua kwa kasi ya gari kufanya polepole (na salama) kuacha. Kumbuka kwamba, kwa kuongeza kasi ya wastani,\(\displaystyle \bar{a}=Δv/Δt\). Wakati wa kusafiri katika gari, polepole kutumia breki kama wewe kuja na kuacha ishara. Kuwa na abiria kumbuka kasi ya awali katika maili kwa saa na muda kuchukuliwa (katika sekunde) kuacha. Kutoka hili, uhesabu kupungua kwa maili kwa saa kwa pili. Badilisha hii kwa mita kwa mraba wa pili na ulinganishe na kupungua kwa kasi nyingine zilizotajwa katika sura hii. Tumia umbali uliosafiri katika kusafisha.

    Zoezi\(\PageIndex{1}\)

    roketi manned kuchochea kasi kwa kiwango cha\(\displaystyle 20 m/s^2\) wakati wa uzinduzi. Inachukua muda gani roketi kufikia kasi ya 400 m/s?

    Jibu

    Ili kujibu hili, chagua equation ambayo inakuwezesha kutatua kwa muda\(\displaystyle t\), kupewa tu\(\displaystyle a, v_0\), na\(\displaystyle v\).

    \(\displaystyle v=v_0+at\)

    Panga upya kutatua kwa\(\displaystyle t\).

    \(\displaystyle t=\frac{v−v_0}{a}=\frac{400 m/s−0 m/s}{20 m/s^2}=20 s\)

    Muhtasari

    • Ili kurahisisha mahesabu tunachukua kasi kuwa mara kwa mara, ili\(\displaystyle \bar{a}=a\) wakati wote.
    • Sisi pia kuchukua muda wa awali kuwa sifuri.
    • Msimamo wa awali na kasi hupewa subscript 0; maadili ya mwisho hawana subscript. Hivyo,

    \(\displaystyle Δt=t\)

    \(\displaystyle Δx=x−x_0\)

    \(\displaystyle Δv=v−v_0\)

    • zifuatazo equations kinematic kwa mwendo na mara kwa mara a ni muhimu:

    \(\displaystyle x=x_0+\bar{v}t\)

    \(\displaystyle \bar{v}=\frac{v_0+v}{2}\)

    \(\displaystyle v=v_0+at\)

    \(\displaystyle x=x_0+v_0t+\frac{1}{2}at^2\)

    \(\displaystyle v^2=v^2_0+2a(x−x_0)\)

    • Katika mwendo wima,\(\displaystyle y\) ni kubadilishwa kwa\(\displaystyle x\).