5.6: Athari ya Doppler
- Page ID
- 176086
Malengo ya kujifunza
Mwishoni mwa sehemu hii, utaweza:
- Eleza kwa nini mistari ya spectral ya photons tunayoona kutoka kwa kitu itabadilika kama matokeo ya mwendo wa kitu kuelekea au mbali na sisi
- Eleza jinsi tunavyoweza kutumia athari ya Doppler ili kubainisha jinsi vitu vya astronomia vinavyotembea angani
sehemu mbili za mwisho ilianzisha wewe dhana nyingi mpya, na tunatarajia kwamba kwa njia ya wale, umeona wazo moja kuu kuibuka. Wanaastronomia wanaweza kujifunza kuhusu mambo katika nyota na galaxi kwa kuamua habari katika mistari yao ya spectral. Kuna sababu ngumu katika kujifunza jinsi ya kufafanua ujumbe wa starlight, hata hivyo. Ikiwa nyota inaelekea kuelekea au mbali nasi, mistari yake itakuwa katika sehemu tofauti kidogo katika wigo na mahali ambapo ingekuwa katika nyota wakati wa kupumzika. Na vitu vingi ulimwenguni vina mwendo fulani unaohusiana na Jua.
mwendo huathiri mawimbi
Mwaka 1842, Christian Doppler alipima kwanza athari za mwendo juu ya mawimbi kwa kukodisha kundi la wanamuziki kucheza kwenye gari la reli wazi wakati lilikuwa likihamia kando ya wimbo. Kisha alitumia kile alichojifunza kwa mawimbi yote, ikiwa ni pamoja na mwanga, na alisema kuwa ikiwa chanzo cha mwanga kinakaribia au kinapungua kutoka kwa mwangalizi, mawimbi ya mwanga yatakuwa, kwa mtiririko huo, yamesongwa kwa karibu zaidi au kuenea. Kanuni ya jumla, inayojulikana sasa kama athari ya Doppler, inaonyeshwa kwenye Kielelezo\(\PageIndex{1}\).
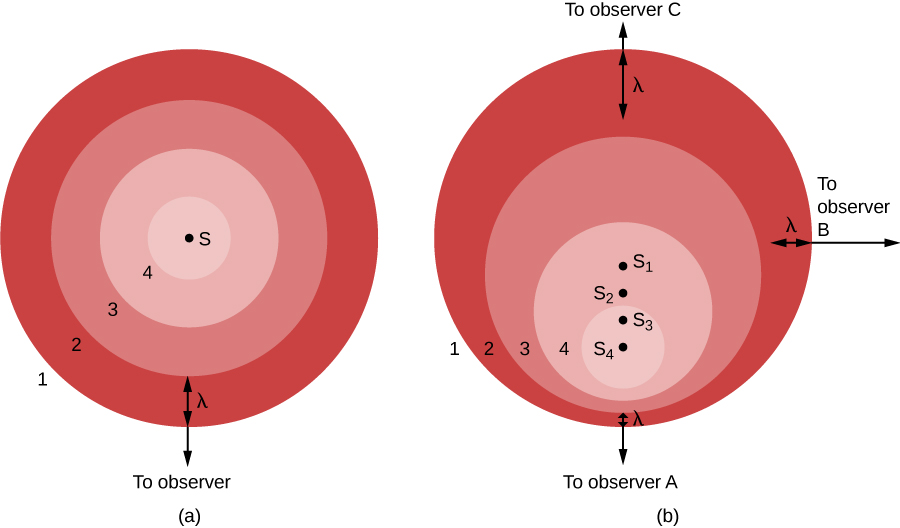
Katika Kielelezo\(\PageIndex{1a}\), chanzo cha mwanga (S) kinapumzika kwa heshima na mwangalizi. Chanzo hutoa mfululizo wa mawimbi, ambao crests tuna lebo 1, 2, 3, na 4. Mawimbi ya mwanga yanaenea sawasawa katika pande zote, kama vile viboko kutoka kwenye bwawa. Vipande vinatenganishwa na umbali, λ, ambapo λ ni wavelength. Mwangalizi, ambaye hutokea kuwa iko katika mwelekeo wa chini ya picha, anaona mawimbi ya mwanga kuja nzuri na sawasawa, wavelength moja mbali. Waangalizi ziko mahali popote bila kuona kitu kimoja.
Kwa upande mwingine, kama chanzo cha mwanga ni kusonga kwa heshima na mwangalizi, kama inavyoonekana katika Kielelezo\(\PageIndex{1b}\), hali ni ngumu zaidi. Kati ya wakati huo kiumbe kimoja kinatolewa na ijayo iko tayari kutokea, chanzo kimehamia kidogo, kuelekea chini ya ukurasa. Kutoka kwa mtazamo wa mwangalizi A, mwendo huu wa chanzo umepungua umbali kati ya viumbe - ni kufinya viumbe pamoja, mwangalizi huyu anaweza kusema.
Katika Kielelezo\(\PageIndex{1b}\), tunaonyesha hali hiyo kwa mtazamo wa waangalizi watatu. Chanzo kinaonekana katika nafasi nne,,\(S_1\),\(S_2\), na\(S_3\)\(S_4\), kila sambamba na chafu ya crest moja ya wimbi. Kuangalia A, mawimbi yanaonekana kufuatana kwa karibu zaidi, kwa wavelength iliyopungua na hivyo kuongezeka kwa mzunguko. (Kumbuka, mawimbi yote ya mwanga husafiri kwa kasi ya mwanga kupitia nafasi tupu, bila kujali nini. Hii inamaanisha kuwa mwendo hauwezi kuathiri kasi, lakini ni wavelength tu na mzunguko. Kama wavelength inapungua, mzunguko lazima uongeze. Ikiwa mawimbi ni mafupi, zaidi itaweza kuhamia wakati wa kila pili.)
Hali si sawa kwa waangalizi wengine. Hebu tuangalie hali hiyo kutoka kwa mtazamo wa mwangalizi C, iko kinyume na mwangalizi A katika Kielelezo\(\PageIndex{1}\). Kwa ajili yake, chanzo kinaondoka mahali pake. Matokeo yake mawimbi hayafanyiki pamoja lakini badala yake yanaenea kwa mwendo wa chanzo. Vipande vinakuja na wavelength iliyoongezeka na kupungua kwa mzunguko. Kuangalia B, kwa uongozi kwenye pembe za kulia kwa mwendo wa chanzo, hakuna athari inayozingatiwa. Wavelength na frequency kubaki sawa na wao walikuwa katika sehemu (a) ya takwimu.
Tunaweza kuona kutoka kwa mfano huu kwamba athari ya Doppler huzalishwa tu na mwendo kuelekea au mbali na mwangalizi, mwendo unaoitwa kasi ya radial. Mwendo wa upande wa pili hauzalishi athari hiyo. Wachunguzi kati ya A na B wangeona baadhi ya kufupisha mawimbi ya mwanga kwa sehemu hiyo ya mwendo wa chanzo ambacho ni pamoja na mstari wao wa kuona. Waangalizi kati ya B na C wangeona kurefusha ya mawimbi ya mwanga ambayo ni pamoja na mstari wao wa kuona.
Huenda umesikia athari ya Doppler na mawimbi ya sauti. Wakati treni filimbi au polisi siren inakaribia wewe na kisha hatua mbali, utaona kupungua kwa lami (ambayo ni jinsi akili za binadamu kutafsiri sauti wimbi frequency) ya mawimbi ya sauti. Ikilinganishwa na mawimbi ya kupumzika, wamebadilika kutoka mara kwa mara zaidi wakati wa kuja kwako, kwa mara kidogo kidogo wakati wa kusonga mbali na wewe.
Mfano mzuri wa mabadiliko haya katika sauti ya filimbi ya treni inaweza kusikilizwa mwishoni mwa wimbo wa kawaida wa Beach Boys “Caroline, No” kwenye albamu yao ya Pet Sauti. Ili kusikia sauti hii, nenda kwenye toleo hili la YouTube la wimbo. Sauti ya treni inaanza saa takriban 2:20.
Mabadiliko ya rangi
Wakati chanzo cha mawimbi kinaelekea kwako, wavelength hupungua kidogo. Ikiwa mawimbi yanayohusika yanaonekana mwanga, basi rangi ya mwanga hubadilika kidogo. Kama wavelength inapungua, wao kuhama kuelekea mwisho wa bluu ya wigo: wanaastronomia wito huu blueshift (tangu mwisho wa wigo ni kweli violet, neno lazima pengine kuwa violetshift, lakini bluu ni rangi ya kawaida zaidi). Wakati chanzo hatua mbali na wewe na wavelength anapata muda mrefu, tunaita mabadiliko katika rangi redshift. Kwa sababu athari ya Doppler ilitumiwa kwanza kwa nuru inayoonekana katika astronomia, maneno “blueshift” na “redshift” yalikuwa imara. Leo hii wanaastronomia hutumia maneno haya kuelezea mabadiliko katika wavelengths ya mawimbi ya redio au eksirei kwa raha kadiri wanavyotumia kuelezea mabadiliko katika nuru inayoonekana.
Zaidi ya mwendo kuelekea au mbali na sisi, zaidi ya mabadiliko ya Doppler. Ikiwa mwendo wa jamaa ni pamoja na mstari wa kuona, formula ya mabadiliko ya Doppler ya mwanga ni
\[\dfrac{\Delta λ}{λ}= \frac{v}{c} \nonumber\]
wapi\(\lambda\) wavelength lilio na chanzo,\(\Delta \lambda\) ni tofauti kati ya\(\lambda\) na wavelength kipimo na mwangalizi,\(c\) ni kasi ya mwanga, na\(v\) ni kasi ya jamaa ya mwangalizi na chanzo katika mstari wa kuona. Variable\(v\) ni kuhesabiwa kama chanya kama kasi ni moja ya uchumi, na hasi kama ni moja ya mbinu. Kutatua equation hii kwa kasi, tunaona
\[ v = c \times \dfrac{\Delta \lambda}{\lambda}. \nonumber\]
Ikiwa nyota inakaribia au ikitoka kwetu, wavelengths ya mwanga katika wigo wake unaoendelea huonekana kufupishwa au kupanuliwa, kwa mtiririko huo, kama vile wale wa mistari ya giza. Hata hivyo, isipokuwa kasi yake ni makumi ya maelfu ya kilomita kwa sekunde, nyota haionekani kuwa blue au nyekundu kuliko kawaida. Kwa hivyo mabadiliko ya Doppler hayatambui kwa urahisi katika wigo unaoendelea na hauwezi kupimwa kwa usahihi katika wigo huo. Wavelengths ya mistari ya ngozi inaweza kupimwa kwa usahihi, hata hivyo, na mabadiliko yao ya Doppler ni rahisi kuchunguza.
Mfano\(\PageIndex{1}\): Athari ya Doppler
Tunaweza kutumia Equation ya athari ya Doppler kuhesabu kasi ya radial ya kitu ikiwa tunajua mambo matatu: kasi ya mwanga, wavelength ya awali (isiyofunguliwa) ya mwanga iliyotolewa, na tofauti kati ya wavelength ya mwanga uliotolewa na wavelength tunayoona. Kwa ajili ya kunyonya au mistari ya uchafu, kwa kawaida tunajua hasa wavelength mstari unao katika maabara yetu duniani, ambapo chanzo cha mwanga hakisonga. Tunaweza kupima wavelength mpya na vyombo vyetu katika darubini, na hivyo tunajua tofauti katika wavelength kutokana na Doppler kuhama. Kwa kuwa kasi ya mwanga ni mara kwa mara ya kawaida, tunaweza kuhesabu kasi ya radial ya nyota.
Mstari fulani wa chafu wa hidrojeni awali unatolewa na wavelength ya 656.3 nm kutoka wingu la gesi. Katika darubini yetu, tunaona wavelength ya mstari wa chafu kuwa 656.6 nm. Je, wingu hili la gesi linasogea haraka kuelekea au mbali na Dunia?
Suluhisho
Kwa sababu mwanga umebadilishwa kwa wavelength ndefu (redtriffed), tunajua wingu hili la gesi linaondoka kwetu. Kasi inaweza kuhesabiwa kwa kutumia formula ya mabadiliko ya Doppler:
\[ν=c×\dfrac{\Delta \lambda}{\lambda}= \left(3.0 \times 10^8 ~ \text{m/s} \right) \left( \dfrac{0.3 ~ \text{nm}}{656.3 ~ \text{nm}} \right)= \left(3.0 \times 10^8 ~ \text{m/s} \right) \left(\dfrac{0.3 \times 10^{–9} ~ \text{m}}{656.3 \times 10^{–9} ~ \text{m}} \right)=140,000 ~ \text{m/s} =140 ~ \text{km/s} \nonumber\]
Zoezi\(\PageIndex{1}\)
Tuseme mstari wa spectral wa hidrojeni, kwa kawaida saa 500 nm, huzingatiwa katika wigo wa nyota kuwa saa 500.1 nm. Je! Nyota inakwenda haraka kuelekea au mbali na Dunia?
- Jibu
-
Kwa sababu mwanga umebadilishwa kwa wavelength ndefu, nyota inaondoka kwetu:
\[ν=c \times \dfrac{\Delta \lambda}{\lambda}= \left(3.0 \times 10^8 ~ \text{m/s} \right) \left(\dfrac{0.1 ~ \text{nm}}{500 ~ \text{nm}} \right)=\left( 3.0 \times 10^8 ~ \text{m/s} \right) \left(\dfrac{0.1 \times 10^{–9} ~ \text{m}}{500 \times 10^{–9} ~ \text{m}} \right)=60,000 ~ \text{m/s}\]
Kasi yake ni 60,000 m/s.
Sasa unaweza kuuliza: kama nyota zote zinasogea na mwendo hubadilisha urefu wa kila mstari wa spectral, je, hii si maafa kwa wanaastronomia wanaojaribu kutambua ni vipi vipi vilivyopo katika nyota? Baada ya yote, ni wavelength sahihi (au rangi) ambayo inaelezea wanaastronomia ambayo mistari ni ya kipengele gani. Na sisi kwanza kupima wavelengths hizi katika vyombo vya gesi katika maabara yetu, ambayo si kusonga. Ikiwa kila mstari katika wigo wa nyota sasa umebadilishwa na mwendo wake kwa wavelength tofauti (rangi), tunawezaje kuwa na uhakika ni mistari gani na mambo gani tunayoyaangalia katika nyota ambayo kasi yake hatujui?
Chukua moyo. Hali hii inaonekana mbaya zaidi kuliko ilivyo kweli. Wanaastronomia mara chache huhukumu uwepo wa elementi katika kitu cha astronomia kwa mstari mmoja. Ni mfano wa mistari ya pekee kwa hidrojeni au kalsiamu ambayo inatuwezesha kutambua kwamba elementi hizo ni sehemu ya nyota au galaksi tunayoyaangalia. Athari ya Doppler haibadili muundo wa mistari kutoka kwa kipengele kilichopewa-inabadilisha tu muundo mzima kidogo kuelekea wavelengths nyekundu au bluer. Mfano uliobadilishwa bado ni rahisi sana kutambua. Bora zaidi, tunapotambua muundo wa kipengele cha kawaida, tunapata bonus: kiasi ambacho muundo umebadilishwa kinaweza kutuwezesha kuamua kasi ya vitu katika mstari wetu wa kuona.
Mafunzo ya wanaastronomia yanajumuisha kazi nyingi juu ya kujifunza kutambua mwanga (na mionzi mingine ya umeme). “Decoder” mwenye ujuzi anaweza kujifunza joto la nyota, ni mambo gani yaliyo ndani yake, na hata kasi yake katika mwelekeo kuelekea sisi au mbali na sisi. Hiyo ni kiasi cha kushangaza cha habari kwa nyota zilizo mbali na miaka ya nuru.
Muhtasari
Ikiwa atomu inaelekea kwetu wakati elektroni inabadilisha mzunguko na inazalisha mstari wa spectral, tunaona mstari huo umebadilishwa kidogo kuelekea bluu ya wavelength yake ya kawaida katika wigo. Kama atomi ni kusonga mbali, tunaona mstari kubadilishwa kuelekea nyekundu. Mabadiliko haya yanajulikana kama athari ya Doppler na inaweza kutumika kupima kasi ya radial ya vitu vya mbali.
faharasa
- Athari ya Doppler
- mabadiliko ya dhahiri katika wavelength au mzunguko wa mionzi kutoka chanzo kutokana na mwendo wake wa jamaa mbali na au kuelekea mwangalizi
- kasi ya radial
- mwendo kuelekea au mbali na mwangalizi; sehemu ya kasi ya jamaa ambayo iko katika mstari wa kuona


