13.6: Theorem ya Binomial
- Page ID
- 177811
- Tumia Theorem ya Binomial.
Polynomial yenye maneno mawili inaitwa binomial. Tayari tumejifunza kuzidisha binomials na kuongeza binomials kwa nguvu, lakini kuongeza binomial kwa nguvu ya juu inaweza kuwa tedious na muda mwingi. Katika sehemu hii, tutajadili njia ya mkato ambayo itatuwezesha kupata\((x+y)^n\) bila kuzidisha binomial kwa\(n\) mara yenyewe.
Kutambua Coefficients Binomial
Katika njia ya mkato ya kutafuta\({(x+y)}^n\), tutahitaji kutumia mchanganyiko ili kupata coefficients ambayo itaonekana katika upanuzi wa binomial. Katika kesi hii, tunatumia notation\(\dbinom{n}{r}\) badala ya\(C(n,r)\), lakini inaweza kuhesabiwa kwa njia ile ile. Hivyo
\[\dbinom{n}{r}=C(n,r)=\dfrac{n!}{r!(n−r)!}\]
Mchanganyiko\(\dbinom{n}{r}\) huitwa mgawo wa binomial. Mfano wa mgawo wa binomial ni:
\(\dbinom{5}{2}=C(5,2)=10\)
Ikiwa\(n\) na\(r\) ni integers kubwa kuliko au sawa\(0\) na\(n≥r\), basi mgawo wa binomial ni
\[\dbinom{n}{r}=C(n,r)=\dfrac{n!}{r!(n−r)!} \label{binomial1}\]
Ndiyo. Kama vile idadi ya mchanganyiko lazima iwe namba nzima, mgawo wa binomial utakuwa nambari nzima.
Pata kila mgawo wa binomial.
- \(\dbinom{5}{3}\)
- \(\dbinom{9}{2}\)
- \(\dbinom{9}{7}\)
Suluhisho
Tumia Equation\ ref {binomial1} kuhesabu kila mgawo wa binomial. Unaweza pia kutumia\(nC_r\) kazi kwenye calculator yako.
- \(\dbinom{5}{3}=\dfrac{5!}{3!(5−3)!}=\dfrac{5⋅4⋅3!}{3!2!}=10\)
- \(\dbinom{9}{2}=\dfrac{9!}{2!(9−2)!}=\dfrac{9⋅8⋅7!}{2!7!}=36\)
- \(\dbinom{9}{7}=\dfrac{9!}{7!(9−7)!}=\dfrac{9⋅8⋅7!}{7!2!}=36\)
Uchambuzi
Kumbuka kwamba tulipata matokeo sawa kwa sehemu (b) na (c). Ikiwa unatazama kwa karibu ufumbuzi wa sehemu hizi mbili, utaona kwamba unaishia na viwanda viwili vilivyofanana katika denominator, lakini utaratibu umebadilishwa, kama vile mchanganyiko.
\[\dbinom{n}{r}=\dbinom{n}{n−r} \nonumber\]
Pata kila mgawo wa binomial.
- \(\dbinom{7}{3}\)
- \(\dbinom{11}{4}\)
- Jibu
-
\(35\)
- Jibu b
-
\(33\)
Kutumia Theorem ya Binomial
Tunapopanua\({(x+y)}^n\) kwa kuzidisha, matokeo huitwa upanuzi wa binomial, na inajumuisha coefficients ya binomial. Kama tulitaka kupanua\({(x+y)}^{52}\), tunaweza kuzidisha\((x+y)\) yenyewe mara hamsini na mbili. Hii inaweza kuchukua masaa! Ikiwa tunachunguza upanuzi wa binomial rahisi, tunaweza kupata ruwaza ambazo zitatuongoza kwenye njia ya mkato ya kutafuta upanuzi wa binomial ngumu zaidi.
\[\begin{align*} {(x+y)}^2 &= x^2+2xy+y^2 \\[4pt] {(x+y)}^3 &= x^3+3x^2y+3xy^2+y^3 \\[4pt] {(x+y)}^4 &= x^4+4x^3y+6x^2y^2+4xy^3+y^4 \end{align*}\]
Kwanza, hebu tuchunguze watazamaji. Kwa kila muda mfululizo, exponent kwa\(x\) itapungua na exponent kwa\(y\) ongezeko. Jumla ya exponents mbili ni\(n\) kwa kila muda.
Kisha, hebu tuchunguze coefficients. Angalia kwamba coefficients huongezeka na kisha hupungua kwa muundo wa ulinganifu. Coefficients kufuata mfano:
\(\dbinom{n}{0}\),\(\dbinom{n}{1}\),\(\dbinom{n}{2}\),...,\(\dbinom{n}{n}.\)
Mwelekeo huu unatuongoza kwenye Theorem ya Binomial, ambayo inaweza kutumika kupanua binomial yoyote.
\[\begin{align*} {(x+y)}^n&=\sum_{k=0}^{n}\dbinom{n}{k}x^{n−k}y^k \\[4pt] &=x^n+\dbinom{n}{1}x^{n−1}y+\dbinom{n}{2}x^{n−2}y^2+...+\dbinom{n}{n−1}xy^{n−1}+y^n \end{align*}\]
Njia nyingine ya kuona coefficients ni kuchunguza upanuzi wa binomial kwa fomu ya jumla\(x+y\),, kwa nguvu za mfululizo\(1\)\(2\),\(3\), na\(4\).
\[\begin{align*} {(x+y)}^1 &= x+y \\ {(x+y)}^2 &= x^2+2xy+y^2 \\ {(x+y)}^3 &= x^3+3x^2y+3xy^2+y^3 \\ {(x+y)}^4 &= x^4+4x^3y+6x^2y^2+4xy^3+y^4 \end{align*}\]
Je, unaweza nadhani upanuzi ijayo kwa binomial\({(x+y)}^5\)?

Kielelezo\(\PageIndex{1}\)
Angalia Kielelezo\(\PageIndex{1}\), ambayo inaonyesha yafuatayo:
- Kuna\(n+1\) suala katika upanuzi wa\({(x+y)}^n\).
- shahada (au jumla ya exponents) kwa kila neno ni\(n\).
- Mamlaka ya\(x\) kuanza\(n\) na kupungua kwa\(0\).
- Mamlaka ya\(y\) kuanza\(0\) na kuongezeka kwa\(n\).
- Coefficients ni sawa.
Kuamua upanuzi juu\({(x+y)}^5\), tunaona\(n=5\), kwa hiyo, kutakuwa na\(5+1=6\) maneno. Kila mrefu ina shahada ya pamoja ya\(5\). Katika utaratibu wa kushuka kwa nguvu za\(x\), mfano ni kama ifuatavyo:
- Kuanzisha\(x^5\), na kisha kwa kila muda mfululizo kupunguza exponent juu\(x\) na\(1\) mpaka\(x^0=1\) ni kufikiwa.
- Kuanzisha\(y^0=1\), na kisha kuongeza exponent juu ya yy na 1 mpaka\(y^5\) ni kufikiwa.
\(x^5, x^4y, x^3y^2, x^2y^3, xy^4, y^5\)
Upanuzi ijayo itakuwa
\({(x+y)}^5=x^5+5x^4y+10x^3y^2+10x^2y^3+5xy^4+y^5\)
Lakini coefficients hizo zinatoka wapi? Coefficients ya binomial ni sawa. Tunaweza kuona coefficients hizi katika safu inayojulikana kama Triangle Pascal ya, inavyoonekana katika Kielelezo\(\PageIndex{2}\).
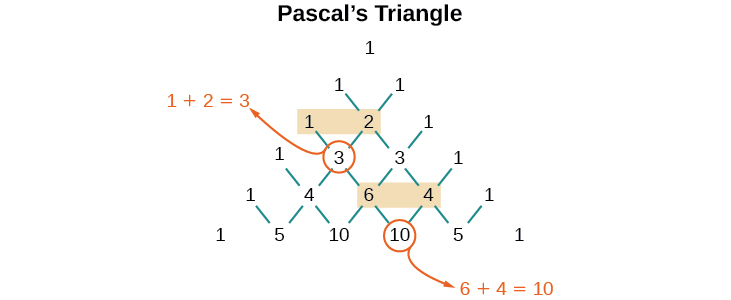
Kielelezo\(\PageIndex{2}\)
Kuzalisha Pascal ya Triangle, sisi kuanza kwa kuandika\(1\). Katika mstari chini, mstari wa 2, tunaandika mbili\(1’s\). Katika mstari wa 3, funga mwisho wa safu na\(1’s\), na uongeze\(1+1\) kupata nambari ya kati,\(2\). Katika\(n^{th}\) mstari, funga mwisho wa mstari na\(1’s\). Kila elementi katika pembetatu ni jumla ya elementi mbili mara moja juu yake.
Kuona uhusiano kati ya Triangle ya Pascal na coefficients ya binomial, hebu tupate upya upanuzi wa binomials kwa fomu ya jumla.
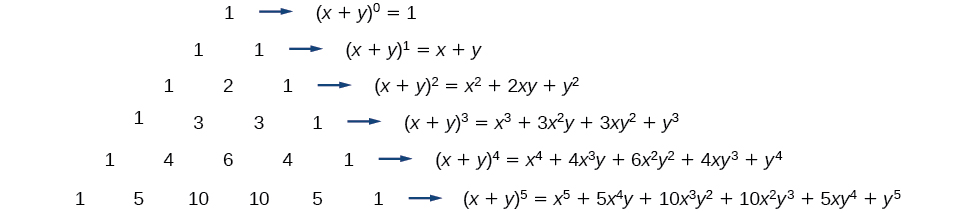
Theorem ya Binomial ni formula ambayo inaweza kutumika kupanua binomial yoyote.
\[ {(x+y)}^n = \sum_{k=0}^{n}\dbinom{n}{k}x^{n−k}y^k = x^n+\dbinom{n}{1}x^{n−1}y+\dbinom{n}{2}x^{n−2}y^2+...+\dbinom{n}{n−1}xy^{n−1}+y^n \]
- Kuamua thamani ya\(n\) kulingana na exponent.
- Tathmini\(k=0\) kupitia kwa\(k=n\) kutumia formula ya Theorem ya Binomial.
- Kurahisisha.
Andika katika fomu iliyopanuliwa.
- \({(x+y)}^5\)
- \({(3x−y)}^4\)
Suluhisho
a. mbadala\(n=5\) katika formula. Tathmini kwa\(k=0\) njia ya\(k=5\) maneno. Kurahisisha.
\[\begin{align*} {(x+y)}^5 &= \dbinom{5}{0}x^5y^0+\dbinom{5}{1}x^4y^1+\dbinom{5}{2}x^3y^2+\dbinom{5}{3}x^2y^3+\dbinom{5}{4}x^1y^4+\dbinom{5}{5}x^0y^5 \\ {(x+y)}^5 &= x^5+5x^4y+10x^3y^2+10x^2y^3+5xy^4+y^5 \end{align*}\]
b Kubadilisha\(n=4\) katika formula. Tathmini kwa\(k=0\) njia ya\(k=4\) maneno. Angalia kwamba\(3x\) ni katika mahali kwamba alikuwa ulichukua\(x\) na kwamba\(–y\) ni katika mahali kwamba alikuwa ulichukua na\(y\). Kwa hiyo tunawabadilisha. Kurahisisha.
\[\begin{align*} {(3x−y)}^4 &= \dbinom{4}{0}{(3x)}^4{(−y)}^0+\dbinom{4}{1}{(3x)}^3{(−y)}^1+\dbinom{4}{2}{(3x)}^2{(−y)}^2+\dbinom{4}{3}{(3x)}^1{(−y)}^3+\dbinom{4}{4}{(3x)}^0{(−y)}^4 \\ {(3x−y)}^4 &= 81x^4−108x^3y+54x^2y^2−12xy^3+y^4 \end{align*}\]
Uchambuzi
Kumbuka ishara alternating katika sehemu b Hii hutokea kwa sababu\((−y)\) kukulia kwa nguvu isiyo ya kawaida ni hasi, lakini\((−y)\) kukulia kwa nguvu hata ni chanya. Hii itatokea wakati wowote binomial ina ishara ya kuondoa.
Andika katika fomu iliyopanuliwa.
- \({(x−y)}^5\)
- \({(2x+5y)}^3\)
- Jibu
-
\(x^5−5x^4y+10x^3y^2−10x^2y^3+5xy^4−y^5\)
- Jibu b
-
\(8x^3+60x^2y+150xy^2+125y^3\)
Kutumia Theorem ya Binomial Kupata Muda Single
Kupanua binomial na exponent juu kama vile\({(x+2y)}^{16}\) inaweza kuwa mchakato mrefu. Wakati mwingine tunavutiwa tu kwa muda fulani wa upanuzi wa binomial. Hatuna haja ya kupanua kikamilifu binomial ili kupata muda mmoja maalum.
Kumbuka mfano wa coefficients katika upanuzi wa\({(x+y)}^5\).
\({(x+y)}^5=x^5+\dbinom{5}{1}x^4y+\dbinom{5}{2}x^3y^2+\dbinom{5}{3}x^2y^3+\dbinom{5}{4}xy^4+y^5\)
Muda wa pili ni\(\dbinom{5}{1}x^4y\). Muda wa tatu ni\(\dbinom{5}{2}x^3y^2\). Tunaweza kuzalisha matokeo haya.
Neno\((r+1)\) la upanuzi wa binomial\({(x+y)}^n\) ni:
\[\dbinom{n}{r}x^{n−r}y^r \label{binomial5}\]
- Kuamua thamani ya nn kulingana na exponent.
- Kuamua\((r+1)\).
- Kuamua\(r\).
- Badilisha nafasi\(r\) katika formula kwa muda\((r+1)\) wa upanuzi wa binomial.
Kupata muda wa kumi wa\({(x+2y)}^{16}\) bila kikamilifu kupanua binomial.
Suluhisho
Kwa sababu sisi ni kuangalia kwa muda wa kumi,\(r+1=10\), tutatumia\(r=9\) katika mahesabu yetu na Equation\ ref {binomial5}.
\(\dbinom{16}{9}x^{16−9}{(2y)}^9=5,857,280x^7y^9\)
Kupata muda wa sita wa\({(3x−y)}^9\) bila kikamilifu kupanua binomial.
- Jibu
-
\(−10,206x^4y^5\)
Kupata rasilimali hizi online kwa maelekezo ya ziada na mazoezi na upanuzi binomial.
Mlinganyo muhimu
| Theorem ya Binomial | \({(x+y)}^n=\sum_{k=0}^n\dbinom{n}{k}x^{n−k}y^k\) |
| \((r+1)\)muda wa upanuzi wa binomial | \(\dbinom{n}{r}x^{n−r}y^r\) |
Key Concepts
- \(\dbinom{n}{r}\) is called a binomial coefficient and is equal to \(C(n,r)\). See Example \(\PageIndex{1}\).
- The Binomial Theorem allows us to expand binomials without multiplying. See Example \(\PageIndex{2}\).
- We can find a given term of a binomial expansion without fully expanding the binomial. See Example \(\PageIndex{3}\).


