13.2: Utaratibu wa hesabu

Last updated
Save as PDF

Page ID: 177848

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Pata tofauti ya kawaida kwa mlolongo wa hesabu.
Andika maneno ya mlolongo wa hesabu.
Tumia formula ya kujirudia kwa mlolongo wa hesabu.
Tumia formula wazi kwa mlolongo wa hesabu.

Makampuni mara nyingi hufanya manunuzi makubwa, kama vile kompyuta na magari, kwa matumizi ya biashara. Thamani ya kitabu cha vifaa hivi hupungua kila mwaka kwa madhumuni ya kodi. Kupungua kwa thamani hii inaitwa kushuka kwa thamani. Njia moja ya kuhesabu kushuka kwa thamani ni kushuka kwa thamani ya mstari wa moja kwa moja, ambapo thamani ya mali hupungua kwa kiasi sawa kila mwaka.

Kwa mfano, fikiria mwanamke ambaye anaanza biashara ndogo ya kuambukizwa. Yeye manunuzi lori mpya kwa ajili ya$$25,000$. Baada ya miaka mitano, yeye anakadiria kwamba atakuwa na uwezo wa kuuza lori kwa$$8,000$. Kwa hiyo kupoteza thamani ya lori itakuwa$$17,000$, ambayo ni$$3,400$ kwa mwaka kwa miaka mitano. Lori itakuwa na thamani$$21,600$ baada ya mwaka wa kwanza;$$18,200$ baada ya miaka miwili;$$14,800$ baada ya miaka mitatu;$$11,400$ baada ya miaka minne; na$$8,000$ mwisho wa miaka mitano. Katika sehemu hii, tutazingatia aina maalum za utaratibu ambazo zitatuwezesha kuhesabu kushuka kwa thamani, kama thamani ya lori.

Kupata Tofauti ya kawaida

Maadili ya lori katika mfano husemekana kuunda mlolongo wa hesabu kwa sababu hubadilika kwa kiasi cha mara kwa mara kila mwaka. Kila neno huongezeka au hupungua kwa thamani sawa ya mara kwa mara inayoitwa tofauti ya kawaida ya mlolongo. Kwa mlolongo huu, tofauti ya kawaida ni$-3,400$.

$Mlolongo, {25000, 21600, 18200, 14800, 8000}, unaoonyesha maneno yanatofautiana tu na -3400.$

Mlolongo hapa chini ni mfano mwingine wa mlolongo wa hesabu. Katika kesi hii, tofauti ya mara kwa mara ni$3$. Unaweza kuchagua muda wowote wa mlolongo, na kuongeza$3$ kupata muda unaofuata.

$Mlolongo {3, 6, 9, 12, 15,...} ambayo inaonyesha maneno yanatofautiana tu na 3.$

MLOLONGO WA HESABU

Mlolongo wa hesabu ni mlolongo ambao una mali ambayo tofauti kati ya maneno yoyote mawili mfululizo ni mara kwa mara. Mara kwa mara hii inaitwa tofauti ya kawaida. Ikiwa$a_1$ ni muda wa kwanza wa mlolongo wa hesabu na$d$ ni tofauti ya kawaida, mlolongo utakuwa:

\[\{a_n\}=\{a_1,a_1+d,a_1+2d,a_1+3d,...\}\]

Mfano$\PageIndex{1}$: Finding Common Differences

Je, kila mlolongo hesabu? Ikiwa ndivyo, pata tofauti ya kawaida.

$\{1,2,4,8,16,...\}$
$\{−3,1,5,9,13,...\}$

Suluhisho

Ondoa kila neno kutoka kwa muda uliofuata ili uone kama tofauti ya kawaida ipo.

Mlolongo sio hesabu kwa sababu hakuna tofauti ya kawaida.

$2-1={\color{red}1} \qquad 4-2={\color{red}2} \qquad 8-4={\color{red}4} \qquad 16-8={\color{red}8}$

Mlolongo ni hesabu kwa sababu kuna tofauti ya kawaida. Tofauti ya kawaida ni$4$.

$1-(-3)={\color{red}4} \qquad 5-1={\color{red}4} \qquad 9-5={\color{red}4} \qquad 13-9={\color{red}4}$

Uchambuzi

Grafu ya kila moja ya utaratibu huu inavyoonekana kwenye Kielelezo$\PageIndex{1}$. Tunaweza kuona kutoka grafu kwamba, ingawa Utaratibu wote kuonyesha ukuaji, (a) si linear ambapo (b) ni linear. Utaratibu wa hesabu una kiwango cha mabadiliko ya mara kwa mara hivyo grafu zao zitakuwa pointi kwenye mstari.

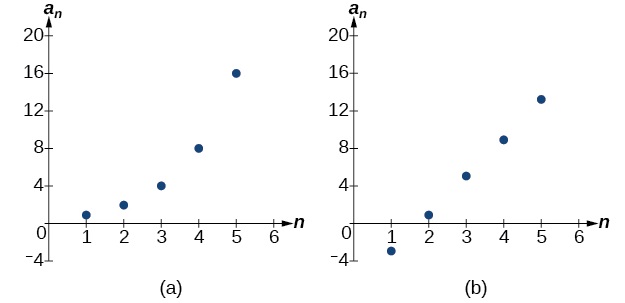
$Grafu mbili za utaratibu wa hesabu. Grafu (a) inakua kwa kiasi kikubwa wakati grafu (b) inakua kwa mstari.$

Kielelezo$\PageIndex{1}$

Q & A

Ikiwa tunaambiwa kuwa mlolongo ni hesabu, je, tunapaswa kuondoa kila neno kutoka kwa muda uliofuata ili kupata tofauti ya kawaida?

Hapana. Ikiwa tunajua kwamba mlolongo ni hesabu, tunaweza kuchagua neno lolote katika mlolongo, na uondoe kutoka kwa muda uliofuata ili kupata tofauti ya kawaida.

Zoezi$\PageIndex{1A}$

Je, mlolongo uliopewa hesabu? Ikiwa ndivyo, pata tofauti ya kawaida.

$\{18, 16, 14, 12, 10,…\}$

Jibu: Mlolongo ni hesabu. Tofauti ya kawaida ni$–2$.

Zoezi$\PageIndex{1B}$

Je, mlolongo uliopewa hesabu? Ikiwa ndivyo, pata tofauti ya kawaida.

$\{1, 3, 6, 10, 15,…\}$

Jibu: Mlolongo sio hesabu kwa sababu$3−1≠6−3$.

Kuandika Masharti ya Utaratibu wa Hesabu

Sasa kwa kuwa tunaweza kutambua mlolongo wa hesabu, tutapata maneno ikiwa tunapewa muda wa kwanza na tofauti ya kawaida. Masharti yanaweza kupatikana kwa kuanzia na muda wa kwanza na kuongeza tofauti ya kawaida mara kwa mara. Kwa kuongeza, neno lolote linaweza pia kupatikana kwa kuziba katika maadili ya$n$ na$d$ katika formula hapa chini.

\[a_n=a_1+(n−1)d\]

Jinsi ya: Kutokana na muda wa kwanza na tofauti ya kawaida ya mlolongo wa hesabu, pata maneno kadhaa ya kwanza.

Ongeza tofauti ya kawaida kwa muda wa kwanza ili kupata muda wa pili.
Ongeza tofauti ya kawaida kwa muda wa pili ili kupata muda wa tatu.
Endelea mpaka maneno yote yaliyotakiwa yanatambuliwa.
Andika maneno yaliyotengwa na koma ndani ya mabano.

Mfano$\PageIndex{2}$: Writing Terms of Arithmetic Sequences

Andika maneno matano ya kwanza ya mlolongo wa hesabu$a_1=17$ na$d=−3$.

Suluhisho

Kuongeza$−3$ ni sawa na kuondoa$3$. Kuanzia na muhula wa kwanza, toa$3$ kutoka kila neno ili upate muda ujao.

Masharti tano ya kwanza ni$\{17,14,11,8,5\}$

Uchambuzi

Kama inavyotarajiwa, grafu ya mlolongo ina pointi kwenye mstari kama inavyoonekana kwenye Kielelezo$\PageIndex{2}$.

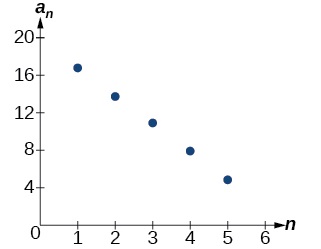
$Grafu ya mlolongo wa hesabu. Pointi huunda mstari hasi.$

Kielelezo$\PageIndex{2}$

Zoezi$\PageIndex{2}$

Andika orodha ya kwanza ya tano ya mlolongo wa hesabu$a_1=1$ na$d=5$.

Jibu: $\{1, 6, 11, 16, 21\}$

Jinsi ya: Kutokana yoyote ya muda wa kwanza na mrefu nyingine yoyote katika mlolongo hesabu, kupata muda fulani.

Badilisha maadili yaliyotolewa kwa$a_1$$a_n$,,$n$ katika fomu ya$a_n=a_1+(n−1)d$ kutatua$d$.
Pata muda uliopewa kwa kubadili maadili sahihi kwa$a_1$,$n$, na$d$ katika fomu$a_n=a_1+(n−1)d$.

Mfano$\PageIndex{3}$: Writing Terms of Arithmetic Sequences

Kutokana$a_1=8$ na$a_4=14$, kupata$a_5$.

Suluhisho

Mlolongo unaweza kuandikwa kwa suala la muda wa awali$8$ na tofauti ya kawaida$d$.

$\{8,8+d,8+2d,8+3d\}$

Tunajua muda wa nne sawa$14$; tunajua muda wa nne una fomu$a_1+3d=8+3d$.

Tunaweza kupata tofauti ya kawaida$d$.

\[\begin{align*} a_n&= a_1+(n-1)d \\ a_4&= a_1+3d \\ a_4&=8+3d\qquad \text{Write the fourth term of the sequence in terms of }a_1 \text{ and } d. \\ 14&=8+3d\qquad \text{Substitute }14 \text{ for } a_4. \\ d&=2\qquad \text{Solve for the common difference.} \end{align*}\]

Pata muda wa tano kwa kuongeza tofauti ya kawaida kwa muda wa nne.

$a_5=a_4+2=16$

Uchambuzi

Angalia kwamba tofauti ya kawaida huongezwa kwa muda wa kwanza mara moja ili kupata muda wa pili, mara mbili kupata muda wa tatu, mara tatu kupata muda wa nne, na kadhalika. Neno la kumi linaweza kupatikana kwa kuongeza tofauti ya kawaida kwa muhula wa kwanza mara tisa au kwa kutumia equation$a_n=a_1+(n−1)d$.

Zoezi$\PageIndex{3}$

Kutokana$a_3=7$ na$a_5=17$, kupata$a_2$.

Jibu: $a_2=2$

Kutumia Fomu za kujirudia kwa Utaratibu wa Hesabu

Utaratibu fulani wa hesabu hufafanuliwa kwa suala la muda uliopita kwa kutumia formula ya kujirudia. Fomu hutoa utawala wa algebraic kwa kuamua masharti ya mlolongo. Fomula ya kujirudia inatuwezesha kupata muda wowote wa mlolongo wa hesabu kwa kutumia kazi ya muda uliopita. Kila neno ni jumla ya muda uliopita na tofauti ya kawaida. Kwa mfano, ikiwa tofauti ya kawaida ni$5$, basi kila neno ni mrefu uliopita pamoja$5$. Kama ilivyo kwa formula yoyote ya kujirudia, muda wa kwanza unapaswa kupewa.

$a_n=a_n−1+d$

kwa$n≥2$

Kumbuka: formula ya kujirudia kwa mlolongo wa hesabu

Fomu ya kujirudia kwa mlolongo wa hesabu na tofauti ya kawaida$d$ ni:

\[a_n=a_n−1+d\]

kwa$n≥2$

Jinsi ya: Kutokana na mlolongo wa hesabu, andika formula yake ya kujirudia.

Ondoa neno lolote kutoka kwa muda uliofuata ili kupata tofauti ya kawaida.
Hali ya muda wa awali na ubadilishe tofauti ya kawaida katika formula ya kujirudia kwa Utaratibu wa hesabu.

Mfano$\PageIndex{4}$: Writing a Recursive Formula for an Arithmetic Sequence

Andika formula ya kujirudia kwa mlolongo wa hesabu.

$\{−18, −7, 4, 15, 26, …\}$

Suluhisho

Neno la kwanza linapewa kama$−18$. Tofauti ya kawaida inaweza kupatikana kwa kuondoa muda wa kwanza kutoka kwa muda wa pili.

$d=−7−(−18)=11$

Badilisha muda wa awali na tofauti ya kawaida katika formula ya kujirudia kwa utaratibu wa hesabu.

$a_1=−18$

$a_n=a_{n−1}+11$

kwa$n≥2$

Uchambuzi

Tunaona kwamba tofauti ya kawaida ni mteremko wa mstari uliofanywa wakati tunapopiga maneno ya mlolongo, kama inavyoonekana kwenye Mchoro$\PageIndex{3}$. Mfano wa ukuaji wa mlolongo unaonyesha tofauti ya mara kwa mara ya vitengo 11.

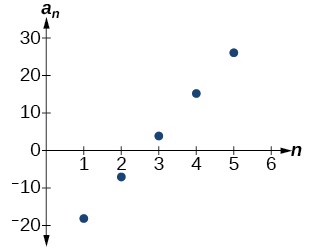
$Grafu ya mlolongo wa hesabu. Pointi huunda mstari mzuri.$

Kielelezo$\PageIndex{3}$

Q & A

Je, tunapaswa kuondoa muda wa kwanza kutoka kwa muda wa pili ili kupata tofauti ya kawaida?

Hapana. Tunaweza kuondoa muda wowote katika mlolongo kutoka kwa muda unaofuata. Hata hivyo, ni kawaida kuondoa muda wa kwanza kutoka kwa muda wa pili kwa sababu mara nyingi ni njia rahisi ya kupata tofauti ya kawaida.

Zoezi$\PageIndex{4}$

Andika formula ya kujirudia kwa mlolongo wa hesabu.

$\{25, 37, 49, 61, …\}$

Jibu: $\begin{align*}a_1 &= 25 \\ a_n &= a_{n−1}+12 , \text{ for }n≥2 \end{align*}$

Kutumia Fomu wazi kwa Utaratibu wa Hesabu

Tunaweza kufikiria mlolongo hesabu kama kazi kwenye uwanja wa idadi ya asili; ni kazi linear kwa sababu ina kiwango cha mara kwa mara ya mabadiliko. Tofauti ya kawaida ni kiwango cha mabadiliko ya mara kwa mara, au mteremko wa kazi. Tunaweza kujenga kazi linear kama tunajua mteremko na intercept wima.

$a_n=a_1+d(n−1)$

Ili kupata$y$ -intercept ya kazi, tunaweza kuondoa tofauti ya kawaida kutoka kwa muda wa kwanza wa mlolongo. Fikiria mlolongo wafuatayo.

$Mlolongo, {200, 150, 100, 50, 0,...}, unaoonyesha maneno yanatofautiana tu na -50.$

Tofauti ya kawaida ni$−50$, hivyo mlolongo inawakilisha kazi linear na mteremko wa$−50$. Ili kupata$y$ -intercept, tunaondoa$−50$ kutoka$200$:$200−(−50)=200+50=250$. Unaweza pia kupata$y$ -intercept kwa graphing kazi na kuamua ambapo mstari unaounganisha pointi bila intersect mhimili wima. Grafu inavyoonyeshwa kwenye Kielelezo$\PageIndex{4}$.

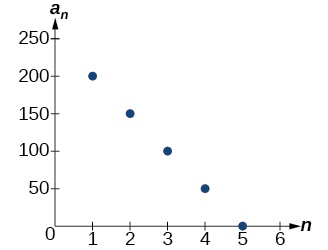
$Grafu ya mlolongo wa hesabu. Pointi huunda mstari hasi.$

Kielelezo$\PageIndex{4}$

Kumbuka mteremka-intercept aina ya mstari ni$y=mx+b$. Wakati wa kushughulika na Utaratibu, tunatumia$a_n$ badala$n$ ya$y$ na badala ya$x$. Ikiwa tunajua mteremko na uingizaji wa wima wa kazi, tunaweza$b$ kuwabadilisha$m$ na katika fomu ya mteremko wa mstari. Kutoa$−50$ kwa mteremko na$250$ kwa kupinga wima, tunapata equation ifuatayo:

$a_n=−50n+250$

Hatuna haja ya kupata intercept wima kuandika formula wazi kwa mlolongo wa hesabu. Fomula nyingine wazi kwa mlolongo huu ni$a_n=200−50(n−1)$, ambayo simplifies kwa$a_n=−50n+250$.

Kumbuka: FORMULA YA WAZI KWA MLOLONGO WA HESABU

Fomu ya wazi kwa$n^{th}$ muda wa mlolongo wa hesabu hutolewa na

\[a_n=a_1+d(n−1)\]

Jinsi ya: Kutokana na maneno kadhaa ya kwanza kwa mlolongo wa hesabu, weka formula wazi.

Kupata tofauti ya kawaida,$a_2−a_1$.
Badilisha tofauti ya kawaida na mrefu ya kwanza katika$a_n=a_1+d(n−1)$.

Mfano$\PageIndex{5}$: Writing the nth Term Explicit Formula for an Arithmetic Sequence

Andika formula wazi kwa mlolongo wa hesabu.

$\{2, 12, 22, 32, 42, …\}$

Suluhisho

Tofauti ya kawaida inaweza kupatikana kwa kuondoa muda wa kwanza kutoka kwa muda wa pili.

\[\begin{align*} d &= a_2−a_1 \\ &= 12−2 \\ &= 10 \end{align*}\]

Tofauti ya kawaida ni$10$. Kuweka tofauti ya kawaida na muda wa kwanza wa mlolongo katika formula na kurahisisha.

\[\begin{align*}a_n &= 2+10(n−1) \\ a_n &= 10n−8 \end{align*}\]

Uchambuzi

Grafu ya mlolongo huu, iliyowakilishwa katika Kielelezo$\PageIndex{5}$, inaonyesha mteremko wa$10$ na kupinga wima ya$−8$.

Grafu ya mlolongo wa hesabu. Pointi huunda mstari mzuri.

Kielelezo$\PageIndex{5}$

Zoezi$\PageIndex{5}$

Andika formula wazi kwa mlolongo wa hesabu zifuatazo.

$\{50,47,44,41,…\}$

Jibu: $a_n=53−3n$

Kutafuta Idadi ya Masharti katika Mlolongo wa Hesabu ya mwisho

Fomu zilizo wazi zinaweza kutumika kuamua idadi ya maneno katika mlolongo wa mwisho wa hesabu. Tunahitaji kupata tofauti ya kawaida, na kisha kuamua mara ngapi tofauti ya kawaida lazima iongezwe kwa muda wa kwanza ili kupata muda wa mwisho wa mlolongo.

Jinsi ya: Kutokana na masharti matatu ya kwanza na muda wa mwisho wa mlolongo wa mwisho wa hesabu, pata idadi ya maneno.

Pata tofauti ya kawaida$d$.
Badilisha tofauti ya kawaida na mrefu ya kwanza katika$a_n=a_1+d(n–1)$.
Badala ya muda wa mwisho kwa$a_n$ na kutatua kwa$n$.

Mfano$\PageIndex{6}$: Finding the Number of Terms in a Finite Arithmetic Sequence

Pata idadi ya maneno katika mlolongo wa mwisho wa hesabu.

$\{8, 1, –6, ..., –41\}$

Suluhisho

Tofauti ya kawaida inaweza kupatikana kwa kuondoa muda wa kwanza kutoka kwa muda wa pili.

$1−8=−7$

Tofauti ya kawaida ni$−7$. Badilisha tofauti ya kawaida na muda wa awali wa mlolongo katika formula ya muda wa nth na kurahisisha.

\[\begin{align*} a_n &= a_1+d(n−1) \\ a_n &= 8+−7(n−1) \\ a_n &= 15−7n \end{align*}\]

Mbadala$−41$ kwa ajili$a_n$ ya na kutatua kwa$n$

\[\begin{align*} -41&=15-7n\\ 8&=n \end{align*}\]

Kuna maneno nane katika mlolongo.

Zoezi$\PageIndex{6}$

Pata idadi ya maneno katika mlolongo wa mwisho wa hesabu.

$\{6, 11, 16, ..., 56\}$

Jibu: Kuna$11$ maneno katika mlolongo.

Kutatua Matatizo ya Maombi na Utaratibu wa Hesabu

Katika matatizo mengi ya maombi, mara nyingi huwa na maana ya kutumia muda wa awali$a_0$ badala ya$a_1$. Katika matatizo haya, sisi kubadilisha formula wazi kidogo kwa akaunti kwa tofauti katika suala awali. Tunatumia formula ifuatayo:

\[a_n=a_0+dn\]

Mfano$\PageIndex{7}$: Solving Application Problems with Arithmetic Sequences

Mtoto mwenye umri wa miaka mitano anapata posho ya$$1$ kila wiki. Wazazi wake wanaahidi ongezeko la kila mwaka la$$2$ kila wiki.

Andika formula kwa posho ya kila wiki ya mtoto katika mwaka uliopewa.
Je, posho ya mtoto itakuwa nini wakati ana umri wa$16$ miaka?

Suluhisho

Hali inaweza kuwa inatokana na mlolongo hesabu na muda wa awali wa$1$ na tofauti ya kawaida ya$2$.
Hebu$A$ kuwa kiasi cha posho na$n$ uwe idadi ya miaka baada ya umri$5$. Kutumia formula iliyo wazi iliyobadilishwa kwa mlolongo wa hesabu tunayopata:

$A_n=1+2n$
Tunaweza kupata idadi ya miaka tangu umri$5$ kwa kuondoa.
$16−5=11$

Tunatafuta posho ya mtoto baada ya$11$ miaka. $11$Kuingiza katika formula ili kupata posho ya mtoto wakati wa umri$16$.

$A_{11}=1+2(11)=23$

Kizuizi cha mtoto wakati wa umri$16$ kitakuwa$$23$ kwa wiki.

Zoezi$\PageIndex{7}$

Mwanamke anaamua kwenda kwa$10$ dakika ya kukimbia kila siku wiki hii na mipango ya kuongeza muda wa kukimbia kwake kila siku kwa$4$ dakika kila wiki. Andika formula kwa wakati wa kukimbia baada ya$n$ wiki. Je, kukimbia kwake kila siku kwa muda gani kuwa$8$ wiki kutoka leo?

Jibu: Fomu ni$T_n=10+4n$, na itachukua$42$ dakika yake.

Media

Fikia rasilimali hii ya mtandaoni kwa maelekezo ya ziada na mazoezi na utaratibu wa hesabu.

Utaratibu wa hesabu

Mlinganyo muhimu

formula ya kujirudia kwa muda wa nth wa mlolongo wa hesabu	$a_n=a_{n−1}+d$$n≥2$
formula wazi kwa muda wa nth wa mlolongo wa hesabu	$a_n=a_1+d(n−1)$

Key Concepts

An arithmetic sequence is a sequence where the difference between any two consecutive terms is a constant.
The constant between two consecutive terms is called the common difference.
The common difference is the number added to any one term of an arithmetic sequence that generates the subsequent term. See Example $\PageIndex{1}$.
The terms of an arithmetic sequence can be found by beginning with the initial term and adding the common difference repeatedly. See Example $\PageIndex{2}$ and Example $\PageIndex{3}$.
A recursive formula for an arithmetic sequence with common difference dd is given by $a_n=a_{n−1}+d$, $n≥2$. See Example $\PageIndex{4}$.
As with any recursive formula, the initial term of the sequence must be given.
An explicit formula for an arithmetic sequence with common difference $d$ is given by $a_n=a_1+d(n−1)$. See Example $\PageIndex{5}$.
An explicit formula can be used to find the number of terms in a sequence. See Example $\PageIndex{6}$.
In application problems, we sometimes alter the explicit formula slightly to $a_n=a_0+dn$. See Example $\PageIndex{7}$.

Contributors and Attributions

Template:ContribOpenStaxPreCalc

MLOLONGO WA HESABU

Mfano\(\PageIndex{1}\): Finding Common Differences

Zoezi\(\PageIndex{1A}\)

Zoezi\(\PageIndex{1B}\)

Jinsi ya: Kutokana na muda wa kwanza na tofauti ya kawaida ya mlolongo wa hesabu, pata maneno kadhaa ya kwanza.

Mfano\(\PageIndex{2}\): Writing Terms of Arithmetic Sequences

Zoezi\(\PageIndex{2}\)

Mfano\(\PageIndex{3}\): Writing Terms of Arithmetic Sequences

Zoezi\(\PageIndex{3}\)

Kumbuka: formula ya kujirudia kwa mlolongo wa hesabu

Jinsi ya: Kutokana na mlolongo wa hesabu, andika formula yake ya kujirudia.

Mfano\(\PageIndex{4}\): Writing a Recursive Formula for an Arithmetic Sequence

Zoezi\(\PageIndex{4}\)

Kumbuka: FORMULA YA WAZI KWA MLOLONGO WA HESABU

Jinsi ya: Kutokana na maneno kadhaa ya kwanza kwa mlolongo wa hesabu, weka formula wazi.

Mfano\(\PageIndex{5}\): Writing the nth Term Explicit Formula for an Arithmetic Sequence

Zoezi\(\PageIndex{5}\)

Jinsi ya: Kutokana na masharti matatu ya kwanza na muda wa mwisho wa mlolongo wa mwisho wa hesabu, pata idadi ya maneno.

Mfano\(\PageIndex{6}\): Finding the Number of Terms in a Finite Arithmetic Sequence

Zoezi\(\PageIndex{6}\)

Mfano\(\PageIndex{7}\): Solving Application Problems with Arithmetic Sequences

Zoezi\(\PageIndex{7}\)

Contributors and Attributions

formula ya kujirudia kwa muda wa nth wa mlolongo wa hesabu	\(a_n=a_{n−1}+d\)\(n≥2\)
formula wazi kwa muda wa nth wa mlolongo wa hesabu	\(a_n=a_1+d(n−1)\)