10.5: Fomu ya Polar ya Hesabu Complex
- Page ID
- 178408
- Panda namba tata katika ndege tata.
- Pata thamani kamili ya idadi tata.
- Andika namba tata katika fomu ya polar.
- Badilisha namba tata kutoka polar hadi fomu ya mstatili.
- Pata bidhaa za namba tata katika fomu ya polar.
- Pata quotients ya idadi tata katika fomu ya polar.
- Pata nguvu za idadi tata katika fomu ya polar.
- Pata mizizi ya namba tata katika fomu ya polar.
“Mungu aliumba integers; yote ni kazi ya mwanadamu.” Nukuu hii maarufu sana na mwanahisabati wa Kijerumani wa karne ya kumi na tisa Leopold Kronecker huweka hatua kwa sehemu hii kwenye fomu ya polar ya namba tata. Idadi tata zuliwa na watu na kuwakilisha zaidi ya miaka elfu ya uchunguzi wa kuendelea na mapambano na wanahisabati kama vile Pythagoras, Descartes, De Moivre, Euler, Gauss, na wengine. Nambari tata zilijibu maswali ambayo kwa karne nyingi zilikuwa zimeshangaa akili kubwa zaidi katika sayansi.
Sisi kwanza tulikutana na idadi tata katika sehemu ya Hesabu Complex. Katika sehemu hii, tutazingatia mechanics ya kufanya kazi na namba tata: tafsiri ya namba tata kutoka kwa fomu ya polar hadi fomu ya mstatili na kinyume chake, tafsiri ya idadi tata katika mpango wa maombi, na matumizi ya Theorem ya De Moivre.
Kupanga Nambari Complex katika Ndege Complex
Kupanga namba tata\(a+bi\) ni sawa na kupanga namba halisi, isipokuwa kwamba mhimili usio na usawa unawakilisha sehemu halisi ya namba\(a\), na mhimili wima unawakilisha sehemu ya kufikiri ya namba,\(bi\).
- Weka mhimili usio na usawa kama mhimili halisi na mhimili wima kama mhimili wa kufikiri.
- Panda hatua katika ndege ngumu kwa kusonga\(a\) vitengo katika mwelekeo usio na usawa na\(b\) vitengo katika mwelekeo wa wima.
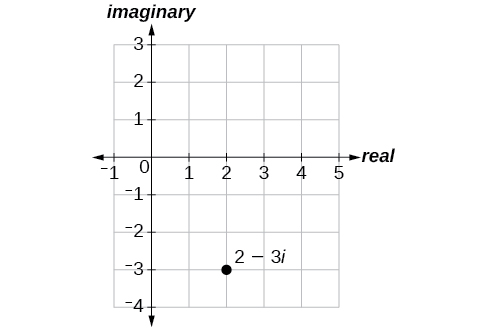
Panda idadi tata\(2−3i\) katika ndege tata.
Suluhisho
Kutoka asili, fanya vitengo viwili katika mwelekeo mzuri wa usawa na vitengo vitatu katika mwelekeo mbaya wa wima. Angalia Kielelezo\(\PageIndex{1}\).
Panda hatua\(1+5i\) katika ndege tata.
- Jibu
-
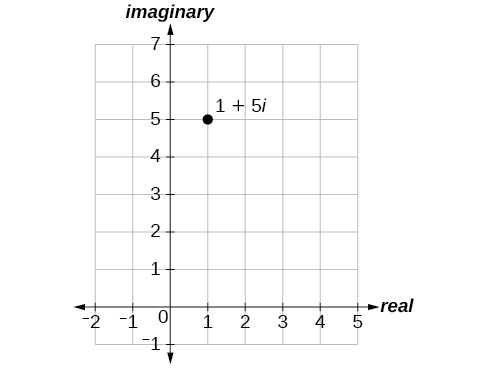
Kielelezo\(\PageIndex{2}\)
Kutafuta Thamani kamili ya Idadi Tata
Hatua ya kwanza kuelekea kufanya kazi na idadi tata katika fomu ya polar ni kupata thamani kamili. Thamani kamili ya idadi tata ni sawa na ukubwa wake, au\(| z |\). Inapima umbali kutoka asili hadi hatua katika ndege. Kwa mfano, grafu ya\(z=2+4i\), katika Kielelezo\(\PageIndex{3}\), inaonyesha\(| z |\).
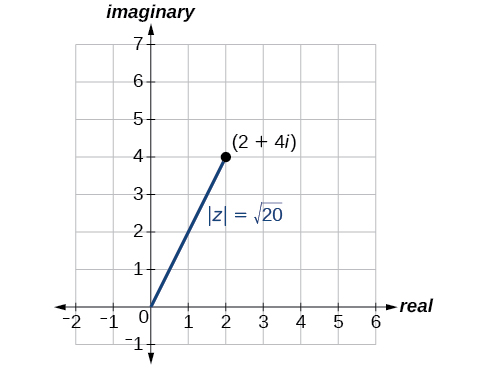
Kutokana\(z=x+yi\), idadi tata, thamani kamili ya\(z\) hufafanuliwa kama
\[| z |=\sqrt{x^2+y^2}\]
Ni umbali kutoka asili hadi hatua\((x,y)\).
Kumbuka kwamba thamani kamili ya idadi halisi inatoa umbali wa idadi kutoka\(0\), wakati thamani kamili ya idadi tata inatoa umbali wa idadi kutoka asili,\((0, 0)\).
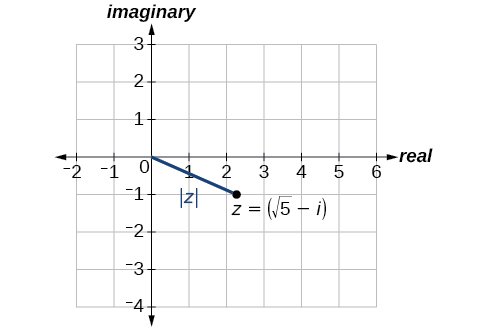
Kupata thamani kamili ya\(z=\sqrt{5}−i\).
Suluhisho
Kutumia formula, tuna
\[\begin{align*} |z| &= \sqrt{x^2+y^2} \\ |z| &= \sqrt{{(\sqrt{5})}^2+{(-1)}^2} \\ |z| &= \sqrt{5+1} \\ |z| &= \sqrt{6} \end{align*}\]
Angalia Kielelezo\(\PageIndex{4}\).
Pata thamani kamili ya idadi tata\(z=12−5i\).
- Jibu
-
\(13\)
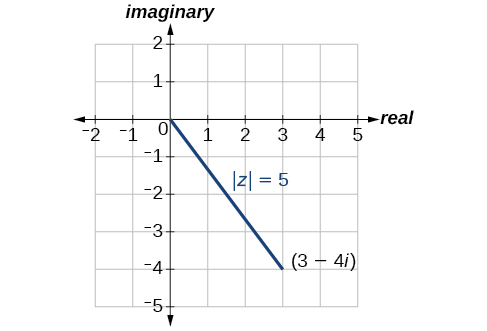
Kutokana\(z=3−4i\), tafuta\(| z |\).
Suluhisho
Kutumia formula, tuna
\[\begin{align*} | z | &= \sqrt{x^2+y^2} \\ | z | &= \sqrt{{(3)}^2+{(-4)}^2} \\ | z | &= \sqrt{9+16} \\ | z | &= \sqrt{25} \\ | z | &= 5 \end{align*}\]
Thamani kamili\(z\) ni\(5\). Angalia Kielelezo\(\PageIndex{5}\).
Kutokana\(z=1−7i\), tafuta\(| z |\).
- Jibu
-
\(| z |=\sqrt{50}=5\sqrt{2}\)
Kuandika Hesabu Complex katika Fomu ya Polar
Fomu ya polar ya nambari tata inaonyesha idadi kwa suala la angle\(\theta\) na umbali wake kutoka kwa asili\(r\). Kutokana na idadi tata katika fomu mstatili walionyesha kama\(z=x+yi\), tunatumia formula sawa uongofu kama sisi kufanya kuandika idadi katika fomu trigonometric:
\[\begin{align*} x &= r \cos \theta \\ y &= r \sin \theta \\ r &= \sqrt{x^2+y^2} \end{align*}\]
Sisi kupitia mahusiano haya katika Kielelezo\(\PageIndex{6}\).
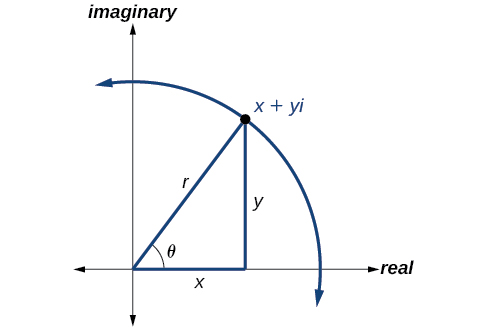
Tunatumia moduli ya neno kuwakilisha thamani kamili ya nambari tata, au umbali kutoka kwa asili hadi hatua\((x,y)\). Moduli, basi, ni sawa na\(r\), radius katika fomu ya polar. Tunatumia\(\theta\) kuonyesha angle ya mwelekeo (kama vile kuratibu polar). Kubadilisha, tuna
\[\begin{align*} z &= x+yi \\ z &= r \cos \theta+(r \sin \theta)i \\ z &= r(\cos \theta+i \sin \theta) \end{align*}\]
Kuandika namba tata katika fomu ya polar inahusisha kanuni zifuatazo za uongofu:
\[\begin{align} x &= r \cos \theta \\ y &= r \sin \theta \\ r &= \sqrt{x^2+y^2} \end{align}\]
Kufanya badala ya moja kwa moja, tuna
\[\begin{align} z &= x+yi \\ z &= (r \cos \theta)+i(r \sin \theta) \\ z &= r(\cos \theta+i \sin \theta) \end{align}\]
\(r\)wapi moduli na\(\theta\) ni hoja. Mara nyingi tunatumia kifupi\(r\; cis \theta\) kuwakilisha\(r(\cos \theta+i \sin \theta)\).
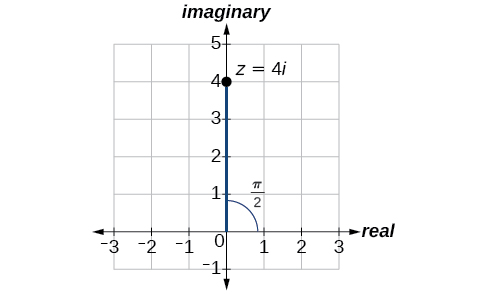
Eleza nambari tata\(4i\) kwa kutumia kuratibu za polar.
Suluhisho
Katika ndege ngumu, idadi hiyo\(z=4i\) ni sawa na\(z=0+4i\). Kuandika kwa fomu ya polar, tunapaswa kuhesabu\(r\) kwanza.
\[\begin{align*} r &= \sqrt{x^2+y^2} \\ r &= \sqrt{0^2+4^2} \\ r &= \sqrt{16} \\ r &= 4 \end{align*}\]
Kisha, tunaangalia\(x\). Ikiwa\(x=r \cos \theta\), na\(x=0\), basi\(\theta=\dfrac{\pi}{2}\). Katika kuratibu polar, idadi tata\(z=0+4i\) inaweza kuandikwa kama\(z=4\left(\cos\left(\dfrac{\pi}{2}\right)+i \sin\left(\dfrac{\pi}{2}\right)\right) \text{ or } 4\; cis\left( \dfrac{\pi}{2}\right)\). Angalia Kielelezo\(\PageIndex{7}\).
Eleza\(z=3i\) kama\(r\space cis \theta\) katika fomu ya polar.
- Jibu
-
\(z=3\left(\cos\left(\dfrac{\pi}{2}\right)+i \sin\left(\dfrac{\pi}{2}\right)\right)\)
Kupata aina polar ya\(−4+4i\).
Suluhisho
Kwanza, kupata thamani ya\(r\).
\[\begin{align*} r &= \sqrt{x^2+y^2} \\ r &= \sqrt{{(−4)}^2+(4^2)} \\ r &= \sqrt{32} \\ r &= 4\sqrt{2} \end{align*}\]
Pata angle\(\theta\) kwa kutumia formula:
\[\begin{align*} \cos \theta &= \dfrac{x}{r} \\ \cos \theta &= \dfrac{−4}{4\sqrt{2}} \\ \cos \theta &= −\dfrac{1}{\sqrt{2}} \\ \theta &= {\cos}^{−1} \left(−\dfrac{1}{\sqrt{2}}\right)\\ &= \dfrac{3\pi}{4} \end{align*}\]
Hivyo, suluhisho ni\(4\sqrt{2}\space cis \left(\dfrac{3\pi}{4}\right)\).
Andika\(z=\sqrt{3}+i\) kwa fomu ya polar.
- Jibu
-
\(z=2\left(\cos\left(\dfrac{\pi}{6}\right)+i \sin\left(\dfrac{\pi}{6}\right)\right)\)
Kubadilisha Idadi Complex kutoka Polar hadi Fomu ya Rectangular
Kubadili namba tata kutoka fomu ya polar hadi fomu ya mstatili ni suala la kutathmini kile kinachopewa na kutumia mali ya usambazaji. Kwa maneno mengine, kutokana\(z=r(\cos \theta+i \sin \theta)\), kwanza tathmini kazi za trigonometric\(\cos \theta\) na\(\sin \theta\). Kisha, kuzidisha kupitia\(r\).
Badilisha fomu ya polar ya nambari tata iliyotolewa kwa fomu ya mstatili:
\(z=12\left(\cos\left(\dfrac{\pi}{6}\right)+i \sin\left(\dfrac{\pi}{6}\right)\right)\)
Suluhisho
Tunaanza kwa kutathmini maneno ya trigonometric.
\[\begin{align*} \cos\left(\dfrac{\pi}{6}\right)&= \dfrac{\sqrt{3}}{2} \text{ and } \sin(\dfrac{\pi}{6})=\dfrac{1}{2}\\ \text {After substitution, the complex number is}\\ z&= 12\left(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}i\right) \end{align*}\]
Tunatumia mali ya usambazaji:
\[\begin{align*} z &= 12\left(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}i\right) \\ &= (12)\dfrac{\sqrt{3}}{2}+(12)\dfrac{1}{2}i \\ &= 6\sqrt{3}+6i \end{align*}\]
Fomu ya mstatili wa hatua iliyotolewa katika fomu ngumu ni\(6\sqrt{3}+6i\).
Pata fomu ya mstatili wa nambari tata iliyotolewa\(r=13\) na\(\tan \theta=\dfrac{5}{12}\).
Suluhisho
Kama\(\tan \theta=\dfrac{5}{12}\), na\(\tan \theta=\dfrac{y}{x}\), sisi kwanza kuamua\(r=\sqrt{x^2+y^2}=\sqrt{122+52}=13\). Sisi kisha kupata\(\cos \theta=\dfrac{x}{r}\) na\(\sin \theta=\dfrac{y}{r}\).
\[\begin{align*} z &= 13\left(\cos \theta+i \sin \theta\right) \\ &= 13\left(\dfrac{12}{13}+\dfrac{5}{13}i\right) \\ &=12+5i \end{align*}\]
Fomu ya mstatili wa nambari iliyotolewa katika fomu ngumu ni\(12+5i\).
Badilisha nambari tata kwa fomu ya mstatili:
\(z=4\left(\cos \dfrac{11\pi}{6}+i \sin \dfrac{11\pi}{6}\right)\)
- Jibu
-
\(z=2\sqrt{3}−2i\)
Kutafuta Bidhaa za Hesabu Complex katika Fomu ya Polar
Sasa kwa kuwa tunaweza kubadilisha namba tata kwa fomu ya polar tutajifunza jinsi ya kufanya shughuli kwa idadi tata katika fomu ya polar. Kwa sehemu hii yote, tutafanya kazi na fomu zilizotengenezwa na mtaalamu wa hisabati wa Kifaransa Abraham de Moivre (1667-1754). Njia hizi zimefanya kufanya kazi na bidhaa, quotients, nguvu, na mizizi ya namba tata rahisi zaidi kuliko zinaonekana. Sheria zinategemea kuzidisha moduli na kuongeza hoja.
Ikiwa\(z_1=r_1(\cos \theta_1+i \sin \theta_1)\) na\(z_2=r_2(\cos \theta_2+i \sin \theta_2)\), basi bidhaa za namba hizi hutolewa kama:
\[\begin{align} z_1z_2 &= r_1r_2[ \cos(\theta_1+\theta_2)+i \sin(\theta_1+\theta_2) ] \\ z_1z_2 &= r_1r_2\space cis(\theta_1+\theta_2) \end{align}\]
Angalia kwamba bidhaa zinaita kuzidisha moduli na kuongeza pembe.
Kupata bidhaa ya\(z_1z_2\), kutokana\(z_1=4(\cos(80°)+i \sin(80°))\) na\(z_2=2(\cos(145°)+i \sin(145°))\).
Suluhisho
Fuata formula
\[\begin{align*} z_1z_2 &= 4⋅2[\cos(80°+145°)+i \sin(80°+145°)] \\ z_1z_2 &= 8[\cos(225°)+i \sin(225°)] \\ z_1z_2 &= 8\left[\cos\left(\dfrac{5\pi}{4}\right)+i \sin\left(\dfrac{5\pi}{4}\right) \right] \\ z_1z_2 &= 8\left[−\dfrac{\sqrt{2}}{2}+i\left(−\dfrac{\sqrt{2}}{2}\right) \right] \\ z_1z_2 &= −4\sqrt{2}−4i\sqrt{2} \end{align*}\]
Kutafuta Quotients ya Hesabu Complex katika Fomu Polar
Kiwango cha namba mbili ngumu katika fomu ya polar ni quotient ya moduli mbili na tofauti ya hoja mbili.
Ikiwa\(z_1=r_1(\cos \theta_1+i \sin \theta_1)\) na\(z_2=r_2(\cos \theta_2+i \sin \theta_2)\), basi quotient ya namba hizi ni
\[\dfrac{z_1}{z_2}=\dfrac{r_1}{r_2}[\cos(\theta_1−\theta_2)+i \sin(\theta_1−\theta_2) ],\space z_2≠0\]
\[\dfrac{z_1}{z_2}=\dfrac{r_1}{r_2}\space cis(\theta_1−\theta_2),\space z_2≠0\]
Angalia kwamba moduli imegawanywa, na pembe zinaondolewa.
- Gawanya\(\dfrac{r_1}{r_2}\).
- Kupata\(\theta_1−\theta_2\).
- Badilisha matokeo katika formula:\(z=r(\cos \theta+i \sin \theta)\). Kuchukua nafasi\(r\) na\(\dfrac{r_1}{r_2}\), na kuchukua nafasi\(\theta\) na\(\theta_1−\theta_2\).
- Tumia maneno mapya ya trigonometric na uongeze kupitia\(r\).
Kupata quotient ya\(z_1=2(\cos(213°)+i \sin(213°))\) na\(z_2=4(\cos(33°)+i \sin(33°))\).
Suluhisho
Kutumia formula, tuna
\[\begin{align*} \dfrac{z_1}{z_2} &= \dfrac{2}{4}[\cos(213°−33°)+i \sin(213°−33°)] \\ \dfrac{z_1}{z_2} &= \dfrac{1}{2}[\cos(180°)+i \sin(180°)] \\ \dfrac{z_1}{z_2} &= \dfrac{1}{2}[−1+0i] \\ \dfrac{z_1}{z_2} &= −\dfrac{1}{2}+0i \\ \dfrac{z_1}{z_2} &= −\dfrac{1}{2} \end{align*}\]
Kupata bidhaa na quotient ya\(z_1=2\sqrt{3}(\cos(150°)+i \sin(150°))\) na\(z_2=2(\cos(30°)+i \sin(30°))\).
- Jibu
-
\(z_1z_2=−4\sqrt{3}\);\(\dfrac{z_1}{z_2}=−\dfrac{\sqrt{3}}{2}+\dfrac{3}{2}i\)
Kupata Nguvu za Hesabu Complex katika Fomu ya Polar
Kupata nguvu za namba tata ni rahisi sana kwa kutumia Theorem ya De Moivre. Inasema kwamba, kwa integer chanya\(n\),\(z^n\) hupatikana kwa kuongeza moduli kwa\(n^{th}\) nguvu na kuzidisha hoja na\(n\). Ni njia ya kawaida inayotumiwa katika hisabati ya kisasa.
Ikiwa\(z=r(\cos \theta+i \sin \theta)\) ni idadi tata, basi
\[\begin{align} z^n &= r^n[\cos(n\theta)+i \sin(n\theta) ] \\ z^n &= r^n\space cis(n\theta) \end{align}\]
ambapo\(n\) ni integer chanya.
Tathmini maneno kwa\({(1+i)}^5\) kutumia Theorem ya De Moivre.
Suluhisho
Kwa kuwa Theorem ya De Moivre inatumika kwa namba tata zilizoandikwa katika fomu ya polar, lazima kwanza tuandike\((1+i)\) kwa fomu ya polar. Hebu kupata\(r\).
\[\begin{align*} r &= \sqrt{x^2+y^2} \\ r &= \sqrt{{(1)}^2+{(1)}^2} \\ r &= \sqrt{2} \end{align*}\]
Kisha sisi kupata\(\theta\). Kutumia formula\(\tan \theta=\dfrac{y}{x}\) inatoa
\[\begin{align*} \tan \theta &= \dfrac{1}{1} \\ \tan \theta &= 1 \\ \theta &= \dfrac{\pi}{4} \end{align*}\]
Tumia Theorem ya De Moivre ili kutathmini usemi.
\[\begin{align*} {(a+bi)}^n &= r^n[\cos(n\theta)+i \sin(n\theta)] \\ {(1+i)}^5 &= {(\sqrt{2})}^5\left[ \cos\left(5⋅\dfrac{\pi}{4}\right)+i \sin\left(5⋅\dfrac{\pi}{4}\right) \right] \\ {(1+i)}^5 &= 4\sqrt{2}\left[ \cos\left(\dfrac{5\pi}{4}\right)+i \sin\left(\dfrac{5\pi}{4}\right) \right] \\ {(1+i)}^5 &= 4\sqrt{2}\left[ −\dfrac{\sqrt{2}}{2}+i\left(−\dfrac{\sqrt{2}}{2}\right) \right] \\ {(1+i)}^5 &= −4−4i \end{align*}\]
Kutafuta Mizizi ya Hesabu Complex katika Fomu ya Polar
Ili kupata\(n^{th}\) mzizi wa idadi tata katika fomu ya polar, tunatumia Theorem ya\(n^{th}\) Mizizi au Theorem ya De Moivre na kuongeza idadi tata kwa nguvu na kielelezo cha busara. Kuna njia kadhaa za kuwakilisha formula ya kutafuta\(n^{th}\) mizizi ya namba tata katika fomu ya polar.
Ili kupata\(n^{th}\) mizizi ya namba tata katika fomu ya polar, tumia fomu iliyotolewa kama
\[z^{\tfrac{1}{n}}=r^{\tfrac{1}{n}}\left[ \cos\left(\dfrac{\theta}{n}+\dfrac{2k\pi}{n}\right)+i \sin\left(\dfrac{\theta}{n}+\dfrac{2k\pi}{n}\right) \right]\]
wapi\(k=0, 1, 2, 3, . . . , n−1\). Tunaongeza\(\dfrac{2k\pi}{n}\)\(\dfrac{\theta}{n}\) ili kupata mizizi ya mara kwa mara.
Kutathmini mizizi mchemraba wa\(z=8\left(\cos\left(\frac{2\pi}{3}\right)+i\sin\left(\frac{2\pi}{3}\right)\right)\).
Suluhisho
Tuna
\[\begin{align*} z^{\frac{1}{3}} &= 8^{\frac{1}{3}}\left[ \cos\left(\frac{\frac{2\pi}{3}}{3}+\frac{2k\pi}{3}\right)+i \sin\left(\frac{\frac{2\pi}{3}}{3}+\frac{2k\pi}{3}\right) \right] \\ z^{\frac{1}{3}} &= 2\left[ \cos\left(\frac{2\pi}{9}+\frac{2k\pi}{3}\right)+i \sin\left(\frac{2\pi}{9}+\frac{2k\pi}{3}\right) \right] \end{align*}\]
Kutakuwa na mizizi mitatu:\(k=0, 1, 2\). Wakati\(k=0\), tuna
\(z^{\frac{1}{3}}=2\left(\cos\left(\dfrac{2\pi}{9}\right)+i \sin\left(\dfrac{2\pi}{9}\right)\right)\)
Wakati\(k=1\), tuna
\[\begin{align*} z^{\frac{1}{3}} &=2\left[ \cos\left(\dfrac{2\pi}{9}+\dfrac{6\pi}{9}\right)+i \sin\left(\dfrac{2\pi}{9}+\dfrac{6\pi}{9}\right) \right] \;\;\;\;\;\;\;\;\; \text{Add }\dfrac{2(1)\pi}{3} \text{ to each angle.} \\ z^{\frac{1}{3}} &= 2\left(\cos\left(\dfrac{8\pi}{9}\right)+i \sin\left(\dfrac{8\pi}{9}\right)\right) \end{align*}\]
Wakati\(k=2\), tuna
\[\begin{align*} z^{\frac{1}{3}} &= 2\left[ \cos\left(\dfrac{2\pi}{9}+\dfrac{12\pi}{9}\right)+i \sin\left(\dfrac{2\pi}{9}+\dfrac{12\pi}{9}\right) \right] \;\;\;\;\;\;\; \text{Add }\dfrac{2(2)\pi}{3} \text{ to each angle.} \\ z^{\frac{1}{3}} &= 2\left(\cos\left(\dfrac{14\pi}{9}\right)+i \sin\left(\dfrac{14\pi}{9}\right)\right) \end{align*}\]
Kumbuka kupata denominator ya kawaida ili kurahisisha sehemu ndogo katika hali kama hii. Kwa\(k=1\), kurahisisha angle ni
\[\begin{align*} \dfrac{\dfrac{2\pi}{3}}{3}+\dfrac{2(1)\pi}{3} &= \dfrac{2\pi}{3}(\dfrac{1}{3})+\dfrac{2(1)\pi}{3}\left(\dfrac{3}{3}\right) \\ &=\dfrac{2\pi}{9}+\dfrac{6\pi}{9} \\ &=\dfrac{8\pi}{9} \end{align*}\]
Kupata nne mizizi ya nne ya\(16(\cos(120°)+i \sin(120°))\).
- Jibu
-
\(z_0=2(\cos(30°)+i \sin(30°))\)
\(z_1=2(\cos(120°)+i \sin(120°))\)
\(z_2=2(\cos(210°)+i \sin(210°))\)
\(z_3=2(\cos(300°)+i \sin(300°))\)
Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na aina za polar za namba tata.
- Bidhaa na Quotient ya Hesabu Complex katika Fomu ya Trigonometric
- Theorem ya De Moivre
Dhana muhimu
- Nambari tata katika fomu\(a+bi\) zimepangwa katika ndege ngumu sawa na njia za kuratibu za mstatili zinapangwa katika ndege ya mstatili. Lebo\(x\) -axis kama mhimili halisi na\(y\) - mhimili kama mhimili wa kufikiri. Angalia Mfano\(\PageIndex{1}\).
- Thamani kamili ya idadi tata ni sawa na ukubwa wake. Ni umbali kutoka asili hadi hatua:\(| z |=\sqrt{a^2+b^2}\). Angalia Mfano\(\PageIndex{2}\) na Mfano\(\PageIndex{3}\).
- Kuandika namba tata katika fomu ya polar, tunatumia formula\(x=r \cos \theta\)\(y=r \sin \theta\), na\(r=\sqrt{x^2+y^2}\). Kisha,\(z=r(\cos \theta+i \sin \theta)\). Angalia Mfano\(\PageIndex{4}\) na Mfano\(\PageIndex{5}\).
- Ili kubadilisha kutoka fomu ya polar hadi fomu ya mstatili, kwanza tathmini kazi za trigonometric. Kisha, kuzidisha kupitia\(r\). Angalia Mfano\(\PageIndex{6}\) na Mfano\(\PageIndex{7}\).
- Ili kupata bidhaa ya namba mbili ngumu, kuzidisha moduli mbili na kuongeza pembe mbili. Tathmini kazi za trigonometric, na uongeze kutumia mali ya usambazaji. Angalia Mfano\(\PageIndex{8}\).
- Ili kupata quotient ya namba mbili ngumu katika fomu ya polar, pata quotient ya moduli mbili na tofauti ya pembe mbili. Angalia Mfano\(\PageIndex{9}\).
- Ili kupata nguvu ya nambari tata\(z^n\), ongeza\(r\) kwa nguvu\(n\), na uongeze\(\theta\) na\(n\). Angalia Mfano\(\PageIndex{10}\).
- Kupata mizizi ya idadi tata ni sawa na kuongeza idadi tata kwa nguvu, lakini kwa kutumia exponent busara. Angalia Mfano\(\PageIndex{11}\).


