10.3: Kuratibu Polar

Last updated
Save as PDF

Page ID: 178388

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Plot pointi kwa kutumia kuratibu polar.
Badilisha kutoka kuratibu za polar hadi kuratibu za mstatili.
Badilisha kutoka kuratibu za mstatili hadi kuratibu za polar.
Kubadilisha equations kati ya aina polar na mstatili.
Tambua na graph equations polar kwa kubadili equations mstatili.

Zaidi ya$12$ kilomita kutoka bandari, baharini hukutana na hali mbaya ya hewa na hupigwa mbali na upepo wa$16$ fundo (angalia Mchoro$\PageIndex{1}$). Mbaharia anawezaje kuonyesha eneo lake kwa Walinzi wa Pwani? Katika sehemu hii, tutachunguza njia ya kuwakilisha eneo ambalo ni tofauti na gridi ya kuratibu ya kawaida.

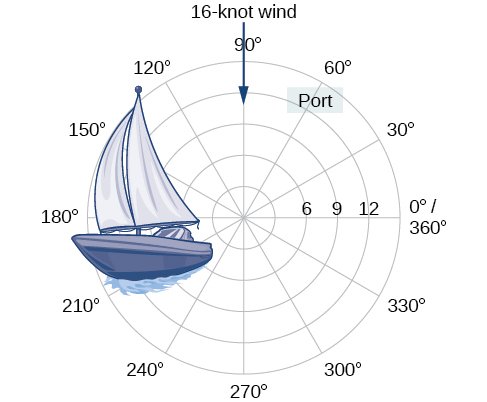
$Mfano wa mashua kwenye gridi ya polar.$

Kielelezo$\PageIndex{1}$

Kupanga Points Kutumia Kuratibu Polar

Tunapofikiri juu ya pointi za kupanga njama kwenye ndege, mara nyingi tunafikiria kuratibu mstatili$(x,y)$ katika ndege ya kuratibu ya Cartesian. Hata hivyo, kuna njia nyingine za kuandika jozi ya kuratibu na aina nyingine za mifumo ya gridi ya taifa. Katika sehemu hii, tunaanzisha kuratibu za polar, ambazo ni pointi zilizoandikwa$(r,\theta)$ na kupangwa kwenye gridi ya polar. Gridi ya polar inawakilishwa kama mfululizo wa miduara ya makini inayotoka nje ya pole, au asili ya ndege ya kuratibu.

Gridi ya polar imeongezwa kama mduara wa kitengo na mhimili mzuri$x$ - sasa unatazamwa kama mhimili wa polar na asili kama pole. Kuratibu kwanza$r$ ni radius au urefu wa sehemu iliyoongozwa ya mstari kutoka kwa pole. Pembe$\theta$, kipimo katika radians, inaonyesha mwelekeo wa$r$. Sisi hoja kinyume chake kutoka mhimili polar kwa angle ya$\theta$, na kupima moja kwa moja line sehemu urefu wa$r$ katika mwelekeo wa$\theta$. Ingawa tunapima$\theta$ kwanza na kisha$r$, hatua ya polar imeandikwa na$r$ -kuratibu kwanza. Kwa mfano, ili kupanga njama$\left(2,\dfrac{\pi}{4}\right)$, tungeweza kusonga$\dfrac{\pi}{4}$ vitengo katika mwelekeo kinyume na kisha urefu wa$2$ kutoka pole. Hatua hii imepangwa kwenye gridi ya taifa katika Kielelezo$\PageIndex{2}$.

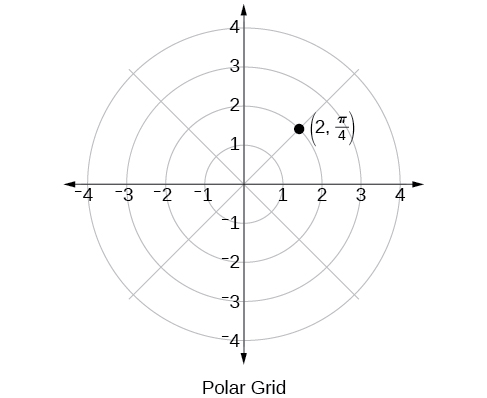
$Gridi ya Polar na uhakika (2, pi/4) walipanga.$

Kielelezo$\PageIndex{2}$

Mfano$\PageIndex{1}$: Plotting a Point on the Polar Grid

Panda hatua$\left(3,\dfrac{\pi}{2}\right)$ kwenye gridi ya polar.

Suluhisho

Pembe$\dfrac{\pi}{2}$ hupatikana kwa kuenea kwa mwelekeo wa kinyume cha mhimili$90°$ kutoka kwa mhimili wa polar. Hatua iko katika urefu wa$3$ vitengo kutoka pole katika$\dfrac{\pi}{2}$ mwelekeo, kama inavyoonekana katika Kielelezo$\PageIndex{3}$.

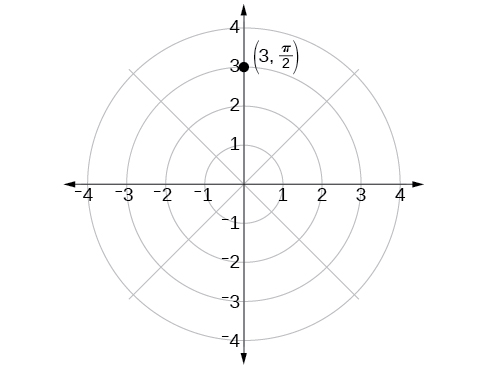
$Gridi ya Polar na uhakika (3, pi/2) walipanga.$

Kielelezo$\PageIndex{3}$

Zoezi$\PageIndex{1}$

Panda hatua$\left(2, \dfrac{\pi}{3}\right)$ katika gridi ya polar.

Jibu

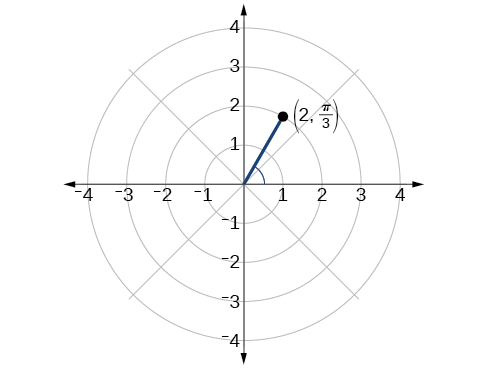
$Gridi ya Polar na uhakika (2, pi/3) walipanga.$

Kielelezo$\PageIndex{4}$

Mfano$\PageIndex{2}$: Plotting a Point in the Polar Coordinate System with a Negative Component

Panda hatua$\left(−2, \dfrac{\pi}{6}\right)$ kwenye gridi ya polar.

Suluhisho

Tunajua kwamba$\dfrac{\pi}{6}$ iko katika roboduara ya kwanza. Hata hivyo,$r=−2$. Tunaweza kukabiliana na kupanga njama kwa hasi$r$ kwa njia mbili:

Panda hatua$\left(2,\dfrac{\pi}{6}\right)$ kwa kuhamia$\dfrac{\pi}{6}$ mwelekeo wa kinyume na kupanua$2$ vitengo vya sehemu ya mstari iliyoelekezwa kwenye quadrant ya kwanza. Kisha retrace sehemu ya mstari iliyoongozwa nyuma kupitia pole, na$2$ uendelee vitengo katika quadrant ya tatu;
Hoja$\dfrac{\pi}{6}$ kwenye mwelekeo wa kinyume chake, na kuteka sehemu iliyoongozwa ya mstari kutoka kwa$2$ vitengo vya pole katika mwelekeo hasi, kwenye quadrant ya tatu.

Angalia Kielelezo$\PageIndex{5a}$. Linganisha hii na grafu ya kuratibu polar$(2,π6)$ inavyoonekana katika Kielelezo$\PageIndex{5b}$.

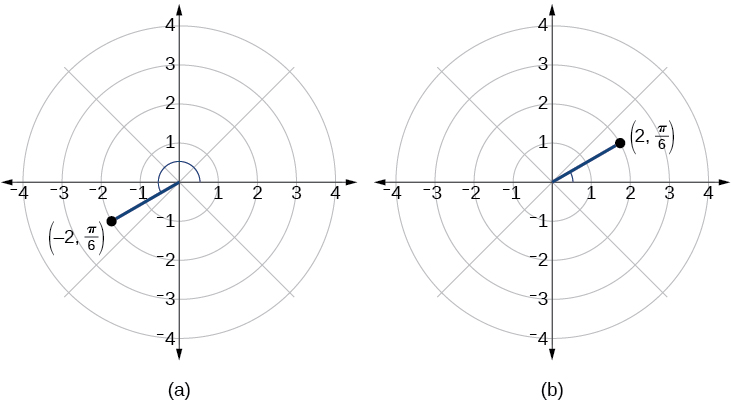
$Gridi mbili za polar. Pointi (2, pi/6) na (-2, pi/6) zimepangwa. Wao ni tafakari katika asili katika Q1 na Q3.$

Kielelezo$\PageIndex{5}$

Zoezi$\PageIndex{2}$

Panda pointi$\left(3,−\dfrac{\pi}{6}\right)$ na$\left(2,\dfrac{9\pi}{4}\right)$ kwenye gridi hiyo ya polar.

Jibu

$Pointi (2, 9pi/4) na (3, -pi/6) hupangwa kwenye gridi ya polar.$

Kielelezo$\PageIndex{6}$

Inabadilisha kutoka kwa Kuratibu za Polar hadi Kuratibu za

Tunapopewa seti ya kuratibu za polar, tunaweza kuhitaji kuzibadilisha kwenye kuratibu za mstatili. Kwa kufanya hivyo, tunaweza kukumbuka mahusiano yaliyopo kati ya vigezo$x$$y$,$r$, na$\theta$.

$\cos \theta=\dfrac{x}{r}\rightarrow x=r \cos \theta$

$\sin \theta=\dfrac{y}{r}\rightarrow y=r \sin \theta$

Kuacha perpendicular kutoka hatua katika ndege hadi x- mhimili huunda pembetatu sahihi, kama ilivyoonyeshwa kwenye Mchoro$\PageIndex{7}$. Njia rahisi ya kukumbuka equations hapo juu ni kufikiria$\cos \theta$ kama upande wa karibu juu ya hypotenuse na$\sin \theta$ kama upande kinyume juu ya hypotenuse.

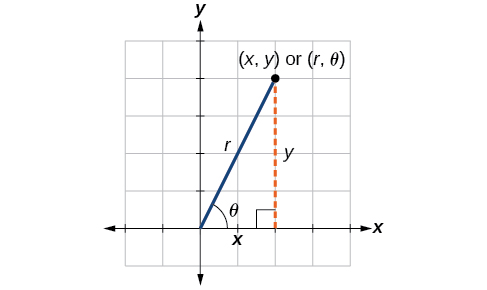
$Kulinganisha kati ya kuratibu polar na kuratibu mstatili. Kuna pembetatu ya kulia iliyopangwa kwenye mhimili wa x, y. Pande ni mstari wa usawa kwenye x-mhimili wa urefu x, mstari wa wima unaoenea kutoka kwa mhimili wa x hadi hatua fulani katika roboduara 1, na hypotenuse r kupanua kutoka asili hadi hatua hiyo katika roboduara 1. Vipeo ni katika asili (0,0), baadhi ya uhakika pamoja x-axis katika (x,0), na hatua hiyo katika roboduara 1. Hatua hii ya mwisho ni (x, y) au (r, theta), kulingana na mfumo gani wa kuratibu unayotumia.$

Kielelezo$\PageIndex{7}$

KUBADILISHA KUTOKA KWA KURATIBU ZA POLAR HADI

Kubadili kuratibu polar$(r, \theta)$ kwa kuratibu mstatili$(x, y)$, basi

\[\cos \theta=\dfrac{x}{r}\rightarrow x=r \cos \theta\]

\[\sin \theta=\dfrac{y}{r}\rightarrow y=r \sin \theta\]

Jinsi ya: Kutokana na kuratibu polar, kubadilisha kwa kuratibu mstatili.

Kutokana na kuratibu polar$(r,\theta)$, kuandika$x=r \cos \theta$ na$y=r \sin \theta$.
Tathmini$\cos \theta$ na$\sin \theta$.
$r$Kuzidisha$\cos \theta$ na kupata$x$ - kuratibu ya fomu ya mstatili.
$r$Kuzidisha$\sin \theta$ na kupata$y$ - kuratibu ya fomu ya mstatili.

Mfano$\PageIndex{3A}$: Writing Polar Coordinates as Rectangular Coordinates

Andika kuratibu za polar$\left(3,\dfrac{\pi}{2}\right)$ kama kuratibu za mstatili.

Suluhisho

Tumia mahusiano sawa.

\[\begin{align*} x&= r \cos \theta\\ x&= 3 \cos \dfrac{\pi}{2}\\ &= 0\\ y&= r \sin \theta\\ y&= 3 \sin \dfrac{\pi}{2}\\ &= 3 \end{align*}\]

Kuratibu mstatili ni$(0,3)$. Angalia Kielelezo$\PageIndex{8}$.

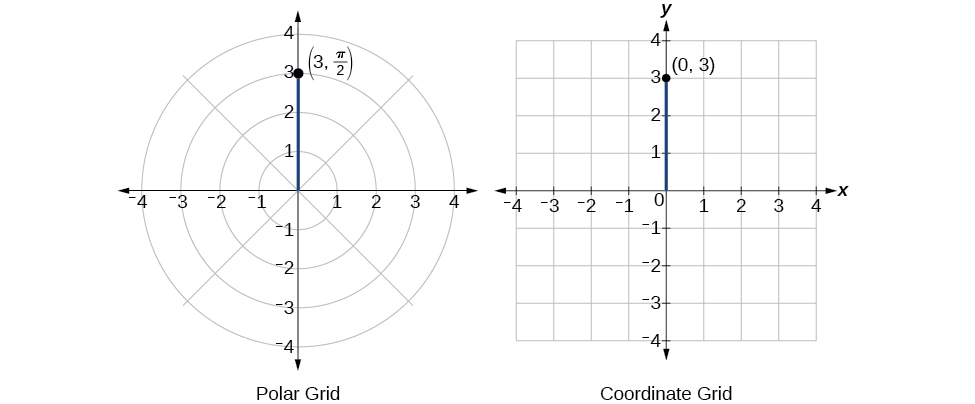
$Mfano wa (3, pi/2) katika kuratibu polar na (0.3) katika kuratibu mstatili - ni hatua sawa!$

Kielelezo$\PageIndex{8}$

Mfano$\PageIndex{3B}$: Writing Polar Coordinates as Rectangular Coordinates

Andika kuratibu za polar$(−2,0)$ kama kuratibu za mstatili.

Suluhisho

Angalia Kielelezo$\PageIndex{9}$. Kuandika kuratibu polar kama mstatili, tuna

\[\begin{align*} x&= r \cos \theta\\ x&= -2 \cos(0)\\ &= -2\\ y&= r \sin \theta\\ y&= -2 \sin(0)\\ &= 0 \end{align*}\]

Kuratibu mstatili pia$(−2,0)$.

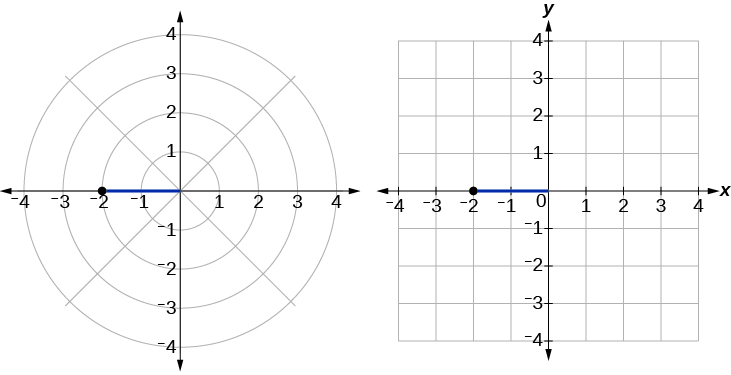
$Mfano wa (-2, 0) katika kuratibu polar na (-2,0) katika kuratibu mstatili - ni hatua sawa!$

Kielelezo$\PageIndex{9}$

Zoezi$\PageIndex{3}$

Andika kuratibu za polar$\left(−1,\dfrac{2\pi}{3}\right)$ kama kuratibu za mstatili.

Jibu: $(x,y)=\left(\dfrac{1}{2},−\dfrac{\sqrt{3}}{2}\right)$

Inabadilisha kutoka Kuratibu za Rectangular hadi Kuratibu

Ili kubadilisha kuratibu mstatili kwa kuratibu polar, tutatumia mahusiano mengine mawili ya kawaida. Kwa uongofu huu, hata hivyo, tunahitaji kuwa na ufahamu kwamba seti ya kuratibu mstatili itatoa zaidi ya hatua moja ya polar.

KUBADILISHA KUTOKA KWA KURATIBU ZA MSTATILI

Kubadilisha kutoka kuratibu mstatili kwa kuratibu polar inahitaji matumizi ya moja au zaidi ya mahusiano yaliyoonyeshwa kwenye Kielelezo$\PageIndex{10}$.

$\cos \theta=\dfrac{x}{r}$au$x=r \cos \theta$

$\sin \theta=\dfrac{y}{r}$au$y=r \sin \theta$

$r^2=x^2+y^2$

$\tan \theta=\dfrac{y}{x}$

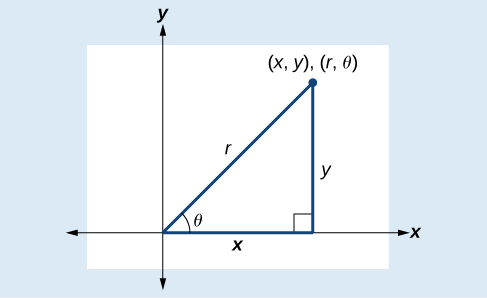
Kielelezo$\PageIndex{10}$

Mfano$\PageIndex{4}$: Writing Rectangular Coordinates as Polar Coordinates

Badilisha kuratibu mstatili$(3,3)$ kwa kuratibu polar.

Suluhisho

Tunaona kwamba hatua ya awali$(3,3)$ iko katika quadrant ya kwanza. Ili kupata$\theta$, tumia formula$\tan \theta=\dfrac{y}{x}$. Hii inatoa

\[\begin{align*} \tan \theta&= \dfrac{3}{3}\\ \tan \theta&= 1\\ {\tan}^{-1}(1)&= \dfrac{\pi}{4} \end{align*}\]

Ili kupata$r$, tunabadilisha maadili$x$ na$y$ katika fomu$r=\sqrt{x^2+y^2}$. Tunajua kwamba$r$ lazima kuwa chanya, kama$\dfrac{\pi}{4}$ ilivyo katika roboduara ya kwanza. Hivyo

\[\begin{align*} r&= \sqrt{3^2+3^2}\\ r&= \sqrt{9+9}\\ r&= \sqrt{18}\\ &= 3\sqrt{2} \end{align*}\]

Kwa hiyo,$r=3\sqrt{2}$ na$\theta=\dfrac{\pi}{4}$, kutupa hatua ya polar$(3\sqrt{2},\dfrac{\pi}{4})$. Angalia Kielelezo$\PageIndex{11}$.

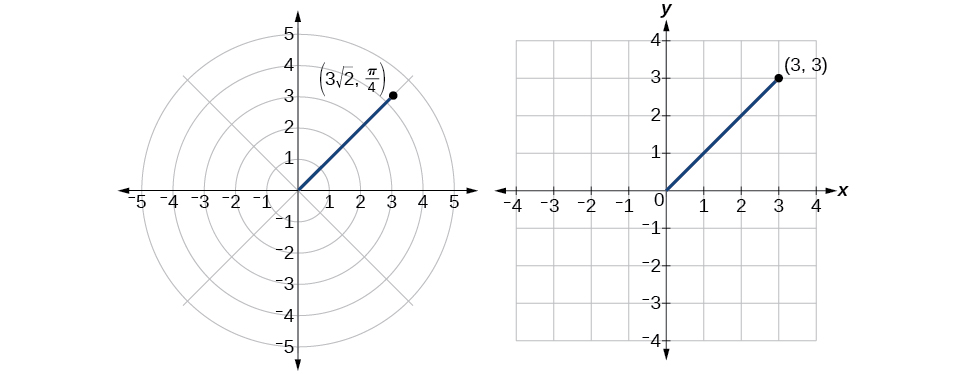
$Mfano wa (3rad2, pi/4) katika kuratibu polar na (3,3) katika kuratibu mstatili - ni hatua sawa!$

Kielelezo$\PageIndex{11}$

Uchambuzi

Kuna seti nyingine za kuratibu polar ambazo zitakuwa sawa na suluhisho letu la kwanza. Kwa mfano, pointi$\left(−3\sqrt{2}, \dfrac{5\pi}{4}\right)$ na$\left(3\sqrt{2},−\dfrac{7\pi}{4}\right)$ itakuwa sanjari na ufumbuzi wa awali wa$\left(3\sqrt{2}, \dfrac{\pi}{4}\right)$. uhakika$\left(−3\sqrt{2}, \dfrac{5\pi}{4}\right)$ inaonyesha hoja zaidi kinyume na$\pi$, ambayo ni moja kwa moja kinyume$\dfrac{\pi}{4}$. Radius inaelezwa kama$−3\sqrt{2}$. Hata hivyo, angle$\dfrac{5\pi}{4}$ iko katika quadrant ya tatu na, kama$r$ ilivyo hasi, tunapanua sehemu ya mstari iliyoongozwa kwa upande mwingine, kwenye quadrant ya kwanza. Hii ni hatua sawa na$\left(3\sqrt{2}, \dfrac{\pi}{4}\right)$. uhakika$\left(3\sqrt{2}, −\dfrac{7\pi}{4}\right)$ ni hoja zaidi clockwise na$−\dfrac{7\pi}{4}$, kutoka$\dfrac{\pi}{4}$. Radi,$3\sqrt{2}$, ni sawa.

Kubadilisha usawa kati ya Fomu za Polar na Rectangular

Sasa tunaweza kubadilisha kuratibu kati ya fomu ya polar na mstatili. Kubadili equations inaweza kuwa ngumu zaidi, lakini inaweza kuwa na manufaa kuwa na uwezo wa kubadilisha kati ya aina mbili. Kwa kuwa kuna idadi ya milinganyo ya polar ambayo haiwezi kuelezwa wazi katika fomu ya Cartesian, na kinyume chake, tunaweza kutumia taratibu sawa tulizotumia kubadili pointi kati ya mifumo ya kuratibu. Tunaweza kisha kutumia calculator graphing kwa grafu ama fomu mstatili au aina polar ya equation.

Jinsi ya: Kutokana na equation katika fomu polar, grafu kwa kutumia calculator graphing

Badilisha MODE kwa POL, anayewakilisha fomu ya polar.
Bonyeza kitufe cha Y = kuleta skrini kuruhusu pembejeo ya milinganyo sita:$r_1$,$r_2$,...,$r_6$.
Ingiza equation polar, kuweka sawa na$r$.
Bonyeza GRAPH.

Mfano$\PageIndex{5A}$: Writing a Cartesian Equation in Polar Form

Andika equation ya Cartesian$x^2+y^2=9$ katika fomu ya polar.

Suluhisho

Lengo ni kuondoa$x$ na$y$ kutoka equation na kuanzisha$r$ na$\theta$. Kimsingi, tunataka kuandika equation$r$ kama kazi ya$\theta$. Ili kupata fomu ya polar, tutatumia uhusiano kati$(x,y)$ na$(r,\theta)$. Tangu$x=r \cos \theta$ na$y=r \sin \theta$, tunaweza mbadala na kutatua kwa$r$.

$\begin{align*} {(r \cos \theta)}^2+{(r \sin \theta)}^2&= 9\\ r^2 {\cos}^2 \theta+r^2 {\sin}^2 \theta&= 9\\ r^2({\cos}^2 \theta+{\sin}^2 \theta)&= 9\\ r^2(1)&= 9\qquad \text {Substitute } {\cos}^2 \theta+{\sin}^2 \theta=1\\ r&= \pm 3\qquad \text {Use the square root property.} \end{align*}$

Hivyo,$x^2+y^2=9$,$r=3$, na$r=−3$ inapaswa kuzalisha grafu sawa. Angalia Kielelezo$\PageIndex{12}$.

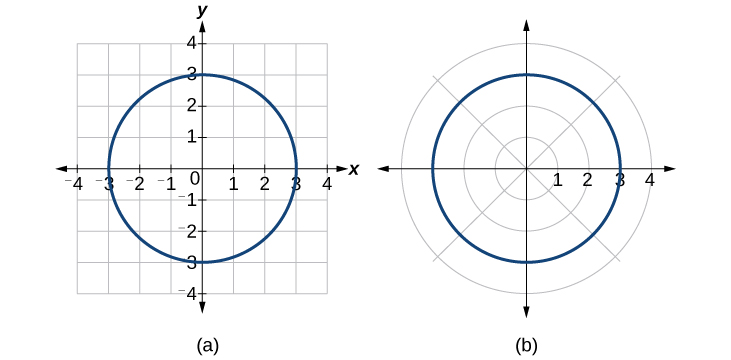
$Kupanga mzunguko wa radius 3 na kituo cha asili katika kuratibu polar na mstatili. Ni sawa katika mifumo yote miwili.$

Kielelezo$\PageIndex{12}$: (a) fomu ya Cartesian$x^2+y^2=9$ (b) Fomu ya Polar$r=3$

Ili kuchora mduara katika fomu ya mstatili, lazima kwanza tufute$y$.

\[\begin{align*} x^2+y^2&= 9\\ y^2&= 9-x^2\\ y&= \pm \sqrt{9-x^2} \end{align*}\]

Kumbuka kuwa hii ni kazi mbili tofauti, kwani mduara unashindwa mtihani wa mstari wa wima. Kwa hiyo, tunahitaji kuingia mizizi nzuri na hasi ya mraba ndani ya calculator tofauti, kama equations mbili katika fomu$Y_1=\sqrt{9−x^2}$ na$Y_2=−\sqrt{9−x^2}$. Bonyeza GRAPH.

Mfano$\PageIndex{5B}$: Rewriting a Cartesian Equation as a Polar Equation

Andika upya equation Cartesian$x^2+y^2=6y$ kama equation Polar.

Suluhisho

Equation hii inaonekana sawa na mfano uliopita, lakini inahitaji hatua tofauti kubadilisha equation.

Bado tunaweza kufuata taratibu hizo ambazo tayari tumejifunza na kufanya mbadala zifuatazo:

$\begin{array}{ll} r^2=6y & \text{Use }x^2+y^2=r^2. \\ r^2=6r \sin \theta & \text{Substitute }y=r \sin \theta. \\ r^2−6r \sin \theta=0 & \text{Set equal to }0. \\ r(r−6 \sin \theta)=0 & \text{Factor and solve.} \\ r=0 & \text{We reject }r=0 \text{, as it only represents one point, }(0,0). \\ \text{or }r=6 \sin \theta \end{array}$

Kwa hiyo, equations$x^2+y^2=6y$ na$r=6 \sin \theta$ inapaswa kutupa grafu hiyo. Angalia Kielelezo$\PageIndex{13}$.

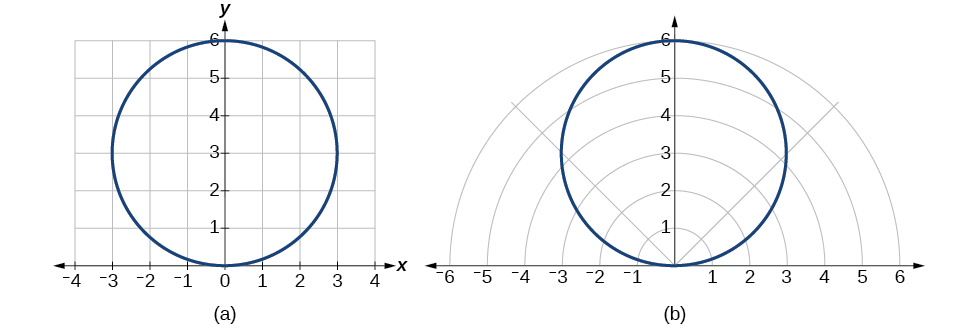
$Viwanja vya equations zilizotajwa hapo juu - viwanja ni sawa katika kuratibu zote za mstatili na polar. Wao ni miduara.$

Kielelezo$\PageIndex{13}$: (a) fomu ya Cartesian$x^2+y^2=6y$ (b) fomu ya polar$r=6 \sin \theta$

Equation ya Cartesian au mstatili imepangwa kwenye gridi ya mstatili, na equation ya polar imepangwa kwenye gridi ya polar. Kwa wazi, grafu zinafanana.

Zoezi$\PageIndex{4A}$:

Kuandika upya Equation ya Cartesian katika Fomu ya Polar

Andika upya equation Cartesian$y=3x+2$ kama equation Polar.

Jibu

Tutatumia mahusiano$x=r \cos \theta$ na$y=r \sin \theta$.

$\begin{array}{cl} y=3x+2 \\ r \sin \theta=3r \cos \theta+2 \\ r \sin \theta−3r \cos \theta=2 \\ r(\sin \theta−3 \cos \theta)=2 & \text{Isolate }r. \\ r=2 \sin \theta−3\cos \theta & \text{Solve for }r. \end{array}$

Zoezi$\PageIndex{4B}$:

Andika upya equation ya Cartesian$y^2=3−x^2$ katika fomu ya polar.

Jibu: $r=\sqrt{3}$

Kutambua na Grafu Ulinganisho wa Polar kwa Kubadilisha kwa Equations Rectangular

Tumejifunza jinsi ya kubadilisha kuratibu mstatili kwa kuratibu polar, na tumeona kwamba pointi ni kweli sawa. Pia tumebadilisha milinganyo ya polar kwa equations mstatili na kinyume chake. Sasa tutaonyesha kwamba grafu zao, wakati zinazotolewa kwenye gridi tofauti, zinafanana.

Mfano$\PageIndex{6A}$: Graphing a Polar Equation by Converting to a Rectangular Equation

Funika equation ya polar$r=2 \sec \theta$ kwa equation mstatili, na kuteka grafu yake sambamba.

Suluhisho

uongofu ni

\[\begin{align*} r &=2 \sec \theta \\ r &= \dfrac{2}{\cos \theta} \\ r \cos \theta &=2 \\ x &=2 \end{align*}\]

Kumbuka kwamba equation$r=2 \sec \theta$ inayotolewa kwenye gridi ya polar ni wazi sawa na mstari wima$x=2$ inayotolewa kwenye gridi ya mstatili (angalia Kielelezo$\PageIndex{14}$). Kama$x=c$ ilivyo fomu ya kawaida ya mstari wa wima katika fomu ya mstatili,$r=c \sec \theta$ ni fomu ya kawaida ya mstari wa wima katika fomu ya polar.

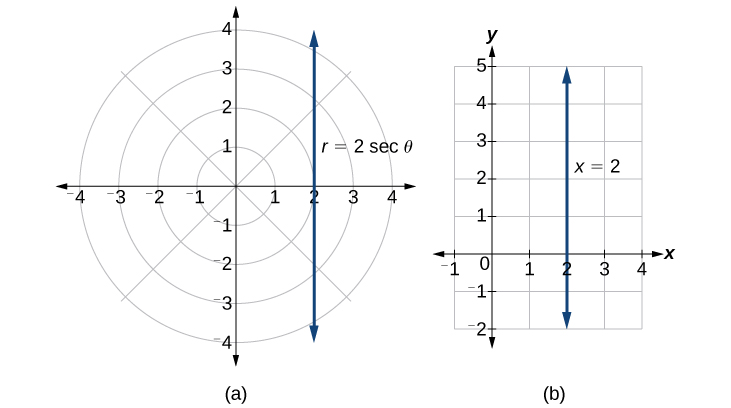
$Viwanja vya equations zilizotajwa hapo juu - viwanja ni sawa katika kuratibu zote za mstatili na polar. Wao ni mistari.$

Kielelezo$\PageIndex{14}$: (a) Gridi ya Polar (b) Mfumo wa kuratibu wa mstatili

Majadiliano kama hayo yataonyesha kwamba grafu ya kazi$r=2 \csc \theta$ itakuwa mstari wa usawa$y=2$. Kwa kweli,$r=c \csc \theta$ ni fomu ya kawaida ya mstari wa usawa katika fomu ya polar, sambamba na fomu ya mstatili$y=c$.

Mfano$\PageIndex{6B}$: Rewriting a Polar Equation in Cartesian Form

Andika upya equation Polar$r=\dfrac{3}{1−2 \cos \theta}$ kama equation Cartesian.

Suluhisho

Lengo ni kuondoa$\theta$ na$r$, na kuanzisha$x$ na$y$. Sisi wazi sehemu, na kisha kutumia badala. Ili kuchukua nafasi$r$$x$ na$y$, tunapaswa kutumia maneno$x^2+y^2=r^2$.

$\begin{array} r =\dfrac{3}{1−2 \cos \theta} \\ r(1−2 \cos \theta)=3 \\ r\left(1−2\left(\dfrac{x}{r}\right)\right)=3 & \text{Use }\cos \theta=\dfrac{x}{r} \text{ to eliminate }\theta. \\ r−2x=3 \\ r=3+2x & \text{Isolate }r. \\ r^2={(3+2x)}^2 & \text{Square both sides.} \\ x^2+y^2={(3+2x)}^2 & \text{Use }x^2+y^2=r^2. \end{array}$

equation Cartesian ni$x^2+y^2={(3+2x)}^2$. Hata hivyo, kwa grafu, hasa kwa kutumia calculator graphing au programu ya kompyuta, tunataka kujitenga$y$.

\[\begin{align*} x^2+y^2 &= {(3+2x)}^2 \\ y^2 &= {(3+2x)}^2-x^2 \\ y &= \pm {(3+2x)}^2-x^2 \end{align*}\]

Wakati equation yetu yote imebadilishwa kutoka$r$ na$\theta$ kwenda$x$ na$y$, tunaweza kuacha, isipokuwa aliuliza kutatua$y$ au kurahisisha. Angalia Kielelezo$\PageIndex{15}$.

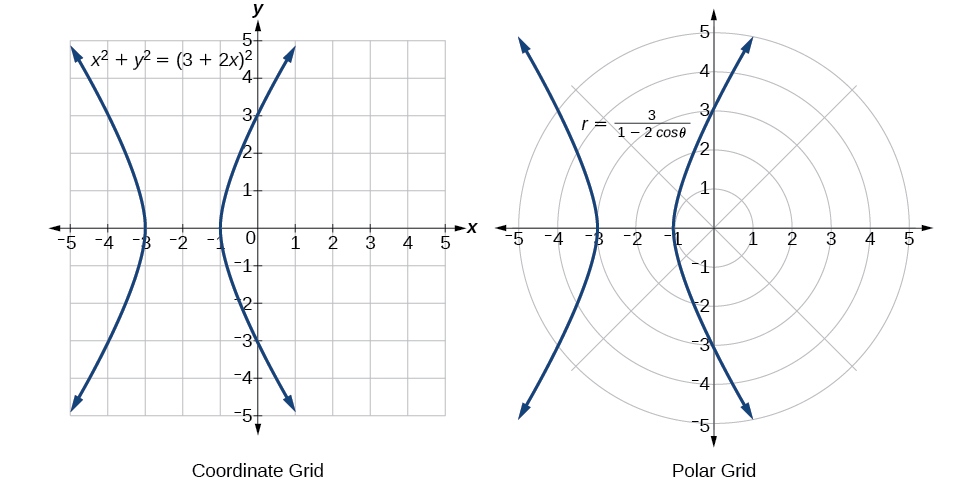
$Viwanja vya equations zilizotajwa hapo juu - viwanja ni sawa katika kuratibu zote za mstatili na polar. Wao ni hyperbolas.$

Kielelezo$\PageIndex{15}$

Sura ya “kioo cha saa” ya grafu inaitwa hyperbola. Hyperbolas zina sifa nyingi za kijiometri na programu, ambazo tutachunguza zaidi katika Jiometri ya Analytic.

Uchambuzi

Katika mfano huu, upande wa kulia wa equation unaweza kupanuliwa na equation rahisi zaidi, kama inavyoonekana hapo juu. Hata hivyo, equation haiwezi kuandikwa kama kazi moja katika fomu ya Cartesian. Tunaweza kutaka kuandika equation mstatili katika fomu ya kawaida ya hyperbola. Ili kufanya hivyo, tunaweza kuanza na equation ya awali.

$\begin{array}{ll} x^2+y^2={(3+2x)}^2 \\ x^2+y^2−{(3+2x)}^2=0 \\ x^2+y^2−(9+12x+4x^2)=0 \\ x^2+y^2−9−12x−4x^2=0 \\ −3x^2−12x+y^2=9 & \text{Multiply through by }−1. \\ 3x^2+12x−y^2=−9 \\ 3(x^2+4x)−y2=−9 & \text{Organize terms to complete the square for }x. \\ 3(x^2+4x+4)−y^2=−9+12 \\ 3{(x+2)}^2−y^2=3 \\ {(x+2)}^2−\dfrac{y^2}{3}=1\end{array}$

Zoezi$\PageIndex{5}$

Andika upya equation ya polar$r=2 \sin \theta$ katika fomu ya Cartesian.

Jibu: $x^2+y^2=2y$au, kwa fomu ya kawaida ya mduara,$x^2+{(y−1)}^2=1$

Mfano$\PageIndex{7}$: Rewriting a Polar Equation in Cartesian Form

Andika upya equation ya polar$r=\sin(2\theta)$ katika fomu ya Cartesian.

Suluhisho

$\begin{array}{cl} r=\sin(2\theta) & \text{Use the double angle identity for sine.} \\ r=2 \sin \theta \cos \theta & \text{Use }\cos \theta=\dfrac{x}{r} \text{ and } \sin \theta=\dfrac{y}{r}. \\ r=2 \dfrac{x}{r})(\dfrac{y}{r}) & \text{ Simplify.} \\ r=\dfrac{2xy}{r^2} & \text{Multiply both sides by }r^2. \\ r^3=2xy \\ {(x^2+y^2)}^3=2xy & \text{As }x^2+y^2=r^2, r=\sqrt{x^2+y^2}. \end{array}$

Equation hii pia inaweza kuandikwa kama

${(x^2+y^2)}^{\frac{3}{2}}=2xy \text{ or }x^2+y^2={(2xy)}^{\frac{2}{3}}$

Media

Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na kuratibu za polar.

Mlinganyo muhimu

Fomu za uongofu

$\cos \theta=\dfrac{x}{r} \rightarrow x=r \cos\theta$

$\sin \theta=\dfrac{y}{r} \rightarrow y=r \sin \theta$

$r^2=x^2+y^2$

$\tan \theta=\dfrac{y}{x}$

Dhana muhimu

Gridi ya polar inawakilishwa kama mfululizo wa miduara ya makini inayotoka nje ya pole, au asili.
Kwa njama uhakika katika fomu$(r,\theta)$$\theta>0$, hoja katika mwelekeo kinyume na mzunguko kutoka mhimili polar kwa angle ya$\theta$, na kisha kupanua moja kwa moja line sehemu kutoka pole urefu wa$r$ katika mwelekeo wa$\theta$. Kama$\theta$ ni hasi, hoja katika mwelekeo clockwise, na kupanua moja kwa moja line sehemu urefu wa$r$ katika mwelekeo wa$\theta$. Angalia Mfano$\PageIndex{1}$.
Kama$r$ ni hasi, kupanua moja kwa moja line sehemu katika mwelekeo kinyume cha$\theta$. Angalia Mfano$\PageIndex{2}$.
Ili kubadilisha kutoka kwa kuratibu za polar hadi kuratibu za mstatili, tumia fomu$x=r \cos \theta$ na$y=r \sin \theta$. Angalia Mfano$\PageIndex{3}$ na Mfano$\PageIndex{4}$.
Ili kubadilisha kutoka kuratibu mstatili kwa kuratibu polar, tumia moja au zaidi ya formula:$\cos \theta=\dfrac{x}{r}$$\sin \theta=\dfrac{y}{r}$,$\tan \theta=\dfrac{y}{x}$,, na$r=\sqrt{x^2+y^2}$. Angalia Mfano$\PageIndex{5}$.
Kubadilisha equations kati ya aina polar na mstatili ina maana ya kufanya mbadala sahihi kulingana na formula zilizopo, pamoja na manipulations algebraic. Angalia Mfano$\PageIndex{6}$, Mfano$\PageIndex{7}$, na Mfano$\PageIndex{8}$.
Kutumia mbadala zinazofaa hufanya iwezekanavyo kuandika upya equation ya polar kama equation ya mstatili, na kisha kuiweka kwenye ndege ya mstatili. Angalia Mfano$\PageIndex{9}$, Mfano$\PageIndex{10}$, na Mfano$\PageIndex{11}$.

Mfano\(\PageIndex{1}\): Plotting a Point on the Polar Grid

Zoezi\(\PageIndex{1}\)

Mfano\(\PageIndex{2}\): Plotting a Point in the Polar Coordinate System with a Negative Component

Zoezi\(\PageIndex{2}\)

KUBADILISHA KUTOKA KWA KURATIBU ZA POLAR HADI

Jinsi ya: Kutokana na kuratibu polar, kubadilisha kwa kuratibu mstatili.

Mfano\(\PageIndex{3A}\): Writing Polar Coordinates as Rectangular Coordinates

Mfano\(\PageIndex{3B}\): Writing Polar Coordinates as Rectangular Coordinates

Zoezi\(\PageIndex{3}\)

KUBADILISHA KUTOKA KWA KURATIBU ZA MSTATILI

Mfano\(\PageIndex{4}\): Writing Rectangular Coordinates as Polar Coordinates

Jinsi ya: Kutokana na equation katika fomu polar, grafu kwa kutumia calculator graphing

Mfano\(\PageIndex{5A}\): Writing a Cartesian Equation in Polar Form

Mfano\(\PageIndex{5B}\): Rewriting a Cartesian Equation as a Polar Equation

Zoezi\(\PageIndex{4A}\):

Zoezi\(\PageIndex{4B}\):

Mfano\(\PageIndex{6A}\): Graphing a Polar Equation by Converting to a Rectangular Equation

Mfano\(\PageIndex{6B}\): Rewriting a Polar Equation in Cartesian Form

Zoezi\(\PageIndex{5}\)

Mfano\(\PageIndex{7}\): Rewriting a Polar Equation in Cartesian Form