10.2: Pembetatu zisizo za haki - Sheria ya Cosines
- Page ID
- 178433
Katika sehemu hii, utakuwa:
- Tumia Sheria ya Cosines kutatua pembetatu za oblique.
- Tatua matatizo yaliyotumika kwa kutumia Sheria ya Cosines.
- Tumia formula ya Heron ili kupata eneo la pembetatu.
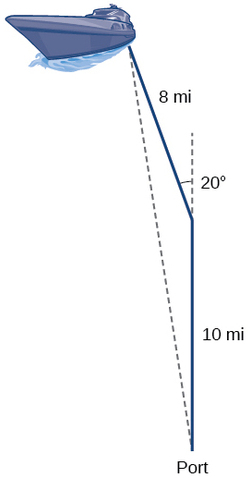
Tuseme mashua majani bandari, husafiri\(10\) maili, zamu\(20\) digrii, na husafiri mwingine 8 maili kama inavyoonekana katika Kielelezo\(\PageIndex{1}\) Jinsi mbali na bandari ni mashua?
Kielelezo\(\PageIndex{1}\)
Kwa bahati mbaya, wakati Sheria ya Sines inatuwezesha kushughulikia kesi nyingi zisizo za kulia za pembetatu, haitusaidia na pembetatu ambapo angle inayojulikana iko kati ya pande mbili zinazojulikana, pembetatu ya SAS (upande wa angle-upande), au wakati pande zote tatu zinajulikana, pembetatu ya SSS (upande wa upande wa upande). Katika sehemu hii, tutachunguza chombo kingine cha kutatua pembetatu za oblique zilizoelezwa na kesi hizi mbili za mwisho.
Kutumia Sheria ya Cosines kutatua Pembetatu za Olique
Chombo tunachohitaji kutatua tatizo la umbali wa mashua kutoka bandari ni Sheria ya Cosines, ambayo inafafanua uhusiano kati ya vipimo vya angle na urefu wa upande katika pembetatu za oblique. Fomu tatu hufanya Sheria ya Cosines. Kwa mtazamo wa kwanza, kanuni zinaweza kuonekana ngumu kwa sababu zinajumuisha vigezo vingi. Hata hivyo, mara tu mfano unaeleweka, Sheria ya Cosines ni rahisi kufanya kazi na kuliko kanuni nyingi katika ngazi hii ya hisabati.
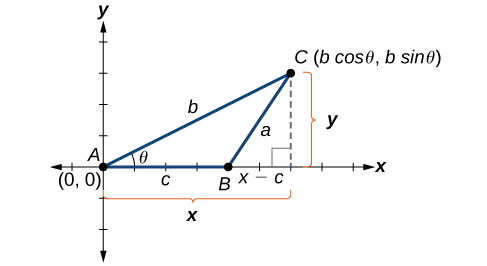
Kuelewa jinsi Sheria ya Cosines inavyotokana itakuwa na manufaa katika kutumia formula. Derivation huanza na Theorem ya jumla ya Pythagorean, ambayo ni ugani wa Theorem ya Pythagorean kwa pembetatu zisizo sahihi. Hapa ni jinsi inavyofanya kazi: holela zisizo haki pembetatu\(ABC\) ni kuwekwa katika kuratibu ndege na kipeo\(A\) katika asili, upande\(c\) inayotolewa pamoja x -axis, na kipeo\(C\) iko katika baadhi ya hatua\((x,y)\) katika ndege, kama inavyoonekana katika Kielelezo\(\PageIndex{2}\). Kwa ujumla, pembetatu zipo popote kwenye ndege, lakini kwa maelezo haya tutaweka pembetatu kama ilivyoelezwa.
Kielelezo\(\PageIndex{2}\)
Tunaweza kuacha perpendicular kutoka\(C\) kwa x- axis (hii ni urefu au urefu). Akikumbuka utambulisho wa msingi wa trigonometric, tunajua kwamba
\(\cos \theta=\dfrac{x(adjacent)}{b(hypotenuse)}\)na\(\sin \theta=\dfrac{y(opposite)}{b(hypotenuse)}\)
Kwa upande wa\(\theta\),\(x=b \cos \theta\) na\(y=b \sin \theta\). \((x,y)\)Hatua iko katika\(C\) ina kuratibu\((b \cos \theta, b \sin \theta)\). Kutumia upande\((x−c)\) kama mguu mmoja wa pembetatu ya kulia na\(y\) kama mguu wa pili, tunaweza kupata urefu wa hypotenuse\(a\) kwa kutumia Theorem ya Pythagorean. Hivyo,
\ (\ kuanza {safu} {ll} a^2= {(x-c)} ^2+y ^ 2\\ [4pt]\;\;\;\;\; = {(b\ cos\ theta-c)} ^2+ {(b\ dhambi\ theta)} ^2 &\ maandishi {mbadala} (b\ cos\ theta)\ maandishi {kwa} x\ maandishi {na} (b\ dhambi\ theta)\ maandishi {kwa} y\\ [4pt]\;\;\;\;\;\;\; = (b ^ 2 {\ cos} ^2\ theta-2bc\ cos\ theta+c ^ 2) +b ^ 2 {\ dhambi} ^2\ theta &\ maandishi {Panua kamili mraba.}\\ [4pt]\;\;\;\; = b ^ 2 {\ cos} ^2\ theta+b ^ 2 {\ dhambi} ^2\ theta+c ^ 218-2bc\ cos\ theta &\ maandishi {Masharti ya kikundi akibainisha kuwa} {\ cos} ^2\ theta+ {\ dhambi} ^2\ theta = 1\\ [4pt]\;\;\;\;\; = b ^ 2 ({\ cos} ^2\ theta+ {\ dhambi} ^2\ theta) +c ^ 2,12bc\ cos\ theta &\ maandishi {Factor nje} b ^ 2\\ [4pt] a
^ 2=b ^ 2+c ^ 2,12bc\ cos\ theta \ mwisho {safu}\)
Fomu inayotokana ni moja ya milinganyo mitatu ya Sheria ya Cosines. Equations nyingine hupatikana kwa mtindo sawa.
Kumbuka kwamba daima ni muhimu kwa mchoro pembetatu wakati wa kutatua kwa pembe au pande. Katika hali halisi ya ulimwengu, jaribu kuteka mchoro wa hali hiyo. Kama habari zaidi inajitokeza, mchoro unaweza kubadilishwa. Fanya mabadiliko hayo kwenye mchoro na, mwishoni, tatizo litakuwa rahisi kutatua.
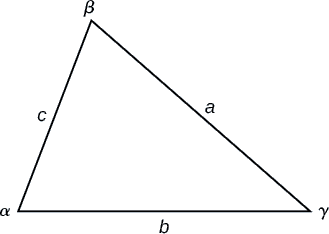
Sheria ya Cosines inasema kwamba mraba wa upande wowote wa pembetatu ni sawa na jumla ya mraba wa pande nyingine mbili bala mara mbili bidhaa za pande nyingine mbili na cosine ya angle iliyojumuishwa.
Kielelezo\(\PageIndex{3}\)
Kwa pembetatu kinachoitwa kama katika Kielelezo\(\PageIndex{3}\), na pembe\(\alpha\),\(\beta\) na\(\gamma\), na kinyume pande sambamba\(a\)\(b\),, na\(c\), kwa mtiririko huo, Sheria ya Cosines inapewa kama equations tatu.
\[a^2=b^2+c^2−2bc \cos \alpha\]
\[b^2=a^2+c^2−2ac \cos \beta\]
\[c^2=a^2+b^2−2ab \cos \gamma\]
Ili kutatua kwa kipimo cha upande usiopotea, kipimo cha kinyume cha angle kinachohitajika kinahitajika.
Wakati wa kutatua kwa angle, kipimo cha upande kinyume kinachohitajika kinahitajika. Tunaweza kutumia toleo jingine la Sheria ya Cosines kutatua kwa angle.
\[\cos \alpha=\dfrac{b^2+c^2−a^2}{2bc}\]
\[\cos \beta=\dfrac{a^2+c^2−b^2}{2ac}\]
\[\cos \gamma=\dfrac{a^2+b^2−c^2}{2ab}\]
- Mchoro pembetatu. Tambua hatua za pande na pembe zinazojulikana. Tumia vigezo kuwakilisha hatua za pande zisizojulikana na pembe.
- Tumia Sheria ya Cosines ili kupata urefu wa upande usiojulikana au angle.
- Tumia Sheria ya Sines au Cosines ili kupata kipimo cha pembe ya pili.
- Futa kipimo cha angle iliyobaki.
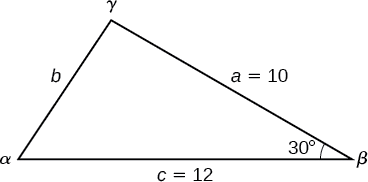
Kupata upande haijulikani na pembe ya pembetatu katika Kielelezo\(\PageIndex{4}\).
Kielelezo\(\PageIndex{4}\)
Suluhisho
Kwanza, tambua kile kinachopewa: pande mbili na angle kati yao. Mpangilio huu umewekwa kama SAS na hutoa data zinazohitajika ili kuomba Sheria ya Cosines.
Kila moja ya sheria tatu za cosines huanza na mraba wa upande usiojulikana kinyume na angle inayojulikana. Kwa mfano huu, upande wa kwanza wa kutatua ni upande\(b\), kama tunavyojua kipimo cha angle kinyume\(\beta\).
\(\begin{array}{ll} b^2=a^2+c^2−2ac \cos \beta \\[4pt] b^2={10}^2+{12}^2−2(10)(12)\cos(30°) & \text{Substitute the measurements for the known quantities.} \\[4pt] b^2=100+144−240 \left(\dfrac{\sqrt{3}}{2}\right) & \text{Evaluate the cosine and begin to simplify.} \\[4pt] b^2=244−120\sqrt{3} \\[4pt] b=\sqrt{244−120\sqrt{3}} & \text{Use the square root property.} \\[4pt] b≈6.013 \end{array}\)
Kwa sababu tunatatua kwa urefu, tunatumia tu mizizi nzuri ya mraba. Sasa kwa kuwa tunajua urefu\(b\), tunaweza kutumia Sheria ya Sines kujaza pembe zilizobaki za pembetatu. Kutatua kwa angle\(\alpha\), tuna
\(\begin{array}{cc} \dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b} \\[4pt] \dfrac{\sin \alpha}{10}=\dfrac{\sin(30°)}{6.013} \\[4pt] \sin \alpha=\dfrac{10\sin(30°)}{6.013} & \text{Multiply both sides of the equation by }10. \\[4pt] \alpha={\sin}^{−1}\left(\dfrac{10\sin(30°)}{6.013}\right) & \text{Find the inverse sine of } \dfrac{10\sin(30°)}{6.013}. \\[4pt] \alpha≈56.3° \end{array}\)
uwezekano mwingine kwa ajili ya\(\alpha\) itakuwa\(\alpha=180°-56.3°≈123.7°\). Katika mchoro wa awali,\(\alpha\) ni karibu na upande mrefu zaidi, hivyo\(\alpha\) ni angle ya papo hapo na, kwa hiyo,\(123.7°\) haina maana. Kumbuka kwamba ikiwa tunachagua kutumia Sheria ya Cosines, tunawasili jibu la pekee. Hatuna kuzingatia uwezekano mwingine, kama cosine ni ya kipekee kwa pembe kati\(0°\) na\(180°\). Kuendelea na\(\alpha≈56.3°\), tunaweza kisha kupata angle ya tatu ya pembetatu.
\[\begin{align*} \gamma&= 180^{\circ}-30^{\circ}-56.3^{\circ}\\ &\approx 93.7^{\circ} \end{align*}\]
Seti kamili ya pembe na pande ni
\(\alpha≈56.3°\)\(a=10\)
\(\beta=30°\)\(b≈6.013\)
\(\gamma≈93.7°\)\(c=12\)
Pata upande usiopotea na pembe za pembetatu iliyotolewa:\(\alpha=30°\),\(b=12\),\(c=24\).
- Jibu
-
\(a≈14.9\),\(\beta≈23.8°\),\(\gamma≈126.2°\).
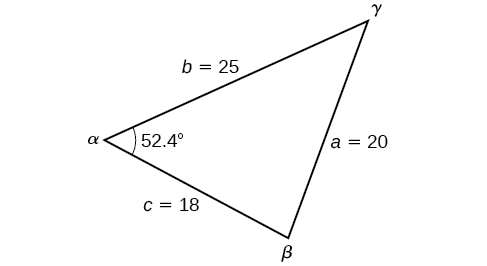
Pata angle\(\alpha\) kwa pembetatu iliyotolewa ikiwa upande\(a=20\), upande\(b=25\), na upande\(c=18\).
Suluhisho
Kwa mfano huu, hatuna pembe. Tunaweza kutatua kwa pembe yoyote kwa kutumia Sheria ya Cosines. Ili kutatua kwa angle\(\alpha\), tuna
\(\begin{array}{ll} a^2=b^2+c^2−2bc \cos \alpha \\[4pt] {20}^2={25}^2+{18}^2−2(25)(18)\cos \alpha & \text{Substitute the appropriate measurements.} \\[4pt] 400=625+324−900 \cos \alpha & \text{ Simplify in each step.} \\[4pt] 400=949−900 \cos \alpha \\[4pt] −549=−900 \cos \alpha & \text{Isolate }\cos \alpha. \\[4pt] 0.61≈\cos \alpha & \text{Find the inverse cosine.} \\[4pt] \alpha≈52.4° \end{array}\)
Angalia Kielelezo\(\PageIndex{5}\).
Kielelezo\(\PageIndex{5}\)
Uchambuzi
Kwa sababu cosine inverse inaweza kurudi angle yoyote kati\(0\) na\(180\) digrii, hakutakuwa na matukio yoyote yasiyofaa kwa kutumia njia hii.
Kutokana\(a=5\),\(b=7\), na\(c=10\), kupata pembe kukosa.
- Jibu
-
\(\alpha≈27.7°\),\(\beta≈40.5°\),\(\gamma≈111.8°\)
Kutatua Matatizo yaliyotumika Kutumia Sheria ya Cosines
Kama vile Sheria ya Sines ilitoa equations sahihi kutatua idadi ya maombi, Sheria ya Cosines inatumika kwa hali ambazo data iliyotolewa inafaa mifano ya cosine. Tunaweza kuona haya katika nyanja za urambazaji, uchunguzi, astronomia, na jiometri, kwa jina chache tu.
Kwa simu nyingi za mkononi na GPS, eneo la takriban linaweza kutolewa kabla ya ishara ya GPS inapokelewa. Hii inafanywa kupitia mchakato unaoitwa triangulation, ambayo inafanya kazi kwa kutumia umbali kutoka pointi mbili zinazojulikana. Tuseme kuna mbili minara ya simu ya mkononi ndani ya aina mbalimbali ya simu ya mkononi. Minara miwili iko\(6000\) miguu mbali kando ya barabara kuu moja kwa moja, inayoendesha mashariki hadi magharibi, na simu ya mkononi iko kaskazini mwa barabara kuu. Kulingana na kuchelewa kwa ishara, inaweza kuamua kuwa ishara ni\(5050\) miguu kutoka mnara wa kwanza na\(2420\) miguu kutoka mnara wa pili. Kuamua nafasi ya simu ya mkononi kaskazini na mashariki ya mnara wa kwanza, na kuamua jinsi mbali na barabara kuu.
Suluhisho
Kwa unyenyekevu, tunaanza kwa kuchora mchoro sawa\(\PageIndex{6}\) na Kielelezo na kuandika maelezo yetu yaliyotolewa.
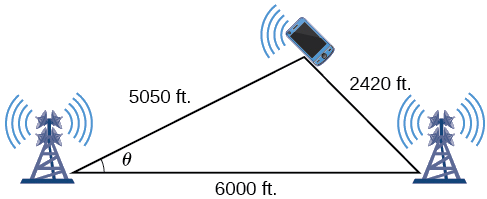
Kielelezo\(\PageIndex{6}\)
Kutumia Sheria ya Cosines, tunaweza kutatua kwa angle\(\theta\). Kumbuka kwamba Sheria ya Cosines inatumia mraba wa upande mmoja ili kupata cosine ya angle kinyume. Kwa mfano huu, basi\(a=2420\),\(b=5050\), na\(c=6000\). Hivyo,\(\theta\) inafanana na upande wa pili\(a=2420\).
\[\begin{align*} a^2 & =b^2+c^2−2bc \cos \theta \\[4pt] {(2420)}^2 &={(5050)}^2+{(6000)}^2−2(5050)(6000) \cos \theta \\[4pt] \cos \theta &≈ 0.9183 \\[4pt] \theta &≈ {\cos}^{−1}(0.9183) \\[4pt] \theta &≈ 23.3° \end{align*}\]
Ili kujibu maswali kuhusu msimamo wa simu kaskazini na mashariki ya mnara, na umbali wa barabara kuu, tone perpendicular kutoka nafasi ya simu ya mkononi, kama katika Kielelezo\(\PageIndex{7}\). Hii inaunda pembetatu mbili za kulia, ingawa tunahitaji tu pembetatu sahihi inayojumuisha mnara wa kwanza kwa tatizo hili.
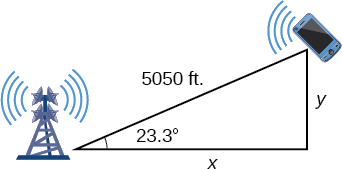
Kielelezo\(\PageIndex{7}\)
Kutumia angle\(\theta=23.3\)° na utambulisho wa msingi wa trigonometric, tunaweza kupata ufumbuzi. Hivyo
\[\begin{align*} \cos(23.3°) &= \dfrac{x}{5050} \\[4pt] x &= 5050\cos(23.3°) \\[4pt] x &≈ 4638.15\, feet\\[4pt] \sin(23.3°) &= \dfrac{y}{5050} \\[4pt] y &= 5050\sin(23.3°) \\[4pt] y &≈1997.5 \, feet \end{align*}\]
Simu ya mkononi ni takriban\(4638\) miguu mashariki na\(1998\) miguu kaskazini ya mnara wa kwanza, na\(1998\) miguu kutoka barabara kuu.
Kurudi tatizo letu mwanzoni mwa sehemu hii, tuseme mashua majani bandari, husafiri\(10\) maili, zamu\(20\) digrii, na husafiri\(8\) maili nyingine. Jinsi mbali na bandari ni mashua? Mchoro unarudiwa hapa kwenye Kielelezo\(\PageIndex{8}\).
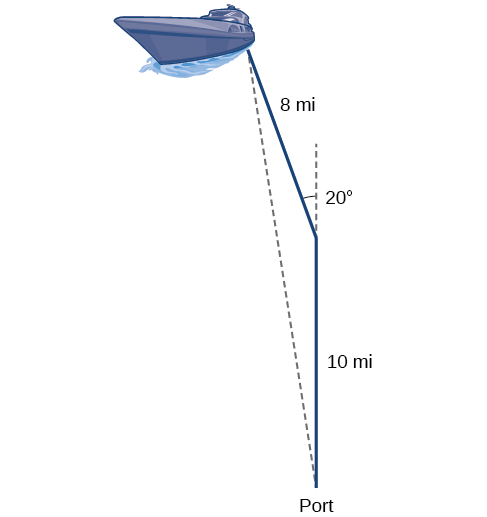
Kielelezo\(\PageIndex{8}\)
Suluhisho
Mashua akageuka digrii 20, hivyo angle obtuse ya pembetatu isiyo ya kulia ni angle ya ziada,\(180°−20°=160°\). Kwa hili, tunaweza kutumia Sheria ya Cosines kupata upande kukosa ya pembetatu obtuse - umbali wa mashua hadi bandari.
\[\begin{align*} x^2 &= 8^2+{10}^2−2(8)(10)\cos(160°) \\[4pt] x^2 &= 314.35 \\[4pt] x &= \sqrt{314.35} \\[4pt] x&≈17.7\, miles \end{align*}\]
mashua ni kuhusu\(17.7\) maili kutoka bandari.
Kutumia Mfumo wa Heron ili Kupata Eneo la Triangle
Tayari tumejifunza jinsi ya kupata eneo la pembetatu ya oblique wakati tunajua pande mbili na angle. Tunajua pia fomu ya kupata eneo la pembetatu kwa kutumia msingi na urefu. Tunapojua pande tatu, hata hivyo, tunaweza kutumia formula ya Heron badala ya kupata urefu. Heron wa Aleksandria alikuwa geometer aliyeishi wakati wa karne ya kwanza B.K.Aligundua formula ya kutafuta eneo la pembetatu za oblique wakati pande tatu zinajulikana.
Fomu ya Heron hupata eneo la pembetatu za oblique ambazo pande\(a\),\(b\), na\(c\) zinajulikana.
\[Area=\sqrt{s(s−a)(s−b)(s−c)}\]
\(s=\dfrac{(a+b+c)}{2}\)wapi nusu ya mzunguko wa pembetatu, wakati mwingine huitwa nusu ya mzunguko.
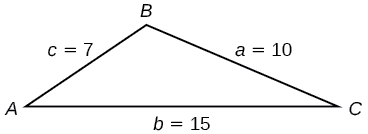
Pata eneo la pembetatu kwenye Kielelezo\(\PageIndex{9}\) ukitumia formula ya Heron.
Kielelezo\(\PageIndex{9}\)
Suluhisho
Kwanza, tunahesabu\(s\).
\[\begin{align*} s&= \dfrac{(a+b+c)}{2}\\ s&= \dfrac{(10+15+7)}{2}\\ &= 16 \end{align*}\]
Kisha tunatumia formula.
\[\begin{align*} Area&= \sqrt{s(s-a)(s-b)(s-c)}\\ Area&= \sqrt{16(16-10)(16-15)(16-7)}\\ Area&\approx 29.4 \end{align*}\]
Eneo hilo ni takriban vitengo vya\(29.4\) mraba.
Tumia formula ya Heron ili kupata eneo la pembetatu na pande za urefu\(a=29.7\) ft,\(b=42.3\) ft, na\(c=38.4\) ft.
- Jibu
-
Eneo = miguu\(552\) mraba
Msanidi wa jiji la Chicago anataka kujenga jengo linalojumuisha mezanine ya msanii kwenye kura ya triangular iliyopakana na Rush Street, Wabash Avenue, na Pearson Street. Frontage kando ya Rush Street ni takriban\(62.4\) mita, kando ya Wabash Avenue ni takriban\(43.5\) mita, na kando ya Pearson Street ni takriban\(34.1\) mita. Ni mita ngapi za mraba zinapatikana kwa msanidi programu? Angalia Kielelezo\(\PageIndex{10}\) kwa mtazamo wa mali ya mji.
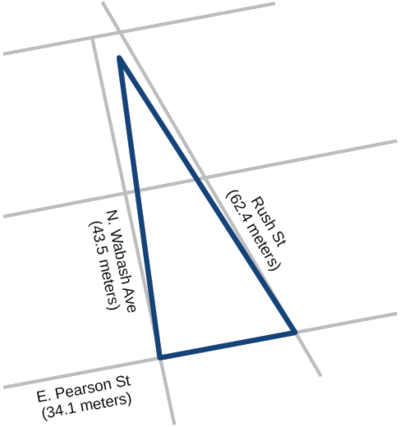
Kielelezo\(\PageIndex{10}\)
Suluhisho
Pata kipimo\(s\), ambacho ni nusu ya mzunguko.
\[\begin{align*} s&= \dfrac{(62.4+43.5+34.1)}{2}\\ s&= 70\; m\\ \text {Apply Heron's formula.}\\ Area&= \sqrt{70(70-62.4)(70-43.5)(70-34.1)}\\ Area&= \sqrt{506,118.2}\\ Area&\approx 711.4 \end{align*}\]
Msanidi programu ana mita za\(711.4\) mraba.
Pata eneo la pembetatu iliyotolewa\(a=4.38\) ft,\(b=3.79\) ft, na\(c=5.22\) ft.
- Jibu
-
kuhusu miguu\(8.15\) ya mraba
Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na Sheria ya Cosines.
Mlinganyo muhimu
| Sheria ya Cosines |
\(a^2=b^2+c^2−2bc \cos \alpha\) \(b^2=a^2+c^2−2ac \cos \beta\) \(c^2=a^2+b^2−2ab \cos \gamma\) |
| Fomu ya Heron |
\(Area=\sqrt{s(s−a)(s−b)(s−c)}\) wapi\(s=\dfrac{(a+b+c)}{2}\) |
Key Concepts
- The Law of Cosines defines the relationship among angle measurements and lengths of sides in oblique triangles.
- The Generalized Pythagorean Theorem is the Law of Cosines for two cases of oblique triangles: SAS and SSS. Dropping an imaginary perpendicular splits the oblique triangle into two right triangles or forms one right triangle, which allows sides to be related and measurements to be calculated. See Example \(\PageIndex{1}\) and Example \(\PageIndex{2}\).
- The Law of Cosines is useful for many types of applied problems. The first step in solving such problems is generally to draw a sketch of the problem presented. If the information given fits one of the three models (the three equations), then apply the Law of Cosines to find a solution. See Example \(\PageIndex{3}\) and Example \(\PageIndex{4}\).
- Heron’s formula allows the calculation of area in oblique triangles. All three sides must be known to apply Heron’s formula. See Example \(\PageIndex{5}\) and See Example \(\PageIndex{6}\).


