10.1: Pembetatu zisizo za haki - Sheria ya Sines
- Page ID
- 178364
- Tumia Sheria ya Sines kutatua pembetatu za oblique.
- Pata eneo la pembetatu ya oblique kwa kutumia kazi ya sine.
- Tatua matatizo yaliyotumika kwa kutumia Sheria ya Sines.
Tuseme vituo rada mbili ziko\(20\) maili mbali kila kuchunguza ndege kati yao. Pembe ya mwinuko inayopimwa na kituo cha kwanza ni\(35\) digrii, ilhali angle ya mwinuko inayopimwa na kituo cha pili ni\(15\) digrii. Tunawezaje kuamua urefu wa ndege? Tunaona katika Kielelezo\(\PageIndex{1}\) kwamba pembetatu sumu na ndege na vituo viwili si pembetatu haki, hivyo hatuwezi kutumia kile tunachokijua kuhusu pembetatu haki. Katika sehemu hii, tutajua jinsi ya kutatua matatizo yanayohusisha pembetatu zisizo sahihi.
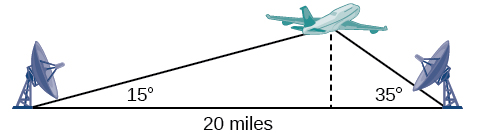
Kielelezo\(\PageIndex{1}\)
Kutumia Sheria ya Sines kutatua Pembetatu za Olique
Katika pembetatu yoyote, tunaweza kuteka urefu, mstari wa perpendicular kutoka vertex moja hadi upande wa pili, na kutengeneza pembetatu mbili za kulia. Itakuwa vyema, hata hivyo, kuwa na mbinu ambazo tunaweza kuomba moja kwa moja kwa pembetatu zisizo za kulia bila ya kwanza kuunda pembetatu sahihi.
Pembetatu yoyote ambayo si pembetatu sahihi ni pembetatu ya oblique. Kutatua pembetatu ya oblique inamaanisha kupata vipimo vya pembe zote tatu na pande zote tatu. Kwa kufanya hivyo, tunahitaji kuanza na angalau tatu ya maadili haya, ikiwa ni pamoja na angalau moja ya pande. Tutachunguza hali tatu za tatizo la oblique pembetatu:
ASA (angle-upande-angle) Tunajua vipimo vya pembe mbili na upande uliojumuishwa. Angalia Kielelezo\(\PageIndex{2}\).
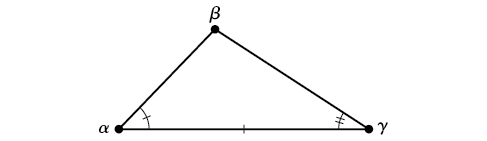
Kielelezo\(\PageIndex{2}\)
AAS (angle-angle-upande) Tunajua vipimo vya pembe mbili na upande usio kati ya pembe zinazojulikana. Angalia Kielelezo\(\PageIndex{3}\).
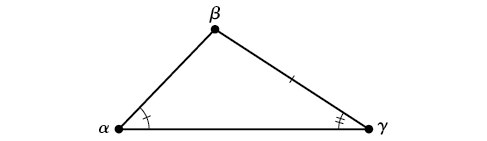
Kielelezo\(\PageIndex{3}\)
SSA (upande-upande-angle) Tunajua vipimo vya pande mbili na pembe ambayo si kati ya pande zinazojulikana. Angalia Kielelezo\(\PageIndex{4}\).
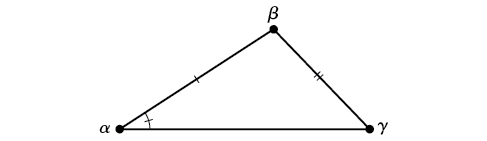
Kielelezo\(\PageIndex{4}\)
Kujua jinsi ya kukabiliana na kila hali hizi hutuwezesha kutatua pembetatu za oblique bila kuacha perpendicular kuunda pembetatu mbili za kulia. Badala yake, tunaweza kutumia ukweli kwamba uwiano wa kipimo cha moja ya pembe kwa urefu wa upande wake wa kinyume utakuwa sawa na uwiano mwingine wa kipimo cha angle kwa upande mwingine. Hebu tuone jinsi kauli hii inatokana na kuzingatia pembetatu inavyoonekana katika Kielelezo\(\PageIndex{5}\).
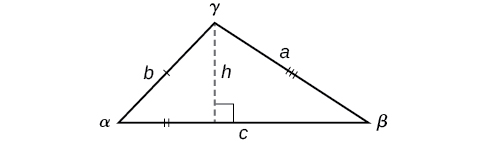
Kielelezo\(\PageIndex{5}\)
Kutumia mahusiano ya pembetatu sahihi, tunajua hilo\(\sin \alpha=\dfrac{h}{b}\) na\(\sin \beta=\dfrac{h}{a}\). Kutatua equations wote kwa\(h\) anatoa maneno mawili tofauti kwa\(h\).
\(h=b \sin \alpha\)na\(h=a \sin \beta\)
Sisi kisha kuweka maneno sawa na kila mmoja.
\[\begin{align*} b \sin \alpha&= a \sin \beta\\ \left(\dfrac{1}{ab}\right)\left(b \sin \alpha\right)&= \left(a \sin \beta\right)\left(\dfrac{1}{ab}\right)\qquad \text{Multiply both sides by } \dfrac{1}{ab}\\ \dfrac{\sin \alpha}{a}&= \dfrac{\sin \beta}{b} \end{align*}\]
Vile vile, tunaweza kulinganisha uwiano mwingine.
\(\dfrac{\sin \alpha}{a}=\dfrac{\sin \gamma}{c}\)na\(\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}\)
Kwa pamoja, mahusiano haya huitwa Sheria ya Sines.
\(\dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}\)
Kumbuka njia ya kawaida ya pembetatu ya kuandika: angle\(\alpha\) (alpha) ni upande wa kinyume\(a\); angle\(\beta\) (beta) ni upande wa pili\(b\); na angle\(\gamma\) (gamma) ni upande wa kinyume\(c\). Angalia Kielelezo\(\PageIndex{6}\).
Wakati wa kuhesabu pembe na pande, hakikisha kubeba maadili halisi kupitia jibu la mwisho. Kwa ujumla, majibu ya mwisho ni mviringo kwa karibu kumi, isipokuwa vinginevyo maalum.
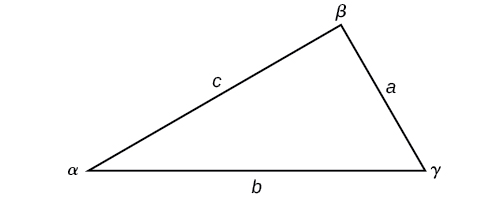
Kielelezo\(\PageIndex{6}\)
Kutokana na pembetatu na pembe na pande kinyume kinachoitwa kama katika Kielelezo\(\PageIndex{6}\), uwiano wa kipimo cha angle hadi urefu wa upande wake wa kinyume utakuwa sawa na uwiano mwingine wa kipimo cha angle kwa upande mwingine. Uwiano wote utakuwa sawa. Sheria ya Sines inategemea uwiano na imewasilishwa kwa njia mbili.
\[\dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}\]
\[\dfrac{a}{\sin \alpha}=\dfrac{b}{\sin \beta}=\dfrac{c}{\sin \gamma}\]
Ili kutatua pembetatu ya oblique, tumia jozi yoyote ya uwiano unaofaa.
Tatua pembetatu iliyoonyeshwa kwenye Kielelezo\(\PageIndex{7}\) hadi kumi ya karibu.
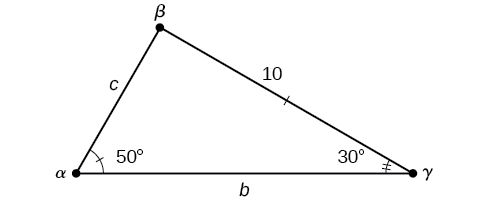
Kielelezo\(\PageIndex{7}\)
Suluhisho
Pembe tatu lazima ziongeze hadi digrii 180. Kutokana na hili, tunaweza kuamua kwamba
\[\begin{align*} \beta &= 180^{\circ} - 50^{\circ} - 30^{\circ}\\ &= 100^{\circ} \end{align*}\]
Ili kupata upande usiojulikana, tunahitaji kujua angle inayofanana na uwiano unaojulikana. Tunajua kwamba angle\(\alpha=50°\) na upande wake sambamba\(a=10\). Tunaweza kutumia uwiano zifuatazo kutoka Sheria ya Sines kupata urefu wa\(c\).
\[\begin{align*} \dfrac{\sin(50^{\circ})}{10}&= \dfrac{\sin(30^{\circ})}{c}\\ c\dfrac{\sin(50^{\circ})}{10}&= \sin(30^{\circ})\qquad \text{Multiply both sides by } c\\ c&= \sin(30^{\circ})\dfrac{10}{\sin(50^{\circ})}\qquad \text{Multiply by the reciprocal to isolate } c\\ c&\approx 6.5 \end{align*}\]
Vile vile, ili kutatua\(b\), tunaanzisha uwiano mwingine.
\[\begin{align*} \dfrac{\sin(50^{\circ})}{10}&= \dfrac{\sin(100^{\circ})}{b}\\ b \sin(50^{\circ})&= 10 \sin(100^{\circ})\qquad \text{Multiply both sides by } b\\ b&= \dfrac{10 \sin(100^{\circ})}{\sin(50^{\circ})}\qquad \text{Multiply by the reciprocal to isolate }b\\ b&\approx 12.9 \end{align*}\]
Kwa hiyo, seti kamili ya pembe na pande ni
\(\begin{matrix} \alpha=50^{\circ} & a=10\\ \beta=100^{\circ} & b\approx 12.9\\ \gamma=30^{\circ} & c\approx 6.5 \end{matrix}\)
Tatua pembetatu iliyoonyeshwa kwenye Kielelezo\(\PageIndex{8}\) hadi kumi ya karibu.
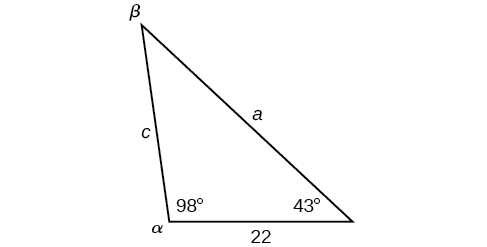
Kielelezo\(\PageIndex{8}\)
- Jibu
-
\(\begin{matrix} \alpha=98^{\circ} & a=34.6\\ \beta=39^{\circ} & b=22\\ \gamma=43^{\circ} & c=23.8 \end{matrix}\)
Kutumia Sheria ya Sines kutatua SSA Pembetatu
Tunaweza kutumia Sheria ya Sines kutatua pembetatu yoyote ya oblique, lakini baadhi ya ufumbuzi hauwezi kuwa moja kwa moja. Katika hali nyingine, zaidi ya pembetatu moja inaweza kukidhi vigezo vilivyopewa, ambavyo tunaelezea kama kesi isiyofaa. Pembetatu zilizowekwa kama SSA, zile ambazo tunajua urefu wa pande mbili na kipimo cha angle kinyume na moja ya pande zilizopewa, zinaweza kusababisha ufumbuzi mmoja au mbili, au hata hakuna suluhisho.
Pembetatu za oblique katika kikundi SSA inaweza kuwa na matokeo manne tofauti. Kielelezo\(\PageIndex{9}\) unaeleza ufumbuzi na pande inayojulikana\(a\)\(b\) na angle inayojulikana\(\alpha\).
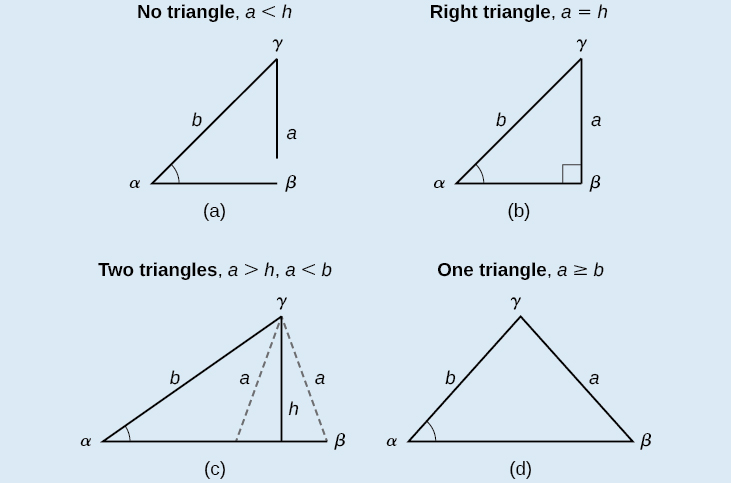
Kielelezo\(\PageIndex{9}\)
Tatua pembetatu kwenye Kielelezo\(\PageIndex{10}\) kwa upande usiopotea na upate hatua za angle zilizopo kwa kumi ya karibu.
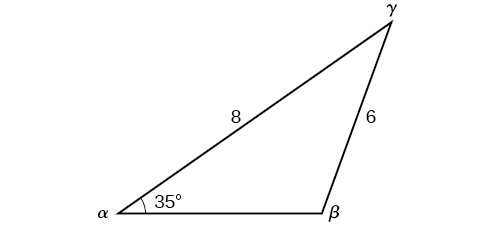
Kielelezo\(\PageIndex{10}\)
Suluhisho
Tumia Sheria ya Sines kupata angle\(\beta\) na angle\(\gamma\), na kisha upande\(c\). Kutatua kwa\(\beta\), tuna uwiano
\[\begin{align*} \dfrac{\sin \alpha}{a}&= \dfrac{\sin \beta}{b}\\ \dfrac{\sin(35^{\circ})}{6}&= \dfrac{\sin \beta}{8}\\ \dfrac{8 \sin(35^{\circ})}{6}&= \sin \beta\\ 0.7648&\approx \sin \beta\\ {\sin}^{-1}(0.7648)&\approx 49.9^{\circ}\\ \beta&\approx 49.9^{\circ} \end{align*}\]
Hata hivyo, katika mchoro, angle\(\beta\) inaonekana kuwa angle ya obtuse na inaweza kuwa kubwa kuliko\(90°\). Jinsi gani sisi kupata angle papo hapo, na jinsi gani sisi kupata kipimo cha\(\beta\)? Hebu tuchunguze zaidi. Kuacha perpendicular kutoka\(\gamma\) na kuangalia pembetatu kutoka mtazamo wa kulia angle, tuna Kielelezo\(\PageIndex{11}\). Inaonekana kwamba kunaweza kuwa na pembetatu ya pili ambayo itafaa vigezo vilivyopewa.
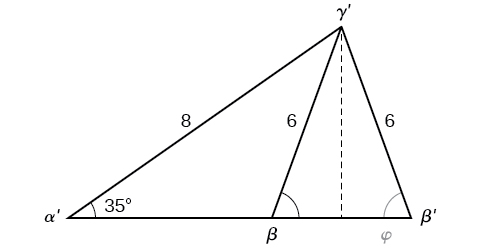
Kielelezo\(\PageIndex{11}\)
Angle ya ziada\(\beta\) ni takriban sawa na\(49.9°\), ambayo ina maana kwamba\(\beta=180°−49.9°=130.1°\). (Kumbuka kwamba kazi ya sine ni chanya katika quadrants ya kwanza na ya pili.) Kutatua kwa\(\gamma\), tuna
\[\begin{align*} \gamma&= 180^{\circ}-35^{\circ}-130.1^{\circ}\\ &\approx 14.9^{\circ} \end{align*}\]
Tunaweza kutumia vipimo hivi kutatua pembetatu nyingine. Tangu\(\beta′\) ni ziada kwa\(\beta\), tuna
\[\begin{align*} \gamma^{'}&= 180^{\circ}-35^{\circ}-49.5^{\circ}\\ &\approx 95.1^{\circ} \end{align*}\]
Sasa tunahitaji kupata\(c\) na\(c′\).
Tuna
\[\begin{align*} \dfrac{c}{\sin(14.9^{\circ})}&= \dfrac{6}{\sin(35^{\circ})}\\ c&= \dfrac{6 \sin(14.9^{\circ})}{\sin(35^{\circ})}\\ &\approx 2.7 \end{align*}\]
Hatimaye,
\[\begin{align*} \dfrac{c'}{\sin(95.1^{\circ})}&= \dfrac{6}{\sin(35^{\circ})}\\ c'&= \dfrac{6 \sin(95.1^{\circ})}{\sin(35^{\circ})}\\ &\approx 10.4 \end{align*}\]
Kwa muhtasari, kuna pembetatu mbili na angle ya\(35°\), upande wa karibu wa 8, na upande kinyume cha 6, kama inavyoonekana katika Kielelezo\(\PageIndex{12}\).
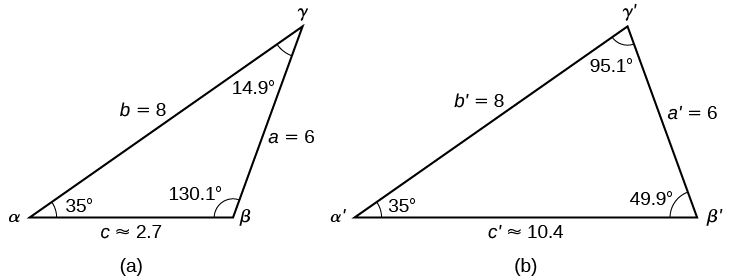
Kielelezo\(\PageIndex{12}\)
Hata hivyo, tulikuwa tunatafuta maadili ya pembetatu na angle ya obtuse\(\beta\). Tunaweza kuwaona katika pembetatu ya kwanza (a) katika Kielelezo\(\PageIndex{12}\).
Kutokana\(\alpha=80°\),\(a=120\), na\(b=121\), kupata upande kukosa na pembe. Ikiwa kuna suluhisho zaidi ya moja iwezekanavyo, onyesha wote wawili.
- Jibu
-
Suluhisho 1
\(\begin{matrix} \alpha=80^{\circ} & a=120\\ \beta\approx 83.2^{\circ} & b=121\\ \gamma\approx 16.8^{\circ} & c\approx 35.2 \end{matrix}\)
Suluhisho 2
\(\begin{matrix} \alpha '=80^{\circ} & a'=120\\ \beta '\approx 96.8^{\circ} & b'=121\\ \gamma '\approx 3.2^{\circ} & c'\approx 6.8 \end{matrix}\)
Katika pembetatu iliyoonyeshwa kwenye Kielelezo\(\PageIndex{13}\), tatua kwa upande usiojulikana na pembe. Pindua majibu yako kwa karibu kumi.
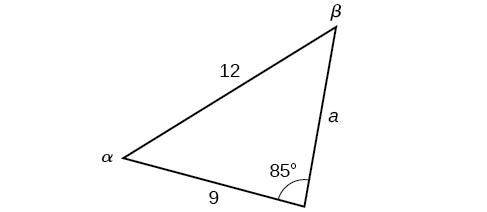
Kielelezo\(\PageIndex{13}\)
Suluhisho
Katika kuchagua jozi ya uwiano kutoka Sheria ya Sines kutumia, angalia habari iliyotolewa. Katika kesi hii, tunajua angle,\(\gamma=85°\), na upande wake sambamba\(c=12\), na tunajua upande\(b=9\). Tutatumia uwiano huu kutatua\(\beta\).
\[\begin{align*} \dfrac{\sin(85^{\circ})}{12}&= \dfrac{\sin \beta}{9}\qquad \text{Isolate the unknown.}\\ \dfrac{9 \sin(85^{\circ})}{12}&= \sin \beta \end{align*}\]
Ili kupata\(\beta\), tumia kazi ya sine inverse. Sine inverse itazalisha matokeo moja, lakini kukumbuka kwamba kunaweza kuwa na maadili mawili kwa\(\beta\). Ni muhimu kuthibitisha matokeo, kwa kuwa kunaweza kuwa na ufumbuzi mbili unaofaa, suluhisho moja tu (kesi ya kawaida), au hakuna ufumbuzi.
\[\begin{align*} \beta&= {\sin}^{-1}\left(\dfrac{9 \sin(85^{\circ})}{12}\right)\\ \beta&\approx {\sin}^{-1} (0.7471)\\ \beta&\approx 48.3^{\circ} \end{align*}\]
Katika kesi hii, ikiwa\(\beta\) tunaondoa\(180°\), tunaona kwamba kunaweza kuwa na suluhisho la pili linalowezekana. Hivyo,\(\beta=180°−48.3°≈131.7°\). Kuangalia suluhisho, toa pembe zote mbili,\(131.7°\) na\(85°\), kutoka\(180°\). Hii inatoa
\[\begin{align*} \alpha&= 180^{\circ}-85^{\circ}-131.7^{\circ}\\ &\approx -36.7^{\circ} \end{align*}\]
ambayo haiwezekani, na hivyo\(\beta≈48.3°\).
Ili kupata maadili yaliyobaki yaliyobaki, tunahesabu\(\alpha=180°−85°−48.3°≈46.7°\). Sasa, upande pekee\(a\) unahitajika. Tumia Sheria ya Sines kutatua\(a\) kwa moja ya idadi.
\[\begin{align*} \dfrac{\sin(85°)}{12}&= \dfrac{\sin(46.7^{\circ})}{a}\\ a\dfrac{\sin(85^{\circ})}{12}&= \sin(46.7^{\circ})\\ a&=\dfrac{12\sin(46.7^{\circ})}{\sin(85^{\circ})}\\ &\approx 8.8 \end{align*}\]
Seti kamili ya ufumbuzi kwa pembetatu iliyotolewa ni
\(\begin{matrix} \alpha\approx 46.7^{\circ} & a\approx 8.8\\ \beta\approx 48.3^{\circ} & b=9\\ \gamma=85^{\circ} & c=12 \end{matrix}\)
Kutokana\(\alpha=80°\),\(a=100\),\(b=10\), kupata upande kukosa na pembe. Ikiwa kuna suluhisho zaidi ya moja iwezekanavyo, onyesha wote wawili. Pindua majibu yako kwa karibu kumi.
- Jibu
-
\(\beta≈5.7°\),\(\gamma≈94.3°\),\(c≈101.3\)
Kupata pembetatu iwezekanavyo kama upande mmoja ina urefu\(4\) kinyume angle ya\(50°\), na upande wa pili ina urefu\(10\).
Suluhisho
Kutumia taarifa iliyotolewa, tunaweza kutatua kwa angle kinyume na upande wa urefu\(10\). Angalia Kielelezo\(\PageIndex{14}\).
\[\begin{align*} \dfrac{\sin \alpha}{10}&= \dfrac{\sin(50^{\circ})}{4}\\ \sin \alpha&= \dfrac{10 \sin(50^{\circ})}{4}\\ \sin \alpha&\approx 1.915 \end{align*}\]
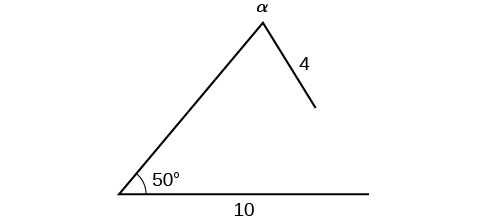
Kielelezo\(\PageIndex{14}\)
Tunaweza kuacha hapa bila kupata thamani ya\(\alpha\). Kwa sababu mbalimbali ya kazi sine ni\([ −1,1 ]\), haiwezekani kwa thamani sine kuwa\(1.915\). Kwa kweli, kuingiza\({\sin}^{−1}(1.915)\) katika calculator ya graphing inazalisha ERROR DOMAIN. Kwa hiyo, hakuna pembetatu inayoweza kupatikana na vipimo vinavyotolewa.
Kuamua idadi ya pembetatu iwezekanavyo kutolewa\(a=31\),\(b=26\),\(\beta=48°\).
- Jibu
-
mbili
Kutafuta Eneo la Triangle ya Olique Kutumia Kazi ya Sine
Sasa kwa kuwa tunaweza kutatua pembetatu kwa maadili ya kukosa, tunaweza kutumia baadhi ya maadili hayo na kazi ya sine ili kupata eneo la pembetatu ya oblique. Kumbuka kwamba formula eneo kwa pembetatu ni kutolewa kama\(Area=\dfrac{1}{2}bh\), ambapo\(b\) ni msingi na\(h\) ni urefu. Kwa pembetatu za oblique, tunapaswa kupata\(h\) kabla ya kutumia formula ya eneo. Kuchunguza pembetatu mbili katika Kielelezo\(\PageIndex{15}\), moja papo hapo na moja obtuse, tunaweza kuacha perpendicular kuwakilisha urefu na kisha kuomba mali trigonometric\(\sin \alpha=\dfrac{opposite}{hypotenuse}\) kuandika equation kwa eneo katika pembetatu oblique. Katika pembetatu ya papo hapo, tuna\(\sin \alpha=\dfrac{h}{c}\) au\(c \sin \alpha=h\). Hata hivyo, katika pembetatu ya obtuse, tunaacha pembetatu nje ya pembetatu na kupanua msingi\(b\) ili kuunda pembetatu sahihi. Pembe inayotumiwa katika hesabu ni\(\alpha′\), au\(180−\alpha\).
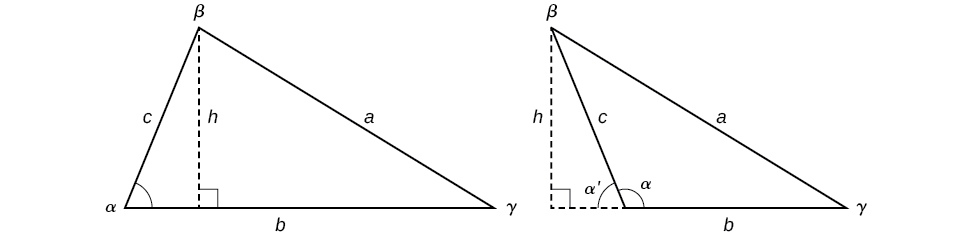
Kielelezo\(\PageIndex{15}\)
Hivyo,
\(Area=\dfrac{1}{2}(base)(height)=\dfrac{1}{2}b(c \sin \alpha)\)
Vile vile,
\(Area=\dfrac{1}{2}a(b \sin \gamma)=\dfrac{1}{2}a(c \sin \beta)\)
Fomu ya eneo la pembetatu ya oblique hutolewa na
\[Area=\dfrac{1}{2}bc \sin \alpha\]
\[Area=\dfrac{1}{2}ac \sin \beta\]
\[Area=\dfrac{1}{2}ab \sin \gamma\]
Hii ni sawa na nusu moja ya bidhaa za pande mbili na sine ya angle yao iliyojumuishwa.
Pata eneo la pembetatu na pande\(a=90\),\(b=52\), na angle\(\gamma=102°\). Pande zote eneo kwa integer iliyo karibu.
Suluhisho
Kutumia formula, tuna
\[\begin{align*} Area&= \dfrac{1}{2}ab \sin \gamma\\ Area&= \dfrac{1}{2}(90)(52) \sin(102^{\circ})\\ Area&\approx 2289\; \text{square units} \end{align*}\]
Pata eneo la pembetatu iliyotolewa\(\beta=42°\),\(a=7.2 ft\),\(c=3.4 ft\). Pande zote eneo hadi kumi ya karibu.
- Jibu
-
kuhusu miguu\(8.2\) ya mraba
Kutatua Matatizo yaliyotumika Kutumia Sheria ya Sines
Zaidi ya sisi kujifunza maombi trigonometric, zaidi sisi kugundua kwamba maombi ni isitoshe. Baadhi ni bapa, hali ya mchoro, lakini maombi mengi katika calculus, uhandisi, na fizikia huhusisha vipimo vitatu na mwendo.
Pata urefu wa ndege katika tatizo lililoletwa mwanzoni mwa sehemu hii, iliyoonyeshwa kwenye Kielelezo\(\PageIndex{16}\). Pande zote urefu hadi kumi ya karibu ya maili.
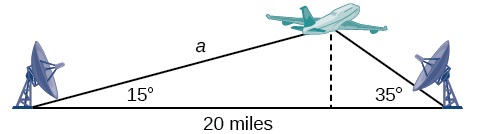
Kielelezo\(\PageIndex{16}\)
Suluhisho
Ili kupata mwinuko wa ndege, sisi kwanza kupata umbali kutoka kituo kimoja kwa ndege, kama vile upande\(a\), na kisha kutumia mahusiano ya pembetatu haki ili kupata urefu wa ndege,\(h\).
Kwa sababu pembe katika pembetatu huongeza hadi\(180\) digrii, angle isiyojulikana lazima iwe\(180°−15°−35°=130°\). Pembe hii ni kinyume na upande wa urefu\(20\), kuruhusu sisi kuanzisha Sheria ya Sines uhusiano.
\[\begin{align*} \dfrac{\sin(130^{\circ})}{20}&= \dfrac{\sin(35^{\circ})}{a}\\ a \sin(130^{\circ})&= 20 \sin(35^{\circ})\\ a&= \dfrac{20 \sin(35^{\circ})}{\sin(130^{\circ})}\\ a&\approx 14.98 \end{align*}\]
Umbali kutoka kituo kimoja hadi ndege ni karibu\(14.98\) maili.
Sasa kwa kuwa tunajua\(a\), tunaweza kutumia mahusiano ya pembetatu ya haki ili kutatua\(h\).
\[\begin{align*} \sin(15^{\circ})&= \dfrac{opposite}{hypotenuse}\\ \sin(15^{\circ})&= \dfrac{h}{a}\\ \sin(15^{\circ})&= \dfrac{h}{14.98}\\ h&= 14.98 \sin(15^{\circ})\\ h&\approx 3.88 \end{align*}\]
Ndege iko kwenye urefu wa\(3.9\) maili takriban.
mchoro inavyoonekana katika Kielelezo\(\PageIndex{17}\) inawakilisha urefu wa blimp flying juu ya uwanja wa mpira wa miguu. Pata urefu wa blimp ikiwa angle ya mwinuko kwenye ukanda wa mwisho wa kusini, kumweka A, ni\(70°\), angle ya mwinuko kutoka ukanda wa mwisho wa kaskazini, hatua B\(62°\), ni, na umbali kati ya pointi za kutazama za maeneo mawili ya mwisho ni\(145\) yadi.
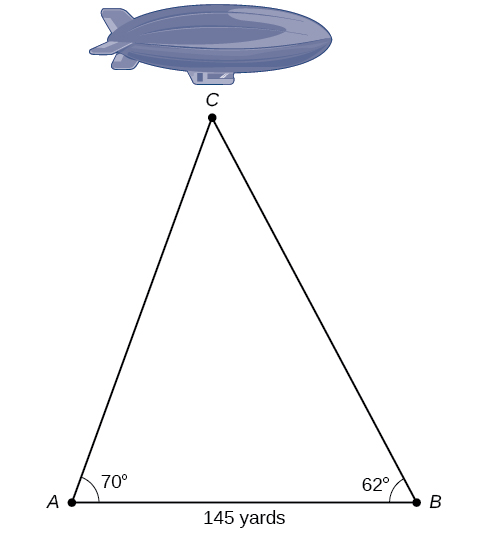
Kielelezo\(\PageIndex{17}\)
- Jibu
-
\(161.9\)yd.
Media
Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na programu za trigonometric.
Mlinganyo muhimu
| Sheria ya Sines |
\(\dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}\) \(\dfrac{a}{\sin \alpha}=\dfrac{b}{\sin \beta}=\dfrac{c}{\sin \gamma}\) |
| Eneo la pembetatu za oblique |
\(Area=\dfrac{1}{2}bc \sin \alpha\) \(=\dfrac{1}{2} ac \sin \beta\) \(=\dfrac{1}{2} ab \sin \gamma\) |
Dhana muhimu
- Sheria ya Sines inaweza kutumika kutatua pembetatu za oblique, ambazo ni pembetatu zisizo sahihi.
- Kwa mujibu wa Sheria ya Sines, uwiano wa kipimo cha moja ya pembe kwa urefu wa upande wake kinyume sawa na uwiano mwingine wa kipimo cha angle kwa upande mwingine.
- Kuna matukio matatu iwezekanavyo: ASA, AAS, SSA. Kulingana na taarifa iliyotolewa, tunaweza kuchagua equation sahihi ili kupata suluhisho lililoombwa. Angalia Mfano\(\PageIndex{1}\).
- Kesi mbaya hutokea wakati pembetatu ya oblique inaweza kuwa na matokeo tofauti.
- Kuna matukio matatu yanayowezekana yanayotokana na utaratibu wa SSA-suluhisho moja, ufumbuzi mbili iwezekanavyo, na hakuna suluhisho. Angalia Mfano\(\PageIndex{2}\) na Mfano\(\PageIndex{3}\).
- Sheria ya Sines inaweza kutumika kutatua pembetatu na vigezo fulani. Angalia Mfano\(\PageIndex{4}\).
- Fomu ya jumla ya eneo la pembetatu hutafsiriwa kwa pembetatu za oblique kwa kwanza kutafuta thamani ya urefu sahihi. Angalia Mfano\(\PageIndex{5}\).
- Kuna maombi mengi ya trigonometric. Mara nyingi huweza kutatuliwa kwa kuchora kwanza mchoro wa habari iliyotolewa na kisha kutumia equation sahihi. Angalia Mfano\(\PageIndex{6}\).


