8.2: Grafu za Kazi nyingine za Trigonometric
- Page ID
- 178081
- Kuchambua grafu ya\(y=\tan x\).
- Graph tofauti ya\(y=\tan x\).
- Kuchambua grafu ya\(y=\sec x\) na\(y=\csc x\).
- Grafu tofauti ya\(y=\sec x\) na\(y=\csc x\).
- Kuchambua grafu ya\(y=\cot x\).
- Graph tofauti ya\(y=\cot x\).
Tunajua kazi ya tangent inaweza kutumika kupata umbali, kama vile urefu wa jengo, mlima, au flagpole. Lakini vipi ikiwa tunataka kupima matukio ya mara kwa mara ya umbali? Fikiria, kwa mfano, gari la polisi lililokuwa limeegeshwa karibu na ghala. Mwanga unaozunguka kutoka gari la polisi ungesafiri kwenye ukuta wa ghala kwa vipindi vya kawaida. Kama pembejeo ni wakati, pato itakuwa umbali boriti ya safari mwanga. Boriti ya mwanga ingeweza kurudia umbali kwa vipindi vya kawaida. Kazi ya tangent inaweza kutumika kwa takriban umbali huu. Asymptotes itahitajika kuonyesha mzunguko wa mara kwa mara wakati boriti inaendesha sambamba na ukuta kwa sababu, inaonekana, boriti ya mwanga inaweza kuonekana kupanua milele. Grafu ya kazi ya tangent ingeonyesha wazi vipindi vya mara kwa mara. Katika sehemu hii, tutazingatia grafu za kazi za tangent na nyingine za trigonometric.
Kuchambua Grafu ya\(y =\tan x\)
Tutaanza na grafu ya kazi ya tangent, pointi za kupanga njama kama tulivyofanya kwa kazi za sine na cosine. Kukumbuka kwamba
\[\tan \, x=\dfrac{\sin \, x}{\cos \, x}\]
Kipindi cha kazi ya tangent ni\(\pi\) kwa sababu grafu inarudia yenyewe kwa vipindi vya\(k\pi\) wapi\(k\) mara kwa mara. Kama sisi graph kazi tangent juu\(−\frac{\pi}{2}\) ya\(\frac{\pi}{2}\), tunaweza kuona tabia ya grafu kwenye mzunguko mmoja kamili. Ikiwa tunaangalia muda wowote mkubwa, tutaona kwamba sifa za grafu hurudia.
Tunaweza kuamua kama tangent ni isiyo ya kawaida au hata kazi kwa kutumia ufafanuzi wa tangent.
\[\begin{align*} \tan(-x)&= \dfrac{\sin(-x)}{\cos(-x)} \qquad \text{Definition of tangent}\\ &= \dfrac{-\sin \, x}{\cos \, x} \qquad \text{Sine is an odd function, cosine is even}\\ &= -\dfrac{\sin \, x}{\cos \, x} \qquad \text{The quotient of an odd and an even function is odd}\\ &= -\tan \, x \qquad \text{Definition of tangent} \end{align*}\]
Kwa hiyo, tangent ni kazi isiyo ya kawaida. Tunaweza kuchambua zaidi tabia ya graphical ya kazi ya tangent kwa kuangalia maadili kwa baadhi ya pembe maalum, kama ilivyoorodheshwa katika Jedwali\(\PageIndex{1}\).
| \(x\) | \(−\dfrac{\pi}{2}\) | \(−\dfrac{\pi}{3}\) | \(−\dfrac{\pi}{4}\) | \(−\dfrac{\pi}{6}\) | 0 | \(\dfrac{\pi}{6}\) | \(\dfrac{\pi}{4}\) | \(\dfrac{\pi}{3}\) | \(\dfrac{\pi}{2}\) |
|---|---|---|---|---|---|---|---|---|---|
| \(\tan x\) | haijafafanuliwa | \(-\sqrt{3}\) | \(–1\) | \(-\dfrac{\sqrt{3}}{3}\) | 0 | \(\dfrac{\sqrt{3}}{3}\) | 1 | \(\sqrt{3}\) | haijafafanuliwa |
Vipengele hivi vitatusaidia kuteka grafu yetu, lakini tunahitaji kuamua jinsi grafu inavyofanya ambapo haijulikani. Kama sisi kuangalia kwa karibu zaidi katika maadili wakati\(\frac{\pi}{3}<x<\frac{\pi}{2}\), tunaweza kutumia meza kuangalia kwa mwenendo. Kwa sababu\(\frac{\pi}{3}≈1.05\) na\(\frac{\pi}{2}≈1.57\), sisi kutathmini\(x\) katika hatua radian\(1.05<x<1.57\) kama inavyoonekana katika Jedwali\(\PageIndex{2}\).
| \(x\) | 1.3 | 1.5 | 1.55 | 1.56 |
|---|---|---|---|---|
| \(\tan x\) | 3.6 | 14.1 | 48.1 | 92.6 |
Kama\(x\) mbinu\(\dfrac{\pi}{2}\), matokeo ya kazi hupata kubwa na kubwa. Kwa sababu\(y=\tan \, x\) ni kazi isiyo ya kawaida, tunaona meza sambamba ya maadili hasi katika Jedwali\(\PageIndex{3}\).
| \(x\) | -1.3 | -1.5 | -1.55 | -1.56 |
|---|---|---|---|---|
| \(\tan x\) | -3.6 | -14.1 | -48.1 | -92.6 |
Tunaweza kuona kwamba, kama\(x\) mbinu\(−\frac{\pi}{2}\), matokeo hupata ndogo na ndogo. Kumbuka kwamba kuna baadhi ya maadili\(x\) ya ambayo\(\cos \, x=0\). Kwa mfano,\(\cos \left (\frac{\pi}{2} \right)=0\) na\(\cos \left (\frac{3\pi}{2} \right )=0\). Kwa maadili haya, kazi ya tangent haijulikani, hivyo grafu ya\(y=\tan \, x\) ina discontinuities saa\(x=\frac{\pi}{2}\) na\(\frac{3\pi}{2}\). Kwa maadili haya, grafu ya tangent ina asymptotes wima. Kielelezo\(\PageIndex{1}\) inawakilisha grafu ya\(y=\tan \, x\). Tangent ni chanya kutoka\(0\) kwenda\(\frac{\pi}{2}\) na kutoka\(\pi\)\(\frac{3\pi}{2}\), sambamba na quadrants I na III ya mduara wa kitengo.
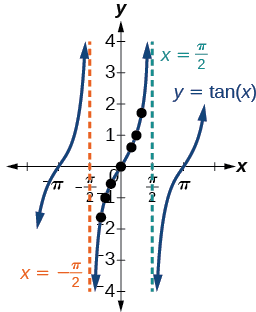
Kielelezo\(\PageIndex{1}\): Grafu ya kazi ya tangent
Graphing Tofauti ya\(y = \tan \, x\)
Kama ilivyo na kazi za sine na cosine, kazi ya tangent inaweza kuelezewa na equation ya jumla.
\[y=A\tan(Bx) \nonumber\]
Tunaweza kutambua stretches usawa na wima na compressions kutumia maadili ya\(A\) na\(B\). Kunyoosha usawa kunaweza kuamua kutoka kipindi cha grafu. Kwa grafu za tangent, mara nyingi ni muhimu kuamua kunyoosha wima kwa kutumia hatua kwenye grafu.
Kwa sababu hakuna maadili ya kiwango cha juu au cha chini cha kazi ya tangent, amplitude ya neno haiwezi kutafsiriwa kama ilivyo kwa kazi za sine na cosine. Badala yake, tutatumia maneno ya kunyoosha/compressing sababu wakati akimaanisha mara kwa mara\(A\).
- Sababu ya kunyoosha ni\(|A|\).
- Kipindi ni\(P=\dfrac{\pi}{|B|}\).
- Kikoa ni namba zote halisi\(x\), ambapo\(x≠\dfrac{\pi}{2| B |}+\dfrac{π}{| B |}k\) vile\(k\) ni integer.
- Mipangilio ni\((−\infty,\infty)\).
- Asymptotes hutokea\(x=\dfrac{\pi}{2| B |}+\dfrac{π}{| B |}k\)\(k\) wapi integer.
- \(y=A\tan(Bx)\)ni kazi isiyo ya kawaida.
Graphing Kipindi kimoja cha Kazi ya Tangent iliyopigwa au iliyosimamishwa
Tunaweza kutumia kile tunachojua kuhusu mali ya kazi ya tangent kwa haraka mchoro wa grafu ya kazi yoyote iliyotambulishwa na/au iliyosimamiwa ya tangent ya fomu\(f(x)=A\tan(Bx)\). Tunazingatia kipindi kimoja cha kazi ikiwa ni pamoja na asili, kwa sababu mali ya mara kwa mara inatuwezesha kupanua grafu kwenye uwanja wote wa kazi ikiwa tunataka. Kikoa chetu kidogo ni kisha muda\(\left (−\dfrac{P}{2},\dfrac{P}{2} \right )\) na grafu ina asymptotes wima\(\pm \dfrac{P}{2}\) wapi\(P=\dfrac{\pi}{B}\). Juu\(\left (−\dfrac{\pi}{2},\dfrac{\pi}{2} \right )\), grafu itakuja kutoka kwa asymptote ya kushoto\(x=−\dfrac{\pi}{2}\), kuvuka kupitia asili, na kuendelea kuongezeka kama inakaribia asymptote sahihi\(x=\dfrac{\pi}{2}\). Ili kufanya mbinu ya kazi asymptotes kwa kiwango sahihi, tunahitaji pia kuweka kiwango cha wima kwa kweli kutathmini kazi kwa angalau hatua moja ambayo grafu itapita. Kwa mfano, tunaweza kutumia
\[f \left (\dfrac{P}{4} \right )=A\tan \left (B\dfrac{P}{4} \right )=A\tan \left (B\dfrac{\pi}{4B} \right )=A \nonumber\]
kwa sababu\(\tan \left (\dfrac{\pi}{4} \right )=1\).
- Tambua sababu ya kuenea,\(| A |\).
- Tambua B na ueleze kipindi,\(P=\dfrac{\pi}{| B |}\).
- Chora asymptotes wima saa\(x=−\dfrac{P}{2}\) na\(x=\dfrac{P}{2}\).
- Kwa\(A>0\), grafu inakaribia asymptote ya kushoto kwa maadili mabaya ya pato na asymptote sahihi katika maadili mazuri ya pato (reverse kwa\(A<0\)).
- Plot pointi kumbukumbu katika\(\left (\dfrac{P}{4},A \right )\)\((0,0)\),, na\(\left (−\dfrac{P}{4},−A \right )\), na kuteka grafu kupitia pointi hizi.
Mchoro grafu ya kipindi kimoja cha kazi\(y=0.5\tan \left (\dfrac{\pi}{2}x \right )\).
Suluhisho
Kwanza, tunatambua\(A\) na\(B\).
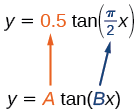
Kielelezo\(\PageIndex{2}\)
Kwa sababu\(A=0.5\) na\(B=\dfrac{\pi}{2}\), tunaweza kupata kunyoosha/compressing sababu na kipindi. Kipindi ni\(\dfrac{\pi}{\dfrac{\pi}{2}}=2\), hivyo asymptotes ni saa\(x=±1\). Katika kipindi cha robo kutoka asili, tuna
\[\begin{align*} f(0.5)&= 0.5\tan \left (\dfrac{0.5\pi}{2} \right )\\ &= 0.5\tan \left (\dfrac{\pi}{4} \right )\\ &= 0.5 \end{align*}\]
Hii ina maana Curve lazima kupita katika pointi\((0.5,0.5)\),\((0,0)\), na\((−0.5,−0.5)\). Njia pekee ya kupigia ni asili. Kielelezo\(\PageIndex{3}\) kinaonyesha grafu ya kipindi kimoja cha kazi.
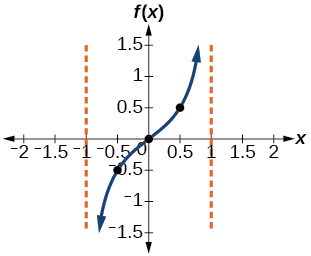
Kielelezo\(\PageIndex{3}\)
Mchoro grafu ya\(f(x)=3\tan \left (\dfrac{\pi}{6}x \right )\).
- Jibu
-

Kielelezo\(\PageIndex{4}\)
Graphing Kipindi kimoja cha Kazi ya Tangent iliyobadilishwa
Sasa kwa kuwa tunaweza graph kazi tangent kwamba ni aliweka au USITUMIE, sisi kuongeza wima na/au usawa (au awamu) kuhama. Katika kesi hii, tunaongeza\(C\) na\(D\) fomu ya jumla ya kazi ya tangent.
\[f(x)=A\tan(Bx−C)+D \nonumber\]
Grafu ya kazi ya tangent iliyobadilishwa ni tofauti na kazi ya msingi ya tangent\(\tan x\) kwa njia kadhaa:
- Sababu ya kunyoosha ni\(| A |\).
- Kipindi ni\(\dfrac{\pi}{| B |}\).
- Kikoa ni\(x≠\dfrac{C}{B}+\dfrac{\pi}{| B |}k\), wapi\(k\) integer.
- Mipangilio ni\((−∞,−| A |]∪[| A |,∞)\).
- Asymptotes wima hutokea saa\(x=\dfrac{C}{B}+\dfrac{\pi}{| B |}k\),\(k\) wapi integer isiyo ya kawaida.
- Hakuna amplitude.
- \(y=A \tan(Bx)\)ni kazi isiyo ya kawaida kwa sababu ni quotient ya kazi isiyo ya kawaida na hata (dhambi na cosine perspectively).
- Eleza kazi iliyotolewa katika fomu\(y=A\tan(Bx−C)+D\).
- Tambua sababu ya kunyoosha/compressing,\(| A |\).
- Tambua\(B\) na kuamua kipindi,\(P=\dfrac{\pi}{|B|}\).
- Tambua\(C\) na kuamua mabadiliko ya awamu,\(\dfrac{C}{B}\).
- Chora grafu ya\(y=A\tan(Bx)\) kubadilishwa kwa haki\(\dfrac{C}{B}\) na juu\(D\).
- Mchoro asymptotes wima, ambayo hutokea katika\(x=\dfrac{C}{B}+\dfrac{\pi}{2| B |}k\), ambapo\(k\) ni integer isiyo ya kawaida.
- Panda pointi yoyote ya kumbukumbu tatu na kuteka grafu kupitia pointi hizi.
Grafu kipindi kimoja cha kazi\(y=−2\tan(\pi x+\pi)−1\).
Suluhisho
- Hatua ya 1. Kazi tayari imeandikwa kwa fomu\(y=A\tan(Bx−C)+D\).
- Hatua ya 2. \(A=—2\), hivyo sababu ya kunyoosha ni\(|A|=2\).
- Hatua ya 3. \(B=\ pi\), hivyo kipindi ni\(P=\dfrac{\pi}{| B |}=\dfrac{\pi}{pi}=1\).
- Hatua ya 4. \(C=\ pi\), hivyo mabadiliko ya awamu ni\(CB=\dfrac{−\pi}{\pi}=−1\).
- Hatua ya 5-7. Asymptotes ni saa\(x=−\dfrac{3}{2}\)\(x=−\dfrac{1}{2}\) na na pointi tatu ilipendekeza kumbukumbu ni\((−1.25,1)\),\((−1,−1)\), na\((−0.75,−3)\). Grafu inavyoonyeshwa kwenye Kielelezo\(\PageIndex{5}\).
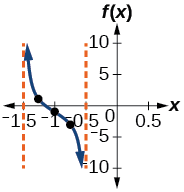
Kielelezo\(\PageIndex{5}\)
Uchambuzi
Kumbuka kuwa hii ni kazi kupungua kwa sababu\(A<0\).
Je, grafu katika Mfano\(\PageIndex{2}\) itaonekanaje tofauti ikiwa tumefanya\(A=2\) badala ya\(−2\)?
- Jibu
-
Itakuwa yalijitokeza katika mstari\(y=−1\), kuwa kazi ya kuongezeka.
- Pata kipindi\(P\) kutoka kwa nafasi kati ya asymptotes ya wima mfululizo au x -intercepts.
- Andika\(f(x)=A\tan \left (\dfrac{\pi}{P}x \right )\).
- Tambua hatua rahisi\((x,f(x))\) kwenye grafu iliyotolewa na uitumie kuamua\(A\).
Kupata formula kwa ajili ya kazi graphed katika Kielelezo\(\PageIndex{6}\).
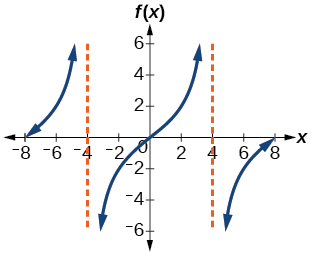
Kielelezo\(\PageIndex{6}\): Kazi ya tangent iliyotiwa
Suluhisho
Grafu ina sura ya kazi ya tangent.
- Hatua ya 1. Mzunguko mmoja unatoka\(–4\) hadi\(4\), hivyo kipindi hicho ni\(P=8\). tangu\(P=\dfrac{\pi}{| B |}\), tuna\(B=\dfrac{π}{P}=\dfrac{\pi}{8}\).
- Hatua ya 2. Equation lazima iwe na fomu\(f(x)=A\tan \left (\dfrac{\pi}{8}x \right )\).
- Hatua ya 3. Ili kupata kunyoosha wima\(A\), tunaweza kutumia uhakika\((2,2)\). \[\begin{align*} 2&=A\tan \left (\dfrac{\pi}{8}\cdot 2 \right )\\ &=A\tan \left (\dfrac{\pi}{4} \right ) \end{align*}\]
Kwa sababu\(\tan \left (\dfrac{\pi}{4} \right )=1\),\(A=2\).
Kazi hii ingekuwa na formula\(f(x)=2\tan \left (\dfrac{\pi}{8}x \right )\).
Pata fomu ya kazi katika Kielelezo\(\PageIndex{7}\).
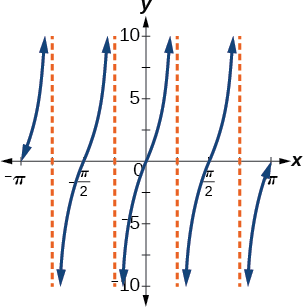
Kielelezo\(\PageIndex{7}\)
- Jibu
-
\(g(x)=4\tan(2x)\)
Kuchambua Grafu ya\(y = \sec x\) na\(y = \csc x\)
Secant ilifafanuliwa na utambulisho wa usawa\(sec \, x=\dfrac{1}{\cos x}\). Kumbuka kwamba kazi haijulikani wakati cosine ni\(0\), na kusababisha asymptotes wima\(1\) katika\(\dfrac{\pi}{2}\),\(\dfrac{3\pi}{2}\) nk Kwa sababu cosine kamwe zaidi ya thamani kamili, secant, kuwa ya usawa, kamwe kuwa chini ya\(1\) thamani kamili.
Tunaweza grafu\(y=\sec x\) kwa kuchunguza grafu ya kazi ya cosine kwa sababu kazi hizi mbili ni za usawa wa kila mmoja. Angalia Kielelezo\(\PageIndex{8}\). Grafu ya cosine inavyoonyeshwa kama wimbi la machungwa lililopigwa ili tuweze kuona uhusiano. Ambapo grafu ya kazi ya cosine inapungua, grafu ya kazi ya secant huongezeka. Ambapo grafu ya kazi ya cosine huongezeka, grafu ya kazi ya secant inapungua. Wakati kazi ya cosine ni sifuri, secant haijulikani.
Grafu ya secant ina asymptotes wima kwa kila thamani ya\(x\) ambapo grafu ya cosine inavuka\(x\) -axis; tunaonyesha haya katika grafu hapa chini na mistari ya wima iliyopigwa, lakini haitaonyesha asymptotes zote wazi kwenye grafu zote za baadaye zinazohusisha secant na cosecant.
Kumbuka kwamba, kwa sababu cosine ni kazi hata, secant pia ni kazi hata. Hiyo ni,\(\sec(−x)=\sec x\).
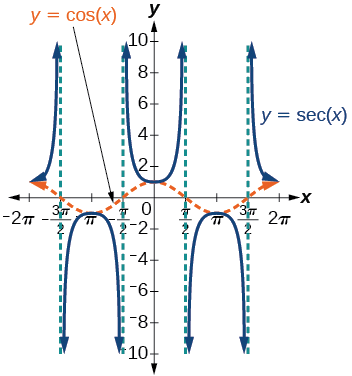
Kielelezo\(\PageIndex{8}\): Grafu ya kazi ya secant,\(f(x)=\sec x=\dfrac{1}{\cos x}\)
Kama tulivyofanya kwa kazi ya tangent, tutataja tena mara kwa mara\(| A |\) kama sababu ya kuenea, sio amplitude.
- Sababu ya kunyoosha ni\(| A |\).
- Kipindi ni\(\dfrac{2\pi}{| B |}\).
- Kikoa ni\(x≠\dfrac{\pi}{2| B |}k\), wapi\(k\) integer isiyo ya kawaida.
- Mipangilio ni\((−∞,−|A|]∪[|A|,∞)\).
- Asymptotes wima hutokea saa\(x=\dfrac{\pi}{2| B |}k\),\(k\) wapi integer isiyo ya kawaida.
- Hakuna amplitude.
- \(y=A\sec(Bx)\)ni kazi hata kwa sababu cosine ni kazi hata.
Sawa na secant, cosecant inaelezwa na utambulisho wa usawa\(\csc x=\dfrac{1}{\sin x}\). Kumbuka kwamba kazi haijulikani wakati sine ni\(0\), na kusababisha asymptote wima katika grafu\(1\) katika\(0\)\(\pi\), nk Kwa kuwa sine kamwe zaidi ya thamani kamili, cosecant, kuwa kubadilishana, kamwe kuwa chini ya\(1\) thamani kamili.
Tunaweza grafu\(y=\csc x\) kwa kuchunguza grafu ya kazi ya sine kwa sababu kazi hizi mbili ni za usawa wa kila mmoja. Angalia Kielelezo\(\PageIndex{7}\). Grafu ya sine inaonyeshwa kama wimbi la machungwa lililopigwa ili tuweze kuona uhusiano. Ambapo grafu ya kazi ya sine inapungua, grafu ya kazi ya cosecant huongezeka. Ambapo grafu ya kazi ya sine huongezeka, grafu ya kazi ya cosecant inapungua.
Grafu ya cosecant ina asymptotes wima kwa kila thamani ya\(x\) ambapo grafu ya sine inavuka\(x\) -axis; tunaonyesha haya katika grafu hapa chini na mistari ya wima iliyopigwa.
Kumbuka kuwa, tangu sine ni kazi isiyo ya kawaida, kazi ya cosecant pia ni kazi isiyo ya kawaida. Hiyo ni,\(\csc(−x)=−\csc x\).
Grafu ya cosecant, ambayo inavyoonyeshwa kwenye Kielelezo\(\PageIndex{9}\), ni sawa na grafu ya secant.
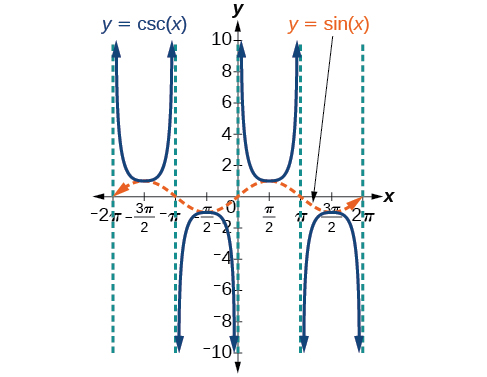
Kielelezo\(\PageIndex{9}\): Grafu ya kazi ya cosecant,\(f(x)=\csc x=\frac{1}{\sin x}\)
- Sababu ya kunyoosha ni\(| A |\).
- Kipindi ni\(\dfrac{2\pi}{|B|}\).
- Kikoa ni\(x≠\dfrac{\pi}{|B|}k\), wapi\(k\) integer.
- Mipangilio ni\((−∞,−|A|]∪[|A|,∞)\).
- Asymptotes hutokea saa\(x=\dfrac{\pi}{| B |}k\),\(k\) wapi integer.
- \(y=A\csc(Bx)\)ni kazi isiyo ya kawaida kwa sababu sine ni kazi isiyo ya kawaida.
Graphing Tofauti ya\(y = \sec x\) na\(y= \csc x\)
Kwa kubadilishwa, USITUMIE, na/au matoleo aliweka ya kazi secant na cosecant, tunaweza kufuata mbinu sawa na wale tulitumia kwa tangent na cotangent. Hiyo ni, tunapata asymptotes wima na pia tathmini kazi kwa pointi chache (hasa extrema ya ndani). Ikiwa tunataka kupiga graph kipindi kimoja tu, tunaweza kuchagua muda kwa kipindi kwa njia zaidi ya moja. Utaratibu wa secant ni sawa sana, kwa sababu utambulisho wa cofunction ina maana kwamba grafu ya secant ni sawa na grafu ya cosecant iliyobadilishwa nusu kipindi upande wa kushoto. Mabadiliko ya wima na awamu yanaweza kutumika kwa kazi ya cosecant kwa njia sawa na kwa kazi za secant na nyingine.Equations kuwa yafuatayo.
\[y=A\sec(Bx−C)+D\]
\[y=A\csc(Bx−C)+D\]
- Sababu ya kunyoosha ni\(|A|\).
- Kipindi ni\(\dfrac{2\pi}{|B|}\).
- Kikoa ni\(x≠\dfrac{C}{B}+\dfrac{\pi}{2| B |}k\), wapi\(k\) integer isiyo ya kawaida.
- Mipangilio ni\((−∞,−|A|]∪[|A|,∞)\).
- Asymptotes wima hutokea saa\(x=\dfrac{C}{B}+\dfrac{π}{2| B |}k\),\(k\) wapi integer isiyo ya kawaida.
- Hakuna amplitude.
- \(y=A\sec(Bx)\)ni kazi hata kwa sababu cosine ni kazi hata.
- Sababu ya kunyoosha ni\(|A|\).
- Kipindi ni\(\dfrac{2\pi}{|B|}\).
- Kikoa ni\(x≠\dfrac{C}{B}+\dfrac{\pi}{2| B |}k\), wapi\(k\) integer.
- Mipangilio ni\((−∞,−|A|]∪[|A|,∞)\).
- Asymptotes wima hutokea saa\(x=\dfrac{C}{B}+\dfrac{\pi}{|B|}k\),\(k\) wapi integer.
- Hakuna amplitude.
- \(y=A\csc(Bx)\)ni kazi isiyo ya kawaida kwa sababu sine ni kazi isiyo ya kawaida.
- Eleza kazi iliyotolewa katika fomu\(y=A\sec(Bx)\).
- Tambua sababu ya kunyoosha/compressing,\(|A|\).
- Tambua\(B\) na kuamua kipindi,\(P=\dfrac{2\pi}{| B |}\).
- Mchoro grafu ya\(y=A\cos(Bx)\).
- Tumia uhusiano wa usawa kati\(y=\cos \, x\) na\(y=\sec \, x\) kuteka grafu ya\(y=A\sec(Bx)\).
- Mchoro asymptotes.
- Panda pointi mbili za kumbukumbu na kuteka grafu kupitia pointi hizi.
Grafu kipindi kimoja cha\(f(x)=2.5\sec(0.4x)\).
Suluhisho
- Hatua ya 1. Kazi iliyotolewa tayari imeandikwa kwa fomu ya jumla,\(y=A\sec(Bx)\).
- Hatua ya 2. \(A=2.5\)hivyo sababu ya kunyoosha ni\(2.5\).
- Hatua ya 3. \(B=0.4\)hivyo\(P=\dfrac{2\pi}{0.4}=5\pi\). Kipindi ni\(5\pi\) vitengo.
- Hatua ya 4. Mchoro grafu ya kazi\(g(x)=2.5\cos(0.4x)\).
- Hatua ya 5. Tumia uhusiano wa usawa wa kazi za cosine na salama ili kuteka kazi ya cosecant.
- Hatua 6-7. Mchoro asymptotes mbili katika\(x=1.25\pi\) na\(x=3.75\pi\). Tunaweza kutumia pointi mbili za kumbukumbu, kiwango cha chini cha ndani\((0,2.5)\) na upeo wa ndani katika\((2.5\pi,−2.5)\). Kielelezo\(\PageIndex{10}\) kinaonyesha grafu.
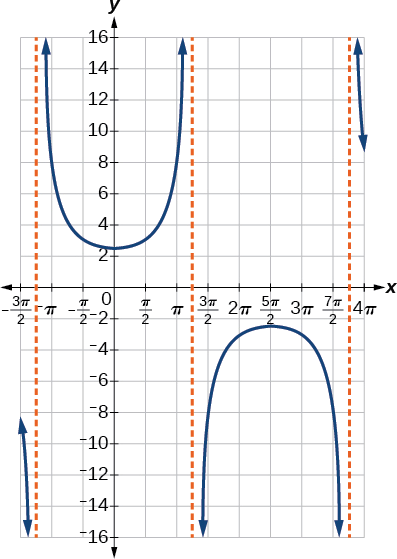
Kielelezo\(\PageIndex{10}\)
Grafu kipindi kimoja cha\(f(x)=−2.5\sec(0.4x)\).
- Jibu
-
Hii ni tafakari ya wima ya grafu iliyotangulia kwa sababu\(A\) ni hasi.
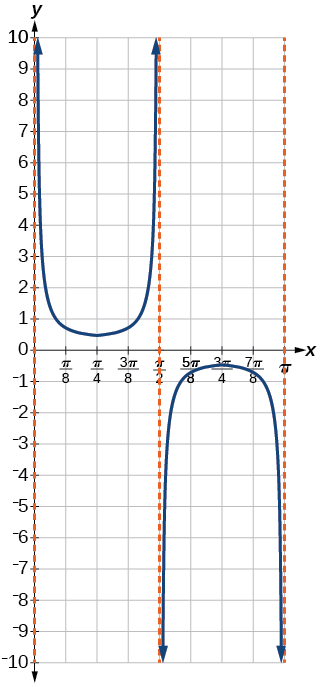
Kielelezo\(\PageIndex{11}\)
Ndiyo. mbalimbali ya\(f(x)=A\sec(Bx−C)+D\) ni\((−∞,−|A|+D]∪[|A|+D,∞)\).
- Eleza kazi iliyotolewa katika fomu\(y=A \sec(Bx−C)+D\).
- Tambua sababu ya kunyoosha/compressing,\(| A |\).
- Tambua\(B\) na kuamua kipindi,\(\dfrac{2\pi}{|B|}\).
- Tambua\(C\) na kuamua mabadiliko ya awamu,\(\dfrac{C}{B}\).
- Chora grafu\(y=A \sec(Bx)\) ya. lakini kuhama kwa haki\(\dfrac{C}{B}\) na kuendelea na\(D\).
- Mchoro asymptotes wima, ambayo hutokea katika\(x=\dfrac{C}{B}+\dfrac{\pi}{2| B |}k\), ambapo\(k\) ni integer isiyo ya kawaida.
Grafu kipindi kimoja cha\(y=4\sec \left (\dfrac{\pi}{3x}−\dfrac{\pi}{2} \right )+1\).
Suluhisho
- Hatua ya 1. Eleza kazi iliyotolewa katika fomu\(y=4\sec \left (\dfrac{\pi}{3x}−\dfrac{\pi}{2} \right )+1\).
- Hatua ya 2. Sababu ya kunyoosha/compressing ni\(| A |=4\).
- Hatua ya 3. Kipindi ni
\[\begin{align*} \dfrac{2\pi}{|B|}&= \dfrac{2\pi}{\dfrac{\pi}{3}}\\ &= 2\pi \cdot \dfrac{3}{\pi}\\ &= 6 \end{align*}\]
- Hatua ya 4. Mabadiliko ya awamu ni
\[\begin{align*} \dfrac{C}{B}&= \dfrac{\dfrac{\pi}{2}}{\dfrac{\pi}{3}}\\ &= \dfrac{\pi}{2}\cdot \dfrac{3}{\pi}\\ &= 1.5 \end{align*}\]
- Hatua ya 5. Chora grafu ya\(y=A\sec(Bx)\), lakini kuhama kwa haki\(\dfrac{C}{B}=1.5\) na kuendelea na\(D=6\).
- Hatua ya 6. Mchoro asymptotes wima, ambayo hutokea saa\(x=0\),\(x=3\), na\(x=6\). Kuna kiwango cha chini ndani katika\((1.5,5)\) na upeo wa ndani katika\((4.5,−3)\). Kielelezo\(\PageIndex{12}\) kinaonyesha grafu.
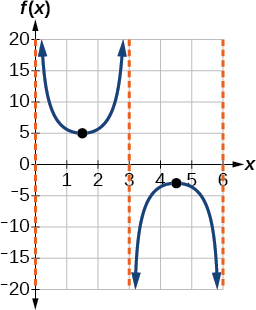
Kielelezo\(\PageIndex{12}\)
Grafu kipindi kimoja cha\(f(x)=−6\sec(4x+2)−8\).
- Jibu
-
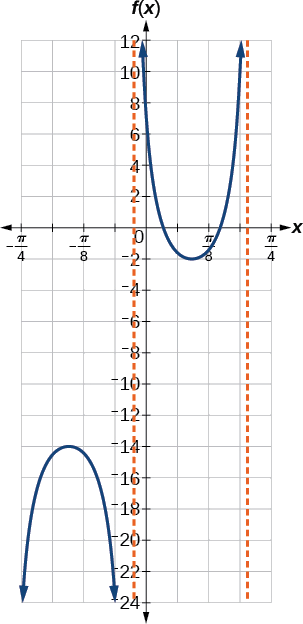
Kielelezo\(\PageIndex{13}\)
Ndiyo. Vipengele vilivyotengwa vya uwanja hufuata asymptotes ya wima. Maeneo yao yanaonyesha mabadiliko ya usawa na ukandamizaji au upanuzi unaotajwa na mabadiliko kwa pembejeo ya kazi ya awali.
- Eleza kazi iliyotolewa katika fomu\(y=A\csc(Bx)\).
- \(|A|\).
- Tambua\(B\) na kuamua kipindi,\(P=\dfrac{2\pi}{| B |}\).
- Chora grafu ya\(y=A\sin(Bx)\).
- Tumia uhusiano wa usawa kati\(y=sin \, x\) na\(y=\csc \, x\) kuteka grafu ya\(y=A\csc(Bx)\).
- Mchoro asymptotes.
- Panda pointi mbili za kumbukumbu na kuteka grafu kupitia pointi hizi.
Grafu kipindi kimoja cha\(f(x)=−3\csc(4x)\).
Suluhisho
- Hatua ya 1. Kazi iliyotolewa tayari imeandikwa kwa fomu ya jumla,\(y=A\csc(Bx)\).
- Hatua ya 2. \(| A |=| −3 |=3\), hivyo sababu ya kunyoosha ni\(3\).
- Hatua ya 3. \(B=4\), hivyo\(P=\dfrac{2\pi}{4}=\dfrac{\pi}{2}\). Kipindi ni\(\dfrac{\pi}{2}\) vitengo.
- Hatua ya 4. Mchoro grafu ya kazi\(g(x)=−3\sin(4x)\).
- Hatua ya 5. Tumia uhusiano wa usawa wa kazi za sine na cosecant ili kuteka kazi ya cosecant.
- Hatua 6-7. Mchoro asymptotes tatu katika\(x=0\)\(x=\dfrac{\pi}{4}\),, na\(x=\dfrac{\pi}{2}\). Tunaweza kutumia pointi mbili kumbukumbu, ndani ya kiwango cha juu katika\(\left (\dfrac{\pi}{8},−3 \right )\) na kiwango cha chini ndani katika\(\left (\dfrac{3\pi}{8},3 \right )\). Kielelezo\(\PageIndex{14}\) kinaonyesha grafu.
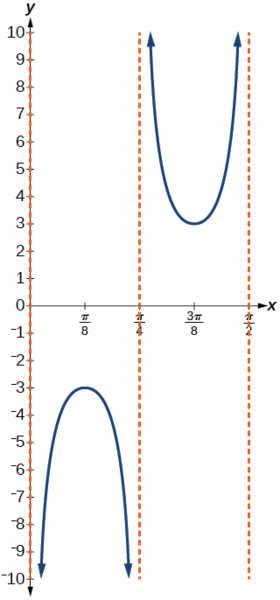
Kielelezo\(\PageIndex{14}\)
Grafu kipindi kimoja cha\(f(x)=0.5\csc(2x)\).
- Jibu
-
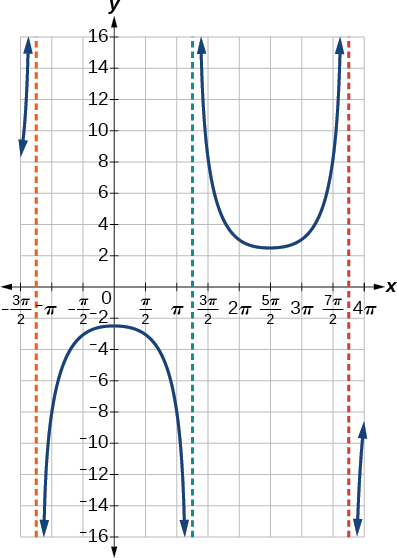
Kielelezo\(\PageIndex{15}\)
- Eleza kazi iliyotolewa katika fomu\(y=A\csc(Bx−C)+D\).
- Tambua sababu ya kunyoosha/compressing,\(|A|\).
- Tambua\(B\) na kuamua kipindi,\(\dfrac{2\pi}{| B |}\).
- Tambua\(C\) na kuamua mabadiliko ya awamu,\(\dfrac{C}{B}\).
- Chora grafu ya\(y=A\csc(Bx)\) lakini kuhama kwa haki na kuendelea na\(D\).
- Mchoro asymptotes wima, ambayo hutokea\(x=\dfrac{C}{B}+\dfrac{\pi}{| B |}k\),\(k\) wapi integer.
Mchoro grafu ya\(y=2\csc \left (\dfrac{\pi}{2}x \right )+1\). Je, ni uwanja na aina gani ya kazi hii?
Suluhisho
- Hatua ya 1. Eleza kazi iliyotolewa katika fomu\(y=2\csc \left (\dfrac{\pi}{2}x \right )+1\).
- Hatua ya 2. Tambua sababu ya kunyoosha/compressing,\(| A |=2\).
- Hatua ya 3. Kipindi ni\(\dfrac{2\pi}{| B |}=\dfrac{2\pi}{\dfrac{\pi}{2}}=2\pi⋅\dfrac{2}{\pi}=4\).
- Hatua ya 4. Mabadiliko ya awamu ni\(\dfrac{0}{\dfrac{\pi}{2}}=0\).
- Hatua ya 5. Chora grafu ya\(y=A\csc(Bx)\) lakini ugeuke\(D=1\).
- Hatua ya 6. Mchoro asymptotes wima, ambayo hutokea saa\(x=0\),\(x=2\),\(x=4\).
Grafu ya kazi hii inavyoonekana kwenye Kielelezo\(\PageIndex{16}\).
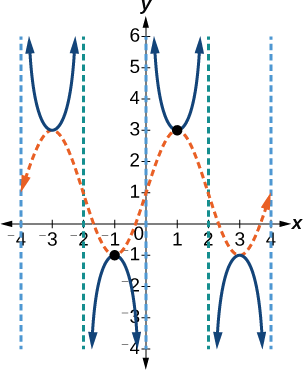
Kielelezo\(\PageIndex{16}\): Kazi iliyobadilishwa ya cosecant
Uchambuzi
Asymptotes wima inavyoonekana kwenye alama ya grafu mbali kipindi kimoja cha kazi, na extrema ya ndani katika kipindi hiki inavyoonyeshwa na dots. Angalia jinsi graph ya cosecant kubadilishwa inahusiana na grafu ya\(f(x)=2\sin \left (\frac{\pi}{2}x \right )+1\), umeonyesha kama machungwa dashed wimbi.
Kutokana na grafu ya\(f(x)=2\cos \left (\frac{\pi}{2}x \right )+1\) inavyoonekana katika Kielelezo\(\PageIndex{17}\), mchoro grafu ya\(g(x)=2\sec \left (\dfrac{\pi}{2}x \right )+1\) juu ya axes sawa.
![Grafu ya vipindi viwili vya kazi ya cosine iliyobadilishwa. Upeo ni [-1,3], umewekwa kutoka x=-4 hadi x=4.](https://math.libretexts.org/@api/deki/files/14146/imageedit_56_4915587648.png)
Kielelezo\(\PageIndex{17}\)
- Jibu
-
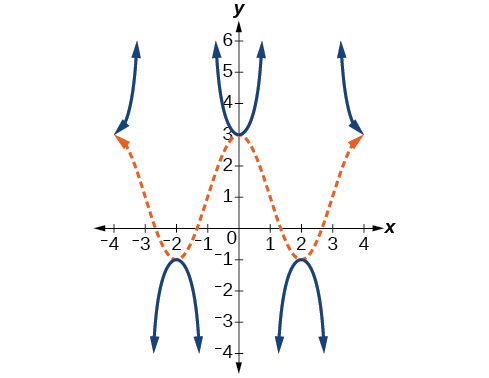
Kielelezo\(\PageIndex{18}\)
Kuchambua Grafu ya\(y = \cot x\)
Kazi ya mwisho ya trigonometric tunayohitaji kuchunguza ni cotangent. Cotangent inaelezwa na utambulisho wa usawa\(cot \, x=\dfrac{1}{\tan x}\). Kumbuka kwamba kazi haijulikani wakati kazi ya tangent ni\(0\), na kusababisha asymptote wima katika grafu saa\(0\)\(\pi\), nk Kwa kuwa pato la kazi ya tangent ni namba zote halisi, pato la kazi ya cotangent pia ni namba zote halisi.
Tunaweza grafu\(y=\cot x\) kwa kuchunguza grafu ya kazi ya tangent kwa sababu kazi hizi mbili ni za usawa wa kila mmoja. Angalia Kielelezo\(\PageIndex{19}\). Ambapo grafu ya kazi ya tangent inapungua, grafu ya kazi ya cotangent huongezeka. Ambapo grafu ya kazi ya tangent huongezeka, grafu ya kazi ya cotangent inapungua.
Grafu ya cotangent ina asymptotes wima kwa kila thamani ya\(x\) wapi\(\tan x=0\); tunaonyesha haya katika grafu hapa chini na mistari iliyopigwa. Kwa kuwa cotangent ni usawa wa tangent,\(\cot x\) ina asymptotes wima katika maadili yote ya\(x\) wapi\(\tan x=0\), na\(\cot x=0\) kwa maadili yote ya\(x\) wapi\(\tan x\) ina asymptotes yake ya wima.
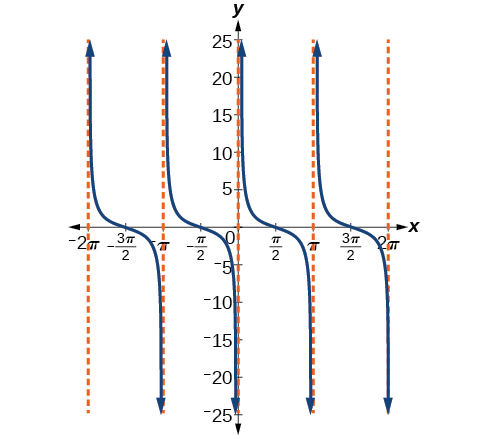
Kielelezo\(\PageIndex{19}\): Kazi ya cotangent
- Sababu ya kunyoosha ni\(|A|\).
- Kipindi ni\(P=\dfrac{\pi}{|B|}\).
- Kikoa ni\(x≠\dfrac{\pi}{|B|}k\), wapi\(k\) integer.
- Mipangilio ni\((−∞,∞)\).
- Asymptotes hutokea saa\(x=\dfrac{\pi}{| B |}k\),\(k\) wapi integer.
- \(y=A\cot(Bx)\)ni kazi isiyo ya kawaida.
Graphing Tofauti ya\(y =\cot x\)
Tunaweza kubadilisha grafu ya cotangent kwa njia sawa na tulivyofanya kwa tangent. Equation inakuwa yafuatayo.
\[y=A\cot(Bx−C)+D\]
- Sababu ya kunyoosha ni\(| A |\).
- Kipindi ni\(\dfrac{\pi}{|B|}\)
- Kikoa ni\(x≠\dfrac{C}{B}+\dfrac{\pi}{| B |}k\), wapi\(k\) integer.
- Mipangilio ni\((−∞,−|A|]∪[|A|,∞)\).
- Asymptotes wima hutokea saa\(x=\dfrac{C}{B}+\dfrac{\pi}{| B |}k\),\(k\) wapi integer.
- Hakuna amplitude.
- \(y=A\cot(Bx)\)ni kazi isiyo ya kawaida kwa sababu ni quotient ya kazi hata na isiyo ya kawaida (cosine na sine, kwa mtiririko huo)
- Eleza kazi katika fomu\(f(x)=A\cot(Bx)\).
- Tambua sababu ya kuenea,\(|A|\).
- Tambua kipindi,\(P=\dfrac{\pi}{|B|}\).
- Chora grafu ya\(y=A\tan(Bx)\).
- Panda pointi zozote mbili za kumbukumbu.
- Tumia uhusiano wa usawa kati ya tangent na cotangent kuteka grafu ya\(y=Acot(Bx)\).
- Mchoro asymptotes.
Kuamua sababu ya kunyoosha, kipindi, na mabadiliko ya awamu ya\(y=3\cot(4x)\), na kisha mchoro grafu.
Suluhisho
- Hatua ya 1. Kuonyesha kazi katika fomu\(f(x)=A\cot(Bx)\) inatoa\(f(x)=3\cot(4x)\).
- Hatua ya 2. Sababu ya kunyoosha ni\(|A|=3\).
- Hatua ya 3. Kipindi ni\(P=\dfrac{\pi}{4}\).
- Hatua ya 4. Mchoro grafu ya\(y=3\tan(4x)\).
- Hatua ya 5. Panda pointi mbili za kumbukumbu. Vipengele viwili vile ni\(\left (\dfrac{\pi}{16},3 \right )\) na\(\left (\dfrac{3\pi}{16},−3 \right )\).
- Hatua ya 6. Tumia uhusiano wa usawa kuteka\(y=3\cot(4x)\).
- Hatua ya 7. Mchoro asymptotes,\(x=0\),\(x=\dfrac{\pi}{4}\).
Grafu ya machungwa katika Kielelezo\(\PageIndex{20}\) inaonyesha\(y=3\tan(4x)\) na grafu ya bluu inaonyesha\(y=3\cot(4x)\).
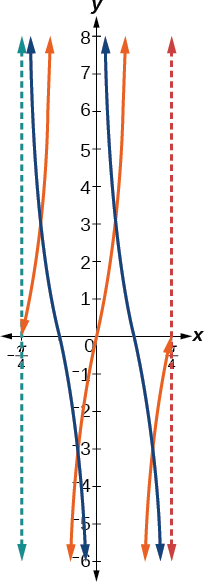
Kielelezo\(\PageIndex{20}\)
- Eleza kazi katika fomu\(f(x)=A\cot(Bx−C)+D\).
- Tambua sababu ya kuenea,\(| A |\).
- Tambua kipindi,\(P=\dfrac{\pi}{|B|}\).
- Tambua mabadiliko ya awamu,\(\dfrac{C}{B}\).
- Chora grafu ya\(y=A\tan(Bx)\) kubadilishwa kwa haki\(\dfrac{C}{B}\) na juu\(D\).
- Mchoro asymptotes\(x=\dfrac{C}{B}+\dfrac{\pi}{| B |}k\),\(k\) wapi integer.
- Panda pointi yoyote ya kumbukumbu tatu na kuteka grafu kupitia pointi hizi.
Mchoro grafu ya kipindi kimoja cha kazi\(f(x)=4\cot \left (\dfrac{\pi}{8}x−\dfrac{\pi}{2} \right )−2\).
Suluhisho
- Hatua ya 1. Kazi tayari imeandikwa kwa fomu ya jumla\(f(x)=A\cot(Bx−C)+D\).
- Hatua ya 2. \(A=4\), hivyo sababu ya kunyoosha ni\(4\).
- Hatua ya 3. \(B=\dfrac{\pi}{8}\), hivyo kipindi ni\(P=\dfrac{\pi}{| B |}=\dfrac{\pi}{\dfrac{\pi}{8}}=8\).
- Hatua ya 4. \(C=\dfrac{\pi}{2}\), hivyo mabadiliko ya awamu ni\(CB=\dfrac{\dfrac{\pi}{2}}{\dfrac{\pi}{8}}=4\).
- Hatua ya 5. Sisi kuteka\(f(x)=4\tan \left (\dfrac{\pi}{8}x−\dfrac{\pi}{2} \right )−2\).
- Hatua ya 6-7. Vipengele vitatu tunaweza kutumia kuongoza grafu ni\((6,2)\),\((8,−2)\), na\((10,−6)\). Tunatumia uhusiano wa usawa wa tangent na cotangent kuteka\(f(x)=4\cot \left (\dfrac{\pi}{8}x−\dfrac{\pi}{2} \right )−2\).
- Hatua ya 8. Asymptotes wima ni\(x=4\) na\(x=12\).
Grafu inavyoonyeshwa kwenye Kielelezo\(\PageIndex{21}\).
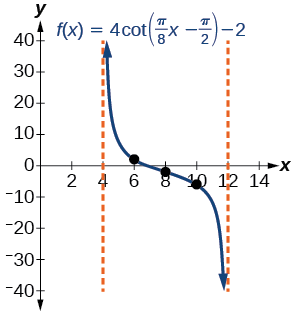
Kielelezo\(\PageIndex{21}\): Kipindi kimoja cha kazi iliyobadilishwa ya cotangent
Kutumia Grafu za Kazi za Trigonometric kutatua Matatizo halisi ya Dunia
Matukio mengi ya ulimwengu halisi yanawakilisha kazi za mara kwa mara na inaweza kuwa inatokana na kazi za trigonometric. Kwa mfano, hebu kurudi kwenye hali kutoka kwa kopo ya sehemu. Je! Umewahi kuona boriti iliyotengenezwa na mwanga unaozunguka kwenye gari la polisi na kujiuliza juu ya harakati ya boriti ya mwanga yenyewe kwenye ukuta? Tabia ya mara kwa mara ya umbali mwanga huangaza kama kazi ya wakati ni dhahiri, lakini tunawezaje kuamua umbali? Tunaweza kutumia kazi tangent.
Tuseme kazi\(y=5\tan(\dfrac{\pi}{4}t)\) alama umbali katika harakati ya boriti mwanga kutoka juu ya gari polisi katika ukuta ambapo\(t\) ni wakati katika sekunde na\(y\) ni umbali katika miguu kutoka hatua juu ya ukuta moja kwa moja hela kutoka gari polisi.
- Pata na kutafsiri sababu ya kuenea na kipindi.
- Grafu juu ya muda\([0,5]\).
- Kutathmini\(f(1)\) na kujadili thamani ya kazi katika pembejeo kwamba.
Suluhisho
- Tunajua kutoka kwa fomu ya jumla ya\(y=A\tan(Bt)\) hiyo\(| A |\) ni sababu ya kuenea na\(\dfrac{\pi}{B}\) ni kipindi.
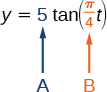
Kielelezo\(\PageIndex{22}\)
Tunaona kwamba sababu ya kunyoosha ni\(5\). Hii ina maana kwamba boriti ya mwanga itahamia\(5\) ft baada ya nusu kipindi.
Kipindi ni\(\dfrac{\pi}{\tfrac{\pi}{4}}=\dfrac{\pi}{1}⋅\dfrac{4}{\pi}=4\). Hii ina maana kwamba kila\(4\) sekunde, boriti ya mwanga inafuta ukuta. Umbali kutoka doa hela kutoka gari la polisi unakua kubwa huku gari la polisi linakaribia.
- Ili kuchora kazi, tunapata asymptote\(t=2\) na kutumia sababu ya kuenea na kipindi. Angalia Kielelezo\(\PageIndex{23}\)
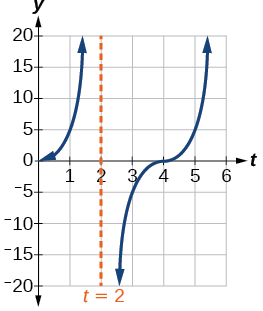
Kielelezo\(\PageIndex{23}\)
- kipindi:\(f(1)=5\tan(\frac{\pi}{4}(1))=5(1)=5\); baada ya\(1\) pili, boriti ya ina wakiongozwa\(5\) ft kutoka doa hela kutoka gari polisi.
Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na grafu za kazi nyingine za trigonometric.
Mlinganyo muhimu
| Kubadilishwa, kusisitizwa, na/au aliweka kazi tangent | \(y=A \tan(Bx−C)+D\) |
| Kubadilishwa, kusisitizwa, na/au aliweka kazi ya secant | \(y=A \sec(Bx−C)+D\) |
| Kubadilishwa, kusisitizwa, na/au aliweka kazi ya cosecant | \(y=A \csc(Bx−C)+D\) |
| Kubadilishwa, kusisitizwa, na/au aliweka kazi ya cotangent | \(y=A \cot(Bx−C)+D\) |
Dhana muhimu
- Kazi ya tangent ina kipindi\(π\).
- \(f( x )=A\tan( Bx−C )+D\)ni tangent na wima na/au usawa kunyoosha/compression na kuhama. Angalia Mfano\(\PageIndex{1}\), Mfano\(\PageIndex{2}\), na Mfano\(\PageIndex{3}\).
- Secant na cosecant ni kazi zote mbili mara kwa mara na kipindi cha\(2\pi\). \(f( x )=A\sec( Bx−C )+D\)anatoa kubadilishwa, USITUMIE, na/au aliweka secant kazi grafu. Angalia Mfano\(\PageIndex{4}\) na Mfano\(\PageIndex{5}\).
- \(f( x )=A\csc( Bx−C )+D\)anatoa kubadilishwa, USITUMIE, na/au aliweka cosecant kazi grafu. Angalia Mfano\(\PageIndex{6}\) na Mfano\(\PageIndex{7}\).
- Kazi ya cotangent ina muda\(\pi\) na asymptotes wima katika\(0,±\pi,±2\pi\),...
- Aina ya cotangent ni\(( −∞,∞ )\), na kazi inapungua kwa kila hatua katika upeo wake.
- Cotangent ni sifuri saa\(±\dfrac{\pi}{2},±\dfrac{3\pi}{2}\),...
- \(f(x)=A\cot(Bx−C)+D\)ni cotangent na wima na/au usawa kunyoosha/compression na kuhama. Angalia Mfano\(\PageIndex{8}\) na Mfano\(\PageIndex{9}\).
- Matukio halisi ya ulimwengu yanaweza kutatuliwa kwa kutumia grafu za kazi za trigonometric. Angalia Mfano\(\PageIndex{10}\).


