Skip to main content
Global

13.2: Constants ya usawa

  1. Last updated
  2. Save as PDF
  • Page ID
    176835

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza
    • Hutumia quotients ya mmenyuko kutoka kwa usawa wa kemikali unaowakilisha athari za kawaida na zisizo za kawaida
    • Tumia maadili ya quotients ya majibu na mara kwa mara ya usawa, kwa kutumia viwango na shinikizo
    • Eleza ukubwa wa mara kwa mara ya usawa kwa mali ya mfumo wa kemikali

    Sasa kwa kuwa tuna ishara (\(\rightleftharpoons\)) kuteua athari zinazobadilishwa, tutahitaji njia ya kueleza hesabu jinsi kiasi cha reactants na bidhaa zinaathiri usawa wa mfumo. Equation ya jumla kwa mmenyuko wa kubadilishwa inaweza kuandikwa kama ifuatavyo:

    \[m\ce{A}+n\ce{B}+ \rightleftharpoons x\ce{C}+y\ce{D} \label{13.3.1} \]

    Tunaweza kuandika majibu quotient (\(Q\)) kwa equation hii. Wakati tathmini kwa kutumia viwango, inaitwa\(Q_c\). Tunatumia mabano ili kuonyesha viwango vya molar vya reactants na bidhaa.

    \[ Q_c=\dfrac{[\ce{C}]^x[\ce{D}]^y}{[\ce{A}]^m[\ce{B}]^n} \label{13.3.2} \]

    Quotient ya mmenyuko ni sawa na viwango vya molar vya bidhaa za equation ya kemikali (kuzidisha pamoja) juu ya reactants (pia huongezeka pamoja), na kila mkusanyiko umeongezeka kwa nguvu ya mgawo wa dutu hiyo katika usawa wa kemikali. Kwa mfano, quotient ya majibu kwa mmenyuko wa kubadilishwa

    \[\ce{2NO}_{2(g)} \rightleftharpoons \ce{N_2O}_{4(g)} \label{13.3.3} \]

    inatolewa na maneno haya:

    \[Q_c=\ce{\dfrac{[N_2O_4]}{[NO_2]^2}} \label{13.3.4} \]

    Mfano\(\PageIndex{1}\): Writing Reaction Quotient Expressions

    Andika maneno kwa quotient ya majibu kwa kila moja ya athari zifuatazo:

    1. \(\ce{3O}_{2(g)} \rightleftharpoons \ce{2O}_{3(g)}\)
    2. \(\ce{N}_{2(g)}+\ce{3H}_{2(g)} \rightleftharpoons \ce{2NH}_{3(g)}\)
    3. \(\ce{4NH}_{3(g)}+\ce{7O}_{2(g)} \rightleftharpoons \ce{4NO}_{2(g)}+\ce{6H_2O}_{(g)}\)
    Suluhisho
    1. \(Q_c=\dfrac{[\ce{O3}]^2}{[\ce{O2}]^3}\)
    2. \( Q_c=\dfrac{[\ce{NH3}]^2}{\ce{[N2][H2]}^3}\)
    3. \( Q_c=\dfrac{\ce{[NO2]^4[H2O]^6}}{\ce{[NH3]^4[O2]^7}}\)
    Zoezi\(\PageIndex{1}\)

    Andika maneno kwa quotient ya majibu kwa kila moja ya athari zifuatazo:

    1. \( \ce{2SO2}(g)+\ce{O2}(g) \rightleftharpoons \ce{2SO3}(g)\)
    2. \( \ce{C4H8}(g) \rightleftharpoons \ce{2C2H4}(g)\)
    3. \( \ce{2C4H10}(g)+\ce{13O2}(g) \rightleftharpoons \ce{8CO2}(g)+\ce{10H2O}(g)\)
    Jibu

    \( Q_c=\dfrac{[\ce{SO3}]^2}{\ce{[SO2]^2[O2]}}\)

    Jibu b

    \( Q_c=\dfrac{[\ce{C2H4}]^2}{[\ce{C4H8}]}\)

    Jibu c

    \( Q_c=\dfrac{\ce{[CO2]^8[H2O]^{10}}}{\ce{[C4H10]^2[O2]^{13}}}\)

    Thamani ya nambari ya\(Q_c\) mmenyuko uliotolewa inatofautiana; inategemea viwango vya bidhaa na majibu yaliyopo wakati\(Q_c\) imedhamiriwa. Wakati reactants safi ni mchanganyiko,\(Q_c\) ni awali sifuri kwa sababu hakuna bidhaa sasa katika hatua hiyo. Kama majibu yanavyoendelea, thamani ya\(Q_c\) ongezeko kama viwango vya ongezeko la bidhaa na viwango vya reactants hupungua wakati huo huo (Kielelezo\(\PageIndex{1}\)). Wakati mmenyuko unafikia usawa, thamani ya quotient ya mmenyuko haibadilika tena kwa sababu viwango havibadilika tena.

    Kielelezo\(\PageIndex{1}\): (a) Mabadiliko katika viwango vya majibu na bidhaa yanaonyeshwa kama\(\ce{2SO2}(g)+\ce{O2}(g) \rightleftharpoons \ce{2SO3}(g)\) majibu yanakaribia usawa. (b) Mabadiliko katika viwango vya reactants na bidhaa yanaonyeshwa kama mmenyuko\(\ce{2SO3}(g) \rightleftharpoons \ce{2SO2}(g)+\ce{O2}(g)\) unakaribia usawa. (c) Grafu inaonyesha mabadiliko katika thamani ya quotient majibu kama majibu inakaribia usawa.
    Grafu tatu zinaonyeshwa na zimeandikwa, “a,” “b,” na “c.” Grafu zote tatu zina mstari wa wima unaozunguka kupitia katikati iliyoandikwa, “Msawazo unafikiwa.” Mhimili wa y kwenye grafu a umeandikwa, “Mkazo,” na x-axis inaitwa, “Muda.” Curves tatu zimepangwa kwenye grafu. kwanza ni kinachoitwa, “[S O Subscript 2];” mstari huu huanza juu ya y-mhimili, mwisho katikati ya y mhimili, ina mwinuko wa awali mteremko na mteremko taratibu zaidi kama inakaribia kulia mbali juu ya x-mhimili. Curve ya pili kwenye grafu hii imeandikwa, “[O subscript 2];” mstari huu huiga kwanza isipokuwa kwamba huanza na kuishia asilimia hamsini chini kwenye mhimili wa y. Curve ya tatu ni inverse ya sura ya kwanza na imeandikwa, “[S O subscript 3].” Mhimili wa y kwenye grafu b ni lebo, “Mkazo,” na x-axis inaitwa, “Muda.” Curves tatu zimepangwa kwenye graph b. kwanza ni kinachoitwa, “[S O Subscript 2];” mstari huu huanza chini juu ya y-mhimili, mwisho katikati ya y mhimili, ina mwinuko wa awali mteremko na mteremko taratibu zaidi kama inakaribia kulia mbali juu ya x-mhimili. Curve ya pili kwenye grafu hii imeandikwa, “[O subscript 2];” mstari huu unaiga kwanza isipokuwa kwamba unakaribia asilimia hamsini chini kwenye mhimili wa y. Curve ya tatu ni inverse ya sura ya kwanza na imeandikwa, “[S O subscript 3].” Mhimili wa y kwenye grafu c ni lebo, “Quotient Reaction,” na x-axis inaitwa, “Muda.” Curve moja imepangwa kwenye grafu c. curve hii huanza chini ya mhimili y na kuongezeka kwa kasi juu karibu na juu ya mhimili y, kisha ngazi mbali katika mstari usawa. Sehemu ya juu ya mstari huu imeandikwa, “k.”

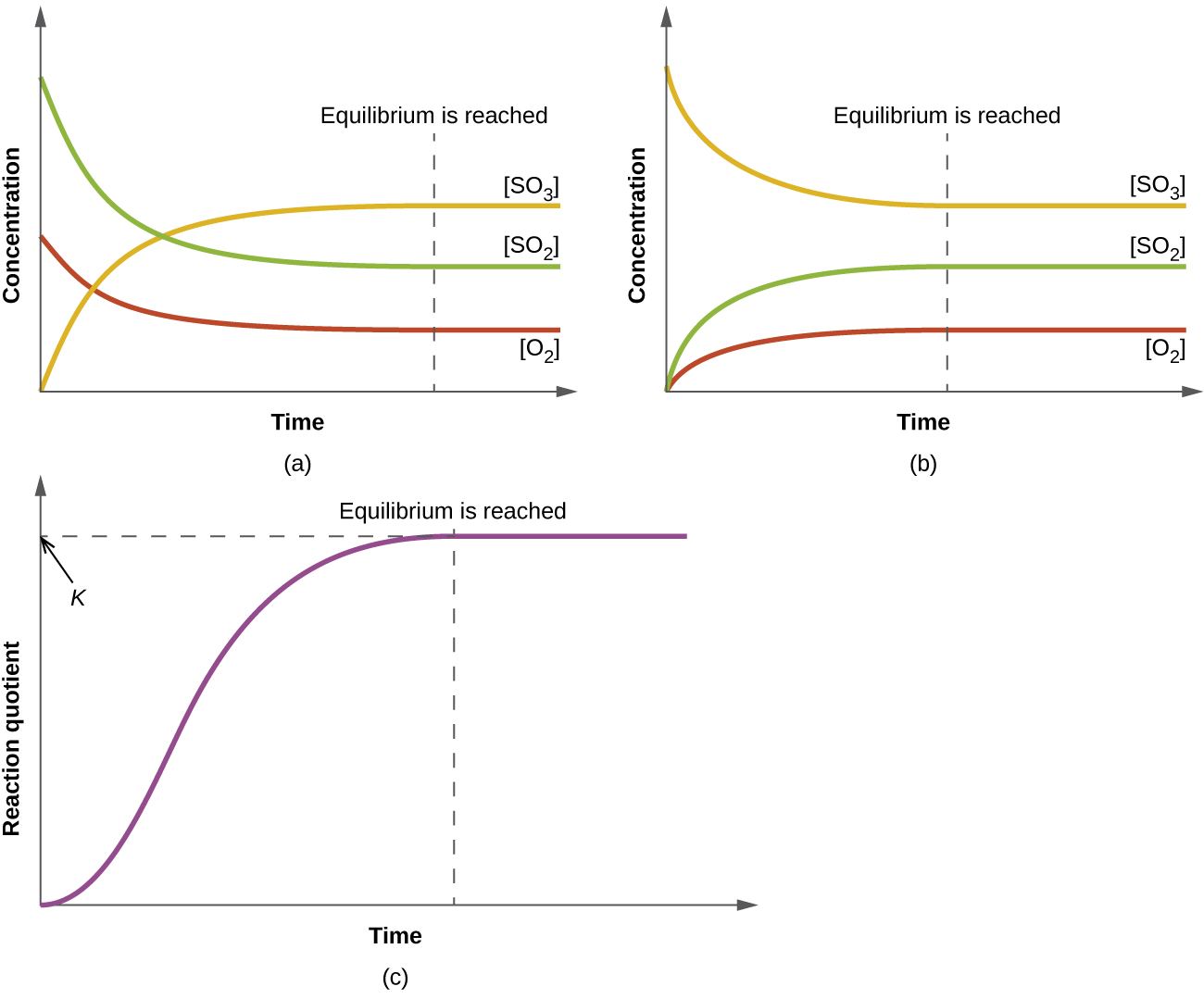
    Wakati mchanganyiko wa reactants na bidhaa za mmenyuko hufikia usawa kwa joto lililopewa, quotient yake ya majibu daima ina thamani sawa. Thamani hii inaitwa mara kwa mara ya usawa (\(K\)) ya mmenyuko kwenye joto hilo. Kama kwa quotient majibu, wakati tathmini katika suala la viwango, ni alibainisha kama\(K_c\).

    Kwamba quotient ya majibu daima inachukua thamani sawa katika usawa inaweza kuelezwa kama:

    \[Q_c \textrm{ at equilibrium}=K_c=\dfrac{[\ce C]^x[\ce D]^y...}{[\ce A]^m[\ce B]^n...} \label{13.3.5} \]

    Equation hii ni taarifa ya hisabati ya sheria ya hatua ya molekuli: Wakati mmenyuko umepata usawa kwenye joto lililopewa, quotient ya majibu kwa majibu daima ina thamani sawa.

    Mfano\(\PageIndex{2}\): Evaluating a Reaction Quotient

    Dioksidi ya nitrojeni ya gesi huunda tetroksidi ya dinitrojeni kulingana na usawa huu:

    \[\ce{2NO}_{2(g)} \rightleftharpoons \ce{N_2O}_{4(g)} \nonumber \]

    Wakati 0.10 mol\(\ce{NO2}\) inapoongezwa kwenye chupa ya 1.0-L saa 25 °C, mkusanyiko hubadilika ili katika usawa, [NO 2] = 0.016 M na [N 2 O 4] = 0.042 M.

    1. Je! Ni thamani gani ya quotient ya majibu kabla ya majibu yoyote hutokea?
    2. Thamani ya mara kwa mara ya usawa kwa majibu ni nini?
    Suluhisho
    1. Kabla ya bidhaa yoyote kuundwa\(\mathrm{[NO_2]=\dfrac{0.10\:mol}{1.0\:L}}=0.10\:M\),, na [N 2 O 4] = 0 M. Hivyo,\[Q_c=\ce{\dfrac{[N2O4]}{[NO2]^2}}=\dfrac{0}{0.10^2}=0 \nonumber \]
    2. Katika usawa, thamani ya mara kwa mara ya usawa ni sawa na thamani ya quotient ya majibu. Katika usawa,\[K_c=Q_c=\ce{\dfrac{[N2O4]}{[NO2]^2}}=\dfrac{0.042}{0.016^2}=1.6\times 10^2. \nonumber \]

    Mara kwa mara ya usawa ni 1.6 × 10 2.

    Kumbuka kuwa uchambuzi wa mwelekeo ungependekeza kitengo cha\(K_c\) thamani hii kinapaswa kuwa M -1. Hata hivyo, ni kawaida ya kuacha vitengo vya\(K_c\) maadili yaliyohesabiwa kama ilivyoelezwa hapa, kwani ni ukubwa wa mara kwa mara ya usawa ambayo hurejesha habari muhimu. Kama itajadiliwa baadaye katika moduli hii, mbinu ukali wa kompyuta constants usawa inatumia kiasi dimensionless inayotokana na shughuli badala ya viwango molar, na hivyo\(K_c\) maadili ni kweli unitless.

    Zoezi\(\PageIndex{2}\)

    Kwa majibu

    \[\ce{2SO2}(g)+\ce{O2}(g) \rightleftharpoons \ce{2SO3}(g) \nonumber \]

    viwango katika usawa ni [SO 2] = 0.90 M, [O 2] = 0.35 M, na [SO 3] = 1.1 M. Nini thamani ya mara kwa mara ya usawa, K c?

    Jibu

    K c = 4.3

    Ukubwa wa mara kwa mara ya usawa ni kipimo cha mavuno ya mmenyuko unapofikia usawa. thamani kubwa kwa\(K_c\) inaonyesha kwamba msawazo ni kupatikana tu baada ya reactants wamekuwa kiasi kikubwa waongofu katika bidhaa. Thamani ndogo ya\(K_c\) -chini ya 1—inaonyesha kuwa usawa unapatikana wakati sehemu ndogo tu ya majibu yamebadilishwa kuwa bidhaa.

    Mara baada ya thamani ya\(K_c\) inajulikana kwa majibu, inaweza kutumika kutabiri mabadiliko directional ikilinganishwa na thamani ya\(Q_c\). Mfumo ambao hauko katika usawa utaendelea katika mwelekeo unaoanzisha usawa. data katika Kielelezo\(\PageIndex{2}\) kuonyesha hii. Wakati joto kwa joto thabiti, 800 °C, tofauti kuanzia mchanganyiko wa\(\ce{CO}\)\(\ce{H_2O}\),\(\ce{CO_2}\), na\(\ce{H_2}\) kuguswa kufikia nyimbo kushikamana na usawa huo (thamani ya\(Q_c\) mabadiliko mpaka ni sawa na thamani ya K c). Thamani hii ni 0.640, mara kwa mara ya usawa kwa majibu chini ya hali hizi.

    \[\ce{CO}(g)+\ce{H2O}(g) \rightleftharpoons \ce{CO2}(g)+\ce{H2}(g) \hspace{20px} K_c=0.640 \hspace{20px} \mathrm{T=800°C} \label{13.3.6} \]

    Ni muhimu kutambua kwamba usawa unaweza kuanzishwa kuanzia ama kutoka kwa reactants au kutoka kwa bidhaa, au kutoka mchanganyiko wa wote wawili. Kwa mfano, usawa ulianzishwa kutoka Mchanganyiko 2 katika Kielelezo\(\PageIndex{2}\) wakati bidhaa za mmenyuko zilipokanzwa kwenye chombo kilichofungwa. Kwa kweli, mbinu moja inayotumiwa kuamua kama mmenyuko ni kweli katika usawa ni kufikia usawa kuanzia na reactants katika jaribio moja na kuanzia na bidhaa katika mwingine. Ikiwa thamani sawa ya quotient ya mmenyuko inazingatiwa wakati viwango vinaacha kubadilisha katika majaribio yote, basi tunaweza kuwa na uhakika kwamba mfumo umefikia usawa.

    Kielelezo\(\PageIndex{2}\): Viwango vya mchanganyiko wa tatu huonyeshwa kabla na baada ya kufikia usawa saa 800 °C kwa kinachojulikana majibu ya mabadiliko ya gesi ya maji (Equation\ ref {13.3.6}).
    Seti mbili za grafu za bar zinaonyeshwa. Kushoto ni lebo, “Kabla ya majibu,” na haki ni lebo, “Katika usawa.” Grafu zote mbili zina y-shoka zilizoandikwa, “Mkazo (M),” na baa tatu kwenye x-axes iliyoandikwa, “Mchanganyiko 1,” “Mchanganyiko 2,” na “Mchanganyiko 3.” Mhimili wa y una kiwango kinachoanza saa 0.00 na kuishia saa 0.10, na vipimo vya kipimo cha 0.02. Vipande kwenye grafu ni rangi ya coded na ufunguo hutolewa kwa hadithi. Red ni kinachoitwa, “C O;” bluu ni kinachoitwa, “H subscript 2 O;” kijani ni kinachoitwa, “C O subscript 2,” na njano ni lebo, “H subscript 2.” Grafu upande wa kushoto inaonyesha bar nyekundu kwa mchanganyiko moja tu juu ya 0.02 na bar ya bluu karibu 0.05. Kwa mchanganyiko mbili, bar ya kijani iko karibu 0.05, na bar ya njano iko karibu 0.09. Kwa mchanganyiko 3, bar nyekundu iko karibu na 0.01, bar ya bluu ni kidogo juu ya kuwa na kijani na njano kuifuta saa 0.02. Kwenye grafu ya kulia, bar ya mchanganyiko moja inaonyesha bar nyekundu kidogo juu ya 0.01, bar ya bluu iliyowekwa juu yake inaongezeka kidogo juu ya 0.02, kijani kinaongezeka karibu 0.04, na bar ya njano ikifikia karibu 0.05. Lebo iliyo juu ya bar hii inasomeka, “Swali ni sawa na 0.640.” Bar kwa mchanganyiko mbili inaonyesha bar nyekundu kidogo juu ya 0.02, bar ya bluu iliyowekwa juu yake inapanda karibu 0.05, kijani kinaongezeka karibu 0.07, na bar ya njano ikifikia karibu 0.10. Lebo iliyo juu ya bar hii inasomeka “Q ni sawa na 0.640.” Bar kwa mchanganyiko tatu inaonyesha bar nyekundu karibu 0.01, bar ya bluu iliyowekwa juu yake inaongezeka kidogo juu ya 0.01, kijani huongezeka karibu 0.02, na bar ya njano kufikia 0.02. Lebo iliyo juu ya bar hii inasomeka “Q ni sawa na 0.640".
    Mfano\(\PageIndex{3}\): Predicting the Direction of Reaction

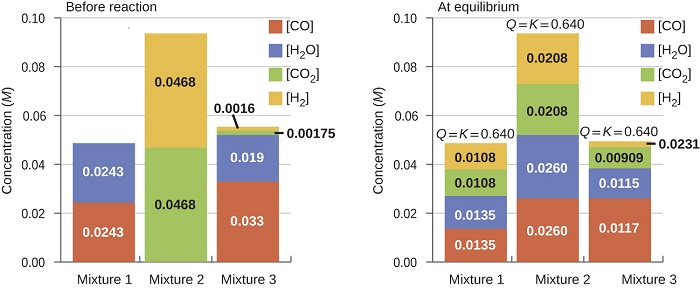
    Kutokana hapa ni viwango vya kuanzia vya reactants na bidhaa kwa ajili ya majaribio matatu yanayohusisha mmenyuko huu:

    \[\ce{CO}(g)+\ce{H2O}(g) \rightleftharpoons \ce{CO2}(g)+\ce{H2}(g) \nonumber \]

    na\(K_c=0.64 \). Kuamua katika mwelekeo gani majibu yanaendelea kama inakwenda kwa usawa katika kila moja ya majaribio matatu yaliyoonyeshwa.

    Reactant/Bidhaa kwa ajili ya majaribio matatu
    Reactants/Bidhaa majaribio 1 majaribio 2 majaribio 3
    [CO] i 0.0203 M 0.011 M 0.0094 M
    [H 2 O] i 0.0203 M 0.0011 M 0.0025 M
    [CO 2] i 0.0040 M 0.037 M 0.0015 M
    [H 2] i 0.0040 M 0.046 M 0.0076 M
    Suluhisho

    Jaribio 1:

    \[Q_c=\ce{\dfrac{[CO2][H2]}{[CO][H2O]}}=\dfrac{(0.0040)(0.0040)}{(0.0203)(0.0203)}=0.039. \nonumber \]

    Q c\(K_c\) <( 0.039 <0.64)

    Majibu yatabadilika kwa haki.

    Jaribio la 2:

    \[Q_c=\ce{\dfrac{[CO2][H2]}{[CO][H2O]}}=\dfrac{(0.037)(0.046)}{(0.011)(0.0011)}=1.4 \times 10^2 \nonumber \]

    Q c >\(K_c\) (140 > 0.64)

    Majibu yatabadilika upande wa kushoto.

    Jaribio la 3:

    \[Q_c=\ce{\dfrac{[CO2][H2]}{[CO][H2O]}}=\dfrac{(0.0015)(0.0076)}{(0.0094)(0.0025)}=0.48 \nonumber \]

    Q c\(K_c\) <( 0.48 <0.64)

    Majibu yatabadilika kwa haki.

    Zoezi\(\PageIndex{3}\)

    Tumia hesabu ya majibu na ueleze mwelekeo ambao kila moja ya athari zifuatazo zitaendelea kufikia usawa.

    (a) chupa ya 1.00-L iliyo na 0.0500 mol ya NO (g), 0.0155 mol ya Cl 2 (g), na 0.500 mol ya NoCl:

    \[\ce{2NO}(g)+\ce{Cl2}(g)⇌\ce{2NOCl}(g)\hspace{20px}K_c=4.6\times 10^4 \nonumber \]

    (b) chupa ya 5.0-L iliyo na 17 g ya NH 3, 14 g ya N 2, na 12 g ya H 2:

    \[\ce{N2}(g)+\ce{3H2}(g)⇌\ce{2NH3}(g)\hspace{20px}K_c=0.060 \nonumber \]

    (c) chupa 2.00-L iliyo na 230 g ya SO 3 (g):

    \[\ce{2SO3}(g)⇌\ce{2SO2}(g)+\ce{O2}(g)\hspace{20px}K_c=0.230 \nonumber \]

    Jibu

    \(Q_c\)= 6.45 × 10 3, mabadiliko ya haki.

    Jibu b

    \(Q_c\)= 0.12, mabadiliko ya kushoto.

    Jibu c

    \(Q_c\)= 0, mabadiliko ya haki

    Katika Mfano\(\PageIndex{2}\), ilitajwa kuwa mazoezi ya kawaida ni kuacha vitengo wakati wa kutathmini quotients ya majibu na constants ya usawa. Ikumbukwe kwamba kutumia viwango katika hesabu hizi ni mbinu rahisi lakini kilichorahisishwa ambayo wakati mwingine husababisha matokeo ambayo inaonekana yanakabiliana na sheria ya hatua ya molekuli. Kwa mfano, usawa unaohusisha ions yenye maji mara nyingi huonyesha vipindi vya usawa ambavyo vinatofautiana kabisa kwa kiasi kikubwa (sio mara kwa mara) katika viwango vya juu vya ufumbuzi. Hii inaweza kuepukwa kwa\(K_c\) maadili ya kompyuta kwa kutumia shughuli za reactants na bidhaa katika mfumo wa usawa badala ya viwango vyao. Shughuli ya dutu ni kipimo cha mkusanyiko wake wa ufanisi chini ya hali maalum. Wakati majadiliano ya kina ya kiasi hiki muhimu ni zaidi ya upeo wa maandishi ya utangulizi, ni muhimu kuwa na ufahamu wa mambo machache muhimu:

    • Shughuli ni dimensionless (unitless) kiasi na ni katika asili “kubadilishwa” viwango.
    • Kwa ufumbuzi wa kiasi kikubwa, shughuli za solute na mkusanyiko wake wa molar ni sawa sawa.
    • Shughuli kwa awamu safi iliyosafishwa (solids na vinywaji) ni sawa na 1.
    • Shughuli za vimumunyisho katika ufumbuzi wa kuondokana ni sawa na 1.

    Kama matokeo ya mambo haya mawili ya mwisho,\(Q_c\) na\(K_c\) maneno hayana maneno ya yabisi au vinywaji au vimumunyisho katika ufumbuzi wa kuondokana (kuwa numerically sawa na 1, maneno haya hayana athari kwa thamani ya kujieleza). Mifano kadhaa ya usawa wa kutoa maneno kama hayo yatakutana katika sehemu hii.

    Ulinganifu wa homogeneous

    Msawazo sawa ni moja ambayo majibu yote na bidhaa zipo katika suluhisho moja (kwa ufafanuzi, mchanganyiko wa homogeneous). Katika sura hii, tutazingatia aina mbili za kawaida za usawa sawa: zile zinazotokea katika ufumbuzi wa awamu ya kioevu na wale wanaohusisha aina pekee za gesi. Majibu kati ya solutes katika ufumbuzi wa kioevu ni aina moja ya usawa sawa. Spishi za kemikali zinazohusika zinaweza kuwa molekuli, ioni, au mchanganyiko wa wote wawili. Mifano kadhaa hutolewa hapa:

    Mfano 1

    \[\ce{C2H2}(aq)+\ce{2Br2}(aq) \rightleftharpoons \ce{C2H2Br4}(aq)\hspace{20px} \label{13.3.7a} \]

    na mara kwa mara ya usawa unaohusishwa

    \[K_c=\ce{\dfrac{[C2H2Br4]}{[C2H2][Br2]^2}} \label{13.3.7b} \]

    Mfano 2

    \[\ce{I2}(aq)+\ce{I-}(aq) \rightleftharpoons \ce{I3-}(aq) \label{13.3.8b} \]

    na mara kwa mara ya usawa unaohusishwa

    \[K_c=\ce{\dfrac{[I3- ]}{[I2][I- ]}} \label{13.3.8c} \]

    Mfano 3

    \[\ce{Hg2^2+}(aq)+\ce{NO3-}(aq)+\ce{3H3O+}(aq) \rightleftharpoons \ce{2Hg^2+}(aq)+\ce{HNO2}(aq)+\ce{4H2O}(l) \label{13.3.9a} \]

    na mara kwa mara ya usawa unaohusishwa

    \[K_c=\ce{\dfrac{[Hg^2+]^2[HNO2]}{[Hg2^2+][NO3- ][H3O+]^3}} \label{13.3.9b} \]

    Mfano 4

    \[\ce{HF}(aq)+\ce{H2O}(l) \rightleftharpoons \ce{H3O+}(aq)+\ce{F-}(aq) \label{13.3.10a} \]

    na mara kwa mara ya usawa unaohusishwa

    \[K_c=\ce{\dfrac{[H3O+][F- ]}{[HF]}} \label{13.3.10b} \]

    Mfano 5

    \[\ce{NH3}(aq)+\ce{H2O}(l) \rightleftharpoons \ce{NH4+}(aq)+\ce{OH-}(aq) \label{13.3.11a} \]

    na mara kwa mara ya usawa unaohusishwa

    \[K_c=\ce{\dfrac{[NH4+][OH- ]}{[NH3]}} \label{13.3.11b} \]

    Katika kila moja ya mifano hii, mfumo wa usawa ni suluhisho la maji, kama ilivyoonyeshwa na maelezo ya aq juu ya formula za solute. Kwa kuwa H 2 O (l) ni kutengenezea kwa ufumbuzi huu, ni kupewa shughuli ya 1, na hivyo haionekani wazi kama neno katika\(K_c\) usemi, kama ilivyojadiliwa mapema, ingawa inaweza pia kuonekana kama reactant au bidhaa katika equation kemikali.

    Majibu ambayo majibu yote na bidhaa ni gesi zinawakilisha darasa la pili la usawa wa homogeneous. Tunatumia viwango vya molar katika mifano ifuatayo, lakini tutaona hivi karibuni kwamba shinikizo la sehemu za gesi zinaweza kutumika pia:

    Mfano 1

    \[\ce{C2H6}(g) \rightleftharpoons \ce{C2H4}(g)+\ce{H2}(g) \label{13.3.12a} \]

    na mara kwa mara ya usawa unaohusishwa

    \[K_c=\ce{\dfrac{[C2H4][H2]}{[C2H6]}} \label{13.3.12b} \]

    Mfano 2

    \[\ce{3O2}(g) \rightleftharpoons \ce{2O3}(g) \label{13.3.13a} \]

    na mara kwa mara ya usawa unaohusishwa

    \[K_c=\ce{\dfrac{[O3]^2}{[O2]^3}} \label{13.3.13b} \]

    Mfano 3

    \[\ce{N2}(g)+\ce{3H2}(g) \rightleftharpoons \ce{2NH3}(g) \label{13.3.14a} \]

    na mara kwa mara ya usawa unaohusishwa

    \[K_c=\ce{\dfrac{[NH3]^2}{[N2][H2]^3}} \label{13.3.14b} \]

    Mfano 4

    \[\ce{C3H8}(g)+\ce{5O2}(g) \rightleftharpoons \ce{3CO2}(g)+\ce{4H2O}(g)\label{13.3.15a} \]

    na mara kwa mara ya usawa unaohusishwa

    \[K_c=\ce{\dfrac{[CO2]^3[H2O]^4}{[C3H8][O2]^5}}\label{13.3.15b} \]

    Kumbuka kuwa mkusanyiko wa\(\ce{H_2O}_{(g)}\) umejumuishwa katika mfano wa mwisho kwa sababu maji sio kutengenezea katika mmenyuko huu wa awamu ya gesi na mabadiliko yake (na shughuli).

    Wakati wowote gesi zinahusika katika mmenyuko, shinikizo la sehemu ya kila gesi linaweza kutumika badala ya mkusanyiko wake katika equation kwa quotient ya mmenyuko kwa sababu shinikizo la sehemu ya gesi ni sawia moja kwa moja na ukolezi wake kwenye joto la mara kwa mara. Uhusiano huu unaweza kuwa inayotokana na bora gesi equation, ambapo M ni mkusanyiko molar ya gesi,\(\dfrac{n}{V}\).

    \[\begin{align} PV&=nRT \label{13.3.16} \\[4pt] P &=\left(\dfrac{n}{V}\right)RT \label{13.3.17} \\[4pt] &=MRT \label{13.3.18} \end{align} \]

    Hivyo, kwa joto la kawaida, shinikizo la gesi ni sawa sawa na ukolezi wake. Kutumia shinikizo la sehemu ya gesi, tunaweza kuandika quotient ya majibu kwa mfumo

    \[\ce{C2H6}(g) \rightleftharpoons \ce{C2H4}(g)+\ce{H2}(g) \label{13.3.19} \]

    kwa kufuata miongozo hiyo kwa ajili ya kupata maneno mkusanyiko makao:

    \[Q_P=\dfrac{P_{\ce{C2H4}}P_{\ce{H2}}}{P_{\ce{C2H6}}} \label{13.3.20} \]

    Katika equation hii tunatumia Q P kuonyesha quotient ya majibu iliyoandikwa na shinikizo la sehemu:\(P_{\ce{C2H6}}\) ni shinikizo la sehemu ya C 2 H 6;\(P_{\ce{H2}}\), shinikizo la sehemu ya H 2; na\(P_{\ce{C2H6}}\), shinikizo la sehemu ya C 2 H 4. Katika usawa:

    \[K_P=Q_P=\dfrac{P_{\ce{C2H4}}P_{\ce{H2}}}{P_{\ce{C2H6}}} \label{13.3.21} \]

    Subscript\(P\) katika ishara\(K_P\) inaashiria mara kwa mara usawa inayotokana na shinikizo sehemu badala ya viwango. Mara kwa mara ya usawa, K P, bado ni mara kwa mara, lakini thamani yake ya nambari inaweza kutofautiana na mara kwa mara ya usawa iliyopatikana kwa majibu sawa kwa kutumia viwango.

    Conversion kati ya thamani kwa\(K_c\), msawazo mara kwa mara walionyesha katika suala la viwango, na thamani ya\(K_P\), mara kwa mara msawazo walionyesha katika suala la shinikizo, ni moja kwa moja (K au Q bila Subscript inaweza kuwa ama mkusanyiko au shinikizo).

    equation zinazohusiana\(K_c\) na\(K_P\) ni inayotokana kama ifuatavyo. Kwa mmenyuko wa awamu ya gesi:

    \[m\ce{A}+n\ce{B} \rightleftharpoons x\ce{C}+y\ce{D} \label{13.3.22} \]

    na

    \[ \begin{align} K_P &=\dfrac{(P_C)^x(P_D)^y}{(P_A)^m(P_B)^n} \label{13.3.23} \\[4pt] &=\dfrac{([\ce C]×RT)^x([\ce D]×RT)^y}{([\ce A]×RT)^m([\ce B]×RT)^n} \label{13.3.24} \\[4pt] &=\dfrac{[\ce C]^x[\ce D]^y}{[\ce A]^m[\ce B]^n}×\dfrac{(RT)^{x+y}}{(RT)^{m+n}} \label{13.3.25} \\[4pt] &=K_c(RT)^{(x+y)−(m+n)} \label{13.3.26} \\[4pt] &=K_c(RT)^{Δn} \label{13.3.27} \end{align} \]

    Uhusiano kati\(K_c\) na\(K_P\) ni

    \[ \color{red} K_P=K_c(RT)^{Δn} \label{13.3.28} \]

    Katika equation hii, Δn ni tofauti kati ya jumla ya coefficients ya bidhaa za gesi na jumla ya coefficients ya majibu ya gesi katika mmenyuko (mabadiliko katika moles ya gesi kati ya reactants na bidhaa). Kwa mmenyuko wa awamu ya gesi\(m\ce{A}+n\ce{B} \rightleftharpoons x\ce{C}+y\ce{D}\), tuna

    \[Δn=(x+y)−(m+n) \label{13.3.29} \]

    Mfano\(\PageIndex{4}\): Calculation of KP

    Andika equations kwa uongofu wa\(K_c\) K P kwa kila moja ya athari zifuatazo:

    1. \(\ce{C2H6}(g) \rightleftharpoons \ce{C2H4}(g)+\ce{H2}(g)\)
    2. \(\ce{CO}(g)+\ce{H2O}(g) \rightleftharpoons \ce{CO2}(g)+\ce{H2}(g)\)
    3. \(\ce{N2}(g)+\ce{3H2}(g) \rightleftharpoons \ce{2NH3}(g)\)
    4. K c ni sawa na 0.28 kwa mmenyuko wafuatayo kwenye 900 °C:

    \[\ce{CS2}(g)+\ce{4H2}(g) \rightleftharpoons \ce{CH4}(g)+\ce{2H2S}(g) \nonumber \]

    K P ni nini katika joto hili?

    Suluhisho

    (a) Δ n = (2) - (1) = 1

    K P =\(K_c\) (RT) Δ n =\(K_c\) (RT) 1 =\(K_c\) (RT)

    (b) Δ n = (2) - (2) = 0

    K P =\(K_c\) (RT) Δ n =\(K_c\) (RT) 0 = K c

    (c) Δ n = (2) - (1 + 3) = -2

    K P =\(K_c\) (RT) Δ n =\(K_c\) (RT) -1 =\(\dfrac{K_c}{(RT)^2}\)

    d) K P =\(K_c\) (RT) Δ n = (0.28) [(0.0821) (1173)] -2 = 3.0 × 10 -5

    Zoezi\(\PageIndex{4}\)

    Andika equations kwa uongofu wa\(K_c\) K P kwa kila moja ya athari zifuatazo, ambazo hutokea katika awamu ya gesi:

    1. \(\ce{2SO2}(g)+\ce{O2}(g) \rightleftharpoons \ce{2SO3}(g)\)
    2. \(\ce{N2O4}(g) \rightleftharpoons \ce{2NO2}(g)\)
    3. \(\ce{C3H8}(g)+\ce{5O2}(g) \rightleftharpoons \ce{3CO2}(g)+\ce{4H2O}(g)\)
    4. Katika 227 °C, mmenyuko wafuatayo una\(K_c\) = 0.0952:

    \[\ce{CH3OH}(g) \rightleftharpoons \ce{CO}(g)+\ce{2H2}(g) \nonumber \]

    Je! Ni thamani gani ya K P kwenye joto hili?

    Jibu

    K P =\(K_c\) (RT) -1

    Jibu b

    K P =\(K_c\) (RT)

    Jibu c

    K P =\(K_c\) (RT);

    Jibu d

    160 au 1.6 × 10 2

    Ulinganifu tofauti

    Msawazo tofauti ni mfumo ambao majibu na bidhaa hupatikana katika awamu mbili au zaidi. Awamu inaweza kuwa mchanganyiko wa awamu imara, kioevu, au gesi, na ufumbuzi. Wakati wa kushughulika na usawa huu, kumbuka kwamba yabisi na vinywaji safi havionekani katika maneno ya mara kwa mara ya usawa (shughuli za yabisi safi, vinywaji safi, na vimumunyisho ni 1).

    Baadhi ya usawa tofauti huhusisha mabadiliko ya kemikali:

    Mfano 1

    \[\ce{PbCl2}(s) \rightleftharpoons \ce{Pb^2+}(aq)+\ce{2Cl-}(aq) \label{13.3.30a} \]

    na mara kwa mara ya usawa unaohusishwa

    \[K_c=\ce{[Pb^2+][Cl- ]^2} \label{13.3.30b} \]

    Mfano 1

    \[\ce{CaO}(s)+\ce{CO2}(g) \rightleftharpoons \ce{CaCO3}(s) \label{13.3.31a} \]

    na mara kwa mara ya usawa unaohusishwa

    \[K_c=\dfrac{1}{[\ce{CO2}]} \label{13.3.31b} \]

    Mfano 1

    \[\ce{C}(s)+\ce{2S}(g) \rightleftharpoons \ce{CS2}(g) \label{13.3.32a} \]

    na mara kwa mara ya usawa unaohusishwa

    \[K_c=\ce{\dfrac{[CS2]}{[S]^2}} \label{13.3.32b} \]

    Mizani mingine isiyo ya kawaida huhusisha mabadiliko ya awamu, kwa mfano, uvukizi wa bromini ya kiowevu, kama inavyoonekana katika equation ifuatayo:

    \[\ce{Br2}(l) \rightleftharpoons \ce{Br2}(g) \label{13.3.33a} \]

    na mara kwa mara ya usawa unaohusishwa

    \[K_c=[\ce{Br2}] \label{13.3.33b} \]

    Tunaweza kuandika equations kwa quotients majibu ya usawa tofauti nyingi zinazohusisha gesi, kwa kutumia shinikizo sehemu badala ya viwango. Mifano miwili ni:

    \[\ce{CaO}(s)+\ce{CO2}(g) \rightleftharpoons \ce{CaCO3}(s)\label{13.3.34a} \]

    na mara kwa mara ya usawa unaohusishwa

    \[K_P=\dfrac{1}{P_{\ce{CO2}}} \label{13.3.34b} \]

    \[\ce{C}(s)+\ce{2S}(g) \rightleftharpoons \ce{CS2}(g)\label{13.3.35a} \]

    na mara kwa mara ya usawa unaohusishwa

    \[K_P=\dfrac{P_{\ce{CS2}}}{(P_{\ce S})^2} \label{13.3.35b} \]

    Muhtasari

    Kwa majibu yoyote ambayo ni katika usawa, quotient ya majibu Q ni sawa na mara kwa mara ya usawa K kwa majibu. Ikiwa reactant au bidhaa ni imara safi, kioevu safi, au kutengenezea katika suluhisho la kuondokana, ukolezi wa sehemu hii hauonekani katika kujieleza kwa mara kwa mara ya usawa. Katika usawa, maadili ya viwango vya reactants na bidhaa ni mara kwa mara. Maadili yao maalum yanaweza kutofautiana kulingana na hali, lakini thamani ya quotient ya mmenyuko daima itakuwa sawa K (K c wakati wa kutumia viwango au K P wakati wa kutumia shinikizo la sehemu).

    Msawazo sawa ni usawa ambao vipengele vyote viko katika awamu moja. Msawazo tofauti ni usawa ambao vipengele viko katika awamu mbili au zaidi. Tunaweza kuamua kama mmenyuko uko katika usawa kwa kulinganisha quotient ya majibu na mara kwa mara ya usawa kwa majibu.

    Mlinganyo muhimu

    • \(Q=\dfrac{[\ce C]^x[\ce D]^y}{[\ce A]^m[\ce B]^n}\hspace{20px}\textrm{where }m\ce A+n\ce B⇌x\ce C+y\ce D\)
    • \(Q_P=\dfrac{(P_C)^x(P_D)^y}{(P_A)^m(P_B)^n}\hspace{20px}\textrm{where }m\ce A+n\ce B⇌x\ce C+y\ce D\)
    • P = MRT
    • K P =\(K_c\) (RT) Δ n

    faharasa

    mara kwa mara ya usawa (K)
    thamani ya quotient mmenyuko kwa mfumo katika usawa
    usawa tofauti
    usawa kati ya reactants na bidhaa katika awamu tofauti
    usawa wa homogeneous
    usawa ndani ya awamu moja
    K c
    usawa wa mara kwa mara kwa athari kulingana na viwango vya reactants na bidhaa
    K P
    mara kwa mara ya usawa kwa athari za awamu ya gesi kulingana na shinikizo la sehemu ya reactants na bidhaa
    sheria ya hatua ya molekuli
    wakati mmenyuko wa kubadilishwa umepata usawa katika joto lililopewa, quotient ya majibu inabakia mara kwa mara
    majibu quotient (Q)
    uwiano wa bidhaa ya viwango vya molar (au shinikizo) ya bidhaa kwa ile ya reactants, kila mkusanyiko (au shinikizo) hufufuliwa kwa nguvu sawa na mgawo katika equation