14.3: Maji, Wiani, na Shinikizo (Sehemu ya 2)
- Page ID
- 177030
Tofauti ya shinikizo na kina katika maji ya wiani wa mara kwa mara
Shinikizo hufafanuliwa kwa majimbo yote ya suala, lakini ni muhimu hasa wakati wa kujadili maji. Tabia muhimu ya maji ni kwamba hakuna upinzani mkubwa kwa sehemu ya nguvu inayotumika sambamba na uso wa maji. Molekuli ya maji inapita tu ili kuzingatia nguvu ya usawa. Nguvu inayotumiwa perpendicular kwa uso compresses au expands maji. Ikiwa unajaribu kuimarisha maji, unapata kwamba nguvu ya mmenyuko inakua kila hatua ndani ya maji katika mwelekeo wa nje, kusawazisha nguvu iliyotumiwa kwenye molekuli kwenye mipaka.
Fikiria maji ya wiani mara kwa mara kama inavyoonekana katika Kielelezo\(\PageIndex{1}\). Shinikizo chini ya chombo ni kutokana na shinikizo la anga (p 0) pamoja na shinikizo kutokana na uzito wa maji. Shinikizo kutokana na maji ni sawa na uzito wa maji yaliyogawanywa na eneo hilo. Uzito wa maji ni sawa na mara zake za wingi kasi kutokana na mvuto.
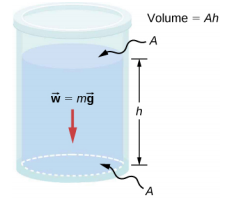
Kwa kuwa wiani ni mara kwa mara, uzito unaweza kuhesabiwa kwa kutumia wiani:
\[w = mg = \rho Vg = \rho Ahg \ldotp\]
Shinikizo chini ya chombo kwa hiyo ni sawa na shinikizo la anga lililoongezwa kwa uzito wa maji iliyogawanywa na eneo:
\[p = p_{0} + \frac{\rho Ahg}{A} = p_{0} + \rho hg \ldotp\]
Equation hii ni nzuri tu kwa shinikizo kwa kina kwa maji ya wiani wa mara kwa mara
Shinikizo kwa kina katika maji ya wiani wa mara kwa mara ni sawa na shinikizo la anga pamoja na shinikizo kutokana na uzito wa maji, au
\[p = p_{0} + \rho hg, \label{14.4}\]
Ambapo p ni shinikizo kwa kina fulani, p 0 ni shinikizo la anga,\(\rho\) ni wiani wa maji, g ni kasi kutokana na mvuto, na h ni kina.

Fikiria shinikizo na nguvu inayofanya bwawa kubaki hifadhi ya maji (Kielelezo\(\PageIndex{2}\)). Tuseme bwawa ni upana wa mita 500 na maji ni kina cha 80.0-m kwenye bwawa, kama ilivyoonyeshwa hapa chini. (a) Shinikizo la wastani kwa bwawa kutokana na maji ni nini? (b) Kuhesabu nguvu exerted dhidi ya bwawa.
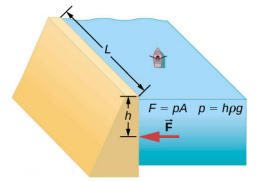
Shinikizo la wastani p kutokana na uzito wa maji ni shinikizo kwa kina cha wastani h cha 40.0 m, kwani shinikizo linaongezeka linearly na kina. Nguvu inayotumiwa kwenye bwawa na maji ni mara shinikizo la wastani eneo la kuwasiliana, F = pA.
Suluhisho
- Shinikizo la wastani kutokana na uzito wa maji ni $$p = h\ rho g\ ldotp\ studio {14.5} $$Kuingia wiani wa maji kutoka Jedwali 14.1 na kuchukua h kuwa kina cha wastani cha 40.0 m, tunapata $$\ kuanza {kupasuliwa} p & = (40.0\; m) (10^ {3}\; kg/m^ {3}) (9.80\; m/s^ {2})\\ & = 3.92\ mara 10^ {5}\; N/m^ {2} = 392\; kPa\ ldotp\ mwisho {mgawanyiko} $$
- Tayari tumepata thamani ya p. eneo la bwawa ni $$A = (80.0\; m)\ mara (500\; m) = 4.00\ mara 10^ {4}\; m^ {2}\ ldotp $$ili $$\ kuanza {mgawanyiko} F & = (3.92\ mara 10^ {5}\; N/m^ {2}) (4.00\ mara 10^ {4}\; m^ {2})\\ & = 1.57\ mara 10^ {10}\; M\ ldotp\ mwisho {mgawanyiko} $$
Umuhimu
Ingawa nguvu hii inaonekana kubwa, ni ndogo ikilinganishwa na 1.96 x 10 13 N uzito wa maji katika hifadhi. Kwa kweli, ni 0.0800% tu ya uzito.
Kama hifadhi katika Mfano\(\PageIndex{1}\) kufunikwa mara mbili eneo, lakini ilihifadhiwa kwa kina sawa, ingekuwa bwawa haja ya kuwa upya?
Shinikizo katika maji ya tuli katika uwanja wa mvuto sare
Maji ya tuli ni maji yasiyo na mwendo. Katika hatua yoyote ndani ya maji tuli, shinikizo pande zote lazima sawa-vinginevyo, maji katika hatua hiyo bila kuguswa na nguvu wavu na kuongeza kasi.
Shinikizo wakati wowote katika maji ya tuli hutegemea tu kina wakati huo. Kama ilivyojadiliwa, shinikizo katika maji karibu na Dunia hutofautiana na kina kutokana na uzito wa maji juu ya kiwango fulani. Katika mifano hapo juu, sisi kudhani wiani kuwa mara kwa mara na wiani wastani wa maji kuwa uwakilishi mzuri wa wiani. Hii ni makadirio ya busara kwa vinywaji kama maji, ambapo vikosi vikubwa vinahitajika kuimarisha kioevu au kubadilisha kiasi. Katika bwawa la kuogelea, kwa mfano, wiani ni takriban mara kwa mara, na maji chini yanasisitizwa kidogo sana na uzito wa maji juu. Kusafiri juu ya anga ni hali tofauti kabisa, hata hivyo. Uzito wa hewa huanza kubadilika kwa kiasi kikubwa umbali mfupi tu juu ya uso wa Dunia.
Ili kupata formula kwa tofauti ya shinikizo na kina katika tank iliyo na maji ya wiani\(\rho\) juu ya uso wa Dunia, lazima tuanze na dhana kwamba wiani wa maji sio mara kwa mara. Maji yaliyo kwenye viwango vya kina yanakabiliwa na nguvu zaidi kuliko maji yaliyo karibu na uso kutokana na uzito wa maji juu yake. Kwa hiyo, shinikizo lililohesabiwa kwa kina kilichopewa ni tofauti na shinikizo lililohesabiwa kwa kutumia wiani wa mara kwa mara.
Fikiria kipengele nyembamba cha maji kwa kina h, kama inavyoonekana kwenye Kielelezo\(\PageIndex{3}\). Hebu kipengele kina eneo la msalaba A na urefu\(\Delta\) y. vikosi vinavyofanya juu ya kipengele ni kutokana na shinikizo p (y) hapo juu na p (y +\(\Delta\) y) chini yake. Uzito wa kipengele yenyewe pia umeonyeshwa kwenye mchoro wa mwili wa bure.
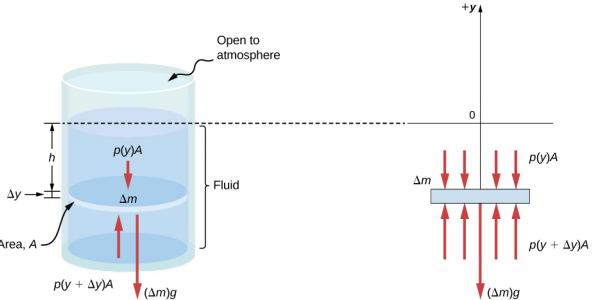
Kwa kuwa kipengele cha maji kati ya y na y +\(\Delta\) y hakizidi kuharakisha, majeshi yana usawa. Kutumia mhimili wa y wa Cartesian unaoelekezwa juu, tunapata equation ifuatayo kwa sehemu ya y:
\[p(y + \Delta y)A - p(y)A - g \Delta m = 0(\Delta y < 0) \ldotp \label{14.6}\]
Kumbuka kwamba kama kipengele kilikuwa na sehemu isiyo ya sifuri y ya kuongeza kasi, upande wa kulia hautakuwa sifuri lakini ingekuwa badala yake kuwa mara nyingi ya kuongeza kasi ya y. Uzito wa kipengele unaweza kuandikwa kwa suala la wiani wa maji na kiasi cha vipengele:
\[\Delta m = |\rho A \Delta y| = - \rho A \Delta y \quad (\Delta y < 0) \ldotp\]
Kuweka maneno haya kwa\(\Delta\) m katika Equation\ ref {14.6} na kisha kugawanya pande zote mbili kwa A\(\Delta\) y, tunaona
\[\frac{p(y + \Delta y) - p(y)}{\Delta y} = - \rho g \ldotp \label{14.7}\]
Kuchukua kikomo cha kipengele cha infinitesimally nyembamba\(\Delta\) y → 0, tunapata equation tofauti yafuatayo, ambayo inatoa tofauti ya shinikizo katika maji:
\[\frac{dp}{dy} = - \rho g \ldotp \label{14.8}\]
Equation hii inatuambia kwamba kiwango cha mabadiliko ya shinikizo katika maji ni sawia na wiani wa maji. Suluhisho la equation hii inategemea kama wiani\(\rho\) ni mara kwa mara au hubadilika kwa kina; yaani, kazi\(\rho\) (y).
Ikiwa kina cha kina kinachochambuliwa sio kubwa sana, tunaweza kudhani wiani kuwa mara kwa mara. Lakini kama kina cha kina ni kikubwa cha kutosha kwa wiani kutofautiana kwa thamani, kama ilivyo katika hali ya anga, kuna mabadiliko makubwa katika wiani na kina. Katika hali hiyo, hatuwezi kutumia makadirio ya wiani mara kwa mara.
Shinikizo katika maji yenye wiani wa mara kwa mara
Hebu tutumie Equation\ ref {14.9} kufanya kazi nje formula kwa shinikizo kwa kina h kutoka uso katika tank ya kiowevu kama vile maji, ambapo wiani wa kiowevu unaweza kuchukuliwa kuwa mara kwa mara.
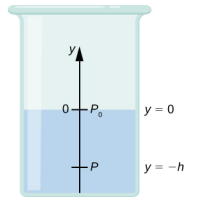
Tunahitaji kuunganisha Equation\ ref {14.9} kutoka y = 0, ambapo shinikizo ni shinikizo la anga (p 0), kwa y = -h, y-kuratibu ya kina:
\[\begin{split} \int_{p_{0}}^{p} dp & = - \int_{0}^{-h} \rho gdy \\ p - p_{0} & = \rho gh \\ p & = p_{0} + \rho gh \ldotp \end{split} \label{14.9}\]
Kwa hiyo, shinikizo kwa kina cha maji juu ya uso wa Dunia ni sawa na shinikizo la anga pamoja na\(\rho\) gh ikiwa wiani wa maji ni mara kwa mara juu ya urefu, kama tulivyopata hapo awali.
Kumbuka kwamba shinikizo katika maji hutegemea tu juu ya kina kutoka kwa uso na si kwa sura ya chombo. Kwa hiyo, katika chombo ambapo maji yanaweza kuhamia kwa uhuru katika sehemu mbalimbali, kioevu kinakaa kwa kiwango sawa katika kila sehemu, bila kujali sura, kama inavyoonekana kwenye Mchoro\(\PageIndex{4}\).

Tofauti ya shinikizo la anga na urefu
Mabadiliko katika shinikizo la anga na urefu ni ya riba fulani. Kutokana joto la hewa kuwa mara kwa mara, na kwamba sheria bora ya gesi ya thermodynamics inaelezea anga kwa makadirio mazuri, tunaweza kupata tofauti ya shinikizo la anga na urefu, wakati joto ni mara kwa mara. (Tunazungumzia sheria bora ya gesi katika sura ya baadaye, lakini tunadhani una ujuzi fulani kutoka shule ya sekondari na kemia.) Hebu p (y) kuwa shinikizo la anga kwa urefu y. wiani\(\rho\) katika y, joto T katika kiwango cha Kelvin (K), na molekuli m ya molekuli ya hewa ni kuhusiana na shinikizo kamili na sheria bora ya gesi, kwa namna
\[p = \rho \frac{k_{B} T}{m}\; (atmosphere), \label{14.10}\]
ambapo k B ni mara kwa mara ya Boltzmann, ambayo ina thamani ya 1.38 x 10 -23 J/K.
Huenda umekutana na sheria bora ya gesi kwa fomu pV = nRT, ambapo n ni idadi ya moles na R ni mara kwa mara ya gesi. Hapa, sheria hiyo imeandikwa kwa fomu tofauti, kwa kutumia wiani\(\rho\) badala ya kiasi V. Kwa hiyo, ikiwa shinikizo p linabadilika na urefu, ndivyo wiani\(\rho\). Kutumia wiani kutoka kwa sheria bora ya gesi, kiwango cha tofauti ya shinikizo na urefu hutolewa kama
\[\frac{dp}{dy} = -p \left(\dfrac{mg}{k_{B} T}\right),\]
ambapo kiasi mara kwa mara wamekusanywa ndani ya mabano. Kubadilisha vipindi hivi kwa ishara moja\(\alpha\), equation inaonekana rahisi zaidi:
\[\begin{split} \frac{dp}{dy} & = - \alpha p \\ \frac{dp}{p} & = - \alpha dy \\ \int_{p_{0}}^{p(y)} \frac{dp}{p} & = \int_{0}^{y} - \alpha dy \\ [\ln (p)]_{p_{0}}^{p(y)} & = [- \alpha y]_{0}^{y} \\ \ln (p) - \ln (p_{0}) & = - \alpha y \\ \ln \left(\dfrac{p}{p_{0}}\right) & = - \alpha y \end{split}\]
Hii inatoa ufumbuzi
\[p(y) = p_{0} e^{- \alpha y} \ldotp\]
Kwa hiyo, shinikizo la anga linapungua kwa urefu, kwani mhimili wa y umeelezwa kutoka chini na y ina maadili mazuri katika anga juu ya usawa wa bahari. shinikizo matone kwa sababu ya\(\frac{1}{e}\) wakati urefu ni\(\frac{1}{\alpha}\), ambayo inatupa tafsiri ya kimwili kwa\(\alpha\): mara kwa mara\(\frac{1}{\alpha}\) ni urefu wadogo kwamba sifa ya jinsi shinikizo inatofautiana na urefu na mara nyingi hujulikana kama shinikizo wadogo urefu.
Tunaweza kupata thamani ya takriban ya\(\alpha\) kwa kutumia wingi wa molekuli ya nitrojeni kama wakala kwa molekuli ya hewa. Katika joto la 27 °C, au 300 K, tunaona
\[\alpha = - \frac{mg}{k_{B} T} = \frac{(4.8 \times 10^{-26}\; kg) \times (9.81\; m/s^{2})}{(1.38 \times 10^{-23}\; J/K) \times (300\; K)} = \frac{1}{8800\; m} \ldotp\]
Kwa hiyo, kwa kila mita 8800, shinikizo la hewa hupungua kwa sababu 1/e, au takriban theluthi moja ya thamani yake. Hii inatupa tu makadirio mabaya ya hali halisi, kwa kuwa tumefikiri joto la mara kwa mara na g ya mara kwa mara juu ya umbali mkubwa kutoka Dunia, wala ambayo ni sahihi kwa kweli.
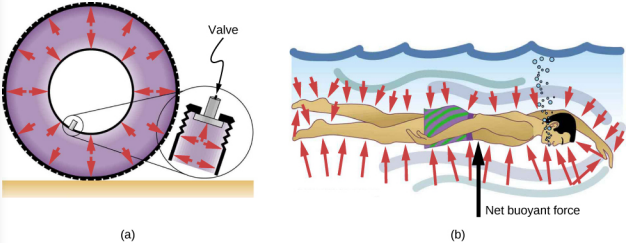
Mwelekeo wa shinikizo katika maji
Shinikizo la maji haina mwelekeo, kuwa wingi wa scalar, wakati nguvu kutokana na shinikizo zina maelekezo vizuri: Wao daima hutumiwa kwa uso wowote. Sababu ni kwamba majimaji hayawezi kuhimili au kutumia vikosi vya kuvikwa. Kwa hiyo, katika maji ya tuli yaliyofungwa ndani ya tank, nguvu inayotumiwa kwenye kuta za tank inatumika kwa uso wa ndani. Vivyo hivyo, shinikizo hutumiwa perpendicular kwa nyuso za kitu chochote ndani ya maji. Kielelezo\(\PageIndex{5}\) inaonyesha shinikizo exerted na hewa juu ya kuta za tairi na kwa maji juu ya mwili wa kuogelea.