Skip to main content
Global

15.7: Transfoma

  1. Last updated
  2. Save as PDF
  • Page ID
    176572

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hiyo, utaweza:

    • Eleza kwa nini mimea ya nguvu hupeleka umeme kwenye voltages ya juu na mikondo ya chini na jinsi wanavyofanya hivyo
    • Kuendeleza mahusiano kati ya sasa, voltage, na idadi ya windings katika transfoma hatua-up na chini-chini

    Ingawa nguvu za umeme zinazalishwa kwa voltages za chini, hutumwa kupitia mistari ya maambukizi kwenye voltages ya juu sana (kama juu ya 500 kV). Nguvu sawa inaweza kupitishwa kwa voltages tofauti kwa sababu nguvu ni bidhaa\(I_{rms}V_{rms}\). (Kwa unyenyekevu, tunapuuza sababu ya awamu\(\cos \, \phi\).) Mahitaji fulani ya nguvu yanaweza kukutana na voltage ya chini na sasa ya juu au kwa voltage ya juu na sasa ya chini. Faida ya uchaguzi wa juu-voltage/chini-sasa ni kwamba husababisha hasara za chini za\(I_{rms}^2R\) ohmic katika mistari ya maambukizi, ambayo inaweza kuwa muhimu katika mistari ambayo ni kilomita nyingi kwa muda mrefu (Kielelezo\(\PageIndex{1}\)).

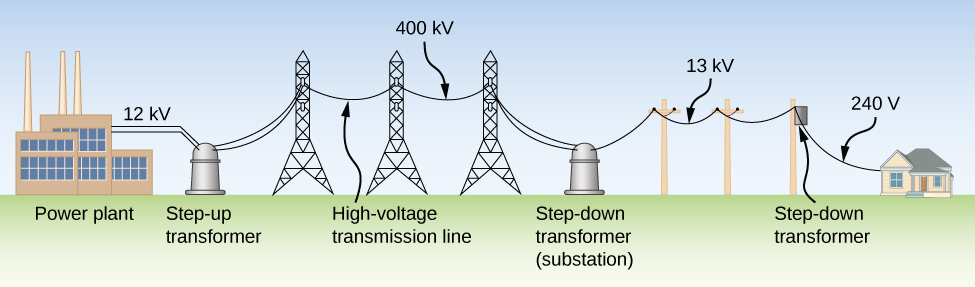
    Kielelezo kinaonyesha mmea wa nguvu upande wa kushoto. Hii imeshikamana na transformer ya hatua kwa njia ya mstari wa kV 12. Transformer imeshikamana na mstari wa maambukizi ya juu ya voltage ya kV 400. Hii imeshikamana na hatua ya chini ya transformer kwenye substation. Kutoka hapa, mstari wa 13 kV huenda kwenye transformer hatua ya chini kwenye pole ya umeme. Kutoka hapa mstari wa 240 V huenda nyumbani.
    Kielelezo\(\PageIndex{1}\): Voltage ya RMS kutoka kwenye mmea wa nguvu hatimaye inahitaji kupitishwa kutoka 12 kV hadi 240 V ili iweze kuletwa salama ndani ya nyumba. Mstari wa maambukizi ya juu-voltage inaruhusu sasa ya chini kupitishwa kupitia substation juu ya umbali mrefu.

    Kwa kawaida, emfs zinazozalishwa kwenye mimea ya nguvu ni “kupitiwa” kwa voltages ya juu sana kabla ya kuambukizwa kupitia mistari ya nguvu; basi, lazima “kupitiwa” kwa maadili salama (110 au 220 V rms) kabla ya kuletwa ndani ya nyumba. Kifaa kinachobadilisha voltages kutoka thamani moja hadi nyingine kwa kutumia induction ni transformer (Kielelezo\(\PageIndex{2}\)).

    Picha ya transfoma kwenye pole ya umeme. Kuna transfoma tatu, kila mmoja imefungwa kwenye chombo cha cylindrical.
    Kielelezo\(\PageIndex{2}\): Transfoma hutumiwa kupungua kwa voltages ya juu katika mistari ya maambukizi kwa 110 hadi 220 V kutumika katika nyumba. (mikopo: mabadiliko ya kazi na “Arobaini Saba” /Flickr)

    Kama Kielelezo\(\PageIndex{3}\) unaeleza, transformer kimsingi lina coils mbili kutengwa, au windings, amefungwa kuzunguka msingi laini chuma. Upepo wa msingi una\(N_p\) matanzi, au hugeuka, na umeunganishwa na voltage inayobadilisha\(v_p(t)\). Upepo wa sekondari\(N_s\) umegeuka na umeunganishwa na kupinga mzigo\(R_s\). Tunadhani kesi nzuri ambayo mistari yote ya shamba la magnetic imefungwa kwa msingi ili flux sawa ya magnetic inapita kila upande wa windings ya msingi na ya sekondari. Pia tunapuuza hasara za nishati kwa hysteresis ya magnetic, kwa joto la ohmic katika windings, na inapokanzwa kwa ohmic ya mikondo ya eddy iliyosababishwa katika msingi. Transformer nzuri inaweza kuwa na hasara chini kama 1% ya nguvu zinazoambukizwa, hivyo hii sio dhana mbaya.

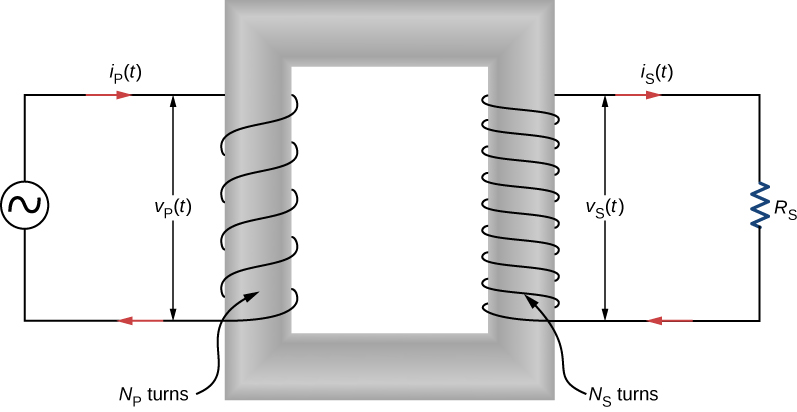
    Kielelezo kinaonyesha msingi wa chuma laini katikati. Hii ni kwa namna ya pete ya mstatili. Kuna windings kwenye mkono wake wa kushoto, unaounganishwa na chanzo cha voltage. Hizi ni kinachoitwa N subscript p zamu. Sasa kwa njia yao ni katika subscript up mabano kwa mabano. voltage katika ncha mbili za windings ni v Subscript p mabano t mabano. windings juu ya mkono wa kulia wa msingi ni kushikamana na resistor R subscript s. windings ni kinachoitwa N subscript s zamu. Hizi ni idadi zaidi kuliko windings upande wa kushoto. Ya sasa katika mzunguko sahihi ni katika usajili kama mabano kwa mabano. voltage katika windings ni v Subscript kama mabano kwa mabano. Ya sasa katika mzunguko wa kushoto inapita ndani ya windings kutoka juu. Ya sasa katika mzunguko sahihi hutoka nje ya vilima kutoka juu.
    Kielelezo\(\PageIndex{3}\): Transformer ya hatua-up (inarudi zaidi katika upepo wa sekondari kuliko katika vilima vya msingi). Windings mbili zimefungwa karibu na msingi wa chuma laini.

    Ili kuchambua mzunguko wa transformer, sisi kwanza tunazingatia upepo wa msingi. Voltage ya pembejeo\(v_p(t)\) ni sawa na tofauti ya uwezo ikiwa katika vilima vya msingi. Kutoka kwa sheria ya Faraday, tofauti ya uwezekano ni\(- N_p (d\Phi /dt)\), wapi\(\Phi\) mtiririko kupitia upande mmoja wa vilima vya msingi. Hivyo,

    \[v_p(t) = -N_p\dfrac{d\Phi}{dt}. \nonumber\]

    Vile vile, voltage ya pato\(v_s(t)\) iliyotolewa kwa kupinga mzigo lazima iwe sawa na tofauti ya uwezo ikiwa katika vilima vya sekondari. Kwa kuwa transformer ni bora, mtiririko kupitia kila upande wa vilima vya sekondari pia\(\Phi\) ni

    \[v_s (t) = -N_s \dfrac{d\Phi}{dt}. \nonumber\]

    Kuchanganya equations mbili za mwisho, tuna

    \[v_s(t) = \dfrac{N_s}{N_p} v_p(t). \label{15.20}\]

    Kwa hiyo, kwa maadili sahihi\(N_s\) na\(N_p\), voltage ya pembejeo\(v_p(t)\) inaweza “kupitiwa”\((N_s > N_p)\) au “imeshuka”\((N_s < N_p)\) kwa\(v_s(t)\), voltage ya pato. Hii mara nyingi hufupishwa kama equation ya transformer,

    \[\dfrac{V_s}{V_p} = \dfrac{N_s}{N_p},\label{transformerEQ}\]

    ambayo inaonyesha kwamba uwiano wa sekondari hadi voltages ya msingi katika transformer sawa na uwiano wa idadi ya zamu katika windings yao. Kwa transformer ya hatua-up, ambayo huongeza voltage na inapungua sasa, uwiano huu ni mkubwa kuliko moja; kwa transformer ya chini-chini, ambayo inapungua voltage na huongeza sasa, uwiano huu ni chini ya moja.

    Kutoka kwa sheria ya uhifadhi wa nishati, nguvu iliyoletwa\(v_p(t)\) kwa papo yoyote na vilima vya msingi lazima iwe sawa na nguvu iliyopigwa katika kupinga kwa mzunguko wa sekondari; hivyo,

    \[i_p(t)v_p(t) = i_s(t)v_s(t). \nonumber\]

    Wakati pamoja na Equation\ ref {TransforMereQ}, hii inatoa

    \[i_s(t) = \dfrac{N_p}{N_s} i_p(t). \label{15.22}\]

    Ikiwa voltage imeongezeka, sasa imeshuka, na kinyume chake.

    Hatimaye, tunaweza kutumia\(i_s(t) = v_s(t)/R_s\), pamoja na Equation\ ref {15.20} na Equation\ ref {15.22}, ili kupata

    \[v_p(t) = i_p \left[\left(\dfrac{N_p}{N_s}\right)^2 R_s\right], \nonumber\]

    ambayo inatuambia kwamba voltage pembejeo\(v_p(t)\) “anaona” si upinzani\(R_s\) bali upinzani

    \[R_p = \left(\dfrac{N_p}{N_s}\right)^2 R_s. \nonumber\]

    Uchunguzi wetu umekuwa msingi wa maadili ya papo hapo ya voltage na ya sasa. Hata hivyo, equations kusababisha si mdogo kwa maadili instantaneous; wao kushikilia pia kwa kiwango cha juu na RMS maadili.

    Mfano\(\PageIndex{1}\): A Step-Down Transformer

    Transformer juu ya pole ya matumizi inachukua voltage ya RMS chini kutoka 12 kV hadi 240 V.

    1. Je! Ni uwiano gani wa idadi ya zamu za sekondari kwa idadi ya zamu za msingi?
    2. Ikiwa pembejeo ya sasa kwa transformer ni 2.0 A, ni nini pato la sasa?
    3. Kuamua kupoteza nguvu katika mstari wa maambukizi ikiwa upinzani wa jumla wa mstari wa maambukizi ni\(200 \, \Omega\).
    4. Je, kupoteza nguvu ingekuwa nini ikiwa mstari wa maambukizi ulikuwa kwenye 240 V urefu mzima wa mstari, badala ya kutoa voltage saa 12 kV? Hii inasema nini kuhusu mistari ya maambukizi?

    Mkakati

    Idadi ya zamu zinazohusiana na voltages hupatikana kutoka Equation\ ref {15.20}. Sasa pato linahesabiwa kwa kutumia Equation\ ref {15.22}.

    Suluhisho

    a. Kutumia Equation\ ref {15.20} na maadili ya RMS\(V_p\) na\(V_s\) tuna\[\dfrac{N_s}{N_p} = \dfrac{240 \, V}{12 \times 10^3 V} = \dfrac{1}{50},\] hivyo vilima vya msingi vina mara 50 idadi ya zamu katika vilima vya sekondari.

    b Kutoka Equation\ ref {15.22}, sasa rms pato\(I_s\) hupatikana kwa kutumia equation transformer na sasa

    \[I_S = \dfrac{N_p}{N_S} I_p \label{15.23}\]

    kama kwamba

    \[I_s = \dfrac{N_p}{N_s}I_p = (50)(2.0 \, A) = 100 \, A. \nonumber\]

    c. kupoteza nguvu katika mstari wa maambukizi ni mahesabu kuwa

    \[P_{loss} = I_p^2R = (2.0 \, A)^2 (200 \, \Omega) = 800 \, W. \nonumber\]

    d Kama hapakuwa na transformer, nguvu ingekuwa kutumwa saa 240 V kufanya kazi kwa nyumba hizi, na kupoteza nguvu itakuwa

    \[P_{loss} = I_s^2R = (100 \, A)^2(200 \, \Omega) = 2 \times 10^6 \, W. \nonumber\]

    Kwa hiyo, wakati nguvu zinahitajika kupitishwa, tunataka kuepuka kupoteza nguvu. Hivyo, mistari hutumwa kwa voltages ya juu na mikondo ya chini na kubadilishwa na transformer kabla ya nguvu kutumwa ndani ya nyumba.

    Umuhimu

    Matumizi haya ya transformer ya chini-chini inaruhusu nyumba ambayo inatumia maduka 240-V kuwa na 100 A inapatikana kuteka juu. Hii inaweza kuimarisha vifaa vingi nyumbani.

    Zoezi\(\PageIndex{1}\)

    A transformer hatua voltage line chini kutoka 110 hadi 9.0 V ili sasa ya 0.50 A inaweza kutolewa kwa mlango.

    1. Je! Ni uwiano gani wa idadi ya zamu katika windings ya msingi na ya sekondari?
    2. Je! Ni sasa gani katika upepo wa msingi?
    3. Ni upinzani gani unaoonekana na chanzo cha 110-V?
    Jibu

    12:1

    Jibu b

    0.042 A

    Jibu c

    \(2.6 \times 10^3 \, \Omega\)