Skip to main content
Global

15.6: Resonance katika mzunguko wa AC

  1. Last updated
  2. Save as PDF
  • Page ID
    176552

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hiyo, utaweza:

    • Kuamua kilele ac resonant angular frequency kwa mzunguko RLC
    • Eleza upana wa nguvu ya wastani dhidi ya pembe ya mzunguko wa angular na umuhimu wake kwa kutumia maneno kama bandwidth na sababu ya ubora

    Katika mzunguko wa mfululizo wa RLC wa Mchoro 15.4.1, amplitude ya sasa ni, kutoka kwa Equation 15.4.7,

    \[I_0 = \dfrac{V_0}{\sqrt{R^2 + (\omega L - 1/\omega C)^2}}. \label{15.15} \]

    Ikiwa tunaweza kutofautiana mzunguko wa jenereta ya ac wakati wa kuweka amplitude ya voltage yake ya pato mara kwa mara, basi mabadiliko ya sasa yanabadilika ipasavyo. njama ya\(I_0\) dhidi\(\omega\) ni inavyoonekana katika Kielelezo\(\PageIndex{1}\).

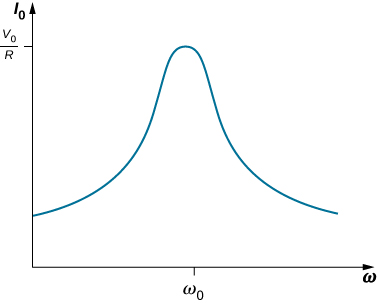
    Kielelezo kinaonyesha grafu ya I0 dhidi ya omega. Curve hupanda hatua kwa hatua, ina kilele kimoja kimoja katikati na kisha hatua kwa hatua hutoka kwa thamani yake ya awali. Thamani ya y kwenye kilele ni V0 na R na thamani ya x ni omega 0.
    Kielelezo\(\PageIndex{1}\): Katika mzunguko wa mzunguko wa RLC\(\omega_0 = \sqrt{1/LC}\), amplitude ya sasa iko katika thamani yake ya juu.

    Katika oscillations, tulikutana na grafu sawa ambapo amplitude ya oscillator ya harmonic iliyopangwa ilipangwa dhidi ya mzunguko wa angular wa nguvu ya kuendesha gari la sinusoidal (tazama. Ufanana huu ni zaidi ya bahati mbaya, kama ilivyoonyeshwa hapo awali na matumizi ya utawala wa kitanzi cha Kirchhoff kwenye mzunguko wa Kielelezo 15.4.1. Hii mavuno

    \[L\dfrac{di}{dt} + iR + \dfrac{q}{C} = V_0 \, \sin \, \omega t, \label{15.16}\]

    au

    \[L\dfrac{d^2q}{dt^2} + R\dfrac{dq}{dt} + \dfrac{1}{C}q = V_0 \, \sin \, \omega t,\]

    ambapo sisi kubadilishwa dq (t)/dt kwa i (t). Ulinganisho wa Equation\ ref {15.16} na, kutoka Oscillations, Oscillations Damped kwa damped harmonic mwendo inaonyesha wazi kwamba inaendeshwa RLC mfululizo mzunguko ni Analog umeme wa inaendeshwa damped harmonic oscillator.

    Mzunguko wa resonant\(f_0\) wa mzunguko wa RLC ni mzunguko ambao amplitude ya sasa ni kiwango cha juu na mzunguko ungeweza kusonga ikiwa sio inaendeshwa na chanzo cha voltage. Kwa ukaguzi, hii inalingana na mzunguko\(\omega_0 = 2\pi f_0\) wa angular ambapo impedance Z katika Equation\ ref {15.15} ni kiwango cha chini, au wakati

    \[\omega_0 L = \dfrac{1}{\omega_0 C} \label{resonantfrequency1}\]

    na

    \[\omega_0 = \sqrt{\dfrac{1}{LC}}.\label{resonantfrequency2}\]

    Hii ni mzunguko wa angular wa mzunguko. Kubadilisha\(\omega_0\) katika Equation 15.4.5, Equation 15.4.7, na Equation 15.4.8, tunaona kwamba katika resonance,

    \[\phi = tan^{-1}(0) = 0, \, I_0 = V_0/R, \, and \, Z = R.\]

    Kwa hiyo, katika resonance, mzunguko wa RLC ni rena resistive, na emf kutumika na sasa katika awamu.

    Ni nini kinachotokea kwa nguvu katika resonance? Equation 15.5.18 inatuambia jinsi nguvu wastani kuhamishwa kutoka ac jenereta kwa mchanganyiko RLC inatofautiana na frequency. Kwa kuongeza,\(P_{ave}\) hufikia kiwango cha juu wakati\(Z\), ambayo inategemea mzunguko, ni kiwango cha chini, yaani, wakati\(X_L = X_C\) na\(Z = R\). Kwa hiyo, kwa resonance, pato la wastani la nguvu la chanzo katika mzunguko wa mfululizo wa RLC ni kiwango cha juu. Kutoka Equation 15.5.18, kiwango cha juu hii ni\(V_{rms}^2 /R\).

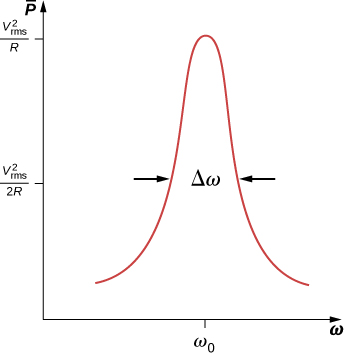
    Kielelezo\(\PageIndex{2}\) ni njama ya kawaida ya\(P_{ave}\) dhidi\(\omega\) katika eneo la pato la juu la nguvu. Bandwidth\(\Delta \omega\) ya kilele cha resonance hufafanuliwa kama aina mbalimbali za masafa\(\omega\) ya angular ambayo nguvu ya wastani\(P_{ave}\) ni kubwa kuliko nusu ya thamani ya juu ya\(P_{ave}\). Ukali wa kilele unaelezewa na kiasi cha dimensionless kinachojulikana kama sababu ya ubora Q ya mzunguko. Kwa ufafanuzi,

    \[Q = \dfrac{\omega_0}{\Delta \omega}, \label{15.18} \]

    \(\omega_0\)wapi mzunguko wa angular wa resonant. Q ya juu inaonyesha kilele cha resonance kali. Tunaweza kutoa Q kwa suala la vigezo vya mzunguko kama

    \[Q = \dfrac{\omega_0L}{R}. \label{15.19} \]

    Kielelezo kinaonyesha grafu ya P bar dhidi ya omega. Curve hupanda hatua kwa hatua, ina kilele kimoja kimoja katikati na kisha hatua kwa hatua hutoka kwa thamani yake ya awali. Thamani ya y katika kilele ni V squared subscript RMS na R na x-thamani ni omega 0. Thamani y karibu katikati ya Curve ni V squared subscript RMS na 2R. Upana wa curve karibu katikati ni kinachoitwa delta omega.
    Kielelezo\(\PageIndex{2}\): Kama sasa, nguvu wastani kuhamishwa kutoka jenereta ac kwa RLC mzunguko peaks katika frequency resonant.

    Mzunguko wa resonant hutumiwa kupitisha au kukataa safu za mzunguko zilizochaguliwa. Hii inafanywa kwa kurekebisha thamani ya moja ya vipengele na hivyo “tuning” mzunguko kwa mzunguko fulani wa resonant. Kwa mfano, katika redio, mpokeaji hutengenezwa kwenye kituo cha taka kwa kurekebisha mzunguko wa resonant wa mzunguko wake ili kufanana na mzunguko wa kituo. Ikiwa mzunguko wa tuning una Q ya juu, itakuwa na bandwidth ndogo, hivyo ishara kutoka vituo vingine kwenye masafa hata tofauti kidogo na mzunguko wa resonant hukutana na impedance ya juu na haipatikani na mzunguko. Simu za mkononi hufanya kazi kwa mtindo sawa, kuwasiliana na ishara za karibu 1 GHz ambazo zinatengenezwa na mzunguko wa inductor-capacitor. Moja ya maombi ya kawaida ya capacitors ni matumizi yao katika nyaya za majira ya joto, kulingana na kufikia mzunguko wa resonant. Detector ya chuma pia hutumia mabadiliko katika mzunguko wa resonance katika kuchunguza metali (Kielelezo\(\PageIndex{3}\)).

    Picha ya diver chini ya maji kwa kutumia detector chuma.
    Kielelezo\(\PageIndex{3}\): Wakati detector ya chuma inakuja karibu na kipande cha chuma, kujitegemea inductance ya moja ya coils yake inabadilika. Hii inasababisha mabadiliko katika mzunguko wa resonant wa mzunguko ulio na coil. Mabadiliko hayo yanagunduliwa na mzunguko na hupitishwa kwa diver kwa njia ya vichwa vya sauti.
    Mfano\(\PageIndex{1}\): Resonance in an RLC Series Circuit
    1. ni mzunguko resonant ya mzunguko wa Mfano 15.3.1 nini?
    2. Ikiwa jenereta ya ac imewekwa kwenye mzunguko huu bila kubadilisha amplitude ya voltage ya pato, ni amplitude gani ya sasa?

    Mkakati

    Mzunguko wa resonant kwa mzunguko wa RLC huhesabiwa kutoka kwa Equation\ ref {resonantfrequency2}, ambayo hutoka kwa usawa kati ya reactances ya capacitor na inductor. Tangu mzunguko ni kwenye resonance, impedance ni sawa na kupinga. Kisha, sasa kilele kinahesabiwa na voltage iliyogawanywa na upinzani.

    Suluhisho

    1. Mzunguko wa resonant hupatikana kutoka kwa Equation\ ref {resonantfrequency2}:\[\begin{align*} f_0 &= \dfrac{1}{2\pi} \sqrt{\dfrac{1}{LC}} \\[4pt] &= \dfrac{1}{2\pi}\sqrt{\dfrac{1}{(3.00 \times 10^{-3} H)(8.00 \times 10^{-4}F)}} \\[4pt] &= 1.03 \times 10^2 \, Hz. \end{align*}\]
    2. Katika resonance, impedance ya mzunguko ni rena resistive, na amplitude ya sasa ni\[I_0 = \dfrac{0.100 \, V}{4.00 \, \Omega} = 2.50 \times 10^{-2}A. \nonumber\]

    Umuhimu

    Ikiwa mzunguko haukuwekwa kwenye mzunguko wa resonant, tutahitaji impedance ya mzunguko mzima ili kuhesabu sasa.

    Mfano\(\PageIndex{2}\): Power Transfer in an RLC Series Circuit at Resonance
    1. ni resonant angular frequency ya mzunguko RLC na nini\( R = 0.200 \, \Omega, \, L = 4.00 \times 10^{-3} H\), na\(C = 2.00 \times 10^{-6}F\)?
    2. Ikiwa chanzo cha ac cha amplitude mara kwa mara 4.00 V kinawekwa kwenye mzunguko huu, ni nguvu gani ya wastani inayohamishiwa kwenye mzunguko?
    3. Tambua Q na bandwidth ya mzunguko huu.

    Mkakati

    Mzunguko wa angular wa resonant huhesabiwa kutoka kwa Equation\ ref {resonantfrequency2}. Nguvu ya wastani imehesabiwa kutoka kwa voltage ya RMS na upinzani katika mzunguko. Sababu ya ubora huhesabiwa kutoka kwa Equation\ ref {15.19} na kwa kujua mzunguko wa resonant. Bandwidth imehesabiwa kutoka kwa Equation\ ref {15.18} na kwa kujua sababu ya ubora.

    Suluhisho

    1. Mzunguko wa angular resonant ni\[ \begin{align*} \omega_0 &= \sqrt{\dfrac{1}{LC}} \\[4pt] &= \sqrt{\dfrac{1}{(4.00 \times 10^{-3}H)(2.00 \times 10^{-6}F)}} \\[4pt] &= 1.12 \times 10^4 \, rad/s. \end{align*}\]
    2. Kwa mzunguko huu, nguvu ya wastani iliyohamishwa kwenye mzunguko ni kiwango cha juu. Ni\[P_{ave} = \dfrac{V_{rms}^2}{R} = \dfrac{[(1/\sqrt{2})(4.00 \, V)]^2}{0.200 \, \Omega} = 40.0 \, W.\]
    3. Sababu ya ubora wa mzunguko ni\[Q = \dfrac{\omega_0L}{R} = \dfrac{(1.12 \times 10^4 \, rad/s)(4.00 \times 10^{-3}H)}{0.200 \, \Omega} = 224. \nonumber\] Sisi kisha kupata kwa bandwidth\[\Delta \omega = \dfrac{\omega_0}{Q} = \dfrac{1.12 \times 10^4 \, rad/s}{224} = 50.0 \, rad/s. \nonumber\]

    Umuhimu

    Ikiwa bandwidth nyembamba inahitajika, upinzani wa chini au inductance ya juu ingesaidia. Hata hivyo, upinzani wa chini huongeza nguvu zilizohamishwa kwenye mzunguko, ambayo inaweza kuwa isiyohitajika, kulingana na nguvu ya juu ambayo inaweza kuhamishwa.

    Zoezi\(\PageIndex{1}\)

    Katika mzunguko wa Kielelezo 15.4.1,\(L = 2.0 \times 10^{-3}H, \, C = 5.0 \times 10^{-4} F\), na\(R = 40 \, \Omega\).

    1. ni frequency resonant nini?
    2. Je, ni impedance ya mzunguko katika resonance?
    3. Ikiwa amplitude ya voltage ni 10 V, ni nini (t) katika resonance?
    4. Mzunguko wa jenereta ya AC sasa umebadilishwa hadi 200 Hz. Tumia tofauti ya awamu kati ya sasa na emf ya jenereta.
    Jibu

    a. 160 Hz; b.\(40 \Omega\); c.\((0.25 A) \, \sin \, 10^3t\); d. 0.023 rad

    Zoezi\(\PageIndex{2}\)

    Ni nini kinachotokea kwa mzunguko wa resonant wa mzunguko wa mfululizo wa RLC wakati kiasi kinachofuata kinaongezeka kwa sababu ya 4: (a) uwezo, (b) kujitegemea, na (c) upinzani?

    Jibu

    a. nusu; b. nusu; c. sawa

    Zoezi\(\PageIndex{3}\)

    Resonant angular frequency ya mzunguko RLC mfululizo ni\(4.0 \times 10^2 \, rad/s\). Chanzo cha ac kinachoendesha mzunguko huu huhamisha nguvu ya\(2.0 \times 10^{-2} W\) wastani ya mzunguko. Upinzani wa mzunguko ni\(0.50 \, \Omega\). Andika maneno kwa emf ya chanzo.

    Jibu

    \(v(t) = (0.14 \, V) \, sin \, (4.0 \times 10^2 t)\)