Skip to main content
Global

14.2: Inductance ya Kuheshimiana

  1. Last updated
  2. Save as PDF
  • Page ID
    176369

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    MALENGO YA KUJIFUNZA

    Mwishoni mwa sehemu hii, utaweza:

    • Unganisha nyaya mbili za karibu ambazo hubeba mikondo ya muda tofauti na emf ikiwa katika kila mzunguko
    • Eleza mifano ambayo inductance ya pamoja inaweza au haipendekezi

    Inductance ni mali ya kifaa kinachotuambia jinsi inavyofanya emf katika kifaa kingine. Kwa maneno mengine, ni kiasi cha kimwili kinachoonyesha ufanisi wa kifaa kilichopewa.

    Wakati mizunguko miwili inayobeba mikondo ya muda tofauti iko karibu na kila mmoja, mtiririko wa magnetic kupitia kila mzunguko unatofautiana kwa sababu ya sasa ya kubadilisha mimi katika mzunguko mwingine. Kwa hiyo, emf inaingizwa katika kila mzunguko na mabadiliko ya sasa katika nyingine. Kwa hiyo aina hii ya emf inaitwa emf ya pande zote, na jambo linalojitokeza linajulikana kama inductance ya pamoja (M). Kwa mfano, hebu tuchunguze coils mbili za jeraha (Kielelezo\(\PageIndex{1}\)). Coils 1 na 2 zina\(N_1\) na\(N_2\) hugeuka na kubeba mikondo\(I_1\) na\(I_2\) kwa mtiririko huo. Flux kupitia upande mmoja wa coil 2 zinazozalishwa na shamba magnetic ya sasa katika coil 1 ni\(\Phi_{12}\), wakati flux kupitia upande mmoja wa coil 1 kutokana na shamba magnetic ya\(I_2\) ni\(\Phi_{12}\).

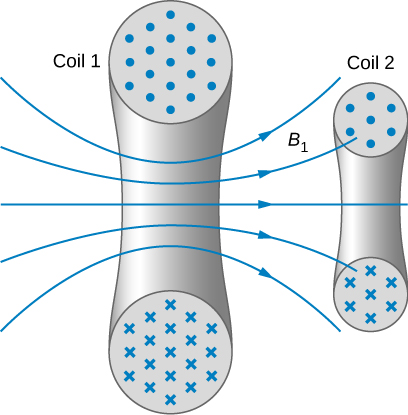
    Kielelezo kinaonyesha sehemu za msalaba wa coil mbili. Katika kila mmoja, sehemu za msalaba wa waya wa coil zinaonyeshwa kama miduara miwili, moja juu na nyingine chini. Dots katika miduara ya juu na misalaba katika chini zinaonyesha mwelekeo wa mtiririko wa sasa. Coil 1 ina mistari shamba kinachoitwa B1 kupita kutoka kati ya duru mbili, kwenda kulia. Baadhi ya hizi hupita kupitia coil 2, ambayo ni ndogo kuliko coil 1
    Kielelezo\(\PageIndex{1}\): Baadhi ya mistari ya shamba la magnetic zinazozalishwa na sasa katika coil 1 hupita kupitia coil 2.

    Kuheshimiana inductance coil 2 kwa heshima\(M_{21}\) ya coil 1 ni uwiano wa flux kupitia\(N_2\) zamu ya coil 2 zinazozalishwa na shamba magnetic ya sasa katika coil 1, kugawanywa na sasa, yaani,

    \[M_{21} = \dfrac{N_2\Phi_{21}}{I_1}. \label{12.24}\]

    Vile vile, inductance ya pamoja ya coil 1 kwa heshima ya coil 2 ni

    \[M_{12} = \dfrac{N_1\Phi_{12}}{I_2}. \label{12.25}\]

    Kama capacitance, inductance ya pamoja ni kiasi cha kijiometri. Inategemea maumbo na nafasi za jamaa za coil mbili, na ni huru ya mikondo katika coils. Kitengo cha SI cha inductance kuheshimiana M kinaitwa henry (H) kwa heshima ya Joseph Henry (1799—1878), mwanasayansi wa Marekani ambaye aligundua ikiwa emf kujitegemea Faraday. Hivyo, tuna\(1 \, H = 1 \, V \cdot s/A\). Kutoka Equations\ ref {12.24} na\ ref {12.25}, tunaweza kuonyesha kwamba\(M_{21} = M_{12}\), kwa kawaida tunatupa michango inayohusishwa na inductance ya pamoja na kuandika

    \[M = \dfrac{N_2\Phi_{21}}{I_1} = \dfrac{N_1 \Phi_{12}}{I_2}.\label{14.3}\]

    EMF iliyoandaliwa katika coil ama inapatikana kwa kuchanganya sheria ya Faraday na ufafanuzi wa inductance ya pamoja. Kwa kuwa\(N_2\Phi_{21}\) ni flux jumla kwa njia ya coil 2 kutokana na\(I_1\), tunapata

    \[\begin{align} \epsilon_2 &= - \dfrac{d}{dt} (N_2 \Phi_{21}) \\[4pt] &= - \dfrac{d}{dt} (MI_1) \\[4pt] & = - M\dfrac{dI_1}{dt} \label{14.4} \end{align} \]

    ambapo tumetumia ukweli kwamba\(M\) ni mara kwa mara ya kujitegemea kwa sababu jiometri ni wakati huru. Vile vile, tuna

    \[\epsilon_1 = - M\dfrac{dI_2}{dt}. \label{14.5}\]

    Katika Equation\ ref {14.5}, tunaweza kuona umuhimu wa maelezo ya awali ya inductance ya pamoja (\(M\)) kama wingi wa kijiometri. Thamani ya\(M\) kuzingatia vizuri mali ya kimwili ya vipengele vya mzunguko na inatuwezesha kutenganisha mpangilio wa kimwili wa mzunguko kutoka kwa kiasi cha nguvu, kama vile emf na sasa. Equation\ ref {14.5} inafafanua inductance kuheshimiana katika suala la mali katika mzunguko, ambapo ufafanuzi uliopita wa inductance kuheshimiana katika Equation\ ref {12.24} hufafanuliwa kwa suala la flux magnetic uzoefu, bila kujali mambo ya mzunguko. Unapaswa kuwa makini wakati wa kutumia equations\ ref {14.4} na\ ref {14.4} kwa sababu\(\epsilon_1\) na\(\epsilon_2\) si lazima kuwakilisha emfs jumla katika coils husika. Kila coil pia inaweza kuwa na emf ikiwa ndani yake kwa sababu ya kujitegemea (kujitegemea inductance itajadiliwa kwa undani zaidi katika sehemu ya baadaye).

    Inductance kubwa ya pamoja M inaweza au haipendekezi. Tunataka transformer kuwa na inductance kubwa ya pamoja. Lakini vifaa, kama vile dryer ya nguo za umeme, vinaweza kusababisha emf hatari kwenye kesi yake ya chuma ikiwa inductance ya pamoja kati ya coils yake na kesi ni kubwa. Njia moja ya kupunguza inductance ya pamoja ni kukabiliana na coils upepo kufuta shamba magnetic zinazozalishwa (Kielelezo\(\PageIndex{2}\)).

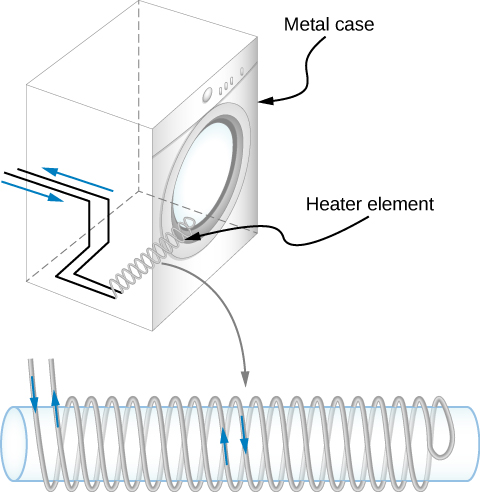
    Kielelezo a inaonyesha coil inapokanzwa ndani ya kesi ya chuma ya dryer nguo. Kielelezo b kinaonyesha coil sawa, imeenea. Coil imejeruhiwa kwenye silinda kwa namna ambayo waya mmoja hujeruhiwa kwa njia yote kwa upande mwingine, inaendelea kuzunguka na kuumiza njia yote ya nyuma. Hivyo, windings mbili karibu na sasa inapita katika mwelekeo kinyume
    Kielelezo\(\PageIndex{2}\): Coils inapokanzwa ya dryer ya nguo za umeme zinaweza kukabiliana na jeraha ili mashamba yao ya magnetic kufuta kila mmoja, kwa kiasi kikubwa kupunguza inductance ya pamoja na kesi ya dryer.

    Usindikaji wa ishara ya digital ni mfano mwingine ambao inductance ya pamoja imepunguzwa na coil coils counter-vilima. Haraka/off emf inayowakilisha 1s na 0 katika mzunguko wa digital inajenga shamba tata la magnetic linalojitegemea wakati. Emf inaweza kuzalishwa katika watendaji wa jirani. Ikiwa kondakta huyo pia anabeba ishara ya digital, emf ikiwa inaweza kuwa kubwa ya kutosha kubadili 1s na 0, na matokeo yanayotokana na hali mbaya hadi ya hatari.

    Mfano\(\PageIndex{1}\): Mutual Inductance

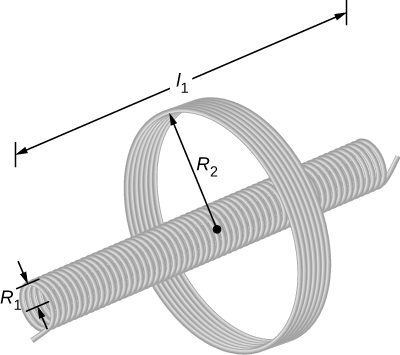
    Kielelezo\(\PageIndex{3}\) kinaonyesha coil ya\(N_2\) zamu na radius\(R_2\) jirani solenoid ndefu ya urefu\(l_1\), radius\(R_1\), na\(N_1\) zamu.

    1. Je, ni inductance ya pamoja ya coils mbili?
    2. Ikiwa\(N_1 = 500 \, turns, \, N_2 = 10 \, turns, \, R_1 = 3.10 \, cm, \, l_1 = 75.0 \, cm\), na sasa katika solenoid inabadilika kwa kiwango cha 200 A/s, ni nini emf ikiwa katika coil jirani?
    Kielelezo kinaonyesha solenoid, kwa namna ya coil ndefu yenye kipenyo kidogo, ambacho kinapangwa kwa makini na coil nyingine, kubwa zaidi. Radi ya solenoid ni R1 na ile ya coil ni R2. Urefu wa solenoid ni l1
    Kielelezo\(\PageIndex{3}\): solenoid iliyozungukwa na coil.

    Mkakati

    Hakuna shamba la magnetic nje ya solenoid, na shamba ndani ina ukubwa\(B_1 = \mu_0(N_1/l_1)I_1\) na inaelekezwa sambamba na mhimili wa solenoid. Tunaweza kutumia uwanja huu wa magnetic kupata flux magnetic kupitia coil jirani na kisha kutumia flux hii kuhesabu inductance kuheshimiana kwa sehemu (a), kwa kutumia Equation\ ref {14.3}. Tunatatua sehemu (b) kwa kuhesabu inductance ya pamoja kutoka kwa kiasi kilichopewa na kutumia Equation\ ref {14.4} ili kuhesabu emf iliyosababishwa.

    Suluhisho

    1. Flux magnetic\(\Phi_{21}\) kupitia coil jirani ni\[\begin{align*} \Phi_{21} &= B_1 \pi R_1^2 \\[4pt] &= \dfrac{\mu_0 N_1I_1}{l_1}\pi R_1^2. \end{align*}\] Sasa kutoka Equation\ ref {14.3}, inductance ya pamoja ni\[\begin{align*} M &= \dfrac{N_2\Phi_{21}}{I_1} \\[4pt] &= \left(\dfrac{N_2}{I_1}\right)\left(\dfrac{\mu_0N_1I_1}{l_1}\right) \pi R_1^2 \nonumber \\[4pt] &= \dfrac{\mu_0N_1N_2 \pi R_1^2}{l_1}.\end{align*} \]
    2. Kutumia maneno ya awali na maadili yaliyotolewa, inductance ya pamoja ni\[\begin{align*} M &= \dfrac{(4\pi \times 10^{-7} \, T \cdot m/A)(500)(10)\pi (0.0310 \, m)^2}{0.750 \, m} \\[4pt] &=2.53 \times 10^{-5} \, H. \nonumber \end{align*} \] Hivyo, kutoka Equation\ ref {14.4}, emf ikiwa katika coil jirani ni\[\begin{align*} \epsilon_2 &= - M\dfrac{dI_1}{dt} \\[4pt] &= - (2.53 \times 10^{-5} H)(200 \, A/s) \\[4pt] &= - 5.06 \times 10^{-3}V. \end{align*} \]

    Umuhimu

    Kumbuka kwamba M katika sehemu (a) ni huru ya radius\(R_2\) ya coil jirani kwa sababu shamba solenoid ya magnetic ni funge kwa mambo yake ya ndani. Kimsingi, tunaweza pia kuhesabu M kwa kutafuta flux magnetic kupitia solenoid zinazozalishwa na sasa katika coil jirani. Njia hii ni ngumu zaidi kwa sababu\(\Phi_{12}\) ni ngumu sana. Hata hivyo\(M_{12} = M_{21}\), tangu, tunajua matokeo ya hesabu hii.

    Zoezi\(\PageIndex{1}\)

    Sasa\(I(t) = (5.0 \, A) \, sin \, ((120\pi \, rad/s)t)\) inapita kupitia solenoid ya sehemu (b) ya Mfano\(\PageIndex{1}\). Je, ni emf ya juu inayoingizwa katika coil inayozunguka?

    Suluhisho

    \(4.77 \times 10^{-2} \, V\)