8.4: Nishati Imehifadhiwa katika Capacitor
- Page ID
- 176420
Mwishoni mwa sehemu hii, utaweza:
- Eleza jinsi nishati inavyohifadhiwa kwenye capacitor
- Tumia mahusiano ya nishati kuamua nishati iliyohifadhiwa kwenye mtandao wa capacitor
Wengi wetu tumeona uigizaji wa wafanyakazi wa matibabu kwa kutumia defibrillator kupitisha sasa umeme kupitia moyo wa mgonjwa ili kuipiga kawaida. Mara nyingi kwa undani kwa undani, mtu anayeomba mshtuko anaongoza mtu mwingine “kuifanya joules 400 wakati huu.” Nishati iliyotolewa na defibrillator imehifadhiwa katika capacitor na inaweza kubadilishwa ili kufanana na hali hiyo. SI vitengo vya joules mara nyingi huajiriwa. Chini ya kiasi kikubwa ni matumizi ya capacitors katika microelectronics kutoa nishati wakati betri ni kushtakiwa (Kielelezo\(\PageIndex{1}\)). Wafanyabiashara pia hutumiwa kutoa nishati kwa taa za flash kwenye kamera.

Nishati\(U_C\) iliyohifadhiwa katika capacitor ni nishati ya uwezo wa umeme na hivyo inahusiana na malipo Q na voltage V kati ya sahani za capacitor. Capitor kushtakiwa huhifadhi nishati katika uwanja wa umeme kati ya sahani zake. Kama capacitor inavyoshtakiwa, uwanja wa umeme hujenga. Wakati capacitor kushtakiwa imekatwa kutoka betri, nishati yake inabaki katika shamba katika nafasi kati ya sahani zake.
Ili kupata ufahamu wa jinsi nishati hii inaweza kuelezwa (kwa suala la Q na V), fikiria capacitor ya kushtakiwa, tupu, sambamba sahani; yaani, capacitor bila dielectric lakini kwa utupu kati ya sahani zake. Nafasi kati ya sahani zake ina kiasi Ad, na imejaa shamba la umeme sare E. Nishati ya jumla\(U_C\) ya capacitor imetolewa ndani ya nafasi hii. Uzito wa nishati\(u_E\) katika nafasi hii\(U_C\) umegawanyika tu na kiasi Ad. Kama tunajua wiani nishati, nishati inaweza kupatikana kama\(U_C = u_E(Ad)\). Tutajifunza katika Mawimbi ya umeme (baada ya kukamilisha utafiti wa equations ya Maxwell) kwamba wiani wa nishati\(u_E\) katika eneo la nafasi ya bure inayotumiwa na uwanja wa umeme E inategemea tu ukubwa wa shamba na ni
\[u_E = \frac{1}{2} \epsilon_0E^2.\]
Ikiwa tunazidisha wiani wa nishati kwa kiasi kati ya sahani, tunapata kiasi cha nishati iliyohifadhiwa kati ya sahani za capacitor ya sambamba\(U_C = u_E(Ad) = \frac{1}{2}\epsilon_0E^2Ad = \frac{1}{2}\epsilon_0\frac{V^2}{d^2}Ad = \frac{1}{2}V^2\epsilon_0 \frac{A}{d} = \frac{1}{2}V^2C\).
Katika derivation hii, tulitumia ukweli kwamba uwanja wa umeme kati ya sahani ni sare ili\(E = V/d\) na\(C = \epsilon_0A/d\). Kwa sababu\(C = Q/V\), tunaweza kueleza matokeo haya kwa aina nyingine sawa:
\[U_C = \frac{1}{2}V^2C = \frac{1}{2}\frac{Q^2}{C} = \frac{1}{2}QV. \label{8.10}\]
Maneno katika Equation\ ref {8.10} kwa nishati iliyohifadhiwa katika capacitor sambamba sahani kwa ujumla ni halali kwa kila aina ya capacitors. Ili kuona hili, fikiria capacitor yoyote isiyojumuishwa (sio aina ya sahani ya sambamba). Kwa papo fulani, tunaiunganisha kwenye betri, na kuifanya tofauti\(V = q/C\) kati ya sahani zake. Awali, malipo kwenye sahani ni\(Q = 0\). Kama capacitor inavyoshtakiwa, malipo hujenga hatua kwa hatua kwenye sahani zake, na baada ya muda fulani, hufikia thamani Swali. Ili kuhamisha malipo ya infinitesimal dq kutoka sahani hasi kwa sahani chanya (kutoka chini hadi uwezo wa juu), kiasi cha kazi dW ambayo lazima ifanyike kwenye dq ni\(dW = W \, dq = \frac{q}{C} dq\).
Kazi hii inakuwa nishati iliyohifadhiwa katika uwanja wa umeme wa capacitor. Ili malipo ya capacitor kwa malipo Swali, kazi ya jumla inahitajika ni
\[W = \int_0^{W(Q)} dW = \int_0^Q \frac{q}{C}dq = \frac{1}{2}\frac{Q^2}{C}.\]
Kwa kuwa jiometri ya capacitor haijainishwa, equation hii inashikilia aina yoyote ya capacitor. Kazi ya jumla W inahitajika kulipa capacitor ni nishati ya uwezo wa umeme\(U_C\) iliyohifadhiwa ndani yake, au\(U_C = W\). Wakati malipo yanaonyeshwa katika coulombs, uwezo unaonyeshwa kwa volts, na uwezo unaonyeshwa katika farads, uhusiano huu hutoa nishati katika joules.
Kujua kwamba nishati iliyohifadhiwa katika capacitor ni\(U_C = Q^2/(2C)\), sasa tunaweza kupata wiani wa nishati\(u_E\) kuhifadhiwa katika utupu kati ya sahani za kushtakiwa sambamba sahani capacitor. Tunapaswa kugawanya\(U_C\) kwa kiasi Ad ya nafasi kati ya sahani zake na kuzingatia kwamba kwa capacitor sambamba sahani, tuna\(E = \sigma/\epsilon_0\) na\(C = \epsilon_0 A/d\). Kwa hiyo, sisi kupata
\[u_E = \frac{U_C}{Ad} = \frac{1}{2} \frac{Q^2}{C} \frac{1}{Ad} = \frac{1}{2} \frac{Q^2}{\epsilon_0A/d} \frac{1}{Ad} = \frac{1}{2} \frac{1}{\epsilon_0} \left(\frac{Q}{A}\right)^2 = \frac{\sigma^2}{2\epsilon_0} = \frac{(E\epsilon_0)^2}{2\epsilon_0} = \frac{\epsilon_0}{2}E^2\]
Tunaona kwamba maneno haya kwa wiani wa nishati kuhifadhiwa katika capacitor sambamba sahani ni kwa mujibu wa uhusiano wa jumla walionyesha katika Equation\ ref {8.9}. Tunaweza kurudia hesabu hii kwa ajili ya capacitor spherical au capacitor cylindrical - au capacitors nyingine-na katika hali zote, tutakuwa kuishia na uhusiano wa jumla iliyotolewa na Equation\ ref {8.9}.
Tumia nishati iliyohifadhiwa kwenye mtandao wa capacitor katika Kielelezo 8.3.4a wakati capacitors ni kushtakiwa kikamilifu na wakati capacitances ni\(C_1 = 12.0 \, \mu F, \, C_2 = 2.0 \, \mu F\), na\(C_3 = 4.0 \, \mu F\), kwa mtiririko huo.
Mkakati
Tunatumia Equation\ ref {8.10} ili kupata nishati\(U_1, \, U_2\), na\(U_3\) kuhifadhiwa katika capacitors 1, 2, na 3, kwa mtiririko huo. Nishati ya jumla ni jumla ya nguvu hizi zote.
Suluhisho Sisi kutambua\(C_1 = 12.0 \, \mu F\)\(V_1 = 4.0 \, V, \, C_2 = 2.0 \, \mu F\) na na\(V_2 = 8.0 \, V, \, C_3 = 4.0 \, \mu F\) na\(V_3 = 8.0 \, V\). Nguvu zilizohifadhiwa katika capacitors hizi ni
\[U_1 = \frac{1}{2}C_1V_1^2 = \frac{1}{2}(12.0 \, \mu F)(4.0 \, V)^2 = 96 \, \mu J,\]
\[U_2 = \frac{1}{2}C_2V_2^2 = \frac{1}{2}(2.0 \, \mu F)(8.0 \, V)^2 = 64 \, \mu J,\]
\[U_3 = \frac{1}{2}C_3V_3^2 = \frac{1}{2}(4.0 \, \mu F)(8.0 \, V)^2 = 130 \, \mu J,\]
Nishati ya jumla iliyohifadhiwa kwenye mtandao huu ni
\[U_C = U_1 + U_2 + U_3 = 96 \, \mu J + 64 \, \mu J + 130 \, \mu J = 0.29 \, mJ.\]
Umuhimu
Tunaweza kuthibitisha matokeo haya kwa kuhesabu nishati iliyohifadhiwa kwenye\(4.0-\mu F\) capacitor moja, ambayo inapatikana kuwa sawa na mtandao mzima. Voltage katika mtandao ni 12.0 V. nishati ya jumla iliyopatikana kwa njia hii inakubaliana na matokeo yetu yaliyopatikana hapo awali,\(U_C = \frac{1}{2}CV^2 = \frac{1}{2}(4.0 \, \mu F)(12.0 \, V)^2 = 0.29 \, mJ\)
Tofauti tofauti katika capacitor 5.0-PF ni 0.40 V. (a) Nishati iliyohifadhiwa katika capacitor hii ni nini? (b) Tofauti ya uwezo sasa imeongezeka hadi 1.20 V. kwa sababu gani nishati iliyohifadhiwa imeongezeka?
- Jibu
-
a.\(4.0 \times 10^{-13}J\); b. Mara 9
Katika dharura ya moyo, kifaa cha elektroniki kinachojulikana kama defibrillator ya nje ya automatiska (AED) inaweza kuwa mwokozi wa maisha. Defibrillator (Kielelezo\(\PageIndex{2}\)) hutoa malipo makubwa kwa kupasuka kwa muda mfupi, au mshtuko, kwa moyo wa mtu kurekebisha rhythm isiyo ya kawaida ya moyo (arrhythmia). Mashambulizi ya moyo yanaweza kutokea kutokana na mwanzo wa kupigwa kwa haraka, kwa kawaida ya moyo-inayoitwa fibrillation ya moyo au ventricular. Kutumia mshtuko mkubwa wa nishati ya umeme unaweza kusitisha arrhythmia na kuruhusu pacemaker ya asili ya mwili kuendelea na rhythm yake ya kawaida. Leo, ni kawaida kwa magari ya wagonjwa kubeba AEDs. AEDs pia hupatikana katika maeneo mengi ya umma. Hizi zimeundwa kutumiwa na watu wa kuweka. Kifaa hiki hutambua moja kwa moja rhythm ya moyo wa mgonjwa na kisha hutumia mshtuko na nishati sahihi na wimbi. CPR (ufufuo wa cardiopulmonary) inapendekezwa katika matukio mengi kabla ya kutumia defibrillator.
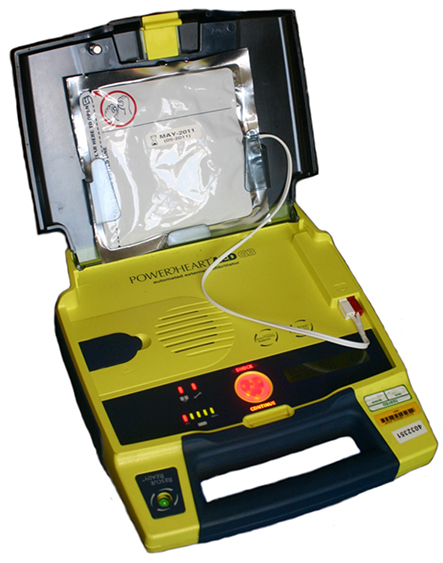
Defibrillator\(4.00 \times 10^2 J\) ya moyo hutoa nishati kwa kuruhusu capacitor awali saa\(1.00 \times 10^4 V\). Uwezo wake ni nini?
Mkakati
Tunapewa\(U_C\) na V, na tunaulizwa kupata capacitance C. Sisi kutatua Equation\ ref {8.10} kwa C na mbadala.
Suluhisho
Kutatua maneno haya kwa C na kuingia maadili yaliyotolewa mavuno\(C = 2\frac{U_C}{V^2} = 2\frac{4.00 \times 10^2 J}{(1.00 \times 10^4V)^2} = 8.00 \, \mu F\).


