Skip to main content
Global

3.6: Uwezo wa joto wa Gesi Bora

  1. Last updated
  2. Save as PDF
  • Page ID
    175612

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Kufafanua uwezo wa joto wa gesi bora kwa mchakato maalum
    • Tumia joto maalum la gesi bora kwa mchakato wa isobaric au isochoric
    • Eleza tofauti kati ya uwezo wa joto wa gesi bora na gesi halisi
    • Tathmini ya mabadiliko katika joto maalum la gesi juu ya safu ya joto

    Tulijifunza kuhusu joto maalum na uwezo wa joto la molar hapo awali; hata hivyo, hatujazingatia mchakato ambao joto huongezwa. Tunafanya hivyo katika sehemu hii. Kwanza, tunachunguza mchakato ambapo mfumo una kiasi cha mara kwa mara, kisha uifanye na mfumo kwa shinikizo la mara kwa mara na uonyeshe jinsi joto lao maalum linahusiana.

    Hebu tuanze na kuangalia Kielelezo\(\PageIndex{1}\), ambacho kinaonyesha vyombo viwili A na B, kila kilicho na 1 mol ya aina moja ya gesi bora kwenye joto T na kiasi V. Tofauti pekee kati ya vyombo viwili ni kwamba pistoni juu ya A ni fasta, wakati moja juu ya B ni huru kuhamia dhidi ya shinikizo la nje la mara kwa mara p. Sasa tunazingatia kinachotokea wakati joto la gesi katika kila chombo linaongezeka polepole\(T + dT\) na kuongeza joto.

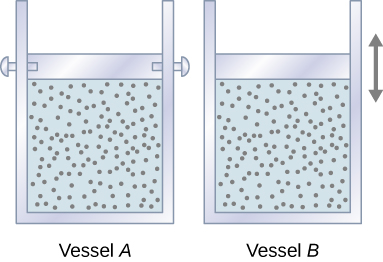
    Vyombo viwili, kinachoitwa Chombo A na Chombo B, vinaonyeshwa. Wote wawili hujazwa na gesi na hufunikwa na pistoni. Katika chombo A, pistoni imefungwa mahali. Katika chombo B, pistoni ni huru kupiga slide, kama ilivyoonyeshwa na mshale ulioongozwa mara mbili karibu na pistoni.
    Kielelezo\(\PageIndex{1}\): Two vessels are identical except that the piston at the top of A is fixed, whereas that atop B is free to move against a constant external pressure p.

    Since the piston of vessel A is fixed, the volume of the enclosed gas does not change. Consequently, the gas does no work, and we have from the first law

    \[dE_{int} = dQ - dW = dQ.\]

    We represent the fact that the heat is exchanged at constant volume by writing

    \[dQ = C_VndT,\] where \(C_V\) is the molar heat capacity at constant volume of the gas. In addition, since \(dE_{int} = dQ\) for this particular process,

    \[dE_{int} = C_VndT. \label{3.9}\]

    We obtained this equation assuming the volume of the gas was fixed. However, internal energy is a state function that depends on only the temperature of an ideal gas. Therefore, \(dE_{int} = C_VndT\) gives the change in internal energy of an ideal gas for any process involving a temperature change dT.

    When the gas in vessel B is heated, it expands against the movable piston and does work \(dW = pdV\). In this case, the heat is added at constant pressure, and we write \[dQ = C_{p}ndT,\] where \(C_p\) is the molar heat capacity at constant pressure of the gas. Furthermore, since the ideal gas expands against a constant pressure,

    \[d(pV) = d(RnT)\] becomes \[pdV = RndT.\]

    Finally, inserting the expressions for dQ and pdV into the first law, we obtain

    \[dE_{int} = dQ - pdV = (C_{p}n - Rn)dT.\]

    We have found \(dE_{int}\) for both an isochoric and an isobaric process. Because the internal energy of an ideal gas depends only on the temperature, \(dE_{int}\) must be the same for both processes. Thus,

    \[C_{V}ndT = (C_{p}n - Rn)dT,\]

    and

    \[C_p = C_V + R. \label{eq50}\]

    The derivation of Equation \ref{eq50} was based only on the ideal gas law. Consequently, this relationship is approximately valid for all dilute gases, whether monatomic like He, diatomic like \(O_2\), or polyatomic like \(CO_2\) or \(NH_3\).

    In the preceding chapter, we found the molar heat capacity of an ideal gas under constant volume to be

    \[C_V = \dfrac{d}{2}R,\]

    where d is the number of degrees of freedom of a molecule in the system. Table \(\PageIndex{1}\) shows the molar heat capacities of some dilute ideal gases at room temperature. The heat capacities of real gases are somewhat higher than those predicted by the expressions of \(C_V\) and \(C_p\) given in Equation \ref{eq50}. This indicates that vibrational motion in polyatomic molecules is significant, even at room temperature. Nevertheless, the difference in the molar heat capacities, \(C_p - C_V\), is very close to R, even for the polyatomic gases.

    Table \(\PageIndex{1}\): Molar Heat Capacities of Dilute Ideal Gases at Room Temperature
    \(C_p\) \(C_V\) \(C_p - C_V\)
    Type of Molecule Gas \(C_p\)" style="text-align:center;" class="lt-phys-4362">(J/mol K) \(C_V\)" style="text-align:center;" class="lt-phys-4362">(J/mol K) \(C_p - C_V\)" style="text-align:center;" class="lt-phys-4362">(J/mol K)
    Monatomic Ideal \(C_p\)" style="text-align:center;" class="lt-phys-4362">\(\frac{5}{2}R = 20.79\) \(C_V\)" style="text-align:center;" class="lt-phys-4362">\(\frac{3}{2}R = 12.47\) \(C_p - C_V\)" style="text-align:center;" class="lt-phys-4362">\(R = 8.31\)
    Diatomic Ideal \(C_p\)" style="text-align:center;" class="lt-phys-4362">\(\frac{7}{2}R = 29.10\) \(C_V\)" style="text-align:center;" class="lt-phys-4362">\(\frac{5}{2}R = 20.79\) \(C_p - C_V\)" style="text-align:center;" class="lt-phys-4362">\(R = 8.31\)
    Polyatomic Ideal \(C_p\)" style="text-align:center;" class="lt-phys-4362">\(4R = 33.26\) \(C_V\)" style="text-align:center;" class="lt-phys-4362">\(3R = 24.04\) \(C_p - C_V\)" style="text-align:center;" class="lt-phys-4362">\(R = 8.31\)

    Glossary

    molar heat capacity at constant pressure
    quantifies the ratio of the amount of heat added removed to the temperature while measuring at constant pressure
    molar heat capacity at constant volume
    quantifies the ratio of the amount of heat added removed to the temperature while measuring at constant volume