9.9: Superconductivity

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Eleza sifa kuu za superconductor
• Eleza nadharia BCS ya superconductivity
• Kuamua uwanja muhimu wa magnetic kwa T = 0 K kutoka data ya shamba la magnetic
• Tumia kiwango cha juu cha emf au sasa kwa waya kubaki superconducting

Upinzani wa umeme unaweza kuchukuliwa kama kipimo cha nguvu ya msuguano katika mtiririko wa sasa wa umeme. Hivyo, upinzani wa umeme ni chanzo kikuu cha ufisadi wa nishati katika mifumo ya umeme kama vile umeme, motors umeme, na mistari ya maambukizi. Waya wa shaba hutumiwa kwa kawaida katika wiring umeme kwa sababu ina moja ya resistivities ya chini kabisa ya chumba cha joto kati ya wasimamizi wa kawaida. (Kwa kweli, fedha ina resistivity chini kuliko shaba, lakini gharama kubwa na upatikanaji mdogo wa fedha outweigh akiba yake katika nishati juu ya shaba.)

Ingawa majadiliano yetu ya conductivity inaonekana kuashiria kwamba vifaa vyote vinapaswa kuwa na upinzani wa umeme, tunajua kwamba hii sio kesi. Wakati joto linapungua chini ya thamani muhimu kwa vifaa vingi, resistivity yao ya umeme hupungua hadi sifuri, na vifaa vinakuwa superconductors.

Tazama video hii ya NOVA Excerpt, Kufanya Stuff Colder, kama utangulizi wa mada ya superconductivity na maombi yake mengi.

Mali ya Superconductors

Mbali na upinzani wa umeme wa sifuri, superconductors pia wana diamagnetism kamili. Kwa maneno mengine, mbele ya shamba la magnetic iliyotumiwa, uwanja wa magnetic wavu ndani ya superconductor daima ni sifuri (Kielelezo\(\PageIndex{1}\)). Kwa hiyo, mistari yoyote ya shamba la magnetic ambayo hupita sampuli ya superconducting wakati iko katika hali yake ya kawaida hufukuzwa mara moja sampuli inakuwa superconducting. Hizi ni maonyesho ya athari ya Meissner, ambayo umejifunza kuhusu sura ya sasa na upinzani.

Kielelezo\(\PageIndex{1}\) :( a) Katika athari ya Meissner, uwanja wa magnetic unafukuzwa kutoka kwenye nyenzo mara moja inakuwa superconducting. (b) Sumaku inaweza levitate juu ya vifaa superconducting, mkono na nguvu kufukuza shamba magnetic.

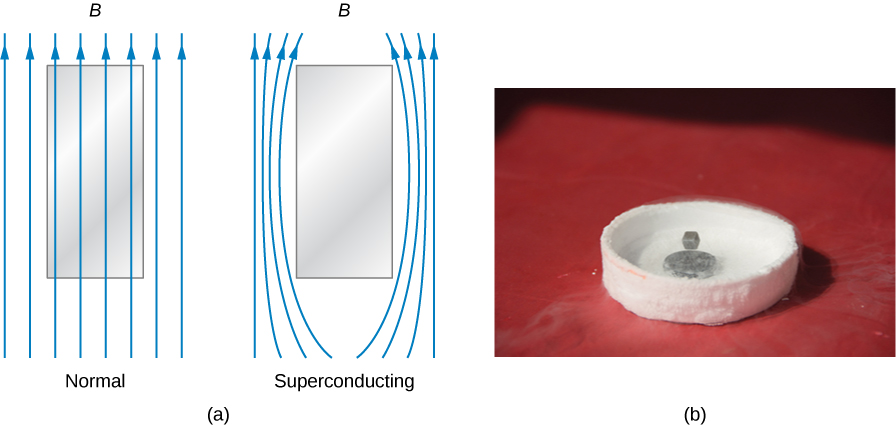
Kushangaza, athari ya Meissner sio matokeo ya upinzani kuwa sifuri. Ili kuona kwa nini, tuseme kwamba sampuli iliyowekwa kwenye uwanja wa magnetic inakabiliwa na mpito ambapo upinzani wake hupungua kwa sifuri. Kutoka kwa sheria ya Ohm, wiani wa sasa, j, katika sampuli unahusiana na uwanja wa umeme wa ndani, E, na resistivity\(\rho\) na\(j = E/\rho\) If\(\rho\) ni sifuri, E lazima pia kuwa sifuri ili j iweze kubaki mwisho. Sasa E na flux magnetic\(\Phi_m\) kupitia sampuli ni kuhusiana na sheria ya Faraday kama

\[\oint E\,dI = - \dfrac{d\Phi_m}{dt} \nonumber \]

Kama E ni sifuri,\(d\Phi_m/dt\) pia sifuri, yaani, flux magnetic kupitia sampuli haiwezi kubadilika. Mistari ya shamba la magnetic ndani ya sampuli haipaswi kufukuzwa wakati mpito hutokea. Kwa hiyo, haifuati kwamba nyenzo ambazo upinzani huenda kwa sifuri unaonyesha athari ya Meissner. Badala yake, athari ya Meissner ni mali maalum ya superconductors.

Mali nyingine muhimu ya vifaa vya superconducting ni joto lake muhimu\(T_c\), joto chini ambayo nyenzo ni superconducting. Aina inayojulikana ya joto kali ni kutoka sehemu ya 1 K hadi kidogo zaidi ya 100 K. superconductors na joto kali karibu na kikomo hiki cha juu hujulikana kama superconductors “high-joto”. Kwa mtazamo wa vitendo, superconductors ambayo\(T_c \gg 77 \, K\) ni muhimu sana. Kwa sasa, maombi yanayohusisha superconductors mara nyingi yanahitaji vifaa vya superconducting viingizwe katika heliamu ya kioevu (4.2 K) ili kuwaweka chini ya joto lao muhimu. Bafu ya heliamu ya kioevu lazima iendelezwe tena kwa sababu ya uvukizi, na gharama za baridi zinaweza kuzidi kwa urahisi akiba kwa kutumia superconductor. Hata hivyo, 77 K ni joto la nitrojeni ya kioevu, ambayo ni mengi zaidi na ya gharama nafuu kuliko heliamu ya kioevu. Itakuwa zaidi ya gharama nafuu kama tunaweza kwa urahisi kuzalisha na kutumia high-joto superconductor vipengele kwamba tu haja ya kuwekwa katika bathi kioevu nitrojeni kudumisha superconductivity yao.

Vifaa vya juu vya joto vya superconducting vinatumika sasa katika matumizi mbalimbali. Mfano ni uzalishaji wa mashamba magnetic katika baadhi ya accelerators chembe. Lengo kuu ni kugundua vifaa ambavyo vina superconducting kwenye joto la kawaida. Bila mahitaji yoyote ya baridi, wingi wa vipengele vya elektroniki na mistari ya maambukizi inaweza kuwa superconducting, na kusababisha ongezeko kubwa na isiyokuwa ya kawaida katika ufanisi na utendaji.

Kielelezo\(\PageIndex{2}\): Utegemezi wa joto wa shamba muhimu kwa superconductors kadhaa. Superconductivity hutokea kwa mashamba magnetic na joto chini curves inavyoonekana.

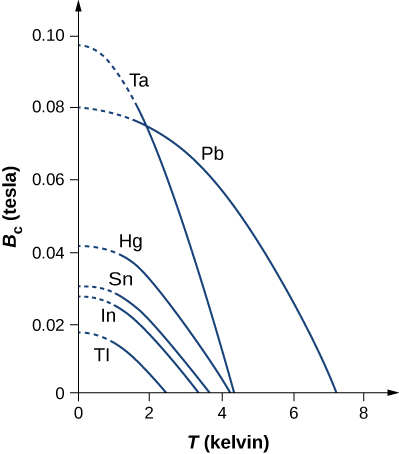
Mali nyingine muhimu ya vifaa vya superconducting ni uwanja wake muhimu wa magnetic\(B_c(T)\), ambayo ni uwanja wa magnetic uliotumiwa kwenye joto T ambayo itawawezesha nyenzo kubaki superconducting. Shamba lililotumiwa ambalo ni kubwa kuliko shamba muhimu litaharibu superconductivity. Sehemu muhimu ni sifuri kwenye joto kali na huongezeka kadiri joto linapungua. Viwanja vya uwanja muhimu dhidi ya joto kwa vifaa kadhaa vya superconducting vinaonyeshwa kwenye Mchoro\(\PageIndex{2}\). Utegemezi wa joto wa shamba muhimu unaweza kuelezewa takriban

\[B_c(T) = B_c(0) \left[1 - \left(\frac{T}{T_c}\right)^2\right] \nonumber \]

ambapo\(B_0\) ni uwanja muhimu katika joto kabisa sifuri. Jedwali\(\PageIndex{1}\) linataja joto kali na mashamba kwa madarasa mawili ya superconductors: aina I superconductor na aina II superconductor. Kwa ujumla, aina I superconductors ni mambo, kama vile alumini na zebaki. Wao ni diamagnetic kikamilifu chini ya uwanja muhimu B _C (T), na kuingia hali ya kawaida isiyo ya superconducting mara moja shamba hilo limezidi. Mashamba muhimu ya aina I superconductors kwa ujumla ni chini kabisa (vizuri chini ya tesla moja). Kwa sababu hii, hawawezi kutumika katika programu zinazohitaji uzalishaji wa mashamba ya juu ya magnetic, ambayo ingeharibu hali yao ya superconducting.

Jedwali\(\PageIndex{1}\): Joto muhimu na Uwanja Muhimu wa Magnetic kwa\(T = 0 \, K\) ajili ya Supercond

Material	Joto muhimu (K)	Uwanja muhimu wa magnetic (T)
Andika I
Al	1.2	0.011
Ga	1.1	0.0051
\(Hg(\alpha)\)	4.2	0.041
Katika	3.4	0.029
Nb	9.3	0.20
Pb	7.2	0.080
Sn	3.7	0.031
Th	1.4	0.00016
Zn	0.87	0.0053
Aina ya II
\(Nb_3Al\)	18	32
\(Nb_3Ge\)	23	38
\(Nb_3Sn\)	18	25
\(NbTi\)	9.3	15
\(YBa_2Cu_3O_7\)	92	>100

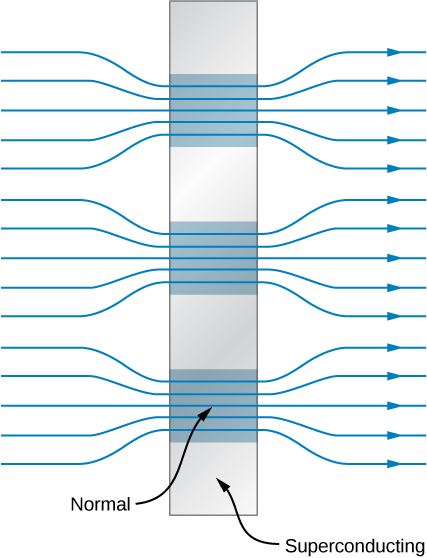
Aina II superconductors ujumla misombo au aloi kuwashirikisha metali mpito au mambo actinide mfululizo. Karibu wote superconductors na joto la juu sana ni aina II. Wana mashamba mawili muhimu, yaliyowakilishwa\(B_{c1}(T)\) na na\(B_{c2}(T)\). Wakati shamba liko chini\(B_{c1}(T)\), aina ya II superconductors ni diamagnetic kikamilifu, na hakuna kupenya kwa magnetic flux ndani ya nyenzo inaweza kutokea. Kwa shamba lililozidi\(B_{c2}(T)\), huendeshwa katika hali yao ya kawaida. Wakati shamba ni kubwa kuliko\(B_{c1}(T)\) lakini chini ya\(B_{c2}(T)\), aina ya II superconductors inasemekana kuwa katika hali mchanganyiko. Ingawa kuna kupenya kwa magnetic flux katika hali iliyochanganywa, upinzani wa nyenzo ni sifuri. Ndani ya superconductor, mikoa kama filament ipo ambayo ina mali ya kawaida ya umeme na magnetic interspersed kati ya mikoa ambayo ni superconducting na diamagnetism kamilifu. Uwakilishi wa hali hii hutolewa katika Kielelezo\(\PageIndex{3}\). Sehemu ya magnetic inafukuzwa kutoka mikoa ya superconducting lakini ipo katika mikoa ya kawaida. Kwa ujumla,\(B_{c2}(T)\) ni kubwa sana ikilinganishwa na mashamba muhimu ya aina I superconductors, hivyo waya alifanya ya aina II superconducting vifaa yanafaa kwa windings ya sumaku high-shamba.

Kielelezo\(\PageIndex{3}\): Uwakilishi wa schematic wa hali ya mchanganyiko wa aina II superconductor. Superconductors (mraba kijivu) hufukuza mashamba ya magnetic katika maeneo yao ya jirani.

Mfano\(\PageIndex{1}\): Niobium Wire

Katika majaribio, waya wa niobium (Nb) wa radius 0.25 mm huingizwa katika heliamu kioevu\(T = 4.2 \, K)\) na inahitajika kubeba sasa ya 300 A. waya hubakia superconducting?

Mkakati

Sehemu ya magnetic iliyotumiwa inaweza kuamua kutoka kwenye radius ya waya na ya sasa. Sehemu muhimu ya magnetic inaweza kuamua kutoka [kiungo], mali ya superconductor, na joto. Ikiwa shamba la magnetic linatumika ni kubwa kuliko shamba muhimu, basi superconductivity katika waya wa Nb imeharibiwa.

Suluhisho

Katika\(T = 4.2 \, K\), uwanja muhimu kwa Nb ni, kutoka Jedwali\(\PageIndex{1}\):

\[B_c(4.2 \, K) = B_c(0)\left[1 - \left(\frac{4.2 \, K}{9.3 \, K}\right)^2\right] = (0.20 \, T)(0.80) = 0.16 \, T. \nonumber \]

Katika sura ya awali, tulijifunza shamba la magnetic ndani ya waya wa sasa wa kubeba radius\(a\) hutolewa na

\[B = \frac{\mu_0I}{2\pi a}, \nonumber \]

ambapo r ni umbali kutoka kwa mhimili wa kati wa waya. Hivyo, shamba kwenye uso wa waya ni\(\frac{\mu_0I}{2\pi a}\). Kwa waya ya niobium, uwanja huu ni

\[B = \frac{(4\pi \times 10^{-7} T m/A)(300 \, A)}{2\pi(2.5 \times 10^{-4}m)} = 0.24 \, T. \nonumber \]

Kwa kuwa hii inazidi muhimu 0.16 T, waya haina kubaki superconducting.

Umuhimu

Superconductivity inahitaji joto la chini na mashamba ya chini magnetic Hali hizi za sawia hukutana kwa urahisi kidogo kwa Nb kuliko kwa metali nyingine nyingi. Kwa mfano, supercontracts alumini katika joto mara 7 chini na magnetic mashamba 18 mara chini.

Zoezi\(\PageIndex{1}\)

Ni hali gani zinazohitajika kwa superconductivity?

Jibu

joto la chini na shamba la chini la magnetic

Nadharia ya wasimamizi

Nadharia ya mafanikio ya superconductivity ilitengenezwa katika miaka ya 1950 na John Bardeen, Leon Cooper, na J. Robert Schrieffer, ambayo walipokea Tuzo ya Nobel mwaka 1972. Nadharia hii inajulikana kama nadharia ya BCS. Nadharia ya BCS ni ngumu, kwa hiyo tunaifupisha kwa usahihi chini.

Katika conductor kawaida, mali ya umeme ya nyenzo ni kutokana na elektroni nguvu zaidi karibu na nishati Fermi. Mwaka wa 1956, Cooper ilionyesha kuwa ikiwa kuna mwingiliano wowote wa kuvutia kati ya elektroni mbili kwenye ngazi ya Fermi, basi elektroni zinaweza kuunda hali iliyofungwa ambayo nishati yao yote ni chini ya 2EF2EF. Elektroni hizo mbili zinajulikana kama jozi la Cooper.

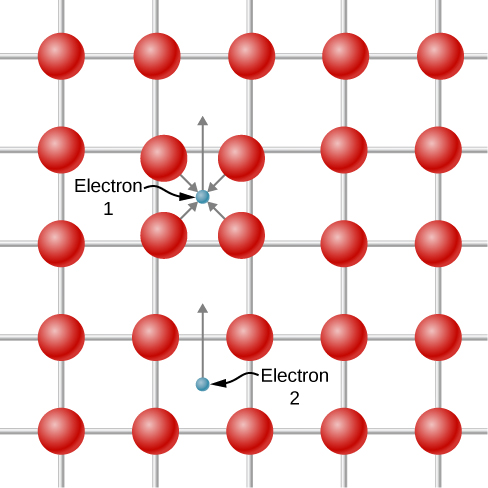
Ni vigumu kufikiria elektroni mbili zinazovutia, kwa kuwa zina kama malipo na zinapaswa kurudisha. Hata hivyo, mwingiliano uliopendekezwa hutokea tu katika mazingira ya bandia ya atomiki. Uchoraji wa kivutio unaonyeshwa kwenye Kielelezo\(\PageIndex{4}\). Electron 1 huhamisha kidogo kiini cha atomiki chaji chanya kuelekea yenyewe kama inasafiri zamani kwa sababu ya kivutio cha Coulomb. Electron 2 “anaona” kanda yenye wiani mkubwa wa malipo mazuri kuhusiana na mazingira na kwa hiyo huvutiwa katika eneo hili na, kwa hiyo, kwa moja kwa moja, kwa elektroni 1. Kwa sababu ya kanuni ya kutengwa, elektroni mbili za jozi ya Cooper lazima iwe na spin kinyume.

Kielelezo\(\PageIndex{4}\): Jozi ya Cooper inaweza kuunda kama matokeo ya uhamisho wa nuclei nzuri ya atomiki. Electron 1 huhamisha kidogo kiini cha atomiki chaji chanya kuelekea yenyewe kama inasafiri zamani kwa sababu ya kivutio cha Coulomb. Electron 2 “anaona” kanda yenye wiani mkubwa wa malipo mazuri kuhusiana na mazingira na kwa hiyo huvutiwa katika eneo hili.

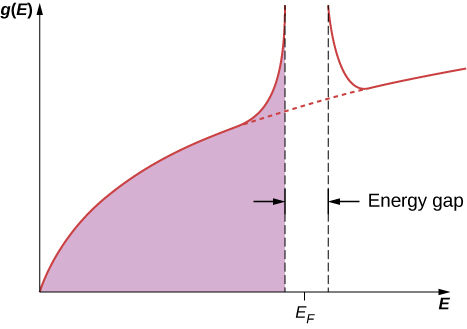
Nadharia ya BCS inaongeza mawazo ya Cooper, ambayo ni kwa jozi moja ya elektroni, hadi gesi nzima ya elektroni huru. Wakati mpito kwa hali ya superconducting hutokea, elektroni zote zinaunganisha ili kuunda jozi za Cooper. Kwa kiwango cha atomiki, umbali kati ya elektroni mbili zinazounda jozi ya Cooper ni kubwa kabisa. Kati ya elektroni hizi ni kawaida kuhusu elektroni\(10^6\) nyingine, kila pia jozi na elektroni mbali. Kwa hiyo, kuna uingiliano mkubwa kati ya kazi za wimbi za jozi za Cooper binafsi, na kusababisha uwiano mkubwa kati ya mwendo wa jozi. Wote huhamia pamoja “kwa hatua,” kama wanachama wa bendi ya kuandamana. Katika mpito wa superconducting, wiani wa majimbo unabadilishwa sana karibu na kiwango cha Fermi. Kama inavyoonekana katika Kielelezo\(\PageIndex{5}\), pengo nishati inaonekana karibu\(E_F\) kwa sababu ukusanyaji wa jozi Cooper ina chini ya ardhi hali ya nishati ya gesi Fermi ya elektroni noninterfactional. Kuonekana kwa pengo hili kunafafanua hali ya superconducting. Ikiwa hali hii imeharibiwa, basi pengo hupotea, na wiani wa majimbo hurudi kwa ile ya gesi ya elektroni ya bure.

Kielelezo\(\PageIndex{5}\): A relatively large energy gap is formed around the Fermi energy when a material becomes superconducting. If this state is destroyed, then the gap disappears, and the density of states reverts to that of the free electron gas.

The BCS theory is able to predict many of the properties observed in superconductors. Examples include the Meissner effect, the critical temperature, the critical field, and, perhaps most importantly, the resistivity becoming zero at a critical temperature. We can think about this last phenomenon qualitatively as follows. In a normal conductor, resistivity results from the interaction of the conduction electrons with the lattice. In this interaction, the energy exchanged is on the order of \(k_BT\), the thermal energy. In a superconductor, electric current is carried by the Cooper pairs. The only way for a lattice to scatter a Cooper pair is to break it up. The destruction of one pair then destroys the collective motion of all the pairs. This destruction requires energy on the order of \(10^{-3}eV\), which is the size of the energy gap. Below the critical temperature, there is not enough thermal energy available for this process, so the Cooper pairs travel unimpeded throughout the superconductor.

Finally, it is interesting to note that no evidence of superconductivity has been found in the best normal conductors, such as copper and silver. This is not unexpected, given the BCS theory. The basis for the formation of the superconducting state is an interaction between the electrons and the lattice. In the best conductors, the electron-lattice interaction is weakest, as evident from their minimal resistivity. We might expect then that in these materials, the interaction is so weak that Cooper pairs cannot be formed, and superconductivity is therefore precluded.