12.5: Theorem ya Binomial
- Page ID
- 175707
Mwishoni mwa sehemu hii, utaweza:
- Tumia Triangle Pascal ya kupanua binomial
- Tathmini mgawo wa binomial
- Tumia Theorem ya Binomial kupanua binomial
Kabla ya kuanza, fanya jaribio hili la utayari.
- Kurahisisha:\(\frac{7 \cdot 6 \cdot 5 \cdot 4}{4 \cdot 3 \cdot 2 \cdot 1}\).
Kama amekosa tatizo hili, mapitio Mfano 1.25. - Panua:\((3 x+5)^{2}\).
Kama amekosa tatizo hili, mapitio Mfano 5.32. - Panua:\((x-y)^{2}\).
Kama amekosa tatizo hili, mapitio Mfano 5.32.
Tumia Triangle ya Pascal kupanua Binomial
Katika kazi yetu ya awali, tuna binomials za mraba ama kwa kutumia FOIL au kwa kutumia Pattern ya Mraba ya Binomial. Tunaweza pia kusema kwamba tulipanua\((a+b)^{2}\).
\((a+b)^{2}=a^{2}+2 a b+b^{2}\)
Kupanua\((a+b)^{3}\), tunatambua kwamba hii ni\((a+b)^{2}(a+b)\) na kuzidisha.
\((a+b)^{3}\)
\((a+b)^{2}(a+b)\)
\(\left(a^{2}+2 a b+b^{2}\right)(a+b)\)
\(a^{3}+2 a^{2} b+a b^{2}+a^{2} b+2 a b^{2}+b^{3}\)
\(a^{3}+3 a^{2} b+3 a b^{2}+b^{3}\)
\((a+b)^{3}=a^{3}+3 a^{2} b+3 a b^{2}+b^{3}\)
Ili kupata njia ambayo haifai sana ambayo itafanya kazi kwa upanuzi wa juu kama\((a+b)^{7}\), sisi tena tunatafuta ruwaza katika upanuzi fulani.
| Idadi ya Masharti | Muda wa Kwanza | Muda wa Mwisho | |
|---|---|---|---|
| \((a+b)^{1}=a+b\) | \(2\) | \(a^{1}\) | \(b^{1}\) |
| \((a+b)^{2}=a^{2}+2 a b+b^{2}\) | \(3\) | \(a^{2}\) | \(b^{2}\) |
| \((a+b)^{3}=a^{3}+3 a^{2} b+3 a b^{2}+b^{3}\) | \(4\) | \(a^{3}\) | \(b^{3}\) |
| \((a+b)^{4}=a^{4}+4 a^{3} b+6 a^{2} b^{2}+4 a b^{3}+b^{4}\) | \(5\) | \(a^{4}\) | \(b^{4}\) |
| \((a+b)^{5}=a^{5}+5 a^{4} b+10 a^{3} b^{2}+10 a^{2} b^{3}+5 a b^{4}+b^{5}\) | \(6\) | \(a^{5}\) | \(b^{5}\) |
| \((a+b)^{n}\) | \(n\) | \(a^{n}\) | \(b^{n}\) |
Angalia maneno ya kwanza na ya mwisho yanaonyesha variable moja tu. Kumbuka kwamba\(a^{0}=1\), ili tuweze kuandika upya masharti ya kwanza na ya mwisho ni pamoja na vigezo vyote viwili. Kwa mfano, tunaweza kupanua\((a+b)^{3}\) kuonyesha kila neno na vigezo vyote viwili.
Kwa ujumla, hatuwezi kuonyesha exponents sifuri, kama sisi kawaida kuandika\(x\) badala ya\(1x\).
Sampuli katika Upanuzi wa\((a+b)^{n}\)
- Idadi ya maneno ni\(n+1\).
- Muda wa kwanza ni\(a^{n}\) na muda wa mwisho ni\(b^{n}\).
- exponents juu ya\(a\) kupungua kwa moja juu ya kila mrefu kwenda kushoto kwenda kulia.
- exponents juu ya\(b\) kuongezeka kwa moja juu ya kila mrefu kwenda kushoto kwenda kulia.
- Jumla ya exponents juu ya muda wowote ni\(n\).
Hebu tuangalie mfano wa kuonyesha mifumo mitatu iliyopita.
Kutoka mwelekeo sisi kutambuliwa, tunaona vigezo katika upanuzi wa\((a+b)^{n}\), itakuwa
\((a+b)^{n}=a^{n}+\_\_\_a^{n-1}b^{1}+\_\_\_a^{n-2}b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n}\).
Ili kupata coefficients ya maneno, tunaandika upanuzi wetu tena kwa kuzingatia coefficients. Tunaandika tena coefficients kwa haki kutengeneza safu ya coefficients.
Safu ya kulia inaitwa Triangle ya Pascal. Angalia kila idadi katika safu ni jumla ya namba mbili karibu katika mstari hapo juu. Tunaweza kupata mstari unaofuata kwa kuanzia na kuishia na moja na kisha kuongeza namba mbili zilizo karibu.
Pembetatu hii inatoa coefficients ya maneno wakati sisi kupanua binomials.
Pembetatu ya Pascal
Katika mfano unaofuata, tutatumia pembetatu hii na mifumo tuliyotambua kupanua binomial.
Tumia Triangle Pascal ya kupanua\((x+y)^{6}\).
Suluhisho:
Tunajua vigezo kwa ajili ya upanuzi huu kufuata mfano sisi kutambuliwa. exponents\(x\) nonzero ya kuanza saa sita na kupungua kwa moja. exponents\(y\) nonzero ya kuanza saa moja na kuongeza hadi sita. Jumla ya exponents katika kila muda itakuwa sita. Katika muundo wetu,\(a=x\) na\(b=y\).
\(\begin{array}{l}{(a+b)^{n}=a^{n}+\_\_\_a^{n-1} b^{1}+\_\_\_a^{n-2} b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n}} \\ {(x+y)^{6}=x^{6}+\_\_\_x^{5} y^{1}+\_\_\_x^{4} y^{2}+\_\_\_x^{3} y^{3}+\_\_\_x^{2} y^{4}+\_\_\_x^{1} y^{5}+y^{6}}\end{array}\)
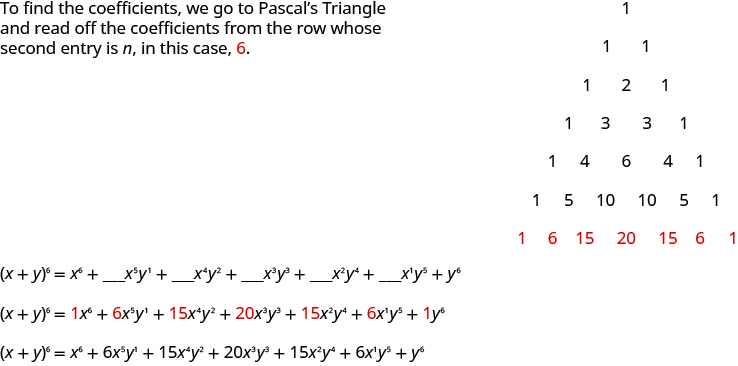
Tumia Triangle Pascal ya kupanua\((x+y)^{5}\).
- Jibu
-
\(\begin{array}{l}{x^{5}+5 x^{4} y+10 x^{3} y^{2}+10 x^{2} y^{3}} {+5 x y^{4}+y^{5}}\end{array}\)
Tumia Triangle Pascal ya kupanua\((p+q)^{7}\).
- Jibu
-
\(\begin{array}{c}{p^{7}+7 p^{6} q+21 p^{5} q^{2}+35 p^{4} q^{3}} {+35 p^{3} q^{4}+21 p^{2} q^{5}+7 p q^{6}+q^{7}}\end{array}\)
Katika mfano unaofuata tunataka kupanua binomial na variable moja na moja ya mara kwa mara. Tunahitaji kutambua\(a\) na\(b\) kutumia kwa makini mfano.
Tumia Triangle Pascal ya kupanua\((x+3)^{5}\).
Suluhisho:
Tunatambua\(a\) na\(b\) ya muundo.
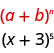
Katika muundo wetu,\(a=x\) na\(b=3\).
Tunajua vigezo kwa ajili ya upanuzi huu kufuata mfano sisi kutambuliwa. Jumla ya exponents katika kila muda itakuwa tano.
\((a+b)^{n}=a^{n}+\_\_\_a^{n-1}b^{1}+\_\_\_a^{n-2}b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n} \)
\((x+3)^{5}=x^{5}+\_\_\_x^{4}\cdot3^{1}+\_\_\_x^{3}\cdot3^{2}+\_\_\_x^{2}\cdot3^{3}+\_\_\_x^{1}\cdot3^{4}+3^{5}\)

Tumia Triangle Pascal ya kupanua\((x+2)^{4}\).
- Jibu
-
\(x^{4}+8 x^{3}+24 x^{2}+32 x+16\)
Tumia Triangle Pascal ya kupanua\((x+1)^{6}\).
- Jibu
-
\(\begin{array}{l}{x^{6}+6 x^{5}+15 x^{4}+20 x^{3}+15 x^{2}} {+6 x+1}\end{array}\)
Katika mfano unaofuata, binomial ni tofauti na muda wa kwanza una mara kwa mara kutofautiana. Mara tu tunatambua\(a\) na\(b\) ya muundo, tunapaswa tena kutumia kwa makini mfano.
Tumia Triangle Pascal ya kupanua\((3x-2)^{4}\).
Suluhisho:
Tunatambua\(a\) na\(b\) ya muundo.
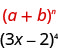
Katika muundo wetu,\(a=3x\) na\(b=-2\).

\((a+b)^{n}=a^{n}+\_\_\_a^{n-1}b^{1}+\_\_\_a^{n-2}b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n} \)
\((3 x-2 )^{4}=1 \cdot\left(\stackrel{3}{x}+4(3 x)^{3}(-2)^{1}+6(3 x)^{2}(-2)^{2}+4(3 x)^{1}(-2)^{3}+1 \cdot(-2)^{4}\right.\)
\((3 x-2)^{4}=81 x^{4}+4\left(27 x^{3}\right)(-2)+6\left(9 x^{2}\right)(4)+4(3 x)(-8)+1 \cdot 16\)
\((3 x-2 )^{4}=81 x^{4}-216 x^{3}+216 x^{2}-96 x+16\)
Tumia Triangle Pascal ya kupanua\((2x-3)^{4}\).
- Jibu
-
\(16 x^{4}-96 x^{3}+216 x^{2}-216 x+81\)
Tumia Triangle Pascal ya kupanua\((2x-1)^{6}\).
- Jibu
-
\(\begin{array}{l}{64 x^{6}-192 x^{5}+240 x^{4}-160 x^{3}} {+60 x^{2}-12 x+1}\end{array}\)
Tathmini ya Mgawo wa Binomial
Wakati Triangle ya Pascal ni njia moja ya kupanua binomial, tutaangalia pia njia nyingine. Kabla ya kupata kwamba, tunahitaji kuanzisha baadhi nukuu zaidi factorial. Nukuu hii haitumiwi tu kupanua binomials, lakini pia katika utafiti na matumizi ya uwezekano.
Ili kupata coefficients ya masharti ya binomials kupanuliwa, tutahitaji kuwa na uwezo wa kutathmini notation\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) ambayo inaitwa mgawo wa binomial. Tunasoma\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) kama “\(n\)kuchagua\(r\)” au “\(n\)kuchukuliwa kwa\(r\) wakati”.
Mgawo wa binomial\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\), wapi\(r\) na\(b\) ni integers na\(0 \leq r \leq n\), hufafanuliwa kama
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)=\frac{n !}{r !(n-r) !}\)
Tunasoma\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) kama\(r\) "\(n\)kuchagua" au "\(n\)kuchukuliwa kwa\(r\) wakati.”
Tathmini:
- \(\left( \begin{array}{l}{5} \\ {1}\end{array}\right)\)
- \(\left( \begin{array}{l}{7} \\ {7}\end{array}\right)\)
- \(\left( \begin{array}{l}{4} \\ {0}\end{array}\right)\)
- \(\left( \begin{array}{l}{8} \\ {5}\end{array}\right)\)
Suluhisho:
Tutatumia ufafanuzi wa mgawo wa binomial,
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)=\frac{n !}{r !(n-r) !}\)
\(\left( \begin{array}{l}{5} \\ {1}\end{array}\right)\)
Tumia ufafanuzi,\(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\), wapi\(n=5, r=1\).
\(\frac{5 !}{1 !(5-1) !}\)
Kurahisisha.
\(\frac{5 !}{1 !(4) !}\)
Andika upya\(5!\) kama\(5\cdot 4!\)
\(\frac{5 \cdot 4 !}{1 ! \cdot 4 !}\)
Kurahisisha, kwa kuondoa mambo ya kawaida.
\(\frac{5\cdot \cancel{4 !}}{1 ! \cdot \cancel{4 !}}\)
Kurahisisha.
\(5\)
\(\left( \begin{array}{l}{5} \\ {1}\end{array}\right)=5\)
b.\(\left( \begin{array}{l}{7} \\ {7}\end{array}\right)\)
Tumia ufafanuzi,\(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\), wapi\(n=7, r=7\).
\(\frac{7 !}{7 !(7-7) !}\)
Kurahisisha.
\(\frac{7 !}{7 !(0) !}\)
Kurahisisha. Kumbuka\(0!=1\).
\(1\)
\(\left( \begin{array}{l}{7} \\ {7}\end{array}\right)=1\)
c.\(\left( \begin{array}{l}{4} \\ {0}\end{array}\right)\)
Tumia ufafanuzi,\(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\), wapi\(n=4, r=0\).
\(\frac{4 !}{0 !(4-0) !}\)
Kurahisisha.
\(\frac{4 !}{0 !(4) !}\)
Kurahisisha.
\(1\)
\(\left( \begin{array}{l}{4} \\ {0}\end{array}\right)=1\)
d.\(\left( \begin{array}{l}{8} \\ {5}\end{array}\right)\)
Tumia ufafanuzi,\(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\), wapi\(n=8, r=5\).
\(\frac{8 !}{5 !(8-5) !}\)
Kurahisisha.
\(\frac{8 !}{5 !(3) !}\)
Andika upya\(8!\) kama\(8\cdot 7\cdot 6\cdot 5!\) na uondoe mambo ya kawaida.
\(\frac{8\cdot7\cdot\cancel{6}\cdot\cancel{5!}}{\cancel{5!}\cdot\cancel{3}\cdot\cancel{2}\cdot1}\)
Kurahisisha.
\(56\)
\(\left( \begin{array}{l}{8} \\ {5}\end{array}\right)=56\)
Tathmini kila mgawo wa binomial:
- \(\left( \begin{array}{l}{6} \\ {1}\end{array}\right)\)
- \(\left( \begin{array}{l}{8} \\ {8}\end{array}\right)\)
- \(\left( \begin{array}{l}{5} \\ {0}\end{array}\right)\)
- \(\left( \begin{array}{l}{7} \\ {3}\end{array}\right)\)
- Jibu
-
- \(6\)
- \(1\)
- \(1\)
- \(35\)
Tathmini kila mgawo wa binomial:
- \(\left( \begin{array}{l}{2} \\ {1}\end{array}\right)\)
- \(\left( \begin{array}{l}{11} \\ {11}\end{array}\right)\)
- \(\left( \begin{array}{l}{9} \\ {0}\end{array}\right)\)
- \(\left( \begin{array}{l}{6} \\ {5}\end{array}\right)\)
- Jibu
-
- \(2\)
- \(1\)
- \(1\)
- \(6\)
Katika mfano uliopita,\((a)\)\((b)\),\((c)\) kuonyesha baadhi ya mali maalum ya coefficients binomial.
Mali ya Coefficients ya Binomial
\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n \quad \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1 \quad \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
Tumia Theorem ya Binomial kupanua Binomial
Sasa tuko tayari kutumia njia mbadala ya kupanua binomials. Theorem ya Binomial inatumia mfano sawa kwa vigezo, lakini hutumia mgawo wa binomial kwa mgawo wa kila neno.
Theorem ya Binomial
Kwa idadi yoyote halisi\(a\) na\(b\), na integer chanya\(n\),
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
Tumia Theorem ya Binomial kupanua\((p+q)^{4}\).
Suluhisho:
Tunatambua\(a\) na\(b\) ya muundo.
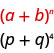
Katika muundo wetu,\(a=p\) na\(b=q\).
Tunatumia Theorem ya Binomial.
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
Mbadala katika maadili\(a=p, b=q\) na\(n=4\).
\((p+q)^{4}=\left( \begin{array}{c}{4} \\ {0}\end{array}\right) p^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right) p^{4-1} q^{1}+\left( \begin{array}{c}{4} \\ {2}\end{array}\right) p^{4-2} q^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right) p^{4-3} q^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right) q^{4}\)
Kurahisisha watetezi.
\((p+q)^{4}=\left( \begin{array}{l}{4} \\ {0}\end{array}\right) p^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right) p^{3} q+\left( \begin{array}{c}{4} \\ {2}\end{array}\right) p^{2} q^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right) p q^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right) q^{4}\)
Tathmini coefficients, kumbuka,\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n, \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1, \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
\((p+q)^{4}=1 p^{4}+4 p^{3} q^{1}+\frac{4 !}{2 !(2) !} p^{2} q^{2}+\frac{4 !}{3 !(4-3) !} p^{1} q^{3}+1 q^{4}\)
\((p+q)^{4}=p^{4}+4 p^{3} q+6 p^{2} q^{2}+4 p q^{3}+q^{4}\)
Tumia Theorem ya Binomial kupanua\((x+y)^{5}\).
- Jibu
-
\(\begin{array}{l}{x^{5}+5 x^{4} y+10 x^{3} y^{2}+10 x^{2} y^{3}} {+5 x y^{4}+y^{5}}\end{array}\)
Tumia Theorem ya Binomial kupanua\((m+n)^{6}\).
- Jibu
-
\(\begin{array}{l}{m^{6}+6 m^{5} n+15 m^{4} n^{2}+20 m^{3} n^{3}} {+15 m^{2} n^{4}+6 m n^{5}+n^{6}}\end{array}\)
Kumbuka kwamba wakati sisi kupanua\((p+q)^{4}\) katika mfano wa mwisho, kwa kutumia Theorem Binomial, tulipata coefficients sawa tunataka kupata kutoka kwa kutumia Pascal ya Triangle.
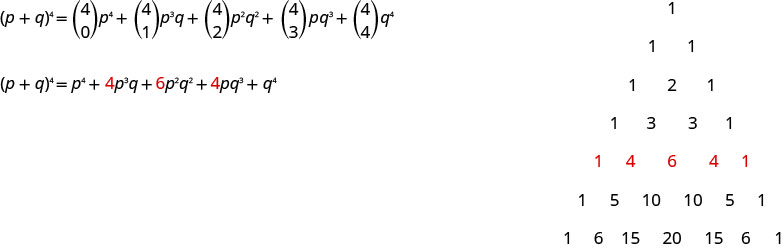
Mfano unaofuata, binomial ni tofauti. Wakati binomial ni tofauti, lazima tuwe makini katika kutambua maadili tutakayotumia katika muundo.
Tumia Theorem ya Binomial kupanua\((x-2)^{5}\).
Suluhisho:
Tunatambua\(a\) na\(b\) ya muundo.
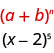
Katika muundo wetu,\(a=x\) na\(b=-2\).
Tunatumia Theorem ya Binomial.
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
Mbadala katika maadili\(a=x, b=-2\), na\(n=5\).
\((x-2)^{5}=\left( \begin{array}{l}{5} \\ {0}\end{array}\right) x^{5}+\left( \begin{array}{c}{5} \\ {1}\end{array}\right) x^{5-1}(-2)^{1}+\left( \begin{array}{c}{5} \\ {2}\end{array}\right) x^{5-2}(-2)^{2}+\left( \begin{array}{c}{5} \\ {3}\end{array}\right) x^{5-3}(-2)^{3}+\left( \begin{array}{c}{5} \\ {4}\end{array}\right) x^{5-4}(-2)^{4}+\left( \begin{array}{c}{5} \\ {5}\end{array}\right)(-2)^{5}\)
Kurahisisha coefficients. Kumbuka,\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n, \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1, \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\).
\((x-2)^{5}=\left( \begin{array}{l}{5} \\ {0}\end{array}\right) x^{5}+\left( \begin{array}{c}{5} \\ {1}\end{array}\right) x^{4}(-2)+\left( \begin{array}{c}{5} \\ {2}\end{array}\right) x^{3}(-2)^{2}+\left( \begin{array}{c}{5} \\ {3}\end{array}\right) x^{2}(-2)^{3}+\left( \begin{array}{c}{5} \\ {4}\end{array}\right) x(-2)^{4}+\left( \begin{array}{c}{5} \\ {5}\end{array}\right)(-2)^{5}\)
\((x-2)^{5}=1 x^{5}+5(-2) x^{4}+\frac{5 !}{2 ! \cdot 3 !}(-2)^{2} x^{3}+\frac{5 !}{3 ! 2 !}(-2)^{3} x^{2}+\frac{5 !}{4 !1 !}(-2)^{4} x+1(-2)^{5}\)
\((x-2)^{5}=x^{5}+5(-2) x^{4}+10 \cdot 4 \cdot x^{3}+10(-8) x^{2}+5 \cdot 16 \cdot x+1(-32)\)
\((x-2)^{5}=x^{5}-10 x^{4}+40 x^{3}-80 x^{2}+80 x-32\)
Tumia Theorem ya Binomial kupanua\((x-3)^{5}\).
- Jibu
-
\(\begin{array}{l}{x^{5}-15 x^{4}+90 x^{3}-270 x^{2}} {+405 x-243}\end{array}\)
Tumia Theorem ya Binomial kupanua\((y-1)^{6}\).
- Jibu
-
\(\begin{array}{l}{y^{6}-6 y^{5}+15 y^{4}-20 y^{3}+15 y^{2}} {-6 y+1}\end{array}\)
Mambo yanaweza kupata messy wakati maneno yote yana mgawo na kutofautiana.
Tumia Theorem ya Binomial kupanua\((2x-3y)^{4}\).
Suluhisho:
Tunatambua\(a\) na\(b\) ya muundo.
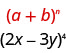
Katika muundo wetu,\(a=2x\) na\(b=-3y\).
Tunatumia Theorem ya Binomial.
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
Mbadala katika maadili\(a=2x, b=-3y\) na\(n=4\).
\((2 x-3 y)^{4}=\left( \begin{array}{l}{4} \\ {0}\end{array}\right)(2 x)^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right)(2 x)^{4-1}(-3 y)^{1}+\left( \begin{array}{c}{4} \\ {2}\end{array}\right)(2 x)^{4-2}(-3 y)^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right)(2 x)^{4-3}(-3 y)^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right) (-3y)^{4}\)
Kurahisisha watetezi.
\((2 x-3 y)^{4}=\left( \begin{array}{l}{4} \\ {0}\end{array}\right)(2 x)^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right)(2 x)^{3}(-3 y)^{1}+\left( \begin{array}{c}{4} \\ {2}\end{array}\right)(2 x)^{2}(-3 y)^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right)(2 x)^{1}(-3 y)^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right)(-3 y)^{4}\)
Tathmini coefficients. Kumbuka,\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n, \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1, \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
\((2 x-3 y)^{4}=1(2 x)^{4}+4(2 x)^{3}(-3 y)^{1}+\frac{4 !}{2 !(2 x) !}(2 x)^{2}+\frac{4 !}{3 !(4-3) !}(2 x)^{3}(-3 y)^{3}+1(-3 y)^{4}\)
\((2 x-3 y)^{4}=16 x^{4}+4 \cdot 8 x^{3}(-3 y)+6\left(4 x^{2}\right)\left(9 y^{2}\right)+4(2 x)\left(-27 y^{3}\right)+81 y^{4}\)
\((2 x-3 y)^{4}=16 x^{4}-96 x^{3} y+216 x^{2} y^{2}-216 x y^{3}+81 y^{4}\)
Tumia Theorem ya Binomial kupanua\((3x-2y)^{5}\).
- Jibu
-
\(\begin{array}{l}{243 x^{5}-810 x^{4} y+1080 x^{3} y^{2}} {-720 x^{2} y^{3}+240 x y^{4}-32 y^{5}}\end{array}\)
Tumia Theorem ya Binomial kupanua\((4x-3y)^{4}\).
- Jibu
-
\(\begin{array}{l}{256 x^{4}-768 x^{3} y+864 x^{2} y^{2}} {-432 x y^{3}+81 y^{4}}\end{array}\)
Uzuri halisi wa Theorem ya Binomial ni kwamba inatoa formula kwa muda wowote wa upanuzi bila ya kukokotoa jumla nzima. Hebu tuangalie mfano katika Theorem ya Binomial.
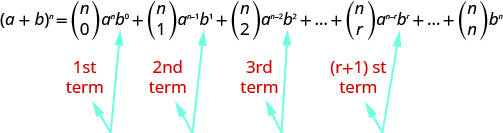
Kumbuka, kwamba katika kila kesi exponent juu ya\(b\) ni moja chini ya idadi ya muda. \((r+1)^{st}\)Neno ni neno ambapo exponent ya\(b\) ni\(r\). Kwa hiyo tunaweza kutumia muundo wa\((r+1)^{st}\) neno ili kupata thamani ya muda maalum.
Pata Muda maalum katika Upanuzi wa Binomial
\((r+1)^{s t}\)Neno katika upanuzi wa\((a+b)^{n}\) ni
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}\)
Kupata muda wa nne wa\((x+y)^{7}\).
Suluhisho:
| Katika muundo wetu,\(n=7, a=x\) na\(b=y\). | 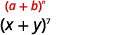 |
|
Tunatafuta muda wa nne. Tangu\(r+1=4\), basi\(r=3\). |
|
| Andika formula | 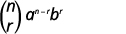 |
| Mbadala katika maadili,\(n=7, r=3, a=x\), na\(b=y\). | 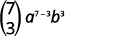 |
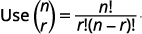 |
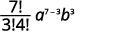 |
| Kurahisisha. | 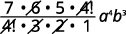 |
| Kurahisisha. |  |
Kupata muda wa tatu wa\((x+y)^{6}\).
- Jibu
-
\(15x^{4}y^{2}\)
Kupata muda wa tano wa\((a+b)^{8}\).
- Jibu
-
\(8ab^{7}\)
Pata mgawo wa\(x^{6}\) muda wa\((x+3)^{9}\).
Suluhisho:
| Katika muundo wetu, basi\(n=9, a=x\), na\(b=3\). |

|
| Tunatafuta mgawo wa\(x^{6}\) muda. tangu\(a=x\), na\(x^{9-r}=x^{6}\), tunajua\(r=3\). | |
| Andika formula. |
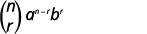
|
| Mbadala katika maadili,\(n=9, 4=3, a=x\), na\(b=3\). |
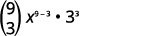
|
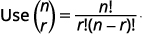
|
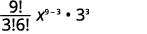
|
| Kurahisisha. |
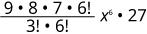
|
| Kurahisisha. |
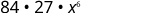
|
| Kurahisisha. |

|
Pata mgawo wa\(x^{5}\) muda wa\((x+4)^{8}\).
- Jibu
-
\(7,168\)
Pata mgawo wa\(x^{4}\) muda wa\((x+2)^{7}\).
- Jibu
-
\(280\)
Kupata rasilimali hizi online kwa maelekezo ya ziada na mazoezi na Utaratibu.
Dhana muhimu
- Sampuli katika upanuzi wa\ ((a+b) ^ {n}\ (
- Idadi ya maneno ni\(n+1\).
- Muda wa kwanza ni\(a^{n}\) na muda wa mwisho ni\(b^{n}\).
- exponents juu ya\(a\) kupungua kwa moja juu ya kila mrefu kwenda kushoto kwenda kulia.
- exponents juu ya\(b\) kuongezeka kwa moja juu ya kila mrefu kwenda kushoto kwenda kulia.
- Jumla ya exponents juu ya muda wowote ni\(n\).
- Pembetatu ya Pascal

- Mgawo wa Binomial \(\left( \begin{array}{l}{\mathbf{n}} \\ {\mathbf{r}}\end{array}\right)\): Mgawo wa binomial\(\left( \begin{array}{l}{\mathbf{n}} \\ {\mathbf{r}}\end{array}\right)\), wapi\(r\) na\(n\) ni integers na\(0≤r≤n\), hufafanuliwa kama
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)=\frac{n !}{r !(n-r) !}\)
Tunasoma\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) kama “\(n\)kuchagua\(r\)” au “\(n\)kuchukuliwa kwa\(r\) wakati”.
- Mali ya Coefficients ya Binomial
\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n \quad \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1 \quad \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
- Theorem ya Binomial:
Kwa idadi yoyote halisi\(a\),\(b\), na integer chanya\(n\),
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)


