Skip to main content
Global

12.2: Utaratibu

  1. Last updated
  2. Save as PDF
  • Page ID
    175631

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Andika maneno machache ya mlolongo
    • Pata fomu kwa muda mrefu (neno la nth) la mlolongo
    • Tumia maelezo ya factorial
    • Pata jumla ya sehemu
    • Tumia maelezo ya muhtasari kuandika jumla

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Tathmini\(2n+3\) kwa integers\(1, 2, 3\), na\(4\).
      Ikiwa umekosa tatizo hili, kagua Mfano 1.6.
    2. Tathmini\((−1)^{n}\) kwa integers\(1, 2, 3\), na\(4\).
      Kama amekosa tatizo hili, mapitio Mfano 1.19.
    3. Kama\(f(n)=n^{2}+2\), kupata\(f(1)+f(2)+f(3)\).
      Kama amekosa tatizo hili, mapitio Mfano 3.49.

    Andika Masharti Machache ya Kwanza ya Mlolongo

    Hebu tuangalie kazi\(f(x)=2x\) na tathmini kwa idadi tu ya kuhesabu.

    \(f(x)=2x\)  
    \(x\) \(2x\)
    \(1\) \(2\)
    \(2\) \(4\)
    \(3\) \(6\)
    \(4\) \(8\)
    \(5\) \(10\)
    \(...\) \(...\)
    Jedwali 12.1.1

    Kama sisi orodha ya maadili ya kazi ili kama\(2, 4, 6, 8\), na\(10\),... tuna mlolongo. Mlolongo ni kazi ambayo uwanja wake ni namba za kuhesabu.

    Ufafanuzi\(\PageIndex{1}\)

    Mlolongo ni kazi ambayo uwanja wake ni namba za kuhesabu.

    Mlolongo unaweza pia kuonekana kama orodha iliyoamriwa ya namba na kila namba katika orodha ni neno. Mlolongo unaweza kuwa na idadi isiyo na kipimo cha maneno au idadi ya mwisho ya maneno. Mlolongo wetu una dots tatu (ellipsis) mwishoni ambayo inaonyesha orodha kamwe mwisho. Ikiwa uwanja ni seti ya namba zote za kuhesabu, basi mlolongo ni mlolongo usio na kipimo. Kikoa chake ni namba zote za kuhesabu na kuna idadi isiyo na kipimo ya idadi ya kuhesabu.

    \(2,4,6,8,10, \dots\)

    Ikiwa tunapunguza kikoa kwa idadi ya mwisho ya idadi ya kuhesabu, basi mlolongo ni mlolongo wa mwisho. Kama sisi kutumia tu kwanza namba nne kuhesabu, mlolongo\(1, 2, 3, 4\) wetu itakuwa mlolongo finite,

    \(2,4,6,8\)

    Mara nyingi wakati wa kufanya kazi na utaratibu hatutaki kuandika maneno yote. Tunataka zaidi kompakt njia ya kuonyesha jinsi kila neno hufafanuliwa. Tulipofanya kazi na kazi, tuliandika\(f(x)=2x\) na tulivyosema maneno\(2x\) yalikuwa utawala unaoelezea maadili katika upeo. Wakati mlolongo ni kazi, hatutumii kawaida kazi nukuu. Badala ya kuandika kazi kama\(f(x)=2x\), tunataka kuandika kama\(a_{n}=2n\). The\(a_{n}\) ni mrefu\(n\) th ya mlolongo, mrefu katika nafasi\(n\) th ambapo\(n\) ni thamani katika uwanja. Fomu ya kuandika muda\(n\) wa mlolongo huitwa neno la jumla au formula ya mlolongo.

    Ufafanuzi\(\PageIndex{2}\)

    Muda wa jumla wa mlolongo hupatikana kutoka kwa fomu ya kuandika muda\(n\) wa mlolongo. \(n\)th mrefu ya mlolongo\(a_{n}\),, ni neno katika nafasi\(n\) th ambapo\(n\) ni thamani katika uwanja.

    Tunapopewa muda wa jumla wa mlolongo, tunaweza kupata maneno kwa kuchukua nafasi\(n\) na namba za kuhesabu kwa utaratibu. Kwa\(a_{n}=2 n\),

    \(n\) \(1\) \(2\) \(3\) \(4\) \(5\) \(6\)
    \(a_{n}\) 2\(\cdot 1\) 2\(\cdot 2\) 2\(\cdot 3\) 2\(\cdot 4\) 2\(\cdot 5\) 2\(\cdot 6\)
      \(2\) \(4\) \(6\) \(8\) \(10\)  
    Jedwali 12.1.2

    \(a_{1}, \quad a_{2}, \quad a_{3}, \quad a_{4}, \quad a_{5}, \ldots, \quad a_{n}, \dots\)

    \(2, \quad 4, \quad 6, \quad 8, \quad10, \dots\)

    Ili kupata maadili ya mlolongo, tunabadilisha nambari za kuhesabu ili katika muda wa jumla wa mlolongo.

    Mfano\(\PageIndex{1}\)

    Andika maneno matano ya kwanza ya mlolongo ambao muda wake ni\(a_{n}=4 n-3\).

    Suluhisho:

    Sisi badala ya maadili\(1, 2, 3, 4\), na\(5\) katika formula,\(a_{n}=4n−3\), kwa utaratibu.

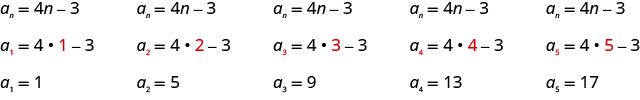
    Takwimu hii inaonyesha safu tatu na nguzo tano. Mstari wa kwanza unasoma neno la nth sawa na mara 4 n bala 3 iliyoandikwa mara tano. Mstari wa pili unasoma ndogo 1 sawa na mara 4 g mara 1 minus 3, ndogo 2 sawa na mara 4 g mara 2 minus 3, ndogo 3 sawa mara 4 g mara 3, ndogo 4 sawa mara 4 g mara 4 minus 3, ndogo 5 sawa mara 4 g mara 4, ndogo 5 sawa mara 4 g mara 5 minus 3. Mstari wa tatu anayesoma, ndogo 1 sawa na 1, ndogo 2 sawa 5, ndogo 3 sawa 9, ndogo 4 sawa 13, ndogo 5 sawa 17.
    Kielelezo 12.1.1

    Jibu:

    Masharti tano ya kwanza ya mlolongo ni\(1, 5, 9, 13\), na\(17\).

    Zoezi\(\PageIndex{1}\)

    Andika maneno matano ya kwanza ya mlolongo ambao muda wake ni\(a_{n}=3n-4\).

    Jibu

    \(-1,2,5,8,11\)

    Zoezi\(\PageIndex{2}\)

    Andika maneno matano ya kwanza ya mlolongo ambao muda wake ni\(a_{n}=2n-5\).

    Jibu

    \(-3,-1,1,3,5\)

    Kwa baadhi ya Utaratibu, variable ni exponent.

    Mfano\(\PageIndex{2}\)

    Andika maneno matano ya kwanza ya mlolongo ambao muda wake ni\(a_{n}=2^{n}+1\).

    Suluhisho:

    Sisi badala ya maadili\(1, 2, 3, 4\), na\(5\) katika formula,\(a_{n}=2^{n}+1\), kwa utaratibu.

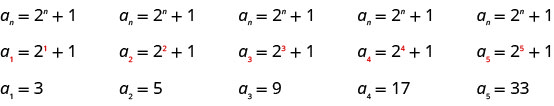
    Takwimu hii inaonyesha safu tatu na nguzo tano. Mstari wa kwanza unasoma “neno la nth linalingana na 2 hadi nguvu ya nth pamoja na 1” iliyoandikwa mara tano. Mstari wa pili unasoma, “ndogo 1 ni sawa na mara 2 1 pamoja na 1, ndogo 2 sawa na 2 kwa nguvu ya 2 pamoja 1, ndogo 3 sawa na 2 kwa nguvu 3 pamoja 1, ndogo 4 sawa na 2 kwa nguvu ya 4 pamoja 1, ndogo 5 sawa na 2 kwa nguvu 5 pamoja 1”. Mstari wa mwisho unasoma “ndogo 1 sawa na 3, ndogo 2 sawa na 5, ndogo 3 sawa 9, ndogo 4 sawa 17, ndogo 5 sawa 33”.
    Kielelezo 12.1.2

    Jibu:

    Masharti tano ya kwanza ya mlolongo ni\(3, 5, 9, 17\), na\(33\).

    Zoezi\(\PageIndex{3}\)

    Andika maneno matano ya kwanza ya mlolongo ambao muda wake ni\(a_{n}=3^{n}+4\).

    Jibu

    \(7,13,31,85,247\)

    Zoezi\(\PageIndex{4}\)

    Andika maneno matano ya kwanza ya mlolongo ambao muda wake ni\(a_{n}=2^{n}-5\).

    Jibu

    \(-3,-1,3,11,27\)

    Sio kawaida kuona maneno\((−1)^{n}\) au\((−1)^{n+1}\) kwa muda wa jumla kwa mlolongo. Ikiwa tunatathmini kila moja ya maneno haya kwa maadili machache, tunaona kwamba maneno haya hubadilisha ishara kwa maneno.

    \(n\) \(1\) \(2\) \(3\) \(4\) \(5\)
    \ (n\) ">\((-1)^{n}\) \ (1\) ">\((-1)^{1}\)
    \(-1\)    		 \ (2\) ">\((-1)^{2}\)
    1    		 \ (3\) ">\((-1)^{3}\)
    \(-1\)    		 \ (4\) ">\((-1)^{4}\)
    \(1\)    		 \ (5\) ">\((-1)^{5}\)
    \(-1\)
    \ (n\) ">\((-1)^{n+1}\) \ (1\) ">\((-1)^{1+1}\)
    1    		 \ (2\) ">\((-1)^{2+1}\)
    \(-1\)    		 \ (3\) ">\((-1)^{3+1}\)
    1    		 \ (4\) ">\((-1)^{4+1}\)
    \(-1\)    		 \ (5\) ">\((-1)^{5+1}\)
    1
    Jedwali 12.1.3

    \(a_{1}, \quad a_{2}, \quad a_{3}, \quad a_{4}, \quad a_{5}, \dots, \quad a_{n}, \dots\)

    \(\begin{array}{rrrr}{-1,} & {1,} & {-1,} & {1,} & {-1 \ldots} \\ {1,} & {-1,} & {1,} & {-1,} & {1 \ldots}\end{array}\)

    Mfano\(\PageIndex{3}\)

    Andika maneno matano ya kwanza ya mlolongo ambao muda wake ni\(a_{n}=(-1)^{n} n^{3}\).

    Suluhisho:

    Sisi badala ya maadili\(1, 2, 3, 4\), na\(5\) katika formula,\(a_{n}=(-1)^{n} n^{3}\), kwa utaratibu.

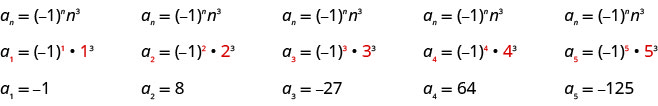
    Takwimu hii inaonyesha safu tatu na nguzo tano. Mstari wa kwanza unasoma “neno la nth linalingana hasi 1 hadi mara ya nguvu ya tisa n cubed” iliyoandikwa mara tano. Mstari wa pili unasoma ndogo 1 sawa na hasi 1 kwa nguvu ya mara 1 g mara 1 cubed, ndogo 2 sawa na hasi 1 squared wakati g mara 2 cubed, ndogo 3 sawa hasi 1 mara cubed g mara 23 cubed, ndogo 4 sawa hasi 1 kwa nguvu ya mara 4 g mara 4 cubed, ndogo 5 sawa hasi 1 kwa nguvu ya 5 mara 3 g mara 5 cubed. Mstari wa mwisho unasoma, “ndogo 1 ni sawa na hasi 1, ndogo 2 sawa na 8, ndogo 3 sawa na hasi 27, ndogo 4 sawa na 64, na ndogo 5 ni sawa na hasi 125.
    Kielelezo 12.1.3

    Jibu:

    Masharti tano ya kwanza ya mlolongo ni\(−1, 8, −27, 64, −1, 8, −27, 64\), na\(−125\).

    Zoezi\(\PageIndex{5}\)

    Andika maneno matano ya kwanza ya mlolongo ambao muda wake ni\(a_{n}=(-1)^{n} n^{2}\).

    Jibu

    \(-1,4,-9,16,-25\)

    Zoezi\(\PageIndex{6}\)

    Andika maneno matano ya kwanza ya mlolongo ambao muda wake ni\(a_{n}=(-1)^{n+1} n^{3}\).

    Jibu

    \(1,-8,27,-64,125\)

    Pata Mfumo wa Muda Mkuu (\(n\)Muda) wa Mlolongo

    Wakati mwingine tuna masharti machache ya mlolongo na itakuwa na manufaa kujua muda wa jumla au\(n\) th mrefu. Ili kupata muda wa jumla, tunatafuta ruwaza katika masharti. Mara nyingi ruwaza huhusisha wingi au nguvu. Tunatafuta pia mfano katika ishara za maneno.

    Mfano\(\PageIndex{4}\)

    Pata muda wa jumla kwa mlolongo ambao maneno matano ya kwanza yanaonyeshwa. \(4,8,12,16,20, \dots\)

    Suluhisho:


      .
      .
    Tunatafuta mfano katika maneno. .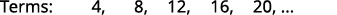
    Idadi ni mafungu yote ya\(4\). .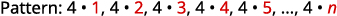
      Neno la jumla la mlolongo ni\(a_{n}=4n\).
    Jedwali 12.1.4

    Jibu:

    Neno la jumla la mlolongo ni\(a_{n}=4n\).

    Zoezi\(\PageIndex{7}\)

    Pata muda wa jumla kwa mlolongo ambao maneno matano ya kwanza yanaonyeshwa.

    \(3,6,9,12,15, \dots\)

    Jibu

    \(a_{n}=3 n\)

    Zoezi\(\PageIndex{8}\)

    Pata muda wa jumla kwa mlolongo ambao maneno matano ya kwanza yanaonyeshwa.

    \(5,10,15,20,25, \dots\)

    Jibu

    \(a_{n}=5 n\)

    Mfano\(\PageIndex{5}\)

    Pata muda wa jumla kwa mlolongo ambao maneno matano ya kwanza yanaonyeshwa. \(2,-4,8,-16,32, \dots\)

    Suluhisho:

     
    .
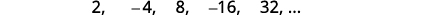
    Kielelezo 12.1.8
     
    .
    Kielelezo 12.1.9
    Tunatafuta mfano katika maneno.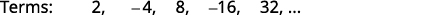
    .
    Kielelezo 12.1.10
    idadi ni nguvu ya\(2\). Ishara zinabadilisha, na hata\(n\) hasi.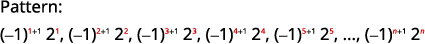
    .
    Kielelezo 12.1.11
      Neno la jumla la mlolongo ni\(a_{n}=(-1)^{n+1} 2^{n}\)
    Jedwali 12.1.5

    Jibu:

    Neno la jumla la mlolongo ni\(a_{n}=(-1)^{n+1}2^{n}\).

    Zoezi\(\PageIndex{9}\)

    Pata muda wa jumla kwa mlolongo ambao maneno matano ya kwanza yanaonyeshwa.

    \(-3,9,-27,81,-243, \dots\)

    Jibu

    \(a_{n}=(-1)^{n} 3^{n}\)

    Zoezi\(\PageIndex{10}\)

    Pata muda wa jumla kwa mlolongo ambao maneno matano ya kwanza yanaonyeshwa

    \(1,-4,9,-16,25, \dots\)

    Jibu

    \(a_{n}=(-1)^{n+1} n^{2}\)

    Mfano\(\PageIndex{6}\)

    Pata muda wa jumla kwa mlolongo ambao maneno matano ya kwanza yanaonyeshwa. \(\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \frac{1}{81}, \frac{1}{243}, \dots\)

    Suluhisho:

     
    .
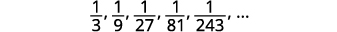
    Kielelezo 12.1.12
     
    .
    Kielelezo 12.1.13
    Tunatafuta mfano katika maneno.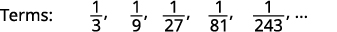
    .
    Kielelezo 12.1.14
    Nambari zote ni zote\(1\).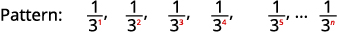
    .
    Kielelezo 12.1.15
    denominators ni nguvu ya\(3\). Neno la jumla la mlolongo ni\(a_{n}=\frac{1}{3^{n}}\).
    Jedwali 12.1.6

    Jibu:

    Neno la jumla la mlolongo ni\(a_{n}=\frac{1}{3^{n}}\).

    Zoezi\(\PageIndex{11}\)

    Pata muda wa jumla kwa mlolongo ambao maneno matano ya kwanza yanaonyeshwa.

    \(\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{32}, \dots\)

    Jibu

    \(a_{n}=\frac{1}{2^{n}}\)

    Zoezi\(\PageIndex{12}\)

    Pata muda wa jumla kwa mlolongo ambao maneno matano ya kwanza yanaonyeshwa.

    \(\frac{1}{1}, \frac{1}{4}, \frac{1}{9}, \frac{1}{16}, \frac{1}{25}, \dots\)

    Jibu

    \(a_{n}=\frac{1}{n^{2}}\)

    Tumia Uthibitishaji wa Kielelezo

    Utaratibu mara nyingi huwa na maneno ambayo ni bidhaa za integers mfululizo. Tunaonyesha bidhaa hizi kwa nukuu maalum inayoitwa notation factorial. Kwa mfano\(5!\), soma\(5\) factorial, ina maana\(5⋅4⋅3⋅2⋅1\). Hatua ya kufurahisha sio punctuation hapa; inaonyesha notation factorial.

    Ufafanuzi\(\PageIndex{3}\)

    Ikiwa\(n\) ni integer chanya, basi\(n!\) ni

    \(n !=n(n-1)(n-2) \dots\)

    Sisi kufafanua\(0!\) kama\(1\), hivyo\(0!=1\).

    Maadili ya\(n!\) integers ya kwanza ya\(5\) chanya yanaonyeshwa.

    \(\begin{array}{ccccc}{1 !} & {2 !} & {3 !} & {4 !} & {5 !} \\ {1} & \quad{2 \cdot 1} & \quad {3 \cdot 2 \cdot 1} & \quad{4 \cdot 3 \cdot 2 \cdot 1} & \quad {5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \\ {1} & {2} & {6} & {24} & {120}\end{array}\)

    Mfano\(\PageIndex{7}\)

    Andika maneno matano ya kwanza ya mlolongo ambao muda wake ni\(a_{n}=\frac{1}{n !}\).

    Suluhisho:

    Sisi badala ya maadili\(1, 2, 3, 4, 5\) katika formula,\(a_{n}=\frac{1}{n !}\), kwa utaratibu.

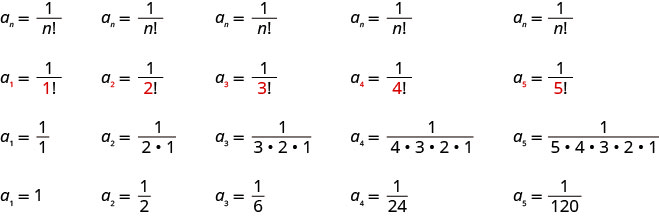
    Takwimu hii inaonyesha safu nne na nguzo tano. Mstari wa kwanza unasoma, “neno la nth linalingana na moja iliyogawanywa na n factorial” iliyoandikwa mara tano. Mstari wa pili unasoma “ndogo 1 sawa na moja iliyogawanywa na factorial 1, ndogo 2 sawa na 1 imegawanywa na 2 factorial, ndogo 3 sawa 1 imegawanywa na 3 factorial, ndogo 4 sawa 1 imegawanywa na 4 factorial, ndogo 5 sawa 1 imegawanywa na 5 factorial”. Mstari wa tatu unasoma “ndogo 1 sawa na 1 iliyogawanywa 1”, “ndogo 2 sawa na 1 imegawanywa na mara 2 g mara 1”, “ndogo 3 sawa na 1 imegawanywa na mara 3 g mara 2 g mara 1”, “ndogo 4 sawa na 1 imegawanywa mara 4 g mara 3 mara g mara 2”, “ndogo 5 sawa na 1 imegawanywa na mara 5 g mara 4 mara 3 g mara 2 g mara 1 “, “ndogo 1 sawa na 1, ndogo 2 sawa na nusu moja”, “ndogo 3 sawa na moja ya sita”, “ndogo 4 sawa 1 imegawanywa na 24", “ndogo 5 sawa 1 imegawanywa na 120".
    Kielelezo 12.1.16

    Jibu:

    Masharti tano ya kwanza ya mlolongo ni\(1, \frac{1}{2}, \frac{1}{6}, \frac{1}{24}, \frac{1}{120}\).

    Zoezi\(\PageIndex{13}\)

    Andika maneno matano ya kwanza ya mlolongo ambao muda wake ni\(a_{n}=\frac{2}{n !}\).

    Jibu

    \(2,1, \frac{1}{3}, \frac{1}{12}, \frac{1}{60}\)

    Zoezi\(\PageIndex{14}\)

    Andika maneno matano ya kwanza ya mlolongo ambao muda wake ni\(a_{n}=\frac{3}{n !}\).

    Jibu

    \(3, \frac{3}{2}, \frac{1}{2}, \frac{1}{8}, \frac{1}{40}\)

    Wakati kuna sehemu na factorials katika nambari na denominator, tunasimamia mambo kwa wima ili kufanya mahesabu yetu iwe rahisi.

    Mfano\(\PageIndex{8}\)

    Andika maneno matano ya kwanza ya mlolongo ambao muda wake ni\(a_{n}=\frac{(n+1) !}{(n-1) !}\).

    Suluhisho:

    Sisi badala ya maadili\(1, 2, 3, 4, 5\) katika formula,\(a_{n}=\frac{(n+1) !}{(n-1) !}\), kwa utaratibu.

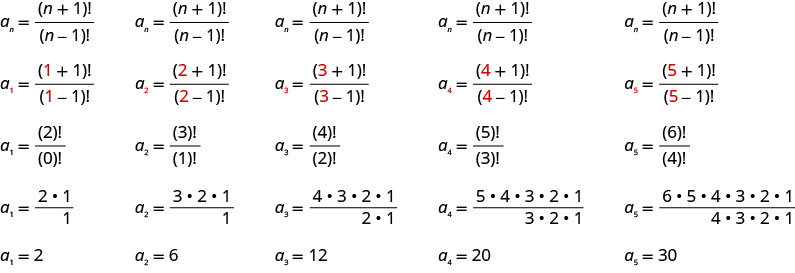
    Takwimu hii inaonyesha nguzo tano na safu tano. Mstari wa kwanza unaonyesha mlolongo “nth mrefu sawa n plus 1 mara factorial kugawanywa na n bala 1 mara factorial” imeandikwa mara tano. Mstari wa pili ni “ndogo 1 sawa na 1 pamoja na mara 1 factorial kugawanywa na 1 bala mara 1 factorial”, “ndogo 2 sawa 2 pamoja 1 mara factorial kugawanywa na 2 bala 1 mara factorial”, “ndogo 3 sawa 3 pamoja na mara 1 factorial kugawanywa na 3 bala 1 mara factorial”, “ndogo 4 sawa 4 pamoja 1 mara factorial kugawanywa na 4 minus 1 mara factorial”, “ndogo 5 sawa 5 pamoja na 1 mara factorial kugawanywa na 5 minus 1 mara factorial”. Mstari wa tatu unasoma “ndogo 1 sawa na mara 2 factorial kugawanywa na mara 0 factorial”, “ndogo 2 sawa na mara 3 factorial kugawanywa na mara 1 factorial”, “ndogo 3 sawa mara 4 factorial kugawanywa na mara 2 factorial”, “ndogo 4 sawa na mara 5 factorial kugawanywa na 3 mara factorial”, “ndogo 5 sawa 6 mara factorial kugawanywa na 4 mara factorial”. Mstari wa nne unasoma, “ndogo 1 sawa na mara 2 g wakati 1 imegawanywa na 1”, “ndogo 2 sawa mara 3 g mara 2 g mara 1 imegawanywa na 1”, “ndogo 3 sawa mara 4 g mara 3 mara g mara 2 g mara 1 kugawanywa na mara 2 g mara 1 “, “ndogo 4 sawa mara 5 g mara 4 mara g mara 3 mara 2 g mara 1 kugawanywa na 3 g mara 2 mara g mara 1 “, na “ndogo 5 sawa mara 6 g mara 5 mara g mara 4 g mara 3 mara g mara 3 g mara 2 mara g mara 1 kugawanywa na mara 4 g mara 3 mara g mara 2 g mara 1”. Mstari wa tano unasoma “ndogo 1 sawa na 2”, “ndogo 2 sawa na 6", “ndogo 3 sawa na 12", “ndogo 4 sawa na 20", “ndogo 5 sawa na 30".
    Kielelezo 12.1.17

    Jibu:

    Masharti tano ya kwanza ya mlolongo ni\(2, 6, 12, 20\), na\(30\).

    Zoezi\(\PageIndex{15}\)

    Andika maneno matano ya kwanza ya mlolongo ambao muda wake ni\(a_{n}=\frac{(n-1) !}{(n+1) !}\)

    Jibu

    \(\frac{1}{2}, \frac{1}{6}, \frac{1}{12}, \frac{1}{20}, \frac{1}{30}\)

    Zoezi\(\PageIndex{16}\)

    Andika maneno matano ya kwanza ya mlolongo ambao muda wake ni\(a_{n}=\frac{n !}{(n+1) !}\).

    Jibu

    \(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{1}{6}\)

    Pata Jumla ya sehemu

    Wakati mwingine katika programu, badala ya kuorodhesha masharti, ni muhimu kwetu kuongeza masharti ya mlolongo. Badala ya kuunganisha masharti na ishara pamoja, tunaweza kutumia maelezo ya muhtasari.

    Kwa mfano,\(a_{1}+a_{2}+a_{3}+a_{4}+a_{5}\) inaweza kuandikwa kama\(\sum_{i=1}^{5} a_{i}\). Tunasoma hii kama “jumla ya\(a\) ndogo\(i\) kutoka\(i\) sawa na moja hadi tano.” Ishara\(∑\) ina maana ya kuongeza na\(i\) ni index ya summation. The\(1\) inatuambia wapi kuanza (thamani ya awali) na\(5\) inatuambia wapi mwisho (terminal thamani).

    Ufafanuzi\(\PageIndex{4}\)

    Jumla ya\(n\) maneno ya kwanza ya mlolongo ambao\(n\) neno lake\(a_{n}\) limeandikwa katika nukuu ya muhtasari kama:

    \(\sum_{i=1}^{n} a_{i}=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+\ldots+a_{n}\)

    The\(i\) ni index ya summation na\(1\) inatuambia wapi kuanza na\(n\) inatuambia wapi mwisho.

    Tunapoongeza idadi ya mwisho ya maneno, tunaita jumla ya jumla ya sehemu.

    Mfano\(\PageIndex{9}\)

    Panua jumla ya sehemu na kupata thamani yake:\(\sum_{i=1}^{5} 2 i\).

    Suluhisho:

      \(\sum_{i=1}^{5} 2 i\)
    Sisi badala ya maadili\(1, 2, 3, 4, 5\) kwa utaratibu. \(2 \cdot 1+2 \cdot 2+2 \cdot 3+2 \cdot 4 + 2 \cdot 5\)
    Kurahisisha. \(2+4+6+8+10\)
    Ongeza. \(\begin{array} {c} 30\\ \sum_{i=1}^{5} 2 i=30 \end{array}\)
    Jedwali 12.1.7

    Jibu:

    \(\begin{array} {c} 30\\ \sum_{i=1}^{5} 2 i=30 \end{array}\)
    Zoezi\(\PageIndex{17}\)

    Panua jumla ya sehemu na kupata thamani yake:\(\sum_{i=1}^{5} 3 i\).

    Jibu

    \(45\)

    Zoezi\(\PageIndex{18}\)

    Panua jumla ya sehemu na kupata thamani yake:\(\sum_{i=1}^{5} 4 i\).

    Jibu

    \(60\)

    index si lazima daima kuwa\(i\) tunaweza kutumia barua yoyote, lakini\(i\) na\(k\) ni kawaida kutumika. Ripoti haifai kuanza na\(1\) aidha - inaweza kuanza na kuishia na integer yoyote nzuri.

    Mfano\(\PageIndex{10}\)

    Panua jumla ya sehemu na kupata thamani yake:\(\sum_{k=0}^{3} \frac{1}{k !}\).

    Suluhisho:

    \(\begin{array}{c c} {}&{\sum_{k=0}^{3} \frac{1}{k !}} \\ {We\:substitute\:the\:values\:0,1,2,3\:in\:order.}&{\frac{1}{1}+\frac{1}{1 !}+\frac{1}{2 !}+\frac{1}{3 !}} \\ {Evaluate\:the\:factorials.}& {\frac{1}{1}+\frac{1}{1}+\frac{1}{2 !}+\frac{1}{6}} \\ {Simplify.}&{1+1+\frac{3}{6}+\frac{1}{6}} \\{Simplify.}& {\frac{16}{6}} \\ {Simplify.}&{\frac{8}{3}} \\{}& {\sum_{k=0}^{3} \frac{1}{k !}=\frac{8}{3}}\end{array}\)

    Zoezi\(\PageIndex{19}\)

    Panua jumla ya sehemu na kupata thamani yake:\(\sum_{k=0}^{3} \frac{2}{k !}\).

    Jibu

    \(\frac{16}{3}\)

    Zoezi\(\PageIndex{20}\)

    Panua jumla ya sehemu na kupata thamani yake:\(\sum_{k=0}^{3} \frac{3}{k !}\).

    Jibu

    \(8\)

    Tumia Notation ya Summation Kuandika Jumla

    Katika mifano miwili iliyopita, tulikwenda kutoka kwa muhtasari wa kuandika jumla. Sasa tutaanza kwa jumla na kuibadilisha kwa maelezo ya muhtasari. Hii ni sawa na kutafuta muda wa jumla wa mlolongo. Tutahitaji kuangalia masharti na kupata mfano. Mara nyingi ruwaza huhusisha wingi au nguvu.

    Mfano\(\PageIndex{11}\)

    Andika jumla kwa kutumia maelezo ya muhtasari:\(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}\).

    Suluhisho:

    \(\begin{array} {}&{ 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}} \\ {}&{n : 1,2,3,4,5} \\ {\text{We look for a pattern in the terms.}}&{\text { Terms: } 1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}} \\ {\text{The numerators are all one.}}&{\text { Pattern: } \frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \ldots \frac{1}{n}} \\ {\text{The denominators are the counting numbers from one to five.}}&{\text{The sum written in summation notation}} \\ {}&{1 + \frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}=\sum^{5}_{n=1} \frac{1}{n}.} \end{array}\)

    Zoezi\(\PageIndex{21}\)

    Andika jumla kwa kutumia maelezo ya muhtasari:\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\).

    Jibu

    \(\sum_{n=1}^{5} \frac{1}{2^{n}}\)

    Zoezi\(\PageIndex{22}\)

    Andika jumla kwa kutumia maelezo ya muhtasari:\(1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\frac{1}{25}\)

    Jibu

    \(\sum_{n=1}^{5} \frac{1}{n^{2}}\)

    Wakati maneno ya jumla yana coefficients hasi, lazima tuchambue kwa makini mfano wa ishara.

    Mfano\(\PageIndex{12}\)

    Andika jumla kwa kutumia maelezo ya muhtasari:\(-1+8-27+64-125\).

    Suluhisho:


     
    .
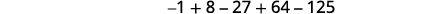
    Kielelezo 12.1.18
     
    .
    Kielelezo 12.1.19
    Tunatafuta mfano katika maneno.
    .
    Kielelezo 12.1.20
    Ishara za maneno mbadala,
    na maneno yasiyo ya kawaida ni hasi.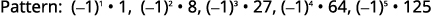
    .
    Kielelezo 12.1.21
    Nambari ni cubes ya namba za
    kuhesabu kutoka moja hadi tano.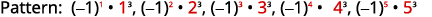
    .
    Kielelezo 12.1.22
     
    .
    Kielelezo 12.1.23
      Jumla iliyoandikwa katika nukuu ya muhtasari ni
      \(-1+8-27+64-125=\sum_{n=1}^{5}(-1)^{n} \cdot n^{3}\)
    Jedwali 12.1.8
    Zoezi\(\PageIndex{23}\)

    Andika kila jumla kwa kutumia muhtasari wa muhtasari:\(1-4+9-16+25\).

    Jibu

    \(\sum_{n=1}^{5}(-1)^{n+1} n^{2}\)

    Zoezi\(\PageIndex{24}\)

    Andika kila jumla kwa kutumia muhtasari wa muhtasari:\(-2+4-6+8-10\).

    Jibu

    \(\sum_{n=1}^{5}(-1)^{n} 2 n\)

    Kupata rasilimali hii online kwa maelekezo ya ziada na mazoezi na Utaratibu.

    https://openstax.org/l/37serseqfindpat

    Dhana muhimu

    • Nukuu ya Kielelezo

    Ikiwa\(n\) ni integer chanya, basi\(n!\) ni

    \(n !=n(n-1)(n-2) \ldots(3)(2)(1)\)

    Sisi kufafanua\(0!\) kama\(1\), hivyo\(0!=1\)

    • Ufafanuzi wa muhtasari

    Jumla ya\(n\) maneno ya kwanza ya mlolongo ambao\(n\) neno lake\(a_{n}\) limeandikwa katika nukuu ya muhtasari kama:

    \(\sum_{i=1}^{n} a_{i}=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+\ldots+a_{n}\)

    The\(i\) ni index ya summation na\(1\) inatuambia wapi kuanza na\(n\) inatuambia wapi mwisho.

    faharasa

    mlolongo wa mwisho
    Mlolongo na uwanja ambao ni mdogo kwa idadi ya mwisho ya idadi ya kuhesabu.
    muda wa jumla wa mlolongo
    Neno la jumla la mlolongo ni formula\(n\) ya kuandika muda wa mlolongo. \(n\)th mrefu ya mlolongo\(a_{n}\),, ni neno katika nafasi\(n\) th ambapo\(n\) ni thamani katika uwanja.
    mlolongo usio
    Mlolongo ambao uwanja wake ni namba zote za kuhesabu na kuna idadi isiyo na kipimo ya namba za kuhesabu.
    jumla ya sehemu
    Tunapoongeza idadi ya mwisho ya maneno ya mlolongo, tunaita jumla ya jumla ya sehemu.
    mlolongo
    Mlolongo ni kazi ambayo uwanja wake ni namba za kuhesabu.