Skip to main content
Global

9.5: Tatua Ulinganisho wa Quadratic katika Fomu ya Quadratic

  1. Last updated
  2. Save as PDF
  • Page ID
    176478

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Tatua usawa katika fomu ya quadratic
    Kabla ya kuanza

    ... kuchukua jaribio hili la utayari.

    1. Sababu kwa badala:\(y^{4}-y^{2}-20\).
    2. Sababu kwa badala:\((y-4)^{2}+8(y-4)+15\).
    3. Kurahisisha
      1. \(x^{\frac{1}{2}} \cdot x^{\frac{1}{4}}\)
      2. \(\left(x^{\frac{1}{3}}\right)^{2}\)
      3. \(\left(x^{-1}\right)^{2}\)

    Tatua Ulinganisho katika Fomu ya Quadratic

    Wakati mwingine tulipofanya trinomials, trinomial haikuonekana kuwa katika\(ax^{2}+bx+c\) fomu. Hivyo sisi factored na badala kuruhusu sisi kufanya hivyo fit\(ax^{2}+bx+c\) fomu. Tulitumia kiwango\(u\) cha ubadilishaji.

    Kwa sababu ya kujieleza\(x^{4}-4 x^{2}-5\), sisi niliona sehemu variable ya muda wa kati ni\(x^{2}\) na mraba wake\(x^{4}\),, ni sehemu variable ya muda wa kwanza. (Tunajua\(\left(x^{2}\right)^{2}=x^{4}\).) Hivyo sisi basi\(u=x^{2}\) na factored.

      \(x^{4}-4 x^{2}-5\)
      \(\left(\color{red}x^2 \color{black} \right)^{2}-4\left( \color{red}x^{2} \color{black}\right)-5\)
    Hebu\(u=x^{2}\) na mbadala. \(\color{red}u \color{black}^{2}-4 \color{red}u \color{black}-5\)
    Sababu ya trinomial. \((u+1)(u-5)\)
    Badilisha nafasi\(u\) na\(x^{2}\). \(\left( \color{red}x^{2} \color{black} + 1\right)\left( \color{red}x^2 \color{black}-5\right)\)

    Vilevile, wakati mwingine equation haipo katika\(ax^{2}+bx+c=0\) fomu lakini inaonekana sana kama equation quadratic. Kisha, tunaweza mara nyingi kufanya badala ya kufikiri ambayo itatuwezesha kuifanya\(ax^{2}+bx+c=0\) fomu hiyo. Ikiwa tunaweza kuifanya fomu hiyo, tunaweza kutumia njia zetu zote kutatua equations quadratic.

    Kumbuka kwamba katika equation quadratic\(ax^{2}+bx+c=0\), muda wa kati ina kutofautiana\(x\),, na mraba wake,\(x^{2}\), ni sehemu ya kutofautiana ya muda wa kwanza. Angalia uhusiano huu unapojaribu kupata nafasi.

    Tena, tutatumia kiwango cha\(u\) kufanya badala ambayo itaweka equation katika fomu quadratic. Kama badala inatupa equation ya fomu\(ax^{2}+bx+c=0\), tunasema equation awali ilikuwa ya fomu quadratic.

    Mfano unaofuata unaonyesha hatua za kutatua equation katika fomu ya quadratic.

    Mfano\(\PageIndex{1}\) How to Solve Equations in Quadratic Form

    Kutatua:\(6 x^{4}-7 x^{2}+2=0\)

    Suluhisho:

    Hatua ya 1: Tambua badala ambayo itaweka equation katika fomu ya quadratic. Tangu\(\left(x^{2}\right)^{2}=x^{4}\), sisi basi\(u=x^{2}\). \(6 x^{4}-7 x^{2}+2=0\)
    Hatua ya 2: Andika upya equation na badala ya kuiweka katika fomu ya quadratic.

    Andika upya ili kujiandaa kwa ajili ya ubadilishaji.

    Mbadala\(u=x^{2}\).

    		 \(\begin{aligned}6\color{black}{\left(\color{red}{x^{2}}\right)}^{2}-7\color{red}{ x^{2}}\color{black}{+}2&=0 \\ \color{black}{6 \color{red}{u}^{2}}-7 \color{red}{u}\color{black}{+}2&=0\end{aligned}\)
    hatua 3: Kutatua equation quadratic kwa\(u\).

    Tunaweza kutatua kwa factoring.

    Tumia mali ya Bidhaa ya Zero.

    		 \(\begin{aligned}(2 u-1)(3 u-2) &=0 \\ 2 u-1=0, 3 u-2&=0 \\ 2 u =1,3 u&=2 \\ u =\frac{1}{2} u&=\frac{2}{3} \end{aligned}\)
    Hatua ya 4: Badilisha variable ya awali nyuma katika matokeo, kwa kutumia badala. Badilisha nafasi\(u\) na\(x^{2}\). \(x^{2}=\frac{1}{2} \quad x^{2}=\frac{2}{3}\)
    Hatua ya 5: Kutatua kwa variable awali. Kutatua kwa\(x\), kwa kutumia Mizizi ya Mizizi ya Mraba.

    \(\begin{array}{ll}{x=\pm \sqrt{\frac{1}{2}}} & {x=\pm \sqrt{\frac{2}{3}}} \\ {x=\pm \frac{\sqrt{2}}{2}} & {x=\pm \frac{\sqrt{6}}{3}}\end{array}\)

    Kuna ufumbuzi nne.

    \(\begin{array}{ll}{x=\frac{\sqrt{2}}{2}} & {x=\frac{\sqrt{6}}{3}} \\ {x=-\frac{\sqrt{2}}{2}} & {x=-\frac{\sqrt{6}}{3}}\end{array}\)
    Hatua ya 6: Angalia ufumbuzi. Angalia ufumbuzi wote wanne. Tutaonyesha hundi moja hapa.

    \(\begin{aligned}x&=\frac{\sqrt{2}}{2} \\ 6 x^{4}-7 x^{2}+2&=0 \\ 6\left(\frac{\sqrt{2}}{2}\right)^{4}-7\left(\frac{\sqrt{2}}{2}\right)^{2}+2 &\stackrel{?}{=} 0\\ 6\left(\frac{4}{16} \right)-7\left(\frac{2}{4} \right)^{2}+2&\stackrel{?}{=}0 \\ \frac{3}{2}-\frac{7}{2}+\frac{4}{2}&\stackrel{?}{=}0 \\ 0&=0 \end{aligned}\)

    Tunaacha hundi nyingine kwako!
    Zoezi\(\PageIndex{1}\)

    Kutatua:\(x^{4}-6 x^{2}+8=0\).

    Jibu

    \(x=\sqrt{2}, x=-\sqrt{2}, x=2, x=-2\)

    Zoezi\(\PageIndex{2}\)

    Kutatua:\(x^{4}-11 x^{2}+28=0\).

    Jibu

    \(x=\sqrt{7}, x=-\sqrt{7}, x=2, x=-2\)

    Sisi muhtasari hatua za kutatua equation katika fomu quadratic.

    Tatua Ulinganisho katika Fomu ya Quadratic
    1. Tambua badala ambayo itaweka equation katika fomu quadratic.
    2. Andika upya equation na badala ya kuiweka katika fomu ya quadratic.
    3. Kutatua equation quadratic kwa\(u\).
    4. Badilisha variable ya awali nyuma katika matokeo, kwa kutumia badala.
    5. Kutatua kwa variable awali.
    6. Angalia ufumbuzi.

    Katika mfano unaofuata, binomial katika muda wa kati,\((x-2)\) ni mraba katika muda wa kwanza. Kama sisi basi\(u=x-2\) na badala, trinomial yetu itakuwa katika\(a x^{2}+b x+c\) fomu.

    Mfano\(\PageIndex{2}\)

    Kutatua:\((x-2)^{2}+7(x-2)+12=0\).

    Suluhisho:

      \((x-2)^{2}+7(x-2)+12=0\)
    Jitayarishe kwa ajili ya ubadilishaji. \(\color{red}(x-2)\color{black}^{2}+7\color{red}(x-2) \color{black} +12=0\)
    Hebu\(u=x-2\) na mbadala. \(\color{red}u^{\color{black}2} \color{black}+ 7 \color{red}u \color{black}+12=0\)
    Kutatua kwa factoring.

    \((u+3)(u+4)=0\)

    \ (\ kuanza {wamekusanyika}
    u+3=0,\ quad u+4=0\\
    u=-3,\ quad u=-4
    \ mwisho {wamekusanyika}\)

    Badilisha nafasi\(u\) na\(x-2\).

    \(x-2=-3, \quad x-2=-4\)

    Kutatua kwa\(x\).

    \(x=-1, \quad x=-2\)

    Angalia: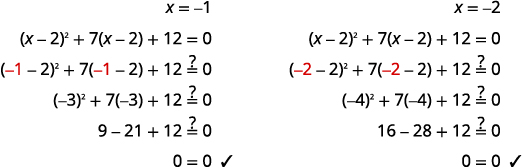

    .
    Kielelezo 9.4.14
    		  
    Zoezi\(\PageIndex{3}\)

    Kutatua:\((x-5)^{2}+6(x-5)+8=0\).

    Jibu

    \(x=3, x=1\)

    Zoezi\(\PageIndex{4}\)

    Kutatua:\((y-4)^{2}+8(y-4)+15=0\).

    Jibu

    \(y=-1, y=1\)

    Katika mfano unaofuata, tunaona hiyo\((\sqrt{x})^{2}=x\). Pia, kumbuka kwamba wakati sisi mraba pande zote mbili za equation, tunaweza kuanzisha mizizi ya nje. Hakikisha kuangalia majibu yako!

    Mfano\(\PageIndex{3}\)

    Kutatua:\(x-3 \sqrt{x}+2=0\).

    Suluhisho:

    \(\sqrt{x}\)Katika muda wa kati, ni mraba katika muda wa kwanza\((\sqrt{x})^{2}=x\). Kama sisi basi\(u=\sqrt{x}\) na badala, trinomial yetu itakuwa katika\(a x^{2}+b x+c=0\) fomu.

      \(x-3 \sqrt{x}+2=0\)
    Andika upya trinomial kujiandaa kwa ajili ya ubadilishaji. .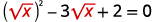
    Hebu\(u=\sqrt{x}\) na mbadala. .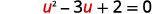
    Kutatua kwa factoring.

    \((u-2)(u-1)=0\)

    \(u-2=0, \quad u-1=0\)
    \(u=2, \quad u=1\)\)
    Badilisha nafasi\(u\) na\(\sqrt{x}\).

    \(\sqrt{x}=2, \quad \sqrt{x}=1\)
    Tatua kwa\(x\), kwa kupiga pande zote mbili. \(x=4, \quad x=1\)

    Angalia: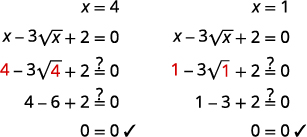

    .
    		  
    Zoezi\(\PageIndex{5}\)

    Kutatua:\(x-7 \sqrt{x}+12=0\).

    Jibu

    \(x=9, x=16\)

    Zoezi\(\PageIndex{6}\)

    Kutatua:\(x-6 \sqrt{x}+8=0\).

    Jibu

    \(x=4, x=16\)

    Substitutions kwa exponents busara pia kutusaidia kutatua equation katika fomu quadratic. Fikiria mali ya exponents kama wewe kuanza mfano unaofuata.

    Mfano\(\PageIndex{4}\)

    Kutatua:\(x^{\frac{2}{3}}-2 x^{\frac{1}{3}}-24=0\).

    Suluhisho:

    \(x^{\frac{1}{3}}\)Katika muda wa kati ni mraba katika muda wa kwanza\(\left(x^{\frac{1}{3}}\right)^{2}=x^{\frac{2}{3}}\). Kama sisi basi\(u=x^{\frac{1}{3}}\) na badala, trinomial yetu itakuwa katika\(a x^{2}+b x+c=0\) fomu.

      \(x^{\frac{2}{3}}-2 x^{\frac{1}{3}}-24=0\)
    Andika upya trinomial kujiandaa kwa ajili ya ubadilishaji. .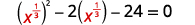
    Hebu\(u=x^{\frac{1}{3}}\) .
    Kutatua kwa factoring.

    \((u-6)(u+4)=0\)

    \(u-6=0, \quad u+4=0\)

    \(u=6, \quad u=-4\)
    Badilisha nafasi\(u\) na\(x^{\frac{1}{3}}\).

    \(x^{\frac{1}{3}}=6, \quad x^{\frac{1}{3}}=-4\)
    Kutatua\(x\) kwa cubing pande zote mbili.

    \(\left(x^{\frac{1}{3}}\right)^{3}=(6)^{3}, \quad\left(x^{\frac{1}{3}}\right)^{3}=(-4)^{3}\)

    \(x=216, \quad x=-64\)

    Angalia: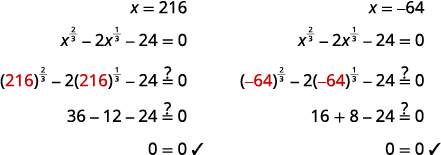

    .
    Kielelezo 9.4.33
    		  
    Zoezi\(\PageIndex{7}\)

    Kutatua:\(x^{\frac{2}{3}}-5 x^{\frac{1}{3}}-14=0\).

    Jibu

    \(x=-8, x=343\)

    Zoezi\(\PageIndex{8}\)

    Kutatua:\(x^{\frac{1}{2}}+8 x^{\frac{1}{4}}+15=0\).

    Jibu

    \(x=81, x=625\)

    Katika mfano unaofuata, tunahitaji kukumbuka ufafanuzi wa exponent hasi pamoja na mali ya exponents.

    Mfano\(\PageIndex{5}\)

    Kutatua:\(3 x^{-2}-7 x^{-1}+2=0\).

    Suluhisho:

    \(x^{−1}\)Katika muda wa kati ni mraba katika muda wa kwanza\(\left(x^{-1}\right)^{2}=x^{-2}\). Kama sisi basi\(u=x^{−1}\) na badala, trinomial yetu itakuwa katika\(a x^{2}+b x+c=0\) fomu.

      \(3 x^{-2}-7 x^{-1}+2=0\)
    Andika upya trinomial kujiandaa kwa ajili ya kubadilisha. .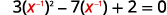
    Hebu\(u=x^{-1}\) na mbadala. .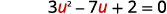
    Kutatua kwa factoring. \((3 u-1)(u-2)=0\)
      \(3 u-1=0, \quad u-2=0\)
      \(u=\frac{1}{3}, \quad u=2\)
    Badilisha nafasi\(u\) na\(x^{-1}\). \(x^{-1}=\frac{1}{3}, \quad x^{-1}=2\)
    Tatua\(x\) kwa kuchukua usawa tangu\(x^{-1}=\frac{1}{x}\). \(x=3, \quad x=\frac{1}{2}\)

    Angalia: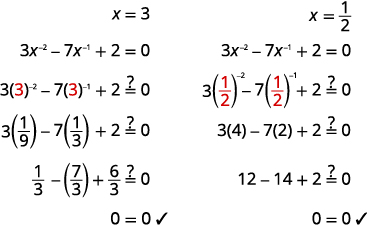

    .
    Kielelezo 9.4.42
    		  
    Zoezi\(\PageIndex{9}\)

    Kutatua:\(8 x^{-2}-10 x^{-1}+3=0\).

    Jibu

    \(x=\frac{4}{3}, x=2\)

    Zoezi\(\PageIndex{10}\)

    Kutatua:\(6 x^{-2}-23 x^{-1}+20=0\).

    Jibu

    \(x=\frac{2}{5}, x=\frac{3}{4}\)

    Pata video hii ya mtandaoni kwa maelekezo ya ziada na mazoezi na kutatua equations quadratic: https://www.youtube.com/watch?v=7X-CZMbpxuw

    Dhana muhimu

    • Jinsi ya kutatua equations katika fomu quadratic.
      1. Tambua badala ambayo itaweka equation katika fomu quadratic.
      2. Andika upya equation na badala ya kuiweka katika fomu ya quadratic.
      3. Kutatua equation quadratic kwa\(u\).
      4. Badilisha variable ya awali nyuma katika matokeo, kwa kutumia badala.
      5. Kutatua kwa variable awali.
      6. Angalia ufumbuzi.