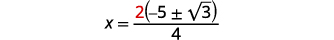9.4: Tatua Ulinganifu wa Quadratic Kutumia Mfumo wa Quadratic

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Tatua usawa wa quadratic kwa kutumia Mfumo wa Quadratic
• Tumia ubaguzi kutabiri idadi na aina ya ufumbuzi wa equation quadratic
• Tambua njia sahihi zaidi ya kutumia kutatua equation quadratic

Kabla ya kuanza, fanya jaribio hili la utayari.

1. Tathmini\(b^{2}-4 a b\)\(a=3\) lini na\(b=−2\).
2. Kurahisisha\(\sqrt{108}\).
3. Kurahisisha\(\sqrt{50}\).

Tatua Ulinganisho wa Quadratic Kutumia Mfumo wa Quadratic

Tulipotatua usawa wa quadratic katika sehemu ya mwisho kwa kukamilisha mraba, tulichukua hatua sawa kila wakati. Mwishoni mwa zoezi la kuweka, huenda umekuwa unashangaa 'je, kuna njia rahisi zaidi ya kufanya hivyo? ' Jibu ni 'ndiyo'. Wanahisabati hutafuta ruwaza wanapofanya mambo tena na tena ili kufanya kazi yao iwe rahisi. Katika sehemu hii tutapata na kutumia formula ili kupata suluhisho la equation ya quadratic.

Tumeona jinsi ya kutatua formula kwa ajili ya kutofautiana maalum 'kwa ujumla', ili tuweze kufanya hatua algebraic mara moja tu, na kisha kutumia formula mpya kupata thamani ya kutofautiana maalum. Sasa tutapitia hatua za kukamilisha mraba kwa kutumia fomu ya jumla ya equation quadratic kutatua equation quadratic kwa\(x\).

Tunaanza na fomu ya kawaida ya equation ya quadratic na kuitatua\(x\) kwa kukamilisha mraba.

	\(ax^2 + bx + c = 0, \quad a \ne 0\)
Sulua maneno ya kutofautiana upande mmoja.	\(ax^2 + bx \quad = -c\)
Fanya mgawo wa\(x^{2}\) sawa na\(1\), kwa kugawa na\(a\).	\(\dfrac{ax^2}{a} + \dfrac{b}{a}x \quad = -\dfrac{c}{a}\)
Kurahisisha.	\(x^2+ \dfrac{b}{a}x \quad = -\dfrac{c}{a}\)
Ili kukamilisha mraba, pata\(\left(\dfrac{1}{2} \cdot \dfrac{b}{a}\right)^{2}\) na uongeze kwa pande zote mbili za equation.
\(\left(\dfrac{1}{2} \dfrac{b}{a}\right)^{2}=\dfrac{b^{2}}{4 a^{2}}\)	\(x^2 + \dfrac{b}{a}x +{\color{red}{\dfrac{b^2}{4a^2}}}{\color{black}{ = -\dfrac{c}{a}\,+\,}}{\color{red}{\dfrac{b^2}{4a^2}}}\)
Upande wa kushoto ni mraba kamilifu, fanya.	\(\left( x + \dfrac{b}{2a}\right)^2 = -\dfrac{c}{a}+\dfrac{b^2}{4a^2}\)
Pata denominator ya kawaida ya upande wa kulia na uandike sehemu ndogo sawa na denominator ya kawaida.	\(\left( x + \dfrac{b}{2a}\right)^2 =\dfrac{b^2}{4a^2}-\dfrac{c\cdot\color{red}{4a}}{a\cdot\color{red}{4a}}\)
Kurahisisha.	\(\left( x + \dfrac{b}{2a}\right)^2 =\dfrac{b^2}{4a^2}-\dfrac{4ac}{4a^2}\)
Kuchanganya kwa sehemu moja.	\(\left( x + \dfrac{b}{2a}\right)^2 =\dfrac{b^2-4ac}{4a^2}\)
Tumia mali ya mizizi ya mraba.	\(x + \dfrac{b}{2a}= \pm\sqrt{\dfrac{b^2-4ac}{4a^2}}\)
Kurahisisha radical.	\(x + \dfrac{b}{2a}= \pm\dfrac{\sqrt{b^2-4ac}}{2a}\)
\(-\dfrac{b}{2a}\)Ongeza pande zote mbili za equation.	\(x = -\dfrac{b}{2a} \pm\dfrac{\sqrt{b^2-4ac}}{2a}\)
Kuchanganya maneno upande wa kulia.	\(x = \dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\)

Equation ya mwisho inaitwa “Mfumo wa Quadratic.”

Ufafanuzi\(\PageIndex{1}\): Quadratic Formula

Ufumbuzi wa equation quadratic ya fomu\(a x^{2}+b x+c=0\), ambapo\(a≠0\) hutolewa na formula:

\[x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \label{quad}\]

Ili kutumia Mfumo wa Quadratic, tunabadilisha maadili ya\(a,b\), na\(c\) kutoka fomu ya kawaida katika kujieleza upande wa kulia wa formula. Kisha sisi kurahisisha kujieleza. Matokeo yake ni jozi ya ufumbuzi wa equation quadratic.

Angalia Mfumo wa Quadratic (Equation\ ref {quad}) ni equation. Hakikisha unatumia pande zote mbili za equation.

Mfano\(\PageIndex{1}\) How to Solve a Quadratic Equation Using the Quadratic Formula

Tatua kwa kutumia Mfumo wa Quadratic:\(2 x^{2}+9 x-5=0\).

Suluhisho:

Hatua ya 1: Andika equation quadratic katika fomu ya kawaida. Tambua\(a,b,c\) maadili.	Equation hii ni katika hali ya kawaida.	\(\begin{aligned} \color{red}{a x^{2}+b x+c =0} \\ 2 x^{2}+9 x-5 =0 \\ a=2, b =9, c=-5 \end{aligned}\)
Hatua ya 2: Andika formula ya quadratic. Kisha mbadala katika maadili ya\(a,b,c\).	Mbadala katika\(a=2, b=9, c=-5\)	\(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\) \(x=\dfrac{-9 \pm \sqrt{9^{2}-4 \cdot 2 \cdot(-5)}}{2 \cdot 2}\)
hatua 3: Kurahisisha sehemu, na kutatua kwa\(x\).		\(\begin{array}{l}{x=\dfrac{-9 \pm \sqrt{81-(-40)}}{4}} \\ {x=\dfrac{-9 \pm \sqrt{121}}{4}} \\ {x=\dfrac{-9 \pm 11}{4}} \\ {x=\dfrac{-9+11}{4}}\quad x=\dfrac{-9-11}{4} \\ {x=\dfrac{2}{4} \quad \quad\:\:\: x=\dfrac{-20}{4}}\\ {x=\dfrac{1}{2} \quad\quad\:\:\: x=-5}\end{array}\)
Hatua ya 4: Angalia ufumbuzi.	Weka kila jibu katika equation ya awali ili uangalie. Mbadala\(x=\color{red}{\dfrac{1}{2}}\) na\(x=\color{red}{-5}\).	\(\begin{aligned}2 x^{2}+9 x-5&=0 \\ 2\color{black}{\left(\color{red}{\dfrac{1}{2}}\right)}^{2}+9 \cdot \color{red}{\dfrac{1}{2}}\color{black}{-}5 &\stackrel{?}{=} 0 \\ 2\cdot\dfrac{1}{4}+0\cdot\dfrac{1}{2}-5&\stackrel{?}{=}0 \\ 2\cdot\dfrac{1}{4}+9\cdot\dfrac{1}{2}-5&\stackrel{?}{=}0 \\ \dfrac{1}{2}+\dfrac{9}{2}-5&\stackrel{?}{=}0 \\ \dfrac{10}{2}-5&\stackrel{?}{=}0 \\5-5&\stackrel{?}{=}0\\0&=0\end{aligned}\) \(\begin{array}{r}{2 x^{2}+9 x-5=0} \\ {2(\color{red}{-5}\color{black}{)}^{2}+9(\color{red}{-5}\color{black}{)}-5\stackrel{?}{=}0} \\ {2 \cdot 25-45-5\stackrel{?}{=}0} \\ {50-45-5\stackrel{?}{=}0} \\ {0=0}\end{array}\)

Zoezi\(\PageIndex{1}\)

Tatua kwa kutumia Mfumo wa Quadratic:\(3 y^{2}-5 y+2=0\).

Jibu

\(y=1, y=\dfrac{2}{3}\)

Zoezi\(\PageIndex{2}\)

Tatua kwa kutumia Mfumo wa Quadratic:\(4 z^{2}+2 z-6=0\).

Jibu

\(z=1, z=-\dfrac{3}{2}\)

HowTo: Tatua Equation ya Quadratic Kutumia Mfumo wa Quadratic

1. Andika equation quadratic katika fomu ya kawaida,\(a x^{2}+b x+c=0\). Tambua maadili ya\(a,b\), na\(c\).
2. Andika Mfumo wa Quadratic. Kisha mbadala katika maadili ya\(a,b\), na\(c\).
3. Kurahisisha.
4. Angalia ufumbuzi.

Kama unasema formula kama wewe kuandika katika kila tatizo, itabidi ni kukariri katika wakati hakuna! Na kumbuka, Mfumo wa Quadratic ni equation. Hakikisha kuanza na “\(x=\)”.

Mfano\(\PageIndex{2}\)

Tatua kwa kutumia Mfumo wa Quadratic:\(x^{2}-6 x=-5\).

Suluhisho:

	\(x^{2}-6 x=-5\)
Andika equation katika fomu ya kawaida\(5\) kwa kuongeza kila upande.	\(x^{2}-6 x+5=0\)
Equation hii ni sasa katika hali ya kawaida.	\({\color{red}{\small{ax^2+bx + c} = \small{0}}}\) \(x^2 - 6x + 5 = 0\)
Tambua maadili ya\(\color{cyan}a\),\(\color{red}b\),\(\color{limegreen}c\).	\({\color{cyan}a=1}\),\({\color{red}b=-6}\),\({\color{limegreen}c=5}\)
Andika Mfumo wa Quadratic.	\(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
Kisha mbadala katika maadili ya\(a, b, c\).	\(x=\dfrac{-\color{red} (-6 ) \color{black} \pm \sqrt{\color{red}(-6) \color{black}^{2}-4 \cdot \color{cyan}1 \color{black} \cdot ( \color{limegreen}5 \color{black})}}{2 \cdot \color{cyan} 1} \)
Kurahisisha.	\(x=\dfrac{6 \pm \sqrt{36-20}}{2}\) \(x=\dfrac{6 \pm \sqrt{16}}{2}\) \(x=\dfrac{6 \pm 4}{2}\)
Andika upya ili kuonyesha ufumbuzi mbili.	\(x=\frac{6+4}{2}, \quad x=\frac{6-4}{2}\)
Kurahisisha.	\(x=\frac{10}{2}, \quad x=\frac{2}{2}\)
	\(x=5, \quad x=1\)
Angalia: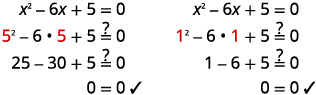

Zoezi\(\PageIndex{3}\)

Tatua kwa kutumia Mfumo wa Quadratic:\(a^{2}-2 a=15\).

Jibu

\(a=-3, a=5\)

Zoezi\(\PageIndex{4}\)

Tatua kwa kutumia Mfumo wa Quadratic:\(b^{2}+24=-10 b\).

Jibu

\(b=-6, b=-4\)

Wakati sisi kutatuliwa equations quadratic kwa kutumia Square Mizizi Mali, sisi wakati mwingine got majibu kwamba alikuwa radicals. Hiyo inaweza kutokea, pia, wakati wa kutumia Mfumo wa Quadratic. Ikiwa tunapata radical kama suluhisho, jibu la mwisho lazima liwe na radical katika fomu yake rahisi.

Mfano\(\PageIndex{3}\)

Tatua kwa kutumia Mfumo wa Quadratic:\(2 x^{2}+10 x+11=0\).

Suluhisho:

Equation hii ni katika hali ya kawaida.
Tambua maadili ya\(a,b\) na\(c\).
Andika Mfumo wa Quadratic.	\(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
Kisha mbadala katika maadili ya\(a, b\), na\(c\).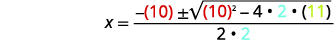
Kurahisisha.	\(x=\dfrac{-10 \pm \sqrt{100-88}}{4}\)
	\(x=\dfrac{-10 \pm \sqrt{12}}{4}\)
Kurahisisha radical.	\(x=\dfrac{-10 \pm 2 \sqrt{3}}{4}\)
Factor nje ya sababu ya kawaida katika nambari.	\(x=\dfrac{\color{red}{2}(-5 \pm \sqrt{3})}{4}\)
Ondoa mambo ya kawaida.	\(x=\dfrac{-5 \pm \sqrt{3}}{2}\)
Andika upya ili kuonyesha ufumbuzi mbili.	\(x=\dfrac{-5+\sqrt{3}}{2}, \quad x=\dfrac{-5-\sqrt{3}}{2}\)
Angalia: Tunaacha hundi kwako!

Zoezi\(\PageIndex{5}\)

Tatua kwa kutumia Mfumo wa Quadratic:\(3 m^{2}+12 m+7=0\).

Jibu

\(m=\dfrac{-6+\sqrt{15}}{3}, m=\dfrac{-6-\sqrt{15}}{3}\)

Zoezi\(\PageIndex{6}\)

Tatua kwa kutumia Mfumo wa Quadratic:\(5 n^{2}+4 n-4=0\).

Jibu

\(n=\dfrac{-2+2 \sqrt{6}}{5}, n=\dfrac{-2-2 \sqrt{6}}{5}\)

\(a, b\)Tunapobadilisha, na\(c\) katika Mfumo wa Quadratic na radicand ni hasi, equation ya quadratic itakuwa na ufumbuzi wa kufikiri au ngumu. Tutaona hili katika mfano unaofuata.

Mfano\(\PageIndex{4}\)

Tatua kwa kutumia Mfumo wa Quadratic:\(3 p^{2}+2 p+9=0\).

Suluhisho:

Jedwali 9.3.5

Equation hii ni katika hali ya kawaida.
Kutambua maadili ya\(a,b,c\).
Andika Mfumo wa Quadratic.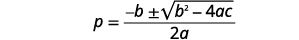
Kisha mbadala katika maadili ya\(a,b,c\).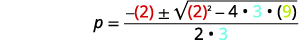
Kurahisisha.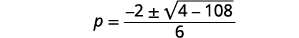
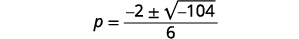Kurahisisha radical kutumia idadi tata.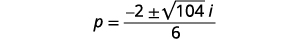
Kurahisisha radical.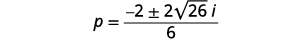
Fanya sababu ya kawaida katika nambari.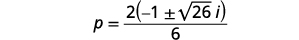
Ondoa mambo ya kawaida.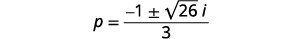
Andika upya kwa\(a+bi\) fomu ya kawaida.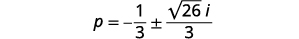
Andika kama ufumbuzi mbili.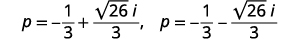

Zoezi\(\PageIndex{7}\)

Tatua kwa kutumia Mfumo wa Quadratic:\(4 a^{2}-2 a+8=0\).

Jibu

\(a=\dfrac{1}{4}+\dfrac{\sqrt{31}}{4} i, \quad a=\dfrac{1}{4}-\dfrac{\sqrt{31}}{4} i\)

Zoezi\(\PageIndex{8}\)

Tatua kwa kutumia Mfumo wa Quadratic:\(5 b^{2}+2 b+4=0\).

Jibu

\(b=-\dfrac{1}{5}+\dfrac{\sqrt{19}}{5} i, \quad b=-\dfrac{1}{5}-\dfrac{\sqrt{19}}{5} i\)

Kumbuka, kutumia Mfumo wa Quadratic, equation lazima iandikwa kwa fomu ya kawaida,\(a x^{2}+b x+c=0\). Wakati mwingine, sisi haja ya kufanya baadhi algebra kupata equation katika hali ya kiwango kabla ya kutumia Mfumo Quadratic.

Mfano\(\PageIndex{5}\)

Tatua kwa kutumia Mfumo wa Quadratic:\(x(x+6)+4=0\).

Suluhisho:

Hatua yetu ya kwanza ni kupata equation katika fomu ya kawaida.

Jedwali 9.3.6

Kusambaza ili kupata equation katika fomu ya kawaida.
Equation hii ni sasa katika hali ya kawaida.
Kutambua maadili ya\(a,b,c\).
Andika Mfumo wa Quadratic.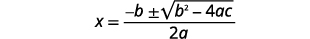
Kisha mbadala katika maadili ya\(a,b,c\).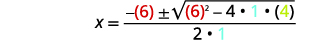
Kurahisisha.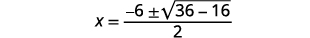
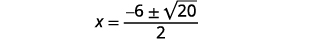Kurahisisha radical.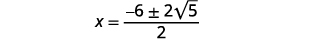
Fanya sababu ya kawaida katika nambari.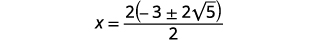
Ondoa mambo ya kawaida.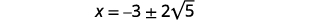
Andika kama ufumbuzi mbili.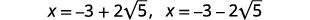
Angalia: Tunaacha hundi kwako!

Zoezi\(\PageIndex{9}\)

Tatua kwa kutumia Mfumo wa Quadratic:\(x(x+2)−5=0\).

Jibu

\(x=-1+\sqrt{6}, x=-1-\sqrt{6}\)

Zoezi\(\PageIndex{10}\)

Tatua kwa kutumia Mfumo wa Quadratic:\(3y(y−2)−3=0\).

Jibu

\(y=1+\sqrt{2}, y=1-\sqrt{2}\)

Wakati sisi kutatuliwa equations linear, kama equation alikuwa FRACTIONS nyingi mno sisi akalipa FRACTIONS kwa kuzidisha pande zote mbili za equation na LCD. Hii alitupa equation sawa - bila FRACTIONS - kutatua. Tunaweza kutumia mkakati huo na equations quadratic.

Mfano\(\PageIndex{6}\)

Tatua kwa kutumia Mfumo wa Quadratic:\(\dfrac{1}{2} u^{2}+\dfrac{2}{3} u=\dfrac{1}{3}\).

Suluhisho:

Hatua yetu ya kwanza ni kufuta sehemu ndogo.

Jedwali 9.3.7

Kuzidisha pande zote mbili na LCD\(6\),, wazi sehemu ndogo.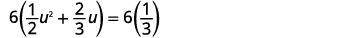
Kuzidisha.
Ondoa\(2\) kupata equation katika fomu ya kawaida.
Tambua maadili ya\(a, b\), na\(c\).
Andika Mfumo wa Quadratic.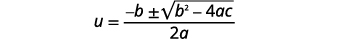
Kisha mbadala katika maadili ya\(a, b,\) na\(c\).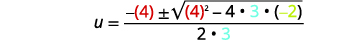
Kurahisisha.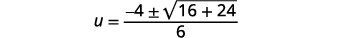
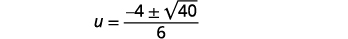Kurahisisha radical.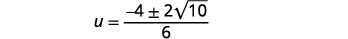
Fanya sababu ya kawaida katika nambari.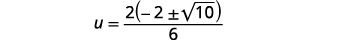
Ondoa mambo ya kawaida.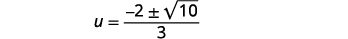
Andika upya ili kuonyesha ufumbuzi mbili.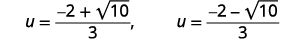
Angalia: Tunaacha hundi kwako!

Zoezi\(\PageIndex{11}\)

Tatua kwa kutumia Mfumo wa Quadratic:\(\dfrac{1}{4} c^{2}-\dfrac{1}{3} c=\dfrac{1}{12}\).

Jibu

\(c=\dfrac{2+\sqrt{7}}{3}, \quad c=\dfrac{2-\sqrt{7}}{3}\)

Zoezi\(\PageIndex{12}\)

Tatua kwa kutumia Mfumo wa Quadratic:\(\dfrac{1}{9} d^{2}-\dfrac{1}{2} d=-\dfrac{1}{3}\).

Jibu

\(d=\dfrac{9+\sqrt{33}}{4}, d=\dfrac{9-\sqrt{33}}{4}\)

Fikiria kuhusu equation\((x-3)^{2}=0\). Tunajua kutoka Zero Bidhaa Mali kwamba equation hii ina ufumbuzi moja tu,\(x=3\).

Tutaona katika mfano unaofuata jinsi ya kutumia Mfumo wa Quadratic kutatua equation ambao fomu ya kawaida ni kamili ya mraba trinomial sawa na\(0\) inatoa suluhisho moja tu. Angalia kwamba mara moja radicand ni rahisi inakuwa\(0\), ambayo inaongoza kwa suluhisho moja tu.

Mfano\(\PageIndex{7}\)

Tatua kwa kutumia Mfumo wa Quadratic:\(4 x^{2}-20 x=-25\).

Suluhisho:

Jedwali 9.3.8

Ongeza\(25\) ili kupata equation katika fomu ya kawaida.
Tambua maadili ya\(a, b\), na\(c\).
Andika formula ya quadratic.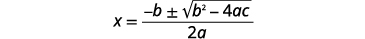
Kisha mbadala katika maadili ya\(a, b\), na\(c\).
Kurahisisha.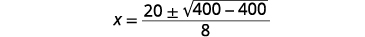
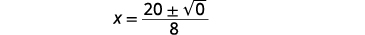Kurahisisha radical.
Kurahisisha sehemu.
Angalia: Tunaacha hundi kwako!

Je, kutambua kwamba\(4 x^{2}-20 x+25\) ni kamili mraba trinomial. Ni sawa na\((2 x-5)^{2}\)? Ikiwa unatatua\(4 x^{2}-20 x+25=0\) kwa kuzingatia na kisha kutumia Mali ya Mizizi ya Mraba, unapata matokeo sawa?

Zoezi\(\PageIndex{13}\)

Tatua kwa kutumia Mfumo wa Quadratic:\(r^{2}+10 r+25=0\).

Jibu

\(r=-5\)

Zoezi\(\PageIndex{14}\)

Tatua kwa kutumia Mfumo wa Quadratic:\(25 t^{2}-40 t=-16\).

Jibu

\(t=\dfrac{4}{5}\)

Tumia Ubaguzi kutabiri Idadi na Aina ya Ufumbuzi wa Equation ya Quadratic

Tulipotatua usawa wa quadratic katika mifano ya awali, wakati mwingine tulipata ufumbuzi wa kweli mbili, suluhisho moja halisi, na wakati mwingine ufumbuzi wawili tata. Je, kuna njia ya kutabiri idadi na aina ya ufumbuzi wa equation quadratic bila kweli kutatua equation?

Ndiyo, maneno chini ya radical ya Mfumo wa Quadratic inafanya iwe rahisi kwetu kuamua idadi na aina ya ufumbuzi. Maneno haya huitwa ubaguzi.

Ufafanuzi\(\PageIndex{2}\)

Kubagua

Kielelezo 9.3.85

Hebu tuangalie ubaguzi wa equations katika baadhi ya mifano na idadi na aina ya ufumbuzi kwa equations hizo quadratic.

Jedwali 9.3.9

Ulinganifu wa Quadratic (kwa fomu ya kawaida)	Discriminat\(b^{2}-4ac\)	Thamani ya Wabaguzi	Idadi na Aina ya Ufumbuzi
\(2 x^{2}+9 x-5=0\)	\ (b ^ {2} -4ac\) ">\(\begin{aligned} 9^{2}-& 4 \cdot 2(-5) \\ & 121 \end{aligned}\)	\(+\)	\(2\)halisi
\(4 x^{2}-20 x+25=0\)	\ (b ^ {2} -4ac\) ">\((-20)^{2}-4 \cdot 4 \cdot 25\) \(0\)	\(0\)	\(1\)halisi
\(3 p^{2}+2 p+9=0\)	\ (b ^ {2} -4ac\) ">\(2^{2}-4 \cdot 3 \cdot 9\) \(-104\)	\(-\)	\(2\)tata

Kielelezo 9.3.86

Kutumia Ubaguzi\(b^{2}-4ac\), Kuamua Idadi na Aina ya Ufumbuzi wa Equation Quadratic

Kwa equation quadratic ya fomu\(ax^{2}+bx+c=0\),\(a \neq 0\),

• Ikiwa\(b^{2}-4 a c>0\), equation ina ufumbuzi\(2\) halisi.
• kama\(b^{2}-4 a c=0\), equation ina ufumbuzi\(1\) halisi.
• ikiwa\(b^{2}-4 a c<0\), equation ina ufumbuzi\(2\) tata.

Mfano\(\PageIndex{8}\)

Kuamua idadi ya ufumbuzi kwa kila equation quadratic.

1. \(3 x^{2}+7 x-9=0\)
2. \(5 n^{2}+n+4=0\)
3. \(9 y^{2}-6 y+1=0\)

Suluhisho:

Kuamua idadi ya ufumbuzi wa kila equation quadratic, tutaangalia ubaguzi wake.

a.

\(3 x^{2}+7 x-9=0\)

Equation iko katika fomu ya kawaida, kutambua\(a, b\), na\(c\).

\(a=3, \quad b=7, \quad c=-9\)

Andika ubaguzi.

\(b^{2}-4 a c\)

Mbadala katika maadili ya\(a, b\), na\(c\).

\((7)^{2}-4 \cdot 3 \cdot(-9)\)

Kurahisisha.

\(49+108\)
\(157\)

Kwa kuwa ubaguzi ni chanya, kuna ufumbuzi\(2\) halisi wa equation.

b.

\(5 n^{2}+n+4=0\)

Equation iko katika fomu ya kawaida, kutambua\(a, b\), na\(c\).

\(a=5, \quad b=1, \quad c=4\)

Andika ubaguzi.

\(b^{2}-4 a c\)

Mbadala katika maadili ya\(a, b\), na\(c\).

\((1)^{2}-4 \cdot 5 \cdot 4\)

Kurahisisha.

\(1-80\)
\(-79\)

Kwa kuwa ubaguzi ni hasi, kuna ufumbuzi\(2\) tata wa equation.

c.

\(9 y^{2}-6 y+1=0\)

Equation iko katika fomu ya kawaida, kutambua\(a, b\), na\(c\).

\(a=9, \quad b=-6, \quad c=1\)

Andika ubaguzi.

\(b^{2}-4 a c\)

Mbadala katika maadili ya\(a, b\), na\(c\).

\((-6)^{2}-4 \cdot 9 \cdot 1\)

Kurahisisha.

\(36-36\)
\(0\)

Kwa kuwa ubaguzi ni\(0\), kuna ufumbuzi\(1\) halisi wa equation.

Zoezi\(\PageIndex{15}\)

Kuamua idadi na aina ya ufumbuzi kwa kila equation quadratic.

1. \(8 m^{2}-3 m+6=0\)
2. \(5 z^{2}+6 z-2=0\)
3. \(9 w^{2}+24 w+16=0\)

Jibu

1. \(2\)ufumbuzi tata
2. \(2\)ufumbuzi halisi
3. \(1\)suluhisho halisi

Zoezi\(\PageIndex{16}\)

Kuamua idadi na aina ya ufumbuzi kwa kila equation quadratic.

1. \(b^{2}+7 b-13=0\)
2. \(5 a^{2}-6 a+10=0\)
3. \(4 r^{2}-20 r+25=0\)

Jibu

1. \(2\)ufumbuzi halisi
2. \(2\)ufumbuzi tata
3. \(1\)suluhisho halisi

Tambua Njia sahihi zaidi ya Kutumia Kutatua Equation ya Quadratic

Sisi muhtasari mbinu nne ambazo tumezitumia kutatua equations quadratic chini.

Njia za Kutatua Ulinganifu wa Quadratic

1. Factoring
2. Mizizi ya mraba Mali
3. Kukamilisha Square
4. Mfumo wa Quadratic

Kutokana na kwamba tuna mbinu nne za kutumia kutatua equation quadratic, unaamuaje ni nani wa kutumia? Kuzingatia mara nyingi ni njia ya haraka zaidi na hivyo tunajaribu kwanza. Ikiwa equation ni\(ax^{2}=k\) au\(a(x−h)^{2}=k\) tunatumia Mizizi ya Mizizi ya Mraba. Kwa equation nyingine yoyote, pengine ni bora kutumia Mfumo Quadratic. Kumbuka, unaweza kutatua equation yoyote ya quadratic kwa kutumia Mfumo wa Quadratic, lakini sio njia rahisi zaidi.

Nini kuhusu njia ya Kukamilisha Square? Watu wengi hupata njia hiyo mbaya na hawapendi kuitumia. Tulihitaji kuiingiza katika orodha ya mbinu kwa sababu tumekamilisha mraba kwa ujumla ili kupata Mfumo wa Quadratic. Utatumia pia mchakato wa Kukamilisha Square katika maeneo mengine ya algebra.

Tambua Njia sahihi zaidi ya Kutatua Equation ya Quadratic

1. Jaribu factoring kwanza. Ikiwa sababu za quadratic kwa urahisi, njia hii ni ya haraka sana.
2. Jaribu Square Mizizi Mali ya. Kama equation inafaa fomu\(ax^{2}=k\) au\(a(x−h)^{2}=k\), inaweza kwa urahisi kutatuliwa kwa kutumia Square Mizizi Mali.
3. Tumia Mfumo wa Quadratic. Equation nyingine yoyote ya quadratic ni bora kutatuliwa kwa kutumia Mfumo wa Quadratic.

Mfano unaofuata unatumia mkakati huu kuamua jinsi ya kutatua kila equation quadratic.

Mfano\(\PageIndex{9}\)

Tambua njia sahihi zaidi ya kutumia kutatua kila equation quadratic.

1. \(5 z^{2}=17\)
2. \(4 x^{2}-12 x+9=0\)
3. \(8 u^{2}+6 u=11\)

Suluhisho:

a.

\(5z^{2}=17\)

Kwa kuwa equation ni katika\(ax^{2}=k\), njia sahihi zaidi ni kutumia Square Mizizi Mali.

b.

\(4 x^{2}-12 x+9=0\)

Tunatambua kwamba upande wa kushoto wa equation ni trinomial kamili ya mraba, na hivyo factoring itakuwa njia sahihi zaidi.

c.

\(8 u^{2}+6 u=11\)

Weka equation katika fomu ya kawaida.

\(8 u^{2}+6 u-11=0\)

Wakati mawazo yetu ya kwanza inaweza kuwa kujaribu factoring, kufikiri juu ya uwezekano wote wa majaribio na kosa njia inatuongoza kuchagua Quadratic Mfumo kama njia sahihi zaidi.

Zoezi\(\PageIndex{17}\)

Tambua njia sahihi zaidi ya kutumia kutatua kila equation quadratic.

1. \(x^{2}+6 x+8=0\)
2. \((n-3)^{2}=16\)
3. \(5 p^{2}-6 p=9\)

Jibu

1. Factoring
2. Mizizi ya mraba Mali
3. Mfumo wa Quadratic

Zoezi\(\PageIndex{18}\)

Tambua njia sahihi zaidi ya kutumia kutatua kila equation quadratic.

1. \(8 a^{2}+3 a-9=0\)
2. \(4 b^{2}+4 b+1=0\)
3. \(5 c^{2}=125\)

Jibu

1. Mfumo wa Quadratic
2. Kuweka au Mizizi ya Mizizi ya Mraba
3. Mizizi ya mraba Mali

Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi kwa kutumia Mfumo wa Quadratic.

• Kutumia Mfumo wa Quadratic
• Tatua Equation ya Quadratic Kutumia Mfumo wa Quadratic na Solutions Complex
• Ubaguzi katika Mfumo wa Quadratic

Dhana muhimu

• Mfumo wa Quadratic
  • Ufumbuzi wa equation quadratic ya fomu\(a x^{2}+b x+c=0, a \neq 0\) hutolewa na formula:

    \(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)

• Jinsi ya kutatua equation quadratic kutumia Mfumo Quadratic.
  1. Andika equation quadratic katika fomu ya kawaida,\(a x^{2}+b x+c=0\). Kutambua maadili ya\(a, b, c\).
  2. Andika Mfumo wa Quadratic. Kisha mbadala katika maadili ya\(a, b, c\).
  3. Kurahisisha.
  4. Angalia ufumbuzi.
• Kutumia Discriminant,\(b^{2}-4 a c\), Kuamua Idadi na Aina ya Solutions ya Equation Quadratic
  • Kwa equation quadratic ya fomu\(a x^{2}+b x+c=0, a \neq 0\),
    • Ikiwa\(b^{2}-4 a c>0\), equation ina ufumbuzi\(2\) halisi.
    • Kama\(b^{2}-4 a c=0\), equation ina ufumbuzi\(1\) halisi.
    • Ikiwa\(b^{2}-4 a c<0\), equation ina ufumbuzi\(2\) tata.
• Njia za Kutatua Ulinganifu wa Quadratic:
  • Factoring
  • Mizizi ya mraba Mali
  • Kukamilisha Square
  • Mfumo wa Quadratic
• Jinsi ya kutambua njia sahihi zaidi ya kutatua equation quadratic.
  1. Jaribu factoring kwanza. Ikiwa sababu za quadratic kwa urahisi, njia hii ni ya haraka sana.
  2. Jaribu Square Mizizi Mali ya. Kama equation inafaa fomu\(a x^{2}=k\) au\(a(x-h)^{2}=k\), inaweza kwa urahisi kutatuliwa kwa kutumia Square Mizizi Mali.
  3. Tumia Mfumo wa Quadratic. Equation nyingine yoyote ya quadratic ni bora kutatuliwa kwa kutumia Mfumo wa Quadratic.

faharasa

kubagua

Katika Mfumo wa Quadratic\(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\), wingi\(b^{2}-4 a c\) huitwa ubaguzi.