Skip to main content
Global

9.3: Tatua Ulinganisho wa Quadratic kwa Kukamilisha Mraba

  1. Last updated
  2. Save as PDF
  • Page ID
    176563

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Jaza mraba wa kujieleza kwa binomial
    • Tatua usawa wa quadratic wa fomu\(x^{2}+bx+c=0\) kwa kukamilisha mraba
    • Tatua usawa wa quadratic wa fomu\(ax^{2}+bx+c=0\) kwa kukamilisha mraba

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Panua:\((x+9)^{2}\).
      Kama amekosa tatizo hili, mapitio Mfano 5.32.
    2. Sababu\(y^{2}-14 y+49\).
      Ikiwa umekosa tatizo hili, kagua Mfano 6.9.
    3. Sababu\(5 n^{2}+40 n+80\).
      Kama amekosa tatizo hili, mapitio Mfano 6.14.

    Hadi sasa tuna kutatuliwa equations quadratic kwa factoring na kutumia Mizizi Square Mali. Katika sehemu hii, tutatatua equations quadratic kwa mchakato unaoitwa kukamilisha mraba, ambayo ni muhimu kwa kazi yetu juu ya conics baadaye.

    Kukamilisha Square ya kujieleza Binomial

    Katika sehemu ya mwisho, tuliweza kutumia Mizizi ya Square Mali ili kutatua equation\((y-7)^{2}=12\) kwa sababu upande wa kushoto ulikuwa mraba kamili.

    \(\begin{aligned}(y-7)^{2} &=12 \\ y-7 &=\pm \sqrt{12} \\ y-7 &=\pm 2 \sqrt{3} \\ y &=7 \pm 2 \sqrt{3} \end{aligned}\)

    Sisi pia kutatuliwa equation ambayo upande wa kushoto ilikuwa kamili mraba trinomial, lakini tulikuwa na kuandika upya\((x−k)^{2}\) fomu ili kutumia Mizizi Square Mali.

    \(\begin{aligned} x^{2}-10 x+25 &=18 \\(x-5)^{2} &=18 \end{aligned}\)

    Nini kinatokea kama variable si sehemu ya mraba kamili? Je, tunaweza kutumia algebra kufanya mraba kamili?

    Hebu tuangalie mifano miwili ili kutusaidia kutambua ruwaza.

    \(\begin{array}{cc}{(x+9)^{2}} & {(y-7)^{2}} \\ {(x+9 )(x+9)} & {(y-7)(y-7)} \\ {x^{2}+9 x+9 x+81} & {y^{2}-7 y-7 y+49} \\ {x^{2}+18 x+81} & {y^{2}-14 y+49}\end{array}\)

    Tunarudia ruwaza hapa kwa ajili ya kumbukumbu.

    Ufafanuzi\(\PageIndex{1}\): Binomial Squares Pattern

    Kama\(a\) na\(b\) ni idadi halisi,

    Kiasi a plus b squared sawa na mraba pamoja na 2 b pamoja na B2 ambapo mraba binomial ni sawa na muda wa kwanza mraba pamoja na mara 2 bidhaa ya maneno pamoja na muda wa pili squared. Kiasi bala b mraba sawa na mraba bala 2 b pamoja na B2 ambapo mraba binomial sawa na muda wa kwanza mraba minus mara 2 bidhaa ya maneno pamoja na muda wa pili squared.

    Tunaweza kutumia ruwaza hii “kufanya” mraba kamilifu.

    Tutaanza na maneno\(x^{2}+6 x\). Kwa kuwa kuna ishara ya pamoja kati ya maneno mawili, tutatumia\((a+b)^{2}\) mfano,\(a^{2}+2 a b+b^{2}=(a+b)^{2}\).

    Maneno kamili ya mraba mraba pamoja na 2 b pamoja na b squared inavyoonyeshwa juu ya kujieleza x squared pamoja 6x pamoja na haijulikani kuruhusu kulinganisha maneno yanayofanana ya maneno.

    Hatimaye tunahitaji kupata muda wa mwisho wa trinomial hii ambayo itafanya kuwa mraba kamili ya trinomial. Ili kufanya hivyo tutahitaji kupata\(b\). Lakini kwanza tunaanza na kuamua\(a\). Kumbuka kwamba muda wa kwanza wa\(x^{2}+6x\) ni mraba,\(x^{2}\). Hii inatuambia kwamba\(a=x\).

    Maneno kamili ya mraba mraba pamoja na 2 b pamoja na b squared inavyoonyeshwa juu ya kujieleza x mraba pamoja na 2 x b + b squared. Kumbuka kuwa x imekuwa kubadilishwa kwa katika equation pili na kulinganisha suala sambamba.

    Nini idadi,\(b\), wakati kuzidisha na\(2x\) anatoa\(6x\)? Inapaswa kuwa\(3\), ambayo ni\(\frac{1}{2}(6)\). Hivyo\(b=3\).

    Maneno kamili ya mraba mraba pamoja na 2 b pamoja na b squared inavyoonyeshwa juu ya kujieleza x squared pamoja mara 2 mara 3 x pamoja thamani haijulikani ili kusaidia kulinganisha maneno.

    Sasa kukamilisha trinomial kamili ya mraba, tutapata muda wa mwisho kwa mraba\(b\), ambayo ni\(3^{2}=9\).

    Maneno kamili ya mraba mraba pamoja na 2 b pamoja na b squared inavyoonyeshwa juu ya kujieleza x squared pamoja 6 x plus 9.

    Sasa tunaweza sababu.

    Maneno yaliyotambuliwa, mraba wa pamoja na b, inavyoonyeshwa juu ya mraba wa maneno x + 3.

    Hivyo tuligundua kwamba kuongeza\(9\) kwa\(x^{2}+6 x\) 'kutimiza mraba', na sisi kuandika kama\((x+3)^{2}\).

    Jinsi ya: Kukamilisha Square of\(x^{2}+bx\)
    1. Tambua\(b\), mgawo wa\(x\).
    2. Kupata\(\left(\frac{1}{2} b\right)^{2}\), idadi ya kukamilisha mraba.
    3. Kuongeza\(\left(\frac{1}{2} b\right)^{2}\) kwa\(x^{2}+bx\).
    4. Fanya trinomial mraba kamili, uiandike kama mraba wa binomial.
    Mfano\(\PageIndex{1}\)

    Kukamilisha mraba kufanya trinomial kamili ya mraba. Kisha kuandika matokeo kama mraba wa binomial.

    1. \(x^{2}-26 x\)
    2. \(y^{2}-9 y\)
    3. \(n^{2}+\frac{1}{2} n\)

    Suluhisho:

    a.

      .
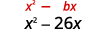    Mgawo wa\(x\) ni -26.  

    Kupata\(\left(\frac{1}{2} b\right)^{2}\).

    \(\left(\frac{1}{2} \cdot(-26)\right)^{2}\)
    \((13)^{2}\)
    169

    		  
    \(169\)Ongeza kwenye binomial ili kukamilisha mraba.

    \(x^{2}-26 x+169\)
    Fanya trinomial mraba kamili, uiandike kama mraba wa binomial.

    \((x-13)^{2}\)

    b.

      .
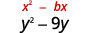    Mgawo wa\(y\) ni\(-9\).  

    Kupata\(\left(\frac{1}{2} b\right)^{2}\).

    \(\left(\frac{1}{2} \cdot(-9)\right)^{2}\)
    \(\left(-\frac{9}{2}\right)^{2}\)
    \(\frac{81}{4}\)

    		  
    \(\frac{81}{4}\)Ongeza kwenye binomial ili kukamilisha mraba.

    \(y^{2}-9 y+\frac{81}{4}\)
    Fanya trinomial mraba kamili, uiandike kama mraba wa binomial.

    \(\left(y-\frac{9}{2}\right)^{2}\)

    c.

      .
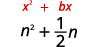    Mgawo wa\(n\) ni\(\frac{1}{2}\).  

    Kupata\(\left(\frac{1}{2} b\right)^{2}\).

    \(\left(\frac{1}{2} \cdot \frac{1}{2}\right)^{2}\)
    \(\left(\frac{1}{4}\right)^{2}\)
    \(\frac{1}{16}\)

    		  
    \(\frac{1}{16}\)Ongeza kwenye binomial ili kukamilisha mraba. \(n^{2}+\frac{1}{2} n+\frac{1}{16}\)
    Andika upya kama mraba wa binomial. \(\left(n+\frac{1}{4}\right)^{2}\)
    Zoezi\(\PageIndex{1}\)

    Kukamilisha mraba kufanya trinomial kamili ya mraba. Kisha kuandika matokeo kama mraba wa binomial.

    1. \(a^{2}-20 a\)
    2. \(m^{2}-5 m\)
    3. \(p^{2}+\frac{1}{4} p\)
    Jibu
    1. \((a-10)^{2}\)
    2. \(\left(b-\frac{5}{2}\right)^{2}\)
    3. \(\left(p+\frac{1}{8}\right)^{2}\)
    Zoezi\(\PageIndex{2}\)

    Kukamilisha mraba kufanya trinomial kamili ya mraba. Kisha kuandika matokeo kama mraba wa binomial.

    1. \(b^{2}-4 b\)
    2. \(n^{2}+13 n\)
    3. \(q^{2}-\frac{2}{3} q\)
    Jibu
    1. \((b-2)^{2}\)
    2. \(\left(n+\frac{13}{2}\right)^{2}\)
    3. \(\left(q-\frac{1}{3}\right)^{2}\)

    Tatua Ulinganisho wa Quadratic wa Fomu\(x^{2}+bx+c=0\) kwa Kukamilisha Square

    Katika kutatua equations, lazima daima kufanya kitu kimoja kwa pande zote mbili za equation. Hii ni kweli, bila shaka, wakati sisi kutatua equation quadratic kwa kukamilisha mraba pia. Wakati sisi kuongeza mrefu kwa upande mmoja wa equation kufanya kamili mraba trinomial, ni lazima pia kuongeza muda huo kwa upande wa pili wa equation.

    Kwa mfano, kama sisi kuanza na equation\(x^{2}+6x=40\), na tunataka kukamilisha mraba upande wa kushoto, sisi kuongeza 9 kwa pande zote mbili za equation.

      .
      .
      .
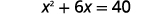    \(9\)Ongeza pande zote mbili ili kukamilisha mraba. .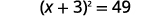

    Sasa equation iko katika fomu ya kutatua kutumia Mizizi ya Mizizi ya Mraba! Kukamilisha mraba ni njia ya kubadilisha equation katika fomu tunahitaji kuwa na uwezo wa kutumia Mizizi ya Mraba Mali.

    Mfano\(\PageIndex{2}\) How to Solve a Quadratic Equation of the Form \(x^{2}+bx+x=0\) by Completing the Square

    Tatua kwa kukamilisha mraba:\(x^{2}+8x=48\).

    Suluhisho:

    Hatua ya 1: Kutenga masharti variable upande mmoja na masharti ya mara kwa mara kwa upande mwingine. Equation hii ina vigezo vyote upande wa kushoto. \(\begin{array}{l}{\color{red}{x^{2}+b x\quad\:\:\: c }} \\ {x^{2}+8 x=48}\end{array}\)
    Hatua ya 2: Tafuta\(\left(\frac{1}{2} \cdot b\right)^{2}\), nambari ya kukamilisha mraba. Kuongeza kwa pande zote mbili za equation.

    Chukua nusu\(8\) na mraba.

    \(4^{2}=16\)

    \(16\)Kuongeza pande zote mbili za equation.

    \(x^{2}+8 x+\frac{}{\color{red}{\left(\frac{1}{2} \cdot 8\right)^{2}}}\color{black}{=}48 \)

    \(x^{2}+8 x\color{red}{+16}\color{black}{=}48\color{red}{+16}\)
    Hatua ya 3: Fanya trinomial mraba kamili kama mraba binomial.

    \(x^{2}+8 x+16=(x+4)^{2}\)

    Ongeza masharti juu ya haki.

    		 \((x+4)^{2}=64\)
    Hatua ya 4: Tumia Mizizi ya Mizizi ya Mraba.   \(x+4=\pm \sqrt{64}\)
    Hatua ya 5: Kurahisisha radical na kisha kutatua equations mbili kusababisha.  

    \(x+4=\pm 8\)

    \(\begin{aligned} x+4 &=8 \quad x+4=-8 \\ x &=4 \quad\quad\:\:\: x=-12 \end{aligned}\)
    Hatua ya 6: Angalia ufumbuzi. Weka kila jibu katika equation ya awali ili uangalie. Mbadala\(x=4\) na\(x=-12\).

    \(\begin{array}{r}{x^{2}+8 x=48} \\ {(\color{red}{4}\color{black}{)}^{2}+8(\color{red}{4}\color{black}{)} \stackrel{?}{=} 48} \\ {16+32\stackrel{?}{=}48} \\ {48=48}\end{array}\)

    \(\begin{array}{r}{x^{2}+8 x=48} \\ {(\color{red}{-12}\color{black}{)}^{2}+8(\color{red}{-12}\color{black}{)}\stackrel{?}{=} 48} \\ {144-96 \stackrel{?}{=} 48} \\ {48=48}\end{array}\)
    Zoezi\(\PageIndex{3}\)

    Tatua kwa kukamilisha mraba:\(x^{2}+4 x=5\).

    Jibu

    \(x=-5, x=-1\)

    Zoezi\(\PageIndex{4}\)

    Tatua kwa kukamilisha mraba:\(y^{2}−10y=−9\).

    Jibu

    \(y=1, y=9\)

    Hatua za kutatua equation ya quadratic kwa kukamilisha mraba zimeorodheshwa hapa.

    Tatua Equation ya Quadratic ya Fomu\(x^{2}+bx+c=0\) kwa Kukamilisha Square

    1. Sulua maneno ya kutofautiana kwa upande mmoja na masharti ya mara kwa mara kwa upande mwingine.
    2. Kupata\(\left(\frac{1}{2} \cdot b\right)^{2}\), idadi zinahitajika kukamilisha mraba. Kuongeza kwa pande zote mbili za equation.
    3. Fanya mraba kamili ya trinomial, uiandike kama mraba wa binomial upande wa kushoto na kurahisisha kwa kuongeza maneno upande wa kulia
    4. Tumia Mizizi ya Mizizi ya Mraba.
    5. Kurahisisha radical na kisha kutatua equations mbili kusababisha.
    6. Angalia ufumbuzi.

    Wakati sisi kutatua equation kwa kukamilisha mraba, majibu si mara zote kuwa integers.

    Mfano\(\PageIndex{3}\)

    Tatua kwa kukamilisha mraba:\(x^{2}+4 x=-21\).

    Suluhisho:

      .

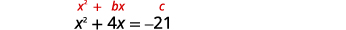    Masharti ya kutofautiana ni upande wa kushoto.

    Chukua nusu\(4\) na mraba.

    		 .
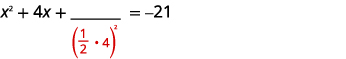    \(\left(\frac{1}{2}(4)\right)^{2}=4\)  
    \(4\)Ongeza pande zote mbili. .
    Fanya trinomial mraba kamili, uiandike kama mraba wa binomial. .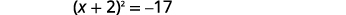
    Tumia Mizizi ya Mizizi ya Mraba. .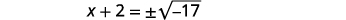
    Kurahisisha kutumia namba tata. .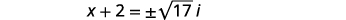
    Ondoa\(2\) kutoka kila upande. .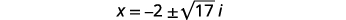
    Andika upya ili kuonyesha ufumbuzi mbili. .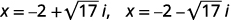
    Tunaacha hundi kwako.  
    Zoezi\(\PageIndex{5}\)

    Tatua kwa kukamilisha mraba:\(y^{2}-10 y=-35\).

    Jibu

    \(y=5+\sqrt{15} i, y=5-\sqrt{15 i}\)

    Zoezi\(\PageIndex{6}\)

    Tatua kwa kukamilisha mraba:\(z^{2}+8 z=-19\).

    Jibu

    \(z=-4+\sqrt{3} i, z=-4-\sqrt{3} i\)

    Katika mfano uliopita, ufumbuzi wetu ulikuwa namba ngumu. Katika mfano unaofuata, ufumbuzi utakuwa nambari zisizo na maana.

    Mfano\(\PageIndex{4}\)

    Tatua kwa kukamilisha mraba:\(y^{2}-18 y=-6\).

    Suluhisho:

      .
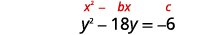    Masharti ya kutofautiana ni upande wa kushoto. Chukua nusu\(-18\) na mraba.
    \(\left(\frac{1}{2}(-18)\right)^{2}=81\) .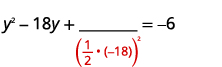
    \(81\)Ongeza pande zote mbili. .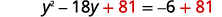
    Fanya trinomial mraba kamili, uiandike kama mraba wa binomial. .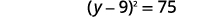
    Tumia Mizizi ya Mizizi ya Mraba. .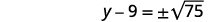
    Kurahisisha radical. .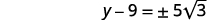
    Kutatua kwa\(y\). .

    Angalia.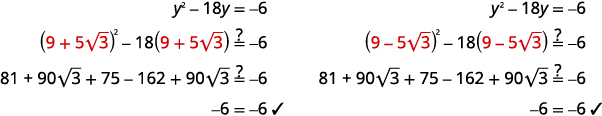

    .
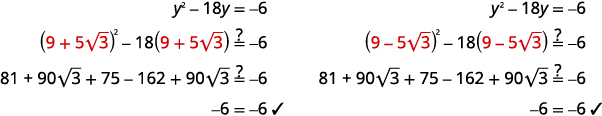    Kielelezo 9.2.35
    		 .

    Njia nyingine ya kuangalia hii itakuwa kutumia calculator. Tathmini\(y^{2}−18y\) kwa ufumbuzi wote. Jibu linapaswa kuwa\(−6\).

    Zoezi\(\PageIndex{7}\)

    Tatua kwa kukamilisha mraba:\(x^{2}-16 x=-16\).

    Jibu

    \(x=8+4 \sqrt{3}, x=8-4 \sqrt{3}\)

    Zoezi\(\PageIndex{8}\)

    Tatua kwa kukamilisha mraba:\(y^{2}+8 y=11\).

    Jibu

    \(y=-4+3 \sqrt{3}, y=-4-3 \sqrt{3}\)

    Tutaanza mfano unaofuata kwa kutenganisha maneno ya kutofautiana upande wa kushoto wa equation.

    Mfano\(\PageIndex{5}\)

    Tatua kwa kukamilisha mraba:\(x^{2}+10 x+4=15\).

    Suluhisho:

      .
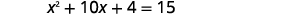    Sulua maneno ya kutofautiana upande wa kushoto. Ondoa\(4\) ili kupata maneno ya mara kwa mara upande wa kulia. .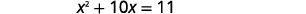
    Chukua nusu\(10\) na mraba.  
    \(\left(\frac{1}{2}(10)\right)^{2}=25\) .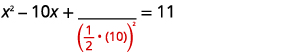
    \(25\)Ongeza pande zote mbili. .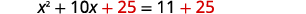
    Fanya trinomial mraba kamili, uiandike kama mraba wa binomial. .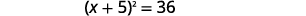
    Tumia Mizizi ya Mizizi ya Mraba. .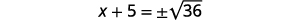
    Kurahisisha radical. .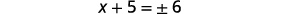
    Kutatua kwa\(x\). .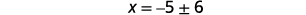
    Andika upya ili kuonyesha ufumbuzi mbili. .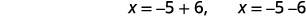
    Tatua equations. .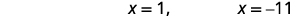

    Angalia: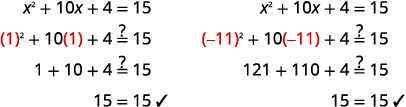

    .
    Kielelezo 9.2.47
    		  
    Zoezi\(\PageIndex{9}\)

    Tatua kwa kukamilisha mraba:\(a^{2}+4 a+9=30\).

    Jibu

    \(a=-7, a=3\)

    Zoezi\(\PageIndex{10}\)

    Tatua kwa kukamilisha mraba:\(b^{2}+8 b-4=16\).

    Jibu

    \(b=-10, b=2\)

    Ili kutatua equation ijayo, ni lazima kwanza kukusanya maneno yote variable upande wa kushoto wa equation. Kisha tunaendelea kama tulivyofanya katika mifano ya awali.

    Mfano\(\PageIndex{6}\)

    Tatua kwa kukamilisha mraba:\(n^{2}=3 n+11\).

    Suluhisho:

      .
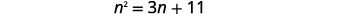    Ondoa\(3n\) ili kupata maneno ya kutofautiana upande wa kushoto. .
    Chukua nusu\(-3\) na mraba.  
    \(\left(\frac{1}{2}(-3)\right)^{2}=\frac{9}{4}\) .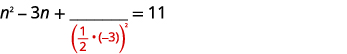
    \(\frac{9}{4}\)Ongeza pande zote mbili. .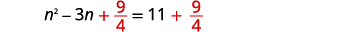
    Fanya trinomial mraba kamili, uiandike kama mraba wa binomial. .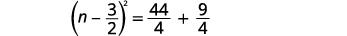
    Ongeza sehemu ndogo upande wa kulia. .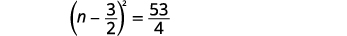
    Tumia Mizizi ya Mizizi ya Mraba. .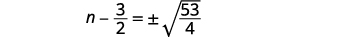
    Kurahisisha radical. .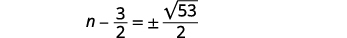
    Kutatua kwa\(n\). .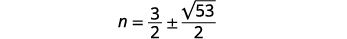
    Andika upya ili kuonyesha ufumbuzi mbili. .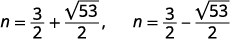

    Angalia:

    Tunaacha hundi kwako!

    		  
    Zoezi\(\PageIndex{11}\)

    Tatua kwa kukamilisha mraba:\(p^{2}=5 p+9\).

    Jibu

    \(p=\frac{5}{2}+\frac{\sqrt{61}}{2}, p=\frac{5}{2}-\frac{\sqrt{61}}{2}\)

    Zoezi\(\PageIndex{12}\)

    Tatua kwa kukamilisha mraba:\(q^{2}=7 q-3\).

    Jibu

    \(q=\frac{7}{2}+\frac{\sqrt{37}}{2}, q=\frac{7}{2}-\frac{\sqrt{37}}{2}\)

    Kumbuka kwamba upande wa kushoto wa equation ya ni katika hali factored. Lakini upande wa kulia sio sifuri. Kwa hivyo, hatuwezi kutumia mali ya Bidhaa ya Zero kwani inasema “Ikiwa\(a⋅b=0\), basi\(a=0\) au\(b=0\).” Badala yake, tunazidisha mambo na kisha kuweka equation katika fomu ya kawaida ya kutatua kwa kukamilisha mraba.

    Mfano\(\PageIndex{7}\)

    Tatua kwa kukamilisha mraba:\((x-3)(x+5)=9\).

    Suluhisho:

      .
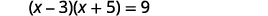    Sisi nyingi binomials upande wa kushoto. .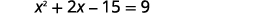
    Ongeza\(15\) kutenganisha masharti ya mara kwa mara juu ya haki. .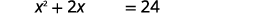
    Chukua nusu\(2\) na mraba.  
    \(\left(\frac{1}{2} \cdot(2)\right)^{2}=1\) .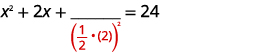
    \(1\)Ongeza pande zote mbili. .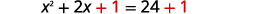
    Fanya trinomial mraba kamili, uiandike kama mraba wa binomial. .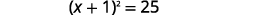
    Tumia Mizizi ya Mizizi ya Mraba. .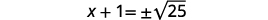
    Kutatua kwa\(x\). .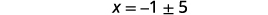
    Andika upya ili kuonyesha ufumbuzi mbili. .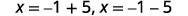
    Kurahisisha. .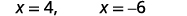

    Angalia:

    Tunaacha hundi kwako!

    		  
    Zoezi\(\PageIndex{13}\)

    Tatua kwa kukamilisha mraba:\((c-2)(c+8)=11\).

    Jibu

    \(c=-9, c=3\)

    Zoezi\(\PageIndex{14}\)

    Tatua kwa kukamilisha mraba:\((d-7)(d+3)=56\).

    Jibu

    \(d=11, d=-7\)

    Tatua Ulinganisho wa Quadratic wa Fomu\(ax^{2}+bx+c=0\) kwa Kukamilisha Square

    Mchakato wa kukamilisha mraba unafanya kazi bora wakati mgawo wa\(x^{2}\) ni\(1\), hivyo upande wa kushoto wa equation ni wa fomu\(x^{2}+bx+c\). Ikiwa\(x^{2}\) neno lina mgawo mwingine isipokuwa\(1\), tunachukua hatua za awali ili kufanya mgawo sawa na\(1\).

    Wakati mwingine mgawo unaweza kuzingatiwa kutoka kwa masharti yote matatu ya trinomial. Hii itakuwa mkakati wetu katika mfano unaofuata.

    Mfano\(\PageIndex{8}\)

    Tatua kwa kukamilisha mraba:\(3 x^{2}-12 x-15=0\).

    Suluhisho:

    Ili kukamilisha mraba, tunahitaji mgawo\(x^{2}\) wa kuwa moja. Ikiwa tunazingatia mgawo wa\(x^{2}\) sababu ya kawaida, tunaweza kuendelea na kutatua equation kwa kukamilisha mraba.

      .
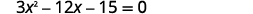    Factor nje kubwa ya kawaida sababu. .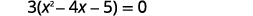
    Gawanya pande zote mbili\(3\) kwa kutenganisha trinomial na mgawo\(1\). .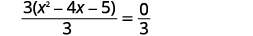
    Kurahisisha. .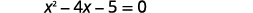
    Ongeza\(5\) ili kupata maneno ya mara kwa mara upande wa kulia. .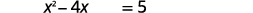
    Chukua nusu ya\(4\) na mraba.  
    \(\left(\frac{1}{2}(-4)\right)^{2}=4\) .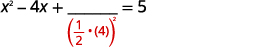
    \(4\)Ongeza pande zote mbili. .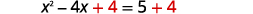
    Fanya trinomial mraba kamili, uiandike kama mraba wa binomial. .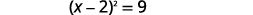
    Tumia Mizizi ya Mizizi ya Mraba. .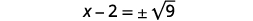
    Kutatua kwa\(x\). .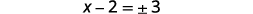
    Andika upya ili kuonyesha ufumbuzi mbili. .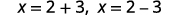
    Kurahisisha. .

    Angalia: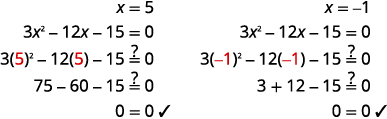

    .
    Kielelezo 9.2.80
    		  
    Zoezi\(\PageIndex{15}\)

    Tatua kwa kukamilisha mraba:\(2 m^{2}+16 m+14=0\).

    Jibu

    \(m=-7, m=-1\)

    Zoezi\(\PageIndex{16}\)

    Tatua kwa kukamilisha mraba:\(4 n^{2}-24 n-56=8\).

    Jibu

    \(n=-2, n=8\)

    Ili kukamilisha mraba, mgawo wa\(x^{2}\) lazima uwe\(1\). Wakati mgawo wa kuongoza sio sababu ya maneno yote, tutagawanya pande zote mbili za equation na mgawo wa kuongoza! Hii itatupa sehemu ya mgawo wa pili. Tumeona jinsi ya kukamilisha mraba na sehemu ndogo katika sehemu hii.

    Mfano\(\PageIndex{9}\)

    Tatua kwa kukamilisha mraba:\(2 x^{2}-3 x=20\).

    Suluhisho:

    Ili kukamilisha mraba tunahitaji mgawo\(x^{2}\) wa kuwa moja. Tutagawanya pande zote mbili za equation na mgawo wa\(x^{2}\). Kisha tunaweza kuendelea na kutatua equation kwa kukamilisha mraba.

      .
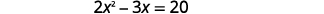    Gawanya pande zote mbili na\(2\) kupata\(x^{2}\) mgawo wa kuwa\(1\). .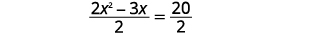
    Kurahisisha. .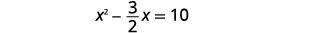
    Chukua nusu ya\(-\frac{3}{2}\) na mraba.  
    \(\left(\frac{1}{2}\left(-\frac{3}{2}\right)\right)^{2}=\frac{9}{16}\) .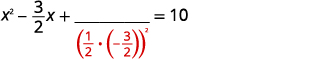
    \(\frac{9}{16}\)Ongeza pande zote mbili. .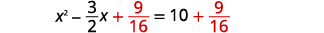
    Fanya trinomial mraba kamili, uiandike kama mraba wa binomial. .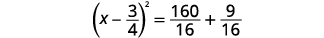
    Ongeza sehemu ndogo upande wa kulia. .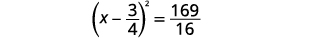
    Tumia Mizizi ya Mizizi ya Mraba. .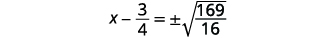
    Kurahisisha radical. .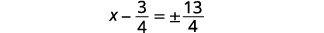
    Kutatua kwa\(x\). .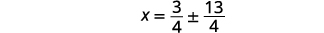
    Andika upya ili kuonyesha ufumbuzi mbili. .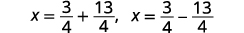
    Kurahisisha. .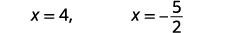

    Angalia:

    Tunaacha hundi kwako!

    		  
    Zoezi\(\PageIndex{17}\)

    Tatua kwa kukamilisha mraba:\(3 r^{2}-2 r=21\).

    Jibu

    \(r=-\frac{7}{3}, r=3\)

    Zoezi\(\PageIndex{18}\)

    Tatua kwa kukamilisha mraba:\(4 t^{2}+2 t=20\).

    Jibu

    \(t=-\frac{5}{2}, t=2\)

    Sasa\(1\) kwa kuwa tumeona kwamba mgawo wa\(x^{2}\) lazima iwe kwetu kukamilisha mraba, tunasasisha utaratibu wetu wa kutatua equation ya quadratic kwa kukamilisha mraba ili kuingiza equations ya fomu\(a x^{2}+b x+c=0\).

    Jinsi ya: Tatua Equation ya Quadratic ya Fomu\(a x^{2}+b x+c=0\) by Completing the Square
    1. Gawanya na aa ili kufanya mgawo wa\(x^{2}\) muda\(1\).
    2. Sulua maneno ya kutofautiana kwa upande mmoja na masharti ya mara kwa mara kwa upande mwingine.
    3. Kupata\(\left(\frac{1}{2} \cdot b\right)^{2}\), idadi zinahitajika kukamilisha mraba. Kuongeza kwa pande zote mbili za equation.
    4. Fanya mraba kamili ya trinomial, uiandike kama mraba wa binomial upande wa kushoto na kurahisisha kwa kuongeza maneno upande wa kulia
    5. Tumia Mizizi ya Mizizi ya Mraba.
    6. Kurahisisha radical na kisha kutatua equations mbili kusababisha.
    7. Angalia ufumbuzi.
    Mfano\(\PageIndex{10}\)

    Tatua kwa kukamilisha mraba:\(3 x^{2}+2 x=4\).

    Suluhisho:

    Tena, hatua yetu ya kwanza itakuwa kufanya mgawo wa\(x^{2}\) moja. Kwa kugawa pande zote mbili za equation na mgawo wa\(x^{2}\), tunaweza kisha kuendelea na kutatua equation kwa kukamilisha mraba.

      .
    Gawanya pande zote mbili\(3\) kwa kufanya mgawo wa\(x^{2}\) sawa\(1\). .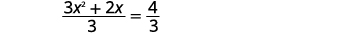
    Kurahisisha. .
    Chukua nusu ya\(\frac{2}{3}\) na mraba.  
    \(\left(\frac{1}{2} \cdot \frac{2}{3}\right)^{2}=\frac{1}{9}\) .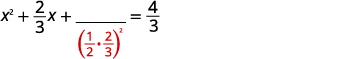
    \(\frac{1}{9}\)Ongeza pande zote mbili. .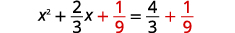
    Fanya trinomial mraba kamili, uiandike kama mraba wa binomial. .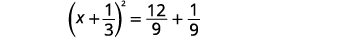
    Tumia Mizizi ya Mizizi ya Mraba. .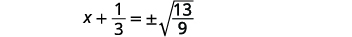
    Kurahisisha radical. .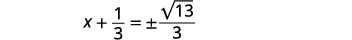
    Kutatua kwa\(x\). .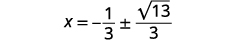
    Andika upya ili kuonyesha ufumbuzi mbili. .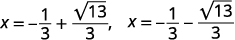

    Angalia:

    Tunaacha hundi kwako!

    		  
    Zoezi\(\PageIndex{19}\)

    Tatua kwa kukamilisha mraba:\(4 x^{2}+3 x=2\).

    Jibu

    \(x=-\frac{3}{8}+\frac{\sqrt{41}}{8}, x=-\frac{3}{8}-\frac{\sqrt{41}}{8}\)

    Zoezi\(\PageIndex{20}\)

    Tatua kwa kukamilisha mraba:\(3 y^{2}-10 y=-5\).

    Jibu

    \(y=\frac{5}{3}+\frac{\sqrt{10}}{3}, y=\frac{5}{3}-\frac{\sqrt{10}}{3}\)

    Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi kwa kukamilisha mraba.

    Dhana muhimu

    • Binomial Mraba Pattern
      Kama\(a\) na\(b\) ni idadi halisi,
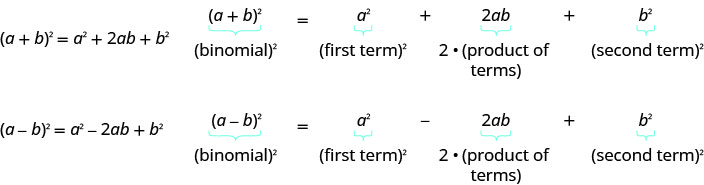
    Kiasi a plus b squared sawa na mraba pamoja na 2 b pamoja na B2 ambapo mraba binomial ni sawa na muda wa kwanza mraba pamoja na mara 2 bidhaa ya maneno pamoja na muda wa pili squared. Kiasi bala b mraba sawa na mraba bala 2 b pamoja na B2 ambapo mraba binomial sawa na muda wa kwanza mraba minus mara 2 bidhaa ya maneno pamoja na muda wa pili squared.
    • Jinsi ya Kukamilisha Square
      1. Tambua\(b\), mgawo wa\(x\).
      2. Kupata\(\left(\frac{1}{2} b\right)^{2}\), idadi ya kukamilisha mraba.
      3. Ongeza\(\left(\frac{1}{2} b\right)^{2}\) kwenye\(x^{2}+bx\)
      4. Andika upya trinomial kama mraba wa binomial
    • Jinsi ya kutatua equation quadratic ya fomu \(a x^{2}+b x+c=0\)kwa kukamilisha mraba.
      1. Gawanya na\(a\) kufanya mgawo wa\(x^{2}\) muda\(1\).
      2. Sulua maneno ya kutofautiana kwa upande mmoja na masharti ya mara kwa mara kwa upande mwingine.
      3. Kupata\(\left(\frac{1}{2} \cdot b\right)^{2}\), idadi zinahitajika kukamilisha mraba. Kuongeza kwa pande zote mbili za equation.
      4. Fanya trinomial mraba kamili, uiandike kama mraba wa binomial upande wa kushoto na kurahisisha kwa kuongeza maneno upande wa kulia.
      5. Tumia Mizizi ya Mizizi ya Mraba.
      6. Kurahisisha radical na kisha kutatua equations mbili kusababisha.
      7. Angalia ufumbuzi.