9.2: Tatua usawa wa Quadratic Kutumia Mali ya Mizizi ya Mraba

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Tatua usawa wa quadratic wa fomu kwa\(ax^{2}=k\) kutumia Mali ya Mizizi ya Mraba
• Tatua usawa wa quadratic wa fomu kwa\(a(x–h)^{2}=k\) kutumia Mali ya Mizizi ya Mraba

Kabla ya kuanza, fanya jaribio hili la utayari.

1. Kurahisisha:\(\sqrt{128}\).
   Kama amekosa tatizo hili, mapitio Mfano 8.13.
2. Kurahisisha:\(\sqrt{\frac{32}{5}}\).
   Kama amekosa tatizo hili, mapitio Mfano 8.50.
3. Sababu:\(9 x^{2}-12 x+4\).
   Kama amekosa tatizo hili, mapitio Mfano 6.23.

equation quadratic ni equation ya fomu\(a x^{2}+b x+c=0\), ambapo\(a≠0\). Ulinganifu wa Quadratic hutofautiana na usawa wa mstari kwa kuingiza muda wa quadratic na kutofautiana kukulia kwa nguvu ya pili ya fomu\(ax^{2}\). Tunatumia mbinu tofauti kutatua equations quadratic kuliko equations linear, kwa sababu tu kuongeza, kuondoa, kuzidisha, na kugawa maneno si kutenganisha kutofautiana.

Tumeona kwamba baadhi ya equations quadratic inaweza kutatuliwa kwa factoring. Katika sura hii, tutajifunza njia nyingine tatu za kutumia ikiwa equation ya quadratic haiwezi kuhesabiwa.

Tatua Ulinganisho wa Quadratic wa Fomu kwa\(ax^{2}=k\) kutumia Mali ya Mizizi ya Mraba

Tayari tumetatua equations za quadratic kwa kuzingatia. Hebu tathmini jinsi tulivyotumia factoring kutatua equation quadratic\(x^{2}=9\).

\(x^{2}=9\)

Weka equation katika fomu ya kawaida.

\(x^{2}-9=0\)

Sababu tofauti ya mraba.

\((x-3)(x+3)=0\)

Tumia mali ya Zero Product.

\(x-3=0 \quad x-3=0\)

Kutatua kila equation.

\(x=3 \quad x=-3\)

Tunaweza kutumia kwa urahisi factoring kupata ufumbuzi wa equations sawa, kama\(x^{2}=16\) na\(x^{2}=25\), kwa sababu\(16\) na\(25\) ni mraba kamilifu. Katika kila kesi, tunataka kupata ufumbuzi mbili,\(x=4, x=-4\) na\(x=5, x=-5\)

Lakini nini kinatokea wakati tuna equation kama\(x^{2}=7\)? Kwa kuwa\(7\) si mraba kamili, hatuwezi kutatua equation kwa factoring.

Hapo awali tulijifunza kwamba tangu\(169\) ni mraba wa\(13\), tunaweza pia kusema kwamba\(13\) ni mizizi ya mraba ya\(169\). Pia,\((-13)^{2}=169\), hivyo pia\(−13\) ni mizizi ya mraba ya\(169\). Kwa hiyo, wote wawili\(13\) na\(−13\) ni mizizi ya mraba ya\(169\). Kwa hiyo, kila idadi nzuri ina mizizi miwili ya mraba-moja chanya na moja hasi. Sisi mapema tulielezea mizizi ya mraba ya namba kwa njia hii:

Ikiwa\(n^{2}=m\), basi\(n\) ni mizizi ya mraba ya\(m\).

Kwa kuwa equations hizi ni wote wa fomu\(x^{2}=k\), mraba mizizi ufafanuzi inatuambia ufumbuzi ni mbili mizizi ya mraba ya\(k\). Hii inasababisha Mali ya Mizizi ya Mraba.

Ufafanuzi\(\PageIndex{1}\)

Mizizi ya mraba Mali

Ikiwa\(x^{2}=k\), basi

\(x=\sqrt{k} \quad\)\(\quad x=-\sqrt{k} \quad\)au\(\quad x=\pm \sqrt{k}\)

Kumbuka kwamba Square Mizizi Mali inatoa ufumbuzi mbili kwa equation ya fomu\(x^{2}=k\), kuu mraba mizizi ya\(k\) na kinyume chake. Tunaweza pia kuandika ufumbuzi kama\(x=\pm \sqrt{k}\). Tunasoma hii kama\(x\) sawa na chanya au hasi mizizi ya mraba ya\(k\).

Sasa sisi kutatua equation\(x^{2}=9\) tena, wakati huu kwa kutumia Mizizi Square Mali.

\(\begin{aligned} &x^{2} =9 \\ \text { Use the Square Root Property. } \quad& x=\pm \sqrt{9} \\& x =\pm 3 \end{aligned}\)

Hivyo\(x=3\) au\(x=-3\)

Nini kinatokea wakati mara kwa mara si mraba kamilifu? Hebu kutumia Mizizi ya Mizizi ya Mraba ili kutatua equation\(x^{2}=7\).

\(x^{2}=7\)

Tumia Mizizi ya Mizizi ya Mraba. \(x=\sqrt{7}, \quad x=-\sqrt{7}\)

Hatuwezi kurahisisha\(\sqrt{7}\), kwa hiyo tunaacha jibu kama radical.

Mfano\(\PageIndex{1}\) How to Solve a Quadratic Equation of the form \(ax^{2}\k\) Using the Square Root Property

Kutatua:\(x^{2}-50=0\).

Suluhisho:

Jedwali 9.1.1

Hatua ya 1: Sulua muda wa quadratic na ufanye mgawo wake mmoja.	\(50\)Ongeza pande zote mbili ili kupata\(x^{2}\) yenyewe.	\(\begin{aligned} x^{2}-50 &=0 \\ x^{2} &=50 \end{aligned}\)
Hatua ya 2: Tumia Mizizi ya Mizizi ya Mraba.	Kumbuka kuandika\(\pm\) ishara.	\(x=\pm \sqrt{50}\)
Hatua ya 3: Kurahisisha radical.	Andika upya ili kuonyesha ufumbuzi mbili.	\(\begin{array}{l}{x=\pm \sqrt{25} \cdot \sqrt{2}} \\ {x=\pm 5 \sqrt{2}} \\ {}x=5\sqrt{2}, \:x=-5\sqrt{2}\end{array}\)
Hatua ya 4: Angalia ufumbuzi.	Mbadala katika\(x=5 \sqrt{2}\) na\(x=-5 \sqrt{2}\)	\(\begin{array}{r}{x^{2}-50=0} \\ {(\color{red}{5 \sqrt{2}}\color{black}{)}^{2}-50 \stackrel{?}{=} 0} \\ {25 \cdot 2-50 \stackrel{?}{=} 0} \\ {0=0}\end{array}\) \(\begin{array}{r}{x^{2}-50=0} \\ {(\color{red}{-5 \sqrt{2}}\color{black}{)}^{2}-50 \stackrel{?}{=} 0} \\ {25 \cdot 2-50 \stackrel{?}{=} 0} \\ {0=0}\end{array}\)

Zoezi\(\PageIndex{1}\)

Kutatua:\(x^{2}-48=0\).

Jibu

\(x=4 \sqrt{3}, x=-4 \sqrt{3}\)

Zoezi\(\PageIndex{2}\)

Kutatua:\(y^{2}-27=0\).

Jibu

\(y=3 \sqrt{3}, y=-3 \sqrt{3}\)

Hatua za kuchukua ili kutumia Mizizi ya Mizizi ya Mraba ili kutatua equation ya quadratic zimeorodheshwa hapa.

Tatua Equation ya Quadratic Kutumia Mizizi ya Mizizi ya

1. Sulua muda wa quadratic na ufanye mgawo wake mmoja.
2. Matumizi Square Mizizi Mali.
3. Kurahisisha radical.
4. Angalia ufumbuzi.

Ili kutumia Mali ya Mizizi ya Mraba, mgawo wa muda wa kutofautiana lazima iwe sawa. Katika mfano unaofuata, tunapaswa kugawanya pande zote mbili za equation kwa mgawo\(3\) kabla ya kutumia Mizizi ya Mizizi ya Mraba.

Mfano\(\PageIndex{2}\)

Kutatua:\(3 z^{2}=108\).

Suluhisho:

Jedwali 9.1.2

	\(3 z^{2}=108\)
Neno la quadratic ni pekee. Gawanya na\(3\) kufanya mgawo wake\(1\).	\(\frac{3 z^{2}}{3}=\frac{108}{3}\)
Kurahisisha.	\(z^{2}=36\)
Tumia Mizizi ya Mizizi ya Mraba.	\(z=\pm \sqrt{36}\)
Kurahisisha radical.	\(z=\pm 6\)
Andika upya ili kuonyesha ufumbuzi mbili.	\(z=6, \quad z=-6\)
Angalia ufumbuzi: Kielelezo 9.1.1

Zoezi\(\PageIndex{3}\)

Kutatua:\(2x^{2}=98\).

Jibu

\(x=7, x=-7\)

Zoezi\(\PageIndex{4}\)

Kutatua:\(5m^{2}=80\).

Jibu

\(m=4, m=-4\)

Mizizi ya Square Mali inasema 'Kama\(x^{2}=k\), 'Nini kitatokea kama\(k<0\)? Hii itakuwa kesi katika mfano unaofuata.

Mfano\(\PageIndex{3}\)

Kutatua:\(x^{2}+72=0\).

Suluhisho:

Jedwali 9.1.3

	\(x^{2}+72=0\)
Sulua muda wa quadratic.	\(x^{2}=-72\)
Tumia Mizizi ya Mizizi ya Mraba.	\(x=\pm \sqrt{-72}\)
Kurahisisha kutumia namba tata.	\(x=\pm \sqrt{72} i\)
Kurahisisha radical.	\(x=\pm 6 \sqrt{2} i\)
Andika upya ili kuonyesha ufumbuzi mbili	\(x=6 \sqrt{2} i, x=-6 \sqrt{2} i\)
Angalia ufumbuzi: 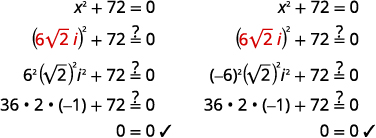Kielelezo 9.1.2

Zoezi\(\PageIndex{5}\)

Kutatua:\(c^{2}+12=0\).

Jibu

\(c=2 \sqrt{3} i, \quad c=-2 \sqrt{3} i\)

Zoezi\(\PageIndex{6}\)

Kutatua:\(q^{2}+24=0\).

Jibu

\(c=2 \sqrt{6} i, \quad c=-2 \sqrt{6} i\)

Njia yetu pia inafanya kazi wakati sehemu ndogo hutokea katika equation, sisi kutatua kama equation yoyote na sehemu ndogo. Katika mfano unaofuata, sisi kwanza hutenganisha muda wa quadratic, na kisha tufanye mgawo sawa na moja.

Mfano\(\PageIndex{4}\)

Kutatua:\(\frac{2}{3} u^{2}+5=17\).

Suluhisho:

Jedwali 9.1.4

	\(\frac{2}{3} u^{2}+5=17\)
Sulua muda wa quadratic.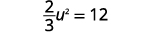
\(\frac{3}{2}\)Kuzidisha na kufanya mgawo\(1\).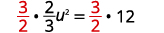
Kurahisisha.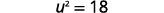
Tumia Mizizi ya Mizizi ya Mraba.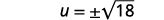
Kurahisisha radical.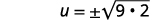
Kurahisisha.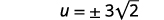
Andika upya ili kuonyesha ufumbuzi mbili.
Angalia: 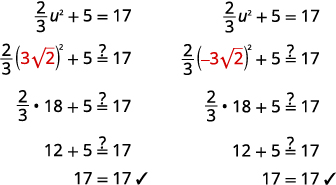Kielelezo 9.1.10

Zoezi\(\PageIndex{7}\)

Kutatua:\(\frac{1}{2} x^{2}+4=24\).

Jibu

\(x=2 \sqrt{10}, x=-2 \sqrt{10}\)

Zoezi\(\PageIndex{8}\)

Kutatua:\(\frac{3}{4} y^{2}-3=18\).

Jibu

\(y=2 \sqrt{7}, y=-2 \sqrt{7}\)

Ufumbuzi wa equations fulani inaweza kuwa na sehemu ndogo ndani ya radicals. Wakati hii itatokea, ni lazima rationalize denominator.

Mfano\(\PageIndex{5}\)

Kutatua:\(2 x^{2}-8=41\).

Suluhisho:

Jedwali 9.1.5

Sulua muda wa quadratic.
Gawanya\(2\) na kufanya mgawo\(1\).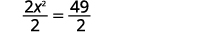
Kurahisisha.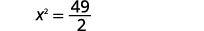
Tumia Mizizi ya Mizizi ya Mraba.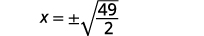
Andika upya radical kama sehemu ya mizizi ya mraba.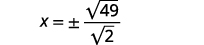
Rationalize denominator.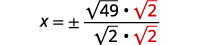
Kurahisisha.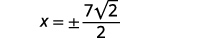
Andika upya ili kuonyesha ufumbuzi mbili.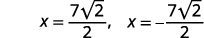
Angalia: Tunaacha hundi kwako.

Zoezi\(\PageIndex{9}\)

Kutatua:\(5 r^{2}-2=34\).

Jibu

\(r=\frac{6 \sqrt{5}}{5}, \quad r=-\frac{6 \sqrt{5}}{5}\)

Zoezi\(\PageIndex{10}\)

Kutatua:\(3 t^{2}+6=70\).

Jibu

\(t=\frac{8 \sqrt{3}}{3}, \quad t=-\frac{8 \sqrt{3}}{3}\)

Tatua usawa wa Quadratic wa Fomu\(a(x-h)^{2}=k\) Kutumia Mizizi ya Mizizi ya Mraba

Tunaweza kutumia Mizizi ya Mizizi ya Mraba ili kutatua equation ya fomu\(a(x-h)^{2}=k\) pia. Angalia kwamba muda wa quadratic,\(x\), katika fomu ya awali\(ax^{2}=k\) inabadilishwa na\((x-h)\).

Kielelezo 9.1.20

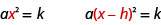
Hatua ya kwanza, kama hapo awali, ni kutenganisha neno ambalo lina mraba wa kutofautiana. Katika kesi hii, binomial ni kuwa mraba. Mara baada ya binomial imetengwa, kwa kugawanya kila upande kwa mgawo wa\(a\), basi Mali ya Mizizi ya Mraba inaweza kutumika\((x-h)^{2}\).

Mfano\(\PageIndex{6}\)

Kutatua:\(4(y-7)^{2}=48\).

Suluhisho:

Jedwali 9.1.6

	\(4(y-7)^{2}=48\)
Gawanya pande zote mbili kwa mgawo\(4\).	\((y-7)^{2}=12\)
Tumia Mizizi ya Mizizi ya Mraba kwenye binomial.	\(y-7=\pm \sqrt{12}\)
Kurahisisha radical.	\(y-7=\pm 2 \sqrt{3}\)
Kutatua kwa\(y\).	\(y=7 \pm 2 \sqrt{3}\)
Andika upya ili kuonyesha ufumbuzi mbili.	\(y=7+2 \sqrt{3}\) \(y=7-2 \sqrt{3}\)
Angalia: 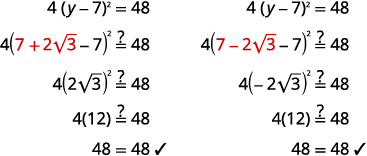Kielelezo 9.1.21

Zoezi\(\PageIndex{11}\)

Kutatua:\(3(a-3)^{2}=54\).

Jibu

\(a=3+3 \sqrt{2}, \quad a=3-3 \sqrt{2}\)

Zoezi\(\PageIndex{12}\)

Kutatua:\(2(b+2)^{2}=80\).

Jibu

\(b=-2+2 \sqrt{10}, \quad b=-2-2 \sqrt{10}\)

Kumbuka tunapochukua mizizi ya mraba ya sehemu, tunaweza kuchukua mizizi ya mraba ya nambari na denominator tofauti.

Mfano\(\PageIndex{7}\)

Kutatua:\(\left(x-\frac{1}{3}\right)^{2}=\frac{5}{9}\).

Suluhisho:

\(\left(x-\frac{1}{3}\right)^{2}=\frac{5}{9}\)

Tumia Mizizi ya Mizizi ya Mraba.

\(x-\frac{1}{3}=\pm \sqrt{\frac{5}{9}}\)

Andika upya radical kama sehemu ya mizizi ya mraba.

\(x-\frac{1}{3}=\pm \frac{\sqrt{5}}{\sqrt{9}}\)

Kurahisisha radical.

\(x-\frac{1}{3}=\pm \frac{\sqrt{5}}{3}\)

Kutatua kwa\(x\).

\(x=\frac{1}{3} \pm \frac{\sqrt{5}}{3}\)

Andika upya ili kuonyesha ufumbuzi mbili.

\(x=\frac{1}{3}+\frac{\sqrt{5}}{3}, x=\frac{1}{3}-\frac{\sqrt{5}}{3}\)

Angalia:

Tunaacha hundi kwako.

Zoezi\(\PageIndex{13}\)

Kutatua:\(\left(x-\frac{1}{2}\right)^{2}=\frac{5}{4}\).

Jibu

\(x=\frac{1}{2}+\frac{\sqrt{5}}{2}, x=\frac{1}{2}-\frac{\sqrt{5}}{2}\)

Zoezi\(\PageIndex{14}\)

Kutatua:\(\left(y+\frac{3}{4}\right)^{2}=\frac{7}{16}\).

Jibu

\(y=-\frac{3}{4}+\frac{\sqrt{7}}{4}, y=-\frac{3}{4}-\frac{\sqrt{7}}{4}\)

Tutaanza suluhisho kwa mfano unaofuata kwa kutenganisha neno la binomial.

Mfano\(\PageIndex{8}\)

Kutatua:\(2(x-2)^{2}+3=57\).

Suluhisho:

\(2(x-2)^{2}+3=57\)

Ondoa\(3\) kutoka pande zote mbili ili kutenganisha neno la binomial.

\(2(x-2)^{2}=54\)

Gawanya pande zote mbili na\(2\).

\((x-2)^{2}=27\)

Tumia Mizizi ya Mizizi ya Mraba.

\(x-2=\pm \sqrt{27}\)

Kurahisisha radical.

\(x-2=\pm 3 \sqrt{3}\)

Kutatua kwa\(x\).

\(x=2 \pm 3 \sqrt{3}\)

Andika upya ili kuonyesha ufumbuzi mbili.

\(x=2+3 \sqrt{3}, x=2-3 \sqrt{3}\)

Angalia:

Tunaacha hundi kwako.

Zoezi\(\PageIndex{15}\)

Kutatua:\(5(a-5)^{2}+4=104\).

Jibu

\(a=5+2 \sqrt{5}, a=5-2 \sqrt{5}\)

Zoezi\(\PageIndex{16}\)

Kutatua:\(3(b+3)^{2}-8=88\).

Jibu

\(b=-3+4 \sqrt{2}, \quad b=-3-4 \sqrt{2}\)

Wakati mwingine ufumbuzi ni namba ngumu.

Mfano\(\PageIndex{9}\)

Kutatua:\((2 x-3)^{2}=-12\).

Suluhisho:

\((2 x-3)^{2}=-12\)

Tumia Mizizi ya Mizizi ya Mraba.

\(2 x-3=\pm \sqrt{-12}\)

Kurahisisha radical.

\(2 x-3=\pm 2 \sqrt{3} i\)

\(3\)Ongeza pande zote mbili.

\(2 x=3 \pm 2 \sqrt{3} i\)

Gawanya pande zote mbili na\(2\).

\(x=\frac{3 \pm 2 \sqrt{3 i}}{2}\)

Andika upya kwa fomu ya kawaida.

\(x=\frac{3}{2} \pm \frac{2 \sqrt{3} i}{2}\)

Kurahisisha.

\(x=\frac{3}{2} \pm \sqrt{3} i\)

Andika upya ili kuonyesha ufumbuzi mbili.

\(x=\frac{3}{2}+\sqrt{3} i, x=\frac{3}{2}-\sqrt{3} i\)

Angalia:

Tunaacha hundi kwako.

Zoezi\(\PageIndex{17}\)

Kutatua:\((3 r+4)^{2}=-8\).

Jibu

\(r=-\frac{4}{3}+\frac{2 \sqrt{2} i}{3}, r=-\frac{4}{3}-\frac{2 \sqrt{2} i}{3}\)

Zoezi\(\PageIndex{18}\)

Kutatua:\((2 t-8)^{2}=-10\).

Jibu

\(t=4+\frac{\sqrt{10} i}{2}, t=4-\frac{\sqrt{10 i}}{2}\)

Pande za kushoto za equations katika mifano miwili ijayo hazionekani kuwa za fomu\(a(x-h)^{2}\). Lakini ni trinomials kamili ya mraba, kwa hiyo tutazingatia kuiweka katika fomu tunayohitaji.

Mfano\(\PageIndex{10}\)

Kutatua:\(4 n^{2}+4 n+1=16\).

Suluhisho:

Tunaona upande wa kushoto wa equation ni kamili mraba trinomial. Tutaifanya kwanza.

Jedwali 9.1.7

	\(4 n^{2}+4 n+1=16\)
Factor kamili mraba trinomial.	\((2 n+1)^{2}=16\)
Tumia Mizizi ya Mizizi ya Mraba.	\(2 n+1=\pm \sqrt{16}\)
Kurahisisha radical.	\(2 n+1=\pm 4\)
Kutatua kwa\(n\).	\(2 n=-1 \pm 4\)
Gawanya kila upande\(2\).	\(\begin{aligned} \frac{2 n}{2} &=\frac{-1 \pm 4}{2} \\ n &=\frac{-1 \pm 4}{2} \end{aligned}\)
Andika upya ili kuonyesha ufumbuzi mbili.	\(n=\frac{-1+4}{2}, n=\frac{-1-4}{2}\)
Kurahisisha kila equation.	\(n=\frac{3}{2}, \quad n=-\frac{5}{2}\)
Angalia: 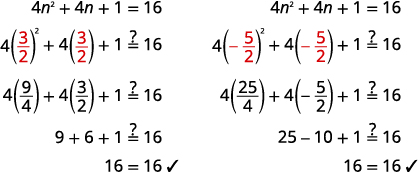Kielelezo 9.1.22

Zoezi\(\PageIndex{19}\)

Kutatua:\(9 m^{2}-12 m+4=25\).

Jibu

\(m=\frac{7}{3}, \quad m=-1\)

Zoezi\(\PageIndex{20}\)

Kutatua:\(16 n^{2}+40 n+25=4\).

Jibu

\(n=-\frac{3}{4}, \quad n=-\frac{7}{4}\)

Fikia rasilimali hii ya mtandaoni kwa maelekezo ya ziada na mazoezi kwa kutumia Mizizi ya Mizizi ya Square kutatua equations quadratic.

• Kutatua Ulinganifu wa Quadratic: Mali ya Mizizi ya Mraba
• Kutumia Mizizi ya Mizizi ya Mraba ili kutatua usawa wa Quadratic

Dhana muhimu

• Mizizi ya mraba Mali
  • Ikiwa\(x^{2}=k\), basi\(x=\sqrt{k}\)\(x=-\sqrt{k}\) au\(x=\pm \sqrt{k}\)
  Jinsi ya kutatua equation quadratic kutumia mali ya mizizi ya mraba.
  1. Sulua muda wa quadratic na ufanye mgawo wake mmoja.
  2. Matumizi Square Mizizi Mali.
  3. Kurahisisha radical.
  4. Angalia ufumbuzi.