6.6E: Mazoezi
- Page ID
- 176114
Mazoezi hufanya kamili
Tumia mali ya Bidhaa ya Zero
Katika mazoezi yafuatayo, tatua.
1. \((3a−10)(2a−7)=0\)
- Jibu
-
\(a=\frac{10}{3},\; a=\frac{7}{2}\)
2. \((5b+1)(6b+1)=0\)
3. \(6m(12m−5)=0\)
- Jibu
-
\(m=0,\; m=\frac{5}{12}\)
4. \(2x(6x−3)=0\)
5. \((2x−1)^2=0\)
- Jibu
-
\(x=\frac{1}{2}\)
6. \((3y+5)^2=0\)
Tatua Ulinganisho wa Quadratic kwa kuzingatia
Katika mazoezi yafuatayo, tatua.
7. \(5a^2−26a=24\)
- Jibu
-
\(a=−\frac{4}{5},\; a=6\)
8. \(4b^2+7b=−3\)
9. \(4m^2=17m−15\)
- Jibu
-
\(m=\frac{5}{4},\; m=3\)
10. \(n^2=5−6n\)
11. \(7a^2+14a=7a\)
- Jibu
-
\(a=−1,\; a=0\)
12. \(12b^2−15b=−9b\)
13. \(49m^2=144\)
- Jibu
-
\(m=\frac{12}{7},\; m=−\frac{12}{7}\)
14. \(625=x^2\)
15. \(16y^2=81\)
- Jibu
-
\(y=−\frac{9}{4},\; y=\frac{9}{4}\)
16. \(64p^2=225\)
17. \(121n^2=36\)
- Jibu
-
\(n=−\frac{6}{11},\; n=\frac{6}{11}\)
18. \(100y^2=9\)
19. \((x+6)(x−3)=−8\)
- Jibu
-
\(x=2,\; x=−5\)
20. \((p−5)(p+3)=−7\)
21. \((2x+1)(x−3)=−4x\)
- Jibu
-
\(x=\frac{3}{2},\; x=−1\)
22. \((y−3)(y+2)=4y\)
23. \((3x−2)(x+4)=12x\)
- Jibu
-
\(x=\frac{3}{2},\; x=−1\)
24. \((2y−3)(3y−1)=8y\)
25. \(20x^2−60x=−45\)
- Jibu
-
\(x=−\frac{2}{3}\)
26. \(3y^2−18y=−27\)
27. \(15x^2−10x=40\)
- Jibu
-
\(x=2,\; x=−\frac{4}{3}\)
28. \(14y^2−77y=−35\)
29. \(18x^2−9=−21x\)
- Jibu
-
\(x=−\frac{3}{2},\; x=\frac{1}{3}\)
30. \(16y^2+12=−32y\)
31. \(16p^3=24p^2-9p\)
- Jibu
-
\(p=0,\; p=\frac{3}{4}\)
32. \(m^3−2m^2=−m\)
33. \(2x^3+72x=24x^2\)
- Jibu
-
\(x=0,\space x=6\)
34. \(3y^3+48y=24y^2\)
35. \(36x^3+24x^2=−4x\)
- Jibu
-
\(x=0,\space x=\frac{1}{3}\)
36. \(2y^3+2y^2=12y\)
Tatua Ulinganisho na Kazi za Polynomial
Katika mazoezi yafuatayo, tatua.
37. Kwa ajili ya kazi\(f(x)=x^2−8x+8\),, ⓐ kupata wakati\(f(x)=−4\) ⓑ Matumizi habari hii kupata pointi mbili kwamba uongo juu ya graph ya kazi.
- Jibu
-
ⓐ\(x=2\) au\(x=6\) ⓑ\((2,−4)\)\((6,−4)\)
38. Kwa ajili ya kazi\(f(x)=x^2+11x+20\),, ⓐ kupata wakati\(f(x)=−8\) ⓑ Matumizi habari hii kupata pointi mbili kwamba uongo juu ya graph ya kazi.
39. Kwa ajili ya kazi\(f(x)=8x^2−18x+5\),, ⓐ kupata wakati\(f(x)=−4\) ⓑ Matumizi habari hii kupata pointi mbili kwamba uongo juu ya graph ya kazi.
- Jibu
-
ⓐ\(x=\frac{3}{2}\) au\(x=\frac{3}{4}\)
ⓑ\((\frac{3}{2},−4)\)\((\frac{3}{4},−4)\)
40. Kwa ajili ya kazi\(f(x)=18x^2+15x−10\),, ⓐ kupata wakati\(f(x)=15\) ⓑ Matumizi habari hii kupata pointi mbili kwamba uongo juu ya graph ya kazi.
Katika mazoezi yafuatayo, kwa kila kazi, tafuta: ⓐ zero za kazi ⓑ\(x\) -intercepts ya grafu ya kazi ⓒ\(y\) -intercept ya grafu ya kazi.
41. \(f(x)=9x^2−4\)
- Jibu
-
ⓐ\(x=\frac{2}{3}\) au\(x=−\frac{2}{3}\)
ⓑ\((\frac{2}{3},0)\),\((−\frac{2}{3},0)\)
ⓒ\((0,−4)\)
42. \(f(x)=25x^2−49\)
43. \(f(x)=6x^2−7x−5\)
- Jibu
-
ⓐ\(x=\frac{5}{3}\) au\(x=−\frac{1}{2}\)
ⓑ\((\frac{5}{3},0)\),\((−\frac{1}{2},0)\)
ⓒ\((0,−5)\)
44. \(f(x)=12x^2−11x+2\)
Kutatua Maombi yanayotokana na equations Quadratic
Katika mazoezi yafuatayo, tatua.
45. Bidhaa ya integers mbili za mfululizo isiyo ya kawaida ni\(143\). Pata integers.
- Jibu
-
\(−13,\space −11\)na\(11,\space 13\)
46. Bidhaa ya integers mbili za mfululizo isiyo ya kawaida ni\(195\). Pata integers.
47. Bidhaa ya integers mbili mfululizo hata ni\(168\). Pata integers.
- Jibu
-
\(−14,\space −12\)na\(12,\space 14\)
48. Bidhaa ya integers mbili mfululizo hata ni\(288\). Pata integers.
49. Eneo la carpet mstatili ni miguu ya\(28\) mraba. Urefu ni miguu mitatu zaidi ya upana. Pata urefu na upana wa carpet.
- Jibu
-
\(−4\)na\(7\)
50. Ukuta wa kubakiza mstatili una eneo la\(15\) mraba miguu. Urefu wa ukuta ni miguu miwili chini ya urefu wake. Pata urefu na urefu wa ukuta.
51. Eneo la ubao wa matangazo ni miguu ya\(55\) mraba. Urefu ni miguu minne chini ya mara tatu upana. Pata urefu na upana wa bodi ya bulletin.
- Jibu
-
\(5,\space 11\)
52. Carport mstatili ina eneo la\(150\) mraba miguu. Urefu wa carport ni miguu mitano chini ya mara mbili urefu wake. Pata urefu na urefu wa carport.
53. Pennant imeumbwa kama pembetatu ya kulia, na\(10\) miguu ya hypotenuse. Urefu wa upande mmoja wa pennant ni urefu wa miguu miwili kuliko urefu wa upande mwingine. Pata urefu wa pande mbili za pennant.
- Jibu
-
\(6,\space 8\)
54. Dirisha la kioo limeumbwa kama pembetatu sahihi. Hypotenuse ni\(15\) feet. One leg is three more than the other. Find the lengths of the legs.
55. Bwawa la kutafakari linaumbwa kama pembetatu ya kulia, na mguu mmoja kando ya ukuta wa jengo. Hypotenuse ni\(9\) miguu ndefu kuliko upande pamoja na jengo hilo. Upande wa tatu ni\(7\) miguu ndefu kuliko upande kando ya jengo. Pata urefu wa pande zote tatu za bwawa la kutafakari.
- Jibu
-
\(8,\space 15,\space 17\)
56. Hifadhi ya mbuzi iko katika sura ya pembetatu sahihi. Mguu mmoja wa enclosure umejengwa dhidi ya upande wa ghalani. Mguu mwingine ni\(4\) miguu zaidi ya mguu dhidi ya ghalani. Hypotenuse ni\(8\) miguu zaidi ya mguu kando ya ghalani. Pata pande tatu za enclosure ya mbuzi.
57. Juli ni kwenda kuzindua mfano roketi katika yadi yake ya nyuma. Wakati yeye yazindua roketi, kazi\(h(t)=−16t^2+32t\) mifano urefu\(h\), ya roketi juu ya ardhi kama kazi ya muda,\(t\). Kupata:
ⓐ zeros ya kazi hii ambayo inatuambia wakati roketi hit ardhi. ⓑ wakati roketi itakuwa\(16\) miguu juu ya ardhi.
- Jibu
-
ⓐ 0, 2 ⓑ 1
58. Gianna ni kwenda kutupa mpira kutoka ghorofa ya juu ya shule yake ya kati. Wakati yeye throws mpira kutoka\(48\) miguu juu ya ardhi, kazi\(h(t)=−16t^2+32t+48\) mifano urefu\(h\), ya mpira juu ya ardhi kama kazi ya muda,\(t\). Kupata:
ⓐ zero za kazi hii ambayo inatuambia wakati mpira utapiga ardhi. ⓑ wakati (s) mpira utakuwa\(48\) miguu juu ya ardhi. ⓒ urefu mpira utakuwa katika\(t=1\) sekunde ambayo ni wakati mpira utakuwa katika hatua yake ya juu.
Mazoezi ya kuandika
59. Eleza jinsi ya kutatua equation quadratic. Ni majibu ngapi unatarajia kupata equation quadratic?
- Jibu
-
Majibu yatatofautiana.
60. Kutoa mfano wa equation quadratic ambayo ina GCF na hakuna ufumbuzi wa equation ni sifuri.
Self Check
ⓐ Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.
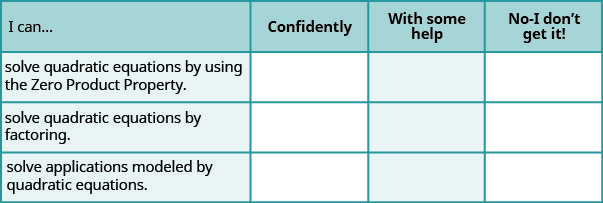
ⓑ Kwa ujumla, baada ya kuangalia orodha, unafikiri umeandaliwa vizuri kwa sehemu inayofuata? Kwa nini au kwa nini?


