6.5: Mkakati Mkuu wa Kufanya Maneno ya Polynomial
- Page ID
- 176051
Mwishoni mwa sehemu hii, utaweza:
- Kutambua na kutumia njia sahihi kwa sababu ya polynomial kabisa
Kutambua na Tumia Njia sahihi ya Kufanya Kipolynomial Kikamilifu
Sasa umejifunza njia zote za kuzingatia ambazo utahitaji katika kozi hii. Chati ifuatayo muhtasari mbinu zote factoring tuna kufunikwa, na muhtasari mkakati unapaswa kutumia wakati factoring polynomials.

- Je, kuna sababu kubwa ya kawaida?
Factor ni nje. - Je, polynomial ni binomial, trinomial, au kuna maneno zaidi ya tatu?
Ikiwa ni binomial:- Je, ni jumla?
Ya mraba? Muhtasari wa mraba hauna sababu.
Ya cubes? Tumia jumla ya muundo wa cubes. - Je, ni tofauti?
Ya mraba? Sababu kama bidhaa ya conjugates.
Ya cubes? Tumia tofauti ya muundo wa cubes.
- Je, ni ya fomu\(x^2+bx+c\)? Tengeneza FOIL.
- Je, ni ya fomu\(ax^2+bx+c\)?
Ikiwa a na c ni mraba, angalia ikiwa inafaa muundo wa mraba wa trinomial.
Tumia jaribio na hitilafu au “\(ac\)” njia.
- Tumia njia ya kikundi.
- Je, ni jumla?
- Angalia.
Je, ni sababu kabisa?
Je! Sababu zinazidisha nyuma ya polynomial ya awali?
Kumbuka, polynomial inaelezewa kabisa ikiwa, isipokuwa monomials, mambo yake ni mkuu!
Sababu kabisa:\(7x^3−21x^2−70x\).
Suluhisho
\(\begin{array} {ll} {7x^3−21x^2−70x} & \\ \text{Is there a GCF? Yes, }7x. & \\ \text{Factor out the GCF.} &7x(x^2−3x−10) \\ \text{In the parentheses, is it a binomial, trinomial,} & \\ \text{or are there more terms?} & \\ \text{Trinomial with leading coefficient 1.} & \\ \text{“Undo” FOIL.} &7x(x\hspace{8mm})(x\hspace{8mm}) \\ &7x(x+2)(x−5) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Neither binomial can be factored.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ & \\ & \\ \hspace{15mm}7x(x+2)(x−5) & \\ \hspace{10mm}7x(x^2−5x+2x−10) & \\ \hspace{15mm}7x(x^2−3x−10) & \\ \hspace{13mm}7x^3−21x^2−70x\checkmark & \end{array} \)
Sababu kabisa:\(8y^3+16y^2−24y\).
- Jibu
-
\(8y(y−1)(y+3)\)
Sababu kabisa:\(5y^3−15y^2−270y\).
- Jibu
-
\(5y(y−9)(y+6)\)
Kuwa makini wakati unapoulizwa kuzingatia binomial kama kuna chaguo kadhaa!
Sababu kabisa:\(24y^2−150\)
Suluhisho
\(\begin{array} {ll} &24y^2−150 \\ \text{Is there a GCF? Yes, }6. & \\ \text{Factor out the GCF.} &6(4y^2−25) \\ \text{In the parentheses, is it a binomial, trinomial} & \\ \text{or are there more than three terms? Binomial.} & \\ \text{Is it a sum? No.} & \\ \text{Is it a difference? Of squares or cubes? Yes, squares.} &6((2y)^2−(5)^2) \\ \text{Write as a product of conjugates.} &6(2y−5)(2y+5) \\ & \\ & \\ \hspace{5mm}\text{Is the expression factored completely?} & \\ \hspace{5mm}\text{Neither binomial can be factored.} & \\ \text{Check:} & \\ & \\ & \\ \hspace{5mm}\text{Multiply.} & \\ & \\ \hspace{15mm}6(2y−5)(2y+5) & \\ & \\ \hspace{18mm}6(4y^2−25) & \\ \hspace{18mm}24y^2−150\checkmark \end{array}\)
Sababu kabisa:\(16x^3−36x\).
- Jibu
-
\(4x(2x−3)(2x+3)\)
Sababu kabisa:\(27y^2−48\).
- Jibu
-
\(3(3y−4)(3y+4)\)
Mfano unaofuata unaweza kuzingatiwa kwa kutumia mbinu kadhaa. Kutambua muundo wa mraba wa trinomial utafanya kazi yako iwe rahisi.
Sababu kabisa:\(4a^2−12ab+9b^2\).
Suluhisho
\(\begin{array} {ll} &4a^2−12ab+9b^2 \\ \text{Is there a GCF? No.} & \\ \text{Is it a binomial, trinomial, or are there more terms?} & \\ \text{Trinomial with }a\neq 1.\text{ But the first term is a perfect square.} \\ \text{Is the last term a perfect square? Yes.} &(2a)^2−12ab+(3b)^2 \\ \text{Does it fit the pattern, }a^2−2ab+b^2?\text{ Yes.} &(2a)^2 −12ab+ (3b)^2 \\ &\hspace{7mm} {\,}^{\searrow}{\,}_{−2(2a)(3b)}{\,}^{\swarrow}\\ \text{Write it as a square.} &(2a−3b)^2 \\ & \\ & \\ \quad\text{Is the expression factored completely? Yes.} & \\ \quad\text{The binomial cannot be factored.} & \\ \text{Check your answer.} \\ & \\ & \\ \quad\text{Multiply.} & \\ \hspace{30mm}(2a−3b)^2 \\ \hspace{20mm} (2a)^2−2·2a·3b+(3b)^2 \\ \hspace{24mm}4a^2−12ab+9b^2\checkmark & \end{array} \)
Sababu kabisa:\(4x^2+20xy+25y^2\).
- Jibu
-
\((2x+5y)^2\)
Sababu kabisa:\(9x^2−24xy+16y^2\).
- Jibu
-
\((3x−4y)^2\)
Kumbuka, kiasi cha mraba hazizingatii, lakini kiasi cha cubes hufanya!
Sababu kabisa\(12x^3y^2+75xy^2\).
Suluhisho
\(\begin{array} {ll} &12x^3y^2+75xy^2 \\ \text{Is there a GCF? Yes, }3xy^2. & \\ \text{Factor out the GCF.} &3xy^2(4x^2+25) \\ \text{In the parentheses, is it a binomial, trinomial, or are} & \\ \text{there more than three terms? Binomial.} & \\ & \\ \text{Is it a sum? Of squares? Yes.} &\text{Sums of squares are prime.} \\ & \\ & \\ \quad\text{Is the expression factored completely? Yes.} & \\ \text{Check:} & \\ & \\ & \\ \quad\text{Multiply.} & \\ \hspace{15mm}3xy^2(4x^2+25) & \\ \hspace{14mm}12x^3y^2+75xy^2\checkmark \end{array} \)
Sababu kabisa:\(50x^3y+72xy\).
- Jibu
-
\(2xy(25x^2+36)\)
Sababu kabisa:\(27xy^3+48xy\).
- Jibu
-
\(3xy(9y^2+16)\)
Wakati wa kutumia jumla au tofauti ya muundo wa cubes, kuwa makini na ishara.
Sababu kabisa:\(24x^3+81y^3\).
Suluhisho
| Je, kuna GCF? Ndiyo, 3. | 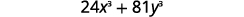 |
| Factor ni nje. | 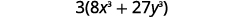 |
| Katika mabano, ni binomial, trinomial, ya kuna maneno zaidi ya tatu? Binomial. |
|
| Je, ni jumla au tofauti? Jumla. | |
| Ya mraba au cubes? Jumla ya cubes. | 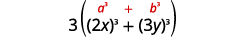 |
| Andika kwa kutumia jumla ya muundo wa cubes. | 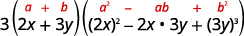 |
| Je! Maneno yanafanywa kabisa? Ndiyo. | 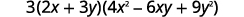 |
| Angalia kwa kuzidisha. |
Sababu kabisa:\(250m^3+432n^3\).
- Jibu
-
\(2(5m+6n)(25m^2−30mn+36n^2)\)
Sababu kabisa:\(2p^3+54q^3\).
- Jibu
-
\(2(p+3q)(p^2−3pq+9q^2)\)
Sababu kabisa:\(3x^5y−48xy\).
Suluhisho
\(\begin{array} {ll} &3x^5y−48xy \\ \text{Is there a GCF? Factor out }3xy &3xy(x^4−16) \\ \begin{array} {l} \text{Is the binomial a sum or difference? Of squares or cubes?} \\ \text{Write it as a difference of squares.} \end{array} &3xy\left((x^2)^2−(4)2\right) \\ \text{Factor it as a product of conjugates} &3xy(x^2−4)(x^2+4) \\ \text{The first binomial is again a difference of squares.} &3xy\left((x)^2−(2)^2\right)(x^2+4) \\ \text{Factor it as a product of conjugates.} &3xy(x−2)(x+2)(x^2+4) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ 3xy(x−2)(x+2)(x^2+4) & \\ 3xy(x^2−4)(x^2+4) & \\ 3xy(x^4−16) & \\ 3x^5y−48xy\checkmark & \end{array}\)
Sababu kabisa:\(4a^5b−64ab\).
- Jibu
-
\(4ab(a^2+4)(a−2)(a+2)\)
Sababu kabisa:\(7xy^5−7xy\).
- Jibu
-
\(7xy(y^2+1)(y−1)(y+1)\)
Sababu kabisa:\(4x^2+8bx−4ax−8ab\).
Suluhisho
\(\begin{array} {ll} &4x^2+8bx−4ax−8ab \\ \text{Is there a GCF? Factor out the GCF, }4. &4(x^2+2bx−ax−2ab) \\ \text{There are four terms. Use grouping.} &4[x(x+2b)−a(x+2b)]4(x+2b)(x−a) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ \hspace{25mm}4(x+2b)(x−a) & \\ \hspace{20mm} 4(x^2−ax+2bx−2ab) & \\ \hspace{20mm}4x^2+8bx−4ax−8ab\checkmark \end{array}\)
Sababu kabisa:\(6x^2−12xc+6bx−12bc\).
- Jibu
-
\(6(x+b)(x−2c)\)
Sababu kabisa:\(16x^2+24xy−4x−6y\).
- Jibu
-
\(2(4x−1)(2x+3y)\)
Kuchukua GCF kamili katika hatua ya kwanza daima kufanya kazi yako rahisi.
Sababu kabisa:\(40x^2y+44xy−24y\).
Suluhisho
\(\begin{array} {ll} &40x^2y+44xy−24y \\ \text{Is there a GCF? Factor out the GCF, }4y. &4y(10x^2+11x−6) \\ \text{Factor the trinomial with }a\neq 1. &4y(10x^2+11x−6) \\ &4y(5x−2)(2x+3) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ \hspace{25mm}4y(5x−2)(2x+3) & \\ \hspace{24mm}4y(10x^2+11x−6) & \\ \hspace{22mm}40x^2y+44xy−24y\checkmark \end{array}\)
Sababu kabisa:\(4p^2q−16pq+12q\).
- Jibu
-
\(4q(p−3)(p−1)\)
Sababu kabisa:\(6pq^2−9pq−6p\).
- Jibu
-
\(3p(2q+1)(q−2)\)
Wakati tumefanya polynomial na maneno manne, mara nyingi tuliitenganisha katika makundi mawili ya maneno mawili. Kumbuka kwamba tunaweza pia kuitenganisha kuwa trinomial na kisha muda mmoja.
Sababu kabisa:\(9x^2−12xy+4y^2−49\).
Suluhisho
\(\begin{array} {ll} &9x^2−12xy+4y^2−49 \\ \text{Is there a GCF? No.} & \\ \begin{array} {l} \text{With more than 3 terms, use grouping. Last 2 terms} \\ \text{have no GCF. Try grouping first 3 terms.} \end{array} &9x^2−12xy+4y^2−49 \\ \begin{array} {l} \text{Factor the trinomial with }a\neq 1. \text{ But the first term is a} \\ \text{perfect square.} \end{array} & \\ \text{Is the last term of the trinomial a perfect square? Yes.} &(3x)^2−12xy+(2y)^2−49 \\ \text{Does the trinomial fit the pattern, }a^2−2ab+b^2? \text{ Yes.} &(3x)^2 −12xy+ (2y)^2−49 \\ &\hspace{7mm} {\,}^{\searrow}{\,}_{−2(3x)(2y))}{\,}^{\swarrow} \\ \text{Write the trinomial as a square.} &(3x−2y)^2−49 \\ \begin{array} {ll} \text{Is this binomial a sum or difference? Of squares or} \\ \text{cubes? Write it as a difference of squares.} \end{array} &(3x−2y)^2−72 \\ \text{Write it as a product of conjugates.} &((3x−2y)−7)((3x−2y)+7) \\ &(3x−2y−7)(3x−2y+7) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ \hspace{23mm}(3x−2y−7)(3x−2y+7) & \\ \hspace{10mm}9x^2−6xy−21x−6xy+4y^2+14y+21x−14y−49 \qquad & \\ \hspace{25mm}9x^2−12xy+4y^2−49\checkmark & \end{array}\)
Sababu kabisa:\(4x^2−12xy+9y^2−25\).
- Jibu
-
\((2x−3y−5)(2x−3y+5)\)
Sababu kabisa:\(16x^2−24xy+9y^2−64\).
- Jibu
-
\((4x−3y−8)(4x−3y+8)\)
Dhana muhimu

- Jinsi ya kutumia mkakati wa jumla wa factoring polynomials.
- Je, kuna sababu kubwa ya kawaida?
Factor ni nje. - Je, polynomial ni binomial, trinomial, au kuna maneno zaidi ya tatu?
Kama ni binomial: Je,
ni jumla?
Ya mraba? Muhtasari wa mraba hauna sababu.
Ya cubes? Tumia jumla ya muundo wa cubes.
Je, ni tofauti?
Ya mraba? Sababu kama bidhaa ya conjugates.
Ya cubes? Tumia tofauti ya muundo wa cubes.
Ikiwa ni trinomial: Je,
ni ya fomu\(x^2+bx+c\)? Tengeneza FOIL.
Je, ni ya fomu\(ax^2+bx+c\)?
Ikiwa a na c ni mraba, angalia ikiwa inafaa muundo wa mraba wa trinomial.
Tumia jaribio na hitilafu au “\(ac\)” njia.
Ikiwa ina maneno zaidi ya tatu:
Tumia njia ya kikundi. - Angalia.
Je, ni sababu kabisa?
Je! Sababu zinazidisha nyuma ya polynomial ya awali?
- Je, kuna sababu kubwa ya kawaida?


