Skip to main content
Global

4.7: Kutatua Mifumo ya Equations Kutumia Maamuzi

  1. Last updated
  2. Save as PDF
  • Page ID
    175917

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Tathmini uamuzi wa tumbo la 2 × 2
    • Tathmini uamuzi wa tumbo la 3 × 3
    • Matumizi Cramer ya Utawala wa kutatua mifumo ya equations
    • Tatua programu kwa kutumia vigezo

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Kurahisisha:\(5(−2)−(−4)(1)\).
      Ikiwa umekosa tatizo hili, tathmini [kiungo].
    2. Kurahisisha:\(−3(8−10)+(−2)(6−3)−4(−3−(−4))\).
      Ikiwa umekosa tatizo hili, tathmini [kiungo].
    3. Kurahisisha:\(\frac{−12}{−8}\).
      Ikiwa umekosa tatizo hili, tathmini [kiungo].

    Katika sehemu hii tutajifunza njia nyingine ya kutatua mifumo ya equations linear inayoitwa utawala wa Cramer. Kabla ya kuanza kutumia utawala, tunahitaji kujifunza baadhi ya ufafanuzi mpya na nukuu.

    Tathmini ya Uamuzi wa\(2×2\) Matrix

    Ikiwa tumbo lina idadi sawa ya safu na nguzo, tunaiita tumbo la mraba. Kila tumbo la mraba lina namba halisi inayohusishwa nayo inayoitwa uamuzi wake. Ili kupata uamuzi wa tumbo la mraba\(\left[ \begin{matrix} a &b \\ c&d \end{matrix} \right] \), sisi kwanza tunaandika kama\(\left| \begin{matrix} a &b \\ c&d \end{matrix} \right| \). Ili kupata thamani halisi ya namba ya kuamua tunaondoa bidhaa za diagonals, kama inavyoonekana.

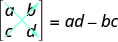
    A 2 na 2 determinant ni show, na mstari wake wa kwanza kuwa a, b na wa pili kuwa c, d. maadili haya yameandikwa kati ya mistari miwili wima badala ya mabano kama ilivyo katika matrices. Mishale miwili imeonyeshwa, moja kutoka kwa d, nyingine kutoka c hadi b. uamuzi huu ni sawa na ad minus bc.

    DETERMINANT

    Uamuzi wa tumbo lolote la mraba\(\left[ \begin{matrix} a &b \\ c&d \end{matrix} \right] \), ambapo a, b, c, na d ni namba halisi, ni

    \[\left| \begin{matrix} a &b \\ c&d \end{matrix} \right| =ad−bc \nonumber \]

    Mfano\(\PageIndex{1}\)

    Tathmini uamuzi wa ⓐ\(\left[ \begin{matrix} 4 &-2 \\ 3&-1 \end{matrix} \right] \) ⓑ\(\left[ \begin{matrix} -3 &-4 \\ -2&0 \end{matrix} \right] \).

    Jibu

    ⓐ

      .
    Andika uamuzi. .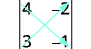
    Ondoa bidhaa za diagonals. .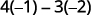
    Kurahisisha. .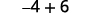
    Kurahisisha. .

    ⓑ

      .
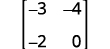
    Andika uamuzi. .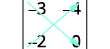
    Ondoa bidhaa za diagonals. .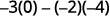
    Kurahisisha. .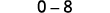
    Kurahisisha. .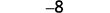
    Mfano\(\PageIndex{2}\)

    Tathmini uamuzi wa ⓐ\(\left[ \begin{matrix} 5&−3\\2&−4 \end{matrix} \right] \) ⓑ\(\left[ \begin{matrix} −4&−6\\0&7 \end{matrix} \right] \).

    Jibu

    ⓐ\(−14\); ⓑ\(−28\)

    Mfano\(\PageIndex{3}\)

    Tathmini uamuzi wa ⓐ\(\left[ \begin{matrix} −1&3\\−2&4 \end{matrix} \right] \) ⓑ\(\left[ \begin{matrix} −7&−3\\−5&0 \end{matrix} \right] \).

    Jibu

    ⓐ 2 ⓑ\(−15\)

    Tathmini ya Uamuzi wa\(3×3\) Matrix

    Ili kutathmini uamuzi wa\(3×3\) tumbo, tunapaswa kuwa na uwezo wa kutathmini mdogo wa kuingia katika uamuzi. Mdogo wa kuingia ni\(2×2\) uamuzi uliopatikana kwa kuondoa mstari na safu katika\(3×3\) uamuzi ambao una kuingia.

    NDOGO YA KUINGIA KATIKA\(3×3\) A DETERMINANT

    Mdogo wa kuingia katika\(3×3\) uamuzi ni\(2×2\) uamuzi uliopatikana kwa kuondoa mstari na safu katika\(3×3\) uamuzi ambao una kuingia.

    Ili kupata mdogo wa kuingia\(a_1\), tunaondoa mstari na safu iliyo nayo. Kwa hiyo tunaondoa mstari wa kwanza na safu ya kwanza. Kisha sisi kuandika\(2×2\) determinant kwamba bado.

    Mstari wa kwanza wa kuamua 3 na 3 ni a1, b1, c1. Row 2 ni a2, b2, c2. Row 3 ni a3, b3, c3. a1 ni yalionyesha. Mistari hupiga mstari wa kwanza na safu ya kwanza. Nini bado inaitwa madogo ya a1. Inaonyeshwa kama uamuzi tofauti ambao mstari wa kwanza ni B2, c2 na mstari wa pili ni b3, c3.

    Ili kupata mdogo wa kuingia\(b_2\), tunaondoa mstari na safu iliyo nayo. Kwa hiyo tunaondoa\(2^{nd}\) mstari na\(2^{nd}\) safu. Kisha sisi kuandika\(2×2\) determinant kwamba bado.

    Mstari wa kwanza wa kuamua 3 na 3 ni a1, b1, c1. Row 2 ni a2, b2, c2. Row 3 ni a3, b3, c3. B2 imeonyeshwa. Mistari hupiga mstari wa pili na safu ya pili. Nini bado ni ndogo ya B2. Imeandikwa kama determinant tofauti ambayo mstari wa kwanza ni a1, c1 na mstari wa pili ni a3, c3.

    Mfano\(\PageIndex{4}\)

    Kwa uamuzi\(\left| \begin{matrix} 4&−2&3\\1&0&−3\\−2&−4&2 \end{matrix} \right|\), tafuta na kisha tathmini mdogo wa ⓐ\(a_1\) ⓑ\(b_3\) ⓒ\(c_2\).

    Jibu

    ⓐ

      .
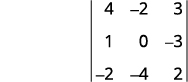
    Ondoa mstari na safu iliyo na\(a_1\). .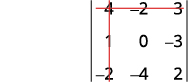
    Andika\(2×2\) uamuzi unaoendelea. .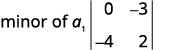
    Tathmini. .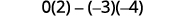
    Kurahisisha. .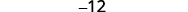

    ⓑ

    Ondoa mstari na safu iliyo na\(b_3\). .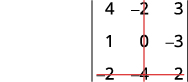
    Andika\(2×2\) uamuzi unaoendelea. .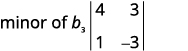
    Tathmini. .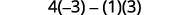
    Kurahisisha. .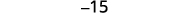

    ⓒ

      .
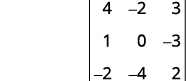
    Ondoa mstari na safu iliyo na\(c_2\). .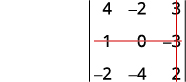
    Andika\(2×2\) uamuzi unaoendelea. .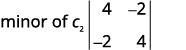
    Tathmini. .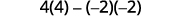
    Kurahisisha. .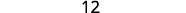
    Mfano\(\PageIndex{5}\)

    Kwa uamuzi\(\left| \begin{matrix} 1&−1&4\\0&2&−1\\−2&−3&3 \end{matrix} \right|\), tafuta na kisha tathmini mdogo wa ⓐ\(a_1\) ⓑ\(b_2\) ⓒ\(c_3\).

    Jibu

    ⓐ 3 ⓑ 11 ⓒ 2

    Mfano\(\PageIndex{6}\)

    Kwa uamuzi\(\left| \begin{matrix} −2&−1&0\\3&0&−1\\−1&−2&3 \end{matrix} \right|\), tafuta na kisha tathmini mdogo wa ⓐ\(a_2\) ⓑ\(b_3\) ⓒ\(c_2\).

    Jibu

    ⓐ\(−3\) ⓑ 2 ⓒ 3

    Sisi sasa ni tayari kutathmini\(3×3\) determinant. Ili kufanya hivyo sisi kupanua na watoto, ambayo inaruhusu sisi kutathmini\(3×3\) determinant kutumia\(2×2\) determinants-ambayo tayari tunajua jinsi ya kutathmini!

    Ili kutathmini\(3×3\) uamuzi kwa kupanua na watoto kando ya mstari wa kwanza, tunatumia muundo wafuatayo:

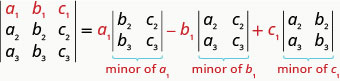
    A 3 na 3 determinant ni sawa na mara A1 madogo ya A1 bala mara b1 madogo ya b1 pamoja na c1 mara madogo ya c1.

    Kumbuka, ili kupata mdogo wa kuingia tunaondoa mstari na safu iliyo na kuingia.

    KUPANUA NA WATOTO PAMOJA MSTARI WA KWANZA KUTATHMINI\(3×3\) DETERMINANT

    Kutathmini\(3×3\) uamuzi kwa kupanua na watoto kando ya mstari wa kwanza, mfano wafuatayo:

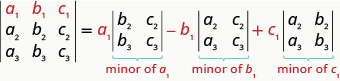
    A 3 na 3 determinant ni sawa na mara A1 madogo ya A1 bala mara b1 madogo ya b1 pamoja na c1 mara madogo ya c1.

    Mfano\(\PageIndex{7}\)

    Tathmini uamuzi\(\left| \begin{matrix} 2&−3&−1\\3&2&0\\−1&−1&−2 \end{matrix} \right|\) kwa kupanua na watoto kando ya mstari wa kwanza.

    Jibu
      .
    Panua na watoto kando ya mstari wa kwanza .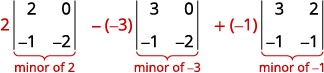
    Tathmini kila determinant. .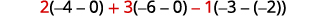
    Kurahisisha. .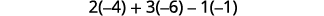
    Kurahisisha. .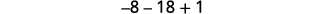
    Kurahisisha. .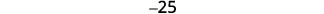
    Mfano\(\PageIndex{8}\)

    Tathmini uamuzi\(\left| \begin{matrix} 3&−2&4\\0&−1&−2\\2&3&−1 \end{matrix} \right|\), kwa kupanua na watoto kando ya mstari wa kwanza.

    Jibu

    37

    Mfano\(\PageIndex{9}\)

    Tathmini uamuzi\(\left| \begin{matrix} 3&−2&−2\\2&−1&4\\−1&0&−3 \end{matrix} \right|\), kwa kupanua na watoto kando ya mstari wa kwanza.

    Jibu

    7

    Kutathmini\(3×3\) determinant tunaweza kupanua na watoto kutumia mstari wowote au safu. Kuchagua mstari au safu nyingine zaidi ya mstari wa kwanza wakati mwingine hufanya kazi iwe rahisi.

    Tunapopanua kwa mstari wowote au safu, lazima tuwe makini kuhusu ishara ya maneno katika upanuzi. Kuamua ishara ya maneno, tunatumia chati ya mfano wa ishara inayofuata.

    \[\left| \begin{matrix} +&−&+\\−&+&−\\+&−&+ \end{matrix} \right|\nonumber\]

    MFANO WA ISHARA

    Wakati wa kupanua na watoto kutumia mstari au safu, ishara ya maneno katika upanuzi hufuata muundo uliofuata. \[\left| \begin{matrix} +&−&+\\−&+&−\\+&−&+ \end{matrix} \right|\nonumber\]

    Angalia kwamba muundo wa ishara katika mstari wa kwanza unafanana na ishara kati ya maneno katika upanuzi kwa mstari wa kwanza.

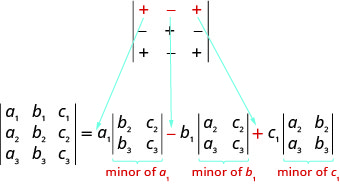
    A 3 na 3 determinant ina mstari 1: pamoja, minus, plus, mstari 2: minus, plus, minus na mstari 3: pamoja, minus, pamoja. Ishara tatu katika mstari wa kwanza kila hatua kwa uamuzi mdogo katika upanuzi wa 3 na 3 determinant. Plus pointi kwa madogo ya a1, minus kwa mdogo wa b1 na pamoja na mdogo wa c1.

    Tangu tunaweza kupanua kwa mstari wowote au safu, tunawezaje kuamua ni mstari au safu ya kutumia? Kawaida tunajaribu kuchukua mstari au safu ambayo itafanya hesabu yetu iwe rahisi. Ikiwa uamuzi una 0, kwa kutumia mstari au safu iliyo na 0 itafanya mahesabu iwe rahisi.

    Mfano\(\PageIndex{10}\)

    Tathmini ya kuamua\(\left| \begin{matrix} 4&−1&−3\\3&0&2\\5&−4&−3 \end{matrix} \right|\) kwa kupanua na watoto.

    Jibu

    Ili kupanua na watoto, tunatafuta mstari au safu ambayo itafanya mahesabu yetu iwe rahisi. Tangu 0 ni katika mstari wa pili na safu ya pili, kupanua na mojawapo ya wale ni uchaguzi mzuri. Kwa kuwa mstari wa pili una vikwazo vichache kuliko safu ya pili, tutapanua kwa mstari wa pili.

      .
    Panua kutumia mstari wa pili.  
    Kuwa makini na ishara. .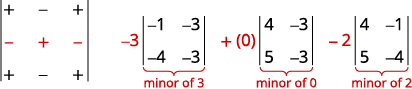
    Tathmini kila determinant. .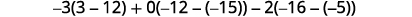
    Kurahisisha. .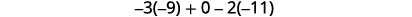
    Kurahisisha. .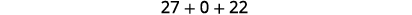
    Ongeza. .
    Mfano\(\PageIndex{11}\)

    Tathmini ya kuamua\(\left| \begin{matrix} 2&−1&−3\\0&3&−4\\3&−4&−3 \end{matrix} \right|\) kwa kupanua na watoto.

    Jibu

    \(−11\)

    Mfano\(\PageIndex{12}\)

    Tathmini ya kuamua\(\left| \begin{matrix} −2&−1&−3\\−1&2&2\\4&−4&0 \end{matrix} \right|\) kwa kupanua na watoto.

    Jibu

    8

    Tumia Utawala wa Cramer wa Kutatua Mifumo ya Equations

    Utawala wa Cramer ni njia ya kutatua mifumo ya equations kwa kutumia vigezo. Inaweza kupatikana kwa kutatua fomu ya jumla ya mifumo ya equations kwa kuondoa. Hapa tutaonyesha utawala wa mifumo miwili ya equations mbili na vigezo viwili na kwa mifumo ya equations tatu na vigezo vitatu.

    Hebu tuanze na mifumo ya equations mbili na vigezo viwili.

    UTAWALA WA CRAMER WA KUTATUA MFUMO WA EQUATIONS MBILI

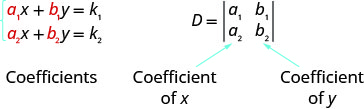
    Kwa mfumo wa equations\(\left\{\begin{array} {l} a_1x+b_1y=k_1 \\ a_2x+b_2y=k_2\end{array}\right.\), suluhisho\((x,y)\) linaweza kuamua na

    x ni Dx juu ya D na y ni Dy juu ya D ambapo D ni kuamua na mstari wa 1: a1, b1 na mstari 2 a2, B2, kutumia coefficients ya vigezo; Dx ni kuamua na mstari 1: k1, b1 na mstari 2: k2, b2, badala ya coefficients x na konsonanti; Dy ni kuamua na mstari 1: a1, k1 na mstari 2: a2, k2 2, badala ya y coefficients na mara kwa mara

    Angalia kwamba ili kuunda D ya kuamua, tunatumia kuchukua coefficients ya vigezo.

    equations ni a1x pamoja b1y sawa na k1 na a2x pamoja b2y sawa k2. Hapa, a1, a2, b1, b2 ni coefficients. Kitambulisho ni D na mstari wa 1: a1, b1 na mstari wa 2: a2, b2. Column 1 ina coefficients ya x na safu 2 ina coefficients ya

    Kumbuka kwamba kuunda uamuzi\(D_x\) na\(D_y\), sisi badala ya constants kwa coefficients ya variable sisi ni kutafuta.

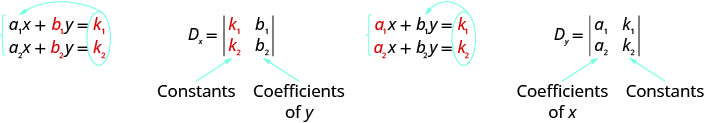
    equations ni a1x pamoja b1y sawa na k1 na a2x pamoja b2y sawa k2. Hapa, a1, a2, b1, b2 ni coefficients. Determinant ni Dx ina mstari 1: k1, b1 na mstari 2: k2, b2. Hapa nguzo 1 na 2 ni mara kwa mara na coefficients ya y kwa mtiririko huo. Determinant Dy ina mstari 1: a1, k1 na mstari 2: a2, k2. Hapa, nguzo 1 na 2 ni coefficients ya x na constants kwa mtiririko huo.

    Mfano\(\PageIndex{13}\): How to Solve a System of Equations Using Cramer’s Rule

    Kutatua kutumia Cramer ya Utawala:\(\left\{ \begin{array} {l} 2x+y=−4\\3x−2y=−6\end{array}\right.\)

    Jibu

    equations ni 2x pamoja y sawa minus 4 na 3x minus 2y sawa minus 6. Hatua ya 1. Tathmini ya kuamua D, kwa kutumia coefficients ya vigezo. D inayoamua ina mstari wa 1:2, 1 na mstari wa 2:3, chini ya 2. Kwa hiyo, D ni chini ya 7.Hatua ya 2. Tathmini Dx inayoamua. Tumia mara kwa mara badala ya coefficients x. Sisi kuchukua nafasi ya coefficients ya x, 2 na 3, na mara kwa mara, hasi 4 na hasi 6. Tunapata Dx sawa na 14.Hatua ya 3. Tathmini Siku ya kuamua. Tumia mara kwa mara badala ya coefficients y. Sisi kuchukua nafasi ya coefficients ya y, 1 na 2, na mara kwa mara, hasi 4 na hasi 6. Tunapata Dy sawa na 0.Hatua ya 4. Pata x na y. maadili ya D, Dx na Dy katika equations x sawa na Dx juu ya D na y sawa na Dy juu ya D, sisi kupata x sawa na minus 2 na y sawa na 0.Hatua ya 5. Andika suluhisho kama jozi iliyoamriwa minus 2, 0.Hatua ya 6. Angalia kwamba jozi iliyoamriwa ni suluhisho la equations zote za awali.

    Mfano\(\PageIndex{14}\)

    Tatua kutumia utawala wa Cramer:\(\left\{\begin{array} {l} 3x+y=−3 \\ 2x+3y=6 \end{array} \right.\)

    Jibu

    \((−\frac{15}{7},\frac{24}{7})\)

    Mfano\(\PageIndex{15}\)

    Tatua kutumia utawala wa Cramer:\(\left\{\begin{array} {l} −x+y=2\\2x+y=−4 \end{array} \right.\)

    Jibu

    \((−2,0)\)

    KUTATUA MFUMO WA EQUATIONS MBILI KWA KUTUMIA UTAWALA WA CRAMER.
    1. Tathmini ya kuamua D, kwa kutumia coefficients ya vigezo.
    2. Tathmini ya kuamua\(D_x\). Tumia mara kwa mara badala ya coefficients x.
    3. Tathmini ya kuamua\(D_y\). Tumia mara kwa mara badala ya coefficients y.
    4. Kupata x na y. \(x=\frac{D_x}{D}\),\(y=\frac{D_y}{D}\)
    5. Andika suluhisho kama jozi iliyoamriwa.
    6. Angalia kwamba jozi iliyoamriwa ni suluhisho la equations zote za awali.

    Ili kutatua mfumo wa milinganyo tatu na vigezo tatu na Utawala Cramer ya, sisi kimsingi kufanya kile tulichofanya kwa mfumo wa milinganyo mbili. Hata hivyo, sasa tunapaswa kutatua kwa vigezo vitatu ili kupata suluhisho. Maamuzi pia yatakuwa\(3×3\) ambayo yatafanya kazi yetu kuvutia zaidi!

    UTAWALA WA CRAMER WA KUTATUA MFUMO WA EQUATIONS TATU

    Kwa mfumo wa equations\(\left\{\begin{array} {l} a_1x+b_1y+c_1z=k_1\\a_2x+b_2y+c_2z=k_2\\a_3x+b_3y+c_3z=k_3\end{array}\right.\), suluhisho\((x,y,z)\) linaweza kuamua na

    x ni Dx juu ya D, y ni Dy juu ya D na z ni Dz juu D, ambapo D ni kuamua na mstari 1: a1, b1, c1, mstari 2: a2, b2, c2, mstari 3: a3, b3, c3, kutumia coefficients ya vigezo; Dx ni kuamua na mstari 1: k1, b1, c1, mstari 2: k2, b2, c2 na rwo 3: k3, b3, c3, badala ya coefficients x na konsonants; Dy ni kuamua na mstari wa 1: a1, k1, c1, mstari wa 2: a2, k2, c2 na mstari wa 3: a3, k3, c3, badala ya coefficients y na mara kwa mara; Dz ni kuamua na mstari wa 1: a1, b1, k1; mstari wa 2: a2, b2, k2, mstari 3: a3, b3, k3; kuchukua nafasi ya coefficients z na conficients stanti.

    Mfano\(\PageIndex{16}\)

    Tatua mfumo wa equations kwa kutumia Kanuni ya Cramer:\(\left\{\begin{array} {l} 3x−5y+4z=5\\5x+2y+z=0\\2x+3y−2z=3 \end{array} \right.\)

    Jibu
    Tathmini ya kuamua D. .
    Panua na watoto kwa kutumia safu ya 1.  
    . .
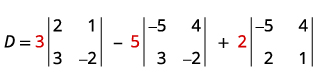
    Tathmini maamuzi. .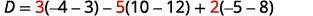
    Kurahisisha. .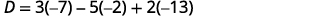
    Kurahisisha. .
    Kurahisisha. .
    Tathmini ya kuamua\(D_x\). Tumia mara kwa
    mara kuchukua nafasi ya coefficients ya x.    		 .
    Panua na watoto kwa kutumia safu ya 1. .
    Tathmini maamuzi. .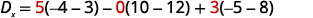
    Kurahisisha. .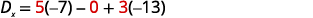
    Kurahisisha. .
    Tathmini Dy.Dy ya kuamua. Tumia mara kwa
    mara kuchukua nafasi ya coefficients ya y.    		 .
    . .
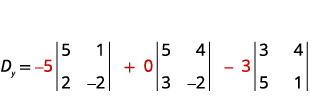
    Tathmini maamuzi. .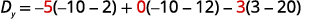
    Kurahisisha. .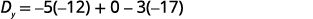
    Kurahisisha. .
    Kurahisisha. .
    Tathmini Dz.Dz inayoamua. Tumia mara kwa
    mara kuchukua nafasi ya coefficients ya z.    		 .
    . .
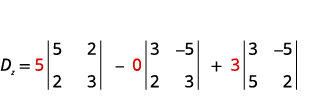
    Tathmini maamuzi. .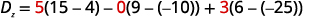
    Kurahisisha. .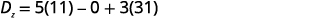
    Kurahisisha. .
    Kurahisisha. .
    Pata x, y, na z. .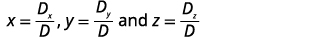
    Mbadala katika maadili. .
    Kurahisisha. .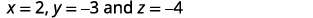
    Andika suluhisho kama mara tatu iliyoamriwa. .
    Angalia kwamba mara tatu zilizoamriwa ni suluhisho la
    milinganyo yote matatu ya awali.    		 Tunaacha hundi kwako.
      Suluhisho ni\((2,−3,−4)\).
    Mfano\(\PageIndex{17}\)

    Tatua mfumo wa equations kwa kutumia Kanuni ya Cramer:\(\left\{\begin{array} {l} 3x+8y+2z=−5\\2x+5y−3z=0\\x+2y−2z=−1 \end{array} \right.\)

    Jibu

    \((−9,3,−1)\)

    Mfano\(\PageIndex{18}\)

    Tatua mfumo wa equations kwa kutumia Kanuni ya Cramer:\(\left\{\begin{array} {l} 3x+y−6z=−3\\2x+6y+3z=0\\3x+2y−3z=−6 \end{array} \right.\)

    Jibu

    \((−6,3,−2)\)

    Utawala Cramer haifanyi kazi wakati thamani ya D determinant ni 0, kama hii itakuwa na maana tutakuwa kugawa na 0. Lakini wakati\(D=0\), mfumo ni ama haiendani au tegemezi.

    Wakati thamani ya\(D=0\)\(D_x,\space D_y\) na D yote ni sifuri, mfumo huo ni thabiti na unategemea na kuna ufumbuzi mkubwa sana.

    Wakati thamani ya\(D=0\)\(D_x,\space D_y\) na\(D_z\) si wote sifuri, mfumo haukubaliani na hakuna suluhisho.

    MIFUMO YA TEGEMEZI NA ISIYO YA KAWAIDA

    Kwa mfumo wowote wa equations, ambapo thamani ya kuamua\(D=0\),

    \[ \begin{array} {lll} \textbf{Value of determinants} &\textbf{Type of system} &\textbf{Solution} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are all zero}} &\text{consistent and dependent} &\text{infinitely many solutions} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are not all zero}} &\text{inconsistent} &\text{no solution} \end{array} \nonumber\]

    Katika mfano unaofuata, tutatumia maadili ya vigezo ili kupata suluhisho la mfumo.

    Mfano\(\PageIndex{19}\)

    Tatua mfumo wa equations kwa kutumia utawala wa Cramer:\(\left\{\begin{array} {l} x+3y=4\\−2x−6y=3 \end{array} \right.\)

    Jibu

    \(\begin{array} {ll} {} &{\left\{\begin{array} {l} x+3y=4\\−2x−6y=3 \end{array} \right.} \\ {\begin{array} {l} \text{Evaluate the determinantD,using the} \\ \text{coefficients of the variables.} \end{array}} &{D=\left|\begin{matrix} 1&3\\−2&−6\end{matrix}\right|} \\ {} &{D=−6−(−6)} \\ {} &{D=0} \end{array} \)

    Hatuwezi kutumia Cramer's Rule kutatua mfumo huu. Lakini kwa kuangalia thamani ya determinants\(D_x\) na\(D_y\), tunaweza kuamua kama mfumo ni tegemezi au haiendani.

    \(\begin{array} {ll} {\text{Evaluate the determinant }D_x.} &{D_x=\left|\begin{matrix} 4&3\\3&−6\end{matrix}\right|} \\ {} &{D_x=−24−9} \\ {} &{D_x=15} \end{array} \)

    Kwa kuwa uamuzi wote sio sifuri, mfumo haukubaliani. Hakuna suluhisho.

    Mfano\(\PageIndex{20}\)

    Tatua mfumo wa equations kwa kutumia utawala wa Cramer:\(\left\{\begin{array} {l} 4x−3y=8\\8x−6y=14 \end{array} \right.\)

    Jibu

    hakuna suluhisho

    Mfano\(\PageIndex{21}\)

    Tatua mfumo wa equations kwa kutumia utawala wa Cramer:\(\left\{\begin{array} {l} x=−3y+4\\2x+6y=8 \end{array} \right.\)

    Jibu

    ufumbuzi usio na mwisho

    Tatua Maombi kwa kutumia Maamuzi

    Matumizi ya kuvutia ya maamuzi inatuwezesha kupima ikiwa pointi ni collinear. pointi tatu\((x_1,y_1)\),\((x_2,y_2)\) na\((x_3,y_3)\) ni collinear kama na tu kama determinant chini ni sifuri.

    \[\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{matrix}\right|=0\nonumber\]

    MTIHANI KWA POINTI COLINEAR

    pointi tatu\((x_1,y_1)\),\((x_2,y_2)\) na\((x_3,y_3)\) ni collinear kama na tu kama

    \[\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{matrix}\right|=0\nonumber\]

    Tutatumia mali hii katika mfano unaofuata.

    Mfano\(\PageIndex{22}\)

    Kuamua kama pointi\((5,−5)\),\((4,−3)\), na\((3,−1)\) ni collinear.

    Jibu
      .
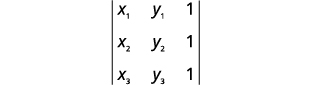
    Badilisha maadili katika uamuzi.
    \((5,−5)\),\((4,−3)\), na\((3,−1)\)    		 .
    Tathmini ya kuamua kwa kupanua
    na watoto kutumia safu ya 3.    		 .
    Tathmini maamuzi. .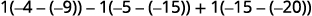
    Kurahisisha. .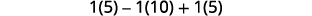
    Kurahisisha. .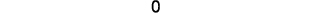
      Thamani ya kuamua ni 0, hivyo
    pointi ni collinear.
    Mfano\(\PageIndex{23}\)

    Kuamua kama pointi\((3,−2)\),\((5,−3)\), na\((1,−1)\) ni collinear.

    Jibu

    ndiyo

    Mfano\(\PageIndex{24}\)

    Kuamua kama pointi\((−4,−1)\),\((−6,2)\), na\((−2,−4)\) ni collinear.

    Jibu

    ndiyo

    Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na mifumo ya kutatua usawa wa mstari kwa kuchora.

    • Kutatua Mifumo ya Usawa wa Linear kwa Graph
    • Mifumo ya kutofautiana kwa mstari

    Dhana muhimu

    • Determinant: Determinant ya tumbo yoyote mraba\(\left[\begin{matrix}a&b\\c&d\end{matrix}\right]\), ambapo a, b, c, na d ni idadi halisi, ni

      \[\left|\begin{matrix}a&b\\c&d\end{matrix}\right|=ad−bc\nonumber\]

    • Kupanua na Watoto pamoja Row Kwanza Kutathmini 3 × 3 Determinant: Kutathmini\(3×3\) determinant kwa kupanua na watoto pamoja mstari wa kwanza, mfano zifuatazo:
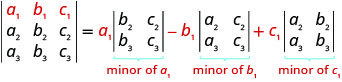
      A 3 na 3 determinant ni sawa na mara A1 madogo ya A1 bala mara b1 madogo ya b1 pamoja na c1 mara madogo ya c1.
    • Ishara Pattern: Wakati kupanua na watoto kutumia mstari au safu, ishara ya maneno katika upanuzi kufuata muundo zifuatazo.

      \[\left|\begin{matrix}+&−&+\\−&+&−\\+&−&+\end{matrix}\right|\nonumber\]

    • Utawala wa Cramer: Kwa mfumo wa equations\(\left\{\begin{array} {l} a_1x+b_1y=k_1\\a_2x+b_2y=k_2\end{array}\right.\), suluhisho\((x,y)\) linaweza kuamua na
      x ni Dx juu ya D na y ni Dy juu ya D ambapo D ni kuamua na mstari wa 1: a1, b1 na mstari 2 a2, B2, kutumia coefficients ya vigezo; Dx ni kuamua na mstari 1: k1, b1 na mstari 2: k2, b2, badala ya coefficients x na konsonanti; Dy ni kuamua na mstari 1: a1, k1 na mstari 2: a2, k2 2, badala ya y coefficients na constants.
      Taarifa kwamba ili kuunda D inayoamua, tunatumia kuchukua coefficients ya vigezo.
    • Jinsi ya kutatua mfumo wa equations mbili kwa kutumia utawala wa Cramer.
      1. Tathmini ya kuamua D, kwa kutumia coefficients ya vigezo.
      2. Tathmini ya kuamua\(D_x\). Tumia mara kwa mara badala ya coefficients x.
      3. Tathmini ya kuamua\(D_y\). Tumia mara kwa mara badala ya coefficients y.
      4. Kupata x na y. \(x=\frac{D_x}{D}\),\(y=\frac{D_y}{D}\).
      5. Andika suluhisho kama jozi iliyoamriwa.
      6. Angalia kwamba jozi iliyoamriwa ni suluhisho la equations zote za awali.
      7. Tegemezi na haiendani Systems ya Equations: Kwa mfumo wowote wa equations, ambapo thamani ya determinant\(D=0\),\[ \begin{array} {lll} \textbf{Value of determinants} &\textbf{Type of system} &\textbf{Solution} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are all zero}} &\text{consistent and dependent} &\text{infinitely many solutions} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are not all zero}} &\text{inconsistent} &\text{no solution} \end{array} \nonumber\]
      8. Mtihani kwa Collinear Points: pointi tatu\((x_1,y_1)\)\((x_2,y_2)\),, na\((x_3,y_3)\) ni collinear kama na tu kama

        \[\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{matrix}\right|=0\nonumber\]

    faharasa

    kiamuzi
    Kila tumbo la mraba lina namba halisi inayohusishwa nayo inayoitwa uamuzi wake.
    madogo ya kuingia katika 3×33×3 determinant
    Mdogo wa kuingia katika determinant 3×33×3 ni determinant 2×22×2 inayopatikana kwa kuondoa mstari na safu katika 3×33×3determinant ambayo ina kuingia.
    matrix mraba
    Matrix ya mraba ni tumbo yenye idadi sawa ya safu na nguzo.