Skip to main content
Global

4.6: Tatua Mifumo ya Equations Kutumia Matrices

  1. Last updated
  2. Save as PDF
  • Page ID
    175801

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Andika tumbo la kuongezeka kwa mfumo wa equations
    • Tumia shughuli za mstari kwenye tumbo
    • Tatua mifumo ya equations kwa kutumia matrices

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Kutatua:\(3(x+2)+4=4(2x−1)+9\).
      Ikiwa umekosa tatizo hili, tathmini [kiungo].
    2. Kutatua:\(0.25p+0.25(x+4)=5.20\).
      Ikiwa umekosa tatizo hili, tathmini [kiungo].
    3. Tathmini\(x=−2\) lini na\(y=3:2x^2−xy+3y^2\).
      Ikiwa umekosa tatizo hili, tathmini [kiungo].

    Andika Matrix iliyoongezwa kwa Mfumo wa Ulinganisho

    Kutatua mfumo wa equations inaweza kuwa operesheni ya kuchochea ambapo kosa rahisi linaweza kuharibu juu ya kutafuta suluhisho. Njia mbadala ambayo inatumia taratibu za msingi za kuondoa lakini kwa notation ambayo ni rahisi inapatikana. Njia hii inahusisha kutumia tumbo. Matrix ni safu ya namba ya mstatili iliyopangwa katika safu na nguzo.

    MATRIX

    Matrix ni safu ya namba ya mstatili iliyopangwa katika safu na nguzo.

    Matrix yenye safu m na nguzo n ina utaratibu\(m\times n\). Matrix upande wa kushoto chini ina safu 2 na nguzo 3 na hivyo ina utaratibu\(2\times 3\). Tunasema ni 2 na 3 Matrix.

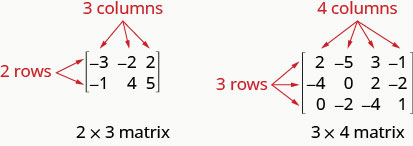
    Kielelezo kinaonyesha matrices mbili. Yule upande wa kushoto ina idadi ndogo ya 3, minus 2 na 2 katika mstari wa kwanza na idadi ndogo ya 1, 4 na 5 katika mstari wa pili. Safu na nguzo zimefungwa ndani ya mabano. Hivyo, ina safu 2 na nguzo 3. Ni kinachoitwa 2 msalaba 3 au 2 na 3 matrix. Matrix upande wa kulia ni sawa lakini kwa safu 3 na nguzo 4. Inaandikwa 3 na 4 matrix.

    Kila namba katika tumbo inaitwa kipengele au kuingia kwenye tumbo.

    Tutatumia tumbo kuwakilisha mfumo wa equations linear. Tunaandika kila equation katika fomu ya kawaida na coefficients ya vigezo na mara kwa mara ya kila equation inakuwa mstari katika tumbo. Kila safu basi itakuwa coefficients ya moja ya vigezo katika mfumo au constants. Mstari wa wima hubadilisha ishara sawa. Tunaita tumbo la kusababisha tumbo la kuongezeka kwa mfumo wa equations.

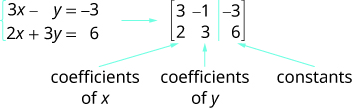
    equations ni 3x pamoja y sawa bala 3 na 2x pamoja 3y sawa 6. Matrix 2 na 3 inavyoonyeshwa. Mstari wa kwanza ni 3, 1, chini ya 3. Mstari wa pili ni 2, 3, 6. Safu ya kwanza ni lebo coefficients ya x. safu ya pili ni lebo coefficients ya y na ya tatu ni kinachoitwa constants.

    Angalia safu ya kwanza imeundwa na coefficients zote za x, safu ya pili ni coefficients yote ya y, na safu ya tatu ni mara kwa mara.

    Mfano\(\PageIndex{1}\)

    ⓐ\(\left\{ \begin{array} {l} 5x−3y=−1 \\ y=2x−2 \end{array} \right. \) ⓑ\( \left\{ \begin{array} {l} 6x−5y+2z=3 \\ 2x+y−4z=5 \\ 3x−3y+z=−1 \end{array} \right. \)

    Jibu

    ⓐ equation pili si katika hali ya kawaida. Tunaandika upya equation ya pili katika fomu ya kawaida.

    \[\begin{aligned} y=2x−2 \\ −2x+y=−2 \end{aligned} \nonumber\]

    Sisi kuchukua nafasi ya equation ya pili na fomu yake ya kawaida. Katika tumbo la kuongezeka, equation ya kwanza inatupa mstari wa kwanza na equation ya pili inatupa mstari wa pili. Mstari wa wima hubadilisha ishara sawa.

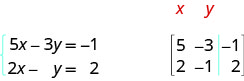
    equations ni 3x pamoja y sawa bala 3 na 2x pamoja 3y sawa 6. Matrix 2 na 3 inavyoonyeshwa. Mstari wa kwanza ni 3, 1, chini ya 3. Mstari wa pili ni 2, 3, 6. Safu ya kwanza ni lebo coefficients ya x. safu ya pili ni lebo coefficients ya y na ya tatu ni kinachoitwa constants.

    ⓑ equations zote tatu ziko katika fomu ya kawaida. Katika tumbo iliyoimarishwa equation ya kwanza inatupa mstari wa kwanza, equation ya pili inatupa mstari wa pili, na equation ya tatu inatupa mstari wa tatu. Mstari wa wima hubadilisha ishara sawa.

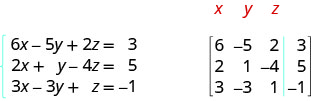
    equations ni 6x minus 5y pamoja 2z sawa 3, 2x pamoja y minus 4z sawa 5 na 3x minus 3y pamoja z sawa bala 1. Matrix 4 na 3 inavyoonyeshwa ambao mstari wa kwanza ni 6, chini ya 5, 2, 3. Mstari wake wa pili ni 2, 1, minus 4, 5. Mstari wake wa tatu ni 3, chini ya 3, 1 na chini ya 1. Nguzo zake tatu za kwanza zimeandikwa x, y na z kwa mtiririko huo.

    Mfano\(\PageIndex{2}\)

    Andika kila mfumo wa equations linear kama tumbo augmented:

    ⓐ\(\left\{ \begin{array} {l} 3x+8y=−3 \\ 2x=−5y−3 \end{array} \right. \) ⓑ\(\left\{ \begin{array} {l} 2x−5y+3z=8 \\ 3x−y+4z=7 \\ x+3y+2z=−3 \end{array} \right. \)

    Jibu

    ⓐ\(\left[ \begin{matrix} 3 &8 &-3 \\ 2 &5 &−3 \end{matrix} \right] \)

    ⓑ\(\left[ \begin{matrix} 2 &3 &1 &−5 \\ −1 &3 &3 &4 \\ 2 &8 &7 &−3 \end{matrix} \right] \)

    Mfano\(\PageIndex{3}\)

    Andika kila mfumo wa equations linear kama tumbo augmented:

    ⓐ\(\left\{ \begin{array} {l} 11x=−9y−5 \\ 7x+5y=−1 \end{array} \right. \) ⓑ\(\left\{ \begin{array} {l} 5x−3y+2z=−5 \\ 2x−y−z=4 \\ 3x−2y+2z=−7 \end{array} \right. \)

    Jibu

    ⓐ\(\left[ \begin{matrix} 11 &9 &−5 \\ 7 &5 &−1 \end{matrix} \right] \)
    ⓑ\(\left[ \begin{matrix} 5 &−3 &2 &−5 \\ 2 &−1 &−1 &4 \\ 3 &−2 &2 &−7 \end{matrix} \right] \)

    Ni muhimu kama sisi kutatua mifumo ya equations kutumia matrices kuwa na uwezo wa kwenda na kurudi kati ya mfumo na tumbo. Mfano unaofuata unatuuliza kuchukua habari katika tumbo na kuandika mfumo wa equations.

    Mfano\(\PageIndex{4}\)

    Andika mfumo wa equations unaofanana na tumbo la kuongezeka:

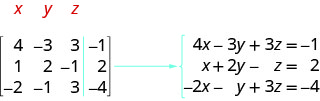
    \(\left[ \begin{array} {ccc|c} 4 &−3 &3 &−1 \\ 1 &2 &−1 &2 \\ −2 &−1 &3 &−4 \end{array} \right] \).

    Jibu

    Tunakumbuka kwamba kila mstari inalingana na equation na kwamba kila kuingia ni mgawo wa kutofautiana au mara kwa mara. Mstari wa wima hubadilisha ishara sawa. Kwa kuwa tumbo hii ni\(4\times 3\), tunajua itakuwa kutafsiri katika mfumo wa milinganyo tatu na vigezo tatu.

    Matrix 3 na 4 inavyoonyeshwa. Mstari wake wa kwanza ni 4, chini ya 3, 3, chini ya 1. Mstari wake wa pili ni 1, 2, chini ya 1, 2. Mstari wake wa tatu ni chini ya 2, chini ya 1, 3, minus 4. equations tatu ni 4x minus 3y pamoja 3z sawa minus 1, x pamoja 2y minus z sawa 2 na minus 2x minus y pamoja 3z sawa minus 4.

    Mfano\(\PageIndex{5}\)

    Andika mfumo wa equations unaofanana na tumbo la kuongezeka:\(\left[ \begin{matrix} 1 &−1 &2 &3 \\ 2 &1 &−2 &1 \\ 4 &−1 &2 &0 \end{matrix} \right] \).

    Jibu

    \(\left\{ \begin{array} {l} x−y+2z=3 \\ 2x+y−2z=1 \\ 4x−y+2z=0 \end{array} \right.\)

    Mfano\(\PageIndex{6}\)

    Andika mfumo wa equations unaofanana na tumbo la kuongezeka:\(\left[ \begin{matrix} 1 &1 &1 &4 \\ 2 &3 &−1 &8 \\ 1 &1 &−1 &3 \end{matrix} \right] \).

    Jibu

    \(\left\{ \begin{array} {l} x+y+z=4 \\ 2x+3y−z=8 \\ x+y−z=3 \end{array} \right.\)

    Matumizi Row Operations juu ya Matrix

    Mara baada ya mfumo wa equations iko katika fomu yake ya tumbo iliyoongezeka, tutafanya shughuli kwenye safu ambazo zitatuongoza kwenye suluhisho.

    Ili kutatua kwa kuondoa, haijalishi ni utaratibu gani tunaweka equations katika mfumo. Vile vile, katika tumbo tunaweza kubadilishana safu.

    Wakati sisi kutatua kwa kuondoa, mara nyingi sisi kuzidisha moja ya equations kwa mara kwa mara. Kwa kuwa kila mstari inawakilisha equation, na tunaweza kuzidisha kila upande wa equation na mara kwa mara, vile vile tunaweza kuzidisha kila kuingia katika mstari na idadi yoyote halisi isipokuwa 0.

    Katika kuondoa, mara nyingi tunaongeza mfululizo wa mstari mmoja hadi mstari mwingine. Katika tumbo tunaweza kuchukua nafasi ya mstari na jumla yake na mfululizo wa mstari mwingine.

    Hatua hizi huitwa shughuli za mstari na zitatusaidia kutumia tumbo kutatua mfumo wa equations.

    SHUGHULI ROW

    Katika tumbo, shughuli zifuatazo zinaweza kufanywa kwenye mstari wowote na tumbo linalosababisha itakuwa sawa na tumbo la awali.

    1. Kubadilishana safu yoyote mbili.
    2. Kuzidisha mstari kwa idadi yoyote halisi isipokuwa 0.
    3. Ongeza nonzero nyingi ya mstari mmoja hadi mstari mwingine.

    Kufanya shughuli hizi ni rahisi kufanya lakini hesabu zote zinaweza kusababisha kosa. Ikiwa tunatumia mfumo wa kurekodi operesheni ya mstari katika kila hatua, ni rahisi kurudi na kuangalia kazi yetu.

    Tunatumia barua kuu na michango ili kuwakilisha kila mstari. Kisha tunaonyesha operesheni upande wa kushoto wa tumbo mpya. Ili kuonyesha kubadilishana mstari:

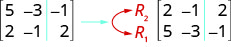
    Matrix 2 na 3 inavyoonyeshwa. Mstari wake wa kwanza, ulioitwa R2 ni 2, chini ya 1, 2. Mstari wake wa pili, ulioitwa R1 ni 5, chini ya 3, chini ya 1.

    Ili kuzidisha mstari wa 2 na\(−3\):

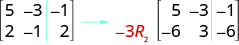
    Matrix 2 na 3 inavyoonyeshwa. Mstari wake wa kwanza ni 5, chini ya 3, chini ya 1. Mstari wake wa pili ni 2, chini ya 1, 2. Mshale wa mshale kutoka kwenye tumbo hili hadi mwingine upande wa kulia. Mstari wa kwanza wa tumbo mpya ni sawa. Mstari wa pili unatanguliwa na chini ya 3 R2. Ni chini ya 6, 3, minus 6.

    Ili kuzidisha mstari wa 2\(−3\) na na uongeze kwenye mstari wa 1:

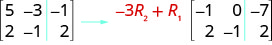
    Matrix 2 na 3 inavyoonyeshwa. Mstari wake wa kwanza ni 5, chini ya 3, chini ya 1. Mstari wake wa pili ni 2, chini ya 1, 2. Mshale wa mshale kutoka kwenye tumbo hili hadi mwingine upande wa kulia. Mstari wa kwanza wa tumbo mpya unatanguliwa na minus 3 R2 pamoja na R1. Ni chini ya 1, 0, minus 7. Mstari wa pili ni 2, chini ya 1, 2.

    Mfano\(\PageIndex{7}\)

    Fanya shughuli zilizoonyeshwa kwenye tumbo la kuongezeka:

    ⓐ Kubadilishana safu 2 na 3.

    ⓑ Kuzidisha mstari 2 na 5.

    ⓒ Ongeza mstari wa 3 na -2—2 na uongeze mstari wa 1.

    \( \left[ \begin{array} {ccc|c} 6 &−5 &2 &3 \\ 2 &1 &−4 &5 \\ 3 &−3 &1 &−1 \end{array} \right] \)

    Jibu

    ⓐ Sisi kubadilishana safu 2 na 3.

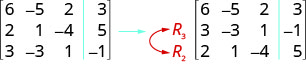
    Mbili 3 na 4 matrices zinaonyeshwa. Katika moja upande wa kushoto, mstari wa kwanza ni 6, chini ya 5, 2, 3. Mstari wa pili ni 2, 1, minus 4, 5. Mstari wa tatu ni 3, chini ya 3, 1, chini ya 1. Matrix ya pili ni sawa isipokuwa kwamba safu 2 na 3 zinabadilishana.

    ⓑ Tunazidisha mstari wa 2 na 5.

    Mbili 3 na 4 matrices zinaonyeshwa. Katika moja upande wa kushoto, mstari wa kwanza ni 6, chini ya 5, 2, 3. Mstari wa pili ni 2, 1, minus 4, 5. Mstari wa tatu ni 3, chini ya 3, 1, chini ya 1. Matrix ya pili ni sawa na ya kwanza isipokuwa mstari huo wa 2, uliotanguliwa na 5 R2, ni 10, 5, chini ya 20, 25.

    ⓒ Tunazidisha mstari wa 3\(−2\) na kuongeza mstari wa 1.

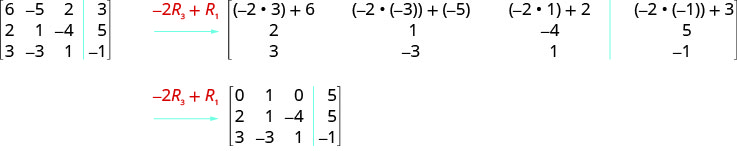
    Katika tumbo la 3 na 4, mstari wa kwanza ni 6, chini ya 5, 2, 3. Mstari wa pili ni 2, 1, minus 4, 5. Mstari wa tatu ni 3, chini ya 3, 1, chini ya 1. Kufanya operesheni minus 2 R3 pamoja na R1 kwenye mstari wa kwanza, mstari wa kwanza unakuwa 6 pamoja na mara 2 minus 3, bala 5 pamoja na mara 2 minus 3, 2 pamoja na bala mara 2 1 na 3 pamoja na mara 2 minus 1. Hii inakuwa 0, 1, 0, 5. Safu mbili zilizobaki za tumbo mpya ni sawa.

    Mfano\(\PageIndex{8}\)

    Fanya shughuli zilizoonyeshwa kwenye tumbo la kuongezeka:

    ⓐ Kubadilishana safu 1 na 3.

    ⓑ Kuzidisha mstari 3 na 3.

    ⓒ Kuzidisha mstari 3 na 2 na kuongeza mstari 2.

    \( \left[ \begin{array} {ccc|c} 5 &−2 &-2 &-2 \\ 4 &-1 &−4 &4 \\ -2 &3 &0 &−1 \end{array} \right] \)

    Jibu

    ⓐ\( \left[ \begin{matrix} −2 &3 &0 &−2 \\ 4 &−1 &−4 &4 \\ 5 &−2 &−2 &−2 \end{matrix} \right] \)

    ⓑ\( \left[ \begin{matrix} −2 &3 &0 &−2 \\ 4 &−1 &−4 &4 \\ 15 &−6 &−6 &−6 \end{matrix} \right] \)

    ⓒ\( \left[ \begin{matrix} -2 &3 &0 &2 & \\ 3 &4 &-13 &-16 &-8 \\ 15 &-6 &-6 &-6 & \end{matrix} \right] \)

    Mfano\(\PageIndex{9}\)

    Fanya shughuli zilizoonyeshwa kwenye tumbo la kuongezeka:

    ⓐ Kubadilishana safu 1 na 2,

    ⓑ Kuzidisha mstari 1 na 2,

    ⓒ Kuzidisha mstari 2 na 3 na kuongeza mstari 1.

    \( \left[ \begin{array} {ccc|c} 2 &−3 &−2 &−4 \\ 4 &1 &−3 &2 \\ 5 &0 &4 &−1 \end{array} \right] \)

    Jibu

    ⓐ\( \left[ \begin{matrix} 4 &1 &−3 &2 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right] \)
    ⓑ\( \left[ \begin{matrix} 8 &2 &−6 &4 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right] \)
    ⓒ\( \left[ \begin{matrix} 14 &−7 &−12 &−8 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right] \)

    Sasa kwa kuwa tumefanya shughuli za mstari, tutaangalia tumbo la kuongezeka na tutafahamu operesheni gani tutakayotumia kufikia lengo. Hii ndio hasa tulivyofanya wakati tulifanya kuondoa. Tuliamua nini idadi ya kuzidisha mstari na ili variable itakuwa kuondolewa wakati sisi aliongeza safu pamoja.

    Kutokana na mfumo huu, ungefanya nini ili kuondoa x?

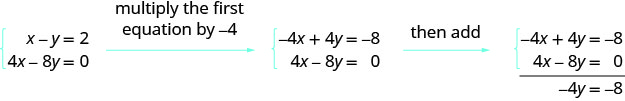
    equations mbili ni x minus y sawa 2 na 4x minus 8y sawa 0. Kuzidisha kwanza kwa minus 4, tunapata minus 4x pamoja na 4y sawa na minus 8. Kuongeza hii kwa equation pili sisi kupata minus 4y sawa minus 8.

    Mfano huu unaofuata kimsingi hufanya kitu kimoja, lakini kwa tumbo.

    Mfano\(\PageIndex{10}\)

    Fanya operesheni inayohitajika ya mstari ambayo itapata kuingia kwanza katika mstari wa 2 kuwa sifuri katika tumbo la kuongezeka:\( \left[ \begin{array} {cc|c} 1 &−1 &2 \\ 4 &−8 &0 \end{array} \right] \)

    Jibu

    Kufanya 4 a 0, tunaweza kuzidisha mstari 1\(−4\) na kisha kuongeza kwa mstari 2.

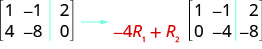
    Matrix 2 na 3 ni 1, minus 1, 2 na 4, minus 8, 0. Kufanya operesheni chini ya 4R1 pamoja na R2 kwenye mstari wa 2, mstari wa pili wa tumbo mpya inakuwa 0, chini ya 4, chini ya 8. Mstari wa kwanza unabaki sawa.

    Mfano\(\PageIndex{11}\)

    Fanya operesheni inayohitajika ya mstari ambayo itapata kuingia kwanza katika mstari wa 2 kuwa sifuri katika tumbo la kuongezeka:\( \left[ \begin{array} {cc|c} 1 &−1 &2 \\ 3 &−6 &2 \end{array} \right] \)

    Jibu

    \( \left[ \begin{matrix} 1 &−1 &2 \\ 0 &−3 &−4 \end{matrix} \right] \)

    Mfano\(\PageIndex{12}\)

    Fanya operesheni inayohitajika ya mstari ambayo itapata kuingia kwanza katika mstari wa 2 kuwa sifuri katika tumbo la kuongezeka:\( \left[ \begin{array} {cc|c} 1 &−1 &3 \\ -2 &−3 &2 \end{array} \right] \)

    Jibu

    \( \left[ \begin{matrix} 1 &−1 &3 \\ 0 &−5 &8 \end{matrix} \right] \)

    Kutatua Mifumo ya Equations Kutumia Matrices

    Ili kutatua mfumo wa equations kwa kutumia matrices, tunabadilisha tumbo la kuongezeka ndani ya tumbo katika fomu ya mstari-echelon kwa kutumia shughuli za mstari. Kwa mfumo thabiti na wa kujitegemea wa milinganyo, tumbo lake la kuongezeka liko katika fomu ya mfululizo wakati upande wa kushoto wa mstari wa wima, kila kuingia kwenye ulalo ni 1 na maingizo yote chini ya ulalo ni zero.

    FOMU YA MSTARI WA ECHELON

    Kwa mfumo thabiti na wa kujitegemea wa milinganyo, tumbo lake la kuongezeka liko katika fomu ya mfululizo wakati upande wa kushoto wa mstari wa wima, kila kuingia kwenye ulalo ni 1 na maingizo yote chini ya ulalo ni zero.

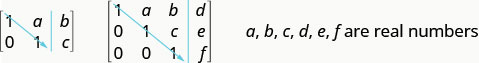
    Matrix 2 na 3 inavyoonyeshwa upande wa kushoto. Mstari wake wa kwanza ni 1, a, b. mstari wake wa pili ni 0, 1, c. mshale pointi diagonally chini na kulia, ukipishana wote 1s katika tumbo. Matrix 3 na 4 inavyoonyeshwa upande wa kulia. Mstari wake wa kwanza ni 1, a, b, d. mstari wake wa pili ni 0, 1, c, e.

    Mara tu sisi kupata tumbo augmented katika mstari-echelon fomu, tunaweza kuandika mfumo sawa wa equations na kusoma thamani ya angalau variable moja. Sisi kisha mbadala thamani hii katika equation mwingine kuendelea kutatua kwa vigezo vingine. Utaratibu huu unaonyeshwa katika mfano unaofuata.

    Jinsi ya Kutatua Mfumo wa Equations Kutumia Matrix

    Tatua mfumo wa equations kwa kutumia tumbo:\(\left\{ \begin{array} {l} 3x+4y=5 \\ x+2y=1 \end{array} \right. \)

    Jibu

    milinganyo ni 3x pamoja 4y sawa 5 na x pamoja 2y sawa 1. Hatua ya 1. Andika tumbo la kuongezeka kwa mfumo wa equations. Tunapata tumbo la 2 na 3 na mstari wa kwanza 3, 4, 5 na mstari wa pili 1, 2, 1.Hatua ya 2. Kutumia shughuli za mstari kupata kuingia katika mstari wa 1, safu ya 1 kuwa 1. Kubadilishana safu R1 na R2.Hatua ya 3. Kutumia shughuli za mstari, pata zero katika safu ya 1 chini ya 1. Panua mstari 1 na minus 3 na uongeze kwenye mstari wa 2. Row 2 inakuwa 0, chini ya 2, 2.Hatua ya 4. Kutumia shughuli za mstari, pata kuingia katika mstari wa 2, safu ya 2 kuwa 1. Panua mstari wa 2 kwa nusu ya chini. Row 2 inakuwa 0, 1, minus 1.Hatua ya 5. Endelea mchakato mpaka tumbo iko katika fomu ya mstari-echelon. Matrix sasa iko katika fomu ya mstari-echelon.Hatua ya 6. Andika mfumo unaofanana wa equations. Tunapata x plus 2y sawa na 1 na y sawa bala 1.Hatua ya 7. Tumia mbadala ili kupata vigezo vilivyobaki. Mbadala y sawa hasi 1 katika x plus 2y sawa 1. X pamoja 2 mara hasi 1 sawa 1. X minus 2 sawa 1. Tunapata x sawa na 3.Hatua ya 8. Andika suluhisho kama jozi iliyoamriwa au mara tatu. Jozi zilizoamriwa ni (3, hasi 1).Hatua ya 9. Angalia kwamba ufumbuzi hufanya milinganyo ya awali ya kweli.

    Mfano\(\PageIndex{14}\)

    Tatua mfumo wa equations kwa kutumia tumbo:\(\left\{ \begin{array} {l} 2x+y=7 \\ x−2y=6 \end{array} \right. \)

    Jibu

    Suluhisho ni\((4,−1)\).

    Mfano\(\PageIndex{15}\)

    Tatua mfumo wa equations kwa kutumia tumbo:\(\left\{ \begin{array} {l} 2x+y=−4 \\ x−y=−2 \end{array} \right. \)

    Jibu

    Suluhisho ni\((−2,0)\).

    Hatua hizi zimefupishwa hapa.

    KUTATUA MFUMO WA EQUATIONS KWA KUTUMIA MATRICES.
    1. Andika tumbo la kuongezeka kwa mfumo wa equations.
    2. Kutumia shughuli za mstari kupata kuingia katika mstari wa 1, safu ya 1 kuwa 1.
    3. Kutumia shughuli za mstari, pata zero katika safu ya 1 chini ya 1.
    4. Kutumia shughuli za mstari, pata kuingia katika mstari wa 2, safu ya 2 kuwa 1.
    5. Endelea mchakato mpaka tumbo iko katika fomu ya mstari-echelon.
    6. Andika mfumo unaofanana wa equations.
    7. Tumia mbadala ili kupata vigezo vilivyobaki.
    8. Andika suluhisho kama jozi iliyoamriwa au mara tatu.
    9. Angalia kwamba ufumbuzi hufanya milinganyo ya awali ya kweli.

    Hapa ni Visual kuonyesha utaratibu wa kupata 1 na 0 katika nafasi sahihi kwa fomu ya mstari-echelon.

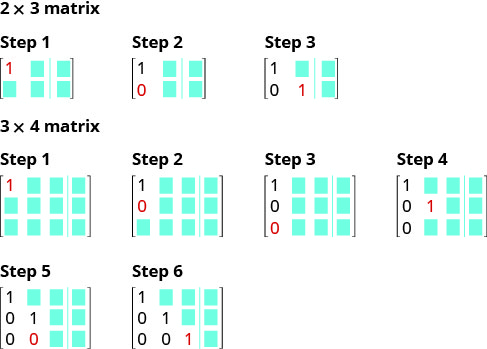
    Takwimu inaonyesha hatua 3 za tumbo la 2 na 3 na hatua 6 kwa tumbo la 3 na 4. Kwa zamani, hatua ya 1 ni kupata 1 mstari 1 safu 1. Hatua ya ni kupata 0 ni mstari 2 safu 1. Hatua ya 3 ni kupata 1 mfululizo 2 safu 2. Kwa matrix 3 na 4, hatua ya 1 ni kupata 1 mfululizo 1 safu 1. Hatua ya 2 ni kupata 0 katika safu ya 2 safu 1. Hatua ya 3 ni kupata 0 mfululizo 3 safu 1. Hatua ya 4 ni kupata 1 mfululizo 2 safu 2. Hatua ya 5 ni kupata 0 mfululizo 3 safu 2. Hatua ya 6 ni kupata 1 mfululizo 3 safu 3.

    Tunatumia utaratibu huo wakati mfumo wa equations una equations tatu.

    Mfano\(\PageIndex{16}\)

    Tatua mfumo wa equations kwa kutumia tumbo:\(\left\{ \begin{array} {l} 3x+8y+2z=−5 \\ 2x+5y−3z=0 \\ x+2y−2z=−1 \end{array} \right. \)

    Jibu
      .
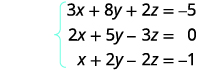
    Andika tumbo la kuongezeka kwa equations. .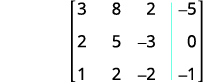
    Interchange mstari 1 na 3 kupata kuingia katika
    mstari wa 1, safu ya 1 kuwa 1.    		 .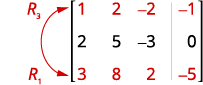
    Kutumia shughuli za mstari, pata zero katika safu ya 1 chini ya 1. .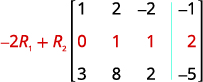
      .
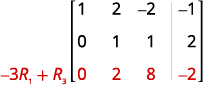
    Kuingia katika mstari wa 2, safu ya 2 sasa ni 1.  
    Endelea mchakato mpaka tumbo
    iko katika fomu ya mstari-echelon.    		 .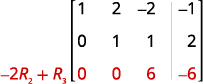
      .
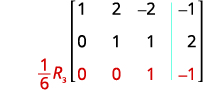
    Matrix sasa iko katika fomu ya mstari-echelon. .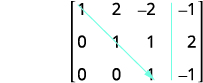
    Andika mfumo unaofanana wa equations. .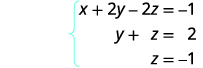
    Tumia mbadala ili kupata vigezo vilivyobaki. .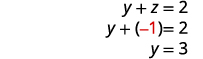
      .
    .
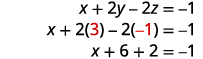
    Andika suluhisho kama jozi iliyoamriwa au mara tatu. .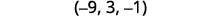
    Angalia kwamba ufumbuzi hufanya milinganyo ya awali ya kweli. Tunaacha hundi kwako.
    Mfano\(\PageIndex{17}\)

    Tatua mfumo wa equations kwa kutumia tumbo:\(\left\{ \begin{array} {l} 2x−5y+3z=8 \\ 3x−y+4z=7 \\ x+3y+2z=−3 \end{array} \right. \)

    Jibu

    \((6,−1,−3)\)

    Mfano\(\PageIndex{18}\)

    Tatua mfumo wa equations kwa kutumia tumbo:\(\left\{ \begin{array} {l} −3x+y+z=−4 \\ −x+2y−2z=1 \\ 2x−y−z=−1 \end{array} \right. \)

    Jibu

    \((5,7,4)\)

    Hadi sasa kazi yetu na matrices imekuwa tu na mifumo ambayo ni thabiti na kujitegemea, ambayo inamaanisha kuwa na suluhisho moja. Hebu sasa angalia nini kinatokea wakati sisi kutumia tumbo kwa mfumo tegemezi au haiendani.

    Mfano\(\PageIndex{19}\)

    Tatua mfumo wa equations kwa kutumia tumbo:\(\left\{ \begin{array} {l} x+y+3z=0 \\ x+3y+5z=0 \\ 2x+4z=1 \end{array} \right. \)

    Jibu
      .
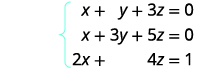
    Andika tumbo la kuongezeka kwa equations. .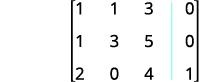
    Kuingia katika mstari wa 1, safu ya 1 ni 1.  
    Kutumia shughuli za mstari, pata zero katika safu ya 1 chini ya 1. .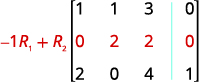
      .
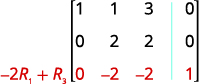
    Endelea mchakato mpaka tumbo iko katika fomu ya mstari-echelon. .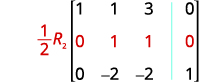
    Panua mstari wa 2 na 2 na uongeze kwenye mstari wa 3. .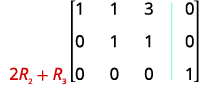
    Kwa hatua hii, tuna zero zote upande wa kushoto wa mstari wa 3.  
    Andika mfumo unaofanana wa equations. .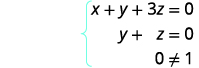
    Kwa kuwa\(0 \neq 1 \) tuna taarifa ya uongo. Kama vile wakati sisi kutatuliwa mfumo kwa kutumia mbinu nyingine, hii inatuambia tuna mfumo haiendani. Hakuna suluhisho.
    Mfano\(\PageIndex{20}\)

    Tatua mfumo wa equations kwa kutumia tumbo:\(\left\{ \begin{array} {l} x−2y+2z=1 \\ −2x+y−z=2 \\ x−y+z=5 \end{array} \right. \)

    Jibu

    hakuna suluhisho

    Mfano\(\PageIndex{21}\)

    Tatua mfumo wa equations kwa kutumia tumbo:\(\left\{ \begin{array} {l} 3x+4y−3z=−2 \\ −2x+3y−z=−1 \\ 2x+y−2z=6 \end{array} \right. \)

    Jibu

    hakuna suluhisho

    Mfumo wa mwisho haukuwa sawa na hivyo haukuwa na ufumbuzi. Mfano unaofuata unategemea na una ufumbuzi mkubwa sana.

    Mfano\(\PageIndex{22}\)

    Tatua mfumo wa equations kwa kutumia tumbo:\(\left\{ \begin{array} {l} x−2y+3z=1 \\ x+y−3z=7 \\ 3x−4y+5z=7 \end{array} \right. \)

    Jibu
      .
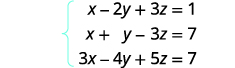
    Andika tumbo la kuongezeka kwa equations. .
    Kuingia katika mstari wa 1, safu ya 1 ni 1.  
    Kutumia shughuli za mstari, pata zero katika safu ya 1 chini ya 1. .
      .
    Endelea mchakato mpaka tumbo iko katika fomu ya mstari-echelon. .
    Panua mstari wa 2\(−2\) na uongeze kwenye mstari wa 3. .
    Kwa hatua hii, tuna zero zote katika mstari wa chini.  
    Andika mfumo unaofanana wa equations. .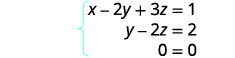
    Kwa kuwa\(0=0\) tuna taarifa ya kweli. Kama vile wakati sisi kutatuliwa na badala, hii inatuambia tuna mfumo tegemezi. Kuna ufumbuzi mkubwa sana.
    Tatua kwa y kwa suala la z katika equation ya pili. .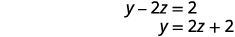
    Kutatua equation kwanza kwa x katika suala la z. .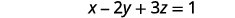
    Mbadala\(y=2z+2\). .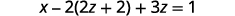
    Kurahisisha. .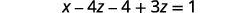
    Kurahisisha. .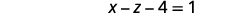
    Kurahisisha. .
    Mfumo una ufumbuzi mkubwa sana\((x,y,z)\), wapi\(x=z+5;\space y=2z+2;\space z\) nambari yoyote halisi.
    Mfano\(\PageIndex{23}\)

    Tatua mfumo wa equations kwa kutumia tumbo:\(\left\{ \begin{array} {l} x+y−z=0 \\ 2x+4y−2z=6 \\ 3x+6y−3z=9 \end{array} \right. \)

    Jibu

    kubwa ufumbuzi wengi\((x,y,z)\), ambapo\(x=z−3;\space y=3;\space z\) ni idadi yoyote halisi.

    Mfano\(\PageIndex{24}\)

    Tatua mfumo wa equations kwa kutumia tumbo:\(\left\{ \begin{array} {l} x−y−z=1 \\ −x+2y−3z=−4 \\ 3x−2y−7z=0 \end{array} \right. \)

    Jibu

    kubwa ufumbuzi wengi\((x,y,z)\), ambapo\(x=5z−2;\space y=4z−3;\space z\) ni idadi yoyote halisi.

    Kupata rasilimali hii online kwa maelekezo ya ziada na mazoezi na Gaussian Kutokomeza.

    • Kuondoa Gaussia

    Dhana muhimu

    • Matrix: Matrix ni safu ya mstatili wa namba zilizopangwa katika safu na nguzo. Matrix yenye safu m na nguzo n ina utaratibu\(m\times n\). Matrix upande wa kushoto chini ina safu 2 na nguzo 3 na hivyo ina utaratibu\(2\times 3\). Tunasema ni 2 na 3 Matrix.
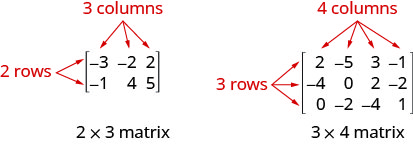
      Kielelezo kinaonyesha matrices mbili. Yule upande wa kushoto ina idadi ndogo ya 3, minus 2 na 2 katika mstari wa kwanza na idadi ndogo ya 1, 4 na 5 katika mstari wa pili. Safu na nguzo zimefungwa ndani ya mabano. Hivyo, ina safu 2 na nguzo 3. Ni kinachoitwa 2 msalaba 3 au 2 na 3 matrix. Matrix upande wa kulia ni sawa lakini kwa safu 3 na nguzo 4. Inaandikwa 3 na 4 matrix.
      Kila namba katika tumbo inaitwa kipengele au kuingia kwenye tumbo.
    • Uendeshaji wa Row: Katika tumbo, shughuli zifuatazo zinaweza kufanywa kwenye mstari wowote na tumbo linalosababisha litakuwa sawa na tumbo la awali.
      • Kubadilishana safu yoyote mbili
      • Panua mstari kwa nambari yoyote halisi isipokuwa 0
      • Ongeza nonzero nyingi ya mstari mmoja hadi mstari mwingine
    • Fomu ya mstari wa Echelon: Kwa mfumo thabiti na wa kujitegemea wa milinganyo, tumbo lake lililoongezeka liko katika fomu ya mstari wa mstari wa mstari wa wima, kila kuingia kwenye ulalo ni 1 na maingizo yote chini ya ulalo ni zero.
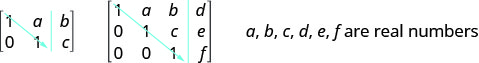
      Kielelezo kinaonyesha matrices mbili. Yule upande wa kushoto ina idadi ndogo ya 3, minus 2 na 2 katika mstari wa kwanza na idadi ndogo ya 1, 4 na 5 katika mstari wa pili. Safu na nguzo zimefungwa ndani ya mabano. Hivyo, ina safu 2 na nguzo 3. Ni kinachoitwa 2 msalaba 3 au 2 na 3 matrix. Matrix upande wa kulia ni sawa lakini kwa safu 3 na nguzo 4. Inaandikwa 3 na 4 matrix.
    • Jinsi ya kutatua mfumo wa equations kutumia matrices.
      1. Andika tumbo la kuongezeka kwa mfumo wa equations.
      2. Kutumia shughuli za mstari kupata kuingia katika mstari wa 1, safu ya 1 kuwa 1.
      3. Kutumia shughuli za mstari, pata zero katika safu ya 1 chini ya 1.
      4. Kutumia shughuli za mstari, pata kuingia katika mstari wa 2, safu ya 2 kuwa 1.
      5. Endelea mchakato mpaka tumbo iko katika fomu ya mstari-echelon.
      6. Andika mfumo unaofanana wa equations.
      7. Tumia mbadala ili kupata vigezo vilivyobaki.
      8. Andika suluhisho kama jozi iliyoamriwa au mara tatu.
      9. Angalia kwamba ufumbuzi hufanya milinganyo ya awali ya kweli.

    faharasa

    tumbo
    Matrix ni safu ya namba ya mstatili iliyopangwa katika safu na nguzo.
    fomu ya mstari-echelon
    Matrix iko katika fomu ya mstari-echelon wakati upande wa kushoto wa mstari wa wima, kila kuingia kwenye ulalo ni 1 na maingizo yote chini ya diagonal ni zero.