Skip to main content
Global

4.2: Tatua Mifumo ya Equations ya Mstari na Vigezo viwili

  1. Last updated
  2. Save as PDF
  • Page ID
    175965

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Kuamua kama jozi iliyoamriwa ni suluhisho la mfumo wa equations
    • Tatua mfumo wa equations linear kwa graphing
    • Tatua mfumo wa equations kwa kubadilisha
    • Tatua mfumo wa equations kwa kuondoa
    • Chagua njia rahisi zaidi ya kutatua mfumo wa equations linear

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Kwa equation\(y=\frac{2}{3}x−4\),
      ⓐ Je, ni\((6,0)\) suluhisho? ⓑ Je\((−3,−2)\), ni suluhisho?
      Ikiwa umekosa tatizo hili, tathmini [kiungo].
    2. Pata mteremko na y -intercept ya mstari\(3x−y=12\).
      Ikiwa umekosa tatizo hili, tathmini [kiungo].
    3. Pata x- na y -intercepts ya mstari\(2x−3y=12\).
      Ikiwa umekosa tatizo hili, tathmini [kiungo].

    Kuamua Kama Jozi Amri ni Suluhisho la Mfumo wa Equations

    Katika Kutatua Equations Linear, tulijifunza jinsi ya kutatua equations linear na variable moja. Sasa tutafanya kazi na equations mbili au zaidi linear makundi pamoja, ambayo inajulikana kama mfumo wa equations linear.

    MFUMO WA EQUATIONS LINEAR

    Wakati equations mbili au zaidi linear ni makundi pamoja, wao huunda mfumo wa equations linear.

    Katika sehemu hii, tutazingatia kazi yetu kwenye mifumo ya equations mbili za mstari katika haijulikani mbili. Sisi kutatua mifumo kubwa ya equations baadaye katika sura hii.

    Mfano wa mfumo wa equations mbili za mstari unaonyeshwa hapa chini. Sisi kutumia brace kuonyesha equations mbili ni makundi pamoja ili kuunda mfumo wa equations.

    \[ \left\{ \begin{aligned} 2x+y & = 7 \\ x−2y & = 6 \end{aligned} \right. \nonumber \]

    Equation linear katika vigezo mbili, kama vile\(2x+y=7\), ina idadi isiyo na mwisho ya ufumbuzi. Grafu yake ni mstari. Kumbuka, kila hatua kwenye mstari ni suluhisho la equation na kila ufumbuzi wa equation ni hatua kwenye mstari.

    Ili kutatua mfumo wa equations mbili za mstari, tunataka kupata maadili ya vigezo ambavyo ni ufumbuzi wa equations zote mbili. Kwa maneno mengine, tunatafuta jozi zilizoamriwa\((x,y)\) ambazo hufanya equations zote mbili kweli. Hizi huitwa ufumbuzi wa mfumo wa equations.

    UFUMBUZI WA MFUMO WA EQUATIONS

    Ufumbuzi wa mfumo wa equations ni maadili ya vigezo vinavyofanya equations zote kuwa kweli. Suluhisho la mfumo wa equations mbili za mstari unawakilishwa na jozi iliyoamriwa\((x,y)\).

    Kuamua kama jozi iliyoamriwa ni suluhisho la mfumo wa milinganyo miwili, tunabadilisha maadili ya vigezo katika kila equation. Ikiwa jozi iliyoamriwa inafanya equations zote mbili kweli, ni suluhisho la mfumo.

    Mfano\(\PageIndex{1}\)

    Kuamua kama jozi iliyoamriwa ni suluhisho la mfumo\(\left \{ \begin{array} {l} x−y = −1 \\ 2x−y = −5 \end{array} \right. \).

    ⓐ\((−2,−1)\) ⓑ\((−4,−3)\)

    Jibu

    ⓐ

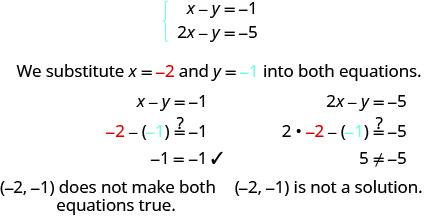
    Equations ni x minus y sawa na minus 1 na 2 x minus y sawa na minus 5. Sisi badala x sawa na minus 2 na y sawa na minus 1 katika equations zote mbili. Kwa hiyo, x minus y sawa na minus 1 inakuwa minus 2 minus mabano wazi minus 1 karibu mabano sawa au si sawa na minus 1. Kurahisisha, tunapata minus 1 sawa na 1 ambayo ni sahihi. Equation 2 x minus y sawa na minus 5 inakuwa mara 2 minus 2 minus mabano wazi minus 1 karibu mabano sawa au si sawa na minus 5. Kurahisisha, tunapata 5 si sawa na minus 5. Kwa hiyo, jozi iliyoamriwa minus 2, minus 1 haifanyi equations zote mbili kweli. Kwa hivyo, sio suluhisho.

    ⓑ

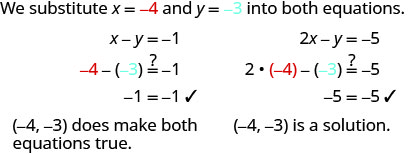
    Sisi badala x sawa na minus 4 na y sawa na minus 3 katika equations zote mbili. Kwa hiyo, x minus y sawa na minus 1 inakuwa minus 4 minus mabano wazi minus 3 karibu mabano sawa au si sawa na minus 1. Kurahisisha, tunapata minus 1 sawa na 1, ambayo ni sahihi. Equation 2 x minus y sawa na minus 5 inakuwa mara 2 minus 4 minus mabano wazi minus 3 karibu mabano sawa au si sawa na minus 5. Kurahisisha, tunapata minus 5 sawa na 5, ambayo ni sahihi. Jozi iliyoamriwa minus 4, minus 3 inafanya equations zote mbili kweli. Kwa hiyo, ni suluhisho.

    Mfano\(\PageIndex{2}\)

    Kuamua kama jozi iliyoamriwa ni suluhisho la mfumo\(\left \{ \begin{array} 3x+y = 0 \\ x+2y = −5 \end{array} \right. \).

    ⓐ\((1,−3)\) ⓑ\((0,0)\)

    Jibu

    ⓐ ndiyo ⓑ hapana

    Mfano\(\PageIndex{3}\)

    Kuamua kama jozi iliyoamriwa ni suluhisho la mfumo\(\left \{ \begin{array} x−3y = −8 \\ −3x−y = 4 \end{array} \right. \).

    ⓐ\((2,−2)\) ⓑ\((−2,2)\)

    Jibu

    ⓐ hapana ⓑ ndiyo

    Tatua Mfumo wa Ulinganisho wa Mstari kwa Graphing

    Katika sehemu hii, tutatumia mbinu tatu za kutatua mfumo wa equations linear. Njia ya kwanza tutatumia ni kuchora.

    Grafu ya equation ya mstari ni mstari. Kila hatua kwenye mstari ni suluhisho la equation. Kwa mfumo wa equations mbili, tutaweka mistari miwili. Basi tunaweza kuona pointi zote kwamba ni ufumbuzi wa kila equation. Na, kwa kutafuta nini mistari inafanana, tutapata suluhisho la mfumo.

    Wengi equations linear katika variable moja na suluhisho moja, lakini tuliona kwamba baadhi equations, aitwaye utata, hawana ufumbuzi na kwa equations nyingine, aitwaye utambulisho, namba zote ni ufumbuzi.

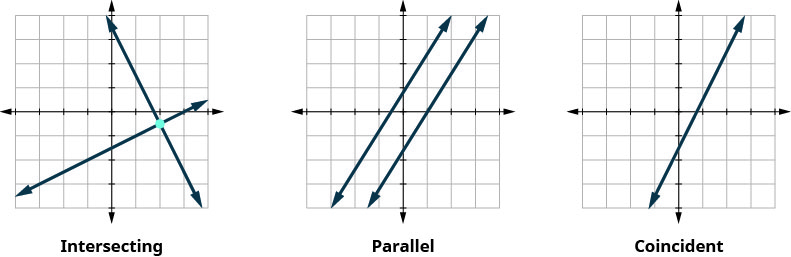
    Vile vile, wakati sisi kutatua mfumo wa equations mbili linear kuwakilishwa na grafu ya mistari miwili katika ndege moja, kuna kesi tatu iwezekanavyo, kama inavyoonekana.

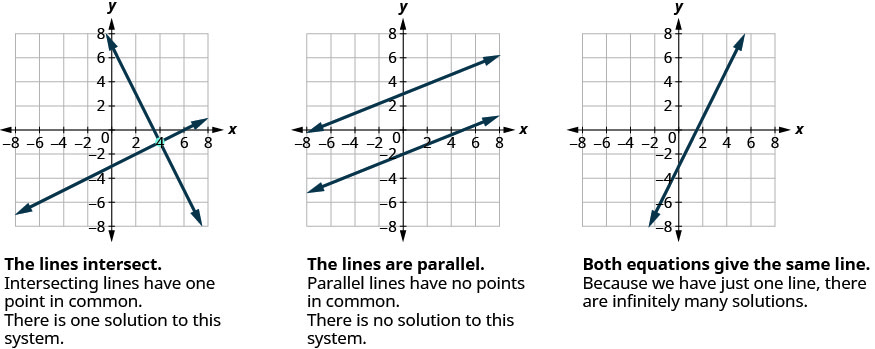
    Kielelezo kinaonyesha grafu tatu. Katika kwanza, mistari inaingiliana kwenye hatua ya 3, chini ya 1. Mstari wa kuingiliana una hatua moja kwa pamoja. Kuna suluhisho moja kwa mfumo. Katika grafu ya pili, mistari ni sawa. Mstari wa sambamba hauna pointi sawa. Hakuna suluhisho kwa mfumo. Grafu ya tatu ina mstari mmoja tu. Hapa, equations zote hutoa mstari huo. Kwa sababu tuna mstari mmoja tu, kuna ufumbuzi usio na mwisho.
    Kielelezo\(\PageIndex{1}\)

    Kila wakati tunapoonyesha njia mpya, tutatumia kwenye mfumo huo wa usawa wa mstari. Mwishoni mwa sehemu utaamua njia ipi ilikuwa njia rahisi zaidi ya kutatua mfumo huu.

    Mfano\(\PageIndex{4}\): How to Solve a System of Equations by Graphing

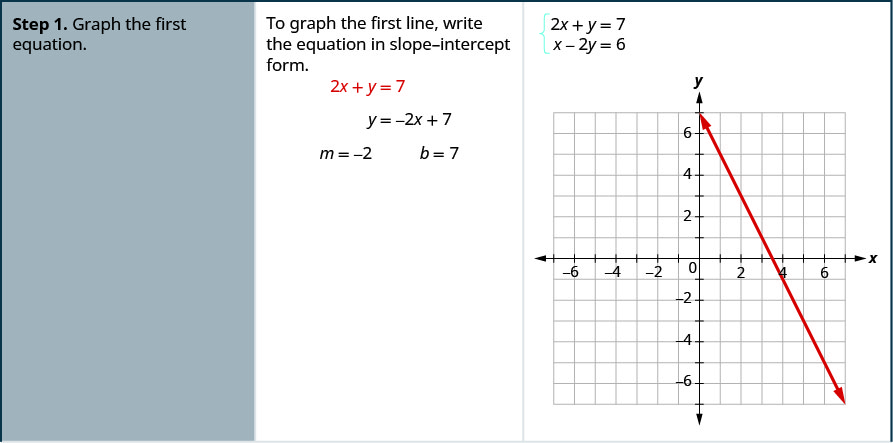
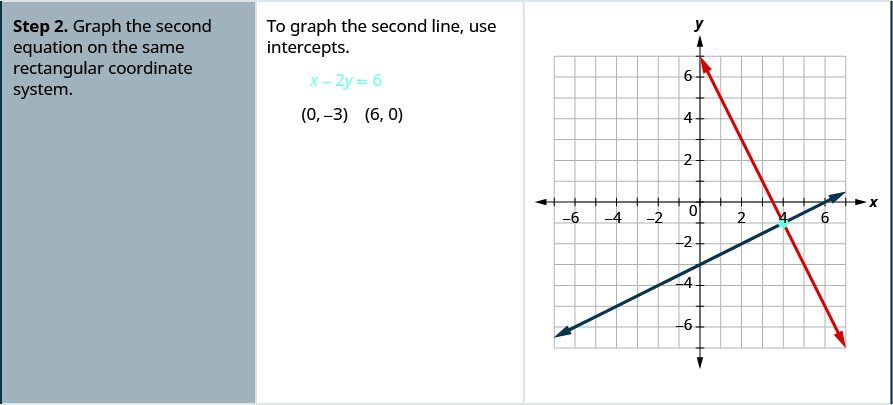
    Tatua mfumo kwa kuchora\( \left\{ \begin{array} {l} 2x+y = 7 \\ x−2y = 6 \end{array} \right. \).

    Jibu

    Hatua ya 1 ni grafu equation kwanza. Ili kuchora mstari wa kwanza, weka equation katika fomu ya kupinga mteremko. Hivyo, 2 x plus y sawa na 7 inakuwa y sawa na minus 2 x plus 7. Hapa, m ni chini ya 2 na b ni 7. Hivyo grafu itakuwa mstari na mteremko sawa na minus 2 na y intercept sawa na 7.Hatua ya 2 ni grafu equation pili kwenye mfumo huo mstatili kuratibu. Ili grafu ya mstari wa pili, tumia matumizi. Kwa x minus 2y sawa na 6, intercepts ni 0, minus 3 na 6, 0.Hatua ya 3 ni kuamua kama mistari intersect, ni sambamba, au ni mstari huo. Hapa, wao huingiliana.Hatua ya 4 ni kutambua suluhisho la mfumo. Ikiwa mistari inakabiliana, tambua hatua ya makutano. Mstari unaingiliana saa 4, chini ya 1. Sasa, angalia ili uhakikishe kuwa ni suluhisho la equations zote mbili. Wakati x na y zinabadilishwa na 4 na chini ya 1 kwa mtiririko huo, equations zote zinashikilia kweli. Hii ni suluhisho la mfumo. Katika hatua ya 4, ikiwa mistari ni sawa, mfumo hauna suluhisho na ikiwa mistari ni sawa, mfumo una idadi isiyo na kipimo ya ufumbuzi.

    Mfano\(\PageIndex{5}\)

    Tatua mfumo kwa kuchora:\( \left\{ \begin{array} {l} x−3y = −3 \\ x+y = 5 \end{array} \right. \).

    Jibu

    \((3,2)\)

    Mfano\(\PageIndex{6}\)

    Tatua mfumo kwa kuchora:\( \left\{ \begin{array} {l} −x+y = 1 \\ 3x+2y = 12 \end{array} \right.\)

    Jibu

    \((2,3)\)

    Hatua za kutumia kutatua mfumo wa equations linear kwa graphing zinaonyeshwa hapa.

    KUTATUA MFUMO WA EQUATIONS LINEAR KWA GRAPHING.
    1. Grafu equation ya kwanza.
    2. Grafu equation ya pili kwenye mfumo huo wa kuratibu mstatili.
    3. Kuamua kama mistari intersect, ni sambamba, au ni mstari huo.
    4. Tambua suluhisho la mfumo.
      • Ikiwa mistari inakabiliana, tambua hatua ya makutano. Hii ni suluhisho la mfumo.
      • Ikiwa mistari ni sawa, mfumo hauna suluhisho.
      • Ikiwa mistari ni sawa, mfumo una idadi isiyo na kipimo ya ufumbuzi.
    5. Angalia suluhisho katika equations zote mbili.

    Katika mfano ijayo, tutaweza kwanza re-kuandika equations katika mteremko - intercept fomu kama hii kufanya ni rahisi kwa sisi haraka graph mistari.

    Mfano\(\PageIndex{7}\)

    Tatua mfumo kwa kuchora:\(\left\{ \begin{array} {l} 3x+y = −1 \\ 2x+y = 0 \end{array}\right.\)

    Jibu

    Tutaweza kutatua wote wa milinganyo haya kwa\(y\) ili tuweze kwa urahisi graph yao kwa kutumia mteremko wao na\(y\) -intercepts.

      .
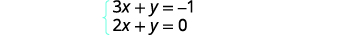
    Tatua equation ya kwanza kwa y. .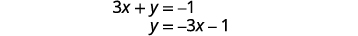
    Pata mteremko na y -intercept. .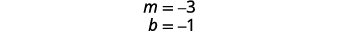
    Tatua equation ya pili kwa y. .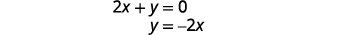
    Pata mteremko na y -intercept. .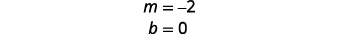
    Grafu mistari. .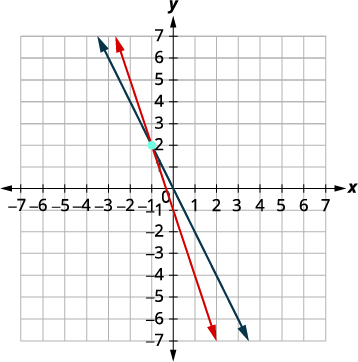
    Kuamua hatua ya makutano. Mstari huingiliana\((−1,2)\).
    Angalia suluhisho katika equations zote mbili.

    .    		  
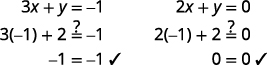
      Suluhisho ni\((−1,2)\).
    Mfano\(\PageIndex{8}\)

    Tatua mfumo kwa kuchora:\(\left\{ \begin{array} {l} −x+y = 1 \\2x+y = 10 \end{array}\right. \).

    Jibu

    \((3,4)\)

    Mfano\(\PageIndex{9}\)

    Tatua mfumo kwa kuchora:\(\left\{ \begin{array} {l} 2x+y = 6 \\x+y = 1 \end{array}\right. \).

    Jibu

    \((5,−4)\)

    Katika mifumo yote ya equations linear hadi sasa, mistari intersected na ufumbuzi ilikuwa hatua moja. Katika mifano miwili ijayo, tutaangalia mfumo wa equations ambayo haina suluhisho na mfumo wa equations ambayo ina idadi isiyo na mwisho ya ufumbuzi.

    Mfano\(\PageIndex{10}\)

    Tatua mfumo kwa kuchora:\(\left\{ \begin{array} {l} y = \tfrac{1}{2}x-3 \\ x-2y = 4 \end{array}\right. \).

    Jibu
      .
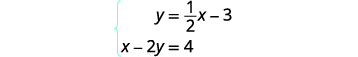
    Ili grafu ya equation ya kwanza, tutatumia
    mteremko wake na y -intercept.    		 .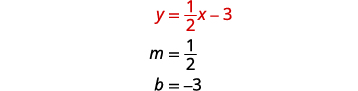
    Ili grafu ya equation ya pili, tutatumia
    intercepts.    		 .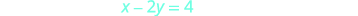
      .
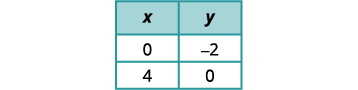
    Grafu mistari. .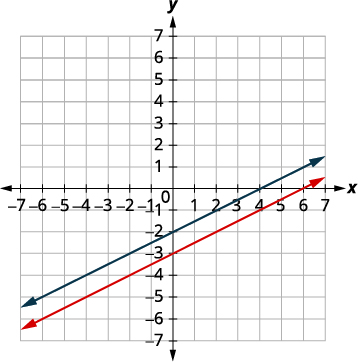
    Tambua pointi za makutano. Mstari ni sawa.
    Kwa kuwa hakuna uhakika ni juu ya mistari yote, hakuna jozi
    awali ambayo inafanya equations wote
    kweli. Hakuna suluhisho la mfumo huu.
    Mfano\(\PageIndex{11}\)

    Tatua mfumo kwa kuchora:\(\left\{ \begin{array} {l} y = -\tfrac{1}{4}x+2 \\ x+4y = 4 \end{array}\right. \).

    Jibu

    hakuna suluhisho

    Mfano\(\PageIndex{12}\)

    Tatua mfumo kwa kuchora:\(\left\{ \begin{array} {l} y = 3x-1 \\ 6x-2y = 6 \end{array}\right. \).

    Jibu

    hakuna suluhisho

    Wakati mwingine equations katika mfumo inawakilisha mstari huo. Kwa kuwa kila hatua kwenye mstari hufanya equations zote mbili kweli, kuna mengi mno awali jozi kwamba kufanya equations wote kweli. Kuna ufumbuzi mkubwa wa mfumo.

    Mfano\(\PageIndex{13}\)

    Tatua mfumo kwa kuchora:\(\left\{ \begin{array} {l} y = 2x-3 \\ -6x+3y = 9 \end{array}\right. \).

    Jibu
      .
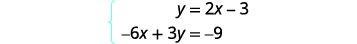
    Pata mteremko na y -intercept ya equation ya kwanza. .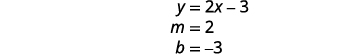
    Pata intercepts ya equation ya pili. .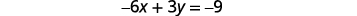
      .
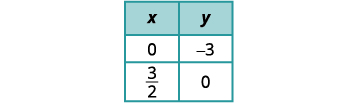
    Grafu mistari. .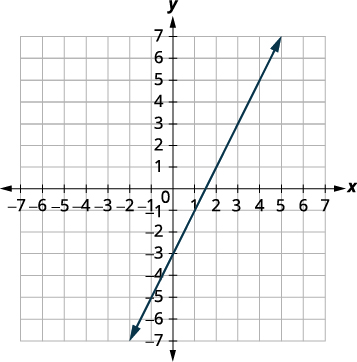
      Mstari ni sawa!
    Kwa kuwa kila hatua kwenye mstari hufanya
    equations zote mbili kweli, kuna mengi mno
    awali jozi kwamba kufanya equations wote kweli.
    Kuna ufumbuzi mkubwa wa mfumo huu.

    Kama kuandika equation pili katika mteremko intercept fomu, unaweza kutambua kwamba equations na mteremko huo na sawa y -intercept.

    Mfano\(\PageIndex{14}\)

    Tatua mfumo kwa kuchora:\(\left\{ \begin{array} {l} y = -3x-6 \\ 6x+2y = -12 \end{array}\right. \).

    Jibu

    ufumbuzi mkubwa sana

    Mfano\(\PageIndex{15}\)

    Tatua mfumo kwa kuchora:\(\left\{ \begin{array} {l} y = \tfrac{1}{2}x-4 \\ 2x-4y = 16 \end{array}\right. \).

    Jibu

    ufumbuzi mkubwa sana

    Tulipopiga mstari wa pili katika mfano wa mwisho, tulivuta haki juu ya mstari wa kwanza. Tunasema mistari miwili ni coincident. Mstari wa mshikamano una mteremko sawa na sawa y- kupinga.

    MISTARI YA KUFANANA

    Mstari wa mshikamano una mteremko sawa na sawa y- kupinga.

    Mifumo ya equations katika Mfano na Mfano kila mmoja alikuwa na mistari miwili intersecting. Kila mfumo ulikuwa na suluhisho moja.

    Katika Mfano, equations alitoa mistari coincident, na hivyo mfumo ulikuwa na ufumbuzi mkubwa sana.

    Mifumo katika mifano hiyo mitatu ilikuwa na angalau suluhisho moja. Mfumo wa equations ambao una angalau suluhisho moja huitwa mfumo thabiti.

    Mfumo wenye mistari sambamba, kama Mfano, hauna suluhisho. Tunaita mfumo wa milinganyo kama hii haiendani. Haina ufumbuzi.

    MIFUMO THABITI NA ISIYO

    Mfumo thabiti wa equations ni mfumo wa equations na angalau suluhisho moja.

    Mfumo usiofaa wa equations ni mfumo wa equations na hakuna suluhisho.

    Sisi pia huainisha equations katika mfumo wa equations kwa kupiga equations huru au tegemezi. Ikiwa equations mbili ni huru, kila mmoja ana seti yao ya ufumbuzi. Mstari wa kuingiliana na mistari sambamba ni huru.

    Ikiwa equations mbili zinategemea, ufumbuzi wote wa equation moja pia ni ufumbuzi wa equation nyingine. Wakati sisi grafu mbili equations tegemezi, sisi kupata mistari coincident.

    Hebu tuangalie hii kwa kuangalia grafu za aina tatu za mifumo. Angalia hapa chini na Jedwali.

    Takwimu inaonyesha grafu tatu. Ya kwanza ina mstari wa kuingiliana mbili. Ya pili ina mistari miwili sambamba. Ya tatu ina mstari mmoja tu. Hii ni kinachoitwa coincident.

    Lines Kuingiliana Sambamba Tukio la bahati mbaya
    Idadi ya ufumbuzi 1 pointi Hakuna ufumbuzi Infinitely wengi
    Thabari/haiendani Thabiti haiendani Thabiti
    Inategemea/huru Independent Independent Tegemezi
    Mfano\(\PageIndex{16}\)

    Bila kuchora, tambua idadi ya ufumbuzi na kisha uainishe mfumo wa equations.

    ⓐ\( \left\{ \begin{array} {l} y = 3x−1 \\ 6x−2y = 12 \end{array}\right. \) ⓑ\( \left\{ \begin{array} {l} 2x+y=−3 \\ x−5y=5 \end{array} \right. \)

    Jibu

    ⓐ Sisi kulinganisha mteremko na intercepts ya mistari miwili.

    \(\begin{array} {lll} {} &{} &{ \left\{ \begin{array} {l} {y=3x-1} \\ {6x−2y=12} \end{array} \right. } \\ {} &{} &{y = 3x-1} \\ {\text{The first equation is already in slope-intercept form.}} &{} &{} \\ {\text{Write the second equation in slope-intercept form.}} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{6x-2y=12} \\ {} &{} &{-2y=-6x+12} \\ {} &{} &{\frac{-2y}{-2}=\frac{-6x+12}{-2}} \\ {} &{} &{y=3x-6} \\ {} &{y=3x-1} &{y=3x-6} \\ {} &{m=3} &{m=3} \\ {} &{b=-1} &{b=-6} \\ {\text{Find the slope and intercept of each line.}} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{\text{Since the slopes are the same andy-intercepts are}} &{} \\ {} &{\text{different, the lines are parallel.}} &{} \\ \end{array}\)

    ⓑ Sisi kulinganisha mteremko na intercepts ya mistari miwili.

    \(\begin{array} {lll} {} &{} &{} \\ {} &{ \left\{ \begin{array} {l} 2x+y=-3 \\ x-5y=5 \\ \end{array} \right. } &{} \\ {\text{Write both equations in slope–intercept form.}} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{2x+y=-3} &{x-5y=5} \\ {} &{y=-2x-3} &{-5y=-x+5} \\ {} &{} &{\frac{-5y}{-5}=\frac{-x+5}{-5}} \\ {} &{} &{y=\frac{1}{5}-1} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {\text{Find the slope and intercept of each line.}} &{} &{} \\ {} &{} &{} \\ {} &{y=-2x-3} &{y=\frac{1}{5}-1} \\ {} &{m=-2} &{m=\frac{1}{5}} \\ {} &{b=-3} &{b=-1} \\ {} &{} &{} \\ {} &{\text{Since the slopes are different, the lines intersect.}} &{} \\ \end{array}\)

    Mfumo wa equations ambao grafu ni intersect ina suluhisho 1 na ni thabiti na kujitegemea.

    Mfano\(\PageIndex{17}\)

    Bila kuchora, tambua idadi ya ufumbuzi na kisha uainishe mfumo wa equations.

    ⓐ\(\left\{ \begin{array} {l} y=−2x−4 \\ 4x+2y=9 \end{array} \right. \) ⓑ\(\left\{ \begin{array} {l} 3x+2y=2 \\ 2x+y=1 \end{array} \right. \)

    Jibu

    ⓐ hakuna ufumbuzi, haiendani, huru ⓑ ufumbuzi mmoja, thabiti, huru

    Mfano\(\PageIndex{18}\)

    Bila kuchora, tambua idadi ya ufumbuzi na kisha uainishe mfumo wa equations.

    ⓐ\(\left\{ \begin{array} {l} y=\frac{1}{3}x−5 \\ x−3y=6 \end{array} \right. \) ⓑ\(\left\{ \begin{array} {l} x+4y=12 \\ −x+y=3 \end{array} \right. \)

    Jibu

    ⓐ hakuna ufumbuzi, haiendani, huru ⓑ ufumbuzi mmoja, thabiti, huru

    Kutatua mifumo ya equations linear kwa graphing ni njia nzuri ya kutazama aina ya ufumbuzi ambayo inaweza kusababisha. Hata hivyo, kuna matukio mengi ambapo kutatua mfumo kwa kuchora picha ni mbaya au isiyo sahihi. Ikiwa grafu zinaenea zaidi ya gridi ndogo na x\(−10\) na y wote kati na 10, kuchora mistari inaweza kuwa mbaya. Na kama ufumbuzi wa mfumo sio integers, inaweza kuwa vigumu kusoma maadili yao kwa usahihi kutoka kwenye grafu.

    Tatua Mfumo wa Ulinganisho kwa Kubadilisha

    Sasa tutatatua mifumo ya equations linear kwa njia ya kubadilisha.

    Tutatumia mfumo huo tuliotumia kwanza kwa kuchora picha.

    \[ \left\{ \begin{array} {l} 2x+y=7 \\ x−2y=6 \end{array} \right. \nonumber \]

    Sisi kwanza kutatua moja ya equations kwa ama x au y. Tunaweza kuchagua ama equation na kutatua kwa aidha variable-lakini tutaweza kujaribu kufanya uchaguzi kwamba kushika kazi rahisi.

    Kisha sisi badala kwamba kujieleza katika equation nyingine. Matokeo yake ni equation na tofauti moja tu-na tunajua jinsi ya kutatua wale!

    Baada ya kupata thamani ya variable moja, sisi badala kwamba thamani katika moja ya equations awali na kutatua kwa variable nyingine. Hatimaye, sisi kuangalia ufumbuzi wetu na kuhakikisha inafanya equations wote kweli.

    Mfano\(\PageIndex{19}\): How to Solve a System of Equations by Substitution

    Tatua mfumo kwa kubadilisha:\( \left\{ \begin{array} {l} 2x+y=7 \\ x−2y=6 \end{array} \right. \)

    Jibu

    equations ni 2 x plus y sawa na 7 na x minus 2y sawa 6. Hatua ya 1 ni kutatua moja ya equations kwa variable ama. Tutaweza kutatua equation ya kwanza kwa y. sisi kupata y sawa 7 minus 2 x.Katika hatua ya 2, badala ya kujieleza kutoka hatua ya 1 katika equation nyingine. Sisi kuchukua nafasi ya y katika equation ya pili na maneno 7 minus 2 x Hivyo, sisi kupata x minus 2 wazi mabano 7 minus 2 x karibu mabano sawa 6.Hatua ya 3 ni kutatua equation kusababisha. Sasa tuna equation na variable tu 1. Sisi kutatua ili kupata x sawa na 4.Hatua ya 4 ni kubadilisha suluhisho katika hatua ya 3 katika moja ya milinganyo ya awali ili kupata variable nyingine. Tutaweza kutumia equation kwanza na kuchukua nafasi ya x na 4. Tunapata, mara 2 4 pamoja na y sawa na 7. Kurahisisha, tunapata y sawa na minus 1.Hatua ya 5 ni kuandika suluhisho kama jozi iliyoamriwa. Jozi iliyoamriwa ni 4, chini ya 1.Hatua ya 6 ni kuangalia kwamba jozi iliyoamriwa ni suluhisho la equations zote za awali. Ili kufanya hivyo sisi mbadala x sawa na 4 na y sawa na minus 1 katika equations wote na kuhakikisha kuwa wote ni kweli.

    Mfano\(\PageIndex{20}\)

    Tatua mfumo kwa kubadilisha:\( \left\{ \begin{array} {l} −2x+y=−11 \\ x+3y=9 \end{array} \right. \)

    Jibu

    \((6,1)\)

    Mfano\(\PageIndex{21}\)

    Tatua mfumo kwa kubadilisha:\( \left\{ \begin{array} {l} 2x+y=−1 \\ 4x+3y=3 \end{array} \right. \)

    Jibu

    \((−3,5)\)

    KUTATUA MFUMO WA EQUATIONS KWA KUBADILISHA.
    1. Kutatua moja ya milinganyo kwa variable ama.
    2. Badilisha usemi kutoka Hatua ya 1 katika equation nyingine.
    3. Tatua equation inayosababisha.
    4. Badilisha ufumbuzi katika Hatua ya 3 katika mojawapo ya milinganyo ya awali ili kupata variable nyingine.
    5. Andika suluhisho kama jozi iliyoamriwa.
    6. Angalia kwamba jozi iliyoamriwa ni suluhisho la equations zote za awali.

    Kuwa makini sana na ishara katika mfano unaofuata.

    Mfano\(\PageIndex{22}\)

    Tatua mfumo kwa kubadilisha:\( \left\{ \begin{array} {l} 4x+2y=4 \\ 6x−y=8 \end{array} \right. \)

    Jibu

    Tunahitaji kutatua equation moja kwa variable moja. Tutatatua equation ya kwanza kwa y.

      .
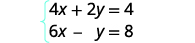
    Tatua equation ya kwanza kwa y.
    Mbadala\(−2x+2\) kwa y katika equation ya pili.    		 .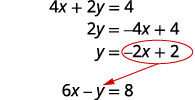
    Badilisha nafasi y na\(−2x+2\). .
    Kutatua equation kwa x. .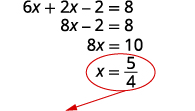
    Mbadala\(x=54\) katika\(4x+2y=4\) kupata y. .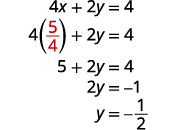
      Jozi iliyoamriwa ni\((54,−12)\).
    Angalia jozi iliyoamriwa katika equations zote mbili.

    .    		  
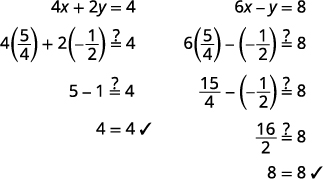
      Suluhisho ni\((54,−12)\).
    Mfano\(\PageIndex{23}\)

    Tatua mfumo kwa kubadilisha:\( \left\{ \begin{array} {l} x−4y=−4 \\ −3x+4y=0 \end{array} \right. \)

    Jibu

    \((2,32)\)

    Mfano\(\PageIndex{24}\)

    Tatua mfumo kwa kubadilisha:\( \left\{ \begin{array} {l} 4x−y=0 \\ 2x−3y=5 \end{array} \right. \)

    Jibu

    \((−12,−2)\)

    Tatua Mfumo wa Equations kwa Kuondoa

    Tumetatua mifumo ya equations linear kwa graphing na kwa badala. Graphing kazi vizuri wakati coefficients variable ni ndogo na ufumbuzi ina maadili integer. Badala kazi vizuri wakati tunaweza kwa urahisi kutatua equation moja kwa moja ya vigezo na kuwa na sehemu nyingi mno katika kujieleza kusababisha.

    Njia ya tatu ya kutatua mifumo ya usawa wa mstari inaitwa Njia ya Kuondoa. Wakati sisi kutatuliwa mfumo kwa badala, sisi ilianza na equations mbili na vigezo mbili na kupunguza kwa equation moja na variable moja. Hii ndio tutafanya na njia ya kuondoa, pia, lakini tutakuwa na njia tofauti ya kufika huko.

    Njia ya Kuondoa inategemea Mali ya Kuongeza ya Usawa. Mali ya Kuongezea ya Usawa inasema kwamba unapoongeza kiasi sawa kwa pande zote mbili za equation, bado una usawa. Tutaongeza Mali ya Kuongeza ya Usawa kusema kwamba unapoongeza kiasi sawa kwa pande zote mbili za equation, matokeo ni sawa.

    Kwa maneno yoyote a, b, c, na d.

    \[\begin{array} {ll} {\text{if}} &{a=b} \\ {\text{and}} &{c=d} \\ {\text{then}} &{a+c=b+d.} \\ \nonumber \end{array}\]

    Ili kutatua mfumo wa equations kwa kuondoa, tunaanza na equations zote mbili katika fomu ya kawaida. Kisha tunaamua ni aina gani ya kutofautiana itakuwa rahisi kuondokana. Tunaamuaje? Tunataka kuwa na coefficients ya variable moja kuwa kinyume, ili tuweze kuongeza equations pamoja na kuondoa kwamba variable.

    Angalia jinsi kwamba kazi wakati sisi kuongeza equations hizi mbili pamoja:

    \[\left\{ \begin{array} {l} 3x+y=5 \\ \underline{2x−y=0} \end{array} \right. \nonumber\]

    \[5x=5 \nonumber\]

    y ya kuongeza sifuri na tuna equation moja na variable moja.

    Hebu jaribu mwingine:

    \[ \left\{ \begin{array} x+4y=2 \\ 2x+5y=−2 \end{array} \right. \nonumber\]

    Wakati huu hatuoni variable ambayo inaweza kuondolewa mara moja kama sisi kuongeza equations.

    Lakini kama sisi kuzidisha equation kwanza na\(−2\), tutafanya coefficients ya kinyume x. Ni lazima kuzidisha kila neno pande zote mbili za equation na\(−2\).

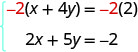
    Minus 2 wazi mabano x pamoja 4y karibu mabano ni minus 2 mara 2. na, 2 x pamoja na 5y ni minus 2.

    Kisha uandike upya mfumo wa equations.

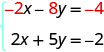
    Minus 2 x minus 8y ni minus 4 na 2 x pamoja 5y ni minus 2.

    Sasa tunaona kwamba coefficients ya maneno x ni kinyume, hivyo x itaondolewa wakati sisi kuongeza equations hizi mbili.

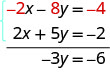
    Minus 2 x minus 8y ni minus 4 na 2 x pamoja 5y ni minus 2. Kuongeza hizi, sisi kupata minus 3y sawa minus 6.

    Mara baada ya sisi kupata equation na variable moja tu, sisi kutatua hilo. Kisha sisi badala kwamba thamani katika moja ya equations awali kutatua kwa variable iliyobaki. Na, kama siku zote, tunaangalia jibu letu ili kuhakikisha kuwa ni suluhisho kwa equations zote za awali.

    Sasa tutaona jinsi ya kutumia kuondoa kutatua mfumo huo wa equations sisi kutatuliwa kwa graphing na badala.

    Zoezi\(\PageIndex{25}\): How to Solve a System of Equations by Elimination

    Tatua mfumo kwa kuondoa:\(\left\{ \begin{array} {l} 2x+y=7 \\ x−2y=6 \end{array} \right. \)

    Jibu

    equations ni 2 x plus y sawa na 7 na x minus 2y sawa 6. Hatua ya 1 ni kuandika equations zote mbili kwa fomu ya kawaida. Wote equations ni katika hali ya kawaida, Ax pamoja By sawa C. coefficients yoyote ni sehemu, wazi yao. Hakuna sehemu ndogo.Hatua ya 2 ni kufanya coefficients ya kupinga moja variable. Kwanza kuamua ambayo variable utaondoa. Kuzidisha equations moja au zote mbili ili coefficients ya kutofautiana kuwa ni kinyume. Tunaweza kuondokana y kwa kuzidisha equation kwanza kwa 2. Tunapata 4x pamoja 2y sawa 14.Hatua ya 3 ni kuongeza equations kutokana na hatua ya 2 ili kuondoa variable moja. Kuongeza, sisi kupata 5x sawa 20.Hatua ya 4 ni kutatua kwa kutofautiana iliyobaki. Kutatua kwa x, tunapata x sawa na 4.Hatua ya 5 ni kubadilisha suluhisho kutoka hatua ya 4 hadi moja ya milinganyo ya awali. Kisha kutatua kwa variable nyingine. Kubadilisha x sawa na 4 katika equation ya pili, tunapata 4 minus 2y sawa na 6. Kutatua kwa y, tunapata y sawa na minus 1.Hatua ya 6 ni kuandika suluhisho kama jozi iliyoamriwa. 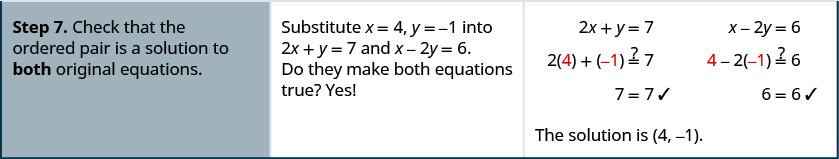Hapa, jozi iliyoamriwa ni 4, chini ya 1.Hatua ya 7 ni kuangalia kwamba jozi iliyoamriwa ni suluhisho la equations zote za awali. Jozi iliyoamriwa hufanya equations zote za awali za kweli.

    Zoezi\(\PageIndex{26}\)

    Tatua mfumo kwa kuondoa:\(\left\{ \begin{array} {l} 3x+y=5 \\ 2x−3y=7 \end{array} \right.\)

    Jibu

    \((2,−1)\)

    Zoezi\(\PageIndex{27}\)

    Tatua mfumo kwa kuondoa:\(\left\{ \begin{array} {l} 4x+y=−5 \\ −2x−2y=−2 \end{array} \right.\)

    Jibu

    \((−2,3)\)

    Hatua zimeorodheshwa hapa kwa ajili ya kumbukumbu rahisi.

    KUTATUA MFUMO WA EQUATIONS KWA KUONDOA.
    1. Andika equations zote mbili kwa fomu ya kawaida. Ikiwa coefficients yoyote ni sehemu ndogo, wazi.
    2. Fanya coefficients ya kinyume kimoja cha kutofautiana.
      • Chagua ni variable gani utaondoa.
      • Kuzidisha equations moja au zote mbili ili coefficients ya kutofautiana kuwa ni kinyume.
    3. Ongeza milinganyo inayotokana na Hatua ya 2 ili kuondoa variable moja.
    4. Tatua kwa kutofautiana iliyobaki.
    5. Badilisha suluhisho kutoka Hatua ya 4 kwenye moja ya milinganyo ya awali. Kisha kutatua kwa variable nyingine.
    6. Andika suluhisho kama jozi iliyoamriwa.
    7. Angalia kwamba jozi iliyoamriwa ni suluhisho la equations zote za awali.

    Sasa tutafanya mfano ambapo tunahitaji kuzidisha equations wote kwa constants ili kufanya coefficients ya kinyume variable moja.

    Zoezi\(\PageIndex{28}\)

    Tatua mfumo kwa kuondoa:\(\left\{ \begin{array} {l} 4x−3y=9 \\ 7x+2y=−6 \end{array} \right. \)

    Jibu

    Katika mfano huu, hatuwezi kuzidisha equation moja tu na mara kwa mara yoyote kupata coefficients kinyume. Hivyo sisi kuweka mikakati ya kuzidisha equations wote kwa constants tofauti kupata kinyume.

      .
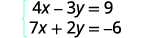
    Equations zote mbili ziko katika fomu ya kawaida.
    Ili kupata coefficients kinyume cha y,
    tutazidisha equation ya kwanza na 2 na equation ya
    pili na 3.    		 .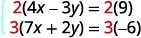
    Kurahisisha. .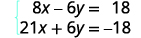
    Ongeza equations mbili ili kuondoa y. .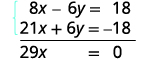
    Kutatua kwa x. .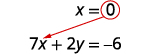
    Mbadala x=0x=0 katika moja ya milinganyo ya awali. .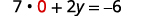
    Kutatua kwa y. .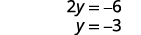
    Andika suluhisho kama jozi iliyoamriwa.

    Jozi iliyoamriwa ni\((0,−3)\).
    Angalia kwamba jozi iliyoamriwa ni suluhisho la equations
    zote za awali.

    .    		  
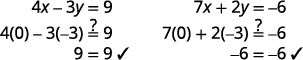
      Suluhisho ni\((0,−3)\).
    Zoezi\(\PageIndex{29}\)

    Tatua mfumo kwa kuondoa:\(\left\{ \begin{array} {l} 3x−4y=−9 \\ 5x+3y=14\end{array} \right. \)

    Jibu

    \((1,3)\)

    Zoezi\(\PageIndex{30}\)

    Tatua kila mfumo kwa kuondoa:\(\left\{ \begin{array} {l} 7x+8y=4 \\ 3x−5y=27 \end{array} \right.\)

    Jibu

    \((4,−3)\)

    Wakati mfumo wa equations una sehemu ndogo, tutaanza kufuta sehemu ndogo kwa kuzidisha kila equation na LCD ya sehemu zote katika equation.

    Zoezi\(\PageIndex{31}\)

    Tatua mfumo kwa kuondoa:\(\left\{ \begin{array} {l} x+\tfrac{1}{2}y=6 \\ \tfrac{3}{2}x+\tfrac{2}{3}y=\tfrac{17}{2} \end{array} \right.\)

    Jibu

    Katika mfano huu, equations zote mbili zina sehemu ndogo. Hatua yetu ya kwanza itakuwa kuzidisha kila equation na LCD ya sehemu zote katika equation ya wazi FRACTIONS.

      .
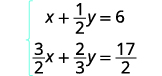
    Ili kufuta sehemu ndogo, kuzidisha kila
    equation na LCD yake.    		 .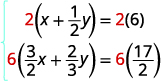
    Kurahisisha. .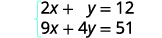
    Sasa tuko tayari kuondokana na moja
    ya vigezo. Kumbuka kwamba equations wote ni katika hali ya
    kawaida.    		  
    Tunaweza kuondokana y kwa kuzidisha equation juu na\(−4\). .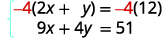
    Kurahisisha na kuongeza.

    Mbadala\(x=3\) katika moja ya milinganyo ya awali.    		 .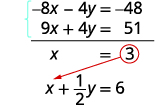
    Kutatua kwa y. .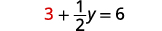
    .
    .
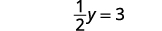
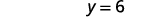
    Andika suluhisho kama jozi iliyoamriwa. Jozi iliyoamriwa ni\((3,6)\).
    Angalia kwamba jozi iliyoamriwa ni suluhisho la equations
    zote za awali.

    .    		  
      Suluhisho ni\((3,6)\).
    Zoezi\(\PageIndex{32}\)

    Tatua kila mfumo kwa kuondoa:\(\left\{ \begin{array} {l} \tfrac{1}{3}x−\tfrac{1}{2}y=1 \\ \tfrac{3}{4}x−y=\tfrac{5}{2} \end{array} \right.\)

    Jibu

    \((6,2)\)

    Zoezi\(\PageIndex{33}\)

    Tatua kila mfumo kwa kuondoa:\(\left\{ \begin{array} {l} x+\tfrac{3}{5}y=−\tfrac{1}{5} \\ −\tfrac{1}{2}x−\tfrac{2}{3}y=\tfrac{5}{6} \end{array} \right.\)

    Jibu

    \((1,−2)\)

    Tulipotatua mfumo kwa kuchora picha, tuliona kwamba sio mifumo yote ya equations linear ina jozi moja iliyoamriwa kama suluhisho. Wakati equations mbili zilikuwa mstari sawa, kulikuwa na ufumbuzi mkubwa sana. Sisi kuitwa kwamba mfumo thabiti. Wakati equations mbili ilivyoelezwa mistari sambamba, hapakuwa na ufumbuzi. Sisi kuitwa kwamba mfumo haiendani.

    Vile vile ni kweli kwa kutumia badala au kuondoa. Ikiwa equation mwishoni mwa mbadala au kuondoa ni kauli ya kweli, tuna mfumo thabiti lakini tegemezi na mfumo wa equations una ufumbuzi mkubwa sana. Ikiwa equation mwishoni mwa kubadilisha au kuondoa ni taarifa ya uongo, tuna mfumo usioendana na mfumo wa equations hauna suluhisho.

    Zoezi\(\PageIndex{34}\)

    Tatua mfumo kwa kuondoa:\(\left\{ \begin{array} {l} 3x+4y=12 \\ y=3−\tfrac{3}{4}x \end{array} \right. \)

    Jibu

    \(\begin{array} {ll} {} &{ \left\{ \begin{array} {l} 3x+4y=12 \\ y=3−\frac{3}{4}x \end{array} \right.} \\ {} &{} \\ {\text{Write the second equation in standard form.}} &{\left\{ \begin{array} {l} 3x+4y=12 \\ \frac{3}{4}x+y=3 \end{array} \right. } \\ {} &{} \\ {\text{Clear the fractions by multiplying the } \\ \text{second equation by 4.}} &{\left\{ \begin{array} {l} 3x+4y=12 \\ 4(\frac{3}{4}x+y)=4(3) \end{array} \right. } \\ {} &{} \\ {\text{Simplify.}} &{\left\{ \begin{array} {l} 3x+4y=12 \\ 3x+4y=12 \end{array} \right. } \\ {} &{} \\ {\text{To eliminate a variable, we multiply the} \\ \text{second equation by−1. Simplify and add.}} &{\begin{array} {l} {\left\{ \begin{array} {l} 3x+4y=12 \\ \underline{-3x-4y=-12 } \end{array} \right.} \\ {\hspace{16mm} 0=0} \end{array}} \\ \end{array} \)

    Hii ni kauli ya kweli. Equations ni thabiti lakini tegemezi. Grafu zao zitakuwa mstari sawa. Mfumo una ufumbuzi mkubwa sana.

    Baada ya kufuta sehemu ndogo katika equation ya pili, je, umeona kwamba equations mbili zilikuwa sawa? Hiyo ina maana tuna mistari coincident.

    Zoezi\(\PageIndex{35}\)

    Tatua mfumo kwa kuondoa:\(\left\{ \begin{array} {l} 5x−3y=15 \\ 5y=−5+\tfrac{5}{3}x \end{array} \right. \)

    Jibu

    ufumbuzi mkubwa sana

    Zoezi\(\PageIndex{36}\)

    Tatua mfumo kwa kuondoa:\(\left\{ \begin{array} {l} x+2y=6 \\ y=−\tfrac{1}{2}x+3\end{array} \right. \)

    Jibu

    ufumbuzi mkubwa sana

    Chagua Njia rahisi zaidi ya Kutatua Mfumo wa Ulinganisho wa Mstari

    Unapotatua mfumo wa usawa wa mstari katika programu, huwezi kuambiwa njia gani ya kutumia. Utahitaji kufanya uamuzi huo mwenyewe. Kwa hivyo utahitaji kuchagua njia ambayo ni rahisi kufanya na kupunguza nafasi yako ya kufanya makosa.

    \[ \textbf{Choose the Most Convenient Method to Solve a System of Linear Equations} \\ \begin{array} {lll} {\underline{\textbf{Graphing}}} &{\underline{\textbf{Substitution}}} &{\underline{\textbf{Elimination}}} \\ {\text{Use when you need a}} &{\text{Use when one equation is}} &{\text{Use when the equations a}} \\ {\text{picture of the situation.}} &{\text{already solved or can be}} &{\text{rein standard form.}} \\ {\text{}} &{\text{easily solved for one}} &{\text{}} \\ {\text{}} &{\text{variable.}} &{\text{}} \\ \end{array} \nonumber \]

    Mfano\(\PageIndex{37}\)

    Kwa kila mfumo wa equations linear, kuamua kama itakuwa rahisi zaidi kutatua kwa kubadilisha au kuondoa. Eleza jibu lako.

    ⓐ\(\left\{ \begin{array} {l} 3x+8y=40 \\ 7x−4y=−32 \end{array} \right.\) ⓑ\(\left\{ \begin{array} {l} 5x+6y=12 \\ y=\tfrac{2}{3}x−1 \end{array} \right.\)

    Jibu

    ⓐ

    \[\left\{ \begin{array} {l} 3x+8y=40 \\ 7x−4y=−32 \end{array} \right.\nonumber\]

    Kwa kuwa equations zote mbili ziko katika fomu ya kawaida, kutumia kuondoa itakuwa rahisi zaidi.

    ⓑ

    \[\left\{ \begin{array} {l} 5x+6y=12 \\ y=\tfrac{2}{3}x−1 \end{array} \right.\nonumber \]

    Kwa kuwa equation moja tayari kutatuliwa kwa y, kutumia badala itakuwa rahisi zaidi.

    Mfano\(\PageIndex{38}\)

    Kwa kila mfumo wa equations linear kuamua kama itakuwa rahisi zaidi kutatua kwa kubadilisha au kuondoa. Eleza jibu lako.

    ⓐ\(\left\{ \begin{array} {l} 4x−5y=−32 \\ 3x+2y=−1 \end{array} \right.\) ⓑ\(\left\{ \begin{array} {l} x=2y−1 \\ 3x−5y=−7 \end{array} \right.\)

    Jibu

    ⓐ Kwa kuwa equations zote mbili ziko katika fomu ya kawaida, kutumia kuondoa itakuwa rahisi zaidi ⓑ Kwa kuwa equation moja tayari kutatuliwa kwa x, kutumia badala itakuwa rahisi zaidi.

    Mfano\(\PageIndex{39}\)

    Kwa kila mfumo wa equations linear kuamua kama itakuwa rahisi zaidi kutatua kwa kubadilisha au kuondoa. Eleza jibu lako.

    ⓐ\(\left\{ \begin{array} {l} y=2x−1 \\ 3x−4y=−6 \end{array} \right.\) ⓑ\(\left\{ \begin{array} {l} 6x−2y=12 \\ 3x+7y=−13 \end{array} \right.\)

    Jibu

    ⓐ Kwa kuwa equation moja tayari kutatuliwa kwa y, kutumia badala itakuwa rahisi zaidi ⓑ Kwa kuwa equations zote mbili ziko katika fomu ya kawaida, kutumia kuondoa itakuwa rahisi zaidi.

    Dhana muhimu

    • Jinsi ya kutatua mfumo wa equations linear kwa graphing.
      1. Grafu equation ya kwanza.
      2. Grafu equation ya pili kwenye mfumo huo wa kuratibu mstatili.
      3. Kuamua kama mistari intersect, ni sambamba, au ni mstari huo.
      4. Tambua suluhisho la mfumo.
        Ikiwa mistari inakabiliana, tambua hatua ya makutano. Hii ni suluhisho la mfumo.
        Ikiwa mistari ni sambamba, mfumo hauna suluhisho.
        Ikiwa mistari ni sawa, mfumo una idadi isiyo na kipimo ya ufumbuzi.
      5. Angalia suluhisho katika equations zote mbili.
    • Jinsi ya kutatua mfumo wa equations kwa kubadilisha.
      1. Kutatua moja ya milinganyo kwa variable ama.
      2. Badilisha usemi kutoka Hatua ya 1 katika equation nyingine.
      3. Tatua equation inayosababisha.
      4. Badilisha ufumbuzi katika Hatua ya 3 katika mojawapo ya milinganyo ya awali ili kupata variable nyingine.
      5. Andika suluhisho kama jozi iliyoamriwa.
      6. Angalia kwamba jozi iliyoamriwa ni suluhisho la equations zote za awali.
    • Jinsi ya kutatua mfumo wa equations kwa kuondoa.
      1. Andika equations zote mbili kwa fomu ya kawaida. Ikiwa coefficients yoyote ni sehemu ndogo, wazi.
      2. Fanya coefficients ya kinyume kimoja cha kutofautiana.
        Chagua ni variable gani utaondoa.
        Kuzidisha equations moja au zote mbili ili coefficients ya kutofautiana kuwa ni kinyume.
      3. Ongeza milinganyo inayotokana na Hatua ya 2 ili kuondoa variable moja.
      4. Tatua kwa kutofautiana iliyobaki.
      5. Badilisha suluhisho kutoka Hatua ya 4 kwenye moja ya milinganyo ya awali. Kisha kutatua kwa variable nyingine.
      6. Andika suluhisho kama jozi iliyoamriwa.
      7. Angalia kwamba jozi iliyoamriwa ni suluhisho la equations zote za awali. \[ \textbf{Choose the Most Convenient Method to Solve a System of Linear Equations} \\ \begin{array} {lll} {\underline{\textbf{Graphing}}} &{\underline{\textbf{Substitution}}} &{\underline{\textbf{Elimination}}} \\ {\text{}} &{\text{Use when one equation is}} &{\text{}} \\ {\text{Use when you need a}} &{\text{already solved or can be}} &{\text{Use when the equations a}} \\ {\text{picture of the situation.}} &{\text{easily solved for one}} &{\text{rein standard form.}} \\ {\text{}} &{\text{variable.}} &{\text{}} \\ \end{array} \nonumber \]

    faharasa

    mistari ya bahati mbaya
    Mstari wa mshikamano una mteremko sawa na sawa y -intercept.
    mifumo thabiti na haiendani
    Mfumo thabiti wa equations ni mfumo wa equations na angalau suluhisho moja; mfumo usioendana wa equations ni mfumo wa equations na hakuna suluhisho.
    ufumbuzi wa mfumo wa equations
    Ufumbuzi wa mfumo wa equations ni maadili ya vigezo vinavyofanya equations zote kweli; suluhisho linawakilishwa na jozi iliyoamriwa (x, y). (x, y).
    mfumo wa equations linear
    Wakati equations mbili au zaidi linear ni makundi pamoja, wao huunda mfumo wa equations linear.