12.R: Introdução ao Cálculo (Revisão)

Last updated
Save as PDF

Page ID: 189241

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

12.1: Encontrando limites - Abordagens numéricas e gráficas

Para os exercícios 1-6, use a Figura abaixo.

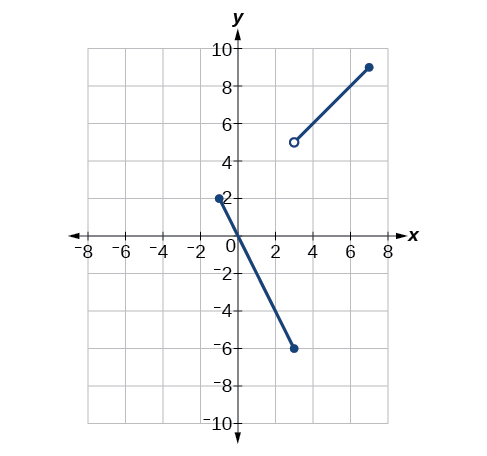
$R 12.1.1.png$

1)$\lim \limits_{x \to -1^+}f(x)$

Responda: $2$

2)$\lim \limits_{x \to -1^-}f(x)$

3)$\lim \limits_{x \to -1}f(x)$

Responda: não existe

4)$\lim \limits_{x \to 3}f(x)$

5) Em quais valores de a função$x$ é descontínua? Qual condição de continuidade é violada?

Responda: Descontínuo em$x=-1\left (\lim \limits_{x \to a}f(x) \text{ does not exist} \right )$$x=3\left (\text{ jump discontinuity} \right )$,$x=7\left (\lim \limits_{x \to a}f(x) \text{ does not exist} \right )$ e.

6) Usando a tabela abaixo, estime$\lim \limits_{x \to 0}f(x)$.

$x$	$F(x)$
\ (x\) ">−0,1	\ (F (x)\) ">2,875
\ (x\) ">−0,01	\ (F (x)\) ">2,92
\ (x\) ">−0,001	\ (F (x)\) ">2,998
\ (x\) ">0	\ (F (x)\) ">Indefinido
\ (x\) ">0,001	\ (F (x)\) ">2,9987
\ (x\) ">0,01	\ (F (x)\) ">2,865
\ (x\) ">0,1	\ (F (x)\) ">2,78145
\ (x\) ">0,15	\ (F (x)\) ">2,678

Responda: $3$

Para os exercícios 7-9, com o uso de um utilitário gráfico, use evidências numéricas ou gráficas para determinar os limites esquerdo e direito da função dada como$x$ abordagens$a$. Se a função tiver limite à medida que$x$ se aproxima$a$, indique-o. Caso contrário, discuta por que não há limite.

7)$f(x)=\begin{cases} \left | x \right |-1 & \text{ if } x\neq 1 \\ x^3 & \text{ if } x= 1 \end{cases} a=1$

8)$f(x)=\begin{cases} \dfrac{1}{x+1} & \text{ if } x= -2 \\ (x+1)^2 & \text{ if } x\neq -2 \end{cases} a=-2$

Responda: $\lim \limits_{x \to -2}f(x)=1$

9)$f(x)=\begin{cases} \sqrt{x+3} & \text{ if } x<1 \\ -\sqrt[3]{x} & \text{ if } x>1 \end{cases} a=1$

12.2: Encontrando limites - Propriedades dos limites

Para os exercícios 1-6, determine os limites se$\lim \limits_{x \to c} f(x)=-3$$\lim \limits_{x \to c} g(x)=5$ e.

1)$\lim \limits_{x \to c} (f(x)+g(x))$

Responda: $2$

2)$\lim \limits_{x \to c} \dfrac{f(x)}{g(x)}$

3)$\underset{x \to c}{\lim } (f(x)\cdot g(x))$

Responda: $-15$

4)$\lim \limits_{x \to 0^+} f(x), f(x)=\begin{cases} 3x^2+2x+1 & x>0 \\ 5x+3 & x<0 \end{cases}$

5)$\lim \limits_{x \to 0^-} f(x), f(x)=\begin{cases} 3x^2+2x+1 & x>0 \\ 5x+3 & x<0 \end{cases}$

Responda: $3$

6)$\lim \limits_{x \to 3^+} (3x-〚x〛)$

Para os exercícios 7-11, avalie os limites usando técnicas algébricas.

7)$\lim \limits_{h \to 0} \left ( \dfrac{(h+6)^2-36}{h} \right )$

Responda: $12$

8)$\lim \limits_{x \to 25} \left ( \dfrac{x^2-625}{\sqrt{x}-5} \right )$

9)$\lim \limits_{x \to 1} \left ( \dfrac{-x^2-9x}{x} \right )$

Responda: $-10$

10)$\lim \limits_{x \to 4} \left ( \dfrac{7-\sqrt{12x+1}}{x-4} \right )$

11)$\lim \limits_{x \to 3} \left ( \dfrac{\frac{1}{3}+\frac{1}{x}}{3+x} \right )$

Responda: $-\dfrac{1}{9}$

12.3: Continuidade

Para os exercícios 1-5, use evidências numéricas para determinar se o limite existe em$x=a$. Caso contrário, descreva o comportamento do gráfico da função em$x=a$.

1)$f(x)=\dfrac{-2}{x-4};\; a=4$

2)$f(x)=\dfrac{-2}{(x-4)^2};\; a=4$

Responda: Em$x=4$, a função tem uma assíntota vertical.

3)$f(x)=\dfrac{-x}{x^2-x-6};\; a=3$

4)$f(x)=\dfrac{6x^2+23x+20}{4x^2-25};\; a=-\dfrac{5}{2}$

Responda: descontinuidade removível em$a=-\dfrac{5}{2}$

5)$f(x)=\dfrac{\sqrt{x}-3}{9-x};\; a=9$

Para os exercícios 6-12, determine onde a função dada$f(x)$ é contínua. Onde não é contínuo, indique quais condições falham e classifique quaisquer descontinuidades.

6)$f(x)=x^2-2x-15$

Responda: contínuo ligado$(-\infty, \infty)$

7)$f(x)=\dfrac{x^2-2x-15}{x-5}$

8)$f(x)=\dfrac{x^2-2x}{x^2-4x+4}$

Responda: descontinuidade removível em$x=2$. $f(2)$não está definido, mas existem limites.

9)$f(x)=\dfrac{x^3-125}{2x^2-12x+10}$

10)$f(x)=\dfrac{x^2-\frac{1}{x}}{2-x}$

Responda: descontinuidade em$x=0$$x=2$ e. Ambos$f(0)$ e não$f(2)$ estão definidos.

11)$f(x)=\dfrac{x+2}{x^2-3x-10}$

12)$f(x)=\dfrac{x+2}{x^3+8}$

Responda: descontinuidade removível em$x=-2$. $f(-2)$não está definido.

12.4: Derivativos

Para os exercícios de 1 a 5, encontre a taxa média de variação$f(x)=\dfrac{f(x+h)-f(x)}{h}$.

1)$f(x)=3x+2$

2)$f(x)=5$

Responda: $0$

3)$f(x)=\dfrac{1}{x+1}$

4)$f(x)=\ln (x)$

Responda: $f(x)=\dfrac{\ln (x+h)-\ln (x)}{h}$

5)$f(x)=e^{2x}$

Para os exercícios 6-7, encontre a derivada da função.

6)$f(x)=4x-6$

Responda: $4$

7)$f(x)=5x^2-3x$

8) Encontre a equação da reta tangente ao gráfico de$f(x)$ no$x$ valor indicado. \[f(x)=-x^3+4x;\; x=2 \nonumber \]

Responda: $y=-8x+16$

9) Para o exercício a seguir, com a ajuda de um utilitário gráfico, explique por que a função não é diferenciável em todos os lugares em seu domínio. Especifique os pontos em que a função não é diferenciável. \[f(x)=\dfrac{x}{\left | x \right |} \nonumber \]

10) Dado que o volume de um cone circular reto é$V=\dfrac{1}{3}\pi r^2h$ e que um determinado cone tem uma altura fixa de$9$ cm e comprimento de raio variável, determine a taxa instantânea de variação de volume em relação ao comprimento do raio quando o raio é$2$ cm. Dê uma resposta exata em termos de$π$.

Responda: $12\pi $

Teste prático

Para os exercícios 1-6, use o gráfico de$f$ na Figura abaixo.

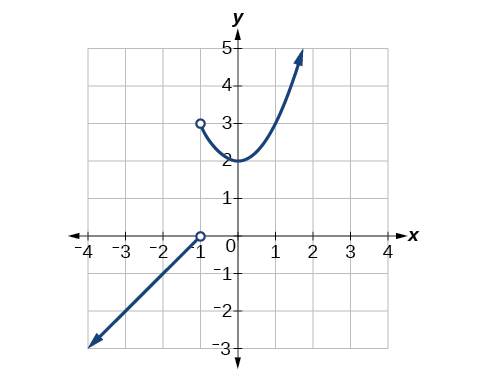
$R Practice.png$

1)$f(1)$

Responda: $3$

2)$\lim \limits_{x \to -1^+} f(x)$

3)$\lim \limits_{x \to -1^-} f(x)$

Responda: $0$

4)$\lim \limits_{x \to -1} f(x)$

5)$\lim \limits_{x \to -2} f(x)$

Responda: $-1$

6) Em quais valores de$x$ é$f$ descontínuo? Qual propriedade de continuidade é violada?

7)$f(x)=\begin{cases} \dfrac{1}{3}-3 & \text{ if } x\leq 2 \\ x^3+1 & \text{ if } x>2 \end{cases} a=2$

Responda

$\lim \limits_{x \to 2^-} f(x)=-\dfrac{5}{2}a$e$\lim \limits_{x \to 2^+} f(x)=9$

Assim, o limite da função como$x$ abordagens$2$ não existe.

8)$f(x)=\begin{cases} x^3+1 & \text{ if } x<1 \\ 3x^2-1 & \text{ if } x=1\; a=1 \\ -\sqrt{x+3}+4 & \text{ if } x>1 \end{cases}$

Para os exercícios 9-11, avalie cada limite usando técnicas algébricas.

9)$\lim \limits_{x \to -5} \left ( \dfrac{\frac{1}{5}+\frac{1}{x}}{10+2x} \right )$

Responda: $-\dfrac{1}{50}$

10)$\lim \limits_{h \to 0} \left ( \dfrac{\sqrt{h^2+25}-5}{h^2} \right )$

11)$\lim \limits_{h \to 0} \left ( \dfrac{1}{h}-\dfrac{1}{h^2+h} \right )$

Responda: $1$

Para os exercícios 12-13, determine se a função dada$f$ é contínua ou não. Se for contínuo, mostre o porquê. Se não for contínuo, indique quais condições falham.

12)$f(x)=\sqrt{x^2-4}$

13)$f(x)=\dfrac{x^3-4x^2-9x+36}{x^3-3x^2+2x-6}$

Responda: descontinuidade removível em$x=3$

Para os exercícios 14-16, use a definição de uma derivada para encontrar a derivada da função dada em$x=a$.

14)$f(x)=\dfrac{3}{5+2x}$

15)$f(x)=\dfrac{3}{\sqrt{x}}$

Responda: $f'(x)=-\dfrac{3}{2a^{\frac{3}{2}}}$

16)$f(x)=2x^2+9x$

17) Para o gráfico na Figura abaixo, determine onde a função é contínua/descontínua e diferenciável/não diferenciável.

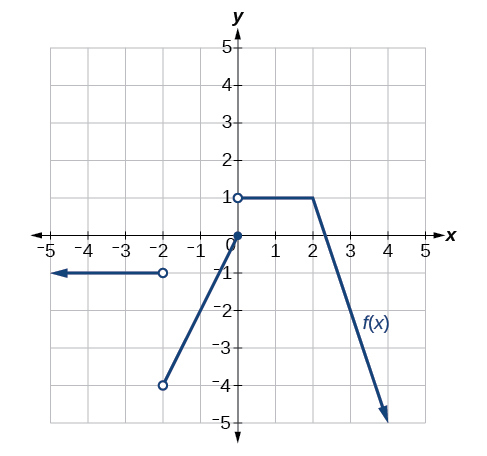
$R Pratique 17.png$

Responda: descontínuo em$-2,0$, não diferenciável em$-2,0, 2$.

Para os exercícios 18-19, com a ajuda de um utilitário gráfico, explique por que a função não é diferenciável em todos os lugares em seu domínio. Especifique os pontos em que a função não é diferenciável.

18)$f(x)=\left | x-2 \right | - \left | x+2 \right |$

19)$f(x)=\dfrac{2}{1+e^{\frac{2}{x}}}$

Responda: não diferenciável em$x=0$ (sem limite)

Para os exercícios 20-24, explique a notação em palavras quando a altura de um projétil em pés$s$,, é uma função do tempo$t$ em segundos após o lançamento e é dada pela função$s(t)$.

20)$s(0)$

21)$s(2)$

Responda: a altura do projétil em$t=2$ segundos

22)$s'(2)$

23)$\dfrac{s(2)-s(1)}{2-1}$

Responda: a velocidade média de$t=1$ até$t=2$

24)$s(t)=0$

Para os exercícios 25-28, use a tecnologia para avaliar o limite.

25)$\lim \limits_{x \to 0}\dfrac{\sin (x)}{3x}$

Responda: $\dfrac{1}{3}$

26)$\lim \limits_{x \to 0}\dfrac{\tan ^2(x)}{2x}$

27)$\lim \limits_{x \to 0}\dfrac{\sin (x)(1-\cos (x))}{2x^2}$

Responda: $0$

28) Avalie o limite manualmente.

\[\lim \limits_{x \to 1}f(x), \text{ where } f(x)=\begin{cases} 4x-7 & x\neq 1 \\ x^2-4 & x= 1 \end{cases} \nonumber \]

Em que valor (es) de a função abaixo$x$ é descontínua?

\[f(x)=\begin{cases} 4x-7 & x\neq 1 \\ x^2-4 & x= 1 \end{cases} \nonumber \]

Para os exercícios 29-32, considere a função cujo gráfico aparece na Figura.

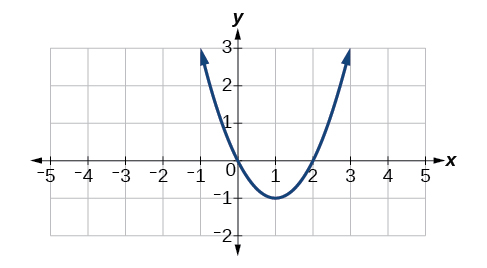
$R Pratique 29-32.png$

29) Encontre a taxa média de variação da função de$x=1$ para$x=3$.

Responda: $2$

30) Encontre todos os valores de$x$ at which$f'(x)=0$.

Responda: $x=1$

31) Encontre todos os valores de$x$ at que$f'(x)$ não existam.

32) Encontre uma equação da reta tangente ao gráfico$f$ do ponto indicado:$f(x)=3x^2-2x-6,\; x=-2$

Responda: $y=-14x-18$

Para os exercícios 33-34, use a função$f(x)=x(1-x)^{\frac{2}{5}}$

33) Faça um gráfico da função$f(x)=x(1-x)^{\tfrac{2}{5}}$ inserindo$f(x)=x\left ((1-x)^2 \right )^{\tfrac{1}{5}}$ e depois inserindo$f(x)=x\left ((1-x)^{\tfrac{1}{5}} \right )^2$.

34) Explore o comportamento do gráfico de$f(x)$ cerca$x=1$ representando graficamente a função nos seguintes domínios$[0.9, 1.1], [0.99, 1.01], [0.999, 1.001]$,$[0.9999, 1.0001]$ e. Use essas informações para determinar se a função parece ser diferenciável em$x=1$.

Responda: O gráfico não é diferenciável em$x=1$ (cúspide).

Para os exercícios 35-42, encontre a derivada de cada uma das funções usando a definição: $\lim \limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h}$

(35)$f(x)=2x-8$

36)$f(x)=4x^2-7$

Responda: $f'(x)=8x$

37)$f(x)=x-\dfrac{1}{2}x^2$

38)$f(x)=\dfrac{1}{x+2}$

Responda: $f'(x)=-\dfrac{1}{(2+x)^2}$

39)$f(x)=\dfrac{3}{x-1}$

40)$f(x)=-x^3+1$

Responda: $f'(x)=-3x^2$

41)$f(x)=x^2+x^3$

(42)$f(x)=\sqrt{x-1}$

Responda: $f'(x)=-\dfrac{1}{2\sqrt{x-1}}$

Contribuidores e atribuições

Template:OpenStaxPreCalc