12.E: Introdução ao cálculo (exercícios)

12.1: Encontrando limites - Abordagens numéricas e gráficas

Nesta seção, examinaremos abordagens numéricas e gráficas para identificar limites.

Verbal

1) Explique a diferença entre um valor em\(x=a\) e o limite conforme\(x\) se aproxima\(a\).

Responda

O valor da função, a saída, at\(x=a\) é\(f(a)\). Quando o\(\lim \limits_{x \to a}f(x)\) é obtido, os valores de\(x\) ficam infinitamente próximos\(a\), mas nunca iguais\(a\). Como os valores de\(x\) aproximação\(a\) da esquerda e da direita, o limite é o valor que a função está se aproximando.

2) Explique por que dizemos que uma função não tem um limite quando\(a\) se\(x\) aproxima se\(a\), à medida que se\(x\) aproxima, o limite esquerdo não é igual ao limite direito.

Gráfica

Para os exercícios 3-14, estime os valores funcionais e os limites do gráfico da função\(f\) fornecido na Figura abaixo.

3)\(\lim \limits_{x \to −2^−} f(x)\)

Responda

\(-4\)

4)\(\lim \limits_{x \to −2^+ }f(x)\)

5)\(\lim \limits_{x \to −2 f(x)}\)

Responda

\(-4\)

6)\(f(−2)\)

7)\(\lim \limits_{x \to −1^− f(x)}\)

Responda

\(2\)

8)\(\lim \limits_{x \to 1^+} f(x)\)

9)\(\lim \limits_{x \to 1} f(x)\)

Responda

não existe

10)\(f(1)\)

11)\(\lim \limits_{x \to 4^−} f(x)\)

Responda

\(4\)

12)\(\lim \limits_{x \to 4^+} f(x)\)

13)\(\lim \limits_{x \to 4} f(x)\)

Responda

não existe

14)\(f(4)\)

Para os exercícios 15-21, desenhe o gráfico de uma função a partir dos valores funcionais e limites fornecidos.

15)\(\lim \limits_{x \to 0^−} f(x)=2, \lim \limits_{x \to 0^+} f(x)=–3, \lim \limits_{x \to 2} f(x)=2, f(0)=4, f(2)=–1, f(–3) \text{ does not exist.}\)

Responda

As respostas podem variar.

16)\(\lim \limits_{x \to 2^−} f(x)=0,\lim \limits_{x \to 2^+} =–2,\lim \limits_{x \to 0} f(x)=3, f(2)=5, f(0)\)

Responda

As respostas podem variar.

17)\(\lim \limits_{ x \to 2^−} f(x)=2, \lim \limits_{ x \to 2^+} f(x)=−3, \lim \limits_{x \to 0} f(x)=5, f(0)=1, f(1)=0\)

Responda

As respostas podem variar.

18)\(\lim \limits_{x \to 3^−} f(x)=0, \lim \limits_{x \to 3^+} f(x)=5, \lim \limits_{x \to 5} f(x)=0, f(5)=4, f(3) \text{ does not exist.}\)

Responda

As respostas podem variar.

19)\( \lim \limits_{ x \to 4} f(x)=6, \lim \limits_{ x \to 6^+} f(x)=−1, \lim \limits_{ x \to 0} f(x)=5, f(4)=6, f(2)=6\)

Responda

As respostas podem variar.

20)\( \lim \limits_{ x \to −3} f(x)=2, \lim \limits_{ x \to 1^+} f(x)=−2, \lim \limits_{ x \to 3} f(x)=–4, f(–3)=0, f(0)=0\)

Responda

As respostas podem variar.

21)\( \lim \limits_{ x \to π} f(x)=π^2, \lim \limits_{ x \to –π} f(x)=\dfrac{π}{2}, \lim \limits_{ x \to 1^-} f(x)=0, f(π)=\sqrt{2}, f(0) \text{ does not exist}.\)

Responda

As respostas podem variar.

Para os exercícios 22-26, use uma calculadora gráfica para determinar o limite de\(5\) casas decimais conforme\(x\) se aproxima\(0\).

22)\(f(x)=(1+x)^{\frac{1}{x}}\)

23)\(g(x)=(1+x)^{\frac{2}{x}}\)

Responda

\(7.38906\)

24)\(h(x)=(1+x)^{\frac{3}{x}}\)

25)\(i(x)=(1+x)^{\frac{4}{x}}\)

Responda

\(54.59815\)

26)\(j(x)=(1+x)^{\frac{5}{x}}\)

27) Com base no padrão que você observou nos exercícios acima, faça uma conjectura quanto ao limite de\(f(x)=(1+x)^{\frac{6}{x}}, g(x)=(1+x)^{\frac{7}{x}},\) e\(h(x)=(1+x)^{\frac{n}{x}}.\)

Responda

\(e^6≈403.428794,e^7≈1096.633158, e^n\)

Para os exercícios 28-29, use um utilitário gráfico para encontrar evidências gráficas para determinar os limites esquerdo e direito da função dada como\(x\) abordagens\(a\). Se a função tiver um limite à medida que\(x\) se aproxima\(a\), indique-o. Caso contrário, discuta por que não há limite.

28)\((x)= \begin{cases} |x|−1, && \text{if }x≠1 \\ x^3, && \text{if }x=1 \end{cases} a=1 \)

29)\((x)= \begin{cases} \frac{1}{x+1}, && \text{if } x=−2 \\ (x+1)^2, && \text{if } x≠−2 \end{cases} a=−2 \)

Responda

\(\lim \limits_{x \to −2} f(x)=1\)

Numérico

Para os exercícios 30-38, use evidências numéricas para determinar se o limite existe em\(x=a\). Caso contrário, descreva o comportamento do gráfico da função near\(x=a\). Arredonde as respostas para duas casas decimais.

30)\(f(x)=\dfrac{x^2−4x}{16−x^2};a=4\)

31)\(f(x)=\dfrac{x^2−x−6}{x^2−9};a=3\)

Responda

\(\lim \limits_{x \to 3} \left (\dfrac{x^2−x−6}{x^2−9} \right )=\dfrac{5}{6}≈0.83\)

32)\(f(x)=\dfrac{x^2−6x−7}{x^2– 7x};a=7\)

33)\(f(x)=\dfrac{x^2–1}{x^2–3x+2};a=1\)

Responda

\(\lim \limits_{x \to 1} \left (\dfrac{x^2−1}{x^2−3x+2} \right )=−2.00\)

34)\(f(x)=\dfrac{1−x^2}{x^2−3x+2};a=1\)

(35)\(f(x)=\dfrac{10−10x^2}{x^2−3x+2};a=1\)

Responda

\(\lim \limits_{x \to 1} \left (\dfrac{10−10x^2}{x^2−3x+2} \right )=20.00\)

36)\(f(x)=\dfrac{x}{6x^2−5x−6};a=\dfrac{3}{2}\)

37)\(f(x)=\dfrac{x}{4x^2+4x+1};a=−\dfrac{1}{2}\)

Responda

\(\lim \limits_{x \to \frac{−1}{2}} \left (\dfrac{x}{4x^2+4x+1} \right )\)não existe. Os valores das funções diminuem sem limite à medida que\(x\) se aproximam\(-0.5\) da esquerda ou da direita.

38)\(f(x)=\frac{2}{x−4}; a=4\)

Para os exercícios 39-41, use uma calculadora para estimar o limite preparando uma tabela de valores. Se não houver limite, descreva o comportamento da função conforme\(x\) se aproxima do valor dado.

39)\(\lim \limits_{x \to 0} \dfrac{7 \tan x}{3x}\)

Responda

\(\lim \limits_{x \to 0} \dfrac{7 \tan x}{3x}=\dfrac{7}{3}\)

40)\(\lim \limits_{x \to 4} \dfrac{x^2}{x−4}\)

Responda

41)\(\lim \limits_{x \to 0}\dfrac{2 \sin x}{4 \tan x}\)

Responda

\(\lim \limits_{x \to 0} \dfrac{2 \sin x}{4 \tan x}=\dfrac{1}{2}\)

Para os exercícios 42-49, use um utilitário gráfico para encontrar evidências numéricas ou gráficas para determinar os limites esquerdo e direito da função dada como\(x\) abordagens\(a\). Se a função tiver um limite à medida que\(x\) se aproxima\(a\), indique-o. Caso contrário, discuta por que não há limite.

42)\(\lim \limits_{x \to 0}e^{e^{\frac{1}{x}}}\)

43)\(\lim \limits_{x \to 0}e^{e^{− \frac{1}{x^2}}}\)

Responda

\(\lim \limits_{x \to 0}e^{e^{− \frac{1}{x^2}}}=1.0\)

44)\(\lim \limits_{x \to 0} \dfrac{|x|}{x}\)

45)\(\lim \limits_{x \to −1} \dfrac{|x+1|}{x+1}\)

Responda

\(\lim \limits_{ x→−1^−}\dfrac{| x+1 |}{x+1}=\dfrac{−(x+1)}{(x+1)}=−1\)e\(\lim \limits_{ x \to −1^+}\dfrac{| x+1 |}{x+1}=\dfrac{(x+1)}{(x+1)}=1\); como o limite direito não é igual ao limite esquerdo,\(\lim \limits_{ x \to −1}\dfrac{|x+1|}{x+1}\) não existe.

46)\(\lim \limits_{ x \to 5} \dfrac{| x−5 |}{5−x}\)

47)\(\lim \limits_{ x \to −1}\dfrac{1}{(x+1)^2}\)

Responda

\(\lim \limits_{ x \to −1} \dfrac{1}{(x+1)^2}\)não existe. A função aumenta sem limites à medida que\(x\) se\(−1\) aproxima de ambos os lados.

48)\(\lim \limits_{ x \to 1} \dfrac{1}{(x−1)^3}\)

49)\(\lim \limits_{ x \to 0} \dfrac{5}{1−e^{\frac{2}{x}}}\)

Responda

\(\lim \limits_{ x \to 0} \dfrac{5}{1−e^{\frac{2}{x}}}\)não existe. Os valores\(5\) da função se aproximam pela esquerda e se\(0\) aproximam pela direita.

50) Use evidências numéricas e gráficas para comparar e contrastar os limites de duas funções cujas fórmulas parecem semelhantes:\(f(x)=\left | \dfrac{1−x}{x} \right |\) e\(g(x)=\left | \dfrac{1+x}{x} \right |\) como\(x\) abordagens\(0\). Use um utilitário gráfico, se possível, para determinar os limites esquerdo e direito das funções\(f(x)\) e\(g(x)\) como\(x\) abordagens\(0\). Se as funções tiverem um limite à medida que\(x\) se aproxima\(0\), indique-o. Caso contrário, discuta por que não há limite.

Extensões

51) De acordo com a Teoria da Relatividade, a massa m m de uma partícula depende de sua velocidade\(v\). Isso é

\[m=\dfrac{m_o}{\sqrt{1−(v^2/c^2)}} \nonumber \]

onde\(m_o\) está a massa quando a partícula está em repouso e\(c\) é a velocidade da luz. Encontre o limite da massa,\(m\), conforme\(v\) se aproxima\(c^−.\)

Responda

Através do exame dos postulados e da compreensão da física relativista, como\(v→c, m→∞. \) Dê um passo adiante para a solução,\[\lim \limits_{v \to c^−}m=\lim \limits_{v \to c^−} \dfrac{m_o}{\sqrt{1−(v^2/c^2)}}=∞ \nonumber \]

52) Permita que a velocidade da luz\(c\),, seja igual\(1.0\) a. Se a massa,\(m\), é\(1\), o que ocorre com\(m\) as\(v \to c\)? Usando os valores listados na Tabela abaixo, faça uma conjectura sobre qual é a massa à medida que\(v\) se aproxima\(1.00\).

\(v\)	\(m\)
\ (v\) ">0,5	\ (m\) ">1,15
\ (v\) ">0,9	\ (m\) ">2,29
\ (v\) ">0,95	\ (m\) ">3,20
\ (v\) ">0,99	\ (m\) ">7,09
\ (v\) ">0,999	\ (m\) ">22,36
\ (v\) ">0,99999	\ (m\) ">223,61

12.2: Encontrando limites - Propriedades dos limites

Representar graficamente uma função ou explorar uma tabela de valores para determinar um limite pode ser complicado e demorado. Quando possível, é mais eficiente usar as propriedades dos limites, que é uma coleção de teoremas para encontrar limites. Conhecer as propriedades dos limites nos permite calcular os limites diretamente.

Verbal

1) Dê um exemplo de um tipo de função\(f\) cujo limite, conforme\(x\) abordagens,\(a,\) é\(f(a)\).

Responda

Se\(f\) for uma função polinomial, o limite de uma função polinomial como\(x\) abordagens sempre\(a\) será\(f(a)\).

2) Quando a substituição direta é usada para avaliar o limite de uma função racional conforme\(x\) se aproxima\(a\) e o resultado é\(f(a)=\dfrac{0}{0}\), isso significa que o limite de\(f\) não existe?

3) O que significa dizer que o limite de\(f(x)\), conforme\(x\) se aproxima\(c\), é indefinido?

Responda

Isso pode significar que (1) os valores da função aumentam ou diminuem sem limites à medida que\(x\) se aproximam\(c,\) ou (2) os limites esquerdo e direito não são iguais.

Algébrico

Para os exercícios 4-30, avalie os limites algebricamente.

4)\(\lim \limits_{x \to 0} (3)\)

5)\(\lim \limits_{x \to 2} \left (\dfrac{−5x}{x^2−1} \right )\)

Responda

\(\dfrac{−10}{3}\)

6)\(\lim \limits_{x \to 2} \left (\dfrac{x^2−5x+6}{x+2} \right )\)

7)\(\lim \limits_{x \to 3} \left (\dfrac{x^2−9}{x−3} \right )\)

Responda

\(6\)

8)\(\lim \limits_{x \to −1} \left (\dfrac{x^2−2x−3}{x+1} \right )\)

9)\(\lim \limits_{x \to \frac{3}{2}} \left (\dfrac{6x^2−17x+12}{2x−3} \right )\)

Responda

\(\dfrac{1}{2}\)

10)\(\lim \limits_{ x \to −\frac{7}{2}} \left (\dfrac{8x^2+18x−35}{2x+7} \right )\)

11)\(\lim \limits_{ x \to 3} \left (\dfrac{x^2−9}{x−5x+6} \right )\)

Responda

\(6\)

12)\(\lim \limits_{ x \to −3} \left (\dfrac{−7x^4−21x^3}{−12x^4+108x^2} \right )\)

13)\(\lim \limits_{ x \to 3} \left (\dfrac{x^2+2x−3}{x−3} \right )\)

Responda

não existe

14)\(\lim \limits_{ h \to 0} \left (\dfrac{(3+h)^3−27}{h} \right )\)

15)\(\lim \limits_{ h \to 0} \left (\dfrac{(2−h)^3−8}{h} \right )\)

Responda

\(−12\)

16)\(\lim \limits_{ h \to 0} \left (\dfrac{(h+3)^2−9}{h} \right )\)

17)\(\lim \limits_{ h \to 0} \left (\dfrac{\sqrt{5−h}−\sqrt{5}}{h} \right )\)

Responda

\(−\dfrac{\sqrt{5}}{10}\)

18)\(\lim \limits_{ x \to 0} \left (\dfrac{\sqrt{3−x}−\sqrt{3}}{x} \right )\)

19)\(\lim \limits_{ x \to 9} \left (\dfrac{x^2−81}{3−x} \right )\)

Responda

\(−108\)

20)\(\lim \limits_{ x \to 1} \left (\dfrac{\sqrt{x}−x^2}{1−\sqrt{x}} \right )\)

21)\(\lim \limits_{ x \to 0}\left ( \dfrac{x}{\sqrt{1+2x}-1} \right )\)

Responda

\(1\)

22)\(\lim \limits_{ x \to \frac{1}{2}} \left (\dfrac{x^2−\tfrac{1}{4}}{2x−1} \right )\)

23)\(\lim \limits_{ x \to 4} \left (\dfrac{x^3−64}{x^2−16} \right )\)

Responda

\(6\)

24)\(\lim \limits_{ x \to 2^−} \left (\dfrac{|x−2|}{x−2} \right )\)

25)\(\lim \limits_{ x \to 2^+} \left (\dfrac{| x−2 |}{x−2} \right )\)

Responda

\(1\)

26)\(\lim \limits_{ x \to 2} \left (\dfrac{| x−2 |}{x−2} \right )\)

27)\(\lim \limits_{ x \to 4^−} \left (\dfrac{| x−4 |}{4−x} \right )\)

Resposta

\(1\)

28)\(\lim \limits_{ x \to 4^+} \left (\dfrac{| x−4 |}{4−x} \right )\)

29)\(\lim \limits_{ x \to 4} \left (\dfrac{| x−4 |}{4−x} \right )\)

Responda

não existe

30)\(\lim \limits_{ x \to 2} \left (\dfrac{−8+6x−x^2}{x−2} \right )\)

Para os exercícios 31-33, use as informações fornecidas para avaliar os limites:\(\lim \limits_{x \to c}f(x)=3, \lim \limits_{x \to c} g(x)=5\)

31)\(\lim \limits_{x \to c} [ 2f(x)+\sqrt{g(x)} ]\)

Responda

\(6+\sqrt{5}\)

32)\(\lim \limits_{x \to c} [ 3f(x)+\sqrt{g(x)} ]\)

33)\(\lim \limits_{x \to c}\dfrac{f(x)}{g(x)}\)

Responda

\(\dfrac{3}{5}\)

Para os exercícios 34-43, avalie os seguintes limites.

34)\(\lim \limits_{x \to 2} \cos (πx)\)

35)\(\lim \limits_{x \to 2} \sin (πx)\)

Responda

\(0\)

36)\(\lim \limits_{x \to 2} \sin \left (\dfrac{π}{x} \right )\)

37)\(f(x)= \begin{cases} 2x^2+2x+1, && x≤0 \\ x−3, && x>0 ; \end{cases} \lim \limits_{x \to 0^+}f(x)\)

Responda

\(−3\)

38)\(f(x)= \begin{cases} 2x^2+2x+1, && x≤0 \\ x−3, && x>0 ; \end{cases} \lim \limits_{x \to 0^−} f(x)\)

39)\(f(x)= \begin{cases} 2x^2+2x+1, && x≤0 \\ x−3, && x>0 ; \end{cases} \lim \limits_{x \to 0}f(x)\)

Responda

não existe; o limite à direita não é o mesmo que o limite esquerdo.

40)\(\lim \limits_{x \to 4} \dfrac{\sqrt{x+5}−3}{x−4}\)

41)\(\lim \limits_{x \to 2^+} (2x−〚x〛)\)

Responda

\(2\)

42)\(\lim \limits_{x \to 2} \dfrac{\sqrt{x+7}−3}{x^2−x−2}\)

43)\(\lim \limits_{x \to 3^+}\dfrac{x^2}{x^2−9}\)

Responda

O limite não existe; o limite se aproxima do infinito.

Para os exercícios 44-53, encontre a taxa média de variação\(\dfrac{f(x+h)−f(x)}{h}\).

44)\(f(x)=x+1\)

45)\(f(x)=2x^2−1\)

Responda

\(4x+2h\)

46)\(f(x)=x^2+3x+4\)

47)\(f(x)=x^2+4x−100\)

Responda

\(2x+h+4\)

48)\(f(x)=3x^2+1\)

49)\(f(x)= \cos (x)\)

Responda

\(\dfrac{\cos (x+h)− \cos (x)}{h}\)

50)\(f(x)=2x^3−4x\)

51)\(f(x)=\dfrac{1}{x}\)

Responda

\(\dfrac{−1}{x(x+h)}\)

52)\(f(x)=\dfrac{1}{x^2}\)

53)\(f(x)=\sqrt{x}\)

Responda

\(\dfrac{−1}{\sqrt{x+h}+\sqrt{x}}\)

Gráfica

54) Encontre uma equação que possa ser representada pela Figura abaixo.

Figura abaixo.

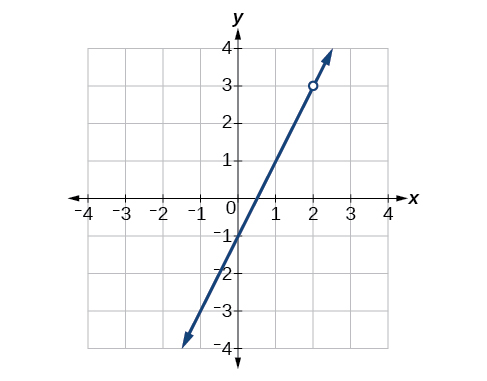
Responda

\(f(x)=\dfrac{x^2+5x+6}{x+3}\)

Para os exercícios 56-57, consulte a Figura abaixo.

56) Qual é o limite direito da função conforme\(x\) se aproxima\(0\)?

57) Qual é o limite esquerdo da função conforme\(x\) se aproxima\(0\)?

Responda

não existe

Aplicativos do mundo real

58) A função de posição\(s(t)=−16t^2+144t\) fornece a posição de um projétil em função do tempo. Encontre a velocidade média (taxa média de variação) no intervalo\([ 1,2 ]\).

59) A altura de um projétil é dada por\(s(t)=−64t^2+192t\) Encontre a taxa média de variação da altura de\(t=1\) segundo para\(t=1.5\) segundos.

Responda

\(52\)

60) A quantia em dinheiro em uma conta após\(t\) anos compostos continuamente com\(4.25\%\) juros é dada pela fórmula\(A=A_0e^{0.0425t}\), onde\(A_0\) é o valor inicial investido. Encontre a taxa média de variação do saldo da conta de\(t=1\) ano para\(t=2\) ano se o valor inicial investido for\(\$1,000.00.\)

12.3: Continuidade

Uma função que permanece nivelada por um intervalo e depois salta instantaneamente para um valor mais alto é chamada de função gradual. Essa função é um exemplo. Uma função que tem qualquer furo ou quebra em seu gráfico é conhecida como função descontínua. Uma função gradual, como taxas de estacionamento em função das horas estacionadas, é um exemplo de função descontínua. Podemos verificar três condições diferentes para decidir se uma função é contínua em um determinado número.

Verbal

1) Declare com suas próprias palavras o que significa para uma função\(f\) ser contínua em\(x=c\).

Responda

Informalmente, se uma função é contínua em\(x=c\), então não há quebra no gráfico da função em\(f(c)\) e\(f(c)\) é definida.

2) Declare com suas próprias palavras o que significa para uma função ser contínua no intervalo\((a,b)\).

Algébrico

Para os exercícios 3-22, determine por que a função\(f\) é descontínua em um determinado ponto\(a\) do gráfico. Indique qual condição falha.

3)\(f(x)=\ln | x+3 |,a=−3\)

Responda

descontínuo em\(a=−3\);\(f(−3)\) não existe

4)\(f(x)= \ln | 5x−2 |,a=\dfrac{2}{5}\)

5)\(f(x)=\dfrac{x^2−16}{x+4},a=−4\)

Responda

descontinuidade removível em não\(a=−4; f(−4)\) está definida

6)\(f(x)=\dfrac{x^2−16x}{x},a=0\)

7)\(f(x)= \begin{cases} x, && x≠3 \\ 2x, && x=3 \end{cases} a=3\)

Responda

Descontínuo em\(a=3; \lim \limits_{x \to 3} f(x)=3,\), mas\(f(3)=6,\) que não é igual ao limite.

8)\(f(x) = \begin{cases} 5, &&x≠0 \\ 3, && x=0 \end{cases} a=0\)

9)\(f(x)= \begin{cases} \dfrac{1}{2−x}, && x≠2 \\ 3, &&x=2 \end{cases} a=2\)

Responda

\(\lim \limits_{x \to 2}f(x)\)não existe.

10)\(f(x)= \begin{cases} \dfrac{1}{x+6}, && x=−6 \\ x^2, && x≠−6 \end{cases} a=−6\)

11)\(f(x)=\begin{cases} 3+x, &&x<1 \\ x, &&x=1 \\ x^2, && x>1 \end{cases} a=1\)

Responda

\(\lim \limits_{x \to 1^−}f(x)=4;\lim \limits_{x \to 1^+}f(x)=1.\)Portanto,\(\lim \limits_{x \to 1}f(x)\) não existe.

12)\(f(x)= \begin{cases} 3−x, && x<1 \\ x, && x=1 \\ 2x^2, && x>1 \end{cases} a=1\)

13)\(f(x)= \begin{cases} 3+2x, && x<1 \\ x, && x=1 \\ −x^2, && x>1 \end{cases} a=1\)

Responda

\(\lim \limits_{x \to 1^−} f(x)=5≠ \lim \limits_{x \to 1^+}f(x)=−1\). Portanto,\(\lim \limits_{x \to 1}f(x)\) não existe.

14)\(f(x)= \begin{cases} x^2, &&x<−2 \\ 2x+1, && x=−2 \\ x^3, && x>−2 \end{cases} a=−2\)

15)\(f(x)= \begin{cases} \dfrac{x^2−9}{x+3}, && x<−3 \\ x−9, && x=−3 \\ \dfrac{1}{x}, && x>−3 \end{cases} a=−3\)

Responda

\(\lim \limits_{x to −3^+}f(x)=−\dfrac{1}{3}\)

Portanto,\(\lim \limits_{x \to −3} f(x)\) não existe.

16)\(f(x)= \begin{cases} \dfrac{x^2−9}{x+3}, && x<−3 \\ x−9, && x=−3\\ −6, && x>−3 \end{cases} a=3\)

17)\(f(x)=\dfrac{x^2−4}{x−2}, a=2\)

Responda

\(f(2)\)não está definido.

18)\(f(x)=\dfrac{25−x^2}{x^2−10x+25}, a=5\)

19)\(f(x)=\dfrac{x^3−9x}{x^2+11x+24}, a=−3\)

Responda

\(f(−3)\)não está definido.

20)\(f(x)=\dfrac{x^3−27}{x^2−3x}, a=3\)

21)\(f(x)=\dfrac{x}{|x|}, a=0\)

Responda

\(f(0)\)não está definido.

22)\(f(x)=\dfrac{2|x+2|}{x+2}, a=−2\)

Para os exercícios 23-35, determine se a função dada\(f\) é contínua ou não em todos os lugares. Se for contínuo em todos os lugares em que está definido, indique para qual faixa ele é contínuo. Se for descontínuo, indique onde é descontínuo.

23)\(f(x)=x^3−2x−15\)

Responda

Contínuo ligado\((−∞,∞)\)

24)\(f(x)=\dfrac{x^2−2x−15}{x−5}\)

25)\(f(x)=2⋅3^{x+4}\)

Responda

Contínuo ligado\((−∞,∞)\)

26)\(f(x)=− \sin (3x)\)

27)\(f(x)=\dfrac{|x−2|}{x^2−2x}\)

Responda

Descontínuo em\(x=0\) e\(x=2\)

28)\(f(x)= \tan (x)+2\)

29)\(f(x)=2x+\dfrac{5}{x}\)

Responda

Descontínuo em\(x=0\)

30)\(f(x)=\log _2 (x)\)

31)\(f(x)= \ln x^2 \)

Responda

Contínuo ligado\((0,∞)\)

32)\(f(x)=e^{2x}\)

33)\(f(x)=\sqrt{x−4}\)

Responda

Contínuo ligado\([4,∞)\)

34)\(f(x)= \sec (x)−3\)

(35)\(f(x)=x^2+ \sin (x)\)

Responda

Ligado continuamente\((−∞,∞)\).

36) Determine os valores de\(b\) e de\(c\) forma que a função a seguir seja contínua em toda a reta do número real.

\[f(x)= \begin{cases}x+1, && 1<x<3 \\ x^2+bx+c, &&|x−2|≥1 \end{cases} \nonumber \]

Gráfica

Para os exercícios 37-39, consulte a Figura abaixo. Cada quadrado representa uma unidade quadrada. Para cada valor de\(a\), determine quais das três condições de continuidade são satisfeitas\(x=a\) e quais não são.

37)\(x=−3\)

Responda

\(1\), mas não\(2\) ou\(3\)

38)\(x=2\)

39)\(x=4\)

Responda

\(1\)e\(2\), mas não\(3\)

Para os exercícios 40-43, use um utilitário gráfico para representar graficamente a função\(f(x)= \sin \left (\dfrac{12π}{x} \right )\), como na Figura. Defina o\(x\) eixo -a uma curta distância antes e depois\(0\) para ilustrar o ponto de descontinuidade.

40) Quais condições de continuidade falham no ponto de descontinuidade?

41) Avalie\(f(0)\).

Responda

\(f(0)\)é indefinido.

42) Resolva\(x\) isso\(f(x)=0\).

43) Qual é o domínio de\(f(x)\)?

Responda

\((−∞,0)∪(0,∞)\)

Para os exercícios 44-45, considere a função mostrada na Figura abaixo.

44) Em quais\(x\) coordenadas a função é descontínua?

45) Que condição de continuidade é violada nesses pontos?

Responda

Em\(x=−1\), o limite não existe. \(x=1, f(1)\)O at não existe.

Em\(x=2\), parece haver uma assíntota vertical e o limite não existe.

46) Considere a função mostrada na Figura abaixo. Em quais\(x\) coordenadas a função é descontínua? Quais condições de continuidade foram violadas?

47) Construa uma função que passe pela origem com uma inclinação constante de\(1\), com descontinuidades removíveis em\(x=−7\)\(x=1\) e.

Responda

\(\dfrac{x^3+6x^2−7x}{(x+7)(x−1)}\)

48) A função\(f(x)=\dfrac{x^3−1}{x−1}\) está representada graficamente na Figura abaixo. Parece ser contínuo no intervalo\([−3,3]\), mas há um\(x\) valor -nesse intervalo no qual a função é descontínua. Determine o valor\(x\) no qual a função é descontínua e explique a armadilha de utilizar a tecnologia ao considerar a continuidade de uma função examinando seu gráfico.

49) Encontre o limite\(\lim \limits_{ x \to 1}f(x)\) e determine se a função a seguir é contínua em\(x=1\):

\[fx= \begin{cases} x^2+4 && x≠1 \\ 2 && x=1\end{cases} \nonumber \]

Responda

A função é descontínua\(x=1\) porque o limite à medida que\(x\) se\(1\) aproxima é\(5\)\(f(1)=2\) e.

50) O gráfico de\(f(x)= \dfrac{\sin (2x)}{x}\) é mostrado na Figura abaixo. A função é\(f(x)\) contínua em\(x=0?\) Por que ou por que não?

12.4: Derivativos

A mudança dividida pelo tempo é um exemplo de taxa. As taxas de variação nos exemplos anteriores são diferentes. Em outras palavras, alguns mudaram mais rápido do que outros. Se fôssemos representar graficamente as funções, poderíamos comparar as taxas determinando as inclinações dos gráficos.

Verbal

1) Como a inclinação de uma função linear é semelhante à derivada?

Responda

A inclinação de uma função linear permanece a mesma. A derivada de uma função geral varia de acordo com\(x\). Tanto a inclinação de uma linha quanto a derivada em um ponto medem a taxa de mudança da função.

2) Qual é a diferença entre a taxa média de variação de uma função no intervalo\([x,x+h]\) e a derivada da função em\(x\)?

3) Um carro percorreu\(110\) milhas durante o período das 14h às 16h. Qual foi a velocidade média do carro? Exatamente às 14h30, a velocidade do carro registrou exatamente\(62\) milhas por hora. Qual é outro nome para a velocidade do carro às 14h30? Por que essa velocidade difere da velocidade média?

Responda

A velocidade média é de\(55\) milhas por hora. A velocidade instantânea às 14h30 é de\(62\) milhas por hora. A velocidade instantânea mede a velocidade do carro em um instante de tempo, enquanto a velocidade média fornece a velocidade do carro em um intervalo.

4) Explique o conceito da inclinação de uma curva no ponto\(x\).

5) Suponha que a água esteja fluindo para um tanque a uma taxa média de\(45\) galões por minuto. Traduza essa afirmação para a linguagem da matemática.

Responda

A taxa média de variação da quantidade de água no tanque é de\(45\) galões por minuto. Se\(f(x)\) for a função que fornece a quantidade de água no tanque a qualquer momento\(t\), então a taxa média de variação\(f(x)\) entre\(t=a\) e\(t=b\) é\(f(a)+45(b−a)\).

Algébrico

Para os exercícios 6-17, use a definição de derivada\(\lim \limits_{ h \to 0}\dfrac{f(x+h)-f(x)}{h}\) para calcular a derivada de cada função.

6)\(f(x)=3x-4\)

7)\(f(x)=-2x+1\)

Responda

\(f'(x)=-2\)

8)\(f(x)=x^2-2x+1\)

9)\(f(x)=2x^2+x-3\)

Responda

\(f'(x)=4x+1\)

10)\(f(x)=2x^2+5\)

11)\(f(x)=\dfrac{-1}{x-2}\)

Responda

\(f'(x)=\dfrac{1}{(x-2)^2}\)

12)\(f(x)=\dfrac{2+x}{1-x}\)

13)\(f(x)=\dfrac{5-2x}{3+2x}\)

Responda

\(\dfrac{-16}{(3+2x)^2}\)

14)\(f(x)=\sqrt{1+3x}\)

15)\(f(x)=3x^3-x^2+2x+5\)

Responda

\(f'(x)=9x^2-2x+2\)

16)\(f(x)=5\)

17)\(f(x)=5\pi\)

Responda

\(f'(x)=0\)

Para os exercícios 18-21, encontre a taxa média de variação entre os dois pontos.

18)\((-2,0)\) e\((-4,5)\)

19)\((4,-3)\) e\((-2,-1)\)

Responda

\(-\dfrac{1}{3}\)

20)\((0,5)\) e\((6,5)\)

21)\((7,-2)\) e\((7,10)\)

Responda

indefinida

Para as funções polinomiais 22-25, encontre as derivadas.

22)\(f(x)=x^3+1\)

23)\(f(x)=-3x^2-7x=6\)

Responda

\(f'(x)=-6x-7\)

24)\(f(x)=7x^2\)

25)\(f(x)=3x^3+2x^2+x-26\)

Responda

\(f'(x)=9x^2+4x+1\)

Para as funções 26-28, encontre a equação da reta tangente à curva\(x\) no ponto dado da curva.

26)\(f(x)=2x^2-3x\; \; x=3\)

27)\(f(x)=x^2+1\; \; x=2\)

Responda

\(y=12x-15\)

28)\(f(x)=\sqrt{x}\; \; x=9\)

29) Para o exercício a seguir, determine de\(k\) forma que a linha dada seja tangente ao gráfico da função.

\[f(x)=x^2-kx\; \; y=4x-9 \nonumber \]

Responda

\(k=-10\)ou\(k=2\)

Gráfica

Para os exercícios 30-33, considere o gráfico da função\(f\) e determine onde a função é contínua/descontínua e diferenciável/não diferenciável.

30)

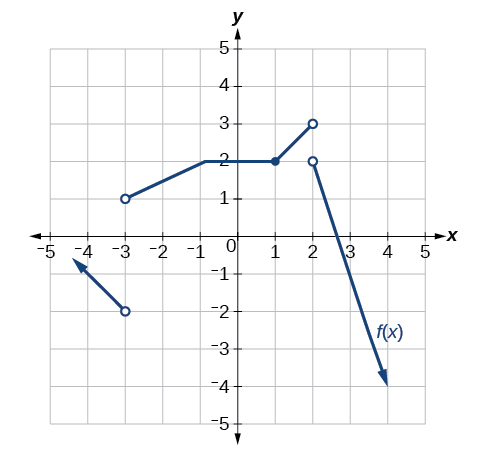
31)

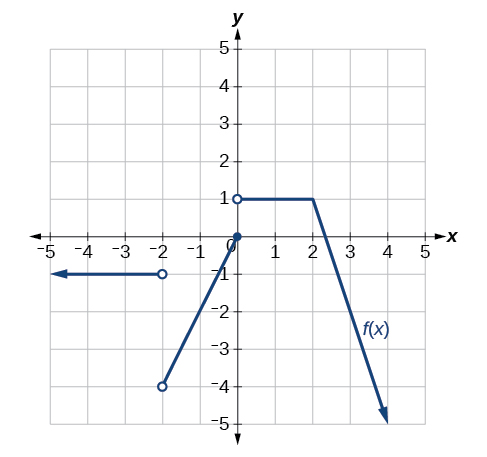
Responda

Descontínuo em\(x=-2\)\(x=0\) e. Não é diferenciável em\(-2, 0, 2\).

32)

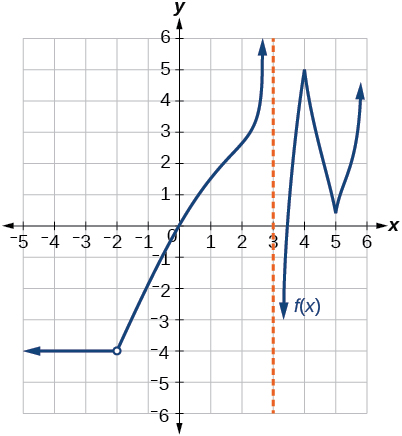
33)

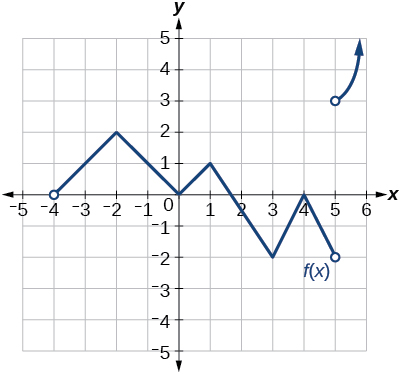
Responda

Descontínuo em\(x=5\). Não é diferenciável em\(-4, -2, 0, 1, 3, 4, 5\).

Para os exercícios 34-43, use a Figura abaixo para estimar a função em um determinado valor de\(x\) ou a derivada em um determinado valor de\(x\), conforme indicado.

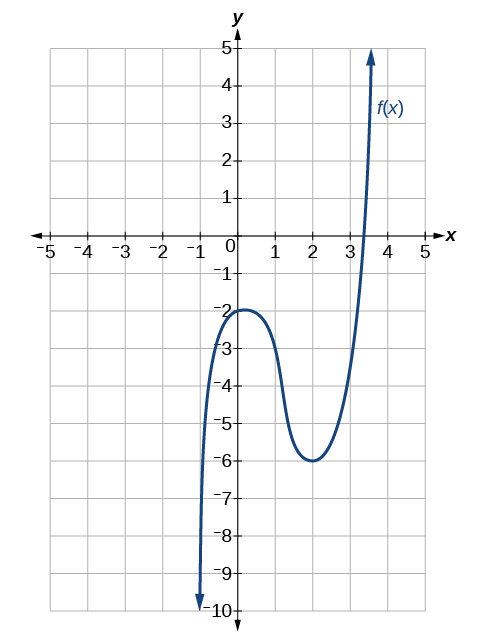
34)\(f(-1)\)

(35)\(f(0)\)

Responda

\(f(0)=-2\)

36)\(f(1)\)

37)\(f(2)\)

Responda

\(f(2)=-6\)

38)\(f(3)\)

39)\(f'(-1)\)

Responda

\(f'(-1)=9\)

40)\(f'(0)\)

41)\(f'(1)\)

Responda

\(f'(1)=-3\)

(42)\(f'(2)\)

43)\(f'(3)\)

Responda

\(f'(3)=9\)

44) Esboce a função com base nas informações abaixo:

\[f'(x)=2x, f(2)=4 \nonumber \]

Tecnologia

45) Avalie numericamente a derivada. Explore o comportamento do gráfico de\(f(x)=x^2\) around\(x=1\) representando graficamente a função nos seguintes domínios:\([0.9,1.1], [0.99,1.01], [0.999,1.001], [0.9999, 1.0001]\). Podemos usar o recurso em nossa calculadora que define automaticamente Ymin e Ymax para os valores Xmin e Xmax que predefinimos. (Em algumas das calculadoras gráficas mais usadas, esse recurso pode ser chamado de ZOOM FIT ou ZOOM AUTO). Ao examinar os valores de intervalo correspondentes para essa janela de visualização, aproxime como a curva muda\(x=1\), ou seja, aproxime a derivada em\(x=1\).

Responda

As respostas variam. A inclinação da reta tangente próxima a\(x=1\) é\(2\).

Aplicativos do mundo real

Para os exercícios 46-50, explique a notação em palavras. O volume\(f(t)\) de um tanque de gasolina, em galões,\(t\) minutos depois do meio dia.

(46)\(f(0)=600\)

47)\(f'(30)=-20\)

Responda

Às 12h30, a taxa de variação do número de galões no tanque é de\(-20\) galões por minuto. Ou seja, o tanque está perdendo\(20\) galões por minuto.

48)\(f(30)=0\)

49)\(f'(200)=30\)

Responda

\(200\)Minutos depois do meio-dia, o volume de galões no tanque está mudando à taxa de\(30\) galões por minuto.

50)\(f(240)=500\)

Para os exercícios 51-55, explique as funções em palavras. A altura,\(s\), de um projétil após\(t\) segundos é dada por\(s(t)=-16t^2+80t\).

51)\(s(2)=96\)

Responda

A altura do projétil após\(2\) segundos é de\(96\) pés.

52)\(s'(2)=16\)

53)\(s(3)=96\)

Responda

A altura do projétil em\(t=3\) segundos é de\(96\) pés.

54)\(s'(3)=-16\)

55)\(s(0)=0, s(5)=0\)

Responda

A altura do projétil é zero\(t=0\) e novamente em\(t=5\). Em outras palavras, o projétil começa no chão e cai na Terra novamente após\(5\) alguns segundos.

Para os exercícios 56-57, o volume\(V\) de uma esfera em relação ao seu raio\(r\) é dado por\(V=\dfrac{4}{3}\pi r^3\).

56) Encontre a taxa média de variação da\(V\) medida que\(r\) muda de\(1\) cm para\(2\) cm.

57) Encontre a taxa instantânea de variação de\(V\) quando\(r=3\) cm.

Responda

\(36\pi \)

Para os exercícios 58-60, a receita gerada pela venda de\(x\) itens é dada por\(R(x)=2x^2+10x\).

58) Encontre a variação média da função de receita à medida que\(x\) muda de\(x=10\) para\(x=20\).

59) Encontre\(R'(10)\) e interprete.

Responda

\(\$50.00\)por unidade, que é a taxa instantânea de variação da receita quando exatamente\(10\) as unidades são vendidas.

60) Encontre\(R'(15)\) e interprete. Compare\(R'(15)\)\(R'(10)\) e explique a diferença.

Para os exercícios 61-63, o custo de produção de\(x\) celulares é descrito pela função\(C(x)=x^2-4x+1000\).

61) Encontre a taxa média de variação no custo total à medida que\(x\) muda de\(x=10\) para\(x=15\).

Responda

\(\$21\)por unidade

62) Encontre o custo marginal aproximado, quando\(15\) os celulares tiverem sido produzidos, de produzir o\(16^{th}\) celular.

63) Encontre o custo marginal aproximado, quando\(20\) os celulares tiverem sido produzidos, de produzir o\(21^{st}\) celular.

Responda

\(\$36\)

Extensão

Para os exercícios 64-67, use a definição da derivada em um ponto\(x=a\),\(\lim \limits_{x \to a}\dfrac{f(x)-f(a)}{x-a}\), para encontrar a derivada das funções.

64)\(f(x)=\dfrac{1}{x^2}\)

65)\(f(x)=5x^2-x+4\)

Responda

\(f'(x)=10a-1\)

66)\(f(x)=-x^2+4x+7\)

67)\(f(x)=\dfrac{-4}{3-x^2}\)

Responda

\(\dfrac{4}{(3-x)^2}\)

Contribuidores e atribuições

• Template:OpenStaxPreCalc