10.3: A parábola

Objetivos de

• Grafe parábolas com vértices na origem.
• Escreva equações de parábolas na forma padrão.
• Grafe parábolas com vértices que não estão na origem.
• Resolva problemas aplicados envolvendo parábolas.

Você sabia que a tocha olímpica é acesa vários meses antes do início dos jogos? O método cerimonial para acender a chama é o mesmo dos tempos antigos. A cerimônia acontece no Templo de Hera, em Olímpia, Grécia, e está enraizada na mitologia grega, prestando homenagem a Prometeu, que roubou fogo de Zeus para dar a todos os humanos. Uma das onze sacerdotisas em exercício coloca a tocha no foco de um espelho parabólico (Figura\(\PageIndex{1}\)), que focaliza os raios de luz do sol para acender a chama.

Figura\(\PageIndex{1}\): A tocha olímpica conclui sua jornada ao redor do mundo quando é usada para acender o caldeirão olímpico durante a cerimônia de abertura. (crédito: Ken Hackman, Força Aérea dos EUA)

Espelhos parabólicos (ou refletores) são capazes de capturar energia e focá-la em um único ponto. As vantagens dessa propriedade são evidenciadas pela vasta lista de objetos parabólicos que usamos todos os dias: antenas parabólicas, pontes suspensas, telescópios, microfones, holofotes e faróis de carros, para citar alguns. Os refletores parabólicos também são usados em dispositivos de energia alternativa, como fogões solares e aquecedores de água, porque são baratos de fabricar e precisam de pouca manutenção. Nesta seção, exploraremos a parábola e seus usos, incluindo projetos solares de baixo custo e com eficiência energética.

Representação gráfica de parábolas com vértices na origem

Anteriormente, vimos que uma elipse é formada quando um plano corta um cone circular reto. Se o plano for paralelo à borda do cone, uma curva ilimitada será formada. Essa curva é uma parábola (Figura\(\PageIndex{2}\)).

Figura\(\PageIndex{2}\): Parabola

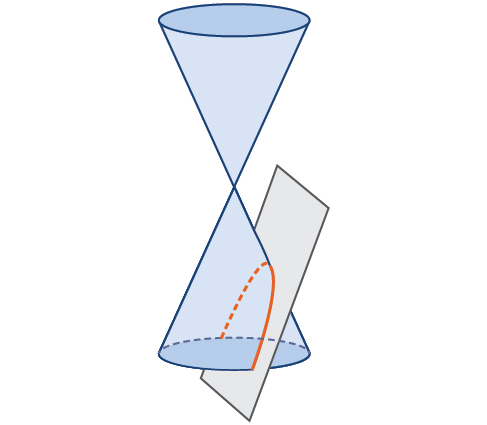
Como a elipse e a hipérbole, a parábola também pode ser definida por um conjunto de pontos no plano coordenado. Uma parábola é o conjunto de todos os pontos\((x,y)\) em um plano que estão à mesma distância de uma linha fixa, chamada diretriz, e um ponto fixo (o foco) que não está na diretriz.

Anteriormente, aprendemos sobre o vértice e o eixo de simetria de uma parábola. Agora, estendemos a discussão para incluir outras características-chave da parábola (Figura\(\PageIndex{3}\)). Observe que o eixo de simetria passa pelo foco e pelo vértice e é perpendicular à diretriz. O vértice é o ponto médio entre a diretriz e o foco. O segmento de linha que passa pelo foco e é paralelo à diretriz é chamado de látus reto. Os pontos finais do latus reto estão na curva. Por definição, o d distanciado do foco a qualquer ponto\(P\) da parábola é igual à distância de\(P\) até a diretriz.

Figura\(\PageIndex{3}\): Principais características da parábola

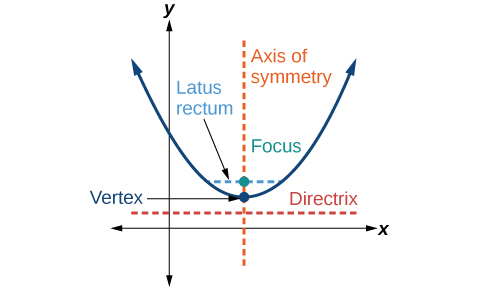
Para trabalhar com parábolas no plano coordenado, consideramos dois casos: aqueles com um vértice na origem e aqueles com um vértice em um ponto diferente da origem. Começamos com o primeiro.

Figura\(\PageIndex{4}\)

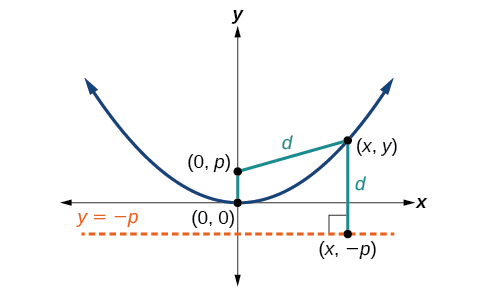
\((x,y)\)Seja um ponto na parábola com vértice\((0,0)\), foco e diretriz\((0,p)\),\(y=−p\) conforme mostrado na Figura\(\PageIndex{4}\). O d distanciado de ponto\((x,y)\) a ponto\((x,−p)\) na diretriz é a diferença dos valores de y:\(d=y+p\). A distância do foco\((0,p)\) até o ponto também\((x,y)\) é igual\(d\) e pode ser expressa usando a fórmula da distância.

\[ \begin{align*} d &=\sqrt{{(x−0)}^2+{(y−p)}^2} \\[4pt] &=\sqrt{x^2+{(y−p)}^2} \end{align*} \]

Defina as duas expressões como\(d\) iguais uma à outra e resolva\(y\) para derivar a equação da parábola. Fazemos isso porque a distância de\((x,y)\) até\((0,p)\) é igual\((x,y)\) à distância de\((x,−p)\) a.

\[\sqrt{x^2+{(y−p)}^2}=y+p \]

Em seguida, quadramos os dois lados da equação, expandimos os termos quadrados e simplificamos combinando termos semelhantes.

\[ \begin{align*} x^2+{(y−p)}^2 &={(y+p)}^2 \\[4pt] x^2+y^2−2py+p^2 &=y^2+2py+p^2 \\[4pt] x^2−2py &=2py \\[4pt] x^2 &=4py \end{align*} \]

As equações das parábolas com vértice\((0,0)\) são\(y^2=4px\) quando o eixo x é o eixo de simetria e\(x^2=4py\) quando o eixo y é o eixo de simetria. Esses formulários padrão são fornecidos abaixo, junto com seus gráficos gerais e características principais.

FORMAS PADRÃO DE PARÁBOLAS COM VÉRTICE\((0,0)\)

A tabela\(\PageIndex{1}\) e a figura\(\PageIndex{5}\) resumem as características padrão das parábolas com um vértice na origem.

Tabela\(\PageIndex{1}\)

Eixo de simetria	Equação	Foco	Directrix	Pontos finais do Latus Rectum
eixo x	\(y^2=4px\)	\((p, 0)\)	\(x=−p\)	\((p, \pm 2p)\)
eixo y	\(x^2=4py\)	\((0, p)\)	\(y=−p\)	\((\pm 2p, p)\)

Figura\(\PageIndex{5}\): (a) Quando\(p>0\) e o eixo de simetria é o eixo x, a parábola se abre à direita. (b) Quando\(p<0\) e o eixo de simetria é o eixo x, a parábola se abre à esquerda. (c) Quando\(p<0\) e o eixo de simetria é o eixo y, a parábola se abre. (d) Quando\(p<0\) e o eixo de simetria é o eixo y, a parábola se abre.

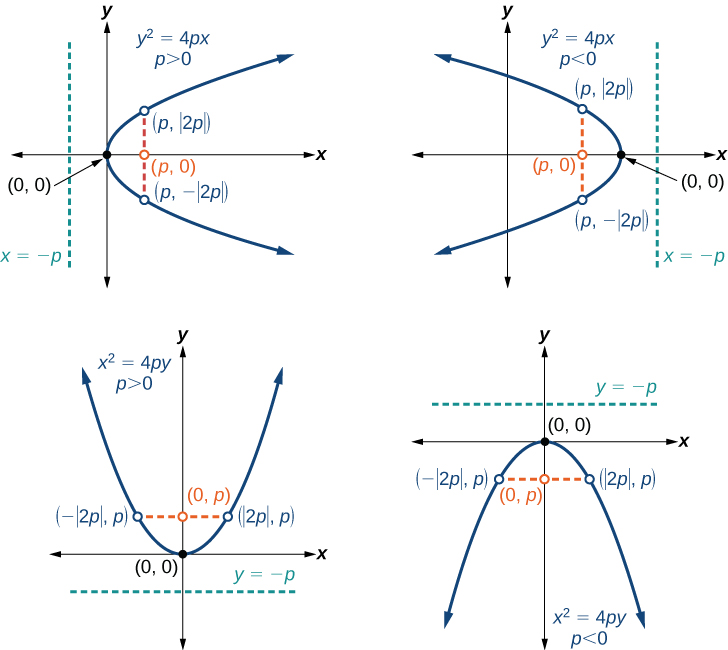
As principais características de uma parábola são seu vértice, eixo de simetria, foco, diretriz e látex reto (Figura\(\PageIndex{5}\)). Quando é dada uma equação padrão para uma parábola centrada na origem, podemos identificar facilmente as principais características para representar graficamente a parábola. Diz-se que uma linha é tangente a uma curva se ela cruzar a curva em exatamente um ponto. Se esboçarmos linhas tangentes à parábola nas extremidades do latus reto, essas linhas se cruzam no eixo de simetria, conforme mostrado na Figura\(\PageIndex{6}\).

Figura\(\PageIndex{6}\)

Como: Dada uma equação de forma padrão para uma parábola centrada em\((0,0)\), sketch the graph

1. Determine qual das formas padrão se aplica à equação dada:\(y^2=4px\) ou\(x^2=4py\).
2. Use a forma padrão identificada na Etapa 1 para determinar o eixo de simetria, foco, equação da diretriz e pontos finais do latus reto.
   • Se a equação estiver no formulário\(y^2=4px\), então
     • o eixo de simetria é o\(x\) eixo -,\(y=0\)
     • conjunto\(4p\) igual ao coeficiente de\(x\) na equação dada para resolver\(p\). Se\(p>0\), a parábola se abre à direita. Se\(p<0\), a parábola se abre para a esquerda.
     • use\(p\) para encontrar as coordenadas do foco,\((p,0)\)
     • use\(p\) para encontrar a equação da diretriz,\(x=−p\)
     • use\(p\) para encontrar os pontos finais do látex reto,\((p,\pm 2p)\). Alternativamente, substitua\(x=p\) na equação original.
   • Se a equação estiver no formulário\(x^2=4py\), então
     • o eixo de simetria é o\(y\) eixo -,\(x=0\)
     • conjunto\(4p\) igual ao coeficiente de\(y\) na equação dada para resolver\(p\). Se\(p>0\), a parábola se abre. Se\(p<0\), a parábola se abre.
     • use\(p\) para encontrar as coordenadas do foco,\((0,p)\)
     • use\(p\) para encontrar a equação da diretriz,\(y=−p\)
     • use\(p\) para encontrar os pontos finais do látex reto,\((\pm 2p,p)\)
3. Faça um gráfico do foco, da diretriz e do látex reto e desenhe uma curva suave para formar a parábola.

-eixo como eixo de simetria

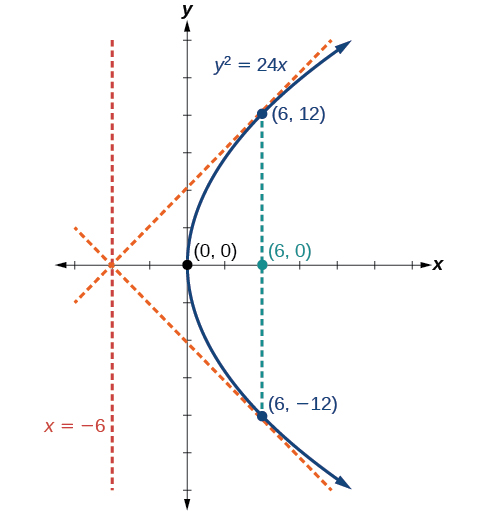
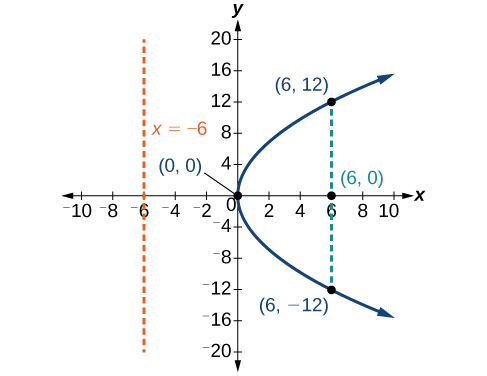
Gráfico\(y^2=24x\). Identifique e rotule o foco, a diretriz e os pontos finais do látex reto.

Solução

A forma padrão que se aplica à equação dada é\(y^2=4px\). Assim, o eixo de simetria é o eixo x. Daqui resulta que:

• \(24=4p\), então\(p=6\). Uma vez que\(p>0\), a parábola se abre à direita
• as coordenadas do foco são\((p,0)=(6,0)\)
• a equação da diretriz é\(x=−p=−6\)
• as extremidades do látex reto têm a mesma coordenada x no foco. Para encontrar os pontos finais,\(x=6\) substitua pela equação original:\((6,\pm 12)\)

Em seguida, traçamos o foco, a diretriz e o látus reto e desenhamos uma curva suave para formar a parábola (Figura\(\PageIndex{7}\)).

Figura\(\PageIndex{7}\)

Exercício\(\PageIndex{1}\)

Gráfico\(y^2=−16x\). Identifique e rotule o foco, a diretriz e os pontos finais do látex reto.

Resposta

• Foco:\((−4,0)\)
• Diretriz:\(x=4\)
• Pontos finais do látex reto:\((−4,\pm 8)\)

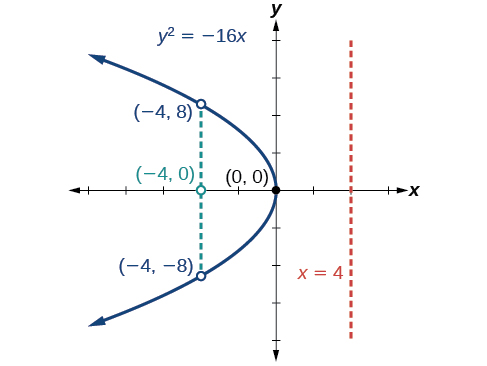
Figura\(\PageIndex{8}\)

-eixo como eixo de simetria

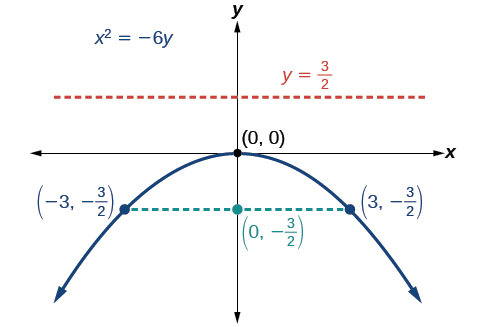
Gráfico\(x^2=−6y\). Identifique e rotule o foco, a diretriz e os pontos finais do látex reto.

Solução

A forma padrão que se aplica à equação dada é\(x^2=4py\). Assim, o eixo de simetria é o\(y\) eixo -. Daqui resulta que:

• \(−6=4p\), então\(p=−\dfrac{3}{2}\). Desde então\(p<0\), a parábola se abre.
• as coordenadas do foco são\((0,p)=(0,−\dfrac{3}{2})\)
• a equação da diretriz é\(y=−p=\dfrac{3}{2}\)
• os pontos finais do látex reto podem ser encontrados\(y=\dfrac{3}{2}\) substituindo-os pela equação original,\((\pm 3,−\dfrac{3}{2})\)

Em seguida, traçamos o foco, a diretriz e o látex reto e desenhamos uma curva suave para formar a parábola.

Figura\(\PageIndex{9}\)

Exercício\(\PageIndex{2}\)

Gráfico\(x^2=8y\). Identifique e rotule o foco, a diretriz e os pontos finais do látex reto.

Resposta

• Foco:\((0,2)\)
• Diretriz:\(y=−2\)
• Extremidades do látex reto:\((\pm 4,2)\).

Figura\(\PageIndex{10}\)

Escrevendo equações de parábolas na forma padrão

Nos exemplos anteriores, usamos a equação de forma padrão de uma parábola para calcular a localização de suas principais características. Também podemos usar os cálculos ao contrário para escrever uma equação para uma parábola, considerando suas principais características.

Como: Dado seu foco e diretriz, escrever a equação para uma parábola na forma padrão

1. Determine se o eixo de simetria é o\(y\) eixo\(x\) - ou -.
   1. Se as coordenadas fornecidas do foco tiverem a forma\((p,0)\), então o eixo de simetria é o\(x\) eixo -. Use o formulário padrão\(y^2=4px\).
   2. Se as coordenadas fornecidas do foco tiverem a forma\((0,p)\), então o eixo de simetria é o\(y\) eixo -. Use o formulário padrão\(x^2=4py\).
2. Multiplique\(4p\).
3. Substitua o valor da Etapa 2 na equação determinada na Etapa 1.

Exemplo\(\PageIndex{3}\): Writing the Equation of a Parabola in Standard Form Given its Focus and Directrix

Qual é a equação da parábola com foco\((−\dfrac{1}{2},0)\) e diretriz\(x=\dfrac{1}{2}\)?

Solução

O foco tem a forma\((p,0)\), então a equação terá a forma\(y^2=4px\).

• Multiplicando\(4p\), temos\(4p=4(−\dfrac{1}{2})=−2\).
• Substituindo por\(4p\), nós temos\(y^2=4px=−2x\). =

Portanto, a equação para a parábola é\(y^2=−2x\).

Exercício\(\PageIndex{3}\)

Qual é a equação da parábola com foco\(\left(0,\dfrac{7}{2}\right)\) e diretriz\(y=−\dfrac{7}{2}\)?

Resposta

\(x^2=14y\).

Representação gráfica de parábolas com vértices que não estão na origem

Como outros gráficos com os quais trabalhamos, o gráfico de uma parábola pode ser traduzido. Se uma parábola for traduzida em\(h\) unidades horizontalmente e\(k\) unidades verticalmente, o vértice será\((h,k)\). Essa tradução resulta na forma padrão da equação que vimos anteriormente com\(x\) substituída por\((x−h)\) e\(y\) substituída por\((y−k)\).

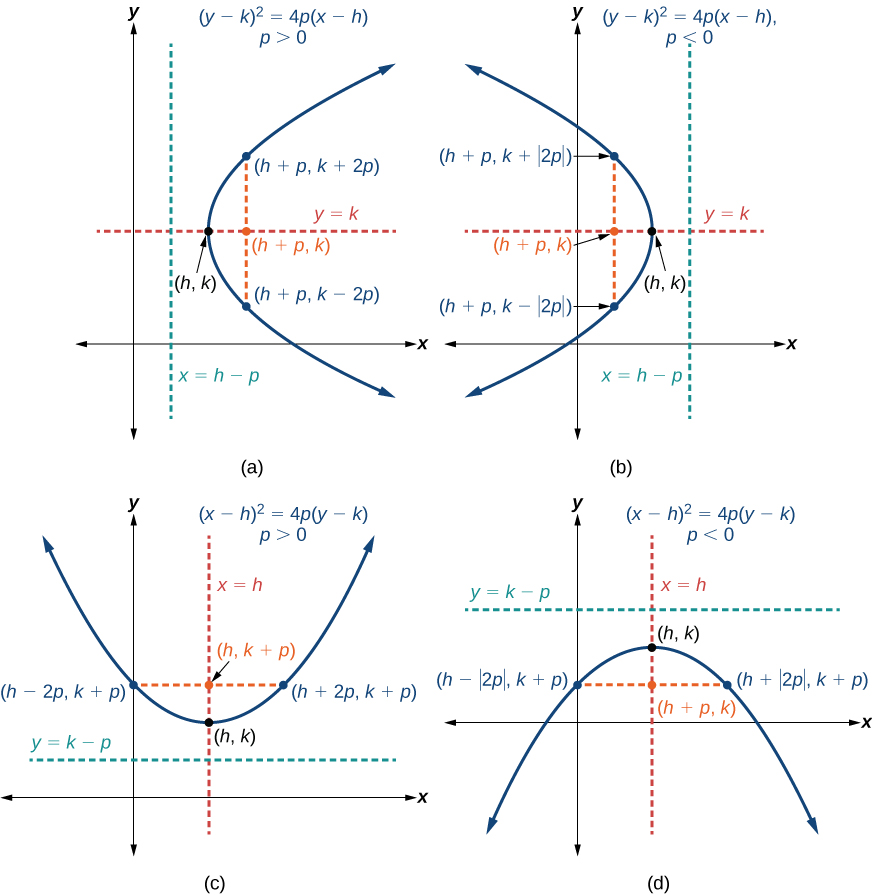
Para representar graficamente parábolas com um vértice\((h,k)\) diferente da origem, usamos a forma padrão\({(y−k)}^2=4p(x−h)\) para parábolas que têm um eixo de simetria paralelo ao\(x\) eixo -e\({(x−h)}^2=4p(y−k)\) para parábolas que têm um eixo de simetria paralelo ao\(y\) eixo -. Esses formulários padrão são fornecidos abaixo, junto com seus gráficos gerais e características principais.

FORMAS PADRÃO DE PARÁBOLAS COM VÉRTICE\((H, K)\)

A tabela\(\PageIndex{2}\) e a figura\(\PageIndex{11}\) resumem as características padrão das parábolas com um vértice em um ponto\((h,k)\).

Tabela\(\PageIndex{2}\)

Eixo de simetria	Equação	Foco	Directrix	Pontos finais do Latus Rectum
\(y=k\)	\({(y−k)}^2=4p(x−h)\)	\((h+p, k)\)	\(x=h−p\)	\((h+p, k\pm 2p)\)
\(x=h\)	\({(x−h)}^2=4p(y−k)\)	\((h, k+p)\)	\(y=k−p\)	\((h\pm 2p, k+p)\)

Figura\(\PageIndex{11}\): (a) Quando\(p>0\), a parábola se abre à direita. (b) Quando\(p<0\), a parábola se abre à esquerda. (c) Quando\(p>0\), a parábola se abre. (d) Quando\(p<0\), a parábola se abre.

Como: Dada uma equação de forma padrão para uma parábola centrada em\((h,k)\), sketch the graph

1. Determine qual das formas padrão se aplica à equação dada:\({(y−k)}^2=4p(x−h)\) ou\({(x−h)}^2=4p(y−k)\).
2. Use a forma padrão identificada na Etapa 1 para determinar o vértice, o eixo de simetria, o foco, a equação da diretriz e os pontos finais do latus reto.
   • Se a equação estiver no formulário\({(y−k)}^2=4p(x−h)\), então:
     • use a equação dada para identificar\(h\) e\(k\) para o vértice,\((h,k)\)
     • use o valor de\(k\) para determinar o eixo de simetria,\(y=k\)
     • conjunto\(4p\) igual ao coeficiente de\((x−h)\) na equação dada para resolver\(p\). Se\(p>0\), a parábola se abre à direita. Se\(p<0\), a parábola se abre para a esquerda.
     • use\(h\),\(k\), e\(p\) para encontrar as coordenadas do foco,\((h+p, k)\)
     • use\(h\) andp p para encontrar a equação da diretriz,\(x=h−p\)
     • use\(h\)\(k\),, e\(p\) para encontrar as extremidades do látex reto,\((h+p,k\pm 2p)\)
   • Se a equação estiver no formulário\({(x−h)}^2=4p(y−k)\), então:
     • use a equação dada para identificar\(h\) e\(k\) para o vértice,\((h,k)\)
     • use o valor de\(h\) para determinar o eixo de simetria,\(x=h\)
     • conjunto\(4p\) igual ao coeficiente de\((y−k)\) na equação dada para resolver\(p\). Se\(p>0\), a parábola se abre. Se\(p<0\), a parábola se abre.
     • use\(h\),\(k\), e\(p\) para encontrar as coordenadas do foco,\((h, k+p)\)
     • use\(k\) e\(p\) para encontrar a equação da diretriz,\(y=k−p\)
     • use\(h\)\(k\),, e\(p\) para encontrar as extremidades do látex reto,\((h\pm 2p, k+p)\)
3. Faça um gráfico do vértice, eixo de simetria, foco, diretriz e latus reto e desenhe uma curva suave para formar a parábola.

Exemplo\(\PageIndex{4}\): Graphing a Parabola with Vertex \((h, k)\) and Axis of Symmetry Parallel to the \(x\)-axis

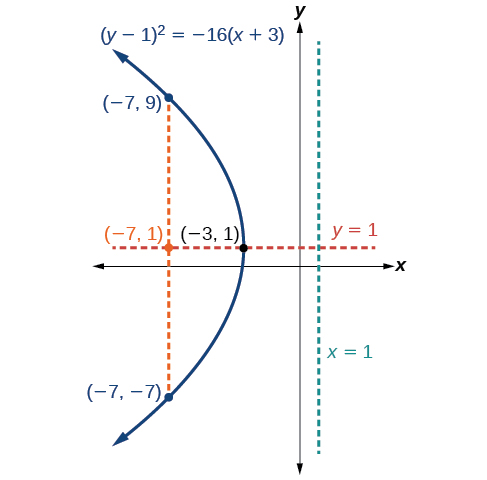
Gráfico\({(y−1)}^2=−16(x+3)\). Identifique e rotule o vértice, o eixo de simetria, o foco, a diretriz e os pontos finais do latus reto.

Solução

A forma padrão que se aplica à equação dada é\({(y−k)}^2=4p(x−h)\). Assim, o eixo de simetria é paralelo ao\(x\) eixo -. Daqui resulta que:

• o vértice é\((h,k)=(−3,1)\)
• o eixo de simetria é\(y=k=1\)
• \(−16=4p\), então\(p=−4\). Desde então\(p<0\), a parábola se abre à esquerda.
• as coordenadas do foco são\((h+p,k)=(−3+(−4),1)=(−7,1)\)
• a equação da diretriz é\(x=h−p=−3−(−4)=1\)
• as extremidades do látex reto são\((h+p,k\pm 2p)=(−3+(−4),1\pm 2(−4))\), ou\((−7,−7)\) e\((−7,9)\)

Em seguida, traçamos o vértice, eixo de simetria, foco, diretriz e latus reto e desenhamos uma curva suave para formar a parábola (Figura\(\PageIndex{10}\)).

Figura\(\PageIndex{12}\)

Exercício\(\PageIndex{4}\)

Gráfico\({(y+1)}^2=4(x−8)\). Identifique e rotule o vértice, o eixo de simetria, o foco, a diretriz e os pontos finais do latus reto.

Resposta

• Vértice:\((8,−1)\)
• Eixo de simetria:\(y=−1\)
• Foco:\((9,−1)\)
• Diretriz:\(x=7\)
• Extremidades do látex reto:\((9,−3)\)\((9,1)\) e.

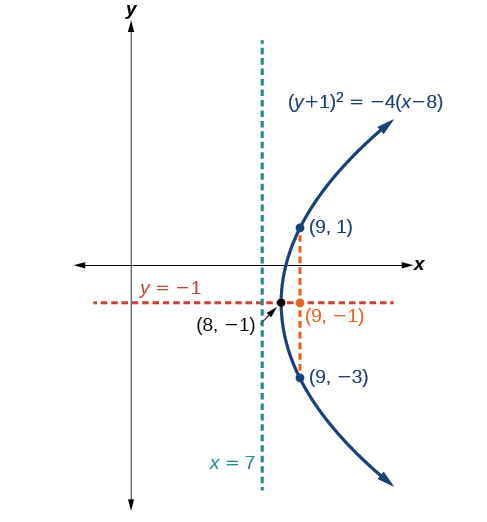
Figura\(\PageIndex{13}\)

Exemplo\(\PageIndex{5}\): Graphing a Parabola from an Equation Given in General Form

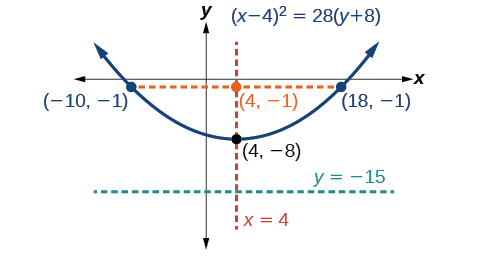
Gráfico\(x^2−8x−28y−208=0\). Identifique e rotule o vértice, o eixo de simetria, o foco, a diretriz e os pontos finais do latus reto.

Solução

Comece escrevendo a equação da parábola na forma padrão. A forma padrão que se aplica à equação dada é\({(x−h)}^2=4p(y−k)\). Assim, o eixo de simetria é paralelo ao\(y\) eixo -. Para expressar a equação da parábola nesta forma, começamos isolando os termos que contêm a variável para\(x\) completar o quadrado.

\[ \begin{align*} x^2−8x−28y−208&=0 \\[4pt] x^2−8x &=28y+208 \\[4pt] x^2−8x+16 &=28y+208+16 \\[4pt] (x−4)^2 &=28y+224 \\[4pt] (x−4)^2 &=28(y+8) \\[4pt] (x−4)^2&= 4⋅7⋅(y+8) \end{align*}\]

Daqui resulta que:

• o vértice é\((h,k)=(4,−8)\)
• o eixo de simetria é\(x=h=4\)
• desde então\(p=7\),\(p>0\) e assim a parábola se abre
• as coordenadas do foco são\((h,k+p)=(4,−8+7)=(4,−1)\)
• a equação da diretriz é\(y=k−p=−8−7=−15\)
• as extremidades do látex reto são\((h\pm 2p,k+p)=(4\pm 2(7),−8+7)\), ou\((−10,−1)\) e\((18,−1)\)

Em seguida, traçamos o vértice, eixo de simetria, foco, diretriz e latus reto e desenhamos uma curva suave para formar a parábola (Figura\(\PageIndex{14}\)).

Figura\(\PageIndex{14}\)

Exercício\(\PageIndex{5}\)

Gráfico\({(x+2)}^2=−20(y−3)\). Identifique e rotule o vértice, o eixo de simetria, o foco, a diretriz e os pontos finais do latus reto.

Resposta

• Vértice:\((−2,3)\)
• Eixo de simetria:\(x=−2\)
• Foco:\((−2,−2)\)
• Diretriz:\(y=8\)
• Extremidades do látex reto:\((−12,−2)\)\((8,−2)\) e.

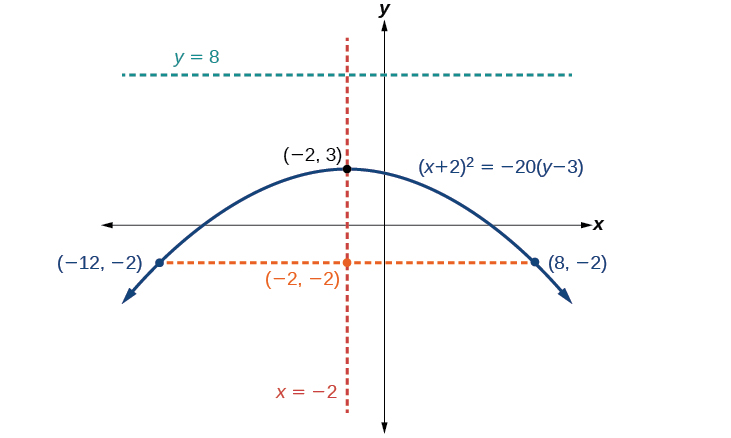
Figura\(\PageIndex{15}\)

Resolvendo problemas aplicados envolvendo parábolas

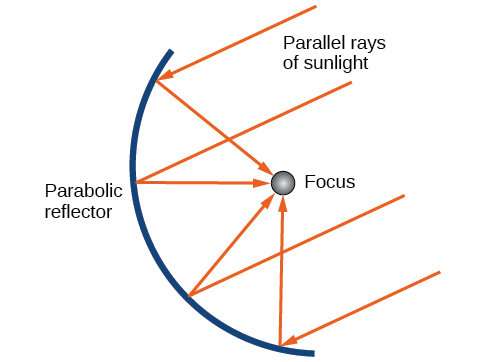
Como mencionamos no início da seção, as parábolas são usadas para projetar muitos objetos que usamos todos os dias, como telescópios, pontes suspensas, microfones e equipamentos de radar. Espelhos parabólicos, como o usado para acender a tocha olímpica, têm uma propriedade refletora muito única. Quando os raios de luz paralelos ao eixo de simetria da parábola são direcionados para qualquer superfície do espelho, a luz é refletida diretamente para o foco (Figura\(\PageIndex{16}\)). É por isso que a tocha olímpica é acesa quando mantida no foco do espelho parabólico.

Figura\(\PageIndex{16}\): Propriedade refletora das parábolas

Os espelhos parabólicos têm a capacidade de focar a energia do sol em um único ponto, elevando a temperatura em centenas de graus em questão de segundos. Assim, os espelhos parabólicos são apresentados em muitos produtos solares de baixo custo e com eficiência energética, como fogões solares, aquecedores solares e até mesmo acionadores de incêndio de tamanho de viagem.

Exemplo\(\PageIndex{6}\): Solving Applied Problems Involving Parabolas

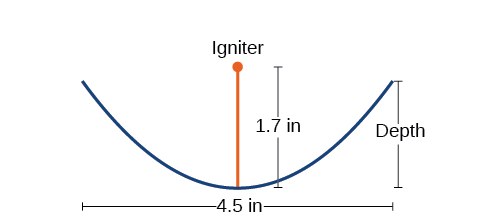
Uma seção transversal de um design para um acionador de incêndio solar de tamanho de viagem é mostrada na Figura\(\PageIndex{17}\). Os raios do sol refletem no espelho parabólico em direção a um objeto preso ao ignitor. Como o ignitor está localizado no foco da parábola, os raios refletidos fazem com que o objeto queime em apenas alguns segundos.

1. Encontre a equação da parábola que modela o acionador de incêndio. Suponha que o vértice do espelho parabólico seja a origem do plano coordenado.
2. Use a equação encontrada na parte (a) para encontrar a profundidade do acionador de incêndio.

Figura\(\PageIndex{17}\) Seção transversal de um acionador de incêndio solar do tamanho de uma viagem

Solução

1. O vértice do prato é a origem do plano coordenado, então a parábola assumirá a forma padrão\(x^2=4py\), onde\(p>0\). O ignitor, que é o foco, está\(1.7\) centímetros acima do vértice do prato. Assim, temos\(p=1.7\).

\[\begin{align*} x^2&=4py\qquad \text{Standard form of upward-facing parabola with vertex } (0,0)\\ x^2&=4(1.7)y\qquad \text{Substitute } 1.7 \text{ for } p\\ x^2&=6.8y\qquad \text{Multiply.} \end{align*}\]

2. O prato se estende por\(\dfrac{4.5}{2}=2.25\) centímetros em cada lado da origem. Podemos substituir\(2.25\) por\(x\) na equação da parte (a) para determinar a profundidade do prato.

\[\begin{align*} x^2&=6.8y\qquad \text{ Equation found in part } (a)\\ {(2.25)}^2&=6.8y\qquad \text{Substitute } 2.25 \text{ for } x\\ y&\approx 0.74\qquad \text{Solve for } y \end{align*}\]

O prato tem cerca de\(0.74\) centímetros de profundidade.

Exercício\(\PageIndex{6}\)

Os fogões solares do tamanho de uma varanda foram projetados para famílias que vivem na Índia. A parte superior de um prato tem um diâmetro de\(1600\) mm. Os raios do sol refletem no espelho parabólico em direção ao “fogão”, que é colocado a\(320\) mm da base.

1. Encontre uma equação que modela uma seção transversal do fogão solar. Suponha que o vértice do espelho parabólico seja a origem do plano coordenado e que a parábola se abra para a direita (ou seja, tenha o eixo x como eixo de simetria).
2. Use a equação encontrada na parte (a) para encontrar a profundidade do fogão.

Responda a um

\(y^2=1280x\)

Resposta b

A profundidade do fogão é\(500\) mm

Equações-chave

Parábola, vértice na origem, eixo de simetria no eixo x	\(y^2=4px\)
Parábola, vértice na origem, eixo de simetria no eixo y	\(x^2=4py\)
Parábola, vértice em\((h,k)\), eixo de simetria no eixo x	\({(y−k)}^2=4p(x−h)\)
Parábola, vértice em\((h,k)\), eixo de simetria no eixo y	\({(x−h)}^2=4p(y−k)\)

Conceitos-chave

• Uma parábola é o conjunto de todos os pontos\((x,y)\) em um plano que estão à mesma distância de uma linha fixa, chamada diretriz, e um ponto fixo (o foco) que não está na diretriz.
• A forma padrão de uma parábola com vértice\((0,0)\) e o eixo x como eixo de simetria pode ser usada para representar graficamente a parábola. Se\(p>0\), a parábola se abre à direita. Se\(p<0\), a parábola se abre para a esquerda. Veja o exemplo\(\PageIndex{1}\).
• A forma padrão de uma parábola com vértice\((0,0)\) e o eixo y como eixo de simetria pode ser usada para representar graficamente a parábola. Se\(p>0\), a parábola se abre. Se\(p<0\), a parábola se abre. Veja o exemplo\(\PageIndex{2}\).
• Quando recebemos o foco e a diretriz de uma parábola, podemos escrever sua equação na forma padrão. Veja o exemplo\(\PageIndex{3}\).
• A forma padrão de uma parábola com vértice\((h,k)\) e eixo de simetria paralelos ao\(x\) eixo -pode ser usada para representar graficamente a parábola. Se\(p>0\), a parábola se abre à direita. Se\(p<0\), a parábola se abre para a esquerda. Veja o exemplo\(\PageIndex{4}\).
• A forma padrão de uma parábola com vértice\((h,k)\) e eixo de simetria paralelos ao\(y\) eixo -pode ser usada para representar graficamente a parábola. Se\(p>0\), a parábola se abre. Se\(p<0\), a parábola se abre. Veja o exemplo\(\PageIndex{5}\).
• Situações do mundo real podem ser modeladas usando as equações padrão das parábolas. Por exemplo, dado o diâmetro e o foco de uma seção transversal de um refletor parabólico, podemos encontrar uma equação que modela seus lados. Veja o exemplo\(\PageIndex{6}\).