10.4: Rotação dos eixos
- Page ID
- 189365
- Identifique seções cônicas não degeneradas dadas suas equações de forma geral.
- Use fórmulas de rotação de eixos.
- Escreva equações de cônicas giradas na forma padrão.
- Identifique cônicas sem eixos rotativos.
Como vimos, seções cônicas são formadas quando um plano cruza dois cones circulares retos alinhados de ponta a ponta e se estendendo infinitamente em direções opostas, o que também chamamos de cone. A forma como cortamos o cone determinará o tipo de seção cônica formada na interseção. Um círculo é formado cortando um cone com um plano perpendicular ao eixo de simetria do cone. Uma elipse é formada cortando um único cone com um plano inclinado não perpendicular ao eixo de simetria. Uma parábola é formada cortando o plano na parte superior ou inferior do cone duplo, enquanto uma hipérbole é formada quando o plano corta a parte superior e inferior do cone (Figura\(\PageIndex{1}\)).
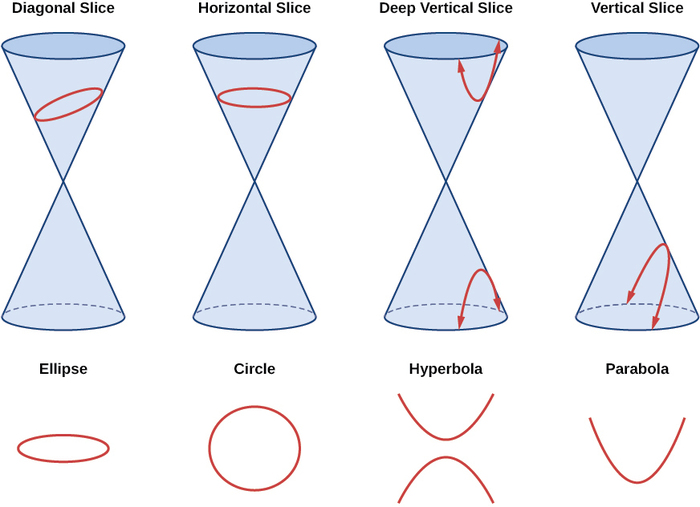
Figura\(\PageIndex{1}\): As seções cônicas não degeneradas
Elipses, círculos, hipérboles e parábolas às vezes são chamadas de seções cônicas não degeneradas, em contraste com as seções cônicas degeneradas, mostradas na Figura\(\PageIndex{2}\). Uma cônica degenerada ocorre quando um plano cruza o cone duplo e passa pelo ápice. Dependendo do ângulo do plano, três tipos de seções cônicas degeneradas são possíveis: um ponto, uma linha ou duas linhas que se cruzam.
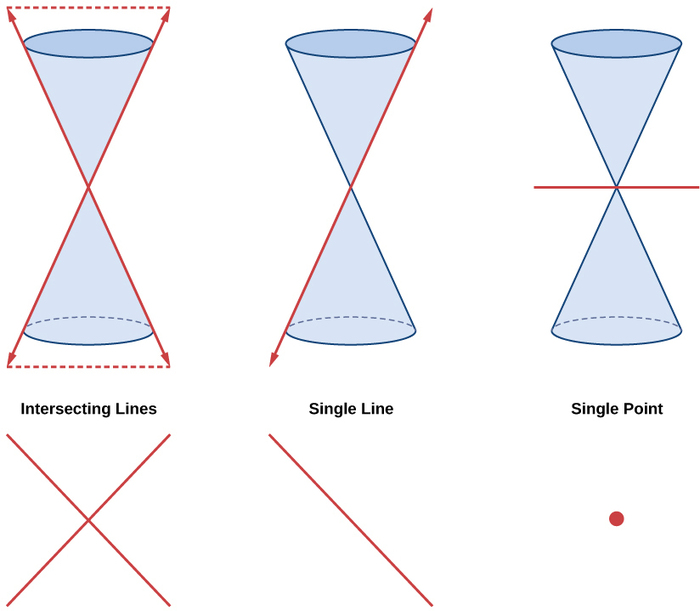
Figura\(\PageIndex{2}\): Seções cônicas degeneradas
Identificação de cônicas não degeneradas na forma geral
Nas seções anteriores deste capítulo, nos concentramos nas equações de forma padrão para seções cônicas não degeneradas. Nesta seção, vamos mudar nosso foco para a equação geral da forma, que pode ser usada para qualquer cônica. A forma geral é definida como igual a zero, e os termos e coeficientes são fornecidos em uma ordem específica, conforme mostrado abaixo.
\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\)
onde\(A\)\(B\), e nem todos\(C\) são zero. Podemos usar os valores dos coeficientes para identificar qual tipo de cônica é representado por uma determinada equação.
Você pode notar que a equação da forma geral tem um\(xy\) termo que não vimos em nenhuma das equações da forma padrão. Como discutiremos mais adiante, o\(xy\) termo gira a cônica sempre que não\(B\) é igual a zero.
| Seções cônicas | Exemplo |
|---|---|
| elipse | \(4x^2+9y^2=1\) |
| circular | \(4x^2+4y^2=1\) |
| hipérbole | \(4x^2−9y^2=1\) |
| parábola | \(4x^2=9y\)ou\(4y^2=9x\) |
| uma linha | \(4x+9y=1\) |
| linhas que se cruzam | \((x−4)(y+4)=0\) |
| linhas paralelas | \((x−4)(x−9)=0\) |
| um ponto | \(4x^2+4y^2=0\) |
| sem gráfico | \(4x^2+4y^2=−1\) |
Uma seção cônica tem a forma geral
\[Ax^2+Bxy+Cy^2+Dx+Ey+F=0 \label{gen}\]
onde\(A\)\(B\), e nem todos\(C\) são zero. A tabela\(\PageIndex{2}\) resume as diferentes seções cônicas onde\(B=0\), e\(A\) e\(C\) são números reais diferentes de zero. Isso indica que a cônica não foi girada.
| elipse | \(Ax^2+Cy^2+Dx+Ey+F=0\),\(A≠C\) e\(AC>0\) |
|---|---|
| circular | \(Ax^2+Cy^2+Dx+Ey+F=0\),\(A=C\) |
| hipérbole | \(Ax^2−Cy^2+Dx+Ey+F=0\)ou\(−Ax^2+Cy^2+Dx+Ey+F=0\), onde\(A\) e\(C\) são positivos |
| parábola | \(Ax^2+Dx+Ey+F=0\)ou\(Cy^2+Dx+Ey+F=0\) |
- Reescreva a equação na forma geral (Equação\ ref {gen}),\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\)
- Identifique os valores de\(A\) e\(C\) a partir do formulário geral.
- Se\(A\) e\(C\) forem diferentes de zero, tiverem o mesmo sinal e não forem iguais entre si, o gráfico pode ser uma elipse.
- Se\(A\) e\(C\) forem iguais e diferentes de zero e tiverem o mesmo sinal, o gráfico poderá ser um círculo.
- Se\(A\) e\(C\) forem diferentes de zero e tiverem sinais opostos, o gráfico pode ser uma hipérbole.
- Se um\(A\) ou\(C\) for zero, o gráfico pode ser uma parábola.
Se\(B=0\), a seção cônica terá eixos verticais e/ou horizontais. Se\(B\) não for igual a 0, conforme mostrado abaixo, a seção cônica é girada. Observe a frase “pode ser” nas definições. Isso ocorre porque a equação pode não representar uma seção cônica, dependendo dos valores de\(A\)\(B\),\(C\),\(D\)\(E\),,\(F\) e. Por exemplo, o caso degenerado de um círculo ou elipse é um ponto:
\[Ax^2+By^2=0,\]
quando\(A\) e\(B\) tem o mesmo sinal.
O caso degenerado de uma hipérbole consiste em duas linhas retas que se cruzam:\(Ax^2+By^2=0\), quando\(A\) e\(B\) têm sinais opostos.
Por outro lado, a equação\(Ax^2+By^2+1=0\), quando\(A\) e\(B\) são positivos não representa nenhum gráfico, pois não há pares reais ordenados que o satisfaçam.
Identifique o gráfico de cada uma das seguintes seções cônicas não degeneradas.
- \(4x^2−9y^2+36x+36y−125=0\)
- \(9y^2+16x+36y−10=0\)
- \(3x^2+3y^2−2x−6y−4=0\)
- \(−25x^2−4y^2+100x+16y+20=0\)
Solução
- Reescrevendo a forma geral (Equação\ ref {gen}), temos\[\begin{align*} \color{red}{A} \color{black}x ^ { 2 } + \color{blue}{B} \color{black}x y + \color{red}{C} \color{black} y ^ { 2 } + \color{blue}{D} \color{black} x + \color{blue}{E} \color{black} y + \color{blue}{F} \color{black} &= 0 \\[4pt] 4 x ^ { 2 } + 0 x y + ( - 9 ) y ^ { 2 } + 36 x + 36 y + ( - 125 ) &= 0 \end{align*}\] com\(A=4\) e\(C=−9\), então observamos isso\(A\) e\(C\) temos sinais opostos. O gráfico dessa equação é uma hipérbole.
- Reescrevendo a forma geral (Equação\ ref {gen}), temos\[\begin{align*} \color{red}{A} \color{black}x ^ { 2 } + \color{blue}{B} \color{black}x y + \color{red}{C} \color{black} y ^ { 2 } + \color{blue}{D} \color{black} x + \color{blue}{E} \color{black} y + \color{blue}{F} \color{black} &= 0 \\[4pt] 0 x ^ { 2 } + 0 x y + 9 y ^ { 2 } + 16 x + 36 y + ( - 10 ) &= 0 \end{align*}\] com\(A=0\)\(C=9\) e. Podemos determinar que a equação é uma parábola, já que\(A\) é zero.
- Reescrevendo a forma geral (Equação\ ref {gen}), temos\[\begin{align*} \color{red}{A} \color{black}x ^ { 2 } + \color{blue}{B} \color{black}x y + \color{red}{C} \color{black} y ^ { 2 } + \color{blue}{D} \color{black} x + \color{blue}{E} \color{black} y + \color{blue}{F} \color{black} &= 0 \\[4pt] 3 x ^ { 2 } + 0 x y + 3 y ^ { 2 } + ( - 2 ) x + ( - 6 ) y + ( - 4 ) &= 0 \end{align*}\] com\(A=3\)\(C=3\) e. Porque\(A=C\) o gráfico dessa equação é um círculo.
- Reescrevendo a forma geral (Equação\ ref {gen}), temos\[\begin{align*} \color{red}{A} \color{black}x ^ { 2 } + \color{blue}{B} \color{black}x y + \color{red}{C} \color{black} y ^ { 2 } + \color{blue}{D} \color{black} x + \color{blue}{E} \color{black} y + \color{blue}{F} \color{black} &= 0 \\[4pt] ( - 25 ) x ^ { 2 } + 0 x y + ( - 4 ) y ^ { 2 } + 100 x + 16 y + 20 &= 0 \end{align*}\] com\(A=−25\)\(C=−4\) e. Porque\(AC>0\) e\(A≠C\), o gráfico dessa equação é uma elipse.
Identifique o gráfico de cada uma das seguintes seções cônicas não degeneradas.
- \(16y^2−x^2+x−4y−9=0\)
- \(16x^2+4y^2+16x+49y−81=0\)
- Responda a um
-
hipérbole
- Resposta b
-
elipse
Encontrando uma nova representação da equação dada após girar em um determinado ângulo
Até agora, analisamos equações de seções cônicas sem um\(xy\) termo, que alinha os gráficos com os eixos x e y. Quando adicionamos um\(xy\) termo, estamos girando a cônica em torno da origem. Se os eixos x e y forem girados em um ângulo, digamos\(\theta\), então cada ponto no plano pode ser considerado como tendo duas representações:\((x,y)\) no plano cartesiano com os eixos x e y originais, e\((x^\prime ,y^\prime )\) no novo plano definido pelos novos eixos girados, chamados de eixo x' e eixo y' (Figura\(\PageIndex{3}\)).
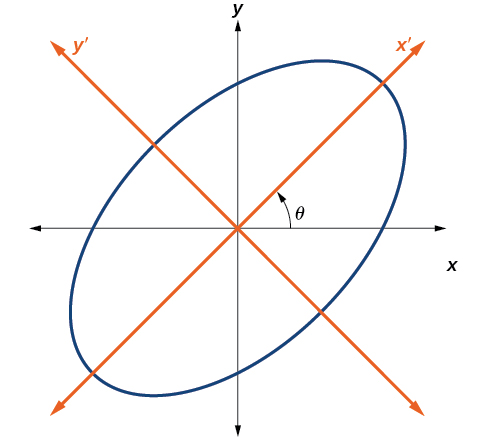
Figura\(\PageIndex{3}\): O gráfico da elipse girada\(x^2+y^2–xy–15=0\)
Encontraremos as relações entre\(x\) e\(y\) no plano cartesiano com\(x^\prime \) e\(y^\prime \) no novo plano rotacionado (Figura\(\PageIndex{4}\)).
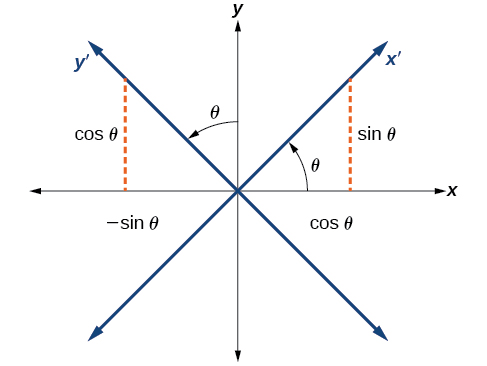
Figura\(\PageIndex{4}\): O plano cartesiano com\(y\) os eixos\(x\) - e -e os eixos\(x^\prime\) − e\(y^\prime\) −resultantes formados por uma rotação por um ângulo\(\theta\).
Os eixos coordenados x - e y originais têm vetores unitários\(\hat{i}\)\(\hat{j}\) e. Os eixos de coordenadas girados têm vetores unitários\(\hat{i}^\prime\)\(\hat{j}^\prime\) e. O ângulo\(\theta\) é conhecido como ângulo de rotação (Figura\(\PageIndex{5}\)). Podemos escrever os novos vetores unitários em termos dos originais.
\[\hat{i}′=\cos \theta \hat{i}+\sin \theta \hat{j}\]
\[\hat{j}′=−\sin \theta \hat{i}+\cos \theta \hat{j}\]
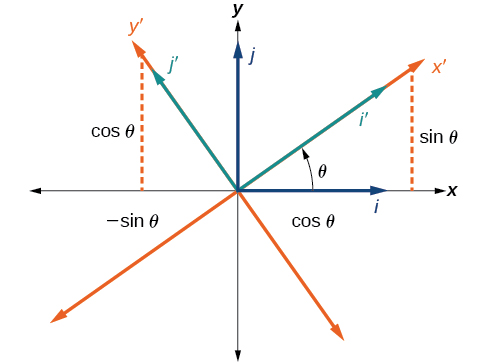
Figura\(\PageIndex{5}\): Relação entre o antigo e o novo plano de coordenadas.
Considere um vetor\(\vec{u}\) no novo plano de coordenadas. Ele pode ser representado em termos de seus eixos coordenados.
\[\begin{align*} \vec{u}&=x^\prime i′+y^\prime j′ \\[4pt] &=x^\prime (i \cos \theta+j \sin \theta)+y^\prime (−i \sin \theta+j \cos \theta) & \text{Substitute.} \\[4pt] &=ix' \cos \theta+jx' \sin \theta−iy' \sin \theta+jy' \cos \theta & \text{Distribute.} \\[4pt] &=ix' \cos \theta−iy' \sin \theta+jx' \sin \theta+jy' \cos \theta & \text{Apply commutative property.} \\[4pt] &=(x' \cos \theta−y' \sin \theta)i+(x' \sin \theta+y' \cos \theta)j & \text{Factor by grouping.} \end{align*}\]
Porque\(\vec{u}=x^\prime i′+y^\prime j′\) temos representações de\(x\) e\(y\) em termos do novo sistema de coordenadas.
\(x=x^\prime \cos \theta−y^\prime \sin \theta\)
e
\(y=x^\prime \sin \theta+y^\prime \cos \theta\)
Se um ponto\((x,y)\) no plano cartesiano for representado em um novo plano coordenado em que os eixos de rotação são formados pela rotação de um ângulo a\(\theta\) partir do eixo x positivo, então as coordenadas do ponto em relação aos novos eixos são\((x^\prime ,y^\prime )\). Podemos usar as seguintes equações de rotação para definir a relação entre\((x,y)\) e\((x^\prime , y^\prime )\):
\[x=x^\prime \cos \theta−y^\prime \sin \theta\]
e
\[y=x^\prime \sin \theta+y^\prime \cos \theta\]
- Encontre\(x\)\(x=x^\prime \cos \theta−y^\prime \sin \theta\) e\(y\) onde\(y=x^\prime \sin \theta+y^\prime \cos \theta\) e.
- Substitua a expressão por\(x\) e\(y\) em na equação dada e, em seguida, simplifique.
- Escreva as equações com\(x^\prime \) e\(y^\prime \) na forma padrão.
Encontre uma nova representação da equação\(2x^2−xy+2y^2−30=0\) depois de girar em um ângulo de\(\theta=45°\).
Solução
Encontre\(x\) e\(y\), onde\(x=x^\prime \cos \theta−y^\prime \sin \theta\)\(y=x^\prime \sin \theta+y^\prime \cos \theta\) e.
Porque\(\theta=45°\),
\[\begin{align*} x &= x^\prime \cos(45°)−y^\prime \sin(45°) \\[4pt] x &= x^\prime \left(\dfrac{1}{\sqrt{2}}\right)−y^\prime \left(\dfrac{1}{\sqrt{2}}\right) \\[4pt] x &=\dfrac{x^\prime −y^\prime }{\sqrt{2}} \end{align*}\]
e
\[\begin{align*} y &= x^\prime \sin(45°)+y^\prime \cos(45°) \\[4pt] y &= x^\prime \left(\dfrac{1}{\sqrt{2}}\right) + y^\prime \left(\dfrac{1}{\sqrt{2}}\right) \\[4pt] y &= \dfrac{x^\prime +y^\prime }{\sqrt{2}} \end{align*}\]
Substitua\(x=x^\prime \cos\theta−y^\prime \sin\theta\) e\(y=x^\prime \sin \theta+y^\prime \cos \theta\) entre\(2x^2−xy+2y^2−30=0\).
\(2{\left(\dfrac{x^\prime −y^\prime }{\sqrt{2}}\right)}^2−\left(\dfrac{x^\prime −y^\prime }{\sqrt{2}}\right)\left(\dfrac{x^\prime +y^\prime }{\sqrt{2}}\right)+2{\left(\dfrac{x^\prime +y^\prime }{\sqrt{2}}\right)}^2−30=0\)
Simplifique.
\(\begin{array}{rl} 2\dfrac{(x^\prime−y^\prime )(x^\prime −y^\prime )}{2}−\dfrac{(x^\prime −y^\prime )(x^\prime +y^\prime )}{2}+2\dfrac{(x^\prime +y^\prime )(x^\prime +y^\prime )}{2}−30=0 & \text{FOIL method} \\[4pt] {x^\prime }^2−2x^\prime y^\prime +{y^\prime }^2−\dfrac{({x^\prime }^2−{y^\prime }^2)}{2}+{x^\prime }^2+2x^\prime y^\prime +{y^\prime }^2−30=0 & \text{Combine like terms.} \\[4pt] 2{x^\prime }^2+2{y^\prime }^2−\dfrac{({x^\prime }^2−{y^\prime }^2)}{2}=30 & \text{Combine like terms.} \\[4pt] 2(2{x^\prime }^2+2{y^\prime }^2−\dfrac{({x^\prime }^2−{y^\prime }^2)}{2})=2(30) & \text{Multiply both sides by 2.} \\[4pt] 4{x^\prime }^2+4{y^\prime }^2−({x^\prime }^2−{y^\prime }^2)=60 & \text{Simplify. } \\[4pt] 4{x^\prime }^2+4{y^\prime }^2−{x^\prime }^2+{y^\prime }2=60 & \text{Distribute.} \\[4pt] \dfrac{3{x^\prime }^2}{60}+\dfrac{5{y^\prime }^2}{60}=\dfrac{60}{60} & \text{Set equal to 1.} \end{array} \)
Escreva as equações com\(x^\prime \) e\(y^\prime \) na forma padrão.
\[\dfrac{{x^\prime }^2}{20}+\dfrac{{y^\prime}^2}{12}=1 \nonumber\]
Essa equação é uma elipse. A figura\(\PageIndex{6}\) mostra o gráfico.
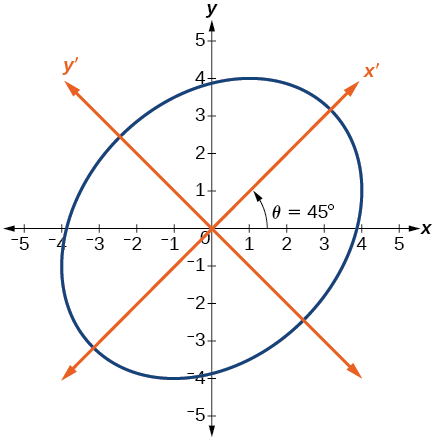
Figura\(\PageIndex{6}\)
Escrevendo equações de cônicas giradas na forma padrão
Agora que podemos encontrar a forma padrão de uma cônica quando recebemos um ângulo de rotação, aprenderemos como transformar a equação de uma cônica dada na forma\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\) em forma padrão girando os eixos. Para fazer isso, reescreveremos a forma geral como uma equação no sistema de\(y^\prime \) coordenadas\(x^\prime \) e sem o\(x^\prime y^\prime \) termo, girando os eixos por uma medida\(\theta\) que satisfaça
\[\cot(2\theta)=\dfrac{A−C}{B}\]
Já aprendemos que qualquer cônica pode ser representada pela equação de segundo grau
\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\)
onde\(A\)\(B\), e nem todos\(C\) são zero. No entanto, se\(B≠0\), então temos um\(xy\) termo que nos impede de reescrever a equação na forma padrão. Para eliminá-lo, podemos girar os eixos em um ângulo agudo\(\theta\) onde\(\cot(2\theta)=\dfrac{A−C}{B}\).
- Se\(\cot(2\theta)>0\), então\(2\theta\) está no primeiro quadrante e\(\theta\) está entre\((0°,45°)\).
- Se\(\cot(2\theta)<0\), então\(2\theta\) está no segundo quadrante e\(\theta\) está entre\((45°,90°)\).
- Se\(A=C\), então\(\theta=45°\).
- Encontre\(\cot(2\theta)\).
- Encontre\(\sin \theta\)\(\cos \theta\) e.
- \(\sin \theta\)Substitua\(x=x^\prime \cos \theta−y^\prime \sin \theta\) e\(\cos \theta\) em\(y=x^\prime \sin \theta+y^\prime \cos \theta\) e.
- Substitua a expressão por\(x\) e\(y\) em na equação dada e, em seguida, simplifique.
- Escreva as equações com\(x^\prime \) e\(y^\prime \) na forma padrão em relação aos eixos girados.
Reescreva a equação\(8x^2−12xy+17y^2=20\) no\(x^\prime y^\prime \) sistema sem um\(x^\prime y^\prime \) termo.
Solução
Primeiro, encontramos\(\cot(2\theta)\).
\(8x^2−12xy+17y^2=20\rightarrow A=8\),\(B=−12\) e\(C=17\)
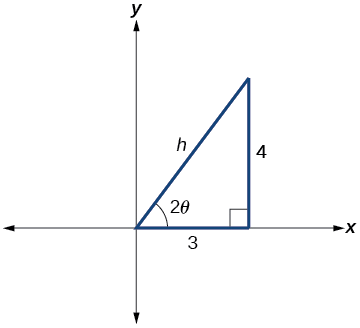
Figura\(\PageIndex{7}\)
Da figura\(\PageIndex{7}\):
\[ \begin{align*} \cot(2\theta) &=\dfrac{A−C}{B}=\dfrac{8−17}{−12} \\[4pt] & =\dfrac{−9}{−12}=\dfrac{3}{4} \end{align*}\]
\(\cot(2\theta)=\dfrac{3}{4}=\dfrac{\text{adjacent}}{\text{opposite}}\)
Então, a hipotenusa é
\[ \begin{align*} 3^2+4^2 &=h^2 \\[4pt] 9+16 &=h^2 \\[4pt] 25&=h^2 \\[4pt] h&=5 \end{align*}\]
Em seguida, encontramos\(\sin \theta\)\(\cos \theta\) e.
\[ \begin{align*} \sin \theta &=\sqrt{\dfrac{1−\cos(2\theta)}{2}}=\sqrt{\dfrac{1−\dfrac{3}{5}}{2}}=\sqrt{\dfrac{\dfrac{5}{5}−\dfrac{3}{5}}{2}}=\sqrt{\dfrac{5−3}{5}⋅\dfrac{1}{2}}=\sqrt{\dfrac{2}{10}}=\sqrt{\dfrac{1}{5}} \\ \sin \theta &= \dfrac{1}{\sqrt{5}} \\ \cos \theta &= \sqrt{\dfrac{1+\cos(2\theta)}{2}}=\sqrt{\dfrac{1+\dfrac{3}{5}}{2}}=\sqrt{\dfrac{\dfrac{5}{5}+\dfrac{3}{5}}{2}}=\sqrt{\dfrac{5+3}{5}⋅\dfrac{1}{2}}=\sqrt{\dfrac{8}{10}}=\sqrt{\dfrac{4}{5}} \\ \cos \theta &= \dfrac{2}{\sqrt{5}} \end{align*}\]
Substitua os valores de\(\sin \theta\)\(x=x^\prime \cos \theta−y^\prime \sin \theta\) e\(\cos \theta\) em\(y=x^\prime \sin \theta+y^\prime \cos \theta\) e.
\[ \begin{align*} x &=x'\cos \theta−y^\prime \sin \theta \\[4pt] &=x^\prime \left(\dfrac{2}{\sqrt{5}}\right)−y^\prime \left(\dfrac{1}{\sqrt{5}}\right) \\[4pt] &=\dfrac{2x^\prime −y^\prime }{\sqrt{5}} \end{align*}\]
e
\[ \begin{align*} y&=x^\prime \sin \theta+y^\prime \cos \theta \\[4pt] &=x^\prime \left(\dfrac{1}{\sqrt{5}}\right)+y^\prime \left(\dfrac{2}{\sqrt{5}}\right) \\[4pt] &=\dfrac{x^\prime +2y^\prime }{\sqrt{5}} \end{align*}\]
Substitua as expressões por\(x\) e\(y\) em na equação dada e, em seguida, simplifique.
\[ \begin{align*} 8{\left(\dfrac{2x^\prime −y^\prime }{\sqrt{5}}\right)}^2−12\left(\dfrac{2x^\prime −y^\prime }{\sqrt{5}}\right)\left(\dfrac{x^\prime +2y^\prime }{\sqrt{5}}\right)+17{\left(\dfrac{x^\prime +2y^\prime }{\sqrt{5}}\right)}^2&=20 \\[4pt] 8\left(\dfrac{(2x^\prime −y^\prime )(2x^\prime −y^\prime )}{5}\right)−12\left(\dfrac{(2x^\prime −y^\prime )(x^\prime +2y^\prime )}{5}\right)+17\left(\dfrac{(x^\prime +2y^\prime )(x^\prime +2y^\prime )}{5}\right)&=20 \\[4pt] 8(4{x^\prime }^2−4x^\prime y^\prime +{y^\prime }^2)−12(2{x^\prime }^2+3x^\prime y^\prime −2{y^\prime }^2)+17({x^\prime }^2+4x^\prime y^\prime +4{y^\prime }^2)&=100 \\[4pt] 32{x^\prime }^2−32x^\prime y^\prime +8{y^\prime }^2−24{x^\prime }^2−36x^\prime y^\prime +24{y^\prime }^2+17{x^\prime }^2+68x^\prime y^\prime +68{y^\prime }^2&=100 \\[4pt] 25{x^\prime }^2+100{y^\prime }^2&=100 \\[4pt] \dfrac{25}{100}{x^\prime }^2+\dfrac{100}{100}{y^\prime }^2&=\dfrac{100}{100} \end{align*}\]
Escreva as equações com\(x^\prime \) e\(y^\prime \) na forma padrão em relação ao novo sistema de coordenadas.
\[\dfrac{{x^\prime }^2}{4}+\dfrac{{y^\prime }^2}{1}=1 \nonumber\]
A figura\(\PageIndex{8}\) mostra o gráfico da elipse.
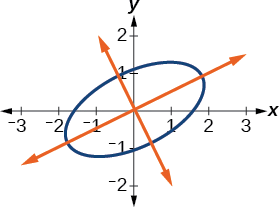
Figura\(\PageIndex{8}\)
Reescreva o\(13x^2−6\sqrt{3}xy+7y^2=16\) no\(x^\prime y^\prime \) sistema sem o\(x^\prime y^\prime \) termo.
- Resposta
-
\(\dfrac{{x^\prime }^2}{4}+\dfrac{{y^\prime }^2}{1}=1\)
Faça um gráfico da seguinte equação em relação ao\(x^\prime y^\prime \) sistema:
\(x^2+12xy−4y^2=30\)
Solução
Primeiro, encontramos\(\cot(2\theta)\).
\(x^2+12xy−4y^2=20\rightarrow A=1\),\(B=12\), e\(C=−4\)
\[\begin{align*} \cot(2\theta) &= \dfrac{A−C}{B} \\ \cot(2\theta) &= \dfrac{1−(−4)}{12} \\ \cot(2\theta) &= \dfrac{5}{12} \end{align*}\]
Porque\(\cot(2\theta)=\dfrac{5}{12}\) podemos desenhar um triângulo de referência como na Figura\(\PageIndex{9}\).
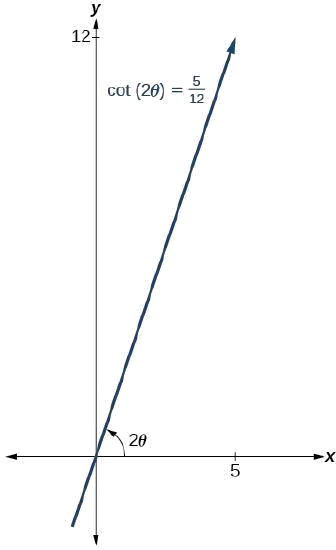
Figura\(\PageIndex{9}\)
\(\cot(2\theta)=\dfrac{5}{12}=\dfrac{adjacent}{opposite}\)
Assim, a hipotenusa é
\[ \begin{align*} 5^2+{12}^2&=h^2 \\[4pt] 25+144 &=h^2 \\[4pt] 169 &=h^2 \\[4pt] h&=13 \end{align*}\]
Em seguida, encontramos\(\sin \theta\)\(\cos \theta\) e. Usaremos identidades de meio ângulo.
\(\sin \theta=\sqrt{\dfrac{1−\cos(2\theta)}{2}}=\sqrt{\dfrac{1−\dfrac{5}{13}}{2}}=\sqrt{\dfrac{\dfrac{13}{13}−\dfrac{5}{13}}{2}}=\sqrt{\dfrac{8}{13}⋅\dfrac{1}{2}}=\dfrac{2}{\sqrt{13}}\)
\(\cos \theta=\sqrt{\dfrac{1+\cos(2\theta)}{2}}=\sqrt{\dfrac{1+\dfrac{5}{13}}{2}}=\sqrt{\dfrac{\dfrac{13}{13}+\dfrac{5}{13}}{2}}=\sqrt{\dfrac{18}{13}⋅\dfrac{1}{2}}=\dfrac{3}{\sqrt{13}}\)
Agora encontramos\(x\)\(y\) e.
\(x=x^\prime \cos \theta−y^\prime \sin \theta\)
\(x=x^\prime \left(\dfrac{3}{\sqrt{13}}\right)−y^\prime \left(\dfrac{2}{\sqrt{13}}\right)\)
\(x=\dfrac{3x^\prime −2y^\prime }{\sqrt{13}}\)
e
\(y=x^\prime \sin \theta+y^\prime \cos \theta\)
\(y=x^\prime \left(\dfrac{2}{\sqrt{13}}\right)+y^\prime \left(\dfrac{3}{\sqrt{13}}\right)\)
\(y=\dfrac{2x^\prime +3y^\prime }{\sqrt{13}}\)
Agora substituímos\(x=\dfrac{3x^\prime −2y^\prime }{\sqrt{13}}\) e\(y=\dfrac{2x^\prime +3y^\prime }{\sqrt{13}}\) entramos\(x^2+12xy−4y^2=30\).
\(\begin{array}{rl} {\left(\dfrac{3x^\prime −2y^\prime }{\sqrt{13}}\right)}^2+12\left(\dfrac{3x^\prime −2y^\prime }{\sqrt{13}}\right)\left(\dfrac{2x^\prime +3y^\prime }{\sqrt{13}}\right)−4{\left(\dfrac{2x^\prime +3y^\prime }{\sqrt{13}}\right)}^2=30 \\ \left(\dfrac{1}{13}\right)[ {(3x^\prime −2y^\prime )}^2+12(3x^\prime −2y^\prime )(2x^\prime +3y^\prime )−4{(2x^\prime +3y^\prime )}^2 ]=30 & \text{Factor.} \\ \left(\dfrac{1}{13}\right)[ 9{x^\prime }^2−12x^\prime y^\prime +4{y^\prime }^2+12(6{x^\prime }^2+5x^\prime y^\prime −6{y^\prime }^2)−4(4{x^\prime }^2+12x^\prime y^\prime +9{y^\prime }^2) ]=30 & \text{Multiply.} \\ \left(\dfrac{1}{13}\right)[ 9{x^\prime }^2−12x^\prime y^\prime +4{y^\prime }^2+72{x^\prime }^2+60x^\prime y^\prime −72{y^\prime }^2−16{x^\prime }^2−48x^\prime y^\prime −36{y^\prime }^2 ]=30 & \text{Distribute.} \\ \left(\dfrac{1}{13}\right)[ 65{x^\prime }^2−104{y^\prime }^2 ]=30 & \text{Combine like terms.} \\ 65{x^\prime }^2−104{y^\prime }^2=390 & \text{Multiply.} \\ \dfrac{{x^\prime }^2}{6}−\dfrac{4{y^\prime }^2}{15}=1 & \text{Divide by 390.} \end{array}\)
A figura\(\PageIndex{10}\) mostra o gráfico da hipérbole\(\dfrac{{x^\prime }^2}{6}−\dfrac{4{y^\prime }^2}{15}=1\)
Figura\(\PageIndex{10}\)
Identificação de cônicas sem eixos rotativos
Agora fechamos o círculo. Como identificamos o tipo de cônica descrito por uma equação? O que acontece quando os eixos são girados? Lembre-se, a forma geral de uma cônica é
\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\)
Se aplicarmos as fórmulas de rotação a essa equação, obtemos a forma
\(A′{x^\prime }^2+B′x^\prime y^\prime +C′{y^\prime }^2+D′x^\prime +E′y^\prime +F′=0\)
Pode ser demonstrado que
\(B^2−4AC={B′}^2−4A′C′\)
A expressão não varia após a rotação, então chamamos a expressão de invariante. O discriminante,\(B^2−4AC\), é invariante e permanece inalterado após a rotação. Como o discriminante permanece inalterado, observar o discriminante nos permite identificar a seção cônica.
Se a equação
\[Ax^2+Bxy+Cy^2+Dx+Ey+F=0\]
é transformado por eixos rotativos na equação
\[A′{x^\prime }^2+B′x^\prime y^\prime +C′{y^\prime }^2+D′x^\prime +E′y^\prime +F′=0\]
então\[B^2−4AC={B′}^2−4A′C′\]
A equação\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\) é uma elipse, uma parábola ou uma hipérbole, ou um caso degenerado de uma delas. Se o discriminante,\(B^2−4AC\), é
- \(<0\), a seção cônica é uma elipse
- \(=0\), a seção cônica é uma parábola
- \(>0\), a seção cônica é uma hipérbole
Identifique a cônica para cada um dos itens a seguir sem eixos rotativos.
- \(5x^2+2\sqrt{3}xy+2y^2−5=0\)
- \(5x^2+2\sqrt{3}xy+12y^2−5=0\)
Solução
a. Vamos começar determinando\(A\)\(B\),\(C\) e.
\(\underbrace{5}_{A}x^2+\underbrace{2\sqrt{3}}_{B}xy+\underbrace{2}_{C}y^2−5=0\)
Agora, encontramos o discriminante.
\[\begin{align*} B^2−4AC &= {(2\sqrt{3})}^2−4(5)(2) \\ &=4(3)−40 \\ &=12−40 \\ &=−28<0 \end{align*}\]
Portanto,\(5x^2+2\sqrt{3}xy+2y^2−5=0\) representa uma elipse.
b. Novamente, vamos começar determinando\(A\)\(B\),\(C\) e.
\(\underbrace{5}_{A}x^2+\underbrace{2\sqrt{3}}_{B}xy+\underbrace{12}_{C}y^2−5=0 \nonumber\)
Agora, encontramos o discriminante.
\[\begin{align*} B^2−4AC &= {(2\sqrt{3})}^2−4(5)(12) \\ &= 4(3)−240 \\ &= 12−240 \\ &=−228<0 \end{align*}\]
Portanto,\(5x^2+2\sqrt{3}xy+12y^2−5=0\) representa uma elipse.
Identifique a cônica para cada um dos itens a seguir sem eixos rotativos.
- \(x^2−9xy+3y^2−12=0\)
- \(10x^2−9xy+4y^2−4=0\)
- Responda a um
-
hipérbole
- Resposta b
-
elipse
Equações chave
| Equação de forma geral de uma seção cônica | \(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\) |
| Rotação de uma seção cônica |
\(x=x^\prime \cos \theta−y^\prime \sin \theta\) \(y=x^\prime \sin \theta+y^\prime \cos \theta\) |
| Ângulo de rotação | \(\theta\), onde\(\cot(2\theta)=\dfrac{A−C}{B}\) |
Conceitos chave
- Quatro formas básicas podem resultar da interseção de um avião com um par de cones circulares retos conectados da cauda à cauda. Eles incluem uma elipse, um círculo, uma hipérbole e uma parábola.
- Uma seção cônica não degenerada tem a forma geral\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\) onde\(A\)\(B\) e nem todas\(C\) são zero. Os valores de\(A\)\(B\), e\(C\) determinam o tipo de cônica. Veja o exemplo\(\PageIndex{1}\).
- Equações de seções cônicas com um\(xy\) termo foram rotacionadas em torno da origem. Veja o exemplo\(\PageIndex{2}\).
- A forma geral pode ser transformada em uma equação no sistema de\(y^\prime \) coordenadas\(x^\prime \) e sem o\(x^\prime y^\prime \) termo. Veja o exemplo\(\PageIndex{3}\) e o exemplo\(\PageIndex{4}\).
- Uma expressão é descrita como invariante se permanecer inalterada após a rotação. Como o discriminante é invariante, observá-lo nos permite identificar a seção cônica. Veja o exemplo\(\PageIndex{5}\).